1. Introduction
In this study, we developed a forecasting method for the time series of counts based on support vector regression (SVR) with particle swarm optimization (PSO), and used it to detect a change in the conditional mean of the time series based on the cumulative sum (CUSUM) test that is calculated from integer-valued autoregressive conditional heteroscedastic (INGARCH) residuals. Over the past few decades, the time series of counts have gained increased attention from researchers in diverse scientific areas. Considering the research conducted by [
1,
2,
3,
4,
5], two classes of models, such as integer-valued autoregressive (INAR) and INGARCH models, have been popular for analyzing the time series of counts. See [
6] for more details. These models have been harnessed to analyze polio data [
7], crime data [
8], car accident traffic data [
9], and financial data [
10].
Although the basic theories and analytical tools for these models are quite well developed in the literature, as seen in [
11,
12,
13,
14,
15], a restriction on their usage exists because both INAR and INGARCH models are mostly assumed to have a linear structure in their conditional mean. In INGARCH models, Poisson and negative binomial distributions have been widely adopted as the conditional distribution of current observations over past information. This is because assuming these distributions is not impractical, as the correct specification of underlying distributions is not essential when attempting to estimate the conditional mean equation, as demonstrated by [
16], who considered the quasi-maximum likelihood estimation (QMLE) method for the time series of counts. However, for the QMLE approach to perform adequately, the conditional mean structure must be correctly specified. As misspecification can potentially lead to false conclusions in real situations, we considered SVR as a nonparametric algorithm for forecasting the time series of counts. To our knowledge, our current study is the first attempt in the literature to use SVR for the prediction of time series of counts based on the INGARCH scheme.
SVR has been one of the most popular nonparametric algorithms for forecasting time series and has been proven to outperform classical time series models, such as autoregressive and moving average (ARMA) and GARCH models, as SVR can approximate nonlinearity without knowing the underlying dynamic structure of time series [
17,
18,
19,
20,
21,
22,
23,
24,
25]. SVR has the merit of implementing the “structural risk minimization principle” [
26] and seeks a balance between model complexity and empirical risk [
27]. Moreover, a smaller number of tuning parameters is required, and determining a global solution is not problematic because it solves a quadratic programming problem (QPP).
SVR has been modified in various manners; for example, smooth SVR [
28], least squares (LS)-SVM [
29], and twin SVR (TSVR) [
30]. TSVR generates two hyperplanes unlike SVR and has a significant advantage over SVR in computational speed. For the relevant references, see [
31,
32,
33]. Here, we harness the SVR and TSVR methods particularly with the particle swarm optimization (PSO) algorithm, originally proposed by [
34], in determining a set of optimal parameters to enhance their efficacy. For an overview of PSO, see [
35,
36].
As an application of our SVR method, we consider the problem of detecting a significant change in the conditional mean of the INGARCH time series. Since [
37], the parameter change detection problem has been a core issue in various research areas. As financial time series often suffer from structural changes, owing to changes in governmental policy and critical social events, and ignoring them leads to a false conclusion, change point tests have been considered as an important research topic in time series analysis. See [
38,
39] for a general review. The CUSUM test has long been used as a tool for detecting a change point, owing to its practical efficiency [
40,
41,
42,
43,
44]. As regards the time series of counts, see [
7,
45,
46,
47,
48,
49,
50].
Among the CUSUM tests, we adopted the residual-based CUSUM test, because the residual method can successfully discard the correlations of time series and enhance the performance of the CUSUM test in terms of both stability and power. See [
51,
52]. The authors of the recent reference [
43,
53] developed a simplistic residual-based CUSUM test for location-scale time series models, based on which the authors of [
21,
22] designated a hybridization of the SVR and CUSUM methods for handling the change point problem for AR and GARCH time series and demonstrated its superiority over classical models. However, their approach is not directly applicable and requires a new modification for effective performance, especially on the proxies used for the GARCH prediction, as seen in
Section 3.4, as simple or exponential moving average type proxies conventionally used for SVR-GARCH models [
22] would not work adequately in our current study. Here, we instead used the proxies obtained through the linear INGARCH fit to time series of counts.
The rest of this paper is organized as follows.
Section 2 reviews the principle of the CUSUM test and CUSUM of squares test for the INGARCH models and then briefly describes how to apply the SVR-INGARCH method for constructing the CUSUM tests.
Section 3 presents the SVR and TSVR-GARCH models for forecasting the conditional mean and describes the SVR and TSVR methods with PSO.
Section 4 discusses the Monte Carlo simulations conducted to evaluate the performance of the proposed method.
Section 5 discusses the performance of the real data analysis, using the return times of extreme events constructed based on the daily log-returns of Goldman Sachs (GS) stock prices. Finally,
Section 6 provides concluding remarks.
2. INGARCH Model-Based Change Point Test
Let
be a time series of counts. In order to make inferences for
, one can consider fitting a parametric model to
, for instance, the INGARCH model with the conditional distribution of the one-parameter exponential family and the link function
, parameterized with
, that describes the conditional expectation, namely,
where
denotes the past information up to time
t,
is defined on
with
, and
is a probability mass function given by
where
is the natural parameter,
and
are known real-valued functions,
is strictly increasing, and
.
and
are the conditional mean and variance of
over past observations, respectively. Symbols
and
are used to emphasize
.
Conventionally,
is assumed to be bounded below by some real number
and to satisfy
for all
and
, where
satisfies
, which, according to [
12], allows
to be strictly stationary and ergodic, required for the consistency of the parameter estimates.
In practice, Poisson or negative binomial (NB) linear INGARCH(1,1) models with , , are frequently used. For the former, we assume , whereas for the latter, we assume , where and NB denotes the negative binomial distribution with its mass function: .
Let
be a true parameter, which is assumed to be an interior point of the compact parameter space
. The
is then estimated using the conditional likelihood function of model (
1), based on the observations
:
where
is updated through the equations:
for
,
with an initial value
.The conditional maximum likelihood estimator (CMLE) of
is then obtained as the maximizer of the likelihood function in Equation (
3):
with
. The authors of the reference [
12,
50] showed that, under certain conditions,
converges to
in probability and
is asymptotically normally distributed as
n tends to
∞. This
is harnessed to make prediction for calculating residuals.
In our current study, we aim to extend Model (
1) to the nonparametric model:
where
and
g are unknown, and
g is implicitly assumed to satisfy Equation (
2). Provided
and
is known a priori, one can estimate
g with
. Even if
is unknown, one can still consider using the Poisson or NB quasi-likelihood estimator (QMLE) method as in [
16]. See also [
54] for various types of CUSUM tests based on the QMLEs. However, when one has no prior information as to
g, the parametric modeling may hamper the inference, and in this case, one can estimate
g with the nonparametric SVR method stated below in
Section 3.
On Model (
1), setting up the null and alternative hypotheses:
remain the same over
vs.
The authors of the reference [
50] considered the problem of detecting a change in
based on the CUSUM test:
with the residuals
and
Furthermore, the authors of the references [
55,
56] employed the residual-based CUSUM of squares test:
with
, and
The authors of the reference [
50] verified that, under the null
,
behaves asymptotically the same as
where
and
. As
forms a sequence of martingale differences, we obtain
in distribution [
57], where
denotes a Brownian bridge, owing to Donsker’s invariance principle, so that, as
, we have
in distribution. For instance,
is rejected if
at the level of 0.05, which is obtainable with Monte Carlo simulations. Similarly, the authors of the reference [
55] verified that
in distribution, so that the same critical values as for the case of
can be harnessed. Provided that a change point exists, the location of change is identified as
This CUSUM framework for parametric models can be easily adopted for nonparametric models as far as the residuals
can be accurately calculated, as seen in [
21,
22] who deal with the change point problem on SVR-ARMA and SVR-GARCH models. Below, when dealing with Model (
4), instead of
in Equation (
5), we use
in the construction of the CUSUM tests in Equations (
5) and (
6).
When estimating
g with SVR and TSVR, we train
either with
and
or
and
, with some proper proxy
. The former has been used for the SVR-GARCH model in [
21], while the latter is newly considered here, inspired by the fact that
, where the error process
is a sequence of martingale differences, which also holds for Model (
1) because we can express
in this case. See Step 3 in
Section 4 below for more details.
4. Simulation Results
In this section, we apply the PSO-SVR and -TSVR models to the INAR(1) and INGARCH(1,1) models, and evaluate the performance of the proposed CUSUM tests. For this task, we generate a time series of length 1000 (
to evaluate the empirical sizes and powers at the nominal level of 0.05. The size and power are calculated as the rejection number of the null hypothesis of no changes out of 500 repetitions. The simulations were conducted with R version 3.6.3, running on Windows 10. Moreover, we use the following R packages: “pso” for the PSO [
60], “kernlab” for the Gaussian kernel [
61], and “osqp” [
62] for solving the quadratic problem. The procedure for the simulation is as follows.
Step 1. Generate a time series of length to train the PSO-SVR and -TSVR models.
Step 2. Apply the estimation scheme described in
Section 4. For the proxy of moving averages, we used
. In this procedure, we divide the given time series into
and
in
Step 1 of
Section 4.
Step 3. Generate a testing time series of length to evaluate the size and power. For computing sizes, we generate a time series of no changes, whereas to examine the power, we generate a time series with a change point in the middle.
Step 4. Apply the estimated model in Step 2 to the time series of Step 3 and conduct the residual CUSUM and CUSUM of squares tests.
Step 5. Repeat the above steps N times, e.g., 500, and then compute the empirical sizes and powers.
We consider the INGARCH(1,1) and INAR(1) models, as these are the most acclaimed models in practice:
Model 1.
Model 2. , where ∘ is a binomial thinning operator and .
Further, upon one referee’s suggestion, we also consider the softplus INGARCH(1,1) model in [
63]:
Under the null hypothesis, we use the parameter settings as follows.
Model 1:
- −
Case 1: ;
- −
Case 2: ;
- −
Case 3: ;
- −
Case 4: ;
Model 2:
- −
Case 1: ;
- −
Case 2: ;
- −
Case 3: ;
Model 3:
- −
.
Under the alternative hypothesis, we only consider the case of one parameter change, while the other parameters remain the same.
Table A1,
Table A2,
Table A3 and
Table A4 in
Appendix A summarize the results for Model 1. Here, MA and ML denote the proxies obtained from the moving average in Equation (
17) and Poisson QMLE in Equation (
18), and
and
, respectively, denote the two targeting methods in Equation (
20) and Equation (
19). The tables show that the difference between the SVR and TSVR methods is marginal. Moreover, in most cases,
appears to be much more stable than
; that is, the latter test suffers from more severe size distortions. In terms of power,
with the ML proxy and
-targeting tends to outperform the others. However, the gap between this test and
is only marginal; therefore, considering the stability of the test,
is highly favored for Model 1.
Table A5,
Table A6 and
Table A7 summarize the result for Model 2, showing that
exhibits a more stable performance for the INAR models than for the INGARCH models. However, it is still not as stable as
and tends to outperform
in terms of power.
Table A8 summarizes the result for Model 3, showing no significant differences from the results of the previous models. This result, to a certain extent, coincides with that of Lee and Lee (2020) who considered parametric INGARCH models for a change point test. Overall, our findings strongly confirm the reliability of using
, particularly with the ML proxy and
-targeting. However, in practice, one can additionally implement
because either test can react more sensitively to a specific situation in comparison to the other.
Table A9 lists the computing times (in seconds) of the SVR and TSVR methods when implemented in R on Windows 10, running on a PC with an Intel i7-3770 processor (3.4 GHz) with 8 GB of RAM, wherein the figures denote the averages of training times in simulations, and the values in the parentheses indicate the sample standard deviations. In each model and parameter setting, the values of the two quickest results are written in boldface. As reported by [
21,
30], the TSVR method is shown to markedly reduce the CPU time. In particular, the results indicate that the computational speed of the TSVR-based method, with the ML proxy and
-targeting, appears to be the fastest in most cases. The result suggests that using the TSVR-based CUSUM tests is beneficial when computational speed is of significance to the implementation.
5. Real Data Analysis
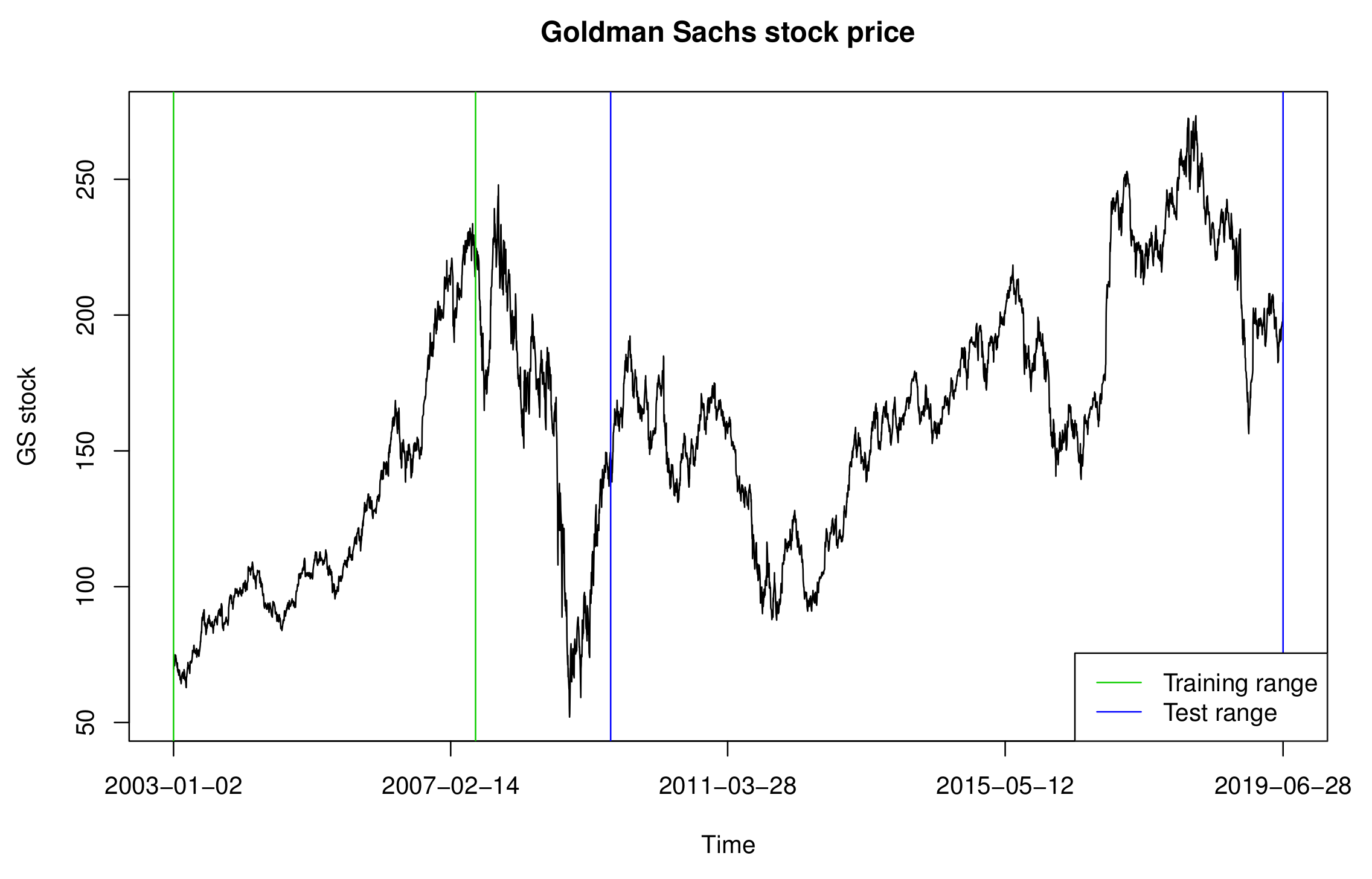
In this section, we analyze the return times of extreme events constructed based on the daily log-returns of GS stock prices from 1 January 2003, to 28 June 2019, obtained using the R package “quantmod.” We used data from 2 January 2003, to 29 June 2007, as the training set and that from 1 July 2009, to 28 June 2019, as the test set.
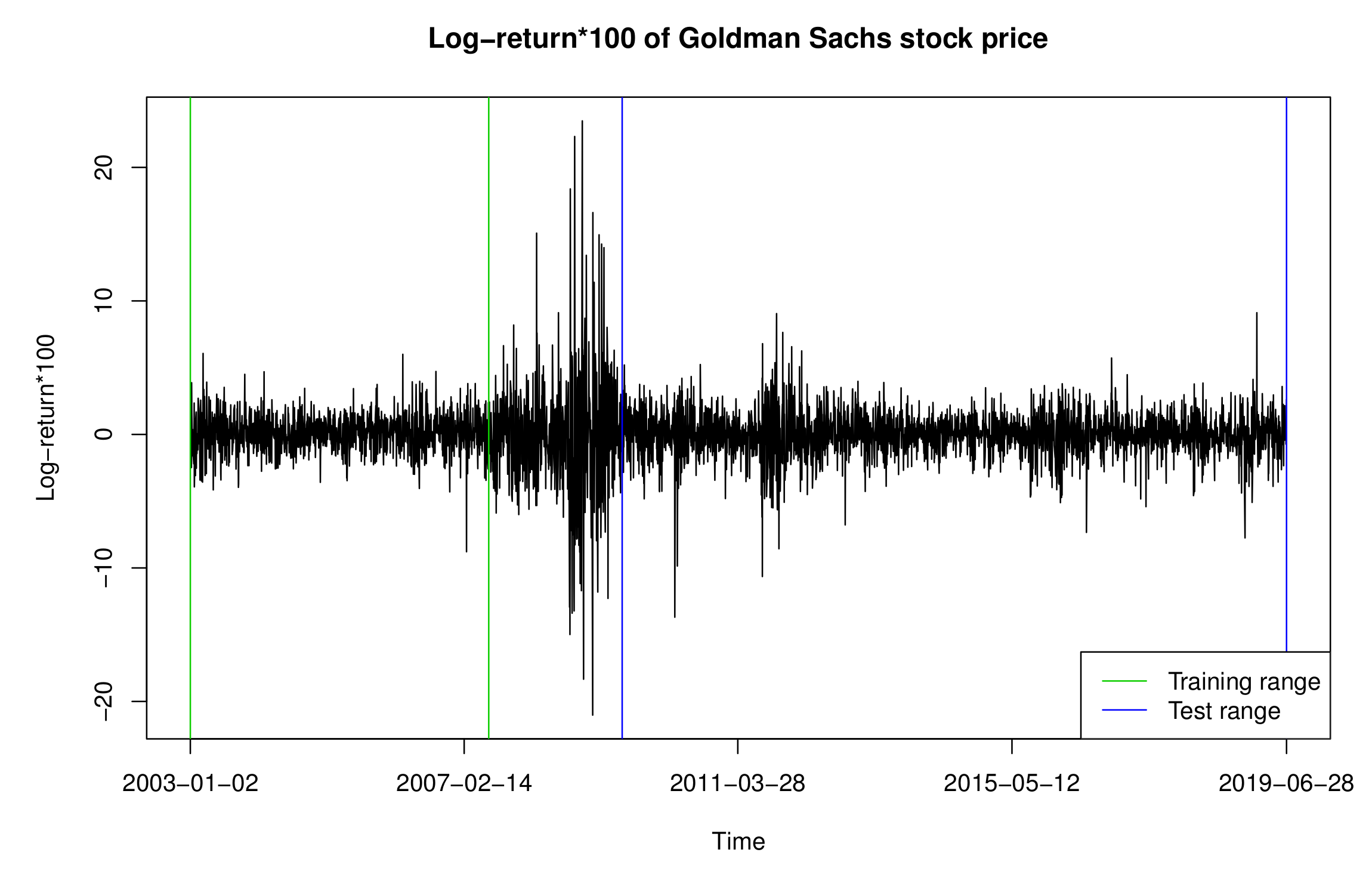
Figure 1 and
Figure 2 exhibit the GS stock prices and 100 times the log-returns, with their ranges denoted by the green and blue vertical lines, respectively. As shown in
Figure 2, the time series between the training and test sets has severe volatility, owing to the financial crisis that occurred in 2008; therefore, it is omitted from our data analysis.
Before applying the PSO-SVR-INGARCH and PSO-TSVR-INGARCH methods, similarly to [
12,
14], we first transform the given time series into the hitting times
, for which the log-returns of the GS stock fall outside the 0.15 and 0.85 quantiles of the training data, that is, -1.242 and 1.440, respectively. More specifically,
,
, where
denote the 100 times log-returns. We then set
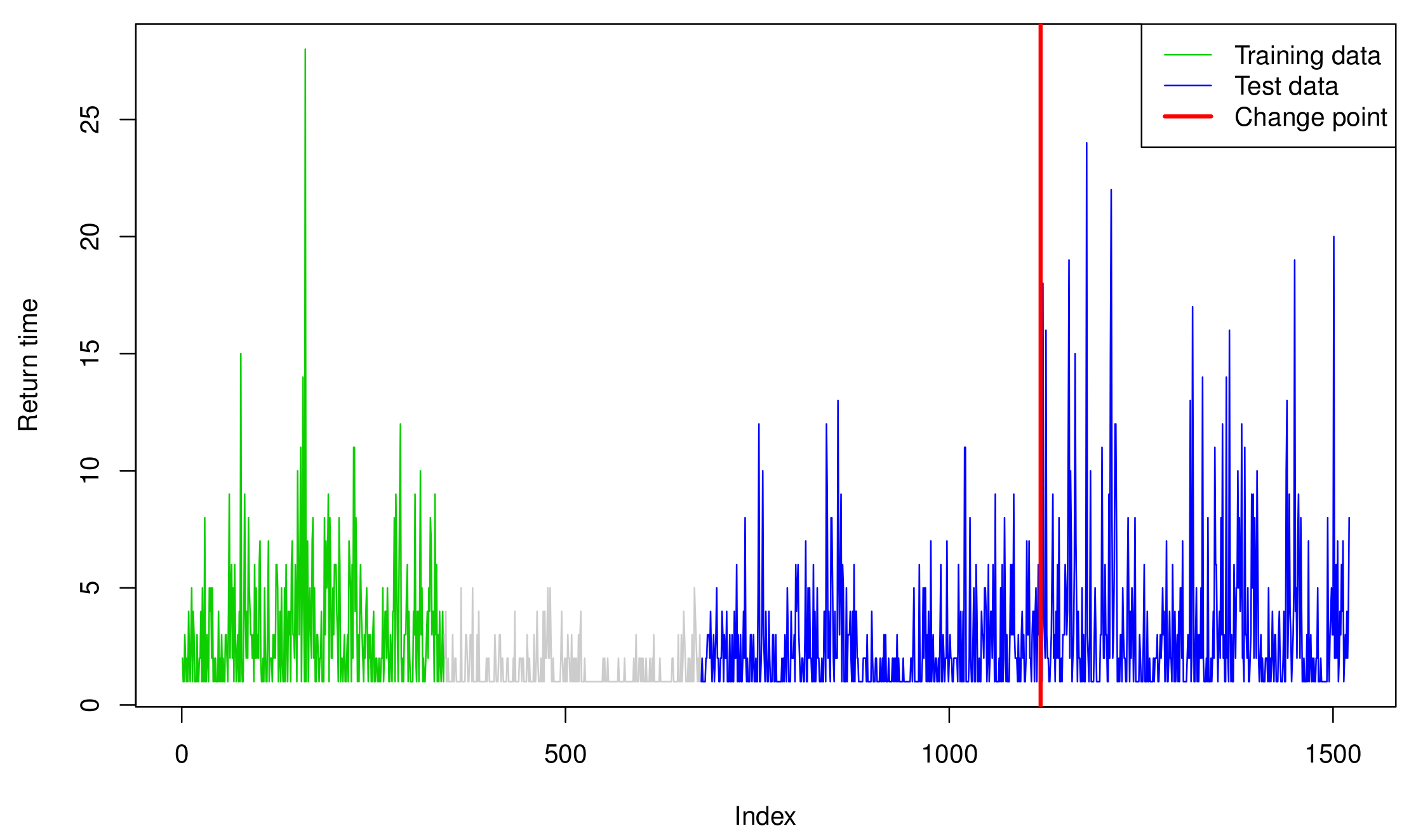
, which forms the return times of these extreme events. Consequently, the training set is transformed into an integer-valued time series of length 341, and the test set is transformed into that of length 844 (see
Figure 2), plotting
.
To determine whether the training set exhibits change, we apply the Poisson QMLE method and CUSUM of squares test from [
54]. The result shows that the CUSUM statistics
has a value of 0.590, which is smaller than the theoretical critical value of 1.358; thus, the null hypothesis of no change is not rejected at the nominal level of 0.05, supporting the adequacy of the training set. The residual-based CUSUM of squares tests based on the SVR and TSVR models with the ML proxy and
-targeting are then applied; subsequently, both tests detect a change point at the 441st observation of the testing data, corresponding to 16 October 2013. The red vertical line in
Figure 3 denotes the detected change point.
To examine how the change affects the dynamic structure of the time series, we fit a Poisson linear INGARCH model to the training and testing time series before and after the change point. For the training time series, the fitted INGARCH model appears to have , and . Conversely, for the testing time series before the change, we obtain , and , which are not as different as those from the training time series case. However, after the change point, the fitted parameters are shown to be , and , thus confirming a significant change in the parameters. For instance, the sum of and in the training data is 0.899, which changes from 0.945 to 0.707 in the testing data.