Dynamics of Ultracold Bosons in Artificial Gauge Fields—Angular Momentum, Fragmentation, and the Variance of Entropy
Abstract
1. Introduction
2. Hamiltonian and Methods
2.1. Setup
2.2. Method
3. Quantities of Interest
- Density, one-body density matrix, and natural occupations:
- Angular momentum:
- Single shots, image entropy and its variance:
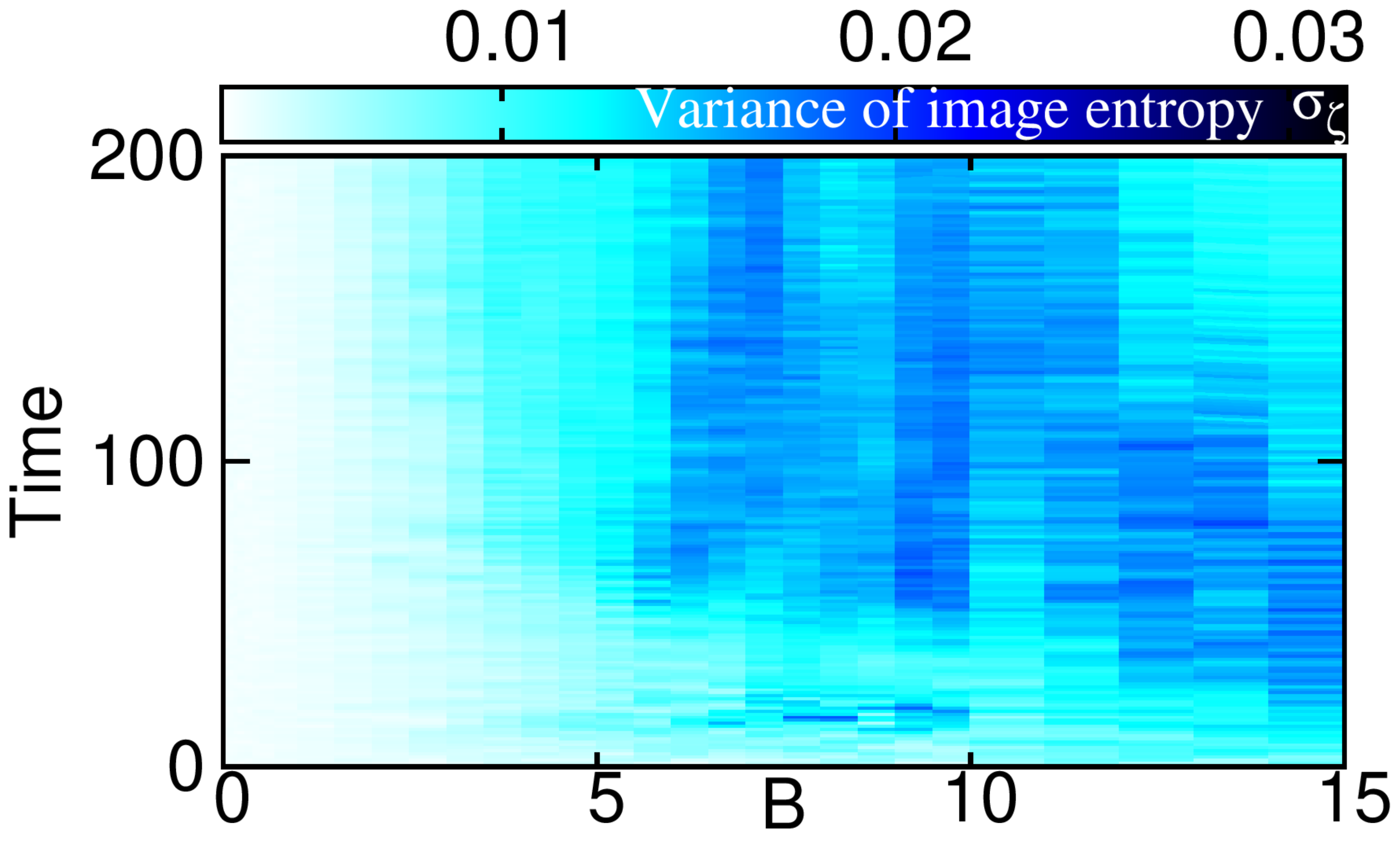
4. Results
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Equations of Motion of the Multiconfigurational Time-Dependent Hartree Method for Indistinguishable Particles
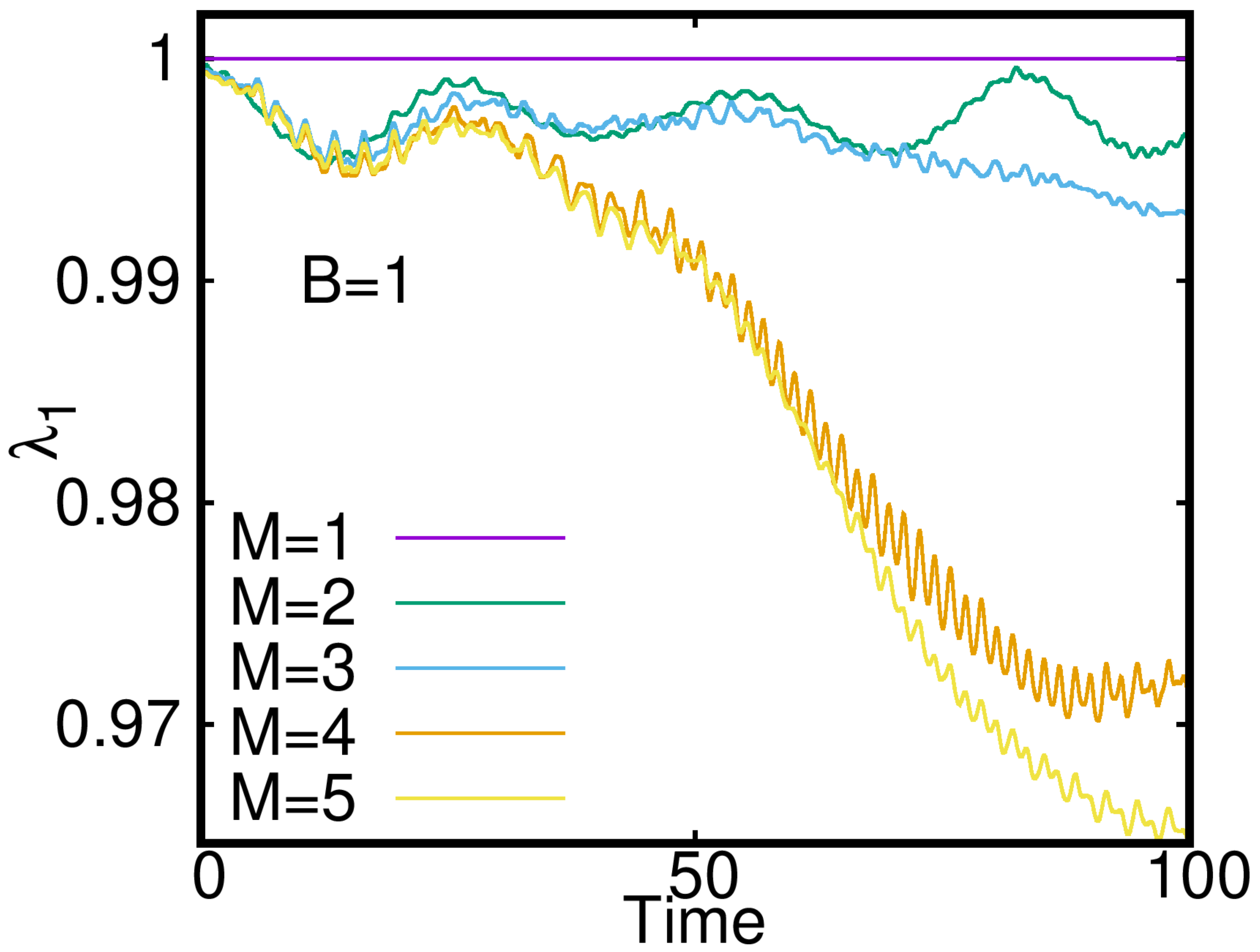
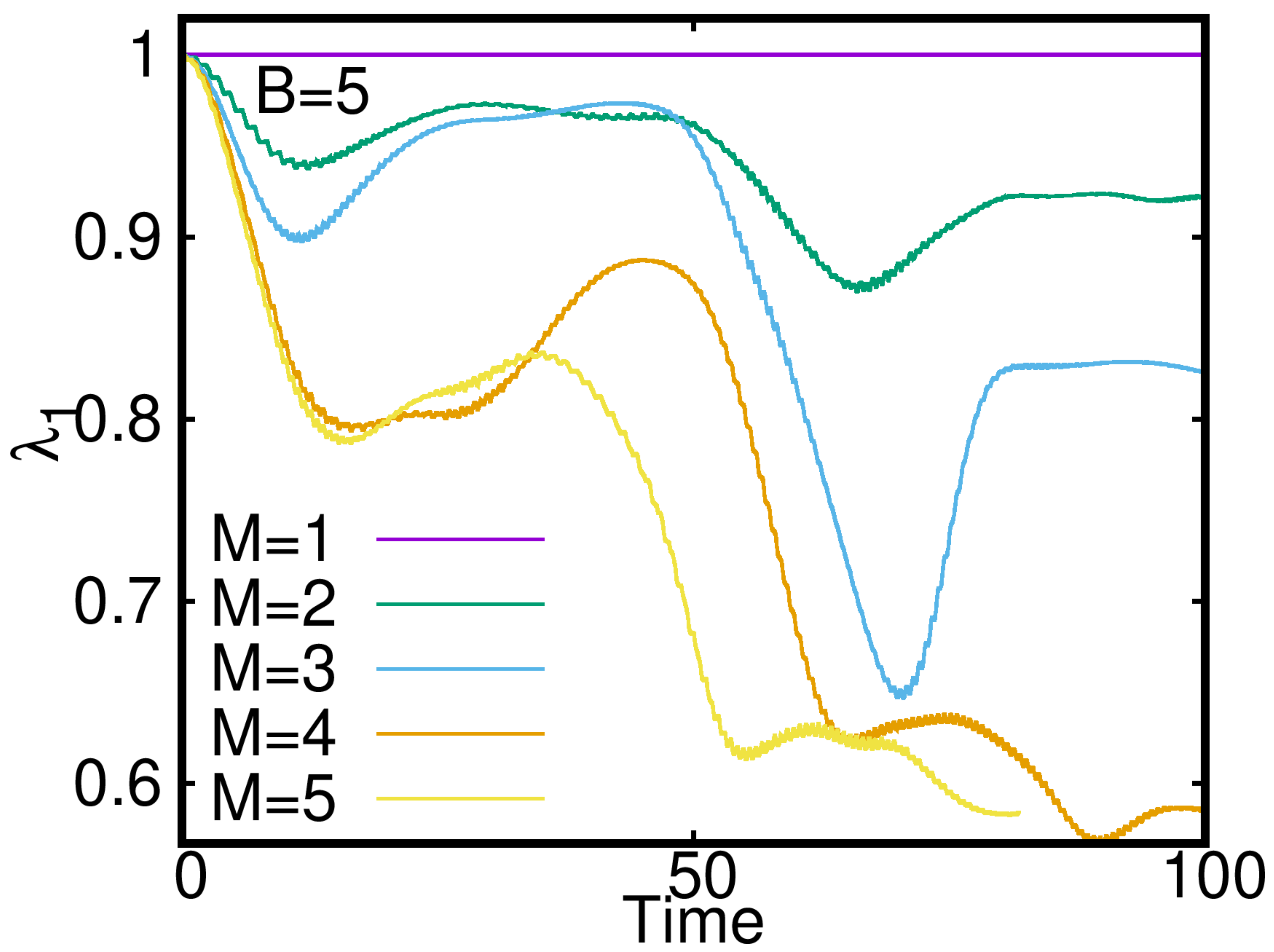
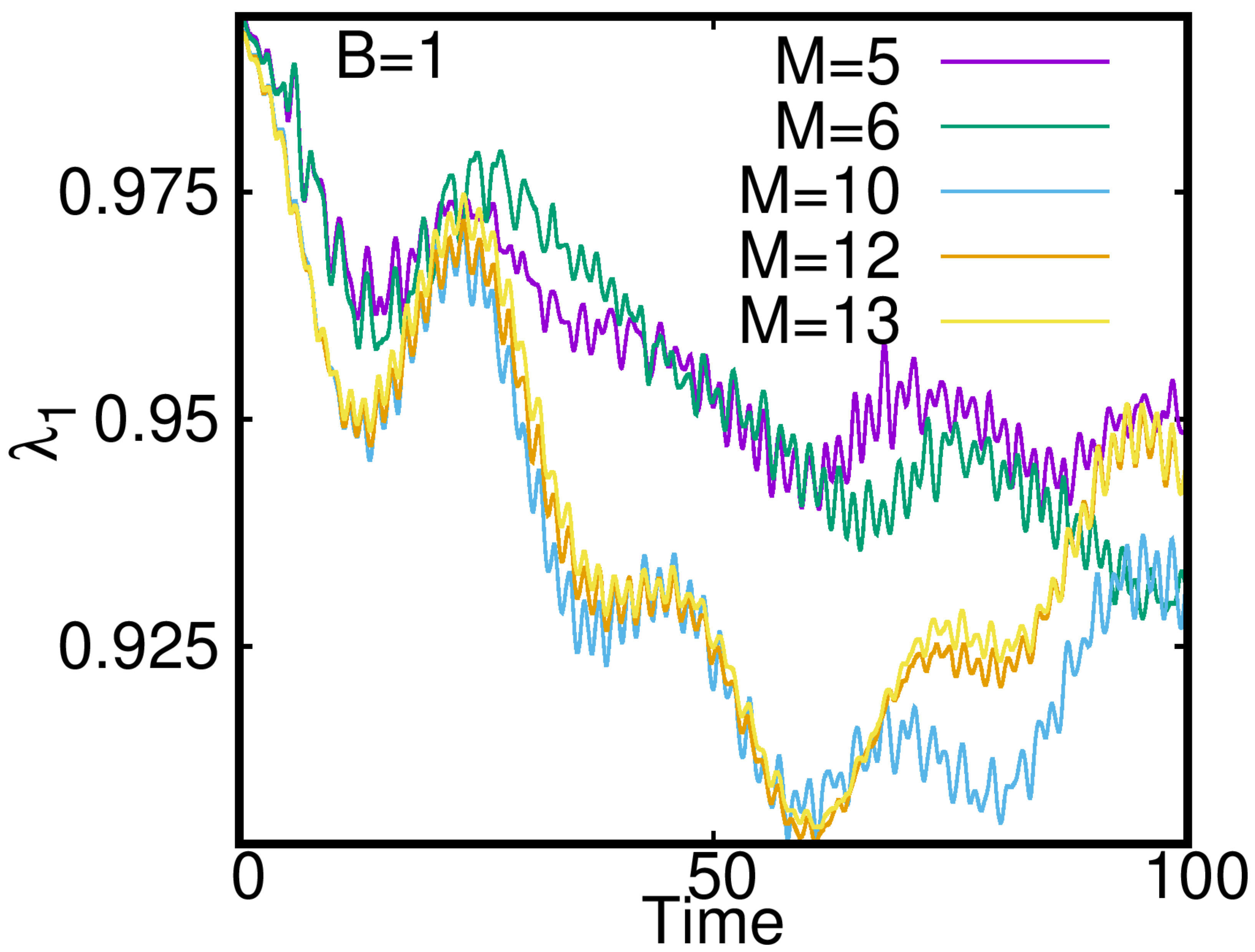
Appendix B. Investigation of Convergence

References
- Davis, K.B.; Mewes, M.O.; Andrews, M.R.; Van Druten, N.J.; Durfee, D.S.; Kurn, D.M.; Ketterle, W. Bose-Einstein condensation in a gas of sodium atoms. Phys. Rev. Lett. 1995, 75, 3969–3973. [Google Scholar] [CrossRef] [PubMed]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of bose-einstein condensation in a dilute atomic vapor. Collect. Pap. Carl Wieman 2008, 269, 453–456. [Google Scholar] [CrossRef]
- Bradley, C.C.; Sackett, C.A.; Tollett, J.J.; Hulet, R.G. Evidence of Bose-Einstein condensation in an atomic gas with attractive interactions. Phys. Rev. Lett. 1995, 75, 1687–1690. [Google Scholar] [CrossRef] [PubMed]
- Jaksch, D.; Bruder, C.; Cirac, J.I.; Gardiner, C.W.; Zoller, P. Cold bosonic atoms in optical lattices. Phys. Rev. Lett. 1998, 81, 3108–3111. [Google Scholar] [CrossRef]
- Greiner, M.; Mandel, O.; Rom, T.; Altmeyer, A.; Widera, A.; Hänsch, T.W.; Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in an ultracold gas of atoms. Phys. B Condens. Matter 2003, 329–333, 11–12. [Google Scholar] [CrossRef]
- Krinner, S.; Stadler, D.; Husmann, D.; Brantut, J.P.; Esslinger, T. Observation of quantized conductance in neutral matter. Nature 2015, 517, 64–67. [Google Scholar] [CrossRef]
- Corman, L.; Fabritius, P.; Häusler, S.; Mohan, J.; Dogra, L.H.; Husmann, D.; Lebrat, M.; Esslinger, T. Quantized conductance through a dissipative atomic point contact. Phys. Rev. A 2019, 100, 053605. [Google Scholar] [CrossRef]
- Baumann, K.; Guerlin, C.; Brennecke, F.; Esslinger, T. Dicke quantum phase transition with a superfluid gas in an optical cavity. Nature 2010, 464, 1301. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Bruder, C. Fragmented Superradiance of a Bose-Einstein Condensate in an Optical Cavity. Phys. Rev. Lett. 2017, 118, 013603. [Google Scholar] [CrossRef]
- Dalibard, J.; Gerbier, F.; Juzeliūnas, G.; Öhberg, P. Colloquium: Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 2011, 83, 1523. [Google Scholar] [CrossRef]
- Aidelsburger, M. Artificial Gauge Fields with Ultracold Atoms in Optical Lattices; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Aidelsburger, M.; Atala, M.; Nascimbène, S.; Trotzky, S.; Chen, Y.A.; Bloch, I. Experimental Realization of Strong Effective Magnetic Fields in an Optical Lattice. Phys. Rev. Lett. 2011, 107, 255301. [Google Scholar] [CrossRef] [PubMed]
- Lim, L.K.; Smith, C.M.; Hemmerich, A. Staggered-Vortex Superfluid of Ultracold Bosons in an Optical Lattice. Phys. Rev. Lett. 2008, 100, 130402. [Google Scholar] [CrossRef]
- Spielman, I.B. Raman processes and effective gauge potentials. Phys. Rev. A 2009, 79, 063613. [Google Scholar] [CrossRef]
- Lin, Y.J.; Compton, R.L.; Jiménez-García, K.; Porto, J.V.; Spielman, I.B. Synthetic magnetic fields for ultracold neutral atoms. Nature 2009, 462, 628–632. [Google Scholar] [CrossRef]
- Lin, Y.J.; Compton, R.; Perry, A.; Phillips, W.; Porto, J.; Spielman, I. Bose-Einstein Condensate in a Uniform Light-Induced Vector Potential. Phys. Rev. Lett. 2009, 102, 130401. [Google Scholar] [CrossRef]
- Gross, E.P. Structure of a quantized vortex in boson systems. Nuovo Cim. Ser. 10 1961, 20, 454. [Google Scholar] [CrossRef]
- Pitaevskii, L.P. Vortex Lines in an imperfect Bose gas. Sov. Phys. JETP 1961, 13, 451. [Google Scholar]
- Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Role of excited states in the splitting of a trapped interacting Bose-Einstein condensate by a time-dependent barrier. Phys. Rev. Lett. 2007, 99, 030402. [Google Scholar] [CrossRef] [PubMed]
- Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Multiconfigurational time-dependent Hartree method for bosons: Many-body dynamics of bosonic systems. Phys. Rev. A 2008, 77, 033613. [Google Scholar] [CrossRef]
- Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Unified view on multiconfigurational time propagation for systems consisting of identical particles. J. Chem. Phys. 2007, 127, 154103. [Google Scholar] [CrossRef]
- Beck, M.H.; Jäckle, A.; Worth, G.A.; Meyer, H.D. The multiconfiguration time-dependent Hartree (MCTDH) method: A highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000, 324, 1–105. [Google Scholar] [CrossRef]
- Wang, H.; Thoss, M. Multilayer formulation of the multiconfiguration time-dependent Hartree theory. J. Chem. Phys. 2003, 119, 1289. [Google Scholar] [CrossRef]
- Manthe, U. A multilayer multiconfigurational time-dependent Hartree approach for quantum dynamics on general potential energy surfaces. J. Chem. Phys. 2008, 128, 164116. [Google Scholar] [CrossRef]
- Wang, H. Multilayer Multiconfiguration Time-Dependent Hartree Theory. J. Phys. Chem. A 2015, 119, 7951–7965. [Google Scholar] [CrossRef] [PubMed]
- Manthe, U.; Weike, T. On the multi-layer multi-configurational time-dependent Hartree approach for bosons and fermions. J. Chem. Phys. 2017, 146, 064117. [Google Scholar] [CrossRef] [PubMed]
- Manthe, U. Wavepacket dynamics and the multi-configurational time-dependent Hartree approach. J. Phys. Condens. Matter 2017, 29, 253001. [Google Scholar] [CrossRef]
- Zanghellini, J.; Kitzler, M.; Fabian, C.; Brabec, T.; Scrinzi, A. An MCTDHF Approach to Multielectron Dynamics in Laser Fields. Laser Phys. 2003, 13, 1064. [Google Scholar]
- Cao, L.; Krönke, S.; Vendrell, O.; Schmelcher, P. The multi-layer multi-configuration time-dependent Hartree method for bosons: Theory, implementation, and applications. J. Chem. Phys. 2013, 139, 134103. [Google Scholar] [CrossRef]
- Cao, L.; Bolsinger, V.; Mistakidis, S.I.; Koutentakis, G.M.; Krönke, S.; Schurer, J.M.; Schmelcher, P. A unified ab initio approach to the correlated quantum dynamics of ultracold fermionic and bosonic mixtures. J. Chem. Phys. 2017, 147, 044106. [Google Scholar] [CrossRef]
- Haxton, D.J.; McCurdy, C.W. Two methods for restricted configuration spaces within the multiconfiguration time-dependent Hartree-Fock method. Phys. Rev. A 2015, 91, 012509. [Google Scholar] [CrossRef]
- Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Multiconfigurational Time-Dependent Hartree Method for Mixtures Consisting of Two Types of Identical Particles; American Physical Society: College Park, MD, USA, 2007; Volume 76, p. 062501. [Google Scholar] [CrossRef]
- Alon, O.E.; Streltsov, A.I.; Sakmann, K.; Lode, A.U.J.; Grond, J.; Cederbaum, L.S. Recursive formulation of the multiconfigurational time-dependent Hartree method for fermions, bosons and mixtures thereof in terms of one-body density operators. Chem. Phys. 2012, 401, 2–14. [Google Scholar] [CrossRef]
- Miyagi, H.; Madsen, L.B. Time-dependent restricted-active-space self-consistent-field theory for laser-driven many-electron dynamics. Phys. Rev. A 2013, 87, 062511. [Google Scholar] [CrossRef]
- Miyagi, H.; Madsen, L.B. Time-Dependent Restricted-Active-Space Self-Consistent-Field Theory With Space Partition; American Physical Society: College Park, MD, USA, 2017; Volume 95, p. 023415. [Google Scholar] [CrossRef]
- Lévêque, C.; Madsen, L.B. Time-dependent restricted-active-space self-consistent-field theory for bosonic many-body systems. New J. Phys. 2017, 19, 043007. [Google Scholar] [CrossRef]
- Lévêque, C.; Madsen, L.B. Multispecies time-dependent restricted-active-space self-consistent-field theory for ultracold atomic and molecular gases. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 155302. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Lévêque, C.; Madsen, L.B.; Streltsov, A.I.; Alon, O.E. Colloquium: Multiconfigurational time-dependent Hartree approaches for indistinguishable particles. Rev. Mod. Phys. 2020, 92, 011001. [Google Scholar] [CrossRef]
- Klaiman, S.; Alon, O.E. Variance as a sensitive probe of correlations. Phys. Rev. A 2015, 91, 063613. [Google Scholar] [CrossRef]
- Klaiman, S.; Streltsov, A.I.; Alon, O.E. Uncertainty Product of an Out-of-Equilibrium Many-Particle System; American Physical Society: College Park, MD, USA, 2016; Volume 93, p. 023605. [Google Scholar] [CrossRef]
- Klaiman, S.; Beinke, R.; Cederbaum, L.S.; Streltsov, A.I.; Alon, O.E. Variance of an anisotropic Bose-Einstein condensate. Chem. Phys. 2018, 509, 45–54. [Google Scholar] [CrossRef]
- Alon, O.E. Condensates in annuli: Dimensionality of the variance. Mol. Phys. 2019, 117, 2108–2120. [Google Scholar] [CrossRef]
- Alon, O.E. Analysis of a trapped Bose-Einstein condensate in terms of position, momentum, and angular-momentum variance. Symmetry 2019, 11, 1344. [Google Scholar] [CrossRef]
- Chatterjee, B.; Lode, A.U.J. Order parameter and detection for a finite ensemble of crystallized one-dimensional dipolar bosons in optical lattices. Phys. Rev. A 2018, 98, 053624. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Cao, L.; Schmelcher, P. Interaction quench induced multimode dynamics of finite atomic ensembles. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 225303. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Cao, L.; Schmelcher, P. Negative-quench-induced excitation dynamics for ultracold bosons in one-dimensional lattices. Phys. Rev. A 2015, 91, 033611. [Google Scholar] [CrossRef]
- Mistakidis, S.I.; Schmelcher, P. Mode coupling of interaction quenched ultracold few-boson ensembles in periodically driven lattices. Phys. Rev. A 2017, 95, 013625. [Google Scholar] [CrossRef]
- Chatterjee, B.; Tsatsos, M.C.; Lode, A.U.J. Correlations of strongly interacting one-dimensional ultracold dipolar few-boson systems in optical lattices. New J. Phys. 2019, 21, 033030. [Google Scholar] [CrossRef]
- Chatterjee, B.; Lévêque, C.; Schmiedmayer, J.; Lode, A.U.J. Detecting One-Dimensional Dipolar Bosonic Crystal Orders via Full Distribution Functions. Phys. Rev. Lett. 2020, 125, 093602. [Google Scholar] [CrossRef] [PubMed]
- Lin, R.; Molignini, P.; Papariello, L.; Tsatsos, M.C.; Lévêque, C.; Weiner, S.E.; Fasshauer, E.; Chitra, R.; Lode, A.U.J. MCTDH-X: The multiconfigurational time-dependent Hartree method for indistinguishable particles software. Quantum Sci. Technol. 2020, 5, 024004. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Diorico, F.S.; Wu, R.; Molignini, P.; Papariello, L.; Lin, R.; Lévêque, C.; Exl, L.; Tsatsos, M.C.; Chitra, R.; et al. Many-body physics in two-component Bose-Einstein condensates in a cavity: Fragmented superradiance and polarization. New J. Phys. 2018, 20, 055006. [Google Scholar] [CrossRef]
- Lin, R.; Papariello, L.; Molignini, P.; Chitra, R.; Lode, A.U.J. Superfluid-Mott-insulator transition of ultracold superradiant bosons in a cavity. Phys. Rev. A 2019, 100, 013611. [Google Scholar] [CrossRef]
- Lin, R.; Molignini, P.; Lode, A.U.J.; Chitra, R. Pathway to chaos through hierarchical superfluidity in blue-detuned cavity-BEC systems. Phys. Rev. A 2020, 101, 061602. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Streltsov, A.I.; Sakmann, K.; Alon, O.E.; Cederbaum, L.S. How an interacting many-body system tunnels through a potential barrier to open space. Proc. Natl. Acad. Sci. USA 2012, 109, 13521. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Klaiman, S.; Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Controlling the velocities and the number of emitted particles in the tunneling to open space dynamics. Phys. Rev. A 2014, 89, 053620. [Google Scholar] [CrossRef]
- Koutentakis, G.M.; Mistakidis, S.I.; Schmelcher, P. Quench-induced resonant tunneling mechanisms of bosons in an optical lattice with harmonic confinement. Phys. Rev. A 2017, 95, 013617. [Google Scholar] [CrossRef]
- Klaiman, S.; Cederbaum, L.S. Overlap of exact and Gross-Pitaevskii wave functions in Bose-Einstein condensates of dilute gases. Phys. Rev. A 2016, 94, 063648. [Google Scholar] [CrossRef]
- Nguyen, J.H.V.; Tsatsos, M.C.; Luo, D.; Lode, A.U.J.; Telles, G.D.; Bagnato, V.S.; Hulet, R.G. Parametric Excitation of a Bose-Einstein Condensate: From Faraday Waves to Granulation. Phys. Rev. X 2019, 9, 011052. [Google Scholar] [CrossRef]
- Bera, S.; Chakrabarti, B.; Gammal, A.; Tsatsos, M.C.; Lekala, M.L.; Chatterjee, B.; Lévêque, C.; Lode, A.U.J. Sorting Fermionization from Crystallization in Many-Boson Wavefunctions. Sci. Rep. 2019, 9, 17873. [Google Scholar] [CrossRef]
- Nozières, P.; St. James, D. Particle Vs. Pair Condensation in Attractive Bose Liquids. J. Phys. Paris 1982, 43, 1133–1148. [Google Scholar] [CrossRef]
- Spekkens, R.W.; Sipe, J.E. Spatial fragmentation of a Bose-Einstein condensate in a double-well potential. Phys. Rev. A 1999, 59, 3868–3877. [Google Scholar] [CrossRef]
- Mueller, E.J.; Ho, T.L.; Ueda, M.; Baym, G. Fragmentation of Bose-Einstein condensates. Phys. Rev. A 2006, 74, 033612. [Google Scholar] [CrossRef]
- Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Efficient generation and properties of mesoscopic quantum superposition states in an attractive Bose-Einstein condensate threaded by a potential barrier. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 091004. [Google Scholar] [CrossRef]
- Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Scattering of an attractive Bose-Einstein condensate from a barrier: Formation of quantum superposition states. Phys. Rev. A 2009, 80, 043616. [Google Scholar] [CrossRef]
- Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Formation and dynamics of many-boson fragmented states in one-dimensional attractive ultracold gases. Phys. Rev. Lett. 2008, 100, 130401. [Google Scholar] [CrossRef]
- Sakmann, K. Many-Body Schrödinger Dynamics of Bose-Einstein Condensates; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Swift loss of coherence of soliton trains in attractive bose-einstein condensates. Phys. Rev. Lett. 2011, 106, 240401. [Google Scholar] [CrossRef] [PubMed]
- Beinke, R.; Klaiman, S.; Cederbaum, L.S.; Streltsov, A.I.; Alon, O.E. Many-body tunneling dynamics of Bose-Einstein condensates and vortex states in two spatial dimensions. Phys. Rev. A 2015, 92, 043627. [Google Scholar] [CrossRef]
- Weiner, S.E.; Tsatsos, M.C.; Cederbaum, L.S.; Lode, A.U.J. Phantom vortices: Hidden angular momentum in ultracold dilute Bose-Einstein condensates. Sci. Rep. 2017, 7, 40122. [Google Scholar] [CrossRef]
- Dutta, S.; Tsatsos, M.C.; Basu, S.; Lode, A.U.J. Management of the correlations of Ultracold Bosons in triple wells. New J. Phys. 2019, 21, 053044. [Google Scholar] [CrossRef]
- Fasshauer, E.; Lode, A.U.J. Multiconfigurational time-dependent Hartree method for fermions: Implementation, exactness, and few-fermion tunneling to open space. Phys. Rev. A 2016, 93, 033635. [Google Scholar] [CrossRef]
- Lode, A.U.J. Multiconfigurational time-dependent Hartree method for bosons with internal degrees of freedom: Theory and composite fragmentation of multicomponent Bose-Einstein condensates. Phys. Rev. A 2016, 93, 063601. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Bruder, C. Dynamics of Hubbard Hamiltonians with the multiconfigurational time-dependent Hartree method for indistinguishable particles. Phys. Rev. A 2016, 94, 013616. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Tsatsos, M.C.; Fasshauer, E.; Lin, R.; Papariello, L.; Molignini, P.; Weiner, S.E.; Lévêque, C. MCTDH-X: The Multiconfigurational Time-Dependent Hartree For Indistinguishable Particles Software. Available online: http://ultracold.org (accessed on 14 March 2021).
- Doganov, R.A.; Klaiman, S.; Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Two trapped particles interacting by a finite-range two-body potential in two spatial dimensions. Phys. Rev. A 2013, 87, 033631. [Google Scholar] [CrossRef]
- Friedman, C.N. Perturbations of the Schroedinger equation by potentials with small support. J. Funct. Anal. 1972, 10, 346–360. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Note on Exchange Phenomena in the Thomas Atom. Math. Proc. Camb. Philos. Soc. 1930, 26, 376. [Google Scholar] [CrossRef]
- Mott, N.F.; Frenkel, J. Wave Mechanics: Advanced General Theory; Clarendon Press: Oxford, UK, 1934; Volume 18, p. 208. [Google Scholar] [CrossRef]
- McLachlan, A.D. A variational solution of the time-dependent Schrodinger equation. Mol. Phys. 1964, 8, 39–44. [Google Scholar] [CrossRef]
- Kramer, P.; Saraceno, M. Geometry of the Time-Dependent Variational Principle in Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Kvaal, S. Variational formulations of the coupled-cluster method in quantum chemistry. Mol. Phys. 2013, 111, 1100–1108. [Google Scholar] [CrossRef]
- Penrose, O.; Onsager, L. Bose-einstein condensation and liquid helium. Phys. Rev. 1956, 104, 576–584. [Google Scholar] [CrossRef]
- Sakmann, K.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Reduced density matrices and coherence of trapped interacting bosons. Phys. Rev. A 2008, 78, 023615. [Google Scholar] [CrossRef]
- Wells, T.; Lode, A.U.J.; Bagnato, V.S.; Tsatsos, M.C. Vortex Reconnections in Anisotropic Trapped Three-Dimensional Bose–Einstein Condensates. J. Low Temp. Phys. 2015, 180, 133–143. [Google Scholar] [CrossRef]
- Sakmann, K.; Kasevich, M. Single-shot simulations of dynamic quantum many-body systems. Nat. Phys. 2016, 12, 451. [Google Scholar] [CrossRef]
- Klaiman, S.; Alon, O.E. Spatially-partitioned many-body vortices. J. Phys. Conf. Ser. 2016, 691, 012015. [Google Scholar] [CrossRef]
- Tsatsos, M.C.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Fragmented many-body states of definite angular momentum and stability of attractive three-dimensional condensates. Phys. Rev. A 2010, 82, 33613. [Google Scholar] [CrossRef]
- Tsatsos, M.C.; Lode, A.U.J. Resonances and Dynamical Fragmentation in a Stirred Bose–Einstein Condensate. J. Low Temp. Phys. 2015, 181, 171–181. [Google Scholar] [CrossRef]
- Gajda, M.; Mostowski, J.; Sowiński, T.; Załuska-Kotur, M. Single-shot imaging of trapped Fermi gas. Europhys. Lett. 2016, 115, 20012. [Google Scholar] [CrossRef]
- Pyzh, M.; Krönke, S.; Weitenberg, C.; Schmelcher, P. Quantum point spread function for imaging trapped few-body systems with a quantum gas microscope. New J. Phys. 2019, 21, 053013. [Google Scholar] [CrossRef]
- Roy, R.; Gammal, A.; Tsatsos, M.C.; Chatterjee, B.; Chakrabarti, B.; Lode, A.U.J. Phases, many-body entropy measures, and coherence of interacting bosons in optical lattices. Phys. Rev. A 2018, 97, 043625. [Google Scholar] [CrossRef]
- Tsubota, M.; Kasamatsu, K.; Ueda, M. Vortex lattice formation in a rotating Bose-Einstein condensate. Phys. Rev. A 2002, 65, 023603. [Google Scholar] [CrossRef]
- Dagnino, D.; Barberán, N.; Lewenstein, M. Vortex nucleation in a mesoscopic Bose superfluid and breaking of the parity symmetry. Phys. Rev. A 2009, 80, 53611. [Google Scholar] [CrossRef]
- Alon, O.E.; Bagnato, V.S.; Beinke, R.; Brouzos, I.; Calarco, T.; Caneva, T.; Cederbaum, L.S.; Kasevich, M.A.; Klaiman, S.; Lode, A.U.J.; et al. MCTDHB physics and technologies: Excitations and vorticity, single-shot detection, measurement of fragmentation, and optimal control in correlated ultra-cold bosonic many-body Systems. In High Performance Computing in Science and Engineering ´15; Springer: Cham, Switzerland, 2016; pp. 23–49. [Google Scholar] [CrossRef]
- Cremon, J.C.; Jackson, A.D.; Karabulut, E.Ö.; Kavoulakis, G.M.; Mottelson, B.R.; Reimann, S.M. Rotating Bose-Einstein condensates: Closing the gap between exact and mean-field solutions. Phys. Rev. A 2015, 91, 033623. [Google Scholar] [CrossRef]
- Alon, O.E.; Beinke, R.; Bruder, C.; Cederbaum, L.S.; Klaiman, S.; Lode, A.U.J.; Sakmann, K.; Theisen, M.; Tsatsos, M.C.; Weiner, S.E.; et al. Many-Body Effects in Fragmented, Depleted, and Condensed Bosonic Systems in Traps and Optical Cavities by MCTDHB and MCTDH-X; Springer: Berlin/Heidelberg, Germany, 2018; pp. 93–115. [Google Scholar] [CrossRef]
- Eriksson, G.; Bengtsson, J.; Kavoulakis, G.M.; Reimann, S.M. Two-state model for vortex nucleation in a rotating Bose-Einstein condensate. Phys. Rev. A 2019, 100, 063638. [Google Scholar] [CrossRef]
- Alon, O.E.; Cederbaum, L.S. Attractive Bose-Einstein condensates in anharmonic traps: Accurate numerical treatment and the intriguing physics of the variance. Chem. Phys. 2018, 515, 287–298. [Google Scholar] [CrossRef]
- Bhowmik, A.; Haldar, S.K.; Alon, O.E. Impact of the transverse direction on the many-body tunneling dynamics in a two-dimensional bosonic Josephson junction. Sci. Rep. 2020, 10, 21476. [Google Scholar] [CrossRef]
- Tsatsos, M.C.; Tavares, P.E.; Cidrim, A.; Fritsch, A.R.; Caracanhas, M.A.; dos Santos, F.E.A.; Barenghi, C.F.; Bagnato, V.S. Quantum turbulence in trapped atomic Bose–Einstein condensates. Phys. Rep. 2016, 622, 1–52. [Google Scholar] [CrossRef]
- Madeira, L.; García-Orozco, A.D.; dos Santos, F.E.A.; Bagnato, V.S. Entropy of a Turbulent Bose-Einstein Condensate. Entropy 2020, 22, 956. [Google Scholar] [CrossRef] [PubMed]
- Caillat, J.; Zanghellini, J.; Kitzler, M.; Koch, O.; Kreuzer, W.; Scrinzi, A. Correlated multielectron systems in strong laser fields: A multiconfiguration time-dependent Hartree-Fock approach. Phys. Rev. A 2005, 71, 012712. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lode, A.U.J.; Dutta, S.; Lévêque, C. Dynamics of Ultracold Bosons in Artificial Gauge Fields—Angular Momentum, Fragmentation, and the Variance of Entropy. Entropy 2021, 23, 392. https://doi.org/10.3390/e23040392
Lode AUJ, Dutta S, Lévêque C. Dynamics of Ultracold Bosons in Artificial Gauge Fields—Angular Momentum, Fragmentation, and the Variance of Entropy. Entropy. 2021; 23(4):392. https://doi.org/10.3390/e23040392
Chicago/Turabian StyleLode, Axel U. J., Sunayana Dutta, and Camille Lévêque. 2021. "Dynamics of Ultracold Bosons in Artificial Gauge Fields—Angular Momentum, Fragmentation, and the Variance of Entropy" Entropy 23, no. 4: 392. https://doi.org/10.3390/e23040392
APA StyleLode, A. U. J., Dutta, S., & Lévêque, C. (2021). Dynamics of Ultracold Bosons in Artificial Gauge Fields—Angular Momentum, Fragmentation, and the Variance of Entropy. Entropy, 23(4), 392. https://doi.org/10.3390/e23040392