The 2-D Cluster Variation Method: Topography Illustrations and Their Enthalpy Parameter Correlations
Abstract
1. Introduction
- How do the configuration variables associated with at-equilibrium patterns compare with the analytically-predicted configuration variables, for the particular set of enthalpy parameters used to drive the initial pattern towards a free energy minimum?
- What is the range of a useful phase space, and (as an extension of question 1), what are the configuration variable values associated with points in this space? and
- How can we visually characterize the resulting topographies themselves; that is, can we identify a correspondence between observed visual patterns and associated configuration variables in an at-equilibrium 2-D grid system?
1.1. A Worked Example: Instance of a Resulting 2-D CVM
1.2. Introducing the Cluster Variation Method
1.3. Background: The Cluster Variation Method (CVM)
- A grid pattern where a key variable is a configurational triplet has at least some possiblity of being correlated with existing cluster description methods, e.g., the clustering coefficient measure first devised by Watts and Strogatz (1998) [16], and
- A triplet configuration is an appropriate modeling unit for neural systems; see discussion in Section 2.3 of Maren (2016) [3] and more specifically in Sporns and Kötter (2004), who note that neural motifs (or functionally- and structurally-connected units) on the order of M = 3 (where M is the number of units) are a useful modeling base [17].
2. Results
- Deviation of computational results from the analytic,
- Identification of a useful parameter range, and
- Intial topography characterization.
- The configuration variables,
- Overview of experimental trials,
- Result 1: computational configuration variable values differ from analytic,
- Result 2: identification of a useful parameter range, and
- Result 3: initial topography characterization.
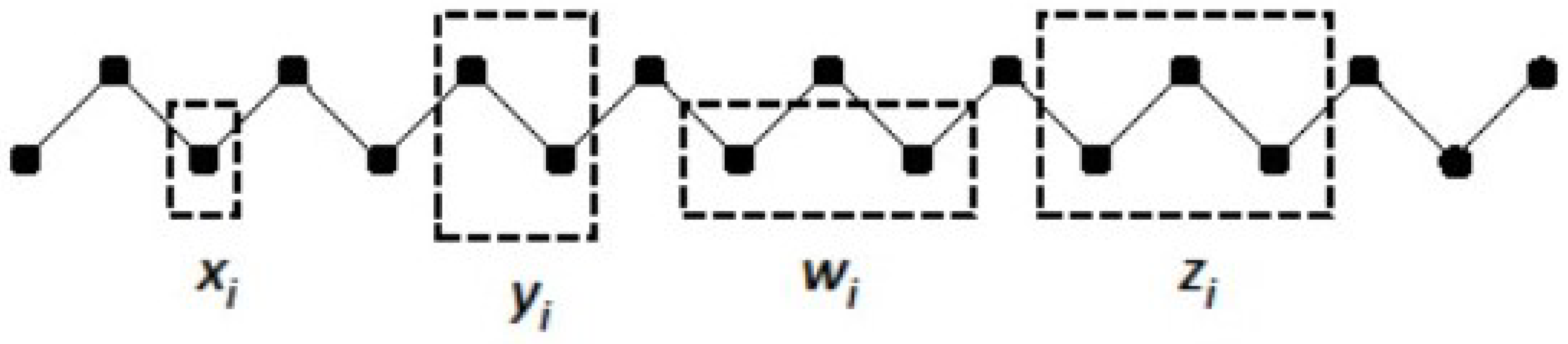
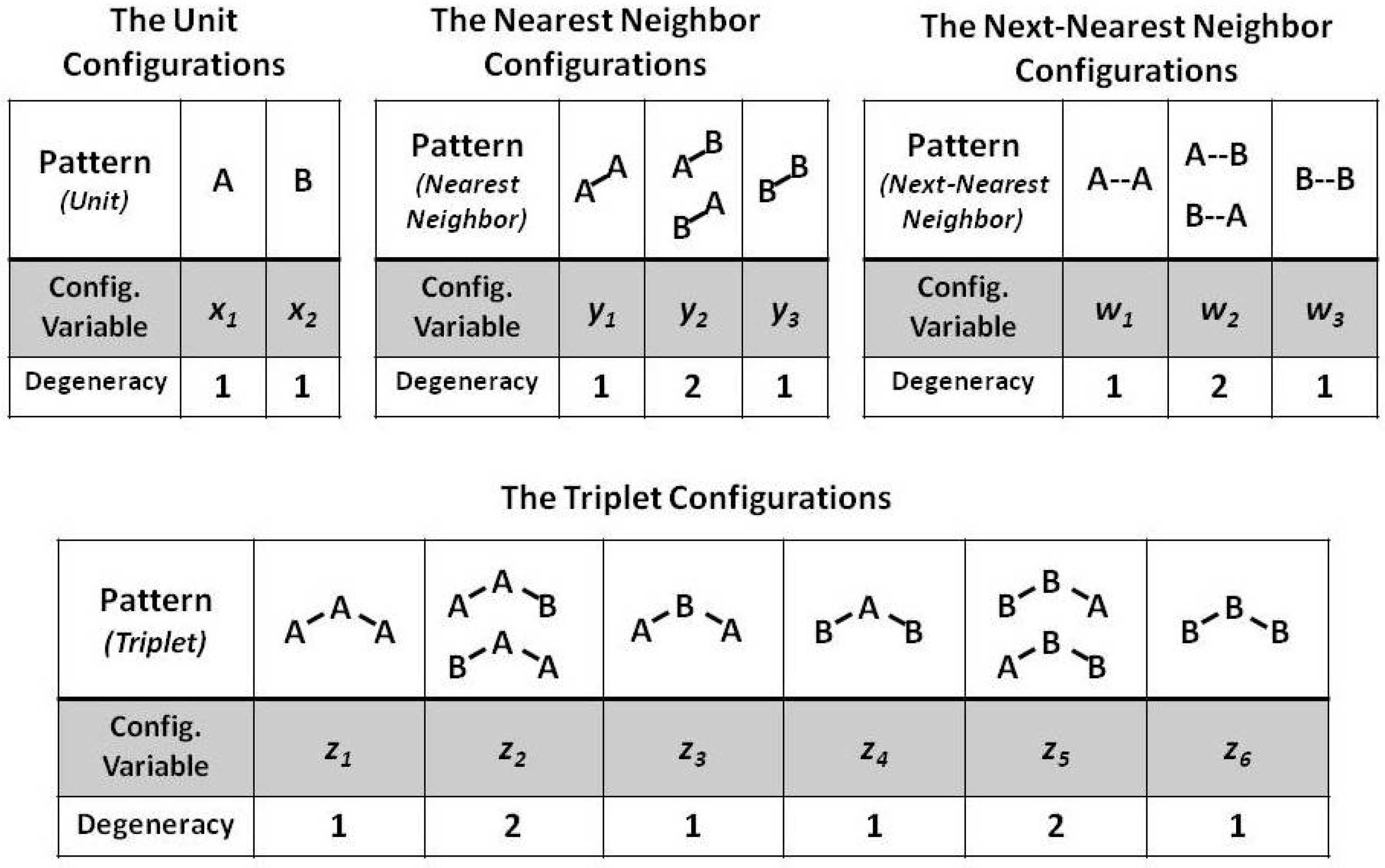
2.1. The Configuration Variables
- Configuration variable definitions–how they show up in the 2-D CVM grid,
- Counting the configuration variables–how each configuration variable is counted, and the verification and validation (V&V) thereof, and
- A brief interpretation–how to interpret configuration variable values.
2.1.1. Introducing the Configuration Variables
- -Single units,
- -Nearest-neighbor pairs,
- -Next-nearest-neighbor pairs, and
- -Triplets.
2.1.2. CVM Topographies: Interpreting Configuration Variables
- -A-A-A triplets; indicates the relative fraction of A units that are included within the interiors of the “islands” or “land masses”; also (indirectly) indicates the compactness of these masses,
- -A-B-A triplets; indicates the relative fraction of A units that are involved in a “jagged” border (one that involves irregular protrusions of A into a B space), or the presence of one or more thin “rivers” of B units extending into landmass(es) of A units, and
- -A-B nearest-neighbor pairs; indicates the relative extent to which the A units are distributed among the surrounding B units. A higher value indicates lots of boundary areas between A and B, and a smaller value indicates more compact “landmasses“ of A units.
2.2. Overview of Experimental Trials
- Scale-free-like, and
- Extreme rich club-like.
- Identify appropriate interaction enthalpy parameters that reasonably corresponded to the two different initial grid patterns,
- Identify the actual configuration variable values for each pattern as each was brought to its respective free energy equilibrium, and
- Characterize the resulting free energy-minimized topographies.
- Comparison of computational results with the analytic, where notable differences have been found,
- Identification of a useful parameter range, which allows us to identify the extent of the phase space that we will ultimately desire to map, and
- Initial topography characterization, which will allow us to correlate h-values with different kinds of topographies, as well as with their associated configuration variable values.
2.3. Result 1: Computational Configuration Variable Values Differ from Analytic
2.3.1. The 2-D CVM Enthalpy
2.3.2. The 2-D CVM Entropy
2.3.3. Free Energy Analytic Solution
2.3.4. Divergence in the Analytic Solution
2.3.5. Significance of h in the Free Energy
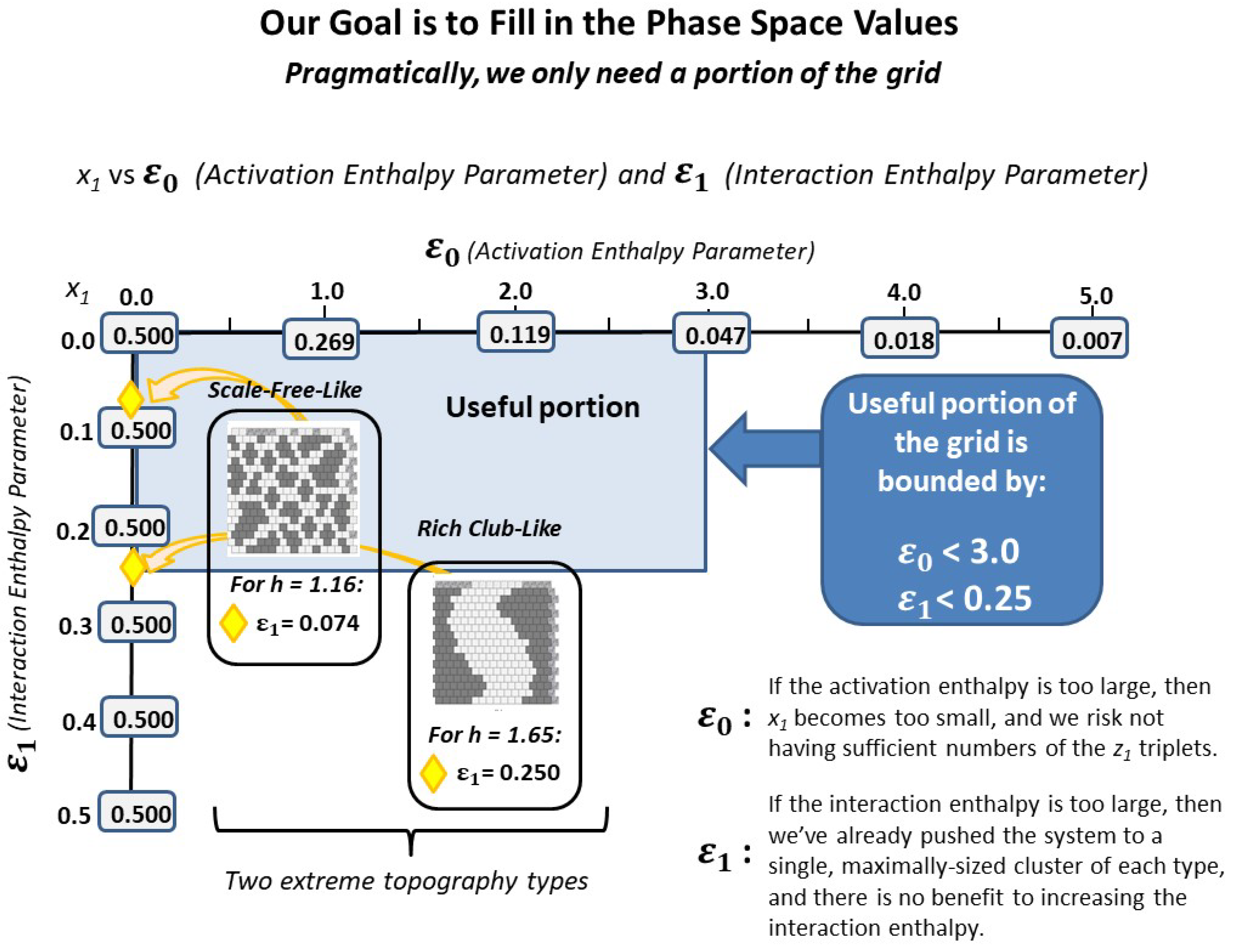
2.4. Result 2: Identification of a Useful Parameter Range
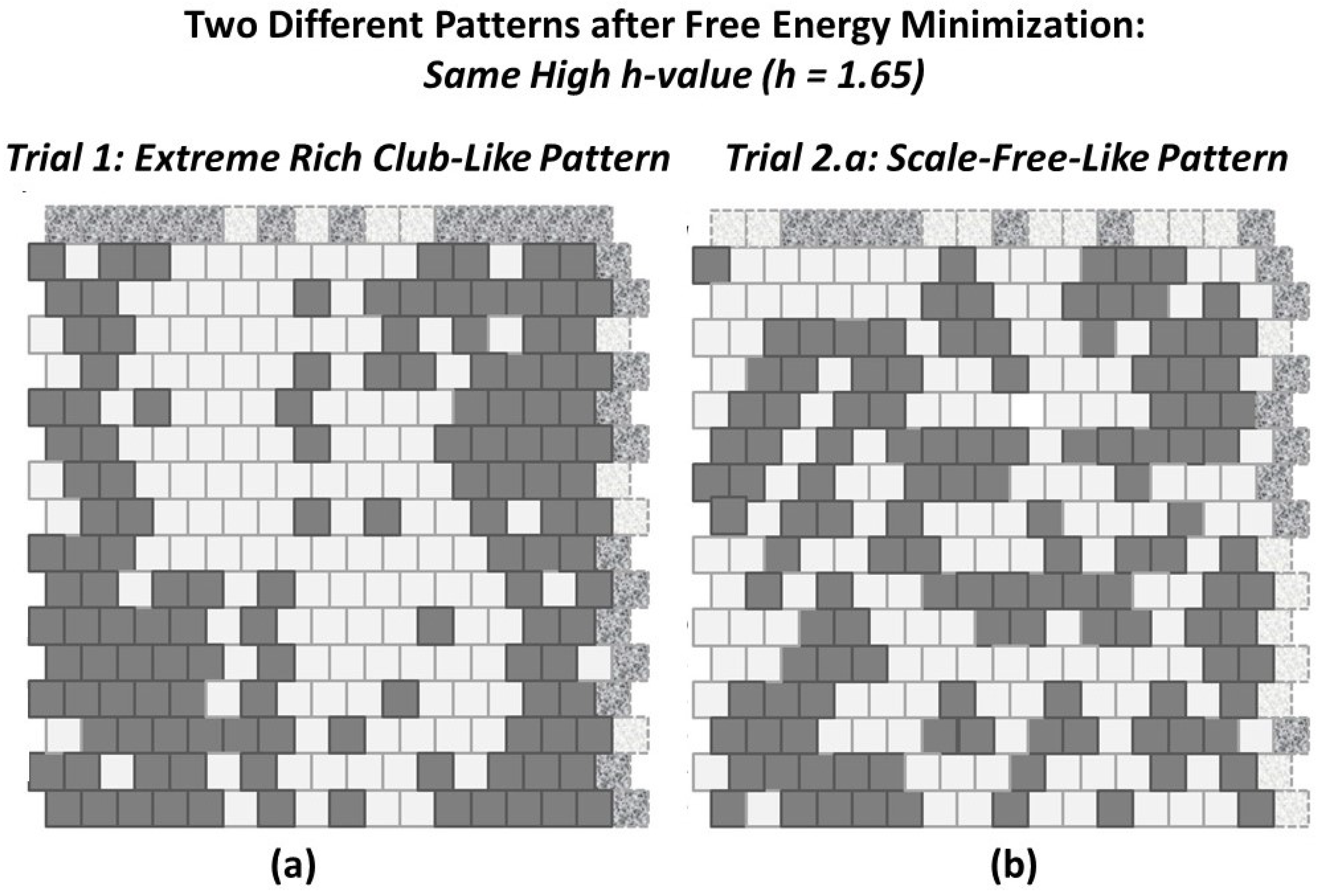
2.4.1. Experimental Trial 1.a: Very Large h-Value
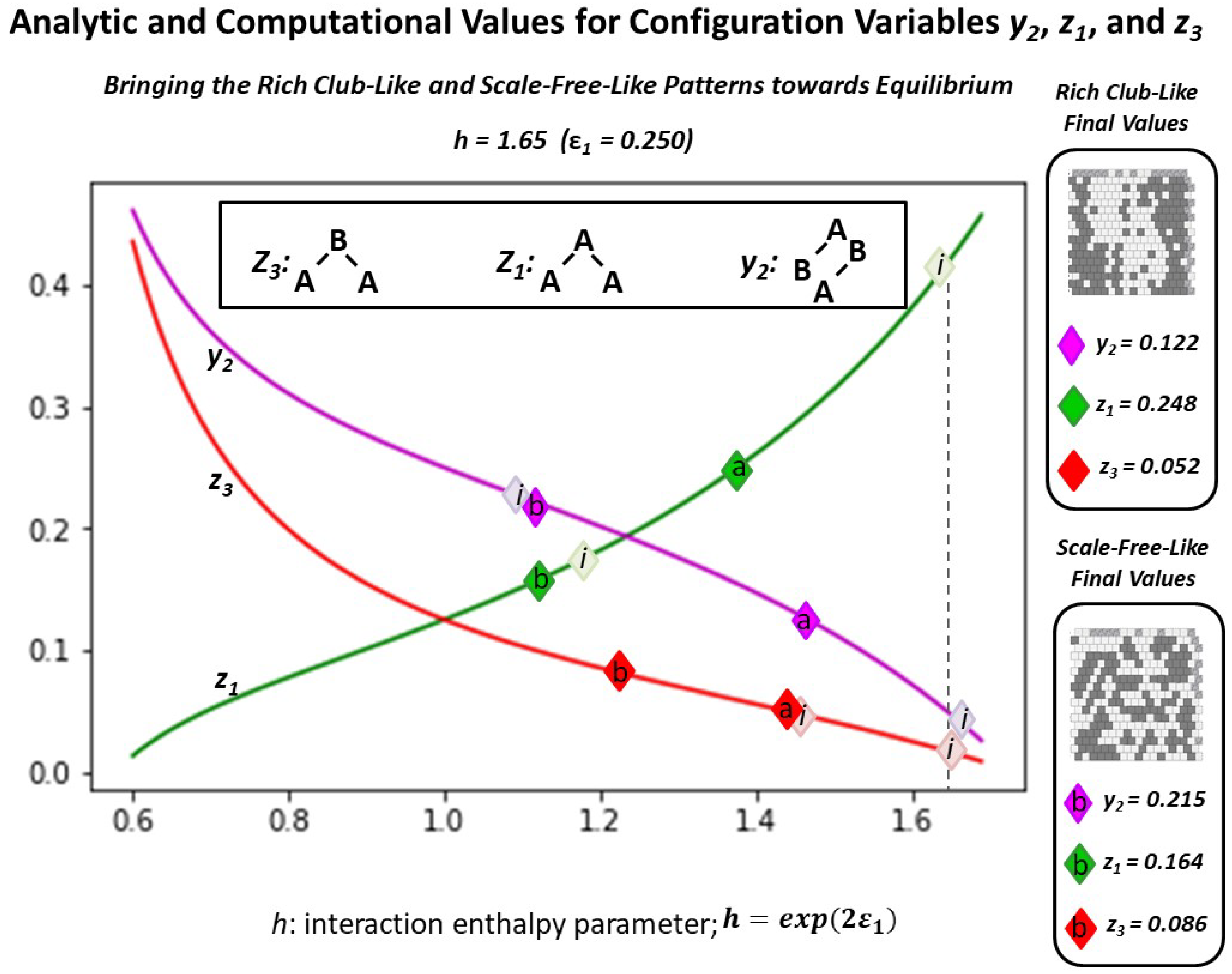
2.4.2. Experimental Trial 1.b: Two Patterns at Same Large h-Value
2.5. Result 3: Topography Characterization
- Sufficient variety in local patterns–this grid size was large enough to illustrate several distinct kinds of topographies (each corresponding to different h-values),
- Sufficient nodes–there were enough nodes so that triplet-configuration extrema could be explored in some detail, e.g., for relatively small numbers of nodes in state A (results not reported in this work), and
- Countability–the verification and validation (V&V) effort required that several early versions of the grid be manually counted for all the configuration values for a given 2-D grid configuration, and matched against the results from the program.
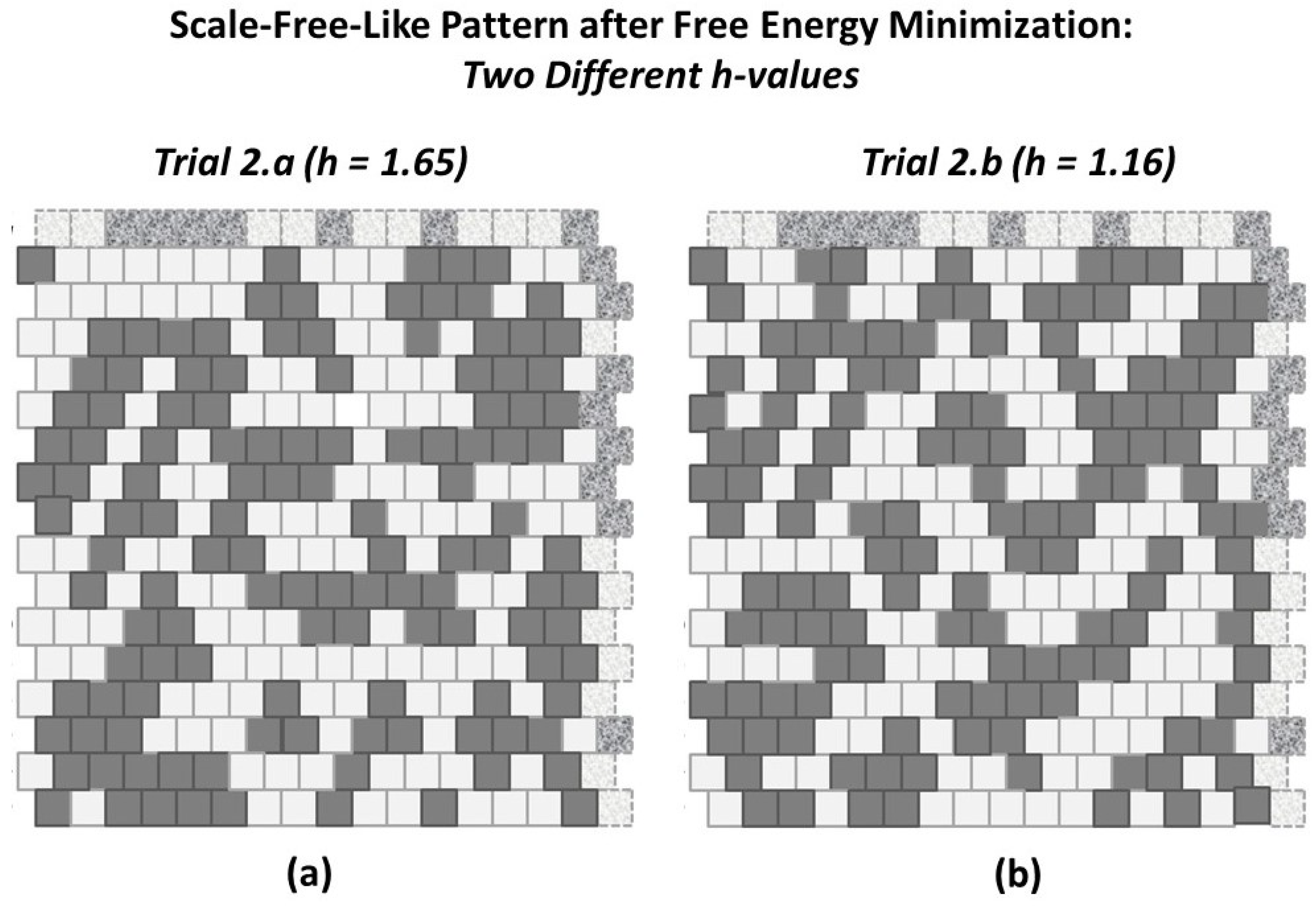
- Trial (2.a): , which was expected to push the system substantially towards increased like-near-like clustering, and
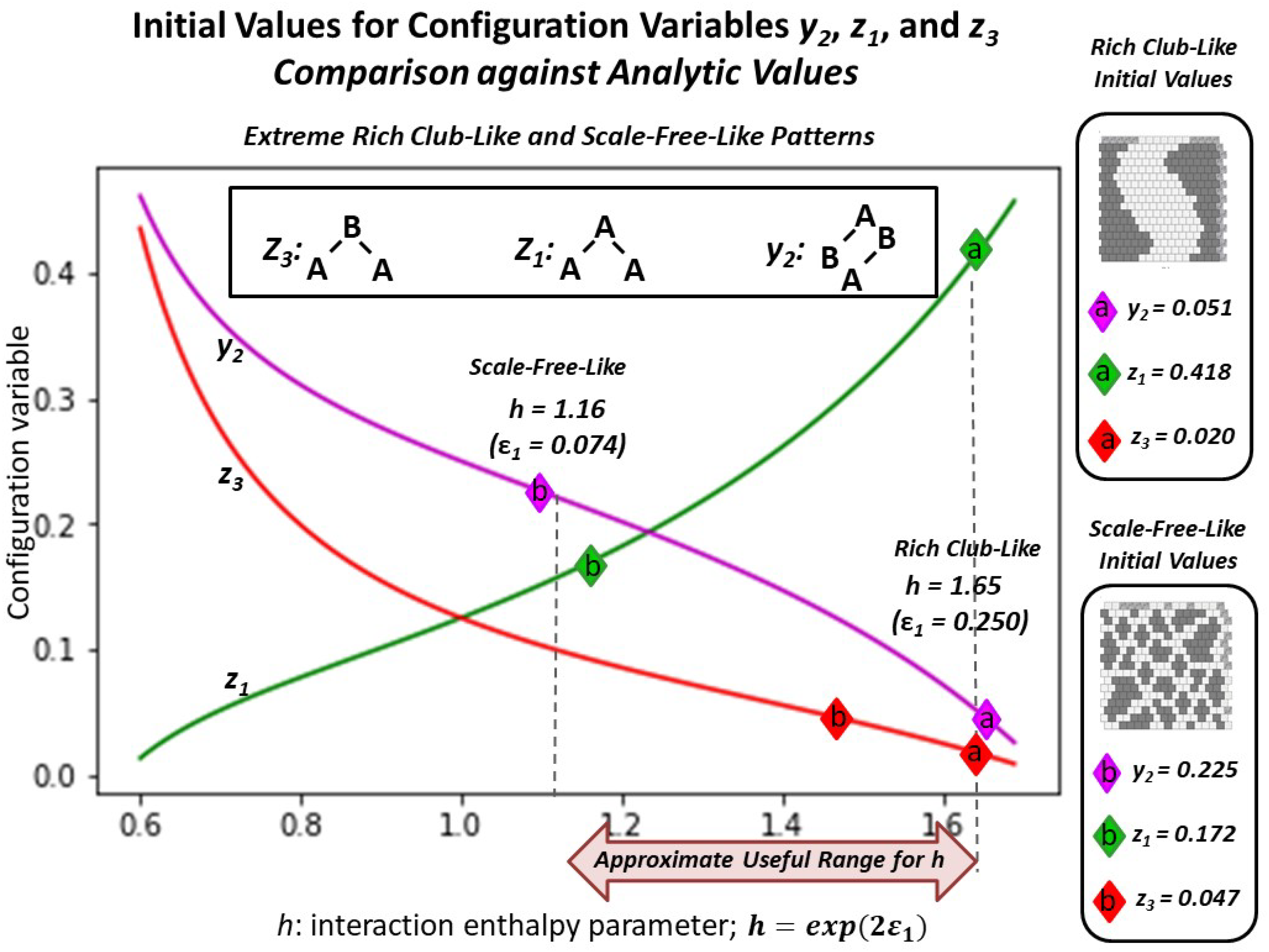
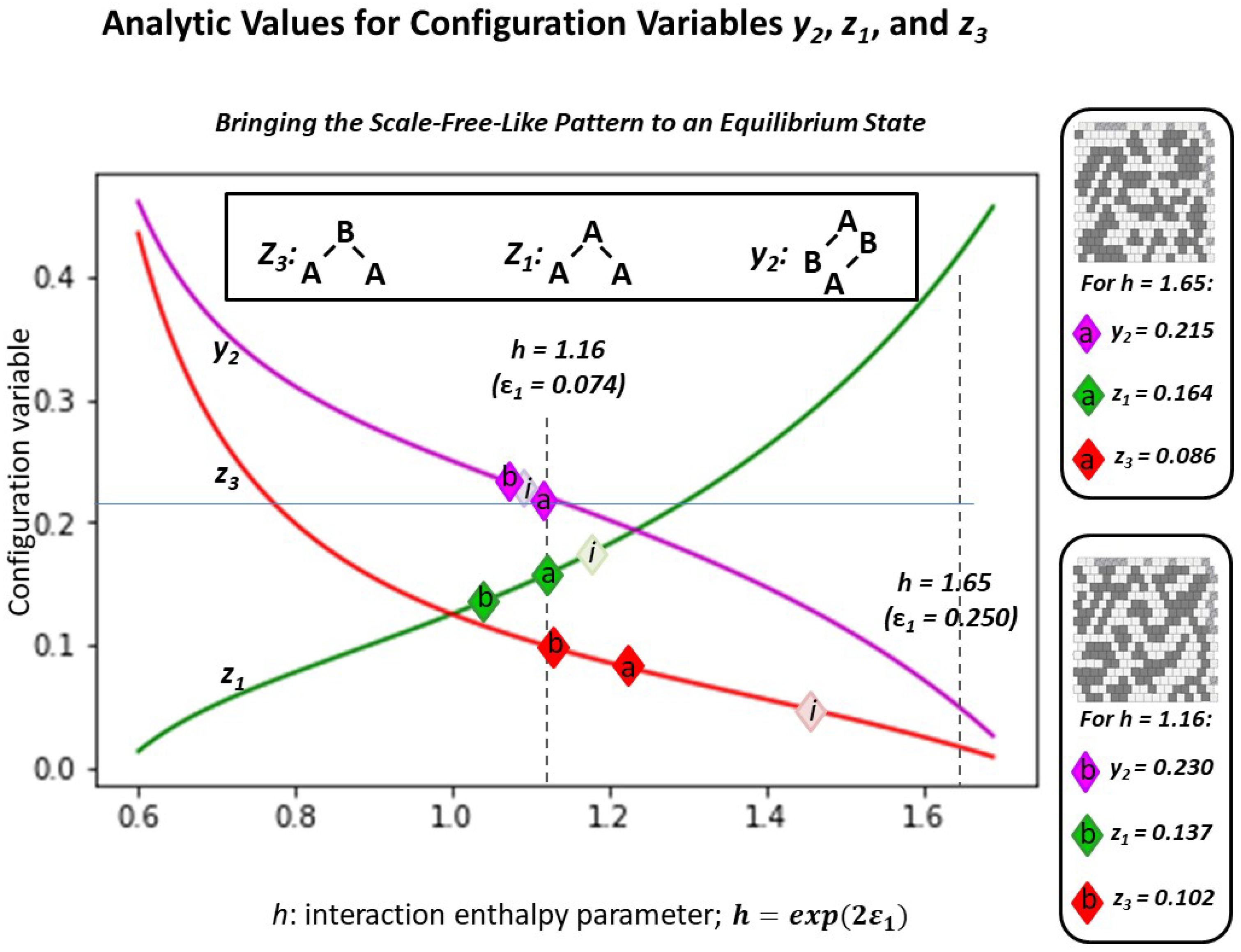
- Trial (2.b): h = 1.16, which was expected would not dramatically change the pattern configuration, as the current configuration values indicate that an h-value of is approximately close to its current state. (See Figure 6; the initial configuration values for the “scale-free-like” pattern approximately surround h = 1.16.)
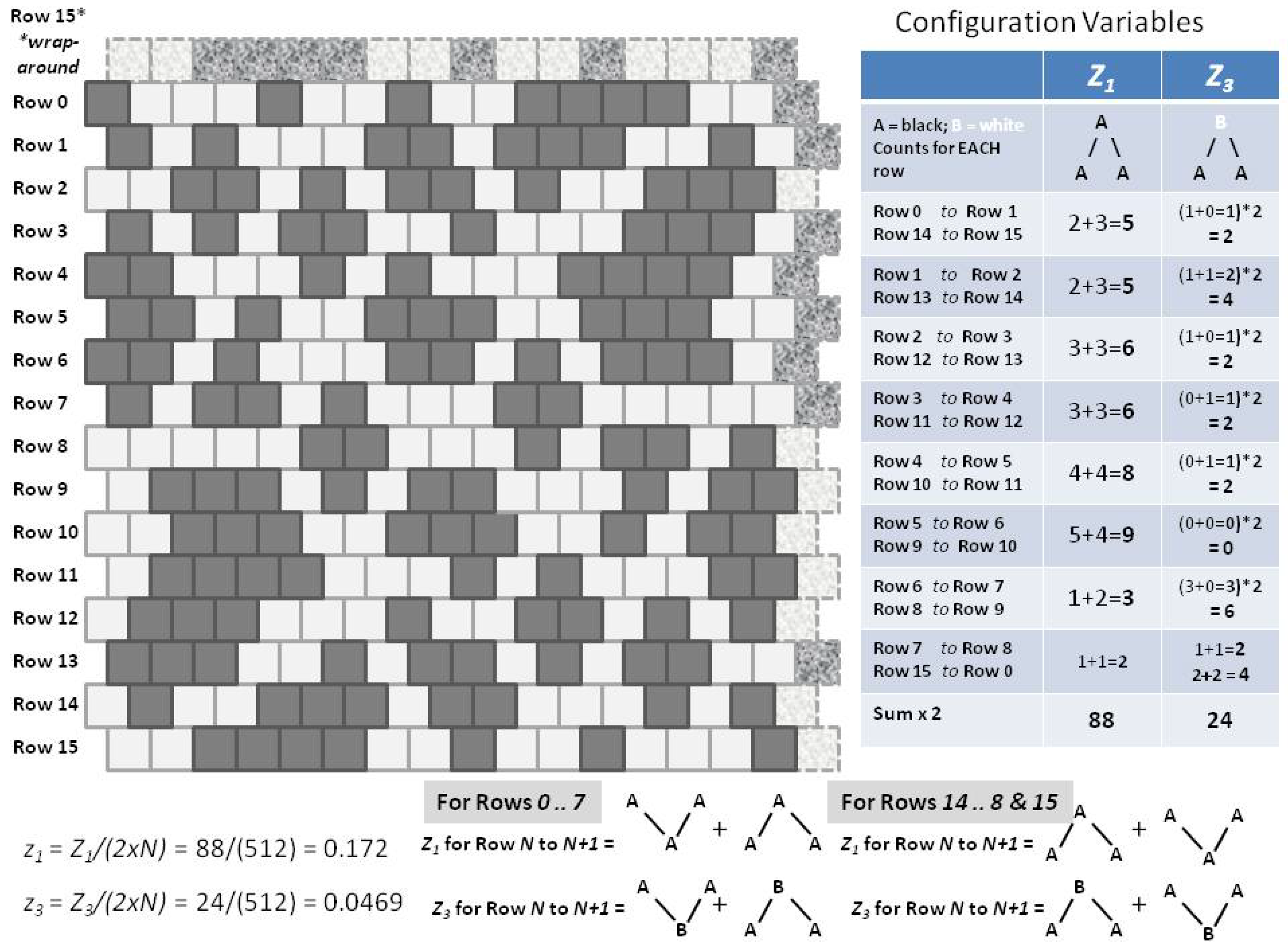
2.5.1. The Configuration Variable Values for the Initial Scale-Free-Like Pattern
2.5.2. Experimental Trial 2.a: “Scale-Free-Like” Grid with h = 1.65
2.5.3. Experimental Trial 2.b: “Scale-Free-Like” Grid with h = 1.16
3. Discussion
- Next steps in characterizing 2-D CVM topographies and their associated configuration variable and parameter space values, as well as strategies to move from one topography to another,
- Potential role of using the 2-D CVM to model certain structural aspects of brain organization, and also addressing the role of free energy minimization within the brain, and
- Next steps to connect 2-D CVM topographies with existing models and characteristics for different forms of structural organization.
3.1. Next Steps in Developing 2-D CVM Topographies and the Associated Parameter Space
- Map the set of configuration variables values to the parameter space (noting that there may be a configuration variable value range, depending on the initial topography),
- Characterize how visual topography features correspond with configuration variable sets, and devise algorithms to characterize topographic elements (e.g., clusters) in terms of variables such as their relative size distributions, compactness, and other measures which are typical in other 2-D grid systems, noting that the algorithms need to be created specific to the grid layout for the 2-D CVM described here, and
- Devise strategies to efficiently transit from one topography to another, as there are changes in the parameters .
- Devising a means to correlate phase space regions with various topograhic descriptions, e.g., “rich club,” and
- Devising strategies to efficiently transit from one topography to another, as there are changes in the parameters .
3.2. Free Energy Minimization in the Brain
- Investigating means to “reverse engineer” empirical timeseries (for example, natural topography evolution) via identifying an enthalpy phase space trajectory, and
- Investigating the potential for dynamic graph generation, via a trajectory through the enthalpy phase space; this could potentially be applied to Bayesian model selection and/or message-passing.
3.3. The Challenge: Efficiently Characterizing Two-Dimensional Topographies
- Rich club,
- Small-world, and
- Scale-free.
3.3.1. Rich Club Topographies
3.3.2. Small-World Topographies
3.3.3. Scale-Free Topographies
4. Materials and Methods
4.1. Method Overview
- Devise an initial pattern, and compute the configuration variables associated with this initial pattern,
- Using this initial set of (not-at-equilibrium) configuration variables (specifically, the set of interpretation variables, , , and ), identify an appropriate h-value that reasonably corresponds to that set of interpretation variables, using both graphical and tabular depictions of the configuration variables as a function of the h-value, and then
- Use that h-value as the key parameter in the code that modifies the pattern until a free energy minimum has been achieved. This new resulting pattern exemplifies how the initial pattern will appear after free energy minimization, and the corresponding set of configuration variable values identify a position in the phase space, associating the selected h-value with a set of configuration variable values.
4.2. Method Illustration
4.2.1. Step 1: Compute Initial Configuration Variable Values
4.2.2. Step 2: Identify Approximate h-Value
4.2.3. Step 3: Perform Free Energy Minimization
4.3. Method for the Case Where the Interaction Enthalpy Is Zero
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
- Various MS PPT decks containing experimental results: github.com/ajmaren/2D-Cluster-Variation-Method (accessed on 3 March 2021).
- Codes for performing free energy minimization on different pre-defined patterns: github.com/ajmaren/2-D-CVM-Defined-Pattern-Configurations (accessed on 3 March 2021).
- Codes for performing perturbation analyses, leading to thermodynamic quantities as an initial randomly-defined grid was brought to free energy equilibrium for a range of different h-values (see Figure 7): github.com/ajmaren/2-D-CVM-Random-Pattern-Configurations (accessed on 3 March 2021).
Appendix A. The Configuration Variables and Method Details
- The configuration varaibles under the equiprobable case,
- (Impact of) Simplifying the ,
- Relationship between the and ,
- Counting the configuration variables: initial verification and validation,
- Experimental trial: very large h-value-details,
- Methods for designing the “scale-free-like” grid,
- Details on experiments using the “scale-free-like” grid,
- Methods for the case where the interaction enthalpy is not zero, and
- Methods for the case where the interaction enthalpy is zero.
Appendix A.1. The Configuration Variables under the Equiprobable Case
- -units in state A equal those in state B,
- -nearest-neighbor pairs A-A equal B-B,
- -next-nearest-neighbor pairs A- -A equal B- -B,
- -triplets A-A-A equal B-B-B,
- -triplets A-B-A equal B-A-B, and
- -triplets A-A-B equal A-B-B.
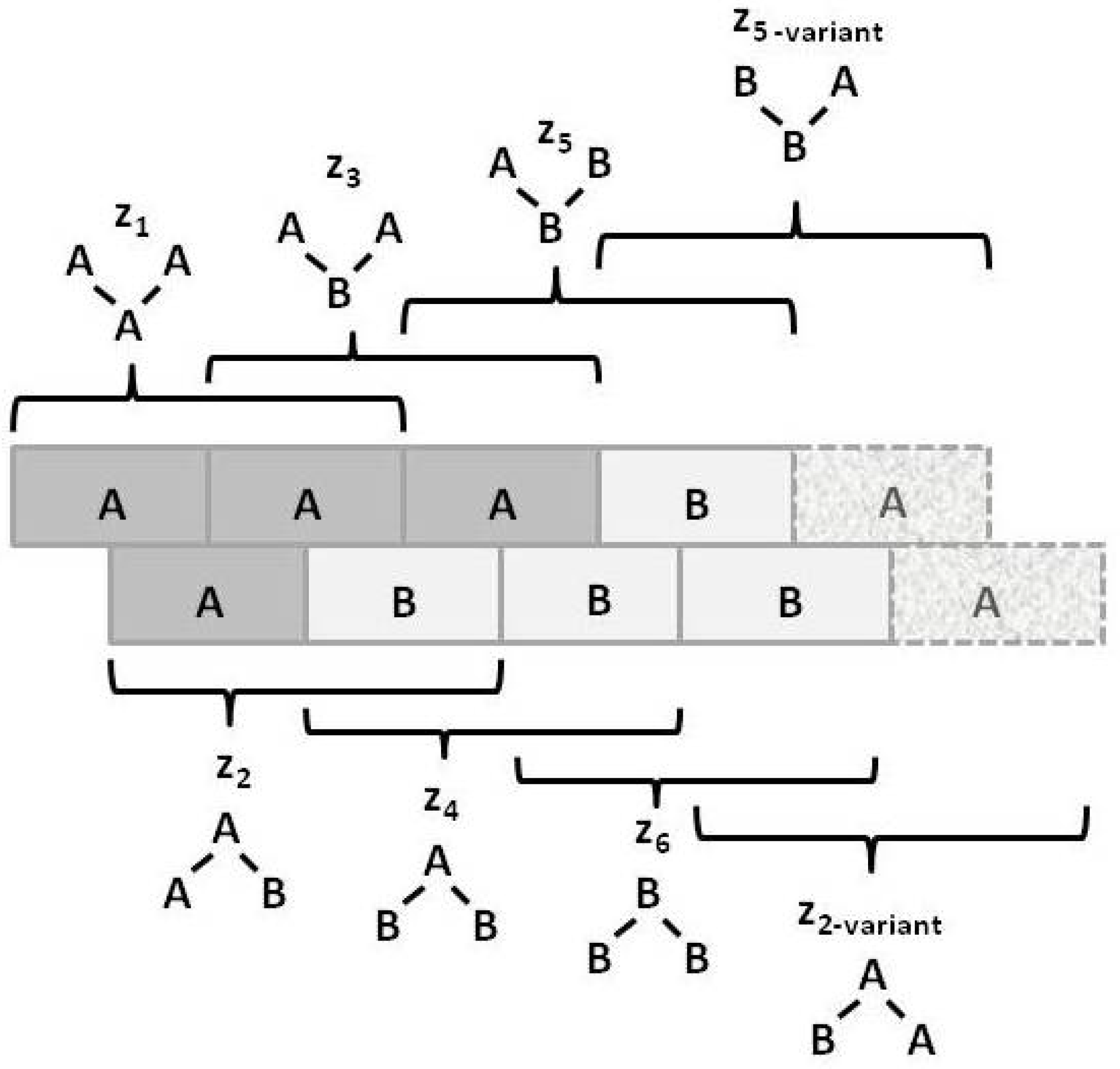
Appendix A.2. Simplifying the Numbers of zi
Appendix A.3. Relationship between yi and wi
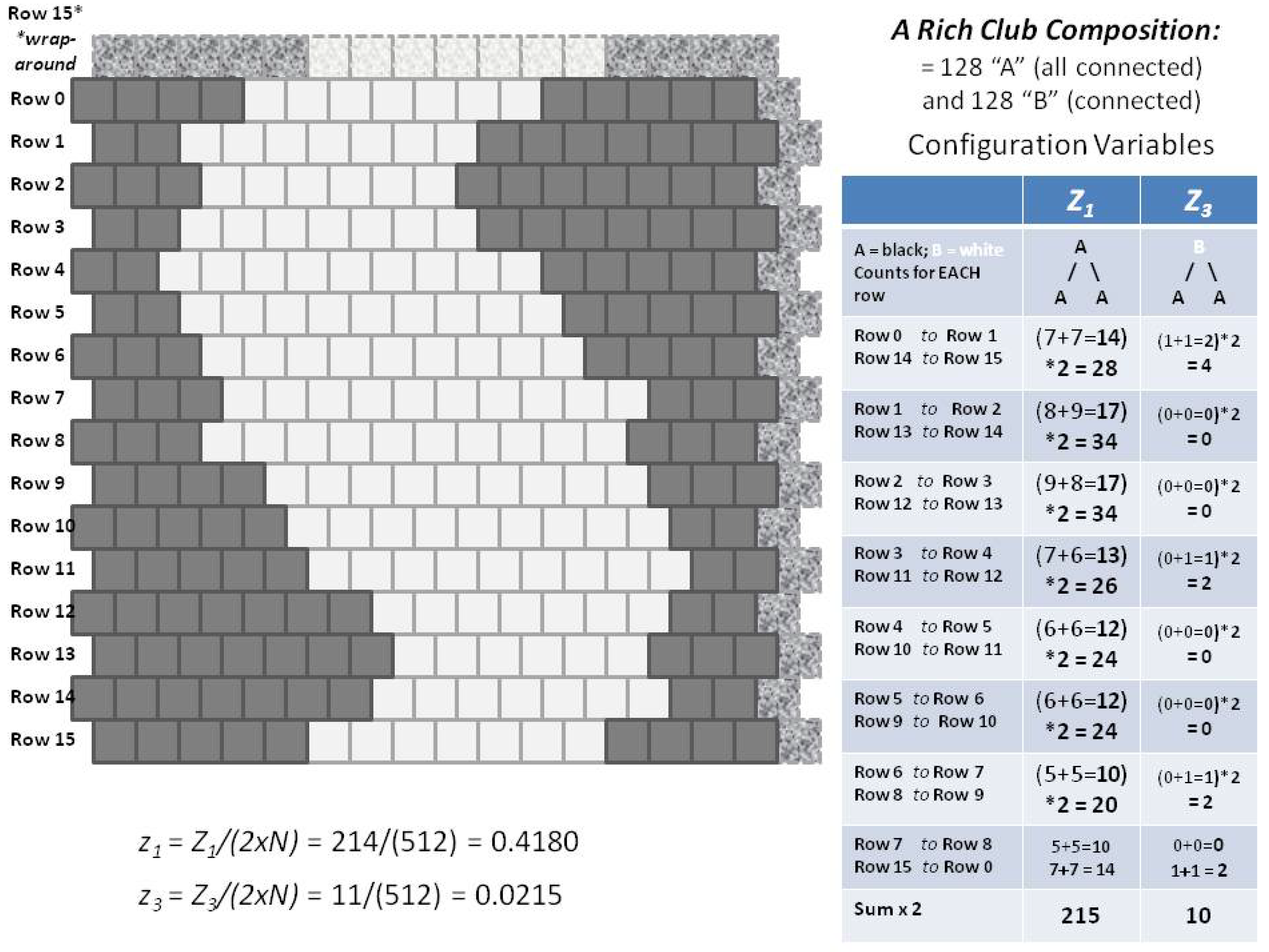
Appendix A.4. Counting the Configuration Variables: Initial Verification and Validation
- Initial Verification and Validation document (Maren (2019c) [60])—results of initial experiments, and also describes both the manually-generated and code-generated results for counting the configuration variables for small grids.
- 2D-CVM-perturb-expt-1-2b-2018-01-12.py-A free energy minimization code that includes perturbations after reaching the first free energy minimum. This was used for a short experimental series confirming that the free energy minimum is stable. The code allows user-specifiable (in **main**) values for , h, , and many other parameters. Detailed results of this experimental series are given in Maren (2019c) [60].
- ,
- , for and , accounting for the degeneracy with which occurs,
- , for and , accounting for the degeneracy with which occurs, and
- , for and , , accounting for the degeneracy with which and occur.
Appendix A.5. Experimental Trial: h-Value—Details
- The equivalence relations introduced that make the analytic solution possible may introduce unusual behaviors in the analytically-derived configuration variables as the h-value moves away from ,
- As the h-value moves towards the value where the analytic solution diverges, the actual at-equilibrium configuration values will diverge from the analytic, and
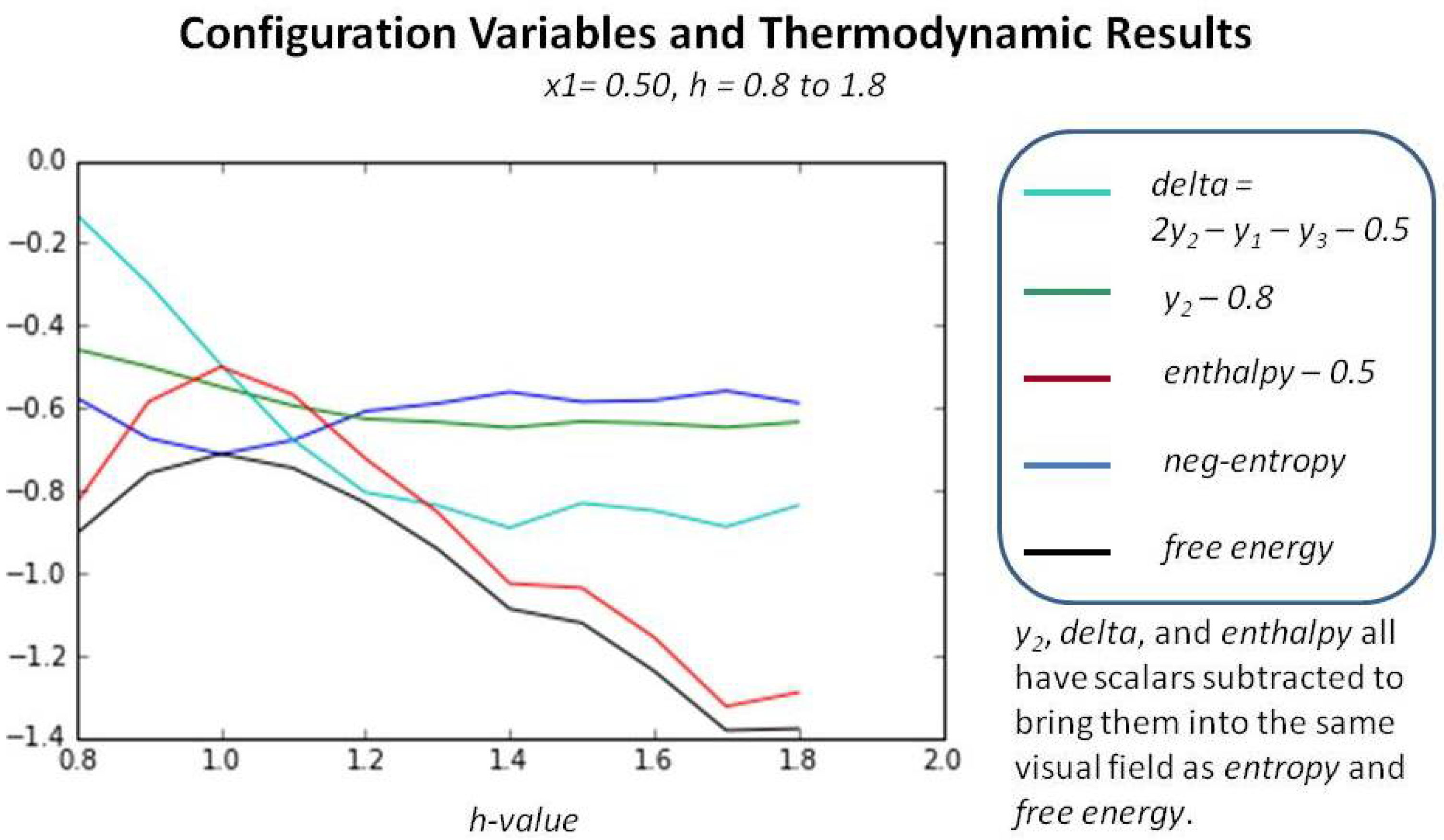
- As shown in Figure 7, as h becomes large, the enthalpy term dominates, and the free energy is reduced by increasing ; this can move the system towards high values faster than would be expected. (This is why the range of usable h-values is limited.)
Appendix A.5.1. Experimental Trial: Very Large h-Value (h = 2.0)
| Variable | Initial | Trial 1 | Trial 2 | Trial 3 |
|---|---|---|---|---|
| 0.4180 | 0.2480 | 0.2500 | 0.2500 | |
| * | 0.0625 | 0.0976 | 0.0898 | 0.0857 |
| 0.0195 | 0.0566 | 0.0703 | 0.0664 | |
| 0.4492 | 0.3457 | 0.3398 | 0.3457 | |
| * | 0.0501 | 0.1543 | 0.1601 | 0.1543 |
| H | −0.5524 | −0.2653 | −0.2491 | −0.2653 |
| −0.1830 | −0.5880 | −0.6162 | −0.6041 | |
| −0.7353 | −0.8533 | −0.8653 | −0.8695 |
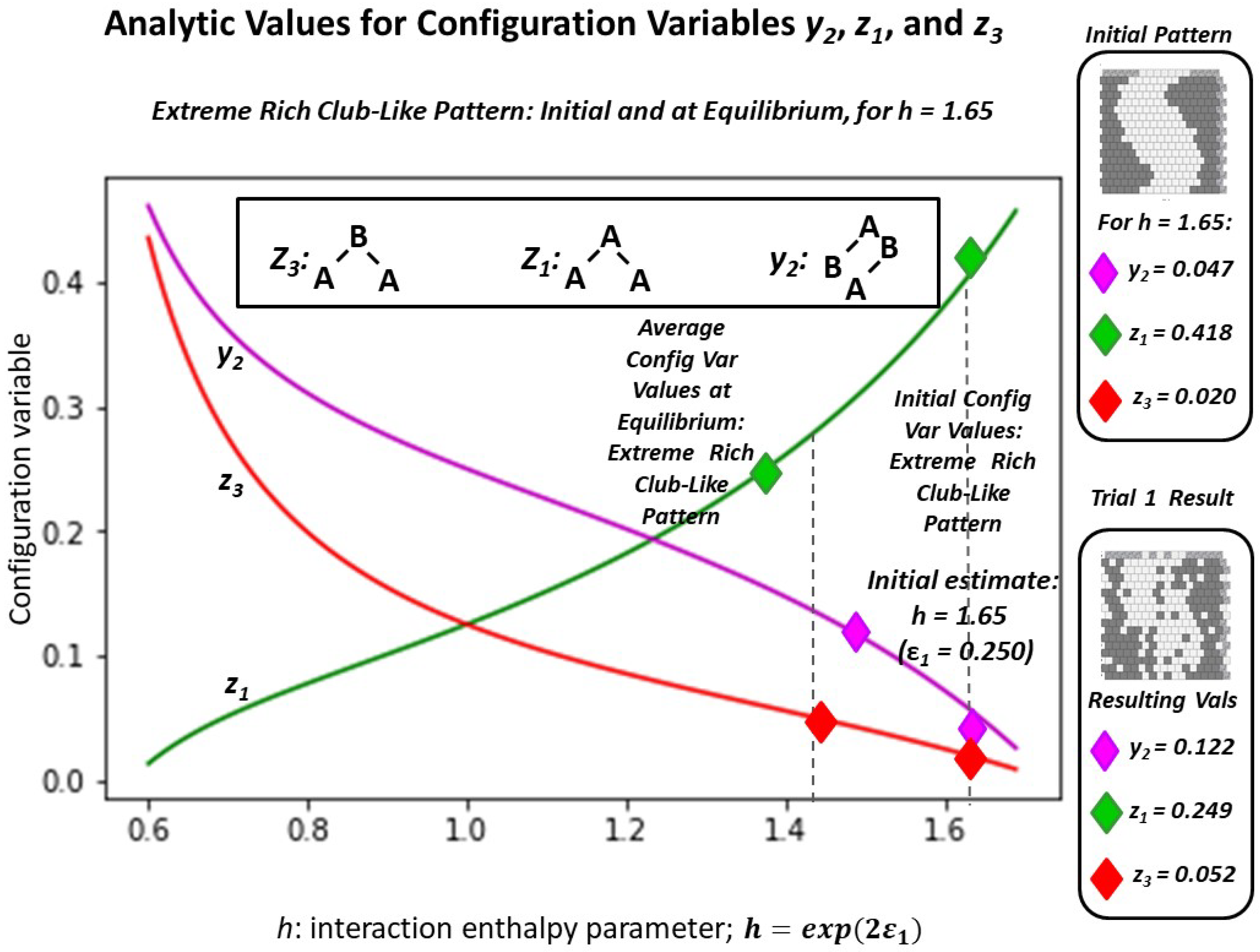
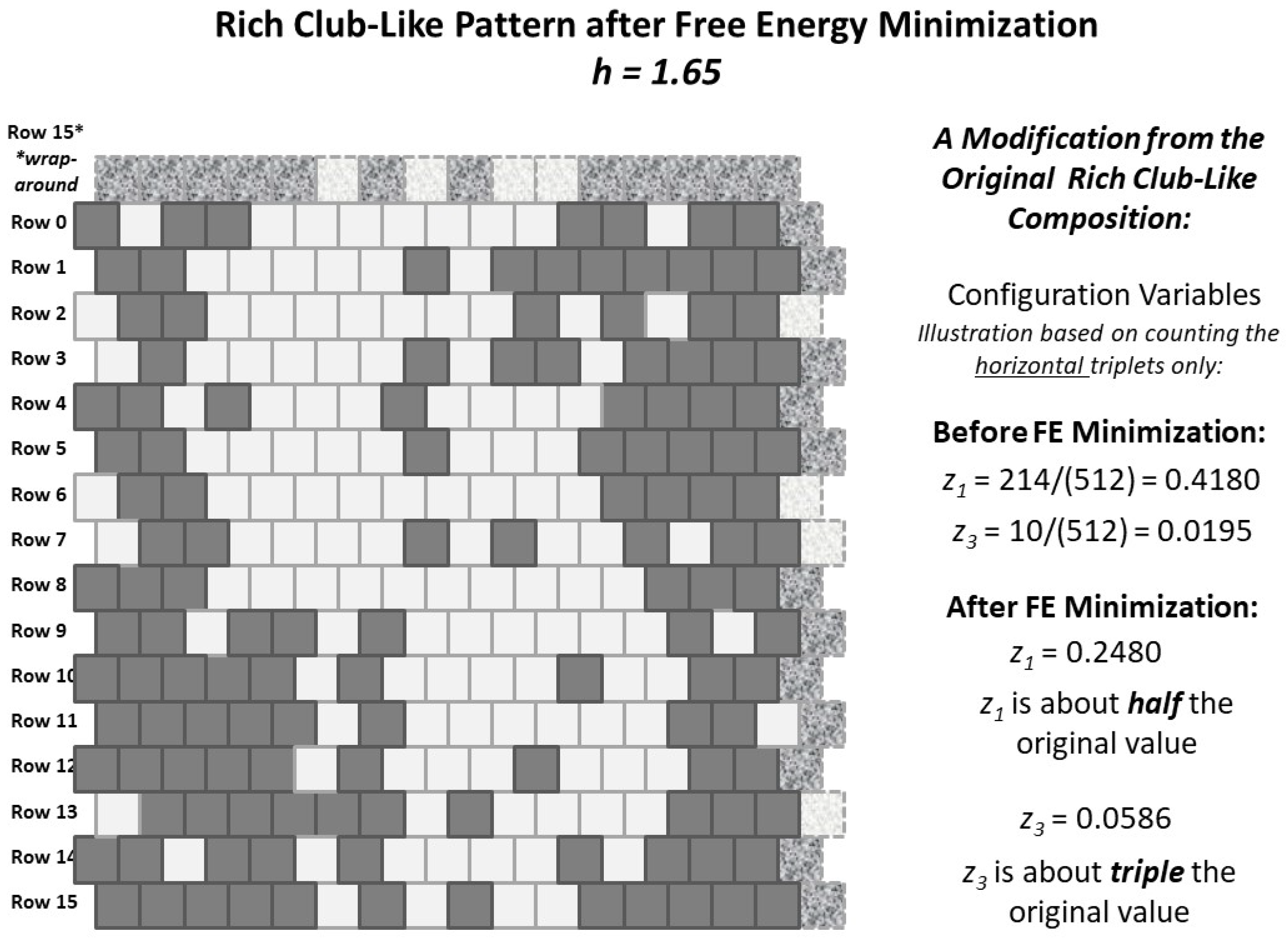
Appendix A.5.2. Experimental Trial: Very Large h-Value (h = 1.65)
| Variable | Initial | Trial 1.a | Trial 1.b | Trial 1.c | Average | Analytic * |
|---|---|---|---|---|---|---|
| 0.4180 | 0.2480 | 0.2500 | 0.2500 | 0.2493 | 0.4209 | |
| 0.0195 | 0.0703 | 0.0664 | 0.0664 | 0.0521 | 0.0664 | |
| * | 0.0508 | 0.1543 | 0.1602 | 0.1543 | 0.1218 | 0.0477 |
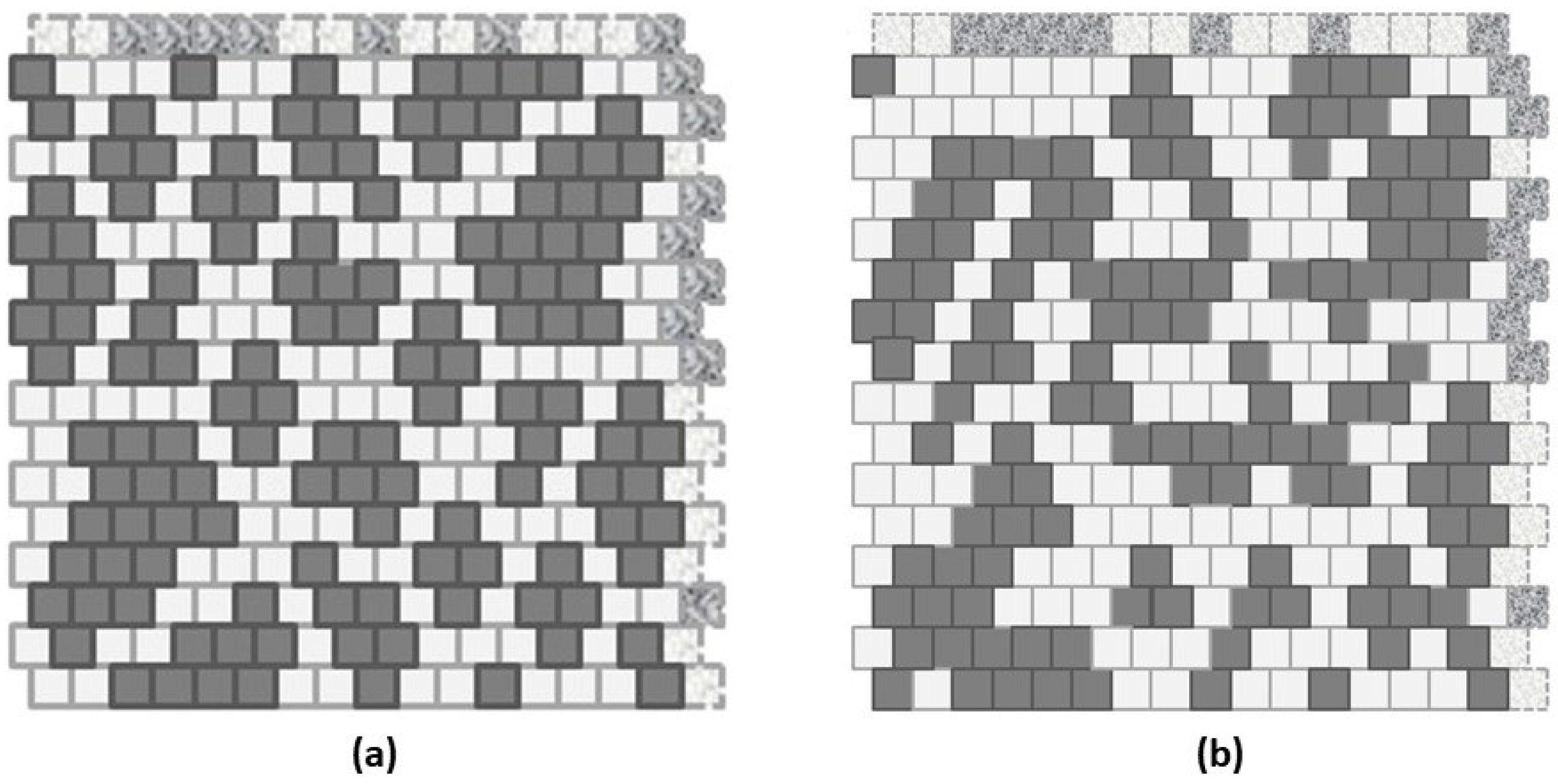
Appendix A.6. Methods for Designing the “Scale-Free-Like” Grid

Appendix A.7. Details on Experiments Using the “Scale-Free-Like” Grid
Appendix A.8. Methods for the Case Where the Interaction Enthalpy Is Not Zero
- 2D-CVM-def-pttrns-anlytc-FE-vary-e0-and-e1-2018-12-12.py (Note: the actual program files have underscores in place of some of the hyphens used in the filename just given; the filenames MAY be updated when the code is released,) This is the first in a series of primary experimental codes for free energy minimization given a starting user-defined 2-D grid, together with user-specified values for and (the h-value). Different programs perform slightly different tasks, with the same overall structure.
- 2D-CVM-def-pttrns-anlytc-FE-vary-e0-and-e1-v1pt1-2018-12-29.py-Together with a similar program, 2D-CVM-def-pttrns-anlytc-FE-vary-e0-and-e1-v1pt3-2018-12-29.py, are variants of the prior program, providing free energy minimization given a starting user-defined 2-D grid, together with user-specified values for and (the h-value).
| Variable | Initial | h = 1.16 Actual | h = 1.16 Analyt. | h = 1.65 Actual | h = 1.65 Analyt. |
|---|---|---|---|---|---|
| 0.1719 | 0.1367 | 0.1830 | 0.1641 | 0.4209 | |
| 0.0469 | 0.1016 | 0.0750 | 0.0859 | 0.0664 | |
| * | 0.2246 | 0.2304 | 0.1866 | 0.2148 | 0.0477 |
Appendix A.9. Methods for the Case where the Interaction Enthalpy Is Zero
- x1-vs-Epsilon0-2018-11-11.xlsx-This simply provides a graphic for the relationship between the fraction of active nodes versus the node activation enthalpy .
References
- Kikuchi, R. A theory of cooperative phenomena. Phys. Rev. 1951, 81, 988. [Google Scholar] [CrossRef]
- Kikuchi, R.; Brush, S. Improvement of the cluster variation method. J. Chem. Phys. 1967, 47, 195. [Google Scholar] [CrossRef]
- Maren, A. The cluster variation method: A primer for neuroscientists. Brain Sci. 2016, 6, 44. [Google Scholar] [CrossRef] [PubMed]
- Maren, A. 2-D cluster variation method free energy: Fundamentals and pragmatics. arXiv 2019, arXiv:1909.09366v1. [Google Scholar]
- Yedidia, J.S.; Freeman, W.T.; Weiss, Y. Generalized Belief Propagation. In Advances in Neural Information Processing Systems; Leen, T.K., Dietterich, T.G., Tresp, V., Eds.; MIT Press: Cambridge, MA, USA, 2001; pp. 689–695. [Google Scholar]
- Yedidia, J.S.; Freeman, W.T.; Weiss, Y. Understanding Belief Propagation and its Generalizations; Technical Report MERL TR-2001-22; Mitsubishi Electric Research Laboratories: Cambridge, MA, USA, 2002; Available online: www.merl.com (accessed on 30 December 2020).
- Yedidia, J.S.; Freeman, W.T.; Weiss, Y. Bethe Free Energy, Kikuchi Approximations, and Belief Propagation Algorithms; Technical Report MERL TR2001-16; Mitsubishi Electric Research Laboratories: Cambridge, MA, USA, 2001; Available online: www.merl.com (accessed on 30 December 2020).
- Yedidia, J.S. An Idiosyncratic Journey Beyond Mean Field Theory. In Advanced Mean Field Methods-Theory and Practice; Saad, D., Opper, M., Eds.; Initially Published as MERL TR-2000-27 June 2000; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Pelizzola, A. Cluster variation method in statistical physics and probabilistic graphical models. J. Phys. A Math. Gen. 2005, 38, R309. [Google Scholar] [CrossRef]
- Wainwright, M.J.; Jordan, M.I. Graphical models, exponential families, and variational inference. Found. Trends Mach. Learn. 2008, 1, 1–305. [Google Scholar] [CrossRef]
- Mohri, T. Cluster variation method. JOM J. Miner. Met. Mater. Soc. 2013, 65, 1510–1522. [Google Scholar] [CrossRef]
- Albers, C.A.; Leisink, M.A.R.; Kappen, H.J. The cluster variation method for efficient linkage analysis on extended pedigrees. NIPS Workshop on New Problems and Methods in Computational Biology. BMC Bioinform. 2006, 7 (Suppl. S1). [Google Scholar] [CrossRef]
- Barton, J.; Cocco, S. Ising models for neural activity inferred via selective cluster expansion: Structural and coding properties. J. Stat. Mech. 2013, 3. [Google Scholar] [CrossRef]
- Balcerzak, T.; Szałowski, K. The pair approximation method for the ferromagnetic Heisenberg model with spin S=1 and arbitrary range of interactions. Application for the magnetic semiconductor CrIAs. J. Magn. Magn. Mater. 2020, 513, 167157. [Google Scholar] [CrossRef]
- Domínguez, E.; Lage-Castellanos, A.; Mulet, R. Random field Ising model in two dimensions: Bethe approximation, cluster variational method and message passing algorithms. J. Stat. Mech. Theory Exp. 2015, 2015, P07003. [Google Scholar] [CrossRef][Green Version]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Sporns, O.; Kötter, R. Motifs in brain networks. PLoS Biol. 2004, 2, e369. [Google Scholar] [CrossRef] [PubMed]
- Sporns, O.; Tononi, G.; Kötter, R. The human connectome: A structural description of the human brain. PLoS Comput. Biol. 2005, 1. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Yin, J. Ht-index for quantifying the fractal or scaling structure of geographic features. Ann. Assoc. Am. Geogr. 2014, 104, 530–540. [Google Scholar] [CrossRef]
- Maren, A. The Cluster Variation Method II: 2-D Grid of Zigzag Chains: Basic Theory, Analytic Solution and Free Energy Variable Distributions at Midpoint (x1 = x2 = 0.5); Technical Report THM TR2014-003 (ajm); Themasis: Kealakekua, HI, USA, 2014. [Google Scholar] [CrossRef]
- Pearl, J. Fusion, Propagation, and Structuring in Belief Networks; Technical Report 850022 (R-42); UCLA Computer Science Dept.: Los Angeles, CA, USA, 1986. [Google Scholar]
- Mendoza Coto, A.; Stariolo, D.; Nicolao, L. Nature of long-range order in stripe-forming systems with long-range repulsive interactions. Phys. Rev. Lett. 2015, 114, 116101. [Google Scholar] [CrossRef] [PubMed]
- Raymond, J.; Ricci-Tersenghi, F. Correcting beliefs in the mean-field and Bethe approximations using linear response. arXiv 2013, arXiv:1302.1911v1. [Google Scholar]
- Parr, T.; Markovic, D.; Kiebel, S.J.; Friston, K.J. Neuronal message passing using mean-field, Bethe, and marginal approximations. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef]
- Peraza-Goicolea, J.A.; Martínez-Montes, E.; Aubert, E.; Valdés-Hernández, P.A.; Mulet, R. Modeling functional resting-state brain networks through neural message passing on the human connectome. Neural Netw. 2020, 123, 52–69. [Google Scholar] [CrossRef]
- Friston, K.J.; Parr, T.; de Vries, B. The graphical brain: Belief propagation and active inference. Netw. Neurosci. 2017, 1, 381–414. [Google Scholar] [CrossRef]
- Kozma, R.; Puljic, M.; Balister, P.; Bollobás, B.; Freeman, W.J. Neuropercolation: A random cellular automata approach to spatio-temporal neurodynamics. Lect. Notes Comput. Sci. 2004, 3305, 435–443. [Google Scholar] [CrossRef]
- Freeman, W.J.; Holmes, M.D.; West, G.A.; Vanhatalo, S. Dynamics of human neocortex that optimizes its stability and flexiblity. Int. J. Intell. Syst. 2006, 21, 881–901. [Google Scholar] [CrossRef]
- Kozma, R.; Puljic, M.; Freeman, W.J. Thermodynamic model of criticality in the cortex based on EEG/ECoG data. In Criticality in Neural Systems; Plenz, D., Ed.; John Wiley: Hoboken, NJ, USA, 2012; Chapter 1; pp. 1–28. [Google Scholar]
- Kozma, R.; Puljic, M. Random graph theory and neuropercolation for modeling brain oscillations at criticality. Curr. Opin. Neurobiol. 2015, 31, 181–188. [Google Scholar] [CrossRef]
- Tognoli, E.; Kelso, J.A.S. The metastable brain. Neuron 2014, 81, 35–48. [Google Scholar] [CrossRef]
- Wilting, J.; Priesemann, V. 25 years of criticality in neuroscience-established results, open controversies, novel concepts. Curr. Opin. Neurobiol. 2019, 58, 105–111. [Google Scholar] [CrossRef]
- Ezaki, T.; dos Reis, E.F.; Watanabe, T.; Sakaki, M.; Masuda, N. Closer to critical resting-state neural dynamics in individuals with higher fluid intelligence. Commun. Biol. 2020, 3, 3067. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. Life as we know it. J. R. Soc. Interface 2013, 10, 0475. [Google Scholar] [CrossRef]
- Friston, K.; Levin, M.; Sengupta, B.; Pezzulo, G. Knowing one’s place: A free-energy approach to pattern regulation. J. R. Soc. Interface 2015, 12, 1383. [Google Scholar] [CrossRef]
- Sajid, N.; Ball, P.J.; Friston, K.J. Active inference: Demystified and compared. arXiv 2020, arXiv:1909.10863v2. [Google Scholar]
- Friston, K.; Breakspear, M.; Deco, G. Perception and self-organized instability. Front. Comput. Neurosci. 2012, 6, 1–19. [Google Scholar] [CrossRef]
- Demekas, D.; Parr, T.; Friston, K.J. An investigation of the free energy principle for emotion recognition. Front. Comput. Neurosci. 2020, 14. [Google Scholar] [CrossRef]
- Biehl, M.; Pollock, F.A.; Kanai, R. A technical critique of the free energy principle as presented in “Life as we know it” and related works. arXiv 2020, arXiv:2001.06408. [Google Scholar]
- Friston, K.J.; Kahan, J.; Razi, A.; Stephan, K.E.; Sporns, O. On nodes and modes in resting state fMRI. NeuroImage 2014, 99, 533–547. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J.; Faberholm, E.D.; Zarghami, T.S.; Parr, T.; Hipólito, I.; Magrou, L.; Razi, A. Parcels and particles: Markov blankets in the brain. arXiv 2020, arXiv:2007.09704v1. [Google Scholar]
- Maren, A. Derivation of the variational Bayes equations. arXiv 2019, arXiv:1906.08804v4. [Google Scholar]
- Kim, D.J.; Min, B.K. Rich-club in the brain’s macrostructure: Insights from graph theoretical analysis. Comput. Struct. Biotechnol. J. 2020, 18, 1761–1773. [Google Scholar] [CrossRef] [PubMed]
- Csigi, M.; Kõrōsi, A.; Bíró, J.; Heszberger, Z.; Malkov, Y.; Gulyás, A. Geometric explanation of the rich-club phenomenon in complex networks. Sci. Rep. 2017, 7, 1730. [Google Scholar] [CrossRef] [PubMed]
- Muldoon, S.F.; Bridgeford, E.W.; Bassett, D.S. Small-world propensity and weighted brain networks. Sci. Rep. 2016, 6, 22057. [Google Scholar] [CrossRef] [PubMed]
- Achard, S.; Salvador, R.; Whitcher, B.; Suckling, J.; Bullmore, E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 2006, 26, 63–72. [Google Scholar] [CrossRef] [PubMed]
- Iturria-Medina, Y.; Sotero, R.C.; Canales-Rodríguez, E.J.; Alemán-Gómez, Y.; Melie-García, L. Studying the human brain anatomical network via diffusion-weighted MRI and graph theory. NeuroImage 2008, 40, 1064–1076. [Google Scholar] [CrossRef] [PubMed]
- Liao, X.; Vasilakos, A.V.; Hea, Y. Small-world human brain networks: Perspectives and challenges. Neurosci. Biobehav. Rev. 2017, 77, 286–300. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Lu, T.; Xie, C.; Wang, Q.; Wang, Y.; Cao, X.; Su, Y.; Wang, Z.; Zhang, Z. Functional disorganization of small-world brain networks in patients with ischemic leukoaraiosis. Front. Aging Neurosci. 2008. [Google Scholar] [CrossRef]
- Friston, K. Functional and effective neuroimaging. Brain Connect. 2011, 1, 13–36. [Google Scholar] [CrossRef]
- Yao, Z.; Hu, B.; Xie, Y.; Moore, P.; Zheng, J. A review of structural and functional brain networks: Small world and atlas. Brain Inform. 2015, 2, 45–57. [Google Scholar] [CrossRef]
- Eguíluz, V.M.; Chialvo, D.R.; Cecchi, G.A.; Baliki, M.; Apkarian, A.V. Scale-free brain functional networks. Phys. Rev. Lett. 2005, 94, 018102. [Google Scholar] [CrossRef]
- Broido, A.D.; Clauset, A. Scale-free networks are rare. Nat. Commun. 2019, 10, 1017. [Google Scholar] [CrossRef]
- Zhou, B.; Meng, X.; Stanley, H.E. Power-law distribution of degree–degree distance: A better representation of the scale-free property of complex networks. Proc. Natl. Acad. Sci. USA 2020, 117, 14812–14818. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance, and Dimension; Freeman: San Francisco, CA, USA, 1977. [Google Scholar]
- Gao, P.; Cushman, S.A.; Liu, G.; Ye, S.; Shen, S.; Cheng, C. FracL: A tool for characterizing the fractality of landscape gradients from a new perspective. ISPRS Int. J. Geo-Inf. 2019, 8, 466. [Google Scholar] [CrossRef]
- Gao, P.; Liu, Z.; Liu, G.; Zhao, H.; Xie, X. Unified metrics for characterizing the fractal nature of geographic features. Ann. Am. Assoc. Geogr. 2017, 107, 1315–1331. [Google Scholar] [CrossRef]
- Gao, P.; Liu, Z.; Xie, M.H.; Tian, K.; Liu, G. CRG index: A more sensitive ht-index for enabling dynamic views of geographic features. Prof. Geogr. 2016, 68, 533–545. [Google Scholar] [CrossRef]
- Maren, A. Free energy minimization using the 2-D cluster variation method: Initial code verification and validation. arXiv 2019, arXiv:1801.08113v2. [Google Scholar]


| Variable | Meaning |
|---|---|
| Activation enthalpy | Enthalpy associated with a single unit (node) |
| ; can be set to 1 for our purposes | |
| Configuration variable(s) | Nearest neighbor, next-nearest neighbor, and triplet patterns |
| Degeneracy | Number of ways in which a configuration variable can appear |
| Enthalpy | Internal energy H results from both per unit and pairwise interactions |
| Entropy | Denoted S; the distribution over all possible states |
| Equilibrium point | By definition, the free energy minimum for a closed system |
| Equilibrium distribution | Configuration variable values when free energy is minimized for given h-value |
| Ergodic distribution | Achieved when a system is allowed to evolve over a long period of time |
| Free energy | F = H-TS; sometimes G (Gibbs free energy) is used instead of F |
| h-value | , where |
| Interaction enthalpy | Between two unlike units, ; influences configuration variables |
| Interaction enthalpy parameter | Another term for the h-value where |
| Boltzmann’s constant | |
| Temperature | Temperature T times Boltzmann’s constant is set equal to one |
| Variable | Scale Free Initial | Scale Free Cmpt-Equil | Rich Club Initial | Rich Club Cmpt-Equil | Analytic Equil * |
|---|---|---|---|---|---|
| 0.1719 | 0.1641 | 0.4180 | 0.2480 | 0.4209 | |
| 0.0469 | 0.0859 | 0.0195 | 0.0566 | 0.0664 | |
| * | 0.2246 | 0.2148 | 0.0508 | 0.1543 | 0.0477 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maren, A.J. The 2-D Cluster Variation Method: Topography Illustrations and Their Enthalpy Parameter Correlations. Entropy 2021, 23, 319. https://doi.org/10.3390/e23030319
Maren AJ. The 2-D Cluster Variation Method: Topography Illustrations and Their Enthalpy Parameter Correlations. Entropy. 2021; 23(3):319. https://doi.org/10.3390/e23030319
Chicago/Turabian StyleMaren, Alianna J. 2021. "The 2-D Cluster Variation Method: Topography Illustrations and Their Enthalpy Parameter Correlations" Entropy 23, no. 3: 319. https://doi.org/10.3390/e23030319
APA StyleMaren, A. J. (2021). The 2-D Cluster Variation Method: Topography Illustrations and Their Enthalpy Parameter Correlations. Entropy, 23(3), 319. https://doi.org/10.3390/e23030319






