A Technical Critique of Some Parts of the Free Energy Principle
Abstract
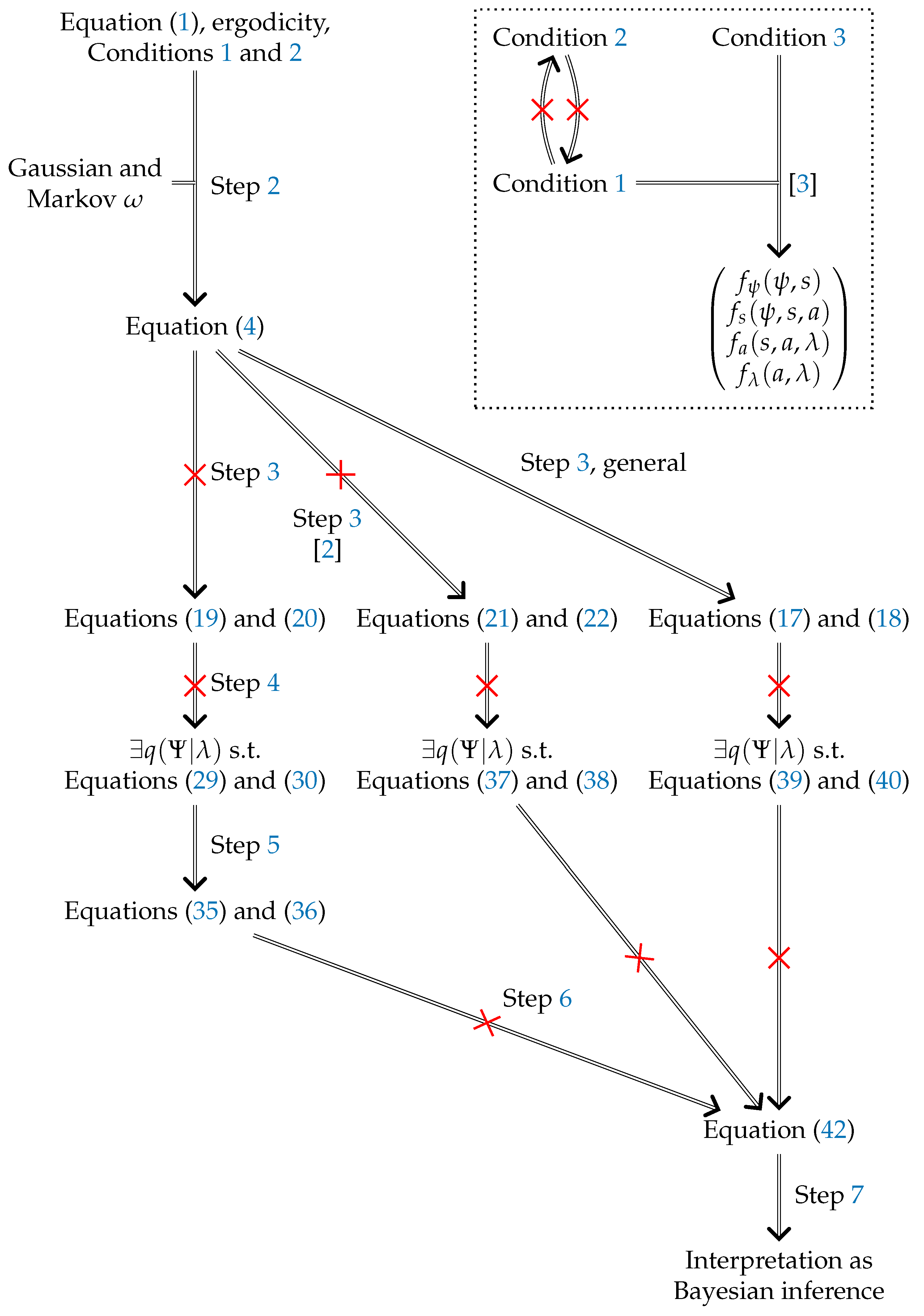
1. Overview
- Step 2
- Rewrite the vector field describing the dynamics of the system in terms of the gradient of the negative logarithm of the ergodic density of that system.
- Step 3
- Rewrite the components and of the vector field in terms of only partial gradients of the negative logarithm of .
- Step 4
- Assert (in the free energy lemma) the existence of a density over the external coordinates parameterized by the internal coordinates and that can again be rewritten, this time in terms of a free energy depending on (here, and whenever it would otherwise be ambiguous, we use a capitalized to indicate full distributions, rather than the probability density for a specific value of ).
- Step 5
- Claim that the equivalence of the equations of motion in Step 3 and Step 4 implies that certain partial gradients of the KL divergence between and the conditional ergodic density must vanish.
- Step 6
- Claim that it follows from Step 5 that and are “rendered” equal.
- Step 7
- Interpret:
- as a posterior over external coordinates given particular values of sensor, active, and internal coordinates,
- as encoding Bayesian beliefs about the external coordinates by the internal coordinates, and
- their equality as the internal coordinates appearing to “solve the problem of Bayesian inference”.
- The re-expression of Equation (1) in the form chosen in Step 2 is derived under restrictive assumptions, including that the system is subject to Gaussian and Markov noise.
- Conditions 1 and 2 are independent of each other.
- Conditions 1 and 3 together lead to a system where the interpretation of s and a as sensory and active coordinates is questionable.
- Under both Conditions 1 and 2, the expressions of and resulting from Step 3 are not as general as those contained in the result of Step 2. The more general alternative expression derived in [2] remains insufficiently general.
- Under both Conditions 1 and 2, the free energy lemma, when taken at face value, is wrong and cannot be salvaged by using alternatives in Step 3.
- Under both Conditions 1 and 2, contrary to Step 6, the vanishing of the gradient of the KL divergence does not imply the equality of and .
- As a consequence, the basic preconditions for the interpretations in Step 7 are not implied by either of the two proposed Markov blankets Conditions 1 and 2.
2. Expression via the Gradient of the Ergodic Density
3. Re-Expression Using Only Partial Gradients
4. Free Energy Lemma
- There is a such that the partial gradients and of the KL divergence between the variational density and the conditional ergodic density are elements of the nullspaces of and , respectively.
- There is a such that the gradients of the KL divergence to are equal to the nullvector:Then, they are always elements of the nullspaces of and , respectively.
- There is a such that (and hence, ), which implies that the KL divergence to vanishes for all and the two partial gradients are always nullvectors and therefore elements of the according nullspaces.
- (i)
- (ii)
- (iii)
5. Vanishing Gradients
6. Equality of and
In other words, the flow of internal and active states minimizes free energy, rendering the variational density equivalent to the posterior density over external states.”
- (i)
- (ii)
- (iii)
7. Interpretation
Because (by Gibbs inequality) this divergence [DKL] cannot be less than zero, the internal flow will appear to have minimized the divergence between the variational and posterior density. In other words, the internal states will appear to have solved the problem of Bayesian inference by encoding posterior beliefs about hidden (external) states, under a generative model provided by the Gibbs energy.
8. Consequences for Friston, K. et al. 2014
- The Markov blanket structure was not explicitly defined via Equation (2). Formally, it was introduced directly (see [4] Equation (10)) in a less general form corresponding to Equations (19) and (20) (at the same time, [1] is referenced in connection to the Markov blanket so there seems to be no intention to replace the original definition with the stronger one). Therefore, our observations concerning Steps 2 to 4 are not directly relevant to this paper.
- The internal coordinate was renamed to r, and the role of matrix R was played by the matrix .
- The proof of the free energy lemma given in [4] was different. It (implicitly) suggested setting the variational density equal to the ergodic conditional posterior.
- The proof of the free energy lemma no longer contained the proposition that the gradient of the KL divergence of the variational density and the ergodic conditional density vanish, i.e., Step 5.
- The proof also no longer contained the claim that the vanishing gradients of the KL divergence of the variational density and the ergodic conditional density imply the equality of those densities, i.e., Step 6 was not present.
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Counterexamples for Observation 1
Appendix B. Counterexample for Step 3
Appendix C. Counterexamples for Step 4
Appendix D. Counterexample for Step 6
Appendix E. Translating Systems into Generalized Coordinate Systems
References
- Friston, K. Life as we know it. J. R. Soc. Interface 2013, 10, 2013.0475. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. A free energy principle for a particular physics. arXiv 2019, arXiv:1906.10184. [Google Scholar]
- Parr, T.; Da Costa, L.; Friston, K. Markov blankets, information geometry and stochastic thermodynamics. Philos. Trans. R. Soc. A 2019, 378, 2019.0159. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Sengupta, B.; Auletta, G. Cognitive Dynamics: From Attractors to Active Inference. Proc. IEEE 2014, 102, 427–445. [Google Scholar] [CrossRef]
- Friston, K.; Rigoli, F.; Ognibene, D.; Mathys, C.; Fitzgerald, T.; Pezzulo, G. Active inference and epistemic value. Cogn. Neurosci. 2015, 6, 187–214. [Google Scholar] [CrossRef] [PubMed]
- Ao, P. Potential in stochastic differential equations: Novel construction. J. Phys. A 2004, 37, L25–L30. [Google Scholar] [CrossRef]
- Kwon, C.; Ao, P.; Thouless, D.J. Structure of stochastic dynamics near fixed points. Proc. Natl. Acad. Sci. USA 2005, 102, 13029–13033. [Google Scholar] [CrossRef] [PubMed]
- Kwon, C.; Ao, P. Nonequilibrium steady state of a stochastic system driven by a nonlinear drift force. Phys. Rev. E 2011, 84, 061106. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.A.; Chen, T.; Fox, E.B. A complete recipe for stochastic gradient MCMC. In Proceedings of the 28th International Conference on Neural Information Processing Systems—Volume 2; MIT Press: Montreal, QC, Canada, 2015; pp. 2917–2925. [Google Scholar]
- Yuan, R.; Tang, Y.; Ao, P. SDE decomposition and A-type stochastic interpretation in nonequilibrium processes. Front. Phys. 2017, 12, 120201. [Google Scholar] [CrossRef]
- Ao, P.; Chen, T.Q.; Shi, J.H. Dynamical Decomposition of Markov Processes without Detailed Balance. Chin. Phys. Lett. 2013, 30, 070201. [Google Scholar] [CrossRef]
- Yuan, R.S.; Ma, Y.A.; Yuan, B.; Ao, P. Lyapunov function as potential function: A dynamical equivalence. Chin. Phys. B 2014, 23, 010505. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning; Information Science and Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- van Kampen, N.G. Stochastic Processes in Physics and Chemistry; North-Holland: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Oberguggenberger, M. Generalized Functions and Stochastic Processes. In Seminar on Stochastic Analysis, Random Fields and Applications. Progress in Probability; Bolthausen, E., Dozzi, M., Russo, F., Eds.; Birkhäuser: Basel, Switzerland, 1995; Volume 36, pp. 215–230. [Google Scholar]
- Cornfeld, I.P.; Fomin, S.V.; Sinai, Y.G. Ergodic Theory; Springer: New York, NY, USA, 1982. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biehl, M.; Pollock, F.A.; Kanai, R. A Technical Critique of Some Parts of the Free Energy Principle. Entropy 2021, 23, 293. https://doi.org/10.3390/e23030293
Biehl M, Pollock FA, Kanai R. A Technical Critique of Some Parts of the Free Energy Principle. Entropy. 2021; 23(3):293. https://doi.org/10.3390/e23030293
Chicago/Turabian StyleBiehl, Martin, Felix A. Pollock, and Ryota Kanai. 2021. "A Technical Critique of Some Parts of the Free Energy Principle" Entropy 23, no. 3: 293. https://doi.org/10.3390/e23030293
APA StyleBiehl, M., Pollock, F. A., & Kanai, R. (2021). A Technical Critique of Some Parts of the Free Energy Principle. Entropy, 23(3), 293. https://doi.org/10.3390/e23030293






