Unidimensional Two-Way Continuous-Variable Quantum Key Distribution Using Coherent States
Abstract
1. Introduction
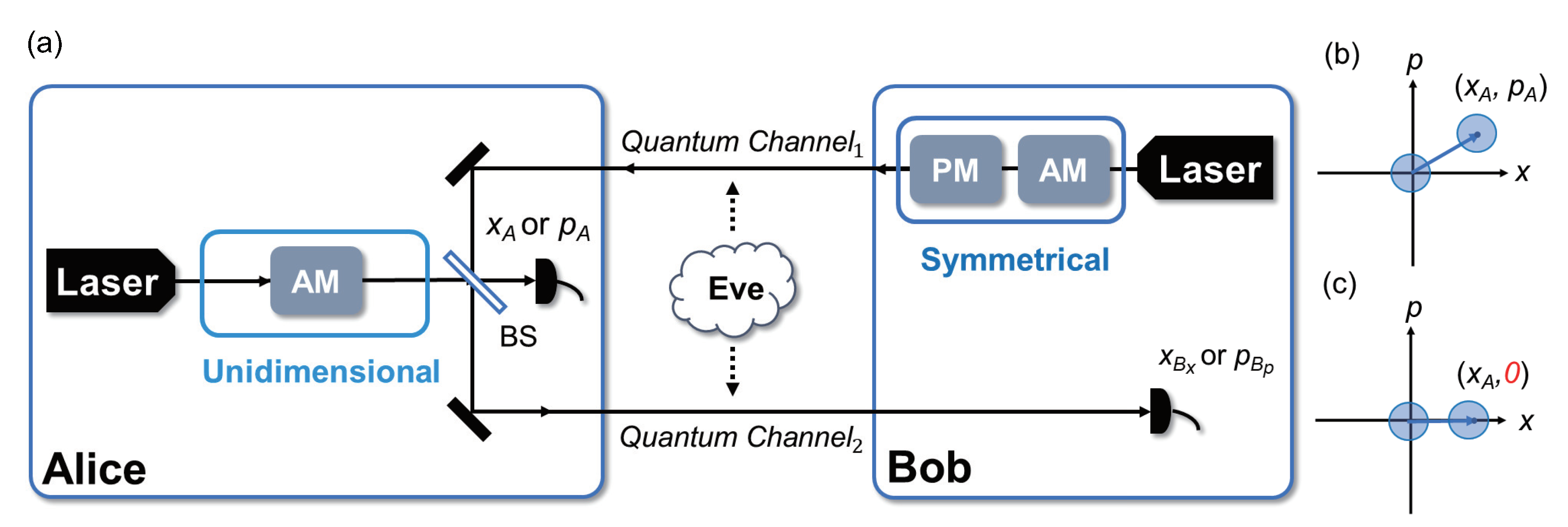
2. The Schemes of Unidimensional Two-Way CV-QKD Protocol
3. Security Analysis of the Protocol Against Two-Mode Attack
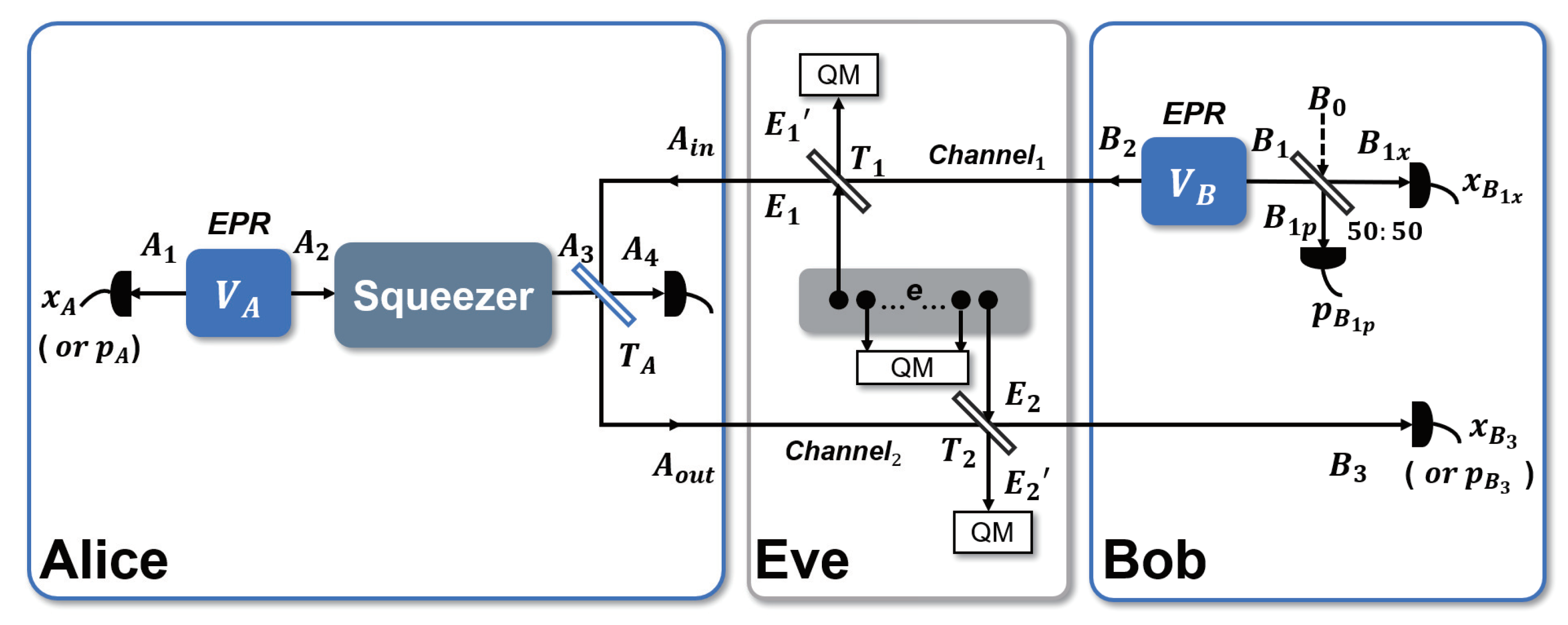
3.1. Two-Mode Attack Strategy
3.2. The Secret Key Rate of the Protocol
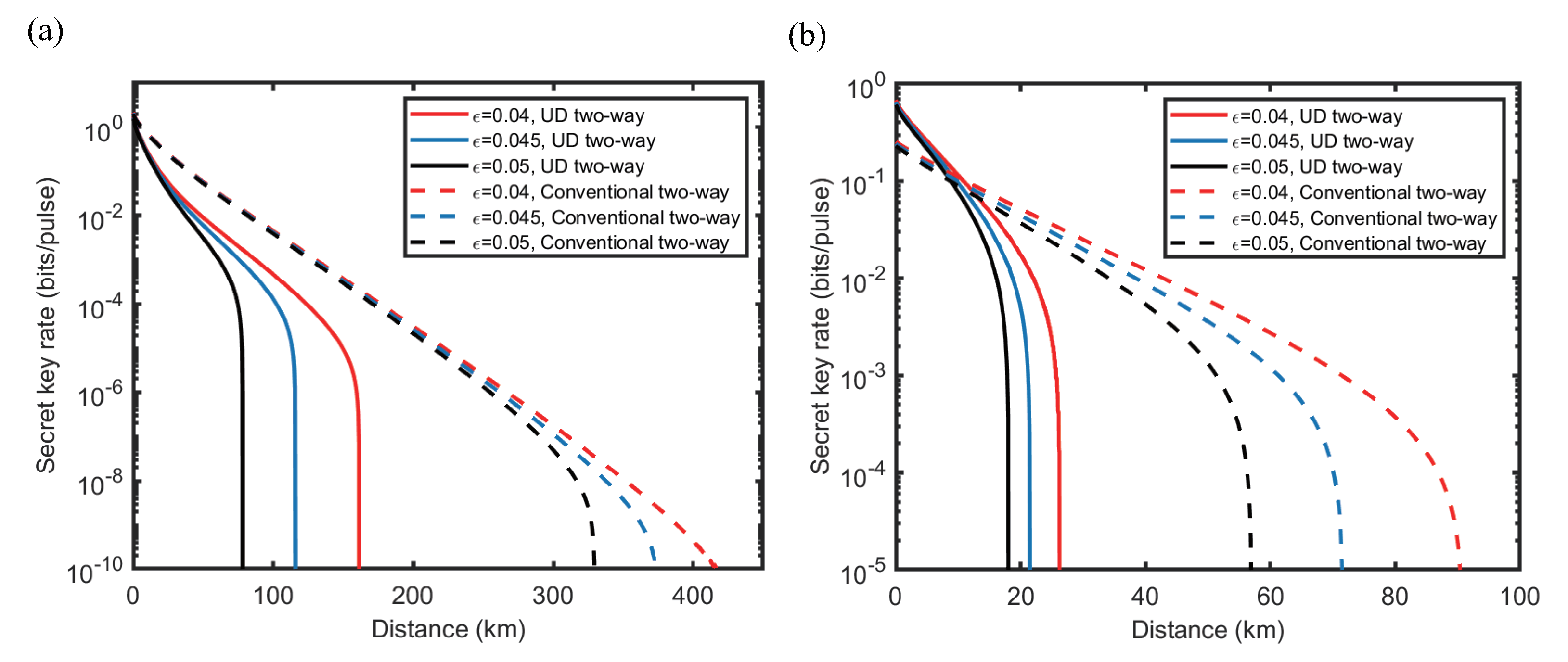
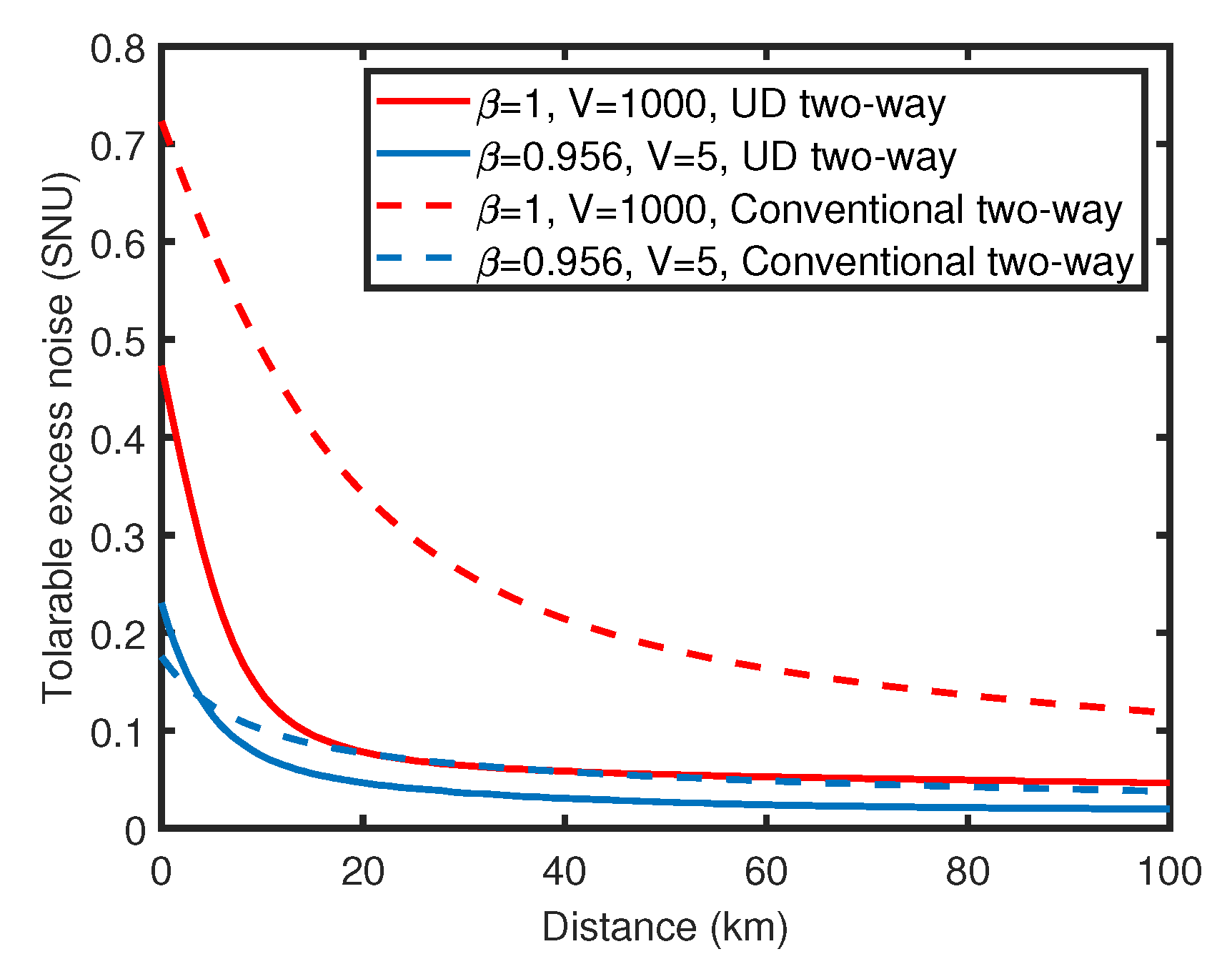
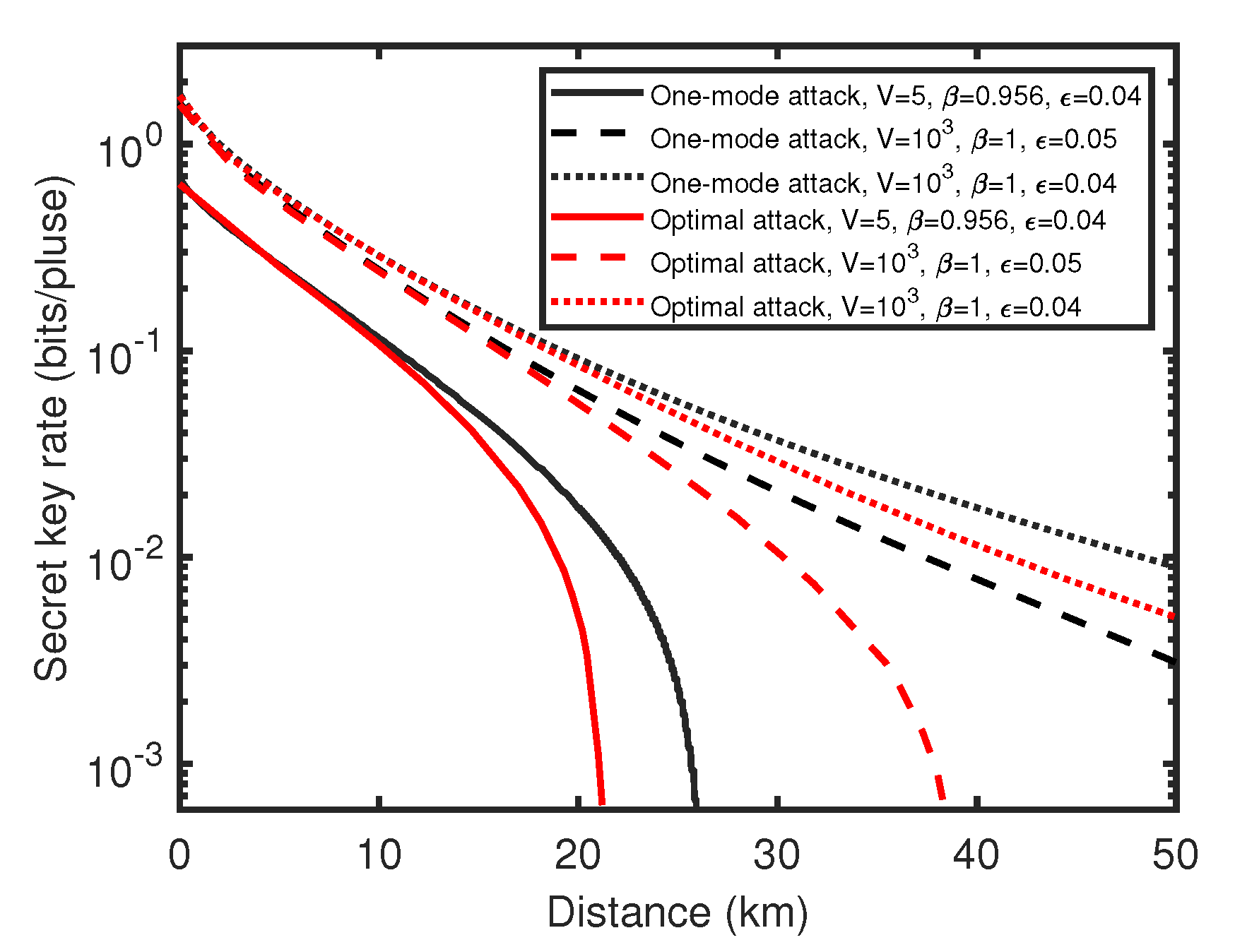
4. Simulation and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 9–12 December 1984; pp. 175–179. [Google Scholar]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photon. 2020, 12, 1012–1236. [Google Scholar] [CrossRef]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.-K.; Pan, J.-W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Diamanti, E.; Leverrier, A. Distributing secret keys with quantum continuous variables: Principle, Security and Implementations. Entropy 2015, 17, 6072–6092. [Google Scholar] [CrossRef]
- Guo, H.; Li, Z.; Yu, S.; Zhang, Y. Toward practical quantum key distribution using telecom components. Fundam. Res. 2021, 1, 96–98. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A.; Grangier, P.; Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photonics 2013, 7, 378. [Google Scholar] [CrossRef]
- Kumar, R.; Qin, H.; Alléaume, R. Coexistence of continuous variable QKD with intense DWDM classical channels. New J. Phys. 2015, 17, 043027. [Google Scholar] [CrossRef]
- Zhang, G.; Haw, J.Y.; Cai, H.; Xu, F.; Assad, S.; Fitzsimons, J.F.; Zhou, X.; Zhang, Y.; Yu, S.; Wu, J. An integrated silicon photonic chip platform for continuous-variable quantum key distribution. Nat. Photonics 2019, 13, 839. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Chen, Z.; Weedbrook, C.; Zhao, Y.; Wang, X.; Huang, Y.; Xu, C.; Zhang, X.; Wang, Z. Continuous-variable QKD over 50 km commercial fiber. Quantum Sci. Technol. 2019, 4, 035006. [Google Scholar] [CrossRef]
- Eriksson, T.A.; Hirano, T.; Puttnam, B.J.; Rademacher, G.; Luís, R.S.; Fujiwara, M.; Namiki, R.; Awaji, Y.; Takeoka, M.; Wada, N. Wavelength division multiplexing of continuous variable quantum key distribution and 18.3 Tbit/s data channels. Commun. Phys. 2019, 2, 9. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Pirandola, S.; Wang, X.; Zhou, C.; Chu, B.; Zhao, Y.; Xu, B.; Yu, S.; Guo, H. Long-distance continuous-variable quantum key distribution over 202.81 km of fiber. Phys. Rev. Lett. 2020, 125, 010502. [Google Scholar] [CrossRef]
- Navascués, M.; Grosshans, F.; Acín, A. Unconditional optimality of gaussian attacks against continuous-variable qantum key distribution. Phys. Rev. Lett. 2006, 97, 190503. [Google Scholar] [CrossRef]
- García-Patrón, R.; Cerf, N.J.; Acín, A. Optimality of gaussian attacks in continuous-variable quantum cryptography. Phys. Rev. Lett. 2006, 97, 190502. [Google Scholar] [CrossRef]
- Leverrier, A. Composable security proof for continuous-variable quantum key distribution with coherent states. Phys. Rev. Lett. 2015, 114, 070501. [Google Scholar] [CrossRef] [PubMed]
- Leverrier, A. Security of continuous-variable quantum key distribution via a Gaussian de Finetti reduction. Phys. Rev. Lett. 2017, 118, 200501. [Google Scholar] [CrossRef] [PubMed]
- Lupo, C.; Ottaviani, C.; Papanastasiou, P.; Pirandola, S. Parameter estimation with almost no public communication for continuous-variable quantum key distribution. Phys. Rev. Lett. 2018, 120, 220505. [Google Scholar] [CrossRef]
- Pirandola, S. Satellite quantum communications: Fundamental bounds and practical security. arXiv 2020, arXiv:2012.01725. [Google Scholar]
- Pirandola, S.; Mancini, S.; Lloyd, S.; Braunstein, S.L. Continuous-variable quantum cryptography using two-way quantum communication. Nat. Phys. 2008, 4, 726. [Google Scholar] [CrossRef]
- Sun, M.; Peng, X.; Shen, Y.; Guo, H. Security of a new two-way continuous-variable quantum key distribution. Int. J. Quantum Inf. 2012, 10, 1250059. [Google Scholar] [CrossRef]
- Sun, M.; Peng, X.; Guo, H. An improved two-way continuous-variable quantum key distribution protocol with added noise in homodyne detection. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 085501. [Google Scholar] [CrossRef]
- Zhang, Y.-C.; Li, Z.; Weedbrook, C.; Yu, S.; Gu, W.; Sun, M.; Peng, X.; Guo, H. Improvement of two-way continuous-variable quantum key distribution using optical amplifiers. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 035501. [Google Scholar] [CrossRef]
- Weedbrook, C.; Ottaviani, C.; Pirandola, S. Two-way quantum cryptography at different wavelengths. Phys. Rev. A 2014, 89, 012309. [Google Scholar] [CrossRef]
- Wang, T.; Yu, S.; Zhang, Y.-C.; Gu, W.; Guo, H. Security of two-way continuous-variable quantum key distribution with source noise. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 215504. [Google Scholar] [CrossRef]
- Ottaviani, C.; Mancini, S.; Pirandola, S. Two-way Gaussian quantum cryptography against coherent attacks in direct reconciliation. Phys. Rev. A 2015, 92, 062323. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Zhao, Y.; Yu, S.; Guo, H. Numerical simulation of the optimal two-mode attacks for two-way continuous-variable quantum cryptography in reverse reconciliation. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 035501. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y.; Li, Z.; Yu, S.; Guo, H. Improvement of two-way continuous-variable quantum key distribution with virtual photon subtraction. Quantum Inf. Process. 2017, 16, 184. [Google Scholar] [CrossRef]
- Usenko, V.; Grosshans, F. Unidimensional continuous-variable quantum key distribution. Phys. Rev. A 2015, 92, 062337. [Google Scholar] [CrossRef]
- Usenko, V. Unidimensional continuous-variable quantum key distribution using squeezed states. Phys. Rev. A 2018, 98, 032321. [Google Scholar] [CrossRef]
- Wang, X.; Cao, Y.; Wang, P.; Li, Y. Advantages of the coherent state compared with squeezed state in unidimensional continuous variable quantum key distribution. Quantum Inf. Process 2018, 17, 344. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, Y.; Chen, Z.; Yu, S. Unidimensional continuous-variable quantum key distribution with untrusted detection under realistic conditions. Entropy 2019, 21, 1100. [Google Scholar] [CrossRef]
- Bai, D.; Huang, P.; Zhu, Y.; Ma, H.; Xiao, T.; Wang, T.; Zeng, G. Unidimensional continuous-variable measurement-device-independent quantum key distribution. Quantum Inf. Process 2020, 19, 53. [Google Scholar] [CrossRef]
- Wang, P.; Wang, X.; Li, J.; Li, Y. Finite-size analysis of unidimensional continuous-variable quantum key distribution under realistic conditions. Optics Express 2017, 25, 27995–28009. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, Y.; Huang, Y.; Jiang, T.; Yu, S. Improvement of unidimensional continuous-variable quantum key distribution systems by using a phase-sensitive amplifier. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 225502. [Google Scholar] [CrossRef]
- Wang, P.; Wang, X.; Li, Y. Security analysis of unidimensional continuous-variable quantum key distribution using uncertainty relations. Entropy 2018, 20, 157. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Liu, W.; Wang, P.; Li, Y. Experimental study on all-fiber-based unidimensional continuous-variable quantum key distribution. Phys. Rev. A 2017, 95, 062330. [Google Scholar] [CrossRef]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.L.; Lloyd, S.; Gehring, T.; Jacobsen, C.S.; Andersen, U.L. High-rate measurement-device-independent quantum cryptography. Nat. Photonics 2015, 9, 397–402. [Google Scholar] [CrossRef]
- Pirandola, S.; Serafini, A.; Lloyd, S. Correlation matrices of two-mode bosonic systems. Phys. Rev. A 2009, 79, 052327. [Google Scholar] [CrossRef]
- Devetak, I.; Winter, A. Distillation of secret key and entanglement from quantum states. Proc. Roy. Soc. A 2005, 461, 207–235. [Google Scholar] [CrossRef]
- Holevo, A.S. Bounds for the quantity of information transmitted by a quantum communication channel. Probl. Inf. Transm. 1973, 9, 177. [Google Scholar]
- Milicevic, M.; Feng, C.; Zhang, L.M.; Gulak, P.G. Quasi-cyclic multi-edge LDPC codes for long-distance quantum cryptography. NPJ Quantum Inf. 2018, 4, 21. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, X.; Zhang, Y.; Zhang, Z.; Yu, S.; Guo, H. Continuous-variable quantum key distribution with rateless reconciliation protocol. Phys. Rev. Appl. 2019, 12, 054013. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, Y.; Huang, L.; Zhang, Y. Unidimensional Two-Way Continuous-Variable Quantum Key Distribution Using Coherent States. Entropy 2021, 23, 294. https://doi.org/10.3390/e23030294
Bian Y, Huang L, Zhang Y. Unidimensional Two-Way Continuous-Variable Quantum Key Distribution Using Coherent States. Entropy. 2021; 23(3):294. https://doi.org/10.3390/e23030294
Chicago/Turabian StyleBian, Yiming, Luyu Huang, and Yichen Zhang. 2021. "Unidimensional Two-Way Continuous-Variable Quantum Key Distribution Using Coherent States" Entropy 23, no. 3: 294. https://doi.org/10.3390/e23030294
APA StyleBian, Y., Huang, L., & Zhang, Y. (2021). Unidimensional Two-Way Continuous-Variable Quantum Key Distribution Using Coherent States. Entropy, 23(3), 294. https://doi.org/10.3390/e23030294





