Robust Multi-Objective Optimization for Response Surface Models Applied to Direct Low-Value Natural Gas Conversion Processes

Abstract

The high proportion of CO₂/CH₄ in low aggregated value natural gas compositions can be used strategically and intelligently to produce more hydrocarbons through oxidative methane coupling (OCM). The main goal of this study was to optimize direct low-value natural gas conversion via CO₂-OCM on metal oxide catalysts using robust multi-objective optimization based on an entropic measure to choose the most preferred Pareto optimal point as the problem’s final solution. The responses of CH₄ conversion, C₂ selectivity, and C₂ yield are modeled using the response surface methodology. In this methodology, decision variables, e.g., the CO₂/CH₄ ratio, reactor temperature, wt.% CaO and wt.% MnO in ceria catalyst, are all employed. The Pareto optimal solution was obtained via the following combination of process parameters: CO₂/CH₄ ratio = 2.50, reactor temperature = 1179.5 K, wt.% CaO in ceria catalyst = 17.2%, wt.% MnO in ceria catalyst = 6.0%. By using the optimal weighting strategy w₁ = 0.2602, w₂ = 0.3203, w₃ = 0.4295, the simultaneous optimal values for the objective functions were: CH₄ conversion = 8.806%, C₂ selectivity = 51.468%, C₂ yield = 3.275%. Finally, an entropic measure used as a decision-making criterion was found to be useful in mapping the regions of minimal variation among the Pareto optimal responses and the results obtained, and this demonstrates that the optimization weights exert influence on the forecast variation of the obtained response.

1. Introduction

A mixture of various hydrocarbons such as methane (CH₄), ethane (C₂H₆), propane (C₃H₈), butane (C₄H₁₀) and inert diluents such as molecular nitrogen (N₂) and carbon dioxide (CO₂) are found in natural gas compositions. Natural gas composition variations are affected by several parameters such as the geographical source, the time of year, and the treatment applied during production or transportation [1,2,3].

CH₄ and CO₂ are believed to contribute to the greenhouse effect [4]. Although the amount of CH₄ in the atmosphere is less than CO₂, its global warming potential is approximately 25 times greater [5]. Large amounts of methane are widely available in nature in the form of natural gas, although methane is a greatly underutilized resource for chemical and liquid fuels [6].

Large amounts of natural gas reserves are located in remote areas [7,8] and pipelines may not be available to transport that remote gas to regions where it can be used, and liquefication for transportation via ship is quite expensive. Almost 11% of this gas is reinjected, while another 4% is flared or vented [5,9,10], generating waste [10].

The conversion of CH₄ and CO₂ into value-added chemicals has attracted attention from the academic community and industries [4,11,12,13]. The abundance of these two gases makes them stand out as raw materials for fuels and chemical synthesis. Furthermore, CH₄ is considered to be the cheapest carbon source for the petrochemical industry [14].

Among these reserves, there are large amounts of low-value natural gas containing a high concentration of CO₂. Currently this natural gas is sold as liquefied natural gas after a carbon dioxide clean up using CO₂ separation facilities. The impurities from both the separation stages are then injected underground to dispose of the waste using a sub-surface aquifer, but at an estimated 49% of the total cost of the project [15]. The high CO₂/CH₄ ratio in low-value natural gas compositions could be strategically utilized to produce value-added chemicals, such as higher hydrocarbons and liquid fuels without having to separate the CO₂ first [16]. The synthesis of liquid fuels and commodity chemicals from CO₂ is a promising approach for clean energy production. For this reason, much academic and industrial effort has been devoted to exploring efficient means of reducing CO₂ [17].

Several studies have been undertaken with the objective of making conversion of methane viable, either by direct or indirect routes. The indirect routes focus on steam reform to produce synthesis gas (CO + H₂), which can be converted into the liquid fuels [18]. The direct route, on the other hand, converts methane into higher hydrocarbons in one step through oxidative methane coupling reactions (OCM). Therefore, it is considered more economically viable and, consequently, it has been the subject of several studies [4,12,14,16,19,20,21,22,23,24,25,26,27,28,29,30,31]. The general reactions for the formation of C₂ hydrocarbons from methane and carbon dioxide are expressed by [24]:

$$2\mathrm{C}{\mathrm{H}}_4+\mathrm{C}{\mathrm{O}}_2\rightleftharpoons {\mathrm{C}}_2{\mathrm{H}}_6+\mathrm{C}\mathrm{O}+{\mathrm{H}}_2\mathrm{O}$$

(1)

$$2\mathrm{C}{\mathrm{H}}_4+2\mathrm{C}{\mathrm{O}}_2\rightleftharpoons {\mathrm{C}}_2{\mathrm{H}}_4+2\mathrm{C}\mathrm{O}+2{\mathrm{H}}_2\mathrm{O}$$

(2)

Although the OCM reaction is a highly exothermic reaction, it requires high temperatures and a suitable catalyst because the binding energy of hydrogen-carbon in methane is very large [32] and the bond dissociation energy of CO-O is also high. Because of the low reactivity of CO₂, the product (C₂H₄, C₂H₆) of the OCM reaction, with CO₂ as an oxidant, is less likely to react with CO₂. Therefore, high C₂ (C₂H₄, C₂H₆) selectivity is expected in the CO₂-OCM [31].

Nevertheless, a possible increase in temperature will result in total oxidation instead of partial oxidation of C₂ hydrocarbons, such as ethylene [6]. We therefore see the importance of catalyst selection for the OCM reaction. The catalyst determines at what temperature and composition the maximum yield and selectivity for the reaction will be defined [30].

Considerable efforts have been placed on developing OCM catalysts in order to make the product yields commercially feasible [4,12,14,19,20,21,23,24,27,29,30,31].

Of the various catalysts for CO₂ activation, ceria (CeO₂) is attracting increased interest due to its high oxygen storage capacity [11]. Indeed, oxidation and reduction reactions of Ce⁴⁺ and Ce³⁺ are effective in activating carbon dioxide to form oxygen active species, while the C₂ selectivity is related to the basicity of a catalyst due to enhanced CO₂ chemisorption on the catalyst surface [11,27]. Wang et al. [25] and Wang et al. [26] proposed using a ceria catalyst modified with CaO. According to these authors the CaO/CeO₂ is the most effective catalyst for conversion at high temperatures of CH₄ to C₂H₆ and C₂H₄ by CO₂ among a series of CeO₂ catalysts modified with alkali and alkaline earth metal oxides. Istadi and Amin [28] and Istadi and Amin [16] proposed using CaO/CeO₂ and MnO/CeO₂ catalysts in the multi-objective optimization of CO₂-OCM process. According to these authors, the optimal operating parameters, such as the CO₂/CH₄ ratio and reactor temperature, and the catalyst compositions in the ceria catalyst, provide essential information for industrial CO₂-OCM processes.

At the same time, multi-objective optimization allows one to find the point that represents the final solution to the problem, in addition to treating the reliability of that solution as an important factor. It then follows that the variance of the prediction would be of great concern [33].

The aim of this study is to optimize the conversion of natural gas, rich in carbon dioxide, using robust multi-criteria decision-making processes, based on an entropic measure, to determine the ideal Pareto point as the final solution to the problem. The normal boundary intersection method (NBI) together with the mixture design of experiments (MDE), will be used to optimize these responses simultaneously.

2. Multi-Objective Optimization

Industrial processes, when translated into optimization problems, are usually treated as multi-objective problems, since they involve more than one desirable resource. When the objective functions are not in conflict, each objective function reaches its optimal value, and a solution is found, without the need for any special method [34]. These objectives are often conflicting [35]. A multi-objective optimization (MOP) problem can be formulated in order to study the tradeoffs between these conflicting objectives, as in:

$$\underset{x\in \mathsf{\Omega }}{Min}\mathsf{\Lambda }=\left\{F_1\left(x\right),F_2\left(x\right),\dots ,F_k\left(x\right)\right\}$$

(3)

where Λ is the vector of the objective functions that comprise the conflicting k criteria and F_i is the vector of the decision variables x belonging to the viable set Ω.

Their restrictions are represented in the form of inequalities or equalities, according to:

$$\mathsf{\Omega }=\{x\in {ℝ}^n|g_r(x)\le 0,r\in I,h_q(x)=0,q\in J\}$$

(4)

where g_r and h_q are the inequality and equality constraint functions, respectively and I and J are the index sets containing as many elements as there are inequality and equality constraints, respectively.

When looking for an MOP solution, the goal is to find efficient solutions. Some variations in the concept of efficiency are concepts of local efficiency, weak efficiency, and weakly local efficiency. Hence, a solution $x^{\ast }\in X$ is locally efficient if $\delta >0$ such that $x^{\ast }$ is efficient in $X\cap N(x^{\ast },\delta )$, where $N(x,\delta )=\left\{y\right|y\in {ℝ}^n,\Vert x-y\Vert <\delta \}$. A solution $x^{\ast }\in X$ is weakly efficient if there is no other point $x\in X$ such that $f(x)<f(x^{\ast })$. A solution $x^{\ast }\in X$ is locally weakly efficient if $\delta >0$ such that $x^{\ast }$ is weakly efficient in $X\cap N(x^{\ast },\delta )$.

However, for a given decision vector $x^{\ast }$ to be the solution to an optimization problem, it must satisfy some conditions, which we call optimality conditions. The simplest situation for which we can define the optimality conditions is that in which we have a single function for which we wish to find the optimal point, and there are no constraints. In the case of unconstrained optimization, the necessary first-order condition is:

If $x^{\ast }$ is to be a local minimizer of the function f(x), differentiable at $x^{\ast }$, then $\nabla f(x^{\ast })=0$.

At this point, Miettinen [34] is used, which shows that a function $f_i:{ℝ}^n\to ℝ$ is differentiable at $x^{\ast }$ if:

$$f_i(x^{\ast }+d)-f_i(x^{\ast })=\nabla f_i{(x^{\ast })}^{T}d+\Vert d\Vert \epsilon (x^{\ast },d)$$

(5)

where $\nabla f_i(x^{\ast })$ is the gradient of $f_i \text{at} x^{\ast }$ and $\epsilon (x^{\ast },d)\to 0$ as $\Vert d\Vert \to 0$.

Furthermore, $f_i$ is continuously differentiable at $x^{\ast }$ if all of its partial derivatives $\frac{\partial f_i(x^{\ast })}{\partial x_j}$$(j=1,\dots ,n)$, i.e., all the gradient components, are continuous at $x^{\ast }$. Still, with respect to the unconstrained optimization, the necessary second-order condition is:

If $x^{\ast }$ is to be a local minimizer of the function f(x), twice differentiable at $x^{\ast }$, then $\nabla f(x^{\ast })=0$ and ${\nabla }^{2}f(x^{\ast })$ must be positive semidefinite, i.e., it has eigenvalues (${\lambda }_i$) greater than or equal to zero.

According to Miettinen [34], a function $f_i:{ℝ}^n\to ℝ$ is twice differentiable at $x^{\ast }$ if:

$$f_i(x^{\ast }+d)-f_i(x^{\ast })=\nabla f_i{(x^{\ast })}^{T}d+\frac{1}{2}{d}^T{\nabla }^2{f}_i(x^{\ast })d+{\Vert d\Vert }^2\epsilon (x^{\ast },d)$$

(6)

where: $\nabla f_i(x^{\ast })$ is the gradient, the symmetric matrix, $n\times n$; ${\nabla }^2{f}_i(x^{\ast })$ is a Hessian matrix of $f_i \text{at} x^{\ast }$; and $\epsilon (x^{\ast },d)\to 0$ as $\Vert d\Vert \to 0$.

The Hessian matrix of a twice differentiable function consists of second-order partial derivatives $\frac{{\partial }^2{f}_i(x^{\ast })}{\partial x_j\partial x_l}(j,l=1,\dots ,n)$, and it can be presented as:

$${\nabla }^2{f}_i(x^{\ast })=\left(\begin{array}{ccc}\frac{{\partial }^2{f}_i(x^{\ast })}{\partial x_1^2}& \cdots & \frac{{\partial }^2{f}_i(x^{\ast })}{\partial x_1\partial x_n}\\ ⋮& \ddots & ⋮\\ \frac{{\partial }^2{f}_i(x^{\ast })}{\partial x_n\partial x_1}& \cdots & \frac{{\partial }^2{f}_i(x^{\ast })}{\partial x_n^2}\end{array}\right)$$

(7)

Furthermore, $f_i$ is twice continuously differentiable at $x^{\ast }$ if all of its second-order partial derivatives are continuous at $x^{\ast }$.

With respect to optimality conditions in unconstrained optimization, we see that only the presented conditions are necessary, since the first and second order terms can be null, still leaving doubt about the nature of $x^{\ast }$. Therefore, a sufficient condition for $x^{\ast }$ to be a strict local minimizer of the function f(x), twice differentiable at $x^{\ast }$, is $\nabla f(x^{\ast })=0$ and ${\nabla }^{2}f(x^{\ast })$ as a positive definite, i.e., it has eigenvalues (${\lambda }_i$) greater than zero.

To analyze the critical points the second order derivatives of the function must exist and be different from zero, which can be verified by performing a Taylor series expansion around the optimal point. Since the first derivative is null, we have:

$$f_i(x)-f_i(x^{\ast })=\frac{1}{2}{(x-x^{\ast })}^T{\nabla }^2{f}_i(x^{\ast })(x-x^{\ast })$$

(8)

The values of the function near the critical point depend on the Hessian. In summary, we have the following relation between the Hessian matrix eigenvalue signals and the critical point:

• if all eigenvalues are positive, we have a minimum point;
• if all eigenvalues are negative, we have a maximum point; and
• if the eigenvalues show different signs, we have a saddle point.

This analysis still allows us to deduce the convexity of the function. Similarly, when working with Response Surface Methodology (RSM), the determination of the convexity of a function is done by characterizing the nature of the stationary point. The stationary point is the level of x₁, x₂, …, x_k, that optimizes the predicted response. This point, if it exists, will be the set of x₁, x₂, …, x_k, for which the partial derivatives are equal to zero. A general mathematical solution for locating the stationary point may be obtained. The second-order model is expressed in the matrix notation as [36]:

$$\widehat{y}={\widehat{\beta }}_0+{\mathbf{x}}^T\mathbf{b}+{\mathbf{x}}^T\mathbf{B}\mathbf{x}$$

(9)

where:

$$\mathbf{x}=\left[\begin{array}{l}{x}_1\\ x_2\\ ⋮\\ x_k\end{array}\right],\mathbf{b}=\left[\begin{array}{l}{\widehat{\beta }}_1\\ {\widehat{\beta }}_2\\ ⋮\\ {\widehat{\beta }}_k\end{array}\right],\mathrm{and}\mathbf{B}=\left[\begin{array}{cccc}{\widehat{\beta }}_{11}& {\widehat{\beta }}_{12}/2& \cdots & {\widehat{\beta }}_{1k}/2\\ {\widehat{\beta }}_{21}/2& {\widehat{\beta }}_{22}& \cdots & {\widehat{\beta }}_{2k}/2\\ ⋮& ⋮& \ddots & ⋮\\ {\widehat{\beta }}_{k1}/2& {\widehat{\beta }}_{k2}/2& \cdots & {\widehat{\beta }}_{kk}\end{array}\right]\mathrm{for}{\widehat{\beta }}_{ij}={\widehat{\beta }}_{ji}$$

(10)

The derivative of $\widehat{y}$ with respect to the elements of the vector x equated to zero is:

$$\frac{\partial \widehat{y}}{\partial \mathbf{x}}=\mathbf{b}+2\mathbf{B}\mathbf{x}=\mathbf{0}$$

(11)

The stationary point described in Equation (12) is the solution of Equation (11):

$${\mathbf{x}}_{\mathrm{s}}=-\frac{1}{2}{\mathbf{B}}^{-1}\mathbf{b}$$

(12)

The predicted response at the stationary point is given by:

$${\widehat{y}}_s={\widehat{\beta }}_0+\frac{1}{2}{\mathbf{x}}_{\mathrm{s}}{}^T\mathbf{b}$$

(13)

In general terms, the nature of a stationary point can be determined from the sign of the eigenvalues or root characteristics of a given matrix B. The eigenvalues (${\lambda }_i$) of the matrix B are the solutions to the following equation:

$$\left|\mathbf{B}-\lambda \mathbf{I}\right|=0$$

(14)

Then, these are defined as follows:

• if the values of ${\lambda }_i$ are all negative, the function is concave and x_S is a maximum point;
• if the values of ${\lambda }_i$ are all positive, the function is convex, and x_S is a minimum point;
• if the values of ${\lambda }_i$ present different signs, the function is neither concave nor convex, and x_S is a saddle point.

In multi-objective optimization two approaches can be used to aid in solving problems: (i) converting all objective functions into a single problem; (ii) optimizing one objective, considering other objectives as constraints [37]. In this second approach, the objective function is prioritized and the relevance of the others is relegated to a lower extent.

According to Shahraki and Noorossana [37], the methods that result in obtaining a set of optimal Pareto solutions are recommended, since they provide the best solutions among all other given options in terms of efficiency. The weighted sum method (WSM) is widely used to obtain optimal Pareto solutions in MOP, as it is easy to implement and interpret. However, if the set of Pareto optimal solutions is nonconvex, the frontier becomes nonconvex and discontinuous, forming clusters of solutions in regions of great curvature, yet discontinuous in the solution space. In such situations, the WSM, which is the standard method for generating the Pareto set in MOP, barely finds solutions in the nonconvex section. Moreover, the WSM cannot generate an equally spaced frontier, even if the distribution of weights is uniform [38,39], which can confuse the decision maker by not clarifying the conflicting behavior and the trade-offs between different objective functions.

Das and Dennis [40] presented the Normal Border Intersection (NBI) method as an option that can overcome the disadvantages presented by the WSM method. This method presents the Pareto surface distributed evenly independent of relative scales and the convexity of the objective functions.

However, Das and Dennis [40] argue that a disadvantage, inherent to methods that seek to find a large number of efficient points in MOP, is that these methods cannot find globally Pareto optimal points. The points generated by the NBI are only locally guaranteed as Pareto optimal points. Nevertheless, we will use the NBI method in this study, given its robustness when working with nonconvex problems.

Thus, the NBI method is used to solve the MOP using the following equation [40]:

$$\begin{array}{ll}\underset{\left(x,D\right)}{Max}& D\hfill \\ s.t.:& \overline{\mathsf{\Phi }}w-D\overline{\mathsf{\Phi }}e=\overline{F}(x)\hfill \\ & x\in \mathsf{\Omega }\hfill \end{array}$$

(15)

where w is the convex weighting; D is the distance between the Utopia line and the Pareto frontier; $\overline{F}(x)$ is the vector containing the individual values of the normalized objectives in each run; $e$ is a column vector of one and $\mathsf{\Phi }$ and $\overline{\mathsf{\Phi }}$ are the payoff and normalized payoff matrices, respectively, and can be written as:

$$\mathsf{\Phi }=\left[\begin{array}{ccc}{f}_1^{*}\left(x_1^{*}\right)& \cdots & f_1^{}\left(x_m^{*}\right)\\ ⋮& \ddots & ⋮\\ f_m^{}\left(x_1^{*}\right)& \cdots & f_m^{*}\left(x_m^{*}\right)\end{array}\right]\Rightarrow \overline{\mathsf{\Phi }}=\left[\begin{array}{ccc}\frac{f_1^{*}\left(x_1^{*}\right)-f_1^{*}\left(x_1^{*}\right)}{f_1^{}\left(x_m^{*}\right)-f_1^{*}\left(x_1^{*}\right)}& \cdots & \frac{f_1\left(x_m^{*}\right)-f_1^{*}\left(x_1^{*}\right)}{f_1^{}\left(x_m^{*}\right)-f_1^{*}\left(x_1^{*}\right)}\\ ⋮& \ddots & ⋮\\ \frac{f_m\left(x_1^{*}\right)-f_m^{*}\left(x_m^{*}\right)}{f_m^{}\left(x_1^{*}\right)-f_m^{*}\left(x_m^{*}\right)}& \cdots & \frac{f_m^{*}\left(x_m^{*}\right)-f_m^{*}\left(x_m^{*}\right)}{f_m^{}\left(x_1^{*}\right)-f_m^{*}\left(x_m^{*}\right)}\end{array}\right]$$

(16)

3. Criteria for Defining the Ideal Pareto Solution

When solving an MOP, there are usually an infinite number of efficient solutions that form the ideal set of Pareto (called efficient set) points [34]. The process that seeks to generate optimal Pareto alternatives is known as multi-objective optimization. From a mathematical standpoint, every Pareto ideal point is an acceptable solution for a MOP, if the objective is to obtain a point as the final solution [41].

It is difficult to define the degree of importance to be attributed to each objective [42]. The definition of the weights for each function can be influenced by the preferences of the decision maker. This affects the influence of weights used to determine the relative importance of the functions, in order to identify the most important parameters during the optimization process, and the preferences are selected [43].

The priority given to the criteria significantly affects the final result, since this result depends on the importance attached to each objective [44,45,46]. This can become a problem as decision makers are often unsure about the exact weights of objective functions [44]. Considerable cognitive effort is necessary [47] in order to obtain information on direct preference from the analyst,

The Pareto set includes rational options, from which the analyst can select the final solution by comparing several objectives with each other [44]. As such, the search is for a set of ideal solutions in the broadest sense (Pareto optimal). Several techniques from literature address optimal Pareto solutions in the solution space. However, the disadvantage of these methods is the variety of solutions from which one must choose. We therefore can identify a need to bridge the gap between exclusive solutions and Pareto ideal sets [44].

When solving a linear multi-objective optimization problem, Zeleny [48,49] sought to answer the following questions: (i) what is the most preferred solution among the generated, non-dominated and extreme solutions? (ii) Can the set of non-dominated solutions be reduced to consist of fewer points to determine a final decision? To answer these questions, he proposed the “traditional measure of entropy” as a parameter to assess the importance of functions and define the weights to be used in solving the problem.

Following a different approach, some authors (see [50,51,52]) used the Shannon entropy index [53] associated with an error measure, to determine the most preferred Pareto ideal point in a MOP in a vertical turning process, resolved using the NBI method. The authors state that Shannon’s entropy index can provide a more reliable assessment of the relative weights of objectives in the absence of analyst preferences. Furthermore, the authors state that when combined with an error measure, it minimized the error of Pareto’s preferred point related to individual optimal responses. The weighting metric ξ is obtained by [50,52]:

$$\begin{array}{ll}Max& \xi =\frac{Entropy}{GPE}\hfill \\ s.t.:& {\displaystyle \sum _{i=1}^n{w}_i}=1\hfill \\ & 0\le w_i\le 1\hfill \end{array}$$

(17)

where w_i are the weights to be assigned to the objectives that are to be optimized.

The Entropy equation can be calculated by [53]:

$$Entropy=-{\displaystyle \sum _{i=1}^m{w}_i\ln w_i}$$

(18)

The GPE equation is represented by [54]:

$$GPE={\displaystyle \sum _{i=1}^m\left|\frac{y_i^{*}}{T_i}-1\right|}$$

(19)

where $y_i^{*}$ is the value of the Pareto-optimal responses; $T_i$ is equal to the defined target and m is equal to the number of objectives.

As discussed earlier, many of the weighting strategies used during the optimization and decision-making process rely on inaccurate and subjective elements in at least one of the stages. Thus, weighting method analysis shows that significant contributions can be made, since a large portion of these strategies still employ elements susceptible to error.

Only Shahraki and Noorossana [34] proposed a way of evaluating any variability parameter when selecting the best Pareto optimal solution. We therefore see the theoretical gap, that we intend to address in this study: the behavior of the prediction variance in relation to the weighting strategies.

Now, consider the following problem [55]:

$$\begin{array}{ll}\underset{x}{Min}& {\displaystyle \sum _{i=1}^n{w}_i{f}_i(x)}\hfill \\ s.t.:& {\displaystyle {\sum }_{i=1}^n{w}_i=1}\hfill \\ & w_i\ge 0,i=1,\dots ,n\hfill \end{array}$$

(20)

where f_i(x) are the objective functions to be optimized and w_i are the weights assigned to each objective function.

In order to calculate the variance for the function described in Equation (20), the following process is considered:

$$\begin{array}{ll}\mathit{Var}\left[{\displaystyle \sum _{i=1}^n{w}_i{f}_i(x)}\right]& ={{\displaystyle \sum _{i=1}^n\left[\frac{\partial w_i{f}_i(x)}{\partial f_i(x)}\right]}}^2{\sigma }_{f_i}^2+2{\displaystyle \sum _i^n{\displaystyle \sum _j^n\left[\frac{\partial w_i{f}_i(x)}{\partial f_i(x)}\right]}\left[\frac{\partial w_j{f}_j(x)}{\partial f_j(x)}\right]}{\sigma }_{f_i{f}_j}\hfill \\ & ={\displaystyle \sum _{i=1}^n{w}_i^2}{\sigma }_{f_i(x)}^2+2{\displaystyle \sum _i^n{\displaystyle \sum _j^n{w}_i{w}_j}}{\sigma }_{f_i{f}_j}\hfill \\ & ={\displaystyle \sum _{i=1}^n{w}_i^2}\mathit{Var}\left[f_i(x)\right]+2{\displaystyle \sum _i^n{\displaystyle \sum _{\ne j}^n{w}_i{w}_j}}{\rho }_{f_i{f}_j}\sqrt{\mathit{Var}\left[f_i(x)\right]\times \mathit{Var}\left[f_j(x)\right]}\hfill \end{array}$$

(21)

where ${\rho }_{f_i{f}_j}$ is the correlation between the functions f_i and f_j.

Considering that it is possible to calculate the variance of f_i (x) at a certain point ${\mathbf{x}}_0{}^T=\left[\begin{array}{ccccc}1& x_{01}& x_{02}& \dots & x_{0k}\end{array}\right]$, as $\mathit{Var}[f_i({\mathbf{x}}_0)]={\widehat{\sigma }}_{f_i}^2{\mathbf{x}}_0{}^T{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{x}}_0$, Equation (21) can be modified to:

$$\begin{array}{l}Var\left[{\displaystyle \sum _{i=1}^n{w}_i{f}_i({\mathbf{x}}_0)}\right]={\displaystyle \sum _{i=1}^n{w}_i^2}\left[{\widehat{\sigma }}_{f_i}^2{\mathbf{x}}_0{}^T{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{x}}_0\right]+\\ 2{\displaystyle \sum _i^n{\displaystyle \sum _{\ne j}^n{w}_i{w}_j}}{\rho }_{f_i{f}_j}\sqrt{\left[{\widehat{\sigma }}_{f_i}^2{\mathbf{x}}_0{}^T{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{x}}_0\right]\times \left[{\widehat{\sigma }}_{f_j}^2{\mathbf{x}}_0{}^T{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{x}}_0\right]}\end{array}$$

(22)

Now, consider the term $\mathit{Var}[f({\mathbf{x}}_0)]={\widehat{\sigma }}_f^2{\mathbf{x}}_0{}^T{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{x}}_0$ as constant for each function at a given point. Analyzing Equation (22), we see that the variance of the estimated responses is minimized by diversification, i.e., by the uniform distribution of weights among the functions involved in the MOP. Furthermore, negative correlations between responses tend to decrease variance. We propose the following: using entropic metrics to choose the optimal weights in MOP can reduce prediction variance.

Figure 1 shows the step-by-step proposal.

4. Experimental Design

The experimental data presented by Istadi and Amin [28] and Istadi and Amin [16] were used in this study. The authors sought to optimize a CO₂-OCM process, by determining the condition that led to maximum CH₄ conversion, C₂ selectivity, and C₂ yield.

The CaO/CeO₂ and MnO/CeO₂ catalysts were prepared by impregnating ceria (CeO₂) with aqueous solutions of Ca(NO₃)₂ and Mn(NO₃)₂, respectively, as described in Istadi and Amin [56] and Istadi and Amin [16]. The catalytic performances were tested in an experimental set-up as described in Istadi and Amin [56]. The CH₄ conversion, C₂ selectivity, and C₂ yield are calculated as defined by Wang et al. [26], considering that the carbon in methane is converted to C₂H₆, C₂H₄ and CO.

The most frequently used experimental design for data collection, for modeling the response surface functions, is a Central Composite Design (CCD). According to Myers et al. [36], a CCD is chosen because it is an efficient design for sequential experimentation, allowing a reasonable amount of information to test the error without requiring a large number of experiments. Additionally, the design accommodates a spherical region with five levels for each factor, which is advantageous from an experimental region point of view. The CCD was then employed in the experimental design. Using CO₂/CH₄ ratio (dimensionless), reactor temperature (K), wt.% CaO in ceria catalyst and wt.% MnO in ceria catalyst as the decision variables, a full factorial design 2⁴ was performed with eight axial points and two center points, generating 26 experiments. The experimental matrix is shown in

Table 1. CCD for CH₄ conversion (y₁), C₂ selectivity (y₂) and C₂ yield (y₃).

N	x1	x2	x3	x4	y1	y2	y3
1	1.5	1048	10	3	2.63	69.01	1.82
2	2.5	1048	10	3	2.68	60.20	1.61
3	1.5	1198	10	3	7.95	32.71	2.60
4	2.5	1198	10	3	9.74	18.73	1.82
5	1.5	1048	20	3	1.76	24.62	0.43
6	2.5	1048	20	3	2.92	55.95	1.63
7	1.5	1198	20	3	9.92	27.84	2.76
8	2.5	1198	20	3	13.41	16.21	2.17
9	1.5	1048	10	7	2.20	78.15	1.72
10	2.5	1048	10	7	2.29	78.37	1.80
11	1.5	1198	10	7	7.80	35.98	2.81
12	2.5	1198	10	7	8.70	33.12	2.88
13	1.5	1048	20	7	1.25	42.64	0.53
14	2.5	1048	20	7	1.55	64.79	1.00
15	1.5	1198	20	7	9.03	34.62	3.13
16	2.5	1198	20	7	10.89	30.78	3.35
17	1.0	1123	15	5	2.27	70.51	1.60
18	3.0	1123	15	5	2.47	65.18	1.61
19	2.0	973	15	5	0.54	24.30	0.13
20	2.0	1273	15	5	16.59	14.32	2.38
21	2.0	1123	5	5	4.33	74.63	3.23
22	2.0	1123	25	5	3.70	66.30	2.45
23	2.0	1123	15	1	4.71	74.07	3.49
24	2.0	1123	15	9	4.53	75.24	3.41
25	2.0	1123	15	5	4.81	72.58	3.49
26	2.0	1123	15	5	5.06	75.64	3.83

in which x₁ is the CO₂/CH₄ ratio, x₂ is the reactor temperature, x₃ is the wt.% CaO in ceria catalyst, x₄ is the wt.% MnO in ceria catalyst, y₁ is the CH₄ conversion (%), y₂ is the C₂ selectivity (%), and y₃ is the C₂ yield (%). The fixed experimental conditions are [16,28]: catalyst weight = 2 g; total feed flow rate = 100 mL/min; total pressure = 1 atm; gas hourly space velocity = 3000 mL/(g h).

It is important to note that the experimental matrix presented in Table 1 was planned using only 2 CP. This can be very detrimental to the stability of the prediction variance. Myers et al. [36] do not recommend using a CCD with only two CP, because this practice does not guarantee good dispersion of the prediction variance throughout the experimental region, and analyzing how the proposed method behaves in such designs is important. This was why we chose this experimental matrix.

The decision variables were analyzed in coded form. They were decoded only at the end of the analyses. This was done using the following equation [51]:

$$X_{uncoded}=\frac{Hi+Lo}{2}+X_{coded}\frac{Hi-Lo}{2}$$

(23)

where: Hi and Lo are related to the values of level +1 and −1, respectively.

The parameters used in the experiments and their levels are shown in

Table 2. Parameters used in the experiments.

Factors	Symbol	Levels
		−2	−1	0	1	2
CO2/CH4 ratio	x1	1	1.5	2	2.5	3
Reactor temperature (K)	x2	973	1048	1123	1198	1273
wt.% CaO (%)	x3	5	10	15	20	25
wt.% MnO (%)	x4	1	3	5	7	9

.

In the search for an optimization model that allows for the simultaneous conversion of CH₄, C₂ selectivity_, and C₂ yield, the decision-making process, based on multiple criteria, proposed by Rocha et al. [52] can be used. The authors sought to build a uniformly distributed Pareto frontier and a way to select the preferred Pareto optimal points as the ideal solution to a given problem. The authors used the NBI method, overcoming the disadvantages of the WSM method. To verify the robustness of the final result obtained, a variance metric was adopted. Although there are different measures of prediction performance to compare experimental designs, SPV is commonly adopted [57]. However, if direct comparisons between the expected variation of estimation are desired, UPV may be more appropriate.

5. Results and Discussion

The analysis of experimental data shown in Table 1 generated the mathematical modeling presented in

Table 3. Objective functions mathematical models.

Terms	y1	y2	y3
Constant	4.9350	74.1100	3.6600
x1	0.4183	0.0800	0.0200
x2	3.8442	−10.9875	0.6450
x3	0.2283	−5.2283	−0.1508
x4	−0.3192	3.9800	0.0925
x1x1	−0.4700	−3.9140	−0.5610
x2x2	1.0788	−16.0477	−0.6485
x3x3	−0.0588	−3.2590	−0.2523
x4x4	0.0925	−2.2115	−0.0998
x1x2	0.4025	−4.8250	−0.1638
x1x3	0.2488	3.9650	0.1338
x1x4	−0.2088	1.1725	0.0763
x2x3	0.7113	5.4150	0.2913
x2x4	−0.1188	−0.9475	0.2038
x3x4	−0.2050	0.2025	−0.0212
p-value	0.000	0.030	0.000
R2 (%)	97.47%	80.29%	94.82%
Lack-of-fit	0.131	0.106	0.483

The values presented in bold represent the significant terms of the model (thus, p-value < 5%).

.

Table 3 shows that the R² values indicate a good fit for the model. The lack-of-fit test is shown in Table 3. In the lack-of-fit test, small p-values are undesirable. At a 5% significance level, all presented models were adequate.

In order to establish a comparison of how each decision variable affects each response, the main effect plots for CH₄ conversion (y₁), C₂ selectivity (y₂) and C₂ yield (y₃) are shown in Figure 2.

According to this analysis, the reactor temperature (x₂) is the most significant factor in increasing CH₄ conversion (y₁). The reactor temperature (x₂) is also an important factor when analyzing C₂ selectivity (y₂) and C₂ yield (y₃), but in a different way. The reactor temperature (x₂) increases the C₂ selectivity (y₂) and C₂ yield (y₃) until reaching 1123 K. When increasing the temperature above 1123 K, C₂ selectivity (y₂) and C₂ yield (y₃) decrease. The drop is greater when analyzing the values of C₂ selectivity (y₂), and this could be attributed to more CH₄ being converted into CO rather than C₂H₄ and/or C₂H₆ [16]. For C₂ selectivity (y₂) and C₂ yield (y₃) the factors wt.% CaO in ceria catalyst (x₃) and wt.% MnO in ceria catalyst (x₄) showed very similar behavior, and the highest values for the responses obtained were extreme factor values, i.e., 5 and 25% CaO, and 1 and 9% MnO in ceria catalyst. The considerable impact that these factors have on C₂ selectivity (y₂) and C₂ yield (y₃) highlights the importance of the catalysts in promoting the product selectivity to C₂H₄ and/or C₂H_6, and in inhibiting the reaction to form CO and H₂O [16]. The CO₂/CH₄ ratio (x₁) had different behavior for C₂ selectivity (y₂) and C₂ yield (y₃). While the highest value for C₂ yield (y₃) was observed for the CO₂/CH₄ ratio (x₁) 2, the highest values for the C₂ selectivity (y₂) obtained were in the extreme CO₂/CH₄ ratio (x₁) range. The 2.5 CO₂/CH₄ ratio (x₁) led to the highest CH₄ (y₁) conversion value with a drop in the value of this response at CO₂/CH₄ ratio (x₁) 3. The abundance of CO₂ in the high CO₂/CH₄ ratio most likely decreased the catalyst activity by covering the catalyst active sites [16]. When analyzing only reactor temperature (x₂), we saw that increased CH₄ conversion (y₁), C₂ selectivity (y₂) and C₂ yield (y₃) would be negatively affected, which corroborates the results presented by other authors [25,26,27]. We can see how these objectives are, thus, conflicting.

Figure 3 shows the response surfaces for CH₄ conversion (y₁), C₂ selectivity (y₂) and C₂ yield (y₃).

In order to check the convexity of the functions, before performing the multi-objective optimization, the nature of the stationary point was analyzed using Equation (14). For CH₄ conversion (y₁) the eigenvalues (${\lambda }_i$) are [1.2205; −0.5222; −0.1821; 0.1263], i.e., the different eigenvalues signs indicate that the function is neither concave nor convex and the stationary point is a saddle point. For C₂ selectivity (y₂) the eigenvalues (${\lambda }_i$) are [−17.1859; −4.6067; −2.3090; −1.3305]. Thus, the eigenvalue signs indicate that the function is concave and the stationary point is a maximum point. For C₂ yield (y₃) the eigenvalues (${\lambda }_i$) are [−0.7656; −0.5133; −0.2047; −0.0781]. The eigenvalue signs indicate that the function is concave and the stationary point is a maximum point. Through an analysis of the nature of the stationary point, we see that the functions have different convexities. Thus, the weighted sum method for multi-objective optimization is not adequate [58]. We therefore adopted the NBI method. To implement the NBI optimization routine, initially, the payoff matrix was estimated, obtaining the results shown in

Table 4. Payoff matrix for the objective functions.

y1	y2	y3
17.118	0.000	2.619
3.376	82.614	2.945
7.793	59.630	3.933

Bold values represent individual optimums.

.

The payoff matrix is an underlying part of the NBI implementation. After this step, a mixture design for the weights of each objective function was defined, as presented in

Table 5. Mixture design.

Weights			y1	y2	y3	Entropy	GPE	$\mathit{\xi }$	UPV
w1	w2	w3
1.000	0.000	0.000	17.118	0.000	2.619	0.0000	1.3341	0.0000	0.5833
0.900	0.100	0.000	15.744	8.261	2.652	0.3251	1.3061	0.2489	0.5833
0.900	0.000	0.100	16.185	5.963	2.750	0.3251	1.2830	0.2534	0.5833
0.800	0.200	0.000	14.370	16.523	2.684	0.5004	1.2781	0.3915	0.5833
0.800	0.100	0.100	14.811	14.224	2.783	0.6390	1.2550	0.5092	0.5833
0.800	0.000	0.200	15.253	11.926	2.882	0.5004	1.2319	0.4062	0.5833
0.700	0.300	0.000	12.995	24.784	2.717	0.6109	1.2501	0.4887	0.5833
0.700	0.200	0.100	13.437	22.486	2.816	0.8018	1.2270	0.6535	0.5833
0.700	0.100	0.200	13.879	20.187	2.914	0.8018	1.2039	0.6660	0.5833
0.700	0.000	0.300	14.320	17.889	3.013	0.6109	1.1807	0.5173	0.5833
0.600	0.400	0.000	11.621	29.734	2.749	0.6730	1.2622	0.5332	0.5833
0.600	0.300	0.100	12.063	30.747	2.848	0.8979	1.1990	0.7489	0.5833
0.600	0.200	0.200	12.505	28.449	2.947	0.9503	1.1758	0.8082	0.5833
0.600	0.100	0.300	12.946	26.151	3.046	0.8979	1.1527	0.7790	0.5833
0.600	0.000	0.400	13.388	23.852	3.145	0.6730	1.1296	0.5958	0.5833
0.500	0.500	0.000	10.247	36.364	2.782	0.6931	1.2539	0.5528	0.5833
0.500	0.400	0.100	10.689	36.248	2.881	0.9433	1.2044	0.7833	0.5833
0.500	0.300	0.200	11.131	36.710	2.980	1.0297	1.1478	0.8970	0.5569
0.500	0.200	0.300	11.572	34.412	3.078	1.0297	1.1247	0.9155	0.3936
0.500	0.100	0.400	12.014	32.113	3.177	0.9433	1.1016	0.8563	0.3420
0.500	0.000	0.500	12.456	29.815	3.276	0.6931	1.0785	0.6427	0.3215
0.400	0.600	0.000	8.873	42.931	2.815	0.6730	1.2464	0.5400	0.5833
0.400	0.500	0.100	9.315	42.340	2.913	0.9433	1.2026	0.7844	0.5833
0.400	0.400	0.200	9.756	44.972	3.012	1.0549	1.1198	0.9420	0.5118
0.400	0.300	0.300	10.198	42.673	3.111	1.0889	1.0967	0.9929	0.4537
0.400	0.200	0.400	10.640	40.375	3.210	1.0549	1.0736	0.9826	0.3384
0.400	0.100	0.500	11.082	38.077	3.309	0.9433	1.0505	0.8980	0.3119
0.400	0.000	0.600	11.523	35.778	3.407	0.6730	1.0274	0.6551	0.3117
0.300	0.700	0.000	7.499	57.830	2.891	0.6109	1.1269	0.5421	0.3459
0.300	0.600	0.100	7.941	55.531	2.946	0.8979	1.1149	0.8054	0.3320
0.300	0.500	0.200	8.382	53.233	3.045	1.0297	1.0918	0.9431	0.3223
0.300	0.400	0.300	8.824	50.935	3.144	1.0889	1.0687	1.0189	0.3171
0.300	0.300	0.400	9.266	48.636	3.242	1.0889	1.0456	1.0414	0.3142
0.300	0.200	0.500	9.707	46.338	3.341	1.0297	1.0225	1.0070	0.3126
0.300	0.100	0.600	10.149	44.040	3.440	0.8979	0.9994	0.8985	0.3120
0.300	0.000	0.700	10.591	41.741	3.539	0.6109	0.9763	0.6257	0.3115
0.200	0.800	0.000	6.125	63.589	2.880	0.5004	1.1403	0.4388	0.3226
0.200	0.700	0.100	6.566	62.391	2.978	0.8018	1.1039	0.7264	0.3162
0.200	0.600	0.200	6.927	61.494	3.077	0.9503	1.0686	0.8893	0.3119
0.200	0.500	0.300	7.450	59.196	3.176	1.0297	1.0407	0.9894	0.3107
0.200	0.400	0.400	7.892	56.898	3.275	1.0549	1.0176	1.0367	0.3108
0.200	0.300	0.500	8.333	54.599	3.374	1.0297	0.9945	1.0354	0.3114
0.200	0.200	0.600	8.775	52.301	3.473	0.9503	0.9714	0.9783	0.3120
0.200	0.100	0.700	9.217	50.003	3.571	0.8018	0.9483	0.8456	0.3122
0.200	0.000	0.800	9.658	47.704	3.670	0.5004	0.9252	0.5409	0.3124
0.100	0.900	0.000	4.751	69.736	2.912	0.3251	1.1379	0.2857	0.3116
0.100	0.800	0.100	5.192	68.568	3.011	0.6390	1.1011	0.5803	0.3107
0.100	0.700	0.200	5.634	67.371	3.110	0.8018	1.0647	0.7531	0.3132
0.100	0.600	0.300	6.076	66.135	3.209	0.8979	1.0287	0.8729	0.3185
0.100	0.500	0.400	6.448	65.159	3.308	0.9433	0.9936	0.9494	0.3271
0.100	0.400	0.500	6.959	62.861	3.406	0.9433	0.9665	0.9761	0.3275
0.100	0.300	0.600	7.401	60.562	3.505	0.8979	0.9434	0.9519	0.3280
0.100	0.200	0.700	7.843	58.264	3.604	0.8018	0.9203	0.8713	0.3274
0.100	0.100	0.800	8.284	55.966	3.703	0.6390	0.8971	0.7123	0.3268
0.100	0.000	0.900	8.726	53.667	3.802	0.3251	0.8740	0.3719	0.3237
0.000	1.000	0.000	3.377	82.614	2.945	0.0000	1.0540	0.0000	0.3984
0.000	0.900	0.100	3.818	80.315	3.044	0.3251	1.0309	0.3153	0.5597
0.000	0.800	0.200	4.260	78.017	3.142	0.5004	1.0078	0.4965	0.5833
0.000	0.700	0.300	4.702	75.719	3.241	0.6109	0.9847	0.6203	0.5833
0.000	0.600	0.400	5.097	73.420	3.340	0.6730	0.9643	0.6979	0.5833
0.000	0.500	0.500	5.447	71.122	3.439	0.6931	0.9465	0.7323	0.5122
0.000	0.400	0.600	5.834	68.824	3.538	0.6730	0.9266	0.7263	0.3236
0.000	0.300	0.700	6.319	66.525	3.637	0.6109	0.9010	0.6780	0.3541
0.000	0.200	0.800	6.910	64.227	3.735	0.5004	0.8691	0.5757	0.3964
0.000	0.100	0.900	7.352	61.929	3.834	0.3251	0.8460	0.3842	0.3562
0.000	0.000	1.000	7.794	59.631	3.933	0.0000	0.8229	0.0000	0.3106
0.333	0.333	0.333	9.429	47.415	3.166	1.0986	1.0703	1.0264	0.3107
0.667	0.167	0.167	13.274	23.707	2.892	0.8676	1.2022	0.7216	0.3697
0.167	0.667	0.167	6.403	63.621	3.055	0.8676	1.0790	0.8040	0.3109
0.167	0.167	0.667	8.611	53.523	3.549	0.8676	0.9466	0.9165	0.3131

.

Table 5 presents the Pareto optimal set for the MOP under analysis. As shown in Rocha et al. [59], the prediction variance was affected by the weights assigned to the objectives.

Table 6. Pearson correlation coefficients.

	Entropy	GPE	$\mathit{\xi }$
GPE	−0.008
	0.950
$\mathit{\xi }$	0.967	−0.232
	0.000	0.054
UPV	−0.228	0.642	−0.378
	0.057	0.000	0.001

shows the Pearson Correlation analysis between the values that were previously presented in Table 5. Using the Pearson Correlation analysis we see that the ξ weighting metric has a statistically negative and significant correlation with the UPV. Therefore, when maximizing this metric, the variance values tend to be lower. This information indicates that the search for the most preferred Pareto optimal point in multi-objective optimization using this metric leads to a robust response from a variability point of view.

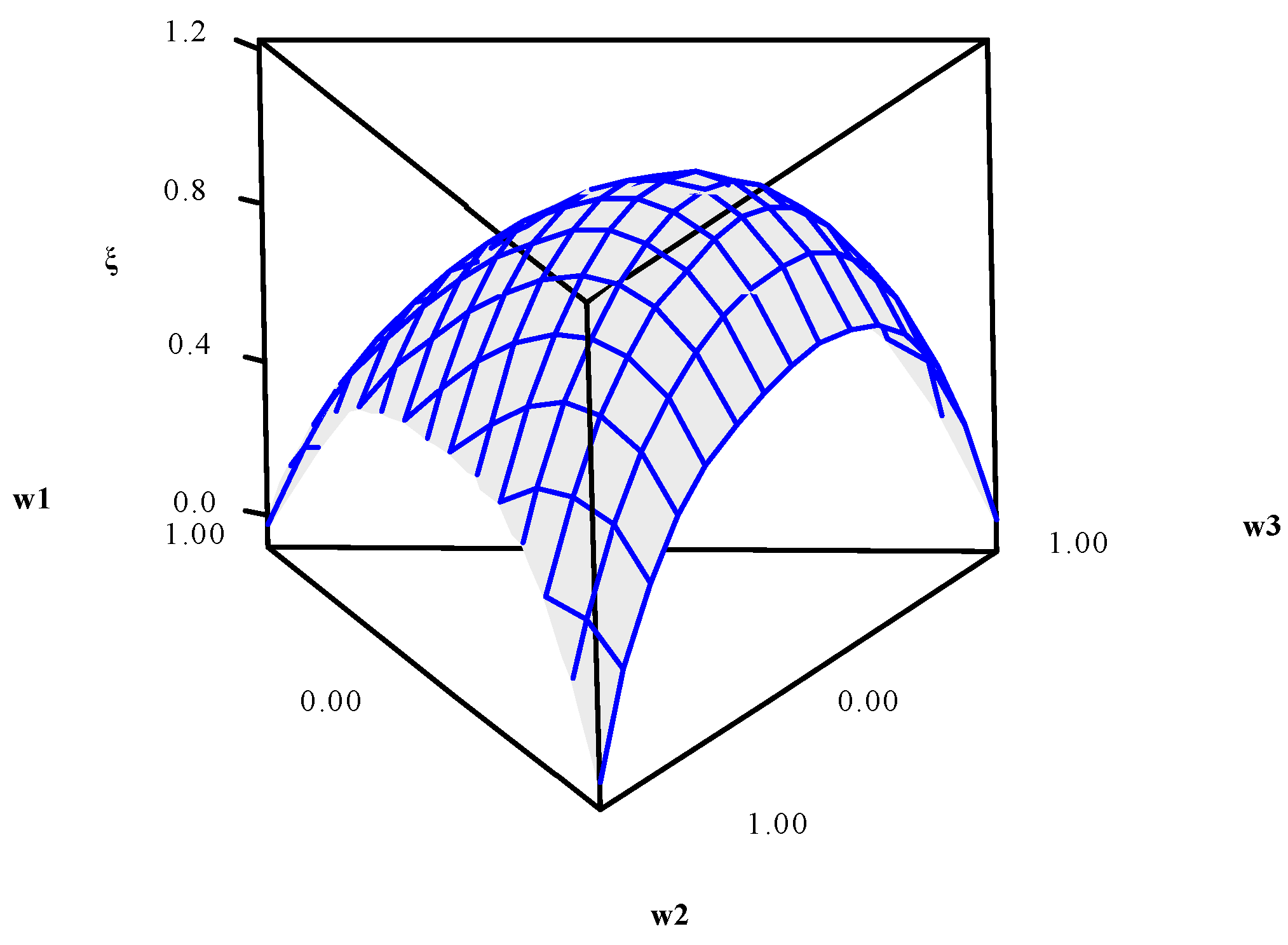
Using data presented in Table 5, the entropy modeling, GPE, weighting metric (ξ), and UPV were performed. Their canonical mixing polynomials (Equations (24)–(27)), response surfaces and contour graphics were obtained (Figure 4, Figure 5, Figure 6 and Figure 7), which are presented below:

$$\begin{array}{ll}Entropy=& -0.0074w_1-0.0074w_2-0.0074w_3+2.7705w_1{w}_2+2.7705w_1{w}_3+\hfill \\ & 2.7705w_2{w}_3+5.4207w_1{w}_1{w}_2{w}_3+5.4207w_1{w}_2{w}_2{w}_3+5.4207w_1{w}_2{w}_3{w}_3+\hfill \\ & 1.4619w_1{w}_2{(w_1-w_2)}^2+1.4619w_1{w}_3{(w_1-w_3)}^2+1.4619w_2{w}_3{(w_2-w_3)}^2\hfill \end{array}$$

(24)

$$\begin{array}{ll}GPE=& 1.3312w_1+1.0624w_2+0.8233w_3+0.1419w_1{w}_2-\hfill \\ & 0.1680w_1{w}_2(w_1-w_2)-1.2977w_1{w}_2{w}_2{w}_3\hfill \end{array}$$

(25)

$$\begin{array}{ll}\xi =& -0.0123w_1-0.0081w_2+0.0016w_3+2.2476w_1{w}_2+2.5539w_1{w}_3+2.9199w_2{w}_3-\hfill \\ & 0.2272w_1{w}_2(w_1-w_2)-0.6622w_1{w}_3(w_1-w_3)-0.3965w_2{w}_3(w_2-w_3)+\hfill \\ & 3.8644w_1{w}_1{w}_2{w}_3+5.3402w_1{w}_2{w}_2{w}_3+6.2119w_1{w}_2{w}_3{w}_3+1.4004w_1{w}_2{(w_1-w_2)}^2+\hfill \\ & 1.5386w_1{w}_3{(w_1-w_3)}^2+1.5177w_2{w}_3{(w_2-w_3)}^2\hfill \end{array}$$

(26)

$$\begin{array}{ll}UPV=& 0.6054w_1+0.4386w_2+0.3849w_3+0.3919w_1{w}_2-0.3719w_1{w}_3+0.2859w_2{w}_3+\hfill \\ & 0.8779w_1{w}_2(w_1-w_2)+0.9531w_1{w}_3(w_1-w_3)+0.9960w_2{w}_3(w_2-w_3)-\hfill \\ & 11.9662w_1{w}_2{w}_2{w}_3-2.6199w_1{w}_2{(w_1-w_2)}^2\hfill \end{array}$$

(27)

It is interesting to note that all canonical polynomials of mixtures showed a good fit, with R² close to 100%. The adopted variance metric, UPV, had the worst adjustments, with an R² value equal to 82.83%. However, this value may be acceptable [36]. This analysis highlights the fact that it is possible to model the variance metric in terms of weights. This is because the weights interfere in the solution space. However, since the optimization of distinct functions is performed simultaneously, the solution space is not the same as the initial area of the DOE, and therefore, its shape is distinguished from the Hat Matrix shape when modeling the variance.

Lastly, when maximizing ξ, as described in Equation (26), weights w₁, w_2, and w₃, related to the final solution, were identified as being w₁ = 0.2603, w₂ = 0.3202, and w₃ = 0.4195. These optimal weights were used in a multi-objective optimization of CH₄ conversion (y₁), C₂ selectivity (y₂), and C₂ yield (y₃), reaching 8.806%, 51.468%, and 3.275%, respectively. This result is different from that obtained by Istadi and Amin [28] and Istadi and Amin [16]. When optimizing the responses using a bio-objective optimization process, the authors neglected the real trade-off behavior between the responses. The lower diversification among the responses almost led to a single-response optimization. The greatest challenge of this process is to achieve both high CH₄ conversion (y₁) and high C₂ selectivity (y₂), since it has been proven that these responses are in conflict one with the other [25,26,27]. Despite this trade-off, the results are acceptable [25] especially with respect to using low-valued natural gas.

The optimal coded values of the decision variables are CO₂/CH₄ ratio (x₁) = 1.0060, reactor temperature (x₂) = 0.7536, wt.% CaO in ceria catalyst (x₃) = 0.4358, and wt.% MnO in ceria catalyst (x₄) = 0.4822. Using Equation (23), the encoded values were transformed into uncoded values. Therefore, the optimal values of the decision variables are CO₂/CH₄ ratio (x₁) = 2.50, reactor temperature (x₂) = 1179.5 K, wt.% CaO in ceria catalyst (x₃) = 17.2%, and wt.% MnO in ceria catalyst (x₄) = 6.0%. The high CO₂/CH₄ ratio (x₁) favors CH₄ conversion (y₁) [26]. A high reactor temperature (x₂) leads to high CH₄ conversion (y₁), but the C₂ yield (y₃) decreases at reactor temperatures higher than 1173 K, due to low C₂ selectivity (y₂) [26,27]. The high wt.% CaO (x₃) and wt.% MnO (x₄) in ceria catalyst increases CH₄ conversion (y₁) and C₂ selectivity (y₂). According to Wang and Ohtsuka [27], these catalysts can activate CO₂ to produce active oxygen for CH₄ conversion (y₁) and their basicity leads to improvements in C₂ selectivity (y₂).

The data presented in Table 5 were used to construct Figure 8. Here, the Pareto frontier constructed using the NBI method is presented, with the ideal point highlighted.

Figure 8 shows the uniform distribution of the optimal Pareto points on the frontier. This also presents the most preferrable Pareto point, which is the final solution for the MOP. The confidence interval values are shown in

Table 7. Confidence interval values for the responses.

Responses	Lower Limit	Mean	Upper Limit
y1	7.583	8.806	10.029
y2	32.802	51.468	70.133
y3	2.845	3.275	3.704

.

For $\alpha =5\%$, the confidence interval of $100(1-\alpha )\%$, for the mean response, at point ${\mathbf{x}}_0{}^T=\left[\begin{array}{ccccc}1& x_{01}& x_{02}& \dots & x_{0k}\end{array}\right]$ is:

$$\widehat{y}({\mathbf{x}}_0)-t_{\alpha /2,n-p}\sqrt{{\widehat{\sigma }}^2{\mathbf{x}}_0{}^T{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{x}}_0}\le {\mu }_{y|{\mathbf{x}}_0}\le \widehat{y}({\mathbf{x}}_0)+t_{\alpha /2,n-p}\sqrt{{\widehat{\sigma }}^2{\mathbf{x}}_0{}^T{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{x}}_0}$$

(28)

When analyzing the question involving variability, the final solution obtained that maximizes the ξ metric is robust, since this metric leads the solution in a region of minimum variance, with less variability, and greater reliability. However, the confidence interval of the C₂ selectivity (y₂) is higher than the other responses. This demonstrates that C₂ selectivity (y₂) is the most difficult parameter to control in the process.

Figure 9 shows the overlap of the different objective functions defining the feasible region for the analyzed problem.

Figure 9 shows the conflicting nature between CH₄ conversion (y₁) and C₂ selectivity (y₂). An increase in CH₄ conversion (y₁) leads to a decrease in C₂ selectivity (y₂). In this study, the optimum point was chosen based on the maximization of metric ξ, and still, it was shown to be the most robust point. However, one can see that the region of maximum C₂ yield (y₃) lies within the feasible region for the problem, and is obtainable, even though this is not the most reliable, from a statistical process control point of view.

6. Conclusions

This paper studied direct low-value natural gas conversion using carbon dioxide oxidative coupling of methane over CaO/CeO₂ and MnO/CeO₂ catalysts to produce C₂ hydrocarbons. The NBI method was adopted to simultaneously optimize CH₄ conversion, C₂ selectivity, and C₂ yield. This method helped build an evenly distributed Pareto frontier for the three responses, regardless of the convexity of the functions.

The mathematical response model showed acceptable fitting, and the functions were proven adequate. Some results described in literature have been corroborated, e.g., the positive influence of reactor temperature in CH₄ conversion, the negative influence of reactor temperature in C₂ selectivity, the synergistic effect between reactor temperature, the wt.% CaO in ceria catalyst in increasing CH₄ conversion and C₂ yield, and the synergistic effect between reactor temperature and wt.% MnO in ceria catalyst in increasing C₂ yield.

An entropic measure was used to select the most preferred ideal Pareto point for the final solution. The decision-making criteria was useful and fundamental in identifying and mapping regions with minimum variation within the optimal Pareto responses obtained in the optimization processes. Furthermore, this study demonstrates that the weights used in the multi-objective optimization process have an influence on the variation in the forecast of the responses obtained. This study also proves the robustness of the weighting process used in choosing the final solution.

The simultaneous optimal values for the objective functions were CH₄ conversion = 8.806%, C₂ selectivity = 51.468%, and C₂ yield = 3.275%. These results were obtained by using the following process parameter combinations: CO₂/CH₄ ratio = 2.50, reactor temperature = 1179.5 K, wt.% CaO in ceria catalyst = 17.2%, and wt.% MnO in ceria catalyst = 6.0%. The analyses of the confidence interval for the responses showed that C₂ selectivity has greater variability, and was the most difficult parameter to control in the process.

From an environmental point of view, this is an efficient process since it helps reduce CO₂ and CH₄ emissions and reduces waste, as hydrocarbon resources, specifically from low-value natural gas, can be used.