Statistical Approach to Crystal Nucleation in Glass-Forming Liquids
Abstract
1. Introduction
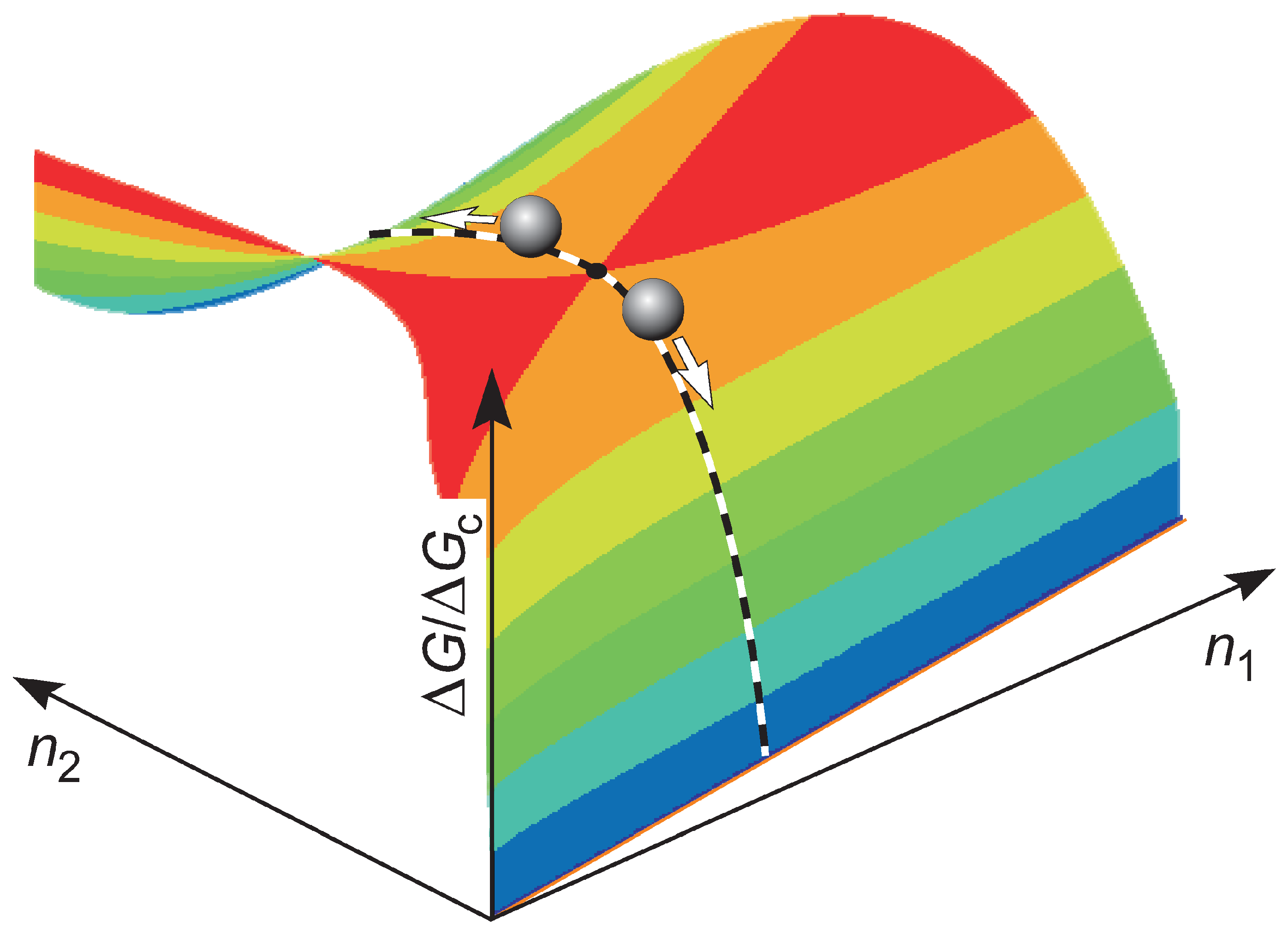
2. Statistical Approach to Crystal Nucleation
2.1. Basic Equations
2.2. Nucleation at Constant Temperature and Pressure
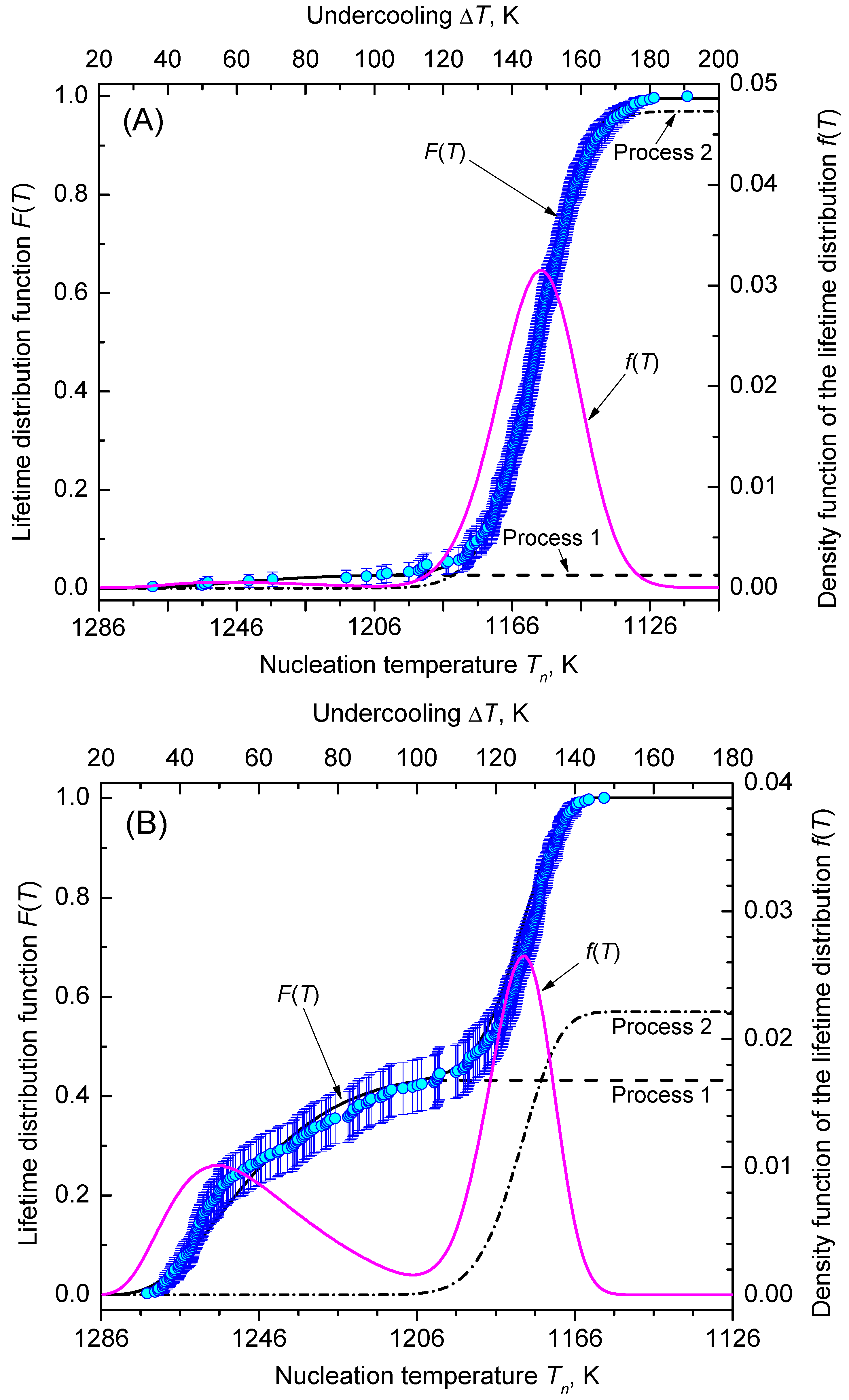
2.2.1. Interpretation in Terms of Times of Formation of the First Supercritical Nucleus
2.2.2. Interpretation in Terms of Lifetime Analysis
2.3. Discussion of Possible Limits of Applicability of the Theoretical Approach
2.3.1. Account of Time-Lag Effects
2.3.2. Account of Finite Times of Growth of Critical Clusters to Observable Sizes
2.4. Nucleation at Cooling or Heating with a Constant Rate of Change of Temperature
2.4.1. Interpretation in Terms of Times of Formation of the First Supercritical Nucleus
2.4.2. Interpretation in Terms of Lifetime Analysis
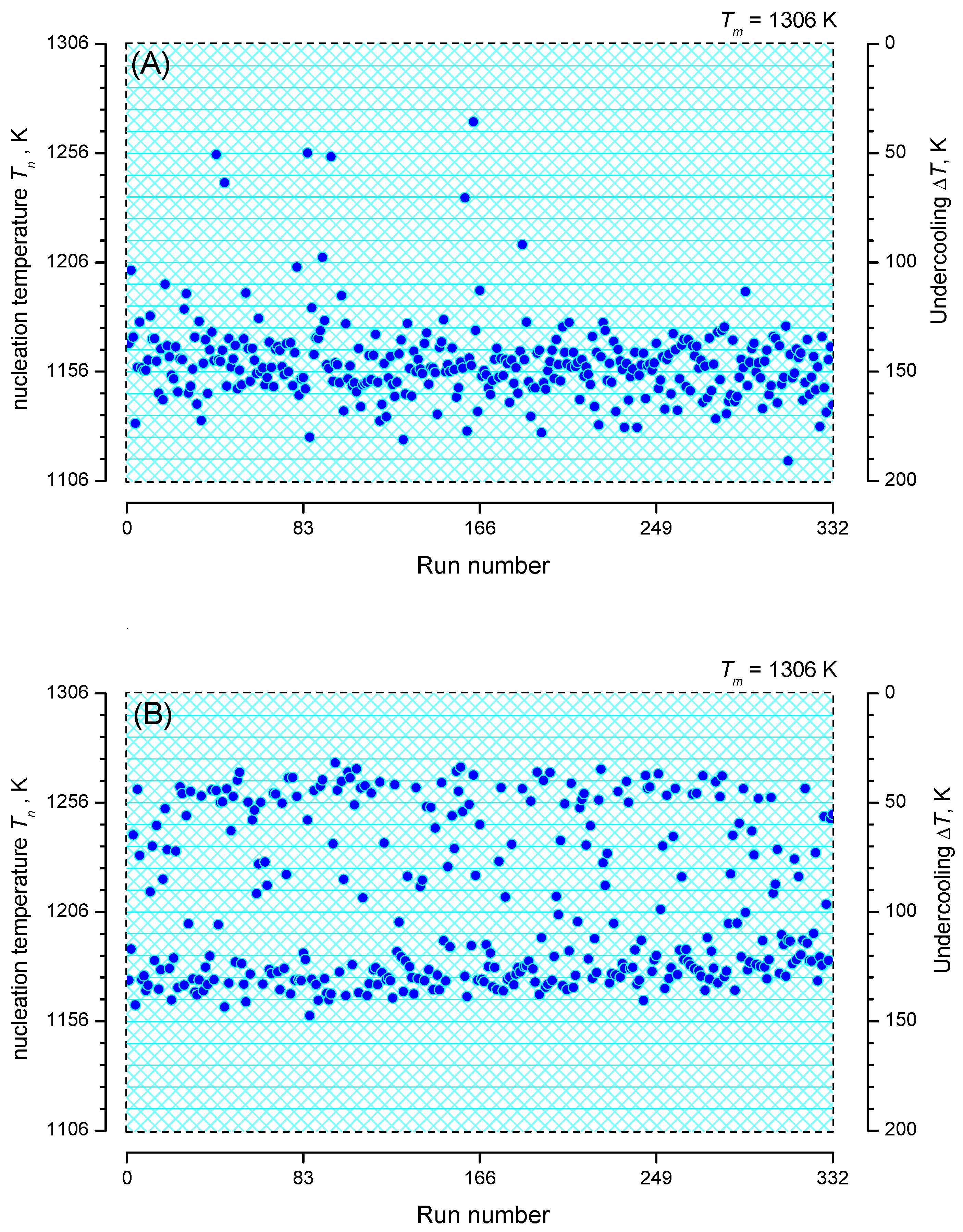
3. Experimental Data and Their Interpretation
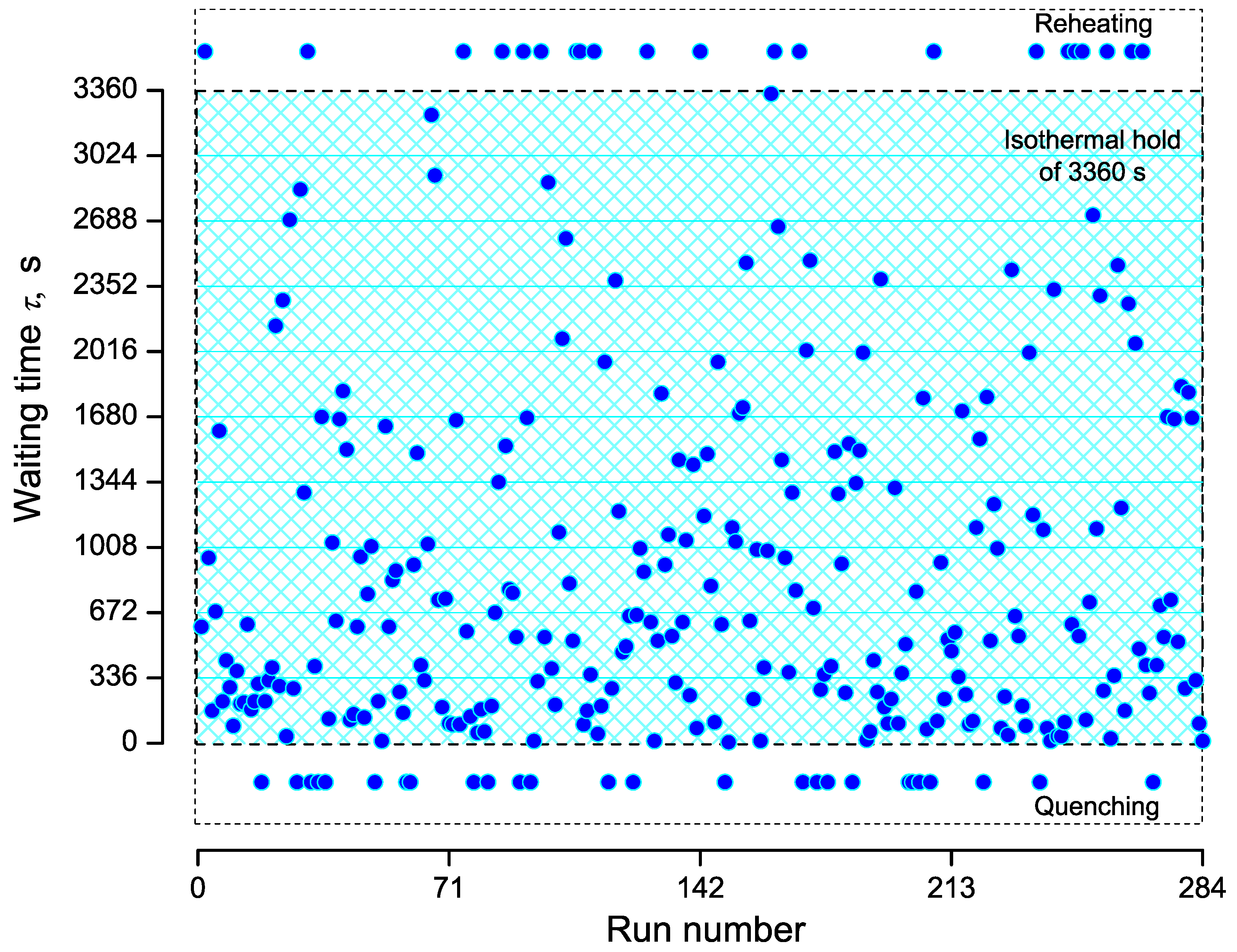
3.1. Brief Description of the Experiments
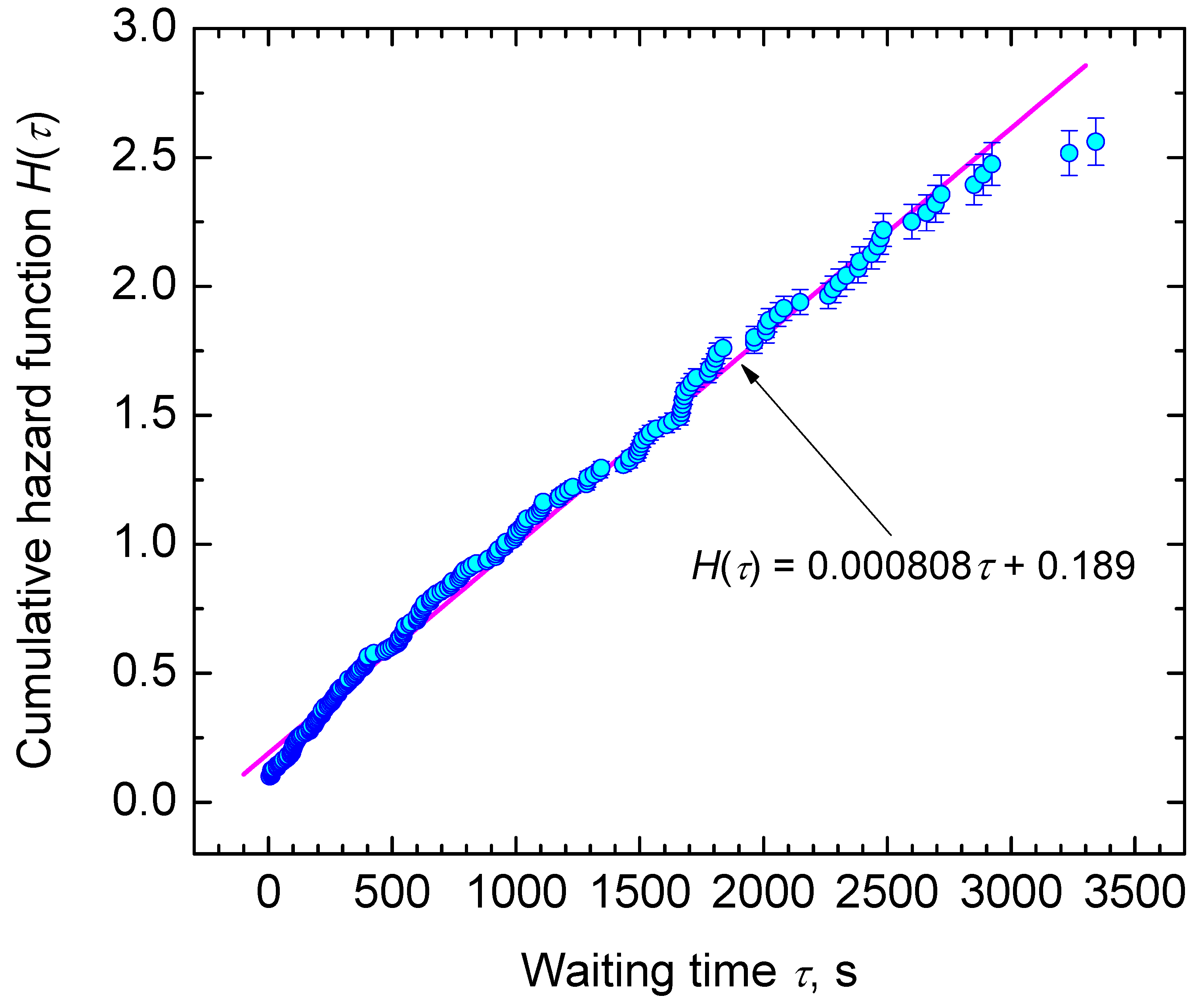
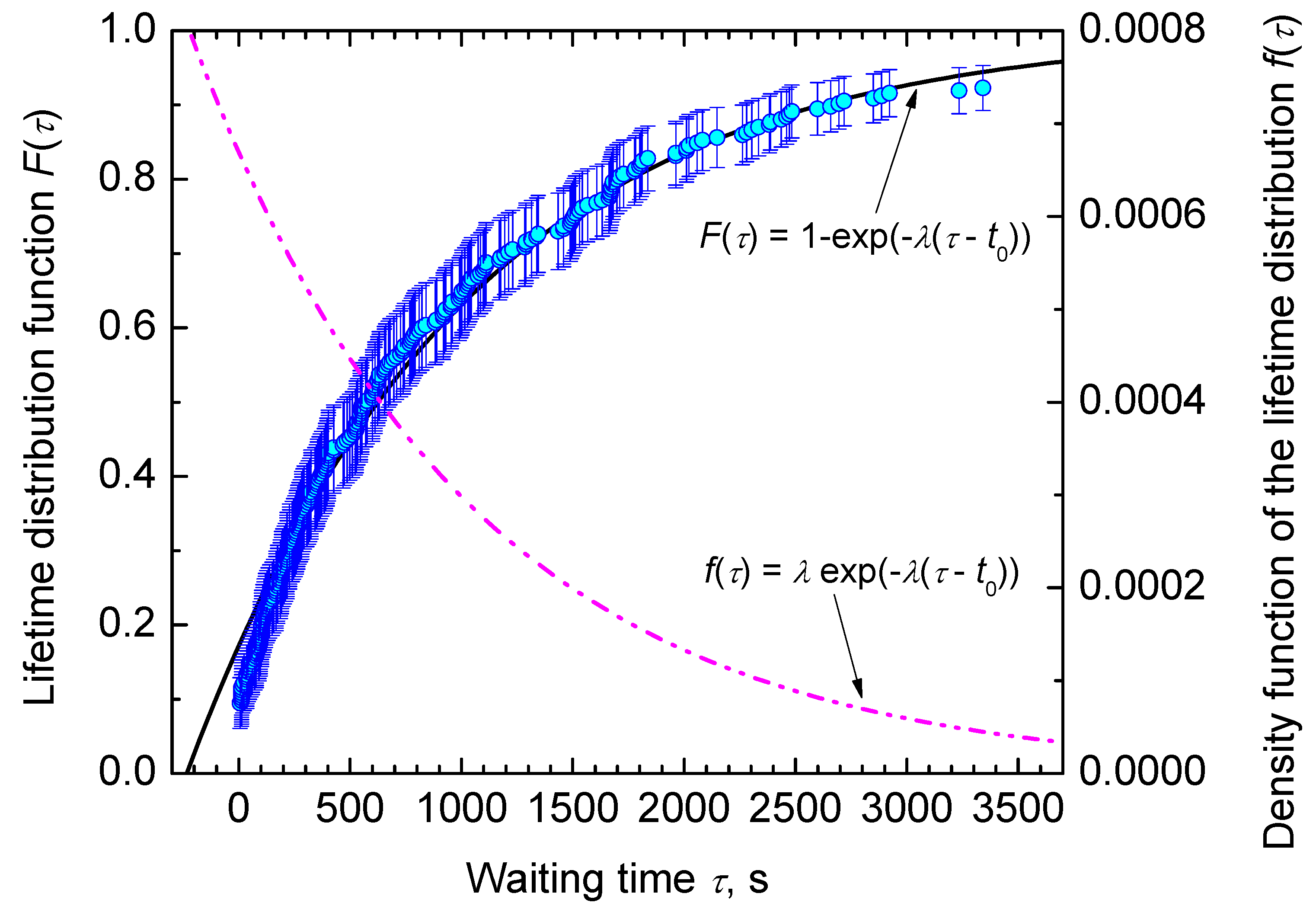
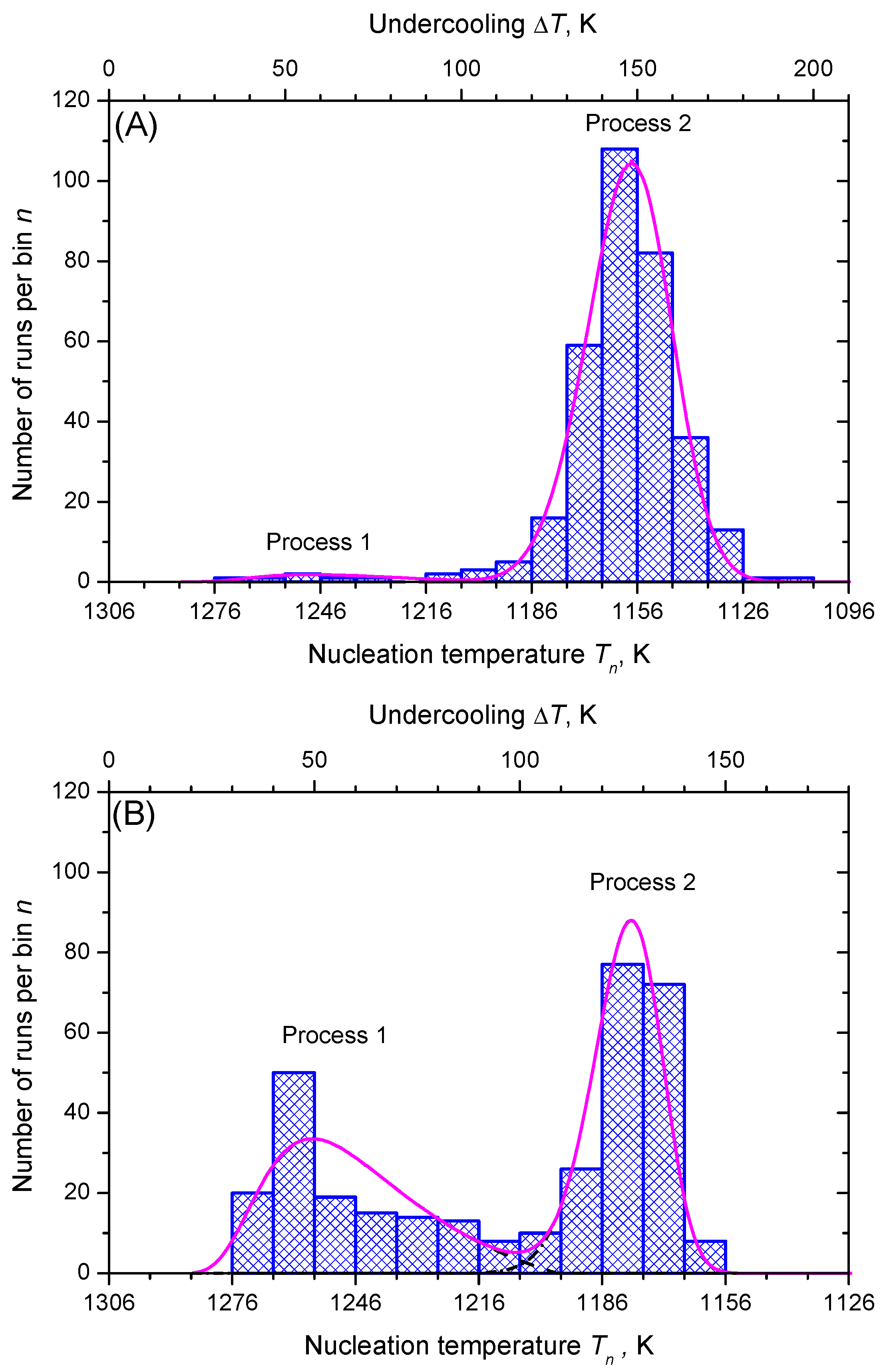
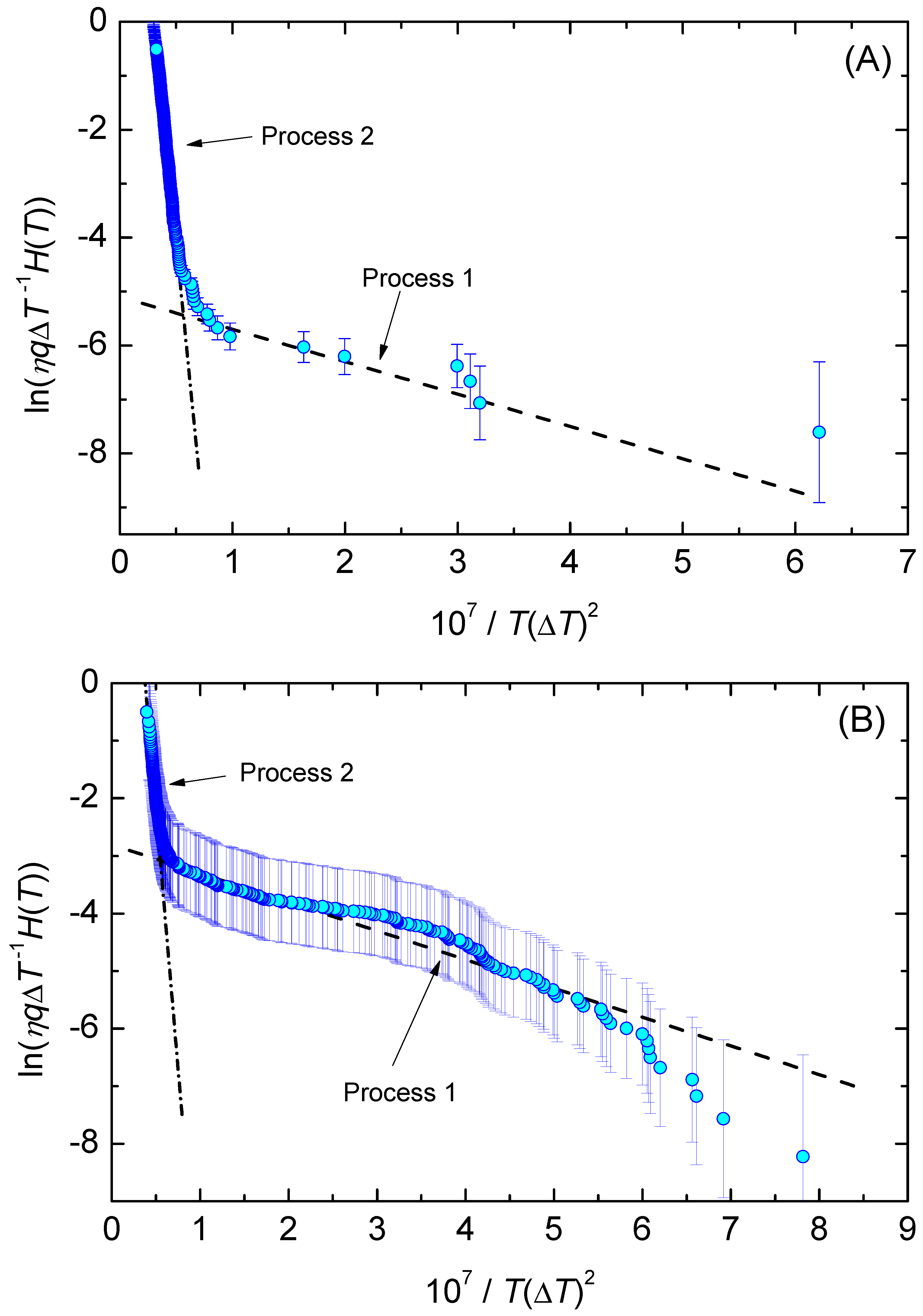
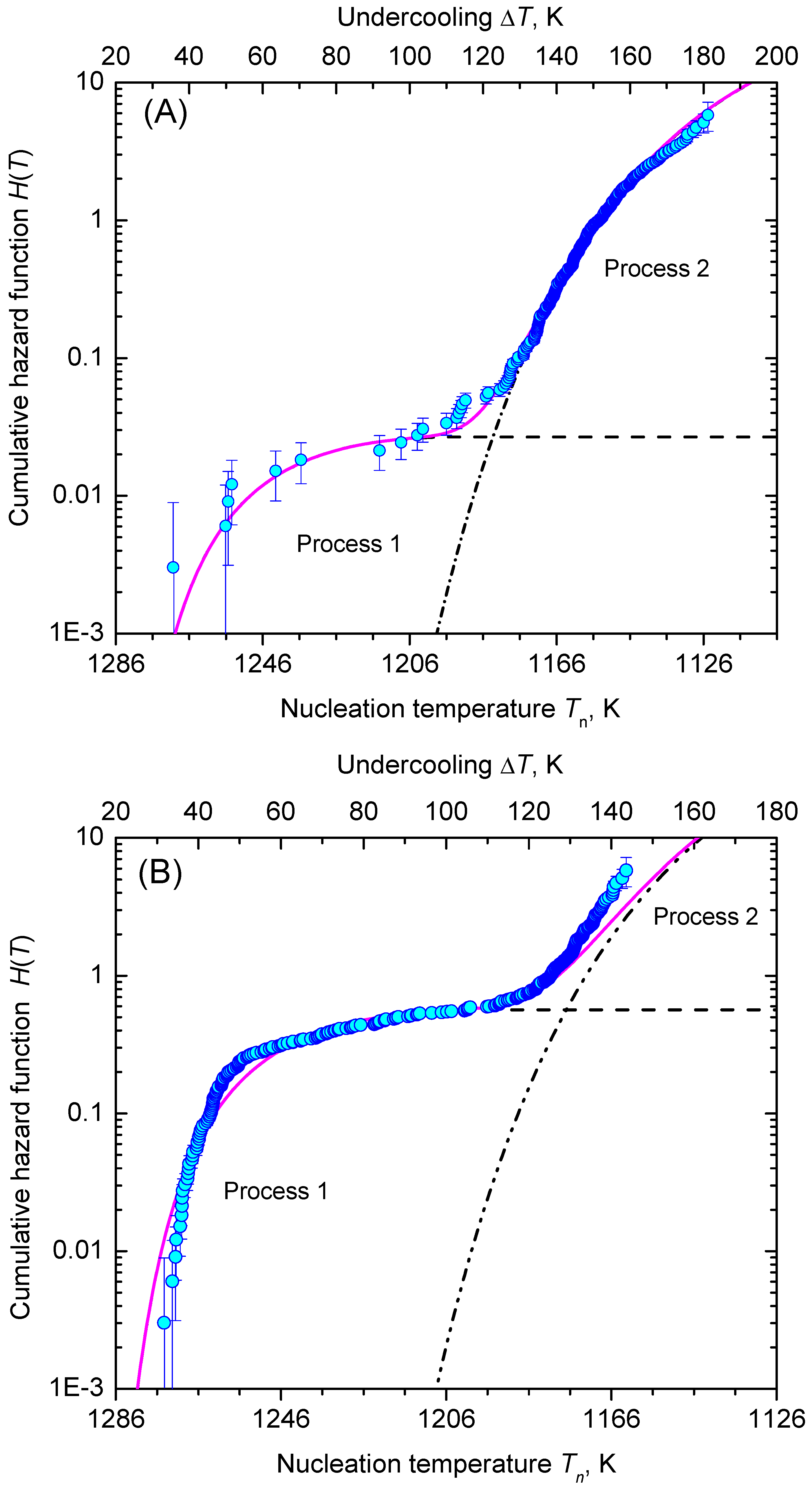
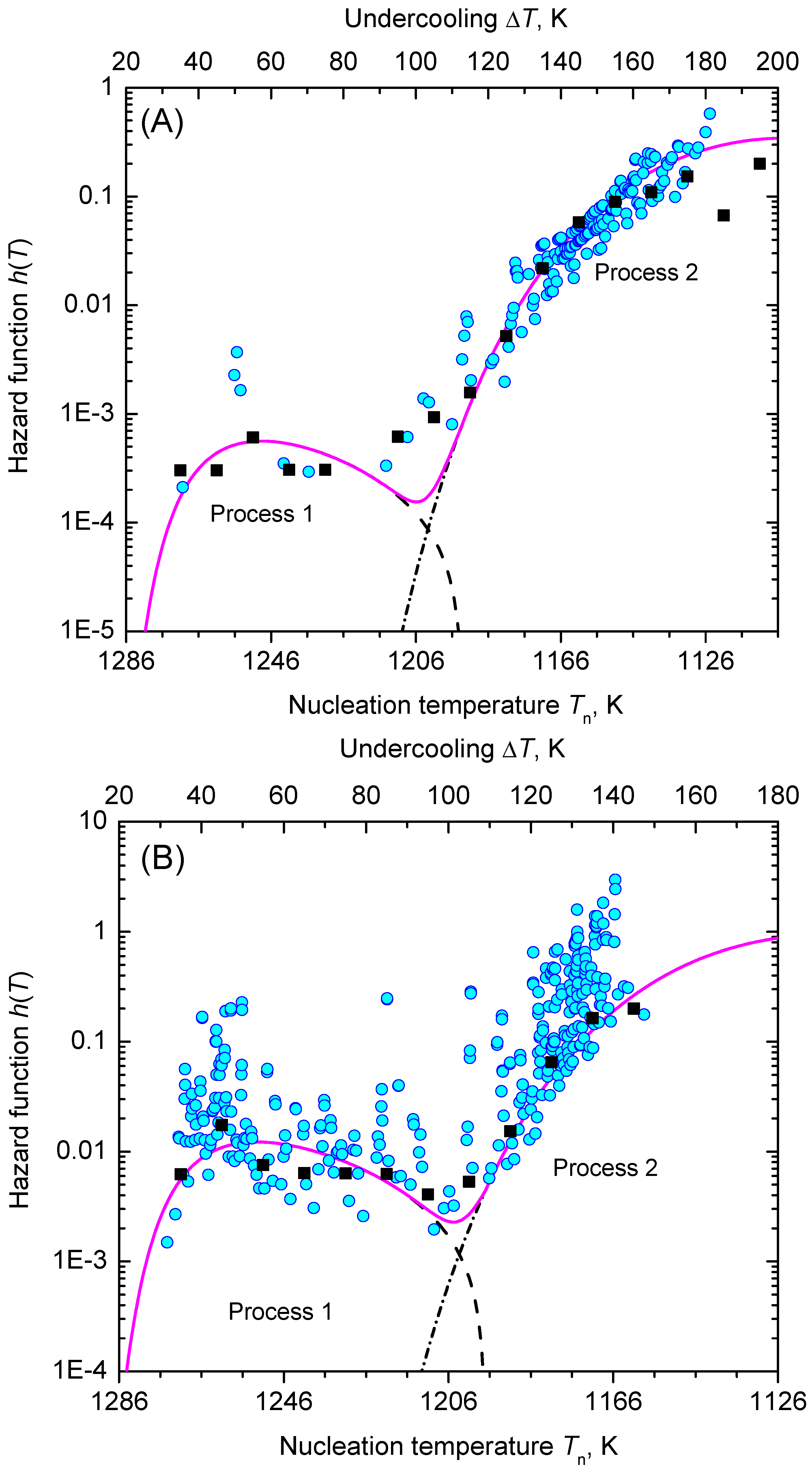
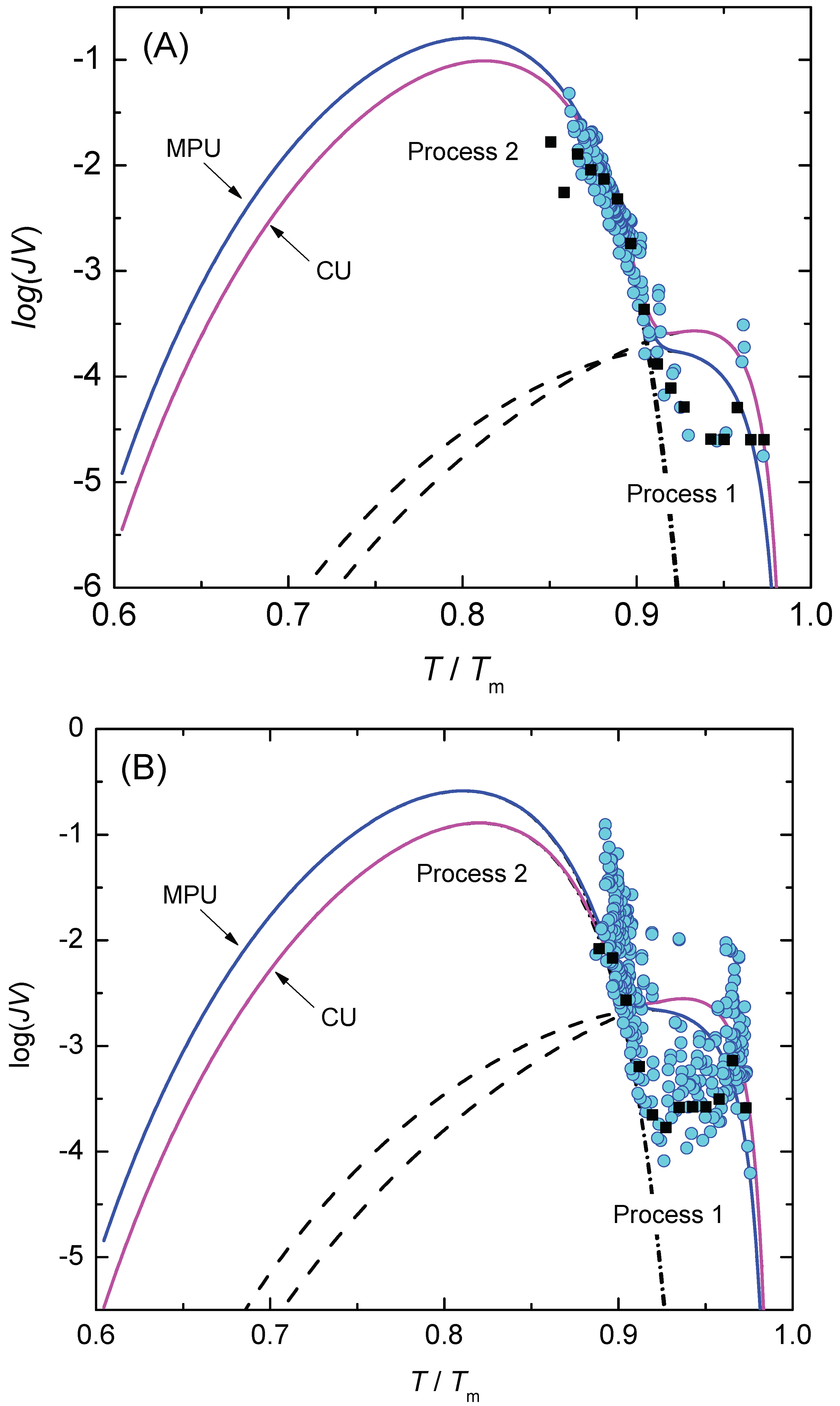
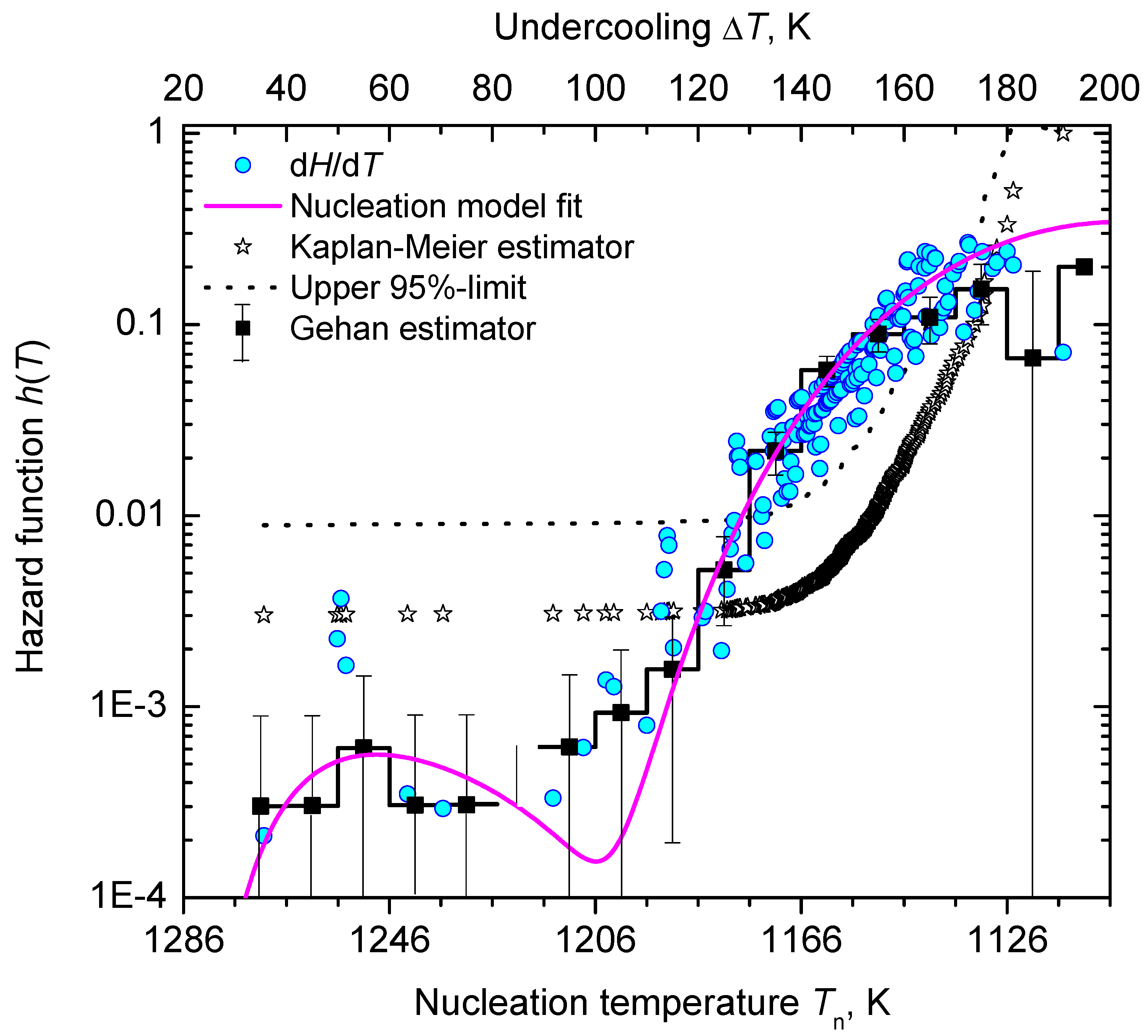
3.2. Nucleation at Constant Temperature
3.3. Nucleation at Cooling with a Constant Cooling Rate
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gibbs, J.W. The Collected Works. In Thermodynamics; Longmans & Green: New York, NY, USA; London, UK; Toronto, ON, Canada, 1928; Volume 1. [Google Scholar]
- Volmer, M. Kinetik der Phasenbildung (Engl.: Kinetics of Phase Formation); Th. Steinkopff: Dresden, Germany, 1939. [Google Scholar]
- Ulbricht, H.; Schmelzer, J.W.P.; Mahnke, R.; Schweitzer, F. Thermodynamics of Finite Systems and the Kinetics of First-Order Phase Transitions; Teubner-Texte zur Physik; Teubner-Verlag: Leipzig, Germany, 1988; Volume 17. [Google Scholar]
- Einstein, A. Zur Theorie der Brownschen Bewegung (Engl: On the theory of Brownian motion). Annalen der Physik 1906, 20, 199–206. [Google Scholar] [CrossRef]
- Einstein, A. Theorie der Opaleszenz von homogenen Flüssigkeiten und Flüssigkeitsgemischen in der Nähe des kritischen Zustandes (Engl: The Theory of the Opalescence of Homogeneous Fluids and Liquid Mixtures near the Critical State). Annalen der Physik 1910, 33, 1275–1298. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifschitz, E.M. Statistische Physik; Akademie-Verlag: Berlin, Germany, 1969; Statistical Physics; Pergamon Press: New York, NY, USA, 1980. [Google Scholar]
- Volmer, M.; Weber, A. Keimbildung in übersättigten Gebilden (Engl.: Nucleation in supersaturated samples). Z. Phys. Chemie 1926, 119, 227–301. [Google Scholar]
- Thomson, J.J. Conduction of Electricity Through Gases, 2nd ed.; Cambridge University Press: Cambridge, UK, 1906. [Google Scholar]
- Schmelzer, J.W.P.; Fokin, V.M.; Abyzov, A.S.; Zanotto, E.D.; Gutzow, I. How Do Crystals Form and Grow in Glass-Forming Liquids: Ostwald’s Rule of Stages and Beyond. Int. J. Appl. Glass Sci. 2010, 1, 16–26. [Google Scholar] [CrossRef]
- Abyzov, A.S.; Schmelzer, J.W.P.; Fokin, V.M.; Zanotto, E.D. Crystallization of supercooled liquids: Self-consistency correction of the steady-state nucleation rate. Entropy 2020, 22, 558. [Google Scholar] [CrossRef]
- Gutzow, I.S.; Schmelzer, J.W.P. The Vitreous State: Thermodynamics, Structure, Rheology, and Crystallization, 1st ed.; Springer: Berlin, Germany, 1995. [Google Scholar]
- Gutzow, I.S.; Schmelzer, J.W.P. The Vitreous State: Thermodynamics, Structure, Rheology, and Crystallization, 2nd ed.; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- James, P.F. Volume nucleation in silicate glasses. In Glasses and Glass-Ceramics; Levis, M.H., Ed.; Chapman and Hall: London, UK, 1989; Chapter 3; pp. 59–105. [Google Scholar]
- Zanotto, E.D.; James, P.F. Experimental tests of the classical nucleation theory for glasses. J. Non-Cryst. Solids 1985, 74, 373–394. [Google Scholar] [CrossRef]
- Deubener, J.; Brückner, R.; Sternitzke, M. Induction-time analysis of nucleation and crystal growth in di- and metasilicate glasses. J. Non-Cryst. Solids 1993, 163, 1–12. [Google Scholar] [CrossRef]
- Fokin, V.M.; Zanotto, E.D.; Yuritsyn, N.S.; Schmelzer, J.W.P. Homogeneous crystal nucleation in silicate glasses: A 40 years perspective. J. Non-Cryst. Solids 2006, 352, 2681–2714. [Google Scholar] [CrossRef]
- Tammann, G. Glasses as supercooled liquids. J. Soc. Glass Technol. 1925, 9, 166–185. [Google Scholar]
- Toschev, S.; Markov, I. Electrolytic nucleation of cadmium. Electrochim. Acta. 1967, 12, 281–286. [Google Scholar] [CrossRef]
- Toschev, S.; Milchev, A.; Stoyanov, S. On some probabilistic aspects of the nucleation process. J. Crystal Growth 1972, 13–14, 123–127. [Google Scholar] [CrossRef]
- Toschev, S.; Gutzow, I. Nichtstationäre Keimbildung: Theorie und Experiment (Engl.: Non-stationary nucleation: Theory and Experiment). Kristall und Technik 1972, 7, 43–73. [Google Scholar] [CrossRef]
- Morton, C.W.; Hofmeister, W.H.; Bayuzick, R.J.; Robinson, M.B. A statistical approach to understanding nucleation phenomena. Mater. Sci. Eng. 1994, A 178, 209–215. [Google Scholar] [CrossRef]
- Uttormark, M.J.; Zanter, J.W.; Perepezko, J.H. Repeated nucleation in an undercooled aluminum droplet. J. Crystal Growth 1997, 177, 258–264. [Google Scholar] [CrossRef]
- Wilde, G.; Sebright, J.L.; Perepezko, J.H. Bulk liquid undercooling and nucleation in gold. Acta Mater. 2006, 54, 4759–4769. [Google Scholar] [CrossRef]
- Wilde, G.; Santhaweesuk, C.; Sebright, J.L.; Bokeloh, J.; Perepezko, J.H. Kinetics of heterogeneous nucleation on intrinsic nucleants in pure fcc-transition metals. J. Phys. Condens. Matter. 2009, 21, 464113. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Gao, Y.L.; Zou, C.D.; Zhai, Q.J.; Zhuravlev, E.; Schick, C. Repeated nucleation in an undercooled tin droplet by fast scanning calorimetry. Mater. Lett. 2009, 63, 2476–2478. [Google Scholar] [CrossRef]
- Yang, B.; Gao, Y.; Zou, C.; Zhai, Q.; Abyzov, A.S.; Zhuravlev, E.; Schmelzer, J.W.P.; Schick, C. Cooling Rate Dependence of Undercooling of Pure Sn Single Drop by Fast Scanning Calorimetry. Appl. Phys. A Mater. Sci. Process. 2011, A 104, 189–196. [Google Scholar] [CrossRef]
- Yang, B.; Abyzov, A.S.; Zhuravlev, E.; Gao, Y.; Schmelzer, J.W.P.; Schick, C. Size Dependent Nucleation of Single Tin Particles by Differential Fast Scanning Calorimetry. J. Chem. Phys. 2013, 138, 054501/1-15. [Google Scholar] [CrossRef] [PubMed]
- Barlow, T.W.; Haymet, A.D.J. ALTA: An automated lag-time apparatus for studying the nucleation of supercooled liquids. Rev. Sci. Instrum. 1995, 66, 2996–3007. [Google Scholar] [CrossRef]
- Heneghan, A.F.; Wilson, P.W.; Wang, G.; Haymet, A.D.J. Liquid-to-crystal nucleation: Automated lag-time apparatus to study supercooled liquids. J. Chem. Phys. 2001, 115, 7599–7608. [Google Scholar] [CrossRef]
- Heneghan, A.F.; Haymet, A.D.J. Liquid-to-crystal nucleation: A new generation lag-time apparatus. J. Chem. Phys. 2002, 117, 5319–5327. [Google Scholar] [CrossRef]
- Heneghan, A.F.; Wilson, P.W.; Haymet, A.D.J. Heterogeneous nucleation of supercooled water, and the effect of an added catalyst. Proc. Natl. Acad. Sci. USA 2002, 99, 9631–9634. [Google Scholar] [CrossRef] [PubMed]
- Wilson, P.W.; Lester, D.; Haymet, A.D.J. Heterogeneous nucleation of clathrates from supercooled tetrahydrofuran (THF)/water mixtures, and the effect of an added catalyst. Chem. Eng. Sci. 2005, 60, 2937–2941. [Google Scholar] [CrossRef]
- Maeda, N.; Wells, D.; Becker, N.C.; Hartley, P.G.; Wilson, P.W.; Haymet, D.J.; Kozielski, K.A. Development of a high pressure automated lag-time apparatus for experimental studies and statistical analyses of nucleation and growth of gas hydrates. Rev. Sci. Instrum. 2011, 82, 065109. [Google Scholar] [CrossRef] [PubMed]
- Maeda, N.; Wells, D.; Hartley, P.G.; Kozielski, K.A. Statistical analysis of supercooling in fuel gas hydrate systems. Energy Fuels. 2012, 26, 1820–1827. [Google Scholar] [CrossRef]
- Krüger, S.; Deubener, J. Stochastic nature of the liquid-to-crystal heterogeneous nucleation of supercooled lithium disilicate liquid. J. Non-Cryst. Solids 2014, 388, 6–9. [Google Scholar] [CrossRef]
- Krüger, S.; Deubener, J. Lag-time to crystal nucleation of supercooled lithium disilicate melts: A test of the classical nucleation theory. J. Non-Cryst. Solids 2015, 426, 1–6. [Google Scholar] [CrossRef]
- Krüger, S.; Deubener, J. The TTT-curves of the heterogeneous and homogeneous crystallization of lithium disilicate—A stochastic approach to crystal nucleation. Front. Mater. 2016, 3, 42. [Google Scholar] [CrossRef][Green Version]
- Krüger, S.; Deubener, J. Thermal analysis of repetitive single crystallization events in glass-forming liquids at low undercooling. J. Non-Cryst. Solids 2018, 501, 36–42. [Google Scholar] [CrossRef]
- Al-Mukadam, R.; Deubener, J. Effects of cooling rate and oxygen partial pressure on heterogeneous crystal nucleation of supercooled lithium disilicate melt in PtRh20-containers. J. Non-Cryst. Solids 2019, 524, 119642. [Google Scholar] [CrossRef]
- Baidakov, V.G. Crystallization of Undercooled Liquids: Results of Molecular Dynamics Simulations. In Glass: Selected Properties and Crystallization; Schmelzer, J.W.P., Ed.; de Gruyter: Berlin, Germany, 2014; pp. 481–520. [Google Scholar]
- Sosso, G.C.; Chen, J.; Cox, S.J.; Fitzner, M.; Pedevilla, P.; Zen, A.; Michaelides, A. Crystal Nucleation in Liquids: Open Questions and Future Challenges in Molecular Dynamics Simulations. Chem. Rev. 2016, 116, 7078–7116. [Google Scholar] [CrossRef] [PubMed]
- Schmelzer, J.W.P.; Abyzov, A.S.; Baidakov, V.G. Time of formation of the first supercritical nucleus, time-lag, and the steady-state nucleation rate. Int. J. Appl. Glass Sci. 2017, 8, 48–60. [Google Scholar] [CrossRef]
- Lee, E.T.; Wang, J.W. Statistical Methods for Survival Data Analysis, 4th ed.; Wiley: Hoboken, NJ, USA, 2013; pp. 1–16. [Google Scholar]
- McPherson, J.W. Reliability Physics and Engineering: Time-to-Failure Modeling; Springer: New York, NY, USA, 2010; pp. 63–93. [Google Scholar]
- Varshneya, A.K.; Mauro, J.C. Fundamentals of Inorganic Glasses, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 487–536. [Google Scholar]
- Skripov, V.P.; Koverda, V.P. Spontaneous Crystallization of Undercooled Liquids; Nauka: Moscow, Russia, 1984. (In Russian) [Google Scholar]
- Baidakov, V.G. Explosive Boiling of Superheated Cryogenic Liquids; WILEY-VCH: Berlin-Weinheim, Germany, 2007. [Google Scholar]
- Schmelzer, J.W.P.; Abyzov, A.S. On the Theoretical Description of Nucleation in Confined Space. Am. Inst. Phys. Adv. 2011, 1, 042160/1-9. [Google Scholar] [CrossRef]
- Zeldovich, Y.B. On the Theory of New Phase Formation: Cavitation. Sov. Phys. JETP 1942, 12, 525–538. [Google Scholar]
- Gutzow, I.S.; Schmelzer, J.W.P.; Dobreva, A. Kinetics of Transient Nucleation in Glass-Forming Liquids: A Retrospective and Recent Results. J. Non-Cryst. Solids 1997, 219, 1–16. [Google Scholar] [CrossRef]
- Yang, B.; Perepezko, J.H.; Schmelzer, J.W.P.; Gao, Y.; Schick, C. Dependence of crystal nucleation on prior liquid overheating by differential fast scanning calorimeter. J. Chem. Phys. 2014, 140, 104513/1-7. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Yang, B.; Zhao, B.; Abyzov, A.S.; Schmelzer, J.W.P.; Schick, C.; Lu, F.; Zhai, Q.; Gao, Y. Rapid solidification behavior of nano-sized Sn droplets embedded in the Al matrix by nanocalorimetry. Mater. Res. Express 2014, 1, 045012/1-15. [Google Scholar] [CrossRef]
- Zhao, B.; Yang, B.; Abyzov, A.S.; Schmelzer, J.W.P.; Rodriguez-Viejo, J.; Zhai, Q.; Schick, C.; Gao, Y. Beating Homogeneous Nucleation and Tuning Atomic Ordering in Glass-Forming Metals by Nanocalorimetry. Nano Lett. 2017, 17, 7751–7760. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Schmelzer, J.W.P.; Zhao, B.; Gao, Y.; Schick, C. Glass transition and primary crystallization of Al86Ni6Y4.5Co2La1.5 metallic glass at heating rates spanning over six orders of magnitude. Scr. Mater. 2019, 162, 146–150. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M.; Schick, C. Kauzmann paradox and the crystallization of glass-forming melts. J. Non-Cryst. Solids 2018, 501, 21–35. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Tropin, T.V. Glass transition, crystallization of glass-forming melts, and entropy. Entropy 2018, 20, 103. [Google Scholar] [CrossRef] [PubMed]
- Schmelzer, J.W.P.; Tropin, T.V.; Fokin, V.M.; Abyzov, A.S.; Zanotto, E.D. Effects of Glass Transition and Structural Relaxation on Crystal Nucleation: Theoretical Description and Model Analysis. Entropy 2020, 22, 1098. [Google Scholar] [CrossRef]
- Bartels, J.; Lembke, U.; Pascova, R.; Schmelzer, J.W.P.; Gutzow, I. Evolution of Cluster Size Distributions in Nucleation and Growth Processes. J. Non-Cryst. Solids 1991, 136, 181–197. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction kinetics in differential thermal analysis. Anal. Chem. 1957, 29, 1702-06. [Google Scholar] [CrossRef]
- Blaine, R.L.; Kissinger, H.E. Homer Kissinger and the Kissinger equation. Thermochim. Acta 2012, 540, 1–6. [Google Scholar] [CrossRef]
- Vyazovkin, S. Kissinger Method in Kinetics of Materials: Things to Beware and Be Aware of. Molecules 2020, 25, 2813. [Google Scholar] [CrossRef] [PubMed]
- Tammann, G. Über die Abhängigkeit der Zahl der Keime, die sich in verschiedenen unterkühlten Flüssigkeiten bilden, von der Temperatur (Engl.: On the dependence on the number of nuclei formed in various undercooled liquids on temperature). Z. Phys. Chem. 1898, 25, 441–473. [Google Scholar]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M.; Schick, C.; Zanotto, E.D. Crystallization in glass-forming liquids: Maxima of nucleation, growth, and overall crystallization rates. J. Non-Cryst. Solids 2015, 429, 24–31. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S. Crystallization of glass-forming melts: New answers to old questions. J. Non-Cryst. Solids 2018, 501, 11–20. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Baidakov, V.G. Entropy and the Tolman Parameter in Nucleation Theory. Entropy 2019, 21, 670. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Schick, C. General concepts of crystallization: Some recent results and possible future developments. In Advances in Dielectrics Series; Crystallization as studied by Broadband Dielectric, Spectroscopy; Kremer, F., Series editor, Ezquerra, T.A., Nogales, A., Eds.; Springer, Nature Switzerland AG: Cham, Switzerland, 2020. [Google Scholar]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M. Thermodynamic aspects of pressure-induced crystallization: Kauzmann pressure. Int. J. Appl. Glass Sci. 2016, 7, 474–485. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S. Pressure dependence of viscosity: A new general relation. Interfacial Phenom. Heat Transf. 2017, 5, 107–112. [Google Scholar] [CrossRef]
- Hellmuth, O.; Schmelzer, J.W.P.; Feistel, R. Ice-Crystal Nucleation in Water: Thermodynamic Driving Force and Surface Tension. Part I: Theoretical Foundation. Entropy 2019, 21, 50. [Google Scholar] [CrossRef]
- Baidakov, V.G.; Tipeev, A.O.; Bobrov, K.S.; Ionov, G.V. Crystal nucleation rate isotherms in Lennard-Jones liquids. J. Chem. Phys. 2010, 132, 234505. [Google Scholar] [CrossRef] [PubMed]
- Baidakov, V.G.; Tipeev, A.O. The Kinetics of the Liquid Phase Nucleation in a Stretched fcc-Crystal: A Molecular Dynamics Simulation. Phys. Solid State 2018, 60, 1853–1860. [Google Scholar] [CrossRef]
- Baidakov, V.G.; Kaverin, A.M. Attainable superheatings and stretchings of methane-hydrogen solutions. Int. J. Heat Mass Transf. 2020, 163, 120498. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S. Crystallization of glass-forming liquids: Thermodynamic driving force. J. Non-Cryst. Solids 2016, 449, 41–49. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M.; Schick, C.; Zanotto, E.D. Crystallization in glass-forming liquids: Effects of decoupling of diffusion and viscosity on crystal growth. J. Non-Cryst. Solids 2015, 429, 45–53. [Google Scholar] [CrossRef]
- Gehan, E.A. Estimating survival functions from the life table. J. Chron. Disease 1969, 21, 629–644. [Google Scholar] [CrossRef]
- Kalbfleisch, J.D.; Prentice, R.L. The Statistical Analysis of Failure Time Data, 2nd ed.; Wiley: New York, NY, USA, 2002; pp. 14–19. [Google Scholar]
- Kaplan, E.L.; Meier, P. Non-parametric estimation from incomplete data. J. Am. Stat. Assoc. 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Greenwood, M. The Natural Duration of Cancer, Report on Public Health and Medical Subjects; Her Majesty’s Stationary Office: London, UK, 1926; Volume 33, pp. 1–26. [Google Scholar]
- Rinne, H. The Hazard Rate: Theory and Inference; Justus-Liebig-Universität Giessen: Giessen, Germany, 2014; pp. 149–151. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deubener, J.; Schmelzer, J.W.P. Statistical Approach to Crystal Nucleation in Glass-Forming Liquids. Entropy 2021, 23, 246. https://doi.org/10.3390/e23020246
Deubener J, Schmelzer JWP. Statistical Approach to Crystal Nucleation in Glass-Forming Liquids. Entropy. 2021; 23(2):246. https://doi.org/10.3390/e23020246
Chicago/Turabian StyleDeubener, Joachim, and Jürn W. P. Schmelzer. 2021. "Statistical Approach to Crystal Nucleation in Glass-Forming Liquids" Entropy 23, no. 2: 246. https://doi.org/10.3390/e23020246
APA StyleDeubener, J., & Schmelzer, J. W. P. (2021). Statistical Approach to Crystal Nucleation in Glass-Forming Liquids. Entropy, 23(2), 246. https://doi.org/10.3390/e23020246






