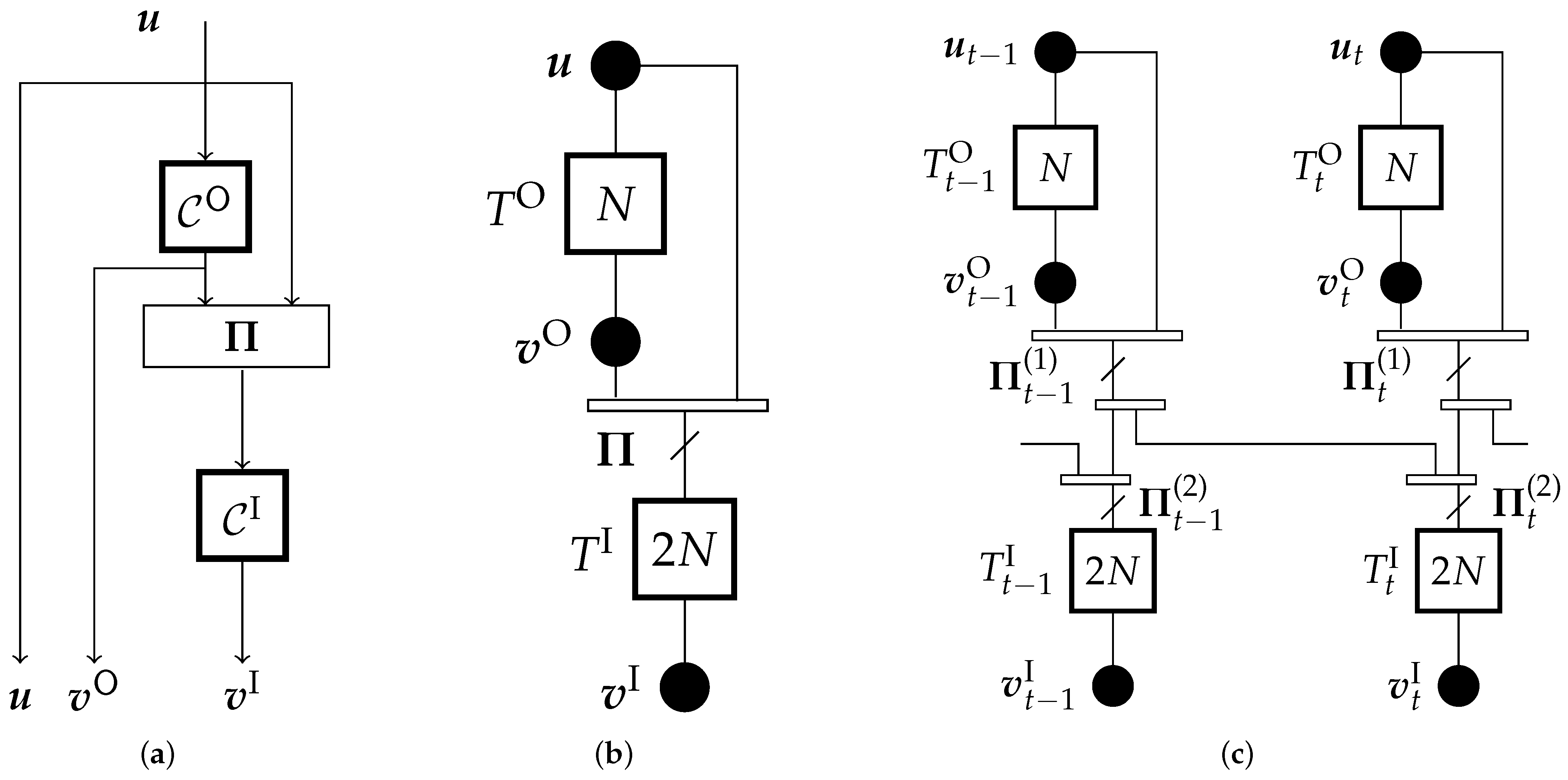
1. Introduction
Turbo-like codes (TCs) [
1]—such as parallel concatenated codes (PCCs) and serially concatenated codes (SCCs)—and low-density parity-check (LDPC) codes [
2] are widely used in communication systems due to their excellent performance and low-complexity decoding. In most cases, the design of these codes is based on the optimization of the iterative belief propagation (BP) decoding threshold, which can be performed via density evolution (DE).
The exact BP thresholds of LDPC codes over the binary erasure channel (BEC) can be easily obtained recursively from a set of DE equations using a scalar representation of the message densities, whereas for the AWGN channel they can be obtained via quantized DE [
3]. Alternatively, the BP threshold may be estimated by means of extrinsic information transfer (EXIT) function analysis [
4,
5], where the densities of the messages are approximated by a Gaussian distribution. For the AWGN channel and binary transmission, the Gaussian approximation yields thresholds close to those obtained via DE, while simplifying the computation. The BP thresholds of the major TC ensembles—PCCs, SCCs, braided convolutional codes (BCCs), and hybrid concatenated codes (HCCs)—over the BEC were computed by Moloudi et al. in [
6,
7] by using the decoder transfer functions of the component codes that map the input and output erasure probabilities of the message sequences. Unfortunately, the decoder transfer functions are not available for the AWGN channel, which hinders the derivation of the exact DE equations. In [
8], a Monte Carlo (MC)-based DE (MC-DE) was proposed for the threshold analysis of BCCs over the AWGN channel. The MC-DE, however, is computationally demanding compared to the simple DE for TCs over the BEC. Moreover, MC-DE for TCs, which entails running BCJR decoding of the component codes, is significantly harder than the quantized DE or the EXIT chart technique for LDPC codes.
Spatial coupling [
9] allows us to construct particularly powerful codes. Thanks to the threshold saturation phenomenon, the BP decoding threshold of a spatially coupled ensemble can achieve the maximum a posteriori (MAP) decoding threshold of the underlying uncoupled ensemble. Remarkably, spatially coupled LDPC codes universally achieve capacity over the class of binary-input memoryless symmetric channels [
10]. The concept of spatial coupling was extended to turbo-like codes in [
6].
Quantized DE for SC-LDPC codes is time consuming, due to the large number of edge types in the corresponding graph. The complexity of MC-DE of spatially coupled (SC) TCs (SC-TCs) is even higher, and hence the computation of the thresholds becomes challenging. Efficient methods that allow to accurately predict the BP thresholds are therefore of practical interest. In [
11], the BP thresholds of randomly-punctured LDPC codes over the AWGN channel were efficiently predicted by using their corresponding BEC thresholds. The same idea was later used in [
8] to predict the thresholds of BCCs over the AWGN channel using the BEC thresholds of BCCs [
6]. The resulting thresholds for SC-BCCs, which have a regular graph representation, are close to those obtained using MC-DE, which can be attributed to the universality of this ensemble.
In this paper, we perform a comprehensive threshold analysis of several classes of uncoupled and coupled TCs—PCCs, SCCs, BCCs, and HCCs—over the AWGN channel, by discussing several efficient methods for threshold computation. More concretely, we review MC-DE with Gaussian approximation and MC-DE where the true densities are estimated using histograms. We also discuss the prediction of the BP thresholds using the thresholds of the corresponding ensembles over the BEC. Further, we discuss the efficient computation of the BP thresholds of punctured TCs from those of the corresponding mother code. We show that for spatially coupled TC ensembles with strong underlying uncoupled code, a very accurate prediction of the BP threshold over the AWGN channel can be efficiently obtained for a large range of coding rates from the BP threshold of the corresponding mother code ensembles over the BEC. We conjecture that the accurate predictions can be attributed to the universality of these code ensembles due to threshold saturation.
The rest of the paper is structured as follows. In
Section 2, the construction of uncoupled and coupled TC ensembles is described using uncoupled and coupled SCCs as an example. A base matrix representation is introduced, which is then used to define the remaining ensembles. In
Section 3, MC-DE for the computation of the BP thresholds of TCs is described in detail. In
Section 4, we discuss threshold prediction methods for randomly punctured TCs. In
Section 5, we compare and discuss the thresholds computed via the different methods for several classes of uncoupled and coupled TCs. Finally,
Section 6 concludes this work.
3. Threshold Computation via Monte Carlo Density Evolution
The BP thresholds can be computed by performing DE. For codes for which the transfer functions of the component codes are not available, MC-DE can be used. In this section, we describe two MC-DE methods and discuss their advantages and shortcomings. The described MC-DE methods are computationally demanding. We hence also discuss an efficient method that provides an approximation of the BP threshold, and compare the thresholds obtained applying the three approaches for uncoupled SCCs.
3.1. Monte-Carlo Density Evolution
MC-DE comprises three key steps [
8], which are performed a number of iterations:
Variable node update: A variable node generates a sequence of extrinsic log-likelihood ratios (LLRs) by properly combining the sequence of Gaussian-distributed channel LLRs and the sequences of extrinsic LLRs—generated according an appropriate distribution—received from the neighboring constraint nodes. In particular, the output LLRs are obtained as the sum of the channel LLR and the LLRs from neighboring constraint nodes.
Constraint node update: A constraint node performs BCJR decoding on the sequences of extrinsic LLRs—used as a-priori information—received from the neighboring variable nodes. The BCJR decoder generates sequences of extrinsic LLRs that are passed to the corresponding neighboring variable nodes.
Density estimation and re-sampling: A sequence of channel LLRs, , and the sequences of extrinsic LLRs, (one for each code sequence), are created from the corresponding probability densities and . These sequences are used in the next MC-DE iteration.
MC-DE tracks the evolution of through the iterative decoding process.
3.2. Monte-Carlo Density Evolution with Gaussian Approximation
In MC-DE with Gaussian approximation (MC-DE-GA), the densities
are approximated by a Gaussian distribution, which can be characterized by its mean
and standard deviation
. Since the extrinsic LLRs are symmetric and consistent, the Gaussian distribution is completely characterized by the single parameter
, which is related to the mean
as
The standard deviation
is computed from the mutual information
between an extrinsic LLR sequence
and the corresponding binary code sequence [
4,
5],
Here
denotes the AWGN channel capacity for a given channel parameter
, which can be computed efficiently using the following series expansion ([
13] Chapter 4):
with
. The mutual information
is computed from [
5]
where
, are the elements of
.
Note that MC-DE-GA is equivalent to an EXIT function analysis. While a threshold computation via the Gaussian assumption becomes highly efficient for LDPC codes, MC-DE-GA has only a minor computational advantage for TCs. Furthermore, for several ensembles, in particular multi-edge type ensembles such as BCCs, SCCs, HCCs, and SC-TCs, the true distributions of the messages may significantly deviate from a Gaussian distribution, leading to inexact decoding thresholds.
3.3. MC-DE with Histogram
A more accurate BP threshold can be obtained by estimating the true densities, which can be performed by means of histograms. We refer to this method as MC-DE-H, which we describe in detail in the following. For ease of notation, let
L be the random variable corresponding to an extrinsic LLR. From the consistency property of the LLRs, we have that
[
5]. The consistency and symmetry properties of
L allow us to determine
from the distribution of
from [
13]
Taking advantage of this symmetry drastically improves the speed of converge of this method.
Without loss of generality, we consider the transmission of the all-zero codeword and approximate the density
in (
6) with a histogram of
M bins and obtain an approximated probability mass function
(For the threshold calculations within this paper we use a fixed number of
bins, divided uniformly between
and
, where
denotes the maximum magnitude among the elements
of the measured sequence. An odd value of
M is recommended to represent erasures accurately. The length of the sequence is chosen adaptively to achieve a desired accuracy). The bit error rate (BER) can be computed from
as
We denote by the approximation of . A sequence of extrinsic LLRs distributed according to can be obtained from by using the probability integral transform. The probability integral transform method states that for a uniformly distributed random variable , and a strictly increasing cumulative distribution function , we have . Samples are generated from by applying the inversion .
3.4. Erasure Channel Prediction
Since MC-DE is time consuming, we are interested in exploring some faster alternatives to predict the BP thresholds of TCs over the AWGN channel. In [
3], the erasure channel prediction (ECP) method was proposed to efficiently predict BP thresholds of codes over the AWGN channel from their corresponding BEC thresholds
. For a given code, the AWGN channel BP threshold
can be obtained from the corresponding
as
where
is the capacity of the BEC.
3.5. Discussion
In
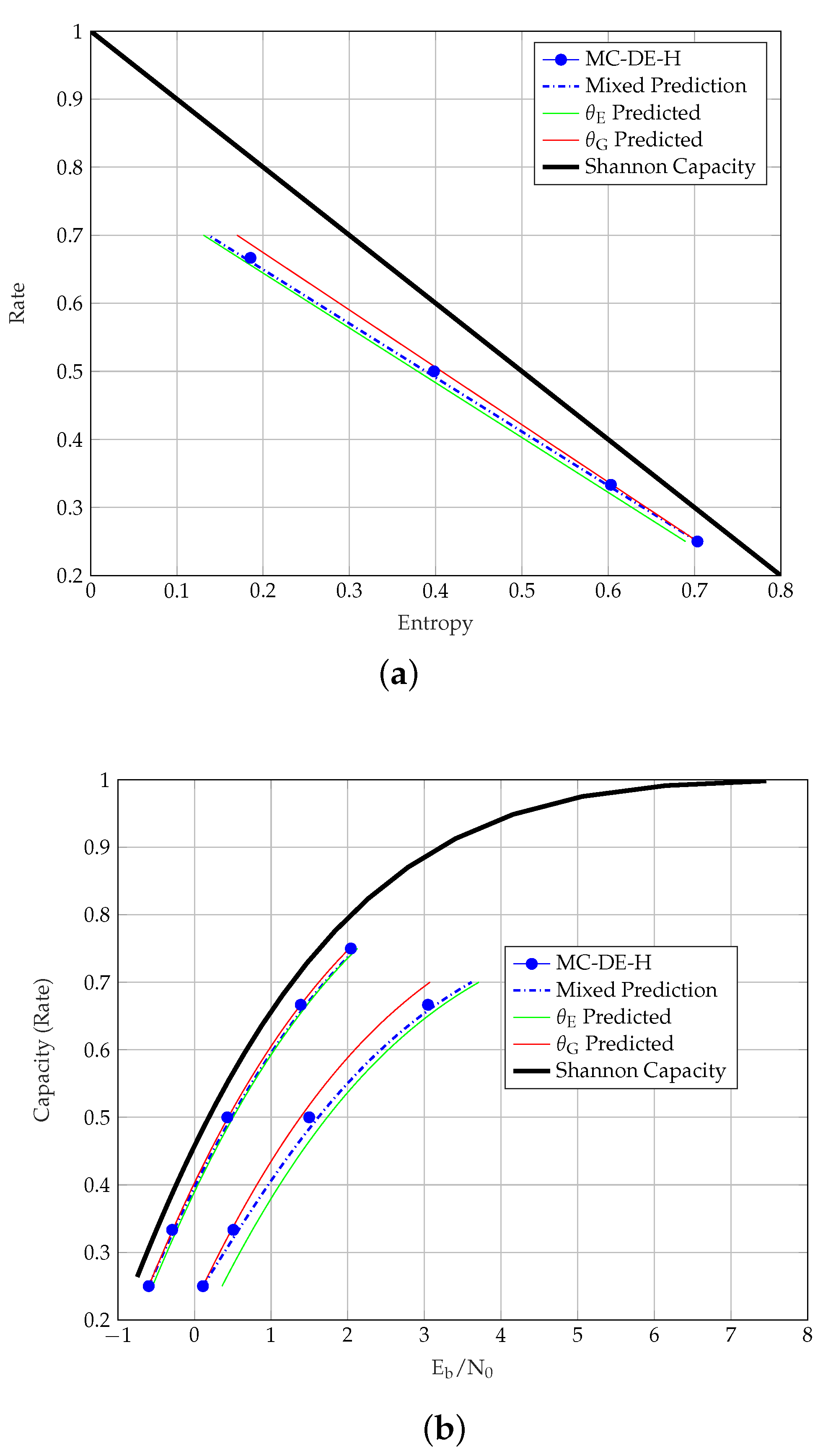
Table 1 we give the BP thresholds of the uncoupled SCCs computed via MC-DE-GA, MC-DE-H, and ECP, for several code rates. We observe that both MC-DE-GA and MC-DE-H yield similar thresholds. However, we remark that the computational complexity of MC-DE-GA and MC-DE-H is similar, as it is primarily dominated by that of the BCJR decoder. Hence, one may resort to MC-DE-H, which does not rely on a Gaussian assumption and gives a more accurate estimation of the threshold provided that the quantization resolution is chosen sufficiently high. The thresholds predicted by the ECP method differ noticeably from those predicted by the MC-DE methods.
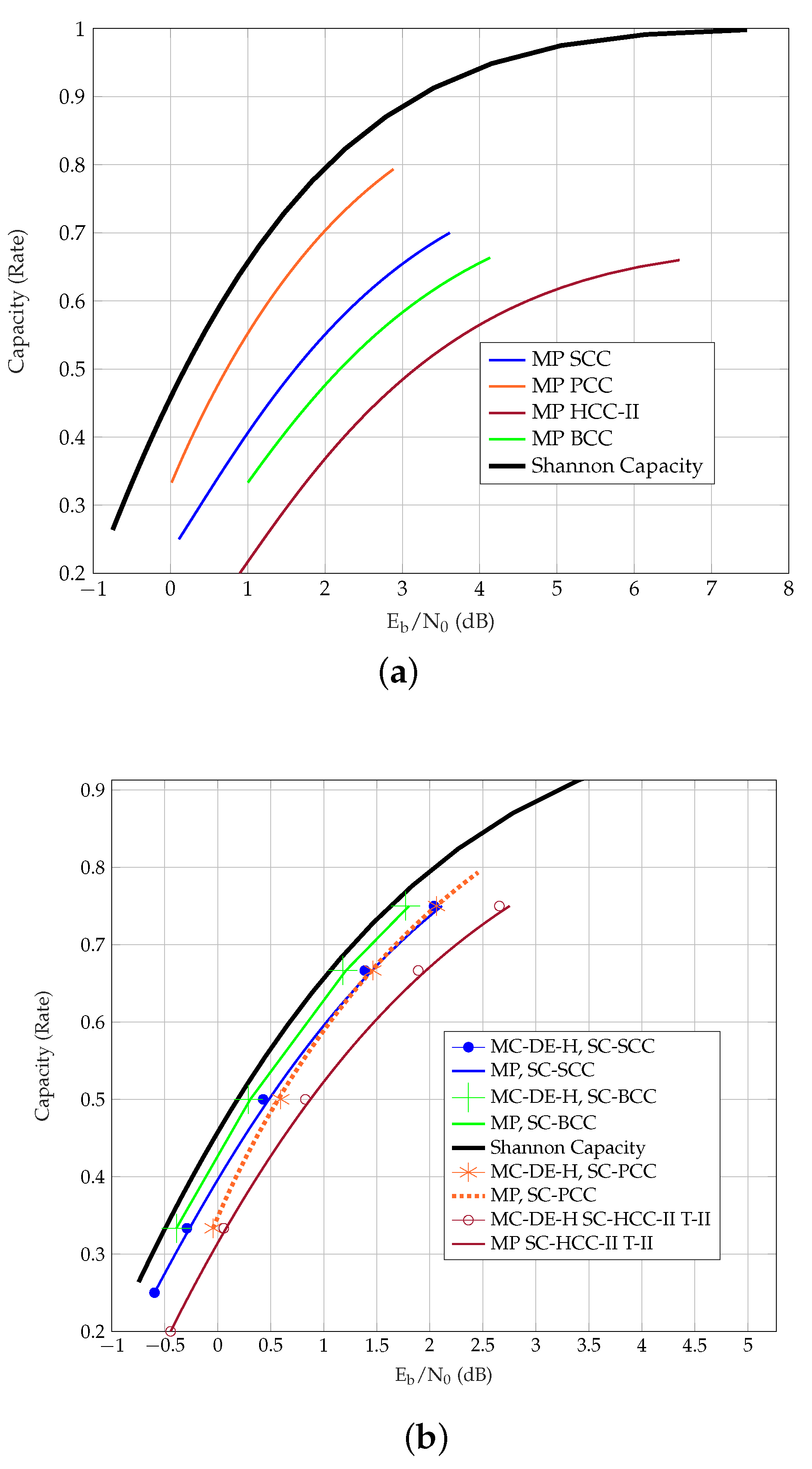
5. Threshold Comparison for Different TC Ensembles
Table 4 presents the MC-DE-H and
predicted thresholds of the coupled TCs. Unlike uncoupled TCs, the predictions are observed to be relatively close to the MC-DE-H thresholds. For this reason, we do not list the
- or MP thresholds of SC-TCs in the table. For the uncoupled ensembles, however, the MP method provides better predicted thresholds than the
method. We further observe that, in general, the
predictions are closer to the Shannon capacity than the
predictions. The exception to this are PCCs, where
predictions are closer to the Shannon capacity than the
predictions, and the gap increases with coupling, as shown in
Figure 3.
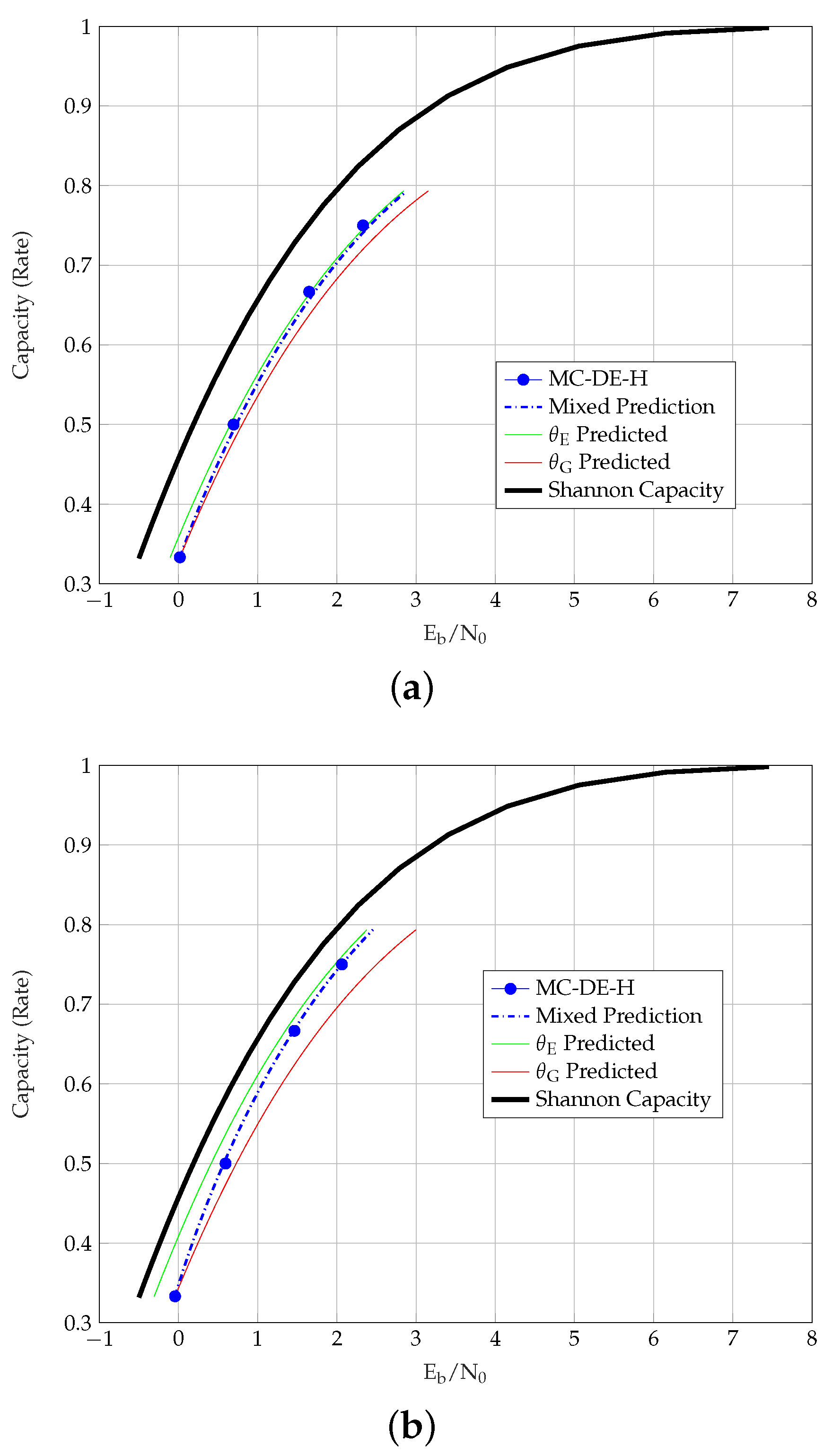
From the thresholds of different TC ensembles, we also observe that the similarity of the MC-DE-H and the predicted thresholds depends on an ensemble’s strength. For stronger TCs, the similarity between the predicted and the MC-DE-H thresholds is clearly observed, as shown for
SC-SCCs in
Figure 4a,
SC-BCCs in
Figure 5, and
SC-HCCs-II type-II in
Figure 4b. We further observe that the predicted and the MC-DE-H thresholds are not alike (1) for PCCs in
Figure 3, as these have BP thresholds close to the MAP thresholds but relatively poor MAP thresholds (2) for other uncoupled TCs in general and SC-HCCs-II type-I in
Figure 4b, as these have strong MAP but poor BP thresholds and (3) for the SC-HCCs-II type-II with
in
Figure 4b, which have a good MAP threshold but require a larger coupling memory.
SC-HCCs-II offer an interesting insight regarding the similarity of predicted and MC-DE-H thresholds of an ensemble. HCCs-II have the strongest MAP thresholds on the BEC among all considered TC ensembles, and we expect the threshold predictions to show strong similarity with spatial coupling. From the thresholds of the SC-HCCs-II in
Figure 4b, however, we observe that this strong similarity is only visible for the SC-HCC-II type-II ensemble with
. The SC-HCC-II type-I ensemble, which uses a different type of coupling than the type-II, shows a weaker BP performance and lower similarity than the type-II, even at a larger coupling memory
. This suggests that in addition to a strong MAP threshold, the capability of an ensemble to exhibit very similar predicted and MC-DE-H thresholds is also linked to its ability of achieving threshold saturation [
14]. For those SC-TCs that demonstrate threshold saturation, we have additionally computed the binary symmetric channel (BSC) thresholds and compare the entropy of the thresholds for the BSC, BEC and AWGN channel in
Table 5. A similar entropy
h at the thresholds of the selected SC-TCs over all three channels confirms our conjecture that a strong similarity between predicted and MC-DE-H thresholds of an ensemble is associated with its capability of achieving threshold saturation.
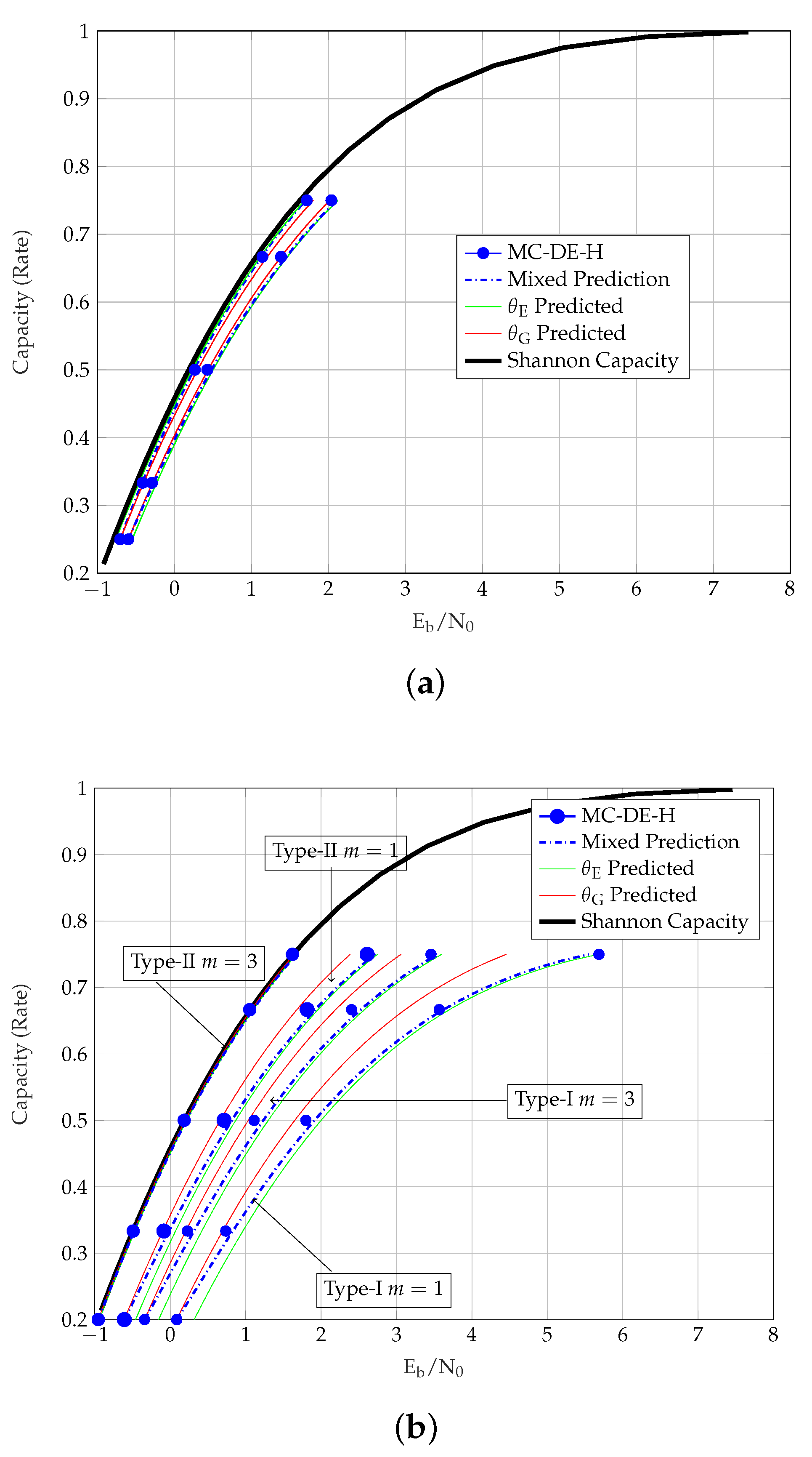
In order to provide an overview over the different ensembles, the MC-DE-H and MP thresholds of uncoupled and coupled TCs with
are plotted in
Figure 6. For coupled TCs with
, BCCs perform best among the considered ensembles, whereas PCCs are the first among the uncoupled ensembles. Interestingly, SC-PCCs approach SC-HCCs at lower rates and SC-SCCs at larger rates. Note that the performance of SC-HCCs-II-TII can be improved by increasing the coupling memory and it is observed that they then outperform SC-BCCs with
.
The threshold observations are further validated by performing some finite length BER performance simulations for SC-HCC-II type-II codes with
, and SC-SCC and SC-BCC codes with
for equal rate
and equal decoding latency. The SC-HCC-II type-II code with
is chosen because the
ensemble has a poor BP performance on both the BEC and the AWGN channel compared to SC-BCCs and SC-SCCs with
. We use sliding window decoding with a window size
, coupling length
, and 20 decoding iterations at each window position. The input block length is
for all ensembles, resulting in an overall structural decoding latency of
code symbols. The BER performance results are shown in
Figure 7. It is observed that the SC-HCC-II type-II code with
has the best performance followed by the SC-BCC code and SC-SCC code with
respectively. The simulations are observed to be consistent with the BP thresholds. However, the gain of the HCC ensemble in terms of the threshold is larger is than in terms of the simulated waterfall performance. This partially can be prescribed to the limited window size.
In
Table 6, we list the BEC and the AWGN channel thresholds of the TCs along with the parameters
,
and
. By using these values together with the prediction methods described in
Section 4, it is possible to immediately reproduce all the continuous threshold curves in
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6. The computation of MC-DE-H thresholds, which are shown as blue dots in these figures, is very time consuming and provided only for validation of the prediction methods. Consider the MP thresholds of rate
SCCs as an example to show how to calculate the predicted thresholds using
Table 6. First, we obtain the noise threshold
of rate
SCCs from its MC-DE-H threshold
. Next, we apply the entropy at the noise threshold
, and
from the
Table 6 to (
14) for
. This gives us
. From the AWGN channel capacity
, we obtain
. Lastly, by using that
we obtain the MP for rate
SCCs in terms of
.
The prediction methods provide a convenient way of comparing the thresholds of mother code ensembles with different rates. A randomly punctured code ensemble is characterized by the parameter
, where
corresponds to a capacity achieving ensemble [
11]. An ensemble with a smaller
and
will outperform an ensemble with larger
and
at all achievable rates.