Estimation for Entropy and Parameters of Generalized Bilal Distribution under Adaptive Type II Progressive Hybrid Censoring Scheme
Abstract
1. Introduction
- Case I: if , where .
- Case II: if and , where .
2. Maximum Likelihood Estimation
Approximate Confidence Interval
3. Bayesian Estimation
3.1. Loss Functions and Posterior Distribution
3.2. Lindley’s Approximation
3.2.1. Squared Error Loss Function
3.2.2. Linex Loss Function
3.2.3. General Entropy Loss Function
3.3. Bayesian Credible Interval
| Algorithm 1 The MCMC method |
| Step 1: Choose the initial value . |
| Step 2: At stage and for the given m, n and ATII-PH censored data, generate from the following: |
| Step 3: Generate from using the following steps. |
| Step 3-1: Generate from . |
| Step 3-2: Generate the from the uniform distribution U(0, 1). |
| Step 3-3: Set , where . |
| Step 4: Set . |
| Step 5: By repeating Steps 2–4 N times, we get . Furthermore, we compute , where and is the Shannon entropy of the GB distribution. |
4. Simulation Study
- CS I:;
- CS II:;
- CS III: if is even or if is odd.
| Algorithm 2. Generating a adaptive Type-II progressive hybrid censored sample from the GB distribution. |
| Step1: Generate independent observations , where follows the uniform distribution , . |
| Step 2: For the known censoring scheme , let . |
| Step 3: By setting , then is a Type-II progressive censored sample from the uniform distribution . |
| Step 4: Using the inverse transformation , , we obtain a Type-II progressive censored sample from the GB distribution; that is, , where denotes the GB distribution’s inverse cumulative functional expression with the parameter . The following theorem1 gives the uniqueness of the solution for the equation , . |
| Step 5: If there exists a real number satisfying , then we set index and record . |
| Step 6: Generate the first order statistics from the truncated distribution with a sample size . |
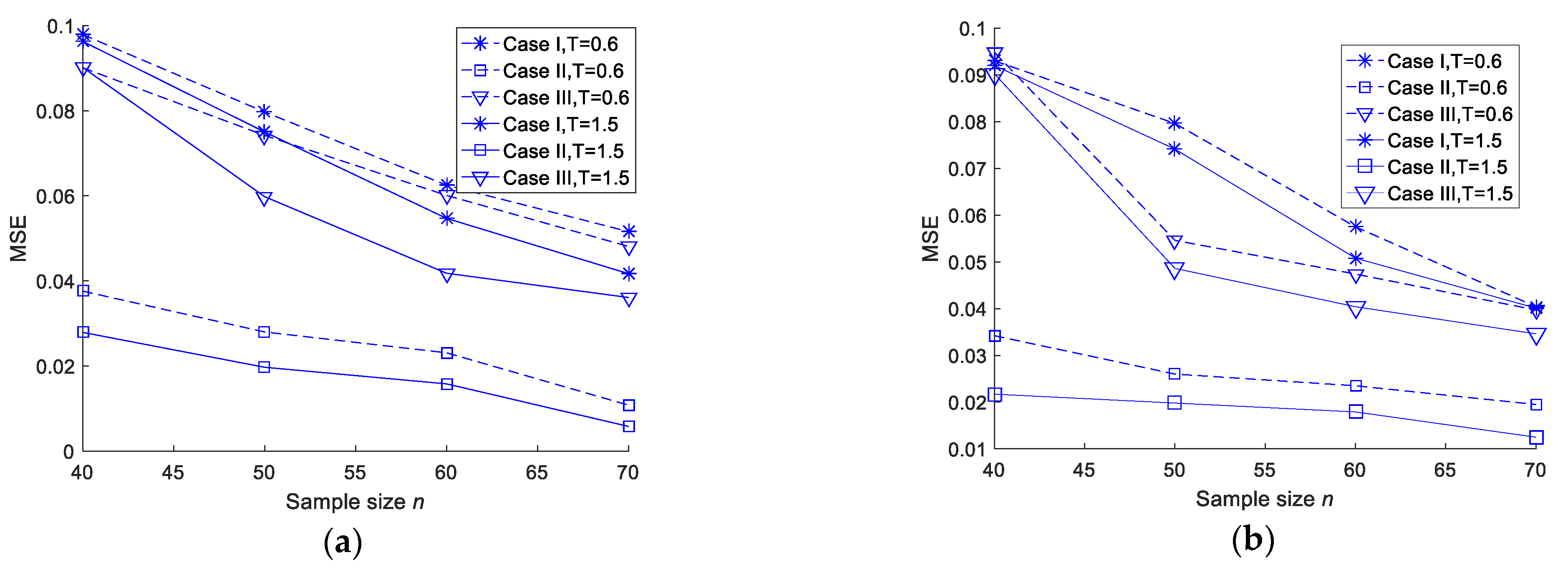
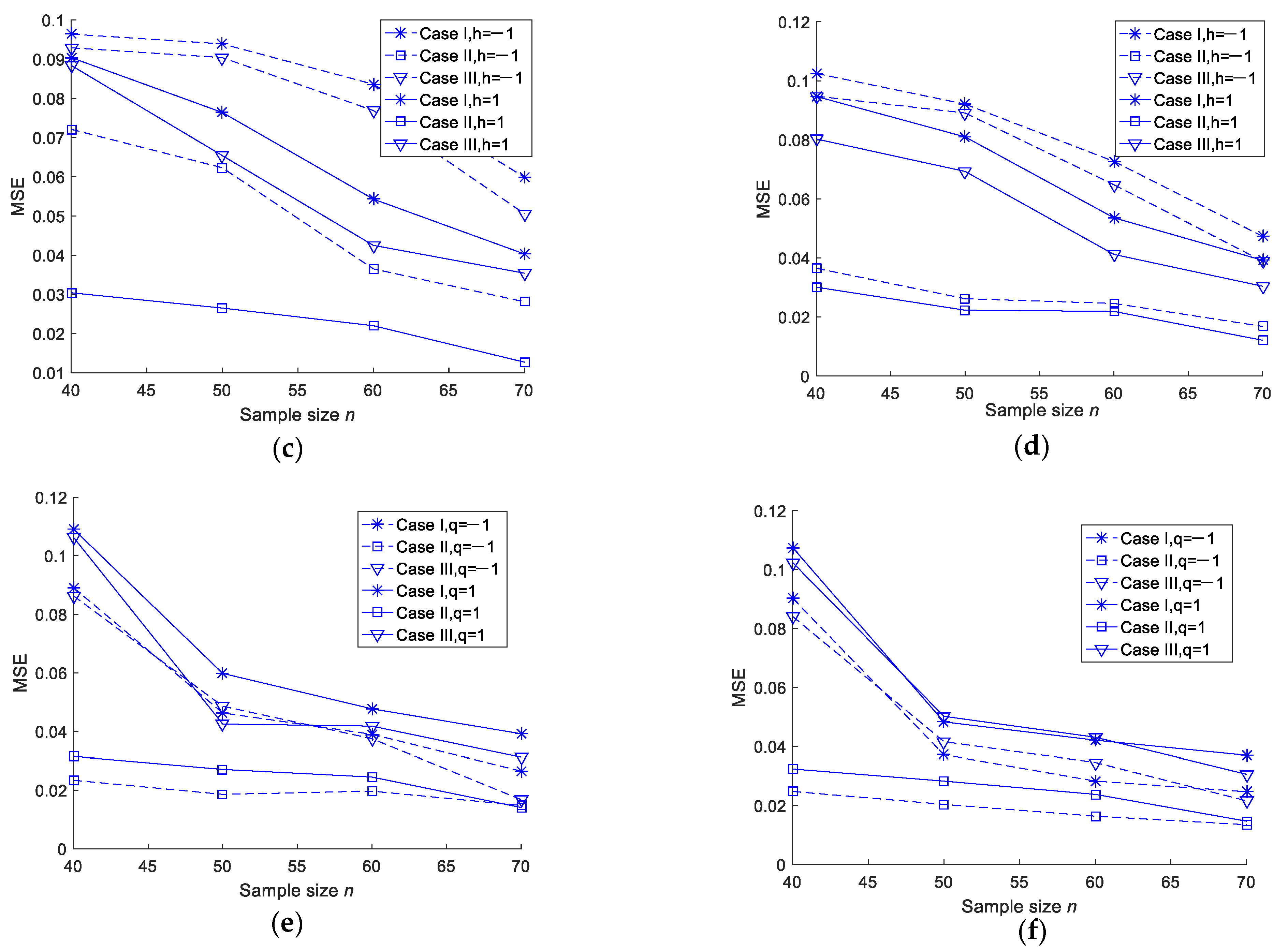
- For the fixed m and T values, the MSEs of the MLEs and Bayesian estimations of the two parameters and the entropy decreased when n increased. As such, we tended to get better estimation results with an increase in the test sample size;
- For the fixed n and m values, when T increased, the MSEs of the MLEs and Bayesian estimations of the two parameters and the entropy did not show any specific trend. This could be due to the fact that the number of observed failures was preplanned, and no additional failures were observed when T increased;
- In most cases, the MSEs of the Bayesian estimations under a squared error loss function were smaller than those of the MLEs. There was no significant difference in the MSEs between the Linex loss and general entropy loss functions;
- For fixed values of n, m and T, Scheme II was smaller than Scheme I and Scheme III in terms of the MSE.
- The coverage probability of the approximate confidence intervals and Bayes credible intervals became bigger when n increased while m and T remain fixed;
- For fixed values of n and m, when T increased, we did not observe any specific trend in the coverage probability of the approximate confidence intervals and Bayesian credible intervals;
- For fixed values of n and T, the average length of the approximate confidence intervals and Bayesian credible intervals were narrowed down when n increased;
- The average length of the Bayesian credible intervals was smaller than that of the asymptotic confidence intervals in most cases;
- For fixed values of n and m, when T increased, we did not observe any specific trend in the average length of the confidence intervals;
- For fixed values of n, m and T, Scheme II was smaller than Scheme I and Scheme III in terms of the average length of the credible interval;
- For fixed values of n, m and T, the coverage probability of the approximate confidence intervals and Bayesian credible intervals were bigger than Scheme I and Scheme III.
5. Real Data Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. The Specific Steps of the Newton–Raphson Iteration Method
Appendix C. The Detailed Derivation of Bayesian Estimates of two Parameters () and the Entropy under the LL Function
Appendix D. The Derivation of Bayesian Estimates of two Parameters and the Entropy under the GEL Function
Appendix E
| (n, m) | SC | β AL | CP | λ AL | CP | H AL | CP |
|---|---|---|---|---|---|---|---|
| (40, 15) | I | (0.6598, 1.5736) 0.9138 | 0.9042 | (1.2220, 3.1773) 1.9573 | 0.9216 | (0.0293, 1.1866) 1.1573 | 0.9184 |
| II | (0.6711, 1.4742) 0.8031 | 0.9253 | (1.4238, 2.8658) 1.4420 | 0.9361 | (0.0393, 0.7733) 0.7340 | 0.929 | |
| III | (0.6343, 1.5347) 0.9004 | 0.9130 | (1.2645, 3.1064) 1.9319 | 0.9281 | (0.0254, 1.1244) 1.0990 | 0.9174 | |
| (50, 15) | I | (0.6421, 1.5458) 0.9037 | 0.9162 | (1.2837, 3.0913) 1.8076 | 0.9314 | (0.0203, 1.0469) 1.0266 | 0.9216 |
| II | (0.7102, 1.3884) 0.6782 | 0.9394 | (1.4416, 2.7246) 1.2830 | 0.9406 | (0.0438, 0.6924) 0.6486 | 0.9392 | |
| III | (0.6914, 1.5147) 0.8233 | 0.9253 | (1.3021, 2.9705) 1.6684 | 0.9370 | (0.0264, 1.0759) 1.0495 | 0.9261 | |
| (60, 30) | I | (0.6377, 1.5335) 0.8958 | 0.9374 | (1.3388, 3.0191) 1.6803 | 0.9487 | (0.0151, 0.9112) 0.8959 | 0.9393 |
| II | (0.7093, 1.3769) 0.6676 | 0.9516 | (1.4807, 2.6886) 1.2069 | 0.9542 | (0.0536, 0.6667) 0.6131 | 0.9461 | |
| III | (0.6934, 1.4786) 0.7852 | 0.9405 | (1.3955, 2.9630) 1.5675 | 0.9506 | (0.0325, 0.8630) 0.8305 | 0.9428 | |
| (70, 30) | I | (0.7329, 1.4293) 0.6964 | 0.9472 | (1.4068, 2.8432) 1.34364 | 0.9534 | (0.0298, 0.7943) 0.7645 | 0.9446 |
| II | (0.7247, 1.2859) 0.5602 | 0.9651 | (1.5369, 2.5891) 1.0522 | 0.9680 | (0.0614, 0.5498) 0.4884 | 0.9632 | |
| III | (0.7392, 1.3486) 0.6154 | 0.9514 | (1.4476, 2.7845) 1.3361 | 0.9573 | (0.0498, 0.7185) 0.6687 | 0.9521 |
| (n, m) | SC | β AL | CP | λ AL | CP | H AL | CP |
|---|---|---|---|---|---|---|---|
| (40, 15) | I | (0.5234, 1.8717) 1.3483 | 0.9231 | (1.2469, 3.2287) 1.9818 | 0.9274 | (0.0284, 1.1887) 1.1603 | 0.9267 |
| II | (0.6662, 1.4576) 0.7914 | 0.9372 | (1.4322, 2.8760) 1.4438 | 0.9405 | (0.0436, 0.7887) 0.7451 | 0.9393 | |
| III | (0.5619, 1.8110) 1.2491 | 0.9252 | (1.2679, 3.2045) 1.9364 | 0.9364 | (0.0212, 1.1173) 1.0961 | 0.9340 | |
| (50, 15) | I | (0.5601, 1.6810) 1.1209 | 0.9230 | (1.3076, 3.0214) 1.7136 | 0.9363 | (0.0245, 0.9304) 0.9059 | 0.9347 |
| II | (0.7124, 1.3705) 0.6581 | 0.9418 | (1.4548, 2.7213) 1.2665 | 0.9462 | (0.0458, 0.6740) 0.6282 | 0.9515 | |
| III | (0.6103, 1.5868) 0.9765 | 0.9336 | (1.3320, 2.9769) 1.6449 | 0.9372 | (0.0259, 0.8461) 0.8202 | 0.9347 | |
| (60, 30) | I | (0.6659, 1.5135) 0.8476 | 0.9418 | (1.3454, 3.0335) 1.6881 | 0.9521 | (0.0206, 1.0400) 1.0194 | 0.9464 |
| II | (0.7051, 1.3680) 0.6619 | 0.9592 | (1.4812, 2.6942) 1.2130 | 0.9574 | (0.0456, 0.6604) 0.6148 | 0.9531 | |
| III | (0.6913, 1.4513) 0.7600 | 0.9431 | (1.3775, 2.8768) 1.4983 | 0.9520 | (0.0237, 0.9934) 0.9697 | 0.9506 | |
| (70, 30) | I | (0.7381, 1.3951) 0.6570 | 0.9492 | (1.4501, 2.7820) 1.3319 | 0.9582 | (0.0321, 0.7553) 0.7232 | 0.9523 |
| II | (0.7573, 1.2850) 0.5277 | 0.9704 | (1.5514, 2.5845) 1.0331 | 0.9726 | (0.0647, 0.5680) 0.5033 | 0.9741 | |
| III | (0.7554, 1.3492) 0.5938 | 0.9546 | (1.4967, 2.7071) 1.2104 | 0.9615 | (0.0410, 0.7147) 0.6737 | 0.9591 |
| (n, m) | SC | β AL | CP | λ AL | CP | H AL | CP |
|---|---|---|---|---|---|---|---|
| (40, 15) | I | (0.5521, 1.2841) 0.7320 | 0.9194 | (1.0215, 2.4593) 1.4378 | 0.9241 | (0.0213, 1.1750) 1.1537 | 0.9263 |
| II | (0.6378, 1.3228) 0.6850 | 0.9433 | (1.2854, 2.5238) 1.2384 | 0.9472 | (0.0395, 0.7752) 0.7357 | 0.9380 | |
| III | (0.5670, 1.2953) 0.7283 | 0.9253 | (1.0579, 2.4762) 1.4183 | 0.9294 | (0.0224, 1.1192) 1.0968 | 0.9308 | |
| (50, 15) | I | (0.5924, 1.2871) 0.6947 | 0.9312 | (1.1731, 2.5054) 1.3323 | 0.9397 | (0.0298, 0.9231) 0.8933 | 0.9386 |
| II | (0.6897, 1.2921) 0.6024 | 0.9491 | (1.3580, 2.4935) 1.1355 | 0.9465 | (0.0548, 0.6751) 0.6203 | 0.9507 | |
| III | (0.6067, 1.2854) 0.6787 | 0.9342 | (1.2051, 2.4718) 1.2667 | 0.9354 | (0.0278, 0.8553) 0.8275 | 0.9326 | |
| (60, 30) | I | (0.6450, 1.2925) 0.6475 | 0.9481 | (1.1389, 2.4565) 1.3176 | 0.9536 | (0.0397, 1.0509) 1.0112 | 0.9394 |
| II | (0.6870, 1.2905) 0.6035 | 0.9614 | (1.3883, 2.4740) 1.0857 | 0.9656 | (0.0578, 0.6717) 0.6139 | 0.9562 | |
| III | (0.6565, 1.2812) 0.6247 | 0.9532 | (1.1919, 2.4423) 1.2504 | 0.9561 | (0.0319, 0.8408) 0.8029 | 0.9528 | |
| (70, 30) | I | (0.7062, 1.2494) 0.5432 | 0.9512 | (1.3068, 2.4374) 1.1306 | 0.9563 | (0.0324, 0.7516) 0.7192 | 0.9536 |
| II | (0.7451, 1.2449) 0.4998 | 0.9711 | (1.4821, 2.4494) 0.9673 | 0.9744 | (0.0701, 0.5672) 0.4971 | 0.9783 | |
| III | (0.7162, 1.2359) 0.5197 | 0.9583 | (1.3597, 2.4443) 1.0846 | 0.9604 | (0.0440, 0.7067) 0.6627 | 0.9578 |
| (n, m) | SC | β AL | CP | λ AL | CP | H AL | CP |
|---|---|---|---|---|---|---|---|
| (40, 15) | I | (0.5554, 1.2954) 0.7400 | 0.9218 | (1.0243, 2.4612) 1.4369 | 0.9354 | (0.0251, 1.1801) 1.1550 | 0.9258 |
| II | (0.6417, 1.3339) 0.6922 | 0.9439 | (1.2824, 2.5169) 1.2345 | 0.9485 | (0.0372, 0.7728) 0.7356 | 0.9394 | |
| III | (0.5696, 1.3033) 0.7337 | 0.9275 | (1.0556, 2.4672) 1.4116 | 0.9318 | (0.0241, 1.1200) 1.0959 | 0.9337 | |
| (50, 15) | I | (0.5954, 1.2947) 0.6993 | 0.9417 | (1.1722, 2.4804) 1.3002 | 0.9420 | (0.0224, 1.0231) 1.0007 | 0.9418 |
| II | (0.68902, 1.2954) 0.6062 | 0.9506 | (1.3599, 2.5034) 1.1435 | 0.9525 | (0.0479, 0.6710) 0.6239 | 0.9526 | |
| III | (0.6045, 1.2801) 0.6756 | 0.9359 | (1.2337, 2.5094) 1.2757 | 0.9364 | (0.0324, 1.0047) 0.9723 | 0.9371 | |
| (60, 30) | I | (0.6418, 1.2835) 0.6417 | 0.9494 | (1.1349, 2.4455) 1.3106 | 0.9548 | (0.0250, 0.9212) 0.8960 | 0.9417 |
| II | (0.6896, 1.2970) 0.6074 | 0.9628 | (1.3987, 2.4911) 1.0924 | 0.9662 | (0.0479, 0.6608) 0.6129 | 0.9573 | |
| III | (0.6600, 1.2856) 0.6256 | 0.9556 | (1.1549, 2.4283) 1.2734 | 0.9571 | (0.0217, 0.8359) 0.8142 | 0.9538 | |
| (70, 30) | I | (0.7061, 1.2472) 0.5411 | 0.9526 | (1.3179, 2.4521) 1.1342 | 0.9571 | (0.0363, 0.7509) 0.7146 | 0.9548 |
| II | (0.7451, 1.2413) 0.4962 | 0.9725 | (1.4663, 2.4268) 0.9605 | 0.9757 | (0.0778, 0.5701) 0.4923 | 0.9793 | |
| III | (0.7154, 1.2267) 0.5113 | 0.9594 | (1.3542, 2.4118) 1.0576 | 0.9624 | (0.0604, 0.7108) 0.6504 | 0.9585 |
References
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring: Theory, Methods, and Applications; Birkhauser: Boston, MA, USA, 2000. [Google Scholar]
- Balakrishnan, N. Progressive censoring methodology: An appraisal. Test 2007, 16, 211–259. [Google Scholar] [CrossRef]
- Kundu, D.; Joarder, A. Analysis of type-II progressively hybrid censored data. Comput. Stat. Data Anal. 2006, 50, 2509–2528. [Google Scholar] [CrossRef]
- Ng, H.K.T.; Kundu, D.; Chan, P.S. Statistical analysis of exponential lifetimes under an adaptive Type II progressive censoring scheme. Naval Res. Logist. 2010, 56, 687–698. [Google Scholar] [CrossRef]
- Nassar, M.; Abo-Kasem, O.; Zhang, C.; Dey, S. Analysis of weibull distribution under adaptive Type-II progressive hybrid censoring scheme. J. Indian Soc. Probab. Stat. 2018, 19, 25–65. [Google Scholar] [CrossRef]
- Zhang, C.; Shi, Y. Estimation of the extended Weibull parameters and acceleration factors in the step-stress accelerated life tests under an adaptive progressively hybrid censoring data. J. Stat Comput. Simulat. 2016, 86, 3303–3314. [Google Scholar] [CrossRef]
- Cui, W.; Yan, Z.; Peng, X. Statistical analysis for constant-stress accelerated life test with Weibull distribution under adaptive Type-II hybrid censored data. IEEE Access 2019. [Google Scholar] [CrossRef]
- Ismail, A.A. Inference for a step-stress partially accelerated life test model with an adaptive Type-II progressively hybrid censored data from Weibull distribution. J. Comput. Appl. Math. 2014, 260, 533–542. [Google Scholar] [CrossRef]
- Zhang, C.; Shi, Y. Inference for constant-stress accelerated life tests with dependent competing risks from bivariate Birnbaum-Saunders distribution based on adaptive progressively hybrid censoring. IEEE Trans. Reliab. 2017, 66, 111–122. [Google Scholar] [CrossRef]
- Ye, Z.S.; Chan, P.S.; Xie, M. Statistical inference for the extreme value distribution under adaptive Type-II progressive censoring schemes. J. Stat. Comput. Simulat. 2014, 84, 1099–1114. [Google Scholar] [CrossRef]
- Sobhi, M.M.; Soliman, A.A. Estimation for the exponentiated Weibull model with adaptive Type-II progressive censored schemes. Appl. Math. Model. 2016, 40, 1180–1192. [Google Scholar] [CrossRef]
- Nassar, M.; Abo-Kasem, O.E. Estimation of the inverse Weibull parameters under adaptive type-II progressive hybrid censoring scheme. J. Comput. Appl. Math. 2017, 315, 228–239. [Google Scholar] [CrossRef]
- Xu, R.; Gui, W.H. Entropy estimation of inverse Weibull Distribution under adaptive Type-II progressive hybrid censoring schemes. Symmetry 2019, 11, 1463. [Google Scholar] [CrossRef]
- Kang, S.B.; Cho, Y.S.; Han, J.T.; Kim, J. An estimation of the entropy for a double exponential distribution based on multiply Type-II censored samples. Entropy 2012, 14, 161–173. [Google Scholar] [CrossRef]
- Cho, Y.; Sun, H.; Lee, K. An estimation of the entropy for a Rayleigh distribution based on doubly-generalized Type-II hybrid censored samples. Entropy 2014, 16, 3655–3669. [Google Scholar] [CrossRef]
- Baratpour, S.; Ahmadi, J.; Arghami, N.R. Entropy properties of record statistics. Stat. Pap. 2017, 48, 197–213. [Google Scholar] [CrossRef]
- Cramer, E.; Bagh, C. Minimum and maximum information censoring plans in progressive censoring. Commun. Stat. Theory Methods 2011, 40, 2511–2527. [Google Scholar] [CrossRef]
- Cho, Y.; Sun, H.; Lee, K. Estimating the entropy of a weibull distribution under generalized progressive hybrid censoring. Entropy 2015, 17, 102–122. [Google Scholar] [CrossRef]
- Yu, J.; Gui, W.H.; Shan, Y.Q. Statistical inference on the Shannon entropy of inverse Weibull distribution under the progressive first-failure censoring. Entropy 2019, 21, 1209. [Google Scholar] [CrossRef]
- Abd-Elrahman, A.M. A new two-parameter lifetime distribution with decreasing, increasing or upside-down bathtub-shaped failure rate. Commun. Stat. Theory Methods 2017, 46, 8865–8880. [Google Scholar] [CrossRef]
- Abd-Elrahman, A.M. Reliability estimation under type-II censored data from the generalized Bilal distribution. J. Egypt. Math. Soc. 2019, 27, 1–15. [Google Scholar] [CrossRef]
- Mahmoud, M.; EL-Sagheer, R.M.; Abdallah, S. Inferences for new Weibull–Pareto distribution based on progressively Type-II censored data. J. Stat. Appl. Probab. 2016, 5, 501–514. [Google Scholar] [CrossRef]
- Ahmed, E.A. Bayesian estimation based on progressive Type-II censoring from two-parameter bathtub-shaped lifetime model: An Markov chain Monte Carlo approach. J. Appl. Stat. 2014, 41, 752–768. [Google Scholar] [CrossRef]
- Gilks, W.R.; Wild, P. Adaptive rejection sampling for Gibbs sampling. J. R. Stat. Soc. 1992, C41, 337–348. [Google Scholar] [CrossRef]
- Koch, K.R. Gibbs sampler by sampling-importance-resampling. J. Geod. 2007, 81, 581–591. [Google Scholar] [CrossRef]
- Martino, L.; Elvira, V.; Camps-Valls, G. The recycling gibbs sampler for efficient learning. Digit. Signal Process. 2018, 74, 1–13. [Google Scholar] [CrossRef]
- Panahi, H.; Moradi, N. Estimation of the inverted exponentiated Rayleigh distribution based on adaptive Type II progressive hybrid censored sample. J. Comput. Appl. Math. 2020, 364, 112345. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equations of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Sandhu, R.A. A simple simulational algorithm for generating progressive Type-II censored samples. Am. Stat. 1995, 49, 229–230. [Google Scholar]
- Hinkley, D. On quick choice of power transformations. Appl. Stat. 1977, 26, 67–96. [Google Scholar] [CrossRef]
- Barreto-Souza, W.; Cribari-Neto, F. A generalization of the exponential-Poisson distribution. Stat. Probab. Lett. 2009, 79, 2493–2500. [Google Scholar] [CrossRef]
| (n, m) | SC | T = 0.6 | T = 1.5 | ||||
|---|---|---|---|---|---|---|---|
MSE | MSE | MSE | MSE | MSE | MSE | ||
| (40, 15) | I | 1.1850 0.1224 | 2.2096 0.1428 | 0.1903 0.0979 | 1.1875 0.1213 | 2.2848 0.1521 | 0.1950 0.0963 |
| II | 1.0727 0.0709 | 2.1448 0.1258 | 0.2015 0.0376 | 1.0619 0.0609 | 2.1541 0.1336 | 0.2017 0.0279 | |
| III | 1.1819 0.1217 | 2.2354 0.1413 | 0.1947 0.0910 | 1.1864 0.1208 | 2.2362 0.1514 | 0.1968 0.0902 | |
| (50, 15) | I | 1.1326 0.1053 | 2.1803 0.1398 | 0.2086 0.0797 | 1.0905 0.0741 | 2.1931 0.1483 | 0.1997 0.0750 |
| II | 1.0498 0.0390 | 2.1017 0.1243 | 0.2281 0.0280 | 1.0390 0.0374 | 2.1076 0.1263 | 0.2169 0.0197 | |
| III | 1.1184 0.1013 | 2.1817 0.1345 | 0.2035 0.0742 | 1.0740 0.0602 | 2.1284 0.1448 | 0.2013 0.0598 | |
| (60, 30) | I | 1.1006 0.0889 | 2.1758 0.1374 | 0.2029 0.0625 | 1.0689 0.0683 | 2.1795 0.1368 | 0.2033 0.0547 |
| II | 1.0451 0.0363 | 2.0847 0.1066 | 0.2260 0.0231 | 1.0476 0.0383 | 2.0877 0.1048 | 0.2170 0.0158 | |
| III | 1.0860 0.0653 | 2.1528 0.1368 | 0.2086 0.0601 | 1.0583 0.0592 | 2.1571 0.1335 | 0.2090 0.0418 | |
| (70, 30) | I | 1.0641 0.0704 | 2.1296 0.1202 | 0.2163 0.0516 | 1.0581 0.0597 | 2.1197 0.1278 | 0.2134 0.0417 |
| II | 1.0246 0.0265 | 2.0785 0.0849 | 0.2294 0.0198 | 1.0231 0.0317 | 2.0715 0.0946 | 0.2245 0.0148 | |
| III | 1.0517 0.0580 | 2.1483 0.1203 | 0.2199 0.0591 | 1.0468 0.0485 | 2.1132 0.1203 | 0.2195 0.0361 | |
| (n, m) | SC | T = 0.6 | T = 1.5 | ||||
|---|---|---|---|---|---|---|---|
MSE | MSE | MSE | MSE | MSE | MSE | ||
| (40, 15) | I | 0.8625 0.0353 | 1.8735 0.1325 | 0.3357 0.0930 | 0.8687 0.0337 | 1.8761 0.1317 | 0.3301 0.0920 |
| II | 0.9480 0.0235 | 1.9583 0.0954 | 0.2630 0.0342 | 0.9546 0.0255 | 1.9531 0.0938 | 0.2616 0.0217 | |
| III | 0.8795 0.0340 | 1.8041 0.1314 | 0.3264 0.0948 | 0.8837 0.0310 | 1.8996 0.1299 | 0.3034 0.0902 | |
| (50, 15) | I | 0.9325 0.0297 | 1.8917 0.1185 | 0.3189 0.0796 | 0.8973 0.0289 | 1.8345 0.0975 | 0.2732 0.0741 |
| II | 0.9645 0.0218 | 1.9907 0.0827 | 0.2580 0.0260 | 0.9694 0.0223 | 1.9763 0.0812 | 0.2303 0.0198 | |
| III | 0.9475 0.0253 | 1.9013 0.1072 | 0.3016 0.0546 | 0.9824 0.0234 | 1.9314 0.0972 | 0.2661 0.0486 | |
| (60, 30) | I | 0.9274 0.0224 | 1.8445 0.1151 | 0.2357 0.0575 | 0.9457 0.0263 | 1.8781 0.0919 | 0.2674 0.0508 |
| II | 0.9671 0.0202 | 1.9932 0.0728 | 0.2398 0.0235 | 0.9688 0.0207 | 2.0176 0.0741 | 0.2235 0.0179 | |
| III | 0.9185 0.0211 | 1.8525 0.1072 | 0.2301 0.0534 | 0.9316 0.0227 | 1.9427 0.0954 | 0.2652 0.0504 | |
| (70, 30) | I | 0.9742 0.0198 | 1.9360 0.0775 | 0.2538 0.0404 | 0.9515 0.0213 | 1.9504 0.0892 | 0.2553 0.0401 |
| II | 0.9895 0.0174 | 2.0413 0.0613 | 0.2506 0.0195 | 0.9804 0.0186 | 2.0378 0.0537 | 0.2260 0.0105 | |
| III | 0.9787 0.0182 | 1.9746 0.0761 | 0.2512 0.0397 | 0.9713 0.0194 | 1.9714 0.0683 | 0.2537 0.0346 | |
| (n, m) | SC | ||||||
|---|---|---|---|---|---|---|---|
MSE | MSE | MSE | MSE | MSE | MSE | ||
| (40, 15) | I | 0.8835 0.0355 | 1.8558 0.1261 | 0.3583 0.0964 | 0.8531 0.0366 | 1.8248 0.1343 | 0.2802 0.0904 |
| II | 0.9740 0.0255 | 1.9161 0.0885 | 0.2587 0.0721 | 0.9308 0.0246 | 1.9092 0.1008 | 0.2469 0.0304 | |
| III | 0.9047 0.0308 | 1.8768 0.1249 | 0.3343 0.0929 | 0.8670 0.0335 | 1.8405 0.1889 | 0.2638 0.0884 | |
| (50, 15) | I | 0.9047 0.0301 | 1.9415 0.1238 | 0.3158 0.0939 | 0.8704 0.0337 | 1.9175 0.1329 | 0.2736 0.0764 |
| II | 0.9852 0.0218 | 2.0538 0.0789 | 0.2502 0.0623 | 0.9674 0.0213 | 1.9201 0.0912 | 0.2358 0.0265 | |
| III | 0.9105 0.0284 | 1.9771 0.0986 | 0.3046 0.0904 | 0.8924 0.0293 | 1.9203 0.1257 | 0.2604 0.0654 | |
| (60, 30) | I | 0.9341 0.0223 | 1.9788 0.1127 | 0.2792 0.0836 | 0.9035 0.0238 | 1.9221 0.1308 | 0.2520 0.0543 |
| II | 0.9834 0.0198 | 2.0465 0.0664 | 0.3743 0.0365 | 0.9609 0.0211 | 1.9447 0.0791 | 0.2118 0.0220 | |
| III | 0.9498 0.0204 | 1.9837 0.0973 | 0.3424 0.0829 | 0.9258 0.0207 | 1.9253 0.1227 | 0.2319 0.0425 | |
| (70, 30) | I | 0.9561 0.0197 | 1.9889 0.0768 | 0.2546 0.0579 | 0.9378 0.0184 | 1.9543 0.0975 | 0.2407 0.0403 |
| II | 0.9957 0.0174 | 2.0312 0.0572 | 0.2371 0.0281 | 0.9798 0.0159 | 2.0164 0.0614 | 0.2410 0.0187 | |
| III | 0.9687 0.0185 | 2.0024 0.0746 | 0.2265 0.0536 | 0.9451 0.0120 | 1.9623 0.0784 | 0.2409 0.0354 | |
| (n, m) | SC | ||||||
|---|---|---|---|---|---|---|---|
MSE | MSE | MSE | MSE | MSE | MSE | ||
| (40, 15) | I | 0.8896 0.0330 | 1.8328 0.1359 | 0.3492 0.1025 | 0.8510 0.0375 | 1.8127 0.1396 | 0.3381 0.0947 |
| II | 0.9638 0.0248 | 1.9177 0.0863 | 0.2743 0.0365 | 0.9272 0.0265 | 1.9167 0.0982 | 0.2657 0.0301 | |
| III | 0.8922 0.0321 | 1.8691 0.1306 | 0.3424 0.0948 | 0.8631 0.0334 | 1.8430 0.1328 | 0.3343 0.0803 | |
| (50, 15) | I | 0.9024 0.0234 | 1.8678 0.1094 | 0.3217 0.0921 | 0.8823 0.0315 | 1.8874 0.1173 | 0.3216 0.0810 |
| II | 0.9713 0.0221 | 1.9401 0.0731 | 0.2601 0.0262 | 0.9418 0.0217 | 1.9824 0.0884 | 0.2632 0.0223 | |
| III | 0.9135 0.0231 | 1.8792 0.090 | 0.3383 0.0921 | 0.8975 0.0314 | 1.8845 0.1121 | 0.3210 0.0693 | |
| (60, 30) | I | 0.9470 0.0219 | 1.8946 0.0951 | 0.3222 0.0727 | 0.9080 0.0234 | 1.9012 0.1075 | 0.3251 0.0536 |
| II | 0.9795 0.0209 | 1.9452 0.0719 | 0.2518 0.0246 | 0.9548 0.0199 | 1.9616 0.0776 | 0.2513 0.0219 | |
| III | 0.9425 0.0213 | 1.8978 0.0906 | 0.3197 0.0648 | 0.9253 0.0213 | 1.9041 0.1069 | 0.3218 0.0412 | |
| (70, 30) | I | 0.9583 0.0184 | 1.9562 0.0748 | 0.3165 0.0473 | 0.9491 0.0179 | 1.9493 0.0861 | 0.3314 0.0392 |
| II | 0.9901 0.0163 | 2.0576 0.0652 | 0.2318 0.0168 | 0.9814 0.0153 | 2.0997 0.0608 | 0.2459 0.0161 | |
| III | 0.9711 0.0175 | 1.9230 0.0697 | 0.3027 0.0389 | 0.9502 0.0162 | 1.9894 0.0841 | 0.3267 0.0304 | |
| (n, m) | SC | ||||||
|---|---|---|---|---|---|---|---|
MSE | MSE | MSE | MSE | MSE | MSE | ||
| (40, 15) | I | 0.8739 0.0341 | 1.8380 0.1348 | 0.3181 0.0891 | 0.8288 0.0437 | 1.8173 0.1381 | 0.3558 0.1091 |
| II | 0.9546 0.0239 | 1.9184 0.0966 | 0.2832 0.0234 | 0.9169 0.0265 | 1.9081 0.1084 | 0.2628 0.0315 | |
| III | 0.8828 0.0324 | 1.8422 0.1306 | 0.3097 0.0863 | 0.8494 0.0389 | 1.8266 0.1361 | 0.3207 0.1063 | |
| (50, 15) | I | 0.9013 0.0305 | 1.8948 0.1191 | 0.3017 0.0463 | 0.8972 0.0380 | 1.8728 0.1231 | 0.3423 0.0598 |
| II | 0.9701 0.0214 | 1.9386 0.0803 | 0.2695 0.0186 | 0.9430 0.0236 | 1.9471 0.0962 | 0.2268 0.0271 | |
| III | 0.9251 0.0263 | 1.8984 0.1093 | 0.3023 0.0486 | 0.8613 0.0308 | 1.8498 0.1176 | 0.3287 0.0525 | |
| (60, 30) | I | 0.9270 0.0232 | 1.9089 0.0824 | 0.2776 0.0390 | 0.8975 0.0276 | 1.8785 0.1127 | 0.3270 0.0477 |
| II | 0.9610 0.0190 | 2.0351 0.0686 | 0.2318 0.0197 | 0.9481 0.0210 | 2.0453 0.0791 | 0.2391 0.0245 | |
| III | 0.9406 0.0210 | 1.9105 0.0874 | 0.2698 0.0375 | 0.9116 0.0231 | 1.8938 0.1109 | 0.3168 0.0418 | |
| (70, 30) | I | 0.9501 0.0171 | 1.9492 0.0778 | 0.2536 0.0265 | 0.9213 0.0202 | 1.9308 0.0840 | 0.2924 0.0392 |
| II | 0.9817 0.0158 | 2.0147 0.0436 | 0.2325 0.0148 | 0.9681 0.0151 | 2, 1489 0.0526 | 0.2410 0.0272 | |
| III | 0.9546 0.0174 | 1.9602 0.0738 | 0.2513 0.0168 | 0.9467 0.0173 | 1.9436 0.0724 | 0.2902 0.0312 | |
| (n, m) | SC | ||||||
|---|---|---|---|---|---|---|---|
MSE | MSE | MSE | MSE | MSE | MSE | ||
| (40, 15) | I | 0.8770 0.0335 | 1.8569 0.1332 | 0.3564 0.0903 | 0.8224 0.0455 | 1.7924 0.1331 | 0.3598 0.1075 |
| II | 0.9560 0.0218 | 1.9221 0.0914 | 0.2729 0.0198 | 0.9112 0.0257 | 1.9038 0.0913 | 0.2786 0.0294 | |
| III | 0.8836 0.0315 | 1.8297 0.1217 | 0.3519 0.0841 | 0.8453 0.0348 | 1.8374 0.1224 | 0.3547 0.1024 | |
| (50, 15) | I | 0.8947 0.0298 | 1.8979 0.0981 | 0.3028 0.0372 | 0.8631 0.0362 | 1.8308 0.1134 | 0.3143 0.0483 |
| II | 0.9685 0.0206 | 1.9793 0.0801 | 0.2610 0.0164 | 0.9377 0.0216 | 1.9467 0.0910 | 0.2656 0.0283 | |
| III | 0.8984 0.0278 | 1.9078 0.0931 | 0.3012 0.0416 | 0.8702 0.0302 | 1.8547 0.1086 | 0.3125 0.0502 | |
| (60, 30) | I | 0.9244 0.0221 | 1.8446 0.0772 | 0.2731 0.0283 | 0.8930 0.0267 | 1.9208 0.1041 | 0.2812 0.0421 |
| II | 0.9767 0.0188 | 2.0526 0.0614 | 0.2554 0.0164 | 0.9440 0.0202 | 2.0658 0.0718 | 0.2627 0.0238 | |
| III | 0.9387 0.0198 | 1.9541 0.0824 | 0.2709 0.0346 | 0.9125 0.0210 | 1.9435 0.0983 | 0.2801 0.0431 | |
| (70, 30) | I | 0.9531 0.0167 | 1.9578 0.0738 | 0.2501 0.0247 | 0.9230 0.0188 | 1.9447 0.0814 | 0.2523 0.0370 |
| II | 0.9814 0.0140 | 2.2263 0.0394 | 0.2309 0.0135 | 0.9675 0.0140 | 2.2680 0.0338 | 0.2352 0.0247 | |
| III | 0.9624 0.0163 | 1.9795 0.0745 | 0.2486 0.0216 | 0.9457 0.0164 | 1.9539 0.0718 | 0.2501 0.0306 | |
| MLEs | Case I | Case II | BEs (Squared Loss) | Case I | Case II |
|---|---|---|---|---|---|
| 0.3289 | 0.3948 | 0.3428 | 0.4044 | ||
| 1.0408 | 1.3373 | 0.9974 | 1.2410 | ||
| 1.5890 | 1.3881 | 1.6230 | 1.4701 |
| BEs Linex Loss | BEs Entropy Loss | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Case I | Case II | Case I | Case II | Case I | Case II | Case I | Case II | ||
| 0.3406 | 0.4031 | 0.3330 | 0.3958 | 0.3369 | 0.4025 | 0.3273 | 0.3852 | ||
| 1.2893 | 1.0217 | 1.2442 | 0.9898 | 1.2618 | 1.0060 | 1.2173 | 0.9765 | ||
| 1.4714 | 1.6681 | 1.4385 | 1.6276 | 1.4608 | 1.6340 | 1.4370 | 1.6249 | ||
| Parameter | ACIs IL | Parameter | BCIs IL | ||
|---|---|---|---|---|---|
| Case I | Case II | Case I | Case II | ||
| β | (0.2406, 0.5409) 0.3003 | (0.1812, 0.4564) 0.2752 | β | (0.2760, 0.5625) 0.2865 | (0.2210, 0.4923) 0.2713 |
| λ | (0.6899, 1.3918) 0.7019 | (0.9884, 1.7863) 0.7979 | λ | (0.7021, 1.3566) 0.6545 | (0.8776, 1.6743) 0.7967 |
| H | (1.2012, 1.9314) 0.7302 | (1.0299, 1.7863) 0.7164 | H | (1.2487, 1.9707) 0.7220 | (1.1266, 1.8671) 0.7405 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Shi, Y.; Zhou, K. Estimation for Entropy and Parameters of Generalized Bilal Distribution under Adaptive Type II Progressive Hybrid Censoring Scheme. Entropy 2021, 23, 206. https://doi.org/10.3390/e23020206
Shi X, Shi Y, Zhou K. Estimation for Entropy and Parameters of Generalized Bilal Distribution under Adaptive Type II Progressive Hybrid Censoring Scheme. Entropy. 2021; 23(2):206. https://doi.org/10.3390/e23020206
Chicago/Turabian StyleShi, Xiaolin, Yimin Shi, and Kuang Zhou. 2021. "Estimation for Entropy and Parameters of Generalized Bilal Distribution under Adaptive Type II Progressive Hybrid Censoring Scheme" Entropy 23, no. 2: 206. https://doi.org/10.3390/e23020206
APA StyleShi, X., Shi, Y., & Zhou, K. (2021). Estimation for Entropy and Parameters of Generalized Bilal Distribution under Adaptive Type II Progressive Hybrid Censoring Scheme. Entropy, 23(2), 206. https://doi.org/10.3390/e23020206





