Error Exponents and α-Mutual Information
Abstract
1. Introduction
1.1. Phase 1: The MIT School
- (a)
- The error exponent functions were expressed as the result of the Karush-Kuhn-Tucker optimization of ad-hoc functions which, unlike mutual information, carried little insight. In particular, during the first phase, center stage is occupied by the parametrized function of the input distribution and the random transformation (or "channel”) ,introduced by Gallager in [8].
- (b)
- Despite the large-deviations nature of the setup, none of the tools from that then-nascent field (other than the Chernoff bound) found their way to the first phase of the work on error exponents; in particular, relative entropy, introduced by Kullback and Leibler [14], failed to put in an appearance.
1.2. Phase 2: Relative Entropy
1.3. Phase 3: Rényi Information Measures
1.4. Cost Constraints
1.5. Organization
2. Relative Information and Information Density
- 1.
- If is a probability space, indicates for all .
- 2.
- If probability measures P and Q defined on the same measurable space satisfy for all such that , we say that P is dominated by Q, denoted as . If P and Q dominate each other, we write . If there is an event such that and , we say that P and Q are mutually singular, and we write .
- 3.
- If , then is the Radon-Nikodym derivative of the dominated measure P with respect to the reference measure Q. Its logarithm is known as the relative information, namely, the random variableAs with the Radon-Nikodym derivative, any identity involving relative informations can be changed on a set of measure zero under the reference measure without incurring in any contradiction. If , then the chain rule of Radon-Nikodym derivatives yieldsThroughout the paper, the base of exp and log is the same and chosen by the reader unless explicitly indicated otherwise. We frequently define a probability measure P from the specification of and sinceIf and , it is often convenient to write instead of . Note thatExample 1.If (Gaussian with mean and variance ) and , then,
- 4.
- Let and be measurable spaces, known as the input and output spaces, respectively. Likewise, and are referred to as the input and output alphabets respectively. The simplified notation denotes a random transformation from to , i.e., for any , is a probability measure on , and for any , is an -measurable function.
- 5.
- We abbreviate by the set of probability measures on , and by the set of probability measures on . If and is a random transformation, the corresponding joint probability measure is denoted by (or, interchangeably, ). The notation simply indicates that the output marginal of the joint probability measure is denoted by , namely,
- 6.
- If and , the information density is defined asFollowing Rényi’s terminology [49], if , the dependence between X and Y is said to be regular, and the information density can be defined on . Henceforth, we assume that is such that the dependence between its input and output is regular regardless of the input probability measure. For example, if , then , and their dependence is not regular, since for any with non-discrete components PXY
PX × PY.
- 7.
- Let , and . The -response to is the output probability measure with relative information given bywhere is a scalar that guarantees that is a probability measure. Invoking (9), we obtainFor brevity, the dependence of on and is omitted. Jensen’s inequality applied to results in for and for . Although the -response has a long record of services to information theory, this terminology and notation were introduced recently in [45]. Alternative terminology and notation were proposed in [42], which refers to the -response as the order Rényi mean. Note that and the 1-response to is . If and denote the densities of and with respect to some common dominating measure, then (13) becomesFor (resp. ) we can think of the normalized version of as a random transformation with less (resp. more) "noise" than .
- 8.
- We will have opportunity to apply the following examples.
3. Relative Entropy and Rényi Divergence
- 9.
- Provided , the relative entropy is the expectation of the relative information with respect to the dominated measurewith equality if and only if . If P
Q, then . As in Item 3, if and , we may write instead of , in the same spirit that the expectation and entropy of P are written as and , respectively.
- 10.
- Arising in the sequel, a common optimization in information theory finds, among the probability measures satisfying an average cost constraint, that which is closest to a given reference measure Q in the sense of . For that purpose, the following result proves sufficient. Incidentally, we often refer to unconstrained maximizations over probability distributions. It should be understood that those optimizations are still constrained to the sets or . As customary in information theory, we will abbreviate by or .Theorem 1.Let and suppose that is a Borel measurable mapping. Then,achieved uniquely by defined byProof.Note that since g is nonnegative, . Furthermore,
- 11.
- Let p and q denote the Radon-Nikodym derivatives of probability measures P and Q, respectively, with respect to a common dominating -finite measure . The Rényi divergence of order between P and Q is defined as [25,50]where (28) and (29) hold if , and in (27), R is a probability measure that dominates both P and Q. Note that (28) and (29) state that and are the cumulant generating functions of the random variables and , respectively. The relative entropy is the limit of as , so it is customary to let . For any , with equality if and only if . Furthermore, is non-decreasing in , satisfies the skew-symmetric propertyand
- 12.
- The expressions in the following pair of examples will come in handy in Section 11 and Section 12.Example 4.Suppose that and . Then,Example 5.Suppose Z is exponentially distributed with unit mean, i.e., its probability density function is . For and α such that we obtain
- 13.
- Intimately connected with the notion of Rényi divergence is the tilted probability measure defined, if , bywhere Q is any probability measure that dominates both and . Although (37) is defined in general, our main emphasis is on the range , in which, as long as P0
P1, the tilted probability measure is defined and satisfies and , with corresponding relative informations
where we have used the chain rule for and . Taking a linear combination of (38)–(41) we conclude that, for all ,Henceforth, we focus particular attention on the case since that is the region of interest in the application of Rényi information measures to the evaluation of error exponents in channel coding for codes whose rate is below capacity. In addition, often proofs simplify considerably for . - 14.
- Much of the interplay between relative entropy and Rényi divergence hinges on the following identity, which appears, without proof, in (3) of [51].Proof.We distinguish three overlapping cases:
- (1)
- : Taking expectation of (42) with respect to , yields (43) becausewhere, thanks to the assumption that , we have invoked Corollary A1 in the Appendix A twice with and , respectively;
- (2)
- : The proof is identical since we are entitled to invoke Corollary A1 to show (45) (resp., (46)) because (resp., ).
- (3)
- and : both sides of (43) are equal to ∞.
- 15.
- Relative entropy and Rényi divergence are related by the following fundamental variational representation.Theorem 3.Fix and . Then, the Rényi divergence between and satisfieswhere the minimum is over . If P0
P1, then the right side of (47) is attained by the tilted measure , and the minimization can be restricted to the subset of probability measures which are dominated by both and .
The variational representation in (47) was observed in [39] in the finite-alphabet case, and, contemporaneously, in full generality in [50]. Unlike Theorem 3, both of those references also deal with . The function , with , is concave in because the right side of (47) is a minimum of affine functions of . - 16.
- Given random transformations , , and a probability measure on the input space, the conditional relative entropy isAnalogously, the conditional Rényi divergence is defined asA word of caution: the notation in (50) conforms to that in [38,45] but it is not universally adopted, e.g., [43] uses the left side of (50) to denote the Rényi generalization of the right side of (49). We can express the conditional Rényi divergence aswhere (52) holds if . Jensen’s inequality applied to (51) results in
- 17.
- Conditional Rényi divergence satisfies the following additive decomposition, originally pointed out, without proof, by Sibson [31] in the setting of finite .Theorem 4.Given , , , and , we haveFurthermore, with as in (14),Proof. Select an arbitrary probability measure that dominates both and , and, therefore, too. Letting , we havewhere (61) follows from (13), and (62) follows from the chain rule of Radon-Nikodym derivatives applied to . Then, (58) follows by specializing , and the proof of (57) is complete, upon plugging (58) into the right side of (63). □
- 18.
- For all , given two inputs and one random transformation , Rényi divergence (and, in particular, relative entropy) satisfies the data processing inequality,where , and . The data processing inequality for Rényi divergence was observed by Csiszár [52] in the more general context of f-divergences. More recently it was stated in [39,50]. Furthermore, given one input and two transformations and , conditioning cannot decrease Rényi divergence,
4. Dependence Measures
- 19.
- The mutual information is
- 20.
- Given , the -mutual information is defined as (see [30,31,32,40,42,45])where (72) and (74) follow from (57); (73) is a special case of (51); (75) follows from Theorem 4; and, (76) is (14). In view of (67) and (69), we let . The notation we use for -mutual information conforms to that used in [40,42,45,53]. Other notations include in [32,38,39] and in [43]. and are defined by taking the corresponding limits.
- 21.
- Theorem 4 and (72) result in the additive decompositionfor any with , thereby generalizing the well-known decomposition for mutual information,which, in contrast to (77), is a simple consequence of the chain rule whenever the dependence between X and Y is regular, and of Lemma A1 in general.
- 22.
- Example 6.Additive independent Gaussian noise. If , where independent of , then, for ,
- 23.
- 24.
- Unlike , we can express directly in terms of its arguments without involving the corresponding output distribution or the -response to . This is most evident in the case of discrete alphabets, in which (76) becomesFor example, if X is discrete and denotes the Rényi entropy of order , then for all ,If X and Y are equiprobable with , then, in bits, , where denotes the binary Rényi entropy.
- 25.
- In the main region of interest, namely, , frequently we use a different parametrization in terms of , with .Theorem 5.For any , we have the upper bound
- 26.
- Before introducing the last dependence measure in this section, recall from Definition 7 and (58) that , the -response (of ) to defined byattains , where the expectation is with respect to . We proceed to define , the -response (of ) to by means ofwith . Note that .
- 27.
- 28.
- The -response satisfies the following identity, which can be regarded as the counterpart of (57) satisfied by the -response.Theorem 6.Fix , and . Then,Proof.For brevity we assume . Otherwise, the proof is similar adopting a reference measure that dominates both and . The definition of unconditional Rényi divergence in Item 11 implies that we can write times the exponential of the left side of (94) aswhere , (96) follows from (92), and (97) follows from the definition of unconditional Rényi divergence in (27). □Theorem 7.Proof.Assume . Jensen’s inequality applied to the right side of (94) results in (98). To show (99), again we assume for brevity , and define the positive functions and ,Note that, with , and ,where (104) uses (100) and (102) and (105) follows from (92). Then,where the expectations are with respect to , and
- (107) follows from the log-sum inequality for integrable non-negative random variables,
- (108) ⇐ (100) and (101).
In the case of finite input-alphabets, a different proof of (99) is given in Appendix B of [54]. - 29.
- Introduced in the unpublished dissertation [36] and rescued from oblivion in [32], the Augustin–Csiszár mutual information of order is defined for aswhere (111) follows from (98) if , and from the reverse of (99) if . We conform to the notation in [40], where was used to denote the difference between entropy and Arimoto-Rényi conditional entropy. In [32,39,43] the Augustin–Csiszár mutual information of order is denoted by . In Augustin’s original notation [36], means , . Independently of [36], Poltyrev [35] introduced a functional (expressed as a maximization over a reverse random transformation) which turns out to be and which he denoted by , although in Gallager’s notation that corresponds to , as we will see in (233). and are defined by taking the corresponding limits.
- 30.
- 31.
- The respective minimizers of (72) and (110), namely, the -response and the -response, are quite different. Most notably, in contrast to Item 7, an explicit expression for is unknown. Instead of defining through (92), [36] defines it, equivalently, as the fixed point of the operator (dubbed the Augustin operator in [43]) which maps the set of probability measures on the output space to itself,where . Although we do not rely on them, Lemma 34.2 of () and Lemma 13 of [43] () claim that the minimizer in (110), referred to in [43] as the Augustin mean of order , is unique and is a fixed point of the operator regardless of . Moreover, Lemma 13(c) of [43] establishes that for and finite input alphabets, repeated iterations of the operator with initial argument converge to .
- 32.
- It is interesting to contrast the next example with the formulas in Examples 2 and 6.Example 7.Additive independent Gaussian noise.If , where independent of , thenThis result can be obtained by postulating a zero-mean Gaussian distribution with variance as and verifying that (92) is indeed satisfied if is chosen as in (116). The first step is to invoke (32), which yieldswhere we have denoted . Since ,
- 33.
- This item gives a variational representation for the Augustin–Csiszár mutual information in terms of mutual information and conditional relative entropy (i.e., non-Rényi information measures). As we will see in Section 10, this representation accounts for the role played by Augustin–Csiszár mutual information in expressing error exponent functions.Theorem 8.For , the Augustin–Csiszár mutual information satisfies the variational representation in terms of conditional relative entropy and mutual information,where the minimum is over all the random transformations from the input to the output spaces.Proof.Averaging over , followed by minimization with respect to yields (128) upon recalling (67). □In the finite-alphabet case with , the representation in (128) is implicit in the appendix of [32], and stated explicitly in [39], where it is shown by means of a minimax theorem. This is one of the instances in which the proof of the result is considerably easier for ; we can take the following route to show (128) for . Neglecting to emphasize its dependence on , denoteInvoking (47) we obtainAveraging (132) with respect to followed by minimization over , results inwhich shows ≥ in (128). If a minimax theorem can be invoked to show equality in (134), then (128) is established for . For that purpose, for fixed , is convex and lower semicontinuous in on the set where it is finite. Rewritingit can be seen that is upper semicontinuous and concave (if ). A different, and considerably more intricate route is taken in Lemma 13(d) of [43], which also gives (128) for assuming finite input alphabets.
- 34.
- Unlike mutual information, neither nor hold in general.Example 8.Erasure transformation. Let ,with , and . Then, we obtain, for ,
- 35.
- It was shown in Theorem 5.2 of [38] that -mutual information satisfies the data processing lemma, namely, if X and Z are conditionally independent given Y, thenAs shown by Csiszár [32] using the data processing inequality for Rényi divergence, the data processing lemma also holds for .
- 36.
- 37.
- The convexity/concavity properties of the generalized mutual informations are summarized next.Theorem 9.
- (a)
- and are concave and monotonically non-decreasing in .
- (b)
- and are concave functions. The same holds for if .
- (c)
- If , then , and are convex functions.
Proof.- (a)
- According to (81) and (128), respectively, with , and are the infima of affine functions with nonnegative slopes.
- (b)
- For mutual information the result goes back to [56] in the finite-alphabet case. In general, it holds since (67) is the infimum of linear functions of . The same reasoning applies to Augustin–Csiszár mutual information in view of (110). For -mutual information with , notice from (51) that is concave in if . Therefore,
- (c)
- The convexity of and follow from the convexity of in for as we saw in Item 18. To show convexity of if , we apply (169) in Item 45 with , and invoke the convexity of :
□
5. Interplay between and
- 38.
- For given and , define , the -adjunct of bywith the constant in (14) and , the -response to .
- 39.
- Example 9.Let with independent of , and . The α-adjunct of the input is
- 40.
- Theorem 10.The -response to is , the α-response to .
- 41.
- For given and , we define , the -adjunct of an input probability measure throughwhere is the -response to and is a normalizing constant so that is a probability measure. According to (9), we must haveHence,
- 42.
- With the aid of the expression in Example 7, we obtainExample 10.Let with independent of , and . Then, the -adjunct of the input iswhich, in contrast to , has larger variance than if .
- 43.
- The following result is the dual of Theorem 10.Theorem 11.The α-response to is , the -response to . Therefore,
- 44.
- By recourse to a minimax theorem, the following representation is given for in the case of finite alphabets in [39], and dropping the restriction on the finiteness of the output space in [43]. As we show, a very simple and general proof is possible for .Theorem 12.Fix , and . Then,where the minimum is attained by , the α-adjunct of defined in (152).Proof.
- 45.
- For finite-input alphabets, Lemma 18(b) of [43] (earlier Theorem 3.4 of [35] gave an equivalent variational characterization assuming, in addition, finite output alphabets) established the following dual to Theorem 12.Theorem 13.Fix , and . Then,The maximum is attained by , the -adjunct of defined by (157).Proof.First observe that (165) implies that ≥ holds in (169). Second, the term in on the right side of (169) evaluated at becomeswhere (170) follows by taking the expectation of minus (157) with respect to . Therefore, ≤ also holds in (169) and the maximum is attained by , as we wanted to show. □Hinging on Theorem 8, Theorems 12 and 13 are given for which is the region of interest in the analysis of error exponents. Whenever, as in the finite-alphabet case, (128) holds for , Theorems 12 and 13 also hold for .Notice that since the definition of involves , the fact that it attains the maximum in (169) does not bring us any closer to finding for a specific input probability measure . Fortunately, as we will see in Section 8, (169) proves to be the gateway to the maximization of in the presence of input-cost constraints.
- 46.
- Focusing on the main range of interest, , we can express (169) aswhere we have defined the function (dependent on , , and )and is the solution toRecall that the maxima over the input distribution in (172) and (175) are attained by the -adjunct defined in Item 41.
- 47.
- At this point it is convenient to summarize the notions of input and output probability measures that we have defined for a given , random transformation , and input probability measure :
- : The familiar output probability measure , defined in Item 5.
- : The -response to , defined in Item 7. It is the unique achiever of the minimization in the definition of -mutual information in (67).
- : The -response to defined in Item 26. It is the unique achiever of the minimization in the definition of Augustin–Csiszár -mutual information in (110).
- : The -adjunct of , defined in (152). The -response to is . Furthermore, achieves the minimum in (165).
- : The -adjunct of , defined in (157). The -response to is . Furthermore, achieves the maximum in (169).
6. Maximization of
- 48.
- The maximization of -mutual information is facilitated by the following result.Theorem 14 ([45]).Given ; a random transformation ; and, a convex set , the following are equivalent.
- (a)
- attains the maximal α-mutual information on ,
- (b)
- For any , and any output distribution ,where is the α-response to .
Moreover, if denotes the α-response to , thenNote that, while may not be maximized by a unique (or, in fact, by any) input distribution, the resulting -response is indeed unique. If is such that none of its elements attain the maximal , it is known [42,45] that the -response to any asymptotically optimal sequence of input distributions converges to . This is the counterpart of a result by Kemperman [58] concerning mutual information. - 49.
- The following example appears in [45].Example 11.Let where independent of X. Fix and . Suppose that the set, , of allowable input probability measures consists of those that satisfy the constraintWe can readily check that satisfies (181) with equality, and as we saw in Example 2, its α-response is . Theorem 14 establishes that does indeed maximize the α-mutual information among all the distributions in , yielding (recall Example 6)Curiously, if, instead of defined by the constraint (181), we consider the more conventional , then the left side of (182) is unknown at present. Numerical evidence shows that it can exceed the right side by employing non-Gaussian inputs.
- 50.
- Recalling (56) and (178) implies that if attains the finite maximal unconstrained -mutual information and its -response is denoted by , then,which requires that , withFor discrete alphabets, this requires that if , then , which is tantamount towith equality for all such that . For finite-alphabet random transformations this observation is equivalent to Theorem 5.6.5 in [9].
- 51.
- Getting slightly ahead of ourselves, we note that, in view of (128), an important consequence of Theorem 15 below, is that, as anticipated in Item 25, the unconstrained maximization of for can be expressed in terms of the solution to an optimization problem involving only conventional mutual information and conditional relative entropy. For ,
7. Unconstrained Maximization of
- 52.
- In view of the fact that it is much easier to determine the -mutual information than the order- Augustin–Csiszár information, it would be advantageous to show that the unconstrained maximum of equals the unconstrained maximum of . In the finite-alphabet setting, in which it is possible to invoke a "minisup” theorem (e.g., see Section 7.1.7 of [59]), Csiszár [32] showed this result for . The assumption of finite output alphabets was dropped in Theorem 1 of [42], and further generalized in Theorem 3 of the same reference. As we see next, for , it is possible to give an elementary proof without restrictions on the alphabets.Theorem 15.Let . If the suprema are over , the set of all probability measures defined on the input space, thenProof. In view of (143), ≥ holds in (187). To show ≤, we assume as, otherwise, there is nothing left to prove. The unconstrained maximization identity in (183) implieswhere is the unique -response to any input that achieves the maximal -mutual information, and if there is no such input, it is the limit of the -responses to any asymptotically optimal input sequence (Item 48). □Furthermore, if is asymptotically optimal for , i.e., , then is also asymptotically optimal for because for any , we can find N, such that for all ,
8. Maximization of Subject to Average Cost Constraints
- 53.
- Given , , a cost function and real scalar , the objective is to maximize the Augustin–Csiszár mutual information allowing only those probability measures that satisfy , namely,Unfortunately, identity (187) no longer holds when the maximizations over the input probability measure are cost-constrained, and, in general, we can only claimA conceptually simple approach to solve for is to
- (a)
- postulate an input probability measure that achieves the supremum in (197);
- (b)
- solve for its -response using (92);
- (c)
- show that is a saddle point for the game with payoff functionwhere and is chosen from the convex subset of of probability measures which satisfy .
Since is already known, by definition, to be the -response to , verifying the saddle point is tantamount to showing that is maximized by among . Theorem 1 of [43] guarantees the existence of a saddle point in the case of finite input alphabets. In addition to the fact that it is not always easy to guess the optimum input (see e.g., Section 12), the main stumbling block is the difficulty in determining the -response to any candidate input distribution, although sometimes this is indeed feasible as we saw in Example 7. - 54.
- Naturally, Theorem 15 impliesIf the unconstrained maximization of is achieved by an input distribution that satisfies , then equality holds in (200), which, in turn, is equal to . In that case, the average cost constraint is said to be inactive. For most cost functions and random transformations of practical interest, the cost constraint is active for all . To ascertain whether it is, we simply verify whether there exists an input achieving the right side of (200), which happens to satisfy the constraint. If so, has been found. The same holds if we can find a sequence such that and . Otherwise, we proceed with the method described below. Thus, henceforth, we assume that the cost constraint is active.
- 55.
- The approach proposed in this paper to solve for for hinges on the variational representation in (172), which allows us to sidestep having to find any -response. Note that once we set out to maximize over , the allowable in the maximization in (175) range over a -blow-up of defined byAs we show in Item 56, we can accomplish such an optimization by solving an unconstrained maximization of the sum of -mutual information and a term suitably derived from the cost function.
- 56.
- It will not be necessary to solve for (176), as our goal is to further maximize (172) over subject to an average cost constraint. The Lagrangian corresponding to the constrained optimization in (197) iswhere on the left side we have omitted, for brevity, the dependence on stemming from the last term on the right side. The Lagrange multiplier method (e.g., [60]) implies that if achieves the supremum in (197), then there exists such that for all on and ,Note from (202) that the right inequality in (203) can only be achieved ifand, consequently,The pivotal result enabling us to obtain without the need to deal with Augustin–Csiszár mutual information is the following.Theorem 16.Given , , , and , denote the functionThen,andProof.Plugging (172) into (197) we obtain, with , and ,where (209) and (213) follow from (202) and (206), respectively, and (212) follows by invoking Theorem 1 with andwhich is nonnegative since and . Finally, (208) follows from (205) and (207). □In conclusion, we have shown that the maximization of Augustin–Csiszár mutual information of order subject to boils down to the unconstrained maximization of a Lagrangian consisting of the sum of -mutual information and an exponential average of the cost function. Circumventing the need to deal with -responses and with Augustin–Csiszár mutual information of order leads to a particularly simple optimization, as illustrated in Section 11 and Section 12.
- 57.
- Theorem 16 solves for the maximal Augustin–Csiszár mutual information of order under an average cost constraint without having to find out the input probability measure that attains it nor its -response (using the notation in Item 53). Instead, it gives the solution asAlthough we are not going to invoke a minimax theorem, with the aid of Theorem 9-(b) we can see that the functional within the inner brackets is concave in ; Furthermore, if , then is easily seen to be convex in with the aid of the Cauchy-Schwarz inequality. Before we characterize the saddle point of the game in (215) we note that can be readily obtained from .Theorem 17.Fix . Let denote the minimizer on the right side of (215), and the input probability measure that attains the maximum in (206) (or (215)) for . Then,
- (a)
- is the -adjunct of .
- (b)
- , the α-response to .
- (c)
- withwhere is a normalizing constant ensuring that is a probability measure.
Proof.- (a)
- We had already established in Theorem 13 that the maximum on the right side of (210) is achieved by the -adjunct of . In the special case , such is . Therefore, , the argument that achieves the maximum in (206) for , is the -adjunct of .
- (b)
- According to Theorem 11, the -response to is the -response to , which is by definition.
- (c)
- For , achieves the supremum in (209) and the infimum in (211). Therefore, (216) follows from Theorem 1 with and given by (214) particularized to .
□The saddle point of (215) admits the following characterization.Theorem 18.If , the saddle point of (215) satisfieswhere is the α-response to , and does not depend on . Furthermore,Proof. First, we show that the scalar that minimizessatisfies (217). If we abbreviate , then the dominated convergence theorem results inTherefore, (217) is equivalent to , which is all we need on account of the convexity of . To show (218), notice that for all ,where (223) is (216) and (224) is (157) with in view of Theorem 17-(b). In conclusion, (218) holds withFinally, (206) implieswhere (227) follows from the definition of -mutual information and Theorem 17-(b), and (228) follows from (218). Plugging (219) into (208) results in (220). □ - 58.
- Typically, the application of Theorem 18 involves
- (a)
- guessing the form of the auxiliary input (modulo some unknown parameter),
- (b)
- obtaining its -response , and
- (c)
- verifying that (217) and (218) are satisfied for some specific choice of the unknown parameter.
With the same approach, we can postulate, for every , an input distribution , whose -response satisfieswhere the only condition we place on is that it not depend on . If this is indeed the case, then the same derivation in (226)–(229) results inand we determine as the solution to , in lieu of (217). Section 11 and Section 12 illustrate the effortless nature of this approach to solve for . Incidentally, (230) can be seen as the -generalization of the condition in Problem 8.2 of [48], elaborated later in [61].
9. Gallager’s Functions and the Maximal Augustin–Csiszár Mutual Information
- 59.
- In his derivation of an achievability result for discrete memoryless channels, Gallager [8] introduced the function (1), which we repeat for convenience,Comparing (82) and (232), we obtainwhich, as we mentioned in Section 1, is the observation by Csiszár in [30] that triggered the third phase in the representation of error exponents. Popularized in [9], the function was employed by Shannon, Gallager and Berlekamp [10] for and by Arimoto [62] for in the derivation of converse results in data transmission, the latter of which considers rates above capacity, a region in which error probability increases with blocklength, approaching one at an exponential rate. For the achievability part, [8] showed upper bounds on the error probability involving for . Therefore, for rates below capacity, the -mutual information only enters the picture for . One exception in which Rényi divergence of order greater than 1 plays a role at rates below capacity was found by Sason [63], where a refined achievability result is shown for binary linear codes for output symmetric channels (a case in which equiprobable maximizes (233)), as a function of their Hamming weight distribution.Although Gallager did not have the benefit of the insight provided by the Rényi information measures, he did notice certain behaviors of reminiscent of mutual information. For example, the derivative of (233) with respect to , at is equal to . As pointed out by Csiszár in [32], in the absence of cost constraints, Gallager’s function in (232) satisfiesin view of (233) and (187).Recall that Gallager’s modified function in the case of cost constraints iswhich, like (232) he introduced in order to show an achievability result. Up until now, no counterpart to (234) has been found with cost constraints and (235). This is accomplished in the remainder of this section.
- 60.
- In the finite alphabet case the following result is useful to obtain a numerical solution for the functional in (206). More importantly, it is relevant to the discussion in Item 61.Theorem 19.In the special case of discrete alphabets, the function in (206) is equal towhere the maximization is over all such thatProof.□
- 61.
- We can now proceed to close the circle between the maximization of Augustin–Csiszár mutual information subject to average cost constraints (Phase 3 in Section 1) and Gallager’s approach (Phase 1 in Section 1).Theorem 20.In the discrete alphabet case, recalling the definitions in (202) and (235), for ,where the maximizations are over .Proof.Withthe maximization of (235) with the respect to the input probability measure yieldswhere
- the maximization on the right side of (247) is over all that satisfy (237), since that constraint is tantamount to enforcing the constraint that on the left side of (247);
- (248) ⟸ Theorem 19;
- (249) ⟸ Theorem 16.
The proof of (242) is complete once (244) is invoked to substitute and from the right side of (249). If we now minimize the outer sides of (245)–(249) with respect to r we obtain, using (205) and (244),□In p. 329 of [9], Gallager poses the unconstrained maximization (i.e., over ) of the LagrangianNote the apparent discrepancy between the optimizations in (243) and (253): the latter is parametrized by r and (in addition to and ), while the maximization on the right side of (243) does not enforce any average cost constraint. In fact, there is no disparity since Gallager loc. cit. finds serendipitously that regardless of r and , and, therefore, just one parameter is enough. - 62.
- The raison d’être for Augustin’s introduction of in [36] was his quest to view Gallager’s approach with average cost constraints under the optic of Rényi information measures. Contrasting (232) and (235) and inspired by the fact that, in the absence of cost constraints, (232) satisfies a variational characterization in view of (69) and (233), Augustin [36] dealt, not with (235), but withAssuming finite alphabets, Augustin was able to connect this quantity with the maximal under cost constraints in an arcane analysis that invokes a minimax theorem. This line of work was continued in Section 5 of [43], which refers to as the Rényi-Gallager information. Unfortunately, since is not a random transformation, the conditional pseudo-Rényi divergence need not satisfy the key additive decomposition in Theorem 4 so the approach of [36,43] fails to establish an identity equating the maximization of Gallager’s function (235) with the maximization of Augustin–Csiszár mutual information, which is what we have accomplished through a crisp and elementary analysis.
10. Error Exponent Functions
- 63.
- If and , the sphere-packing error exponent function is (e.g., (10.19) of [48])
- 64.
- As a function of , the basic properties of (254) for fixed are as follows.
- (a)
- If , then ;
- (b)
- If , then ;
- (c)
- The infimum of the arguments for which the sphere-packing error exponent function is finite is denoted by ;
- (d)
- On the interval , is convex, strictly decreasing, continuous, and equal to (254) where the constraint is satisfied with equality. This implies that for R belonging to that interval, we can find so that for all ,
- 65.
- In view of Theorem 8 and its definition in (254), it is not surprising that is intimately related to the Augustin–Csiszár mutual information, through the following key identity.Theorem 21.Proof.First note that ≥ holds in (256) because from (128) we obtain, for all ,where (260) follows from the definition in (254). To show ≤ in (256) for those R such that , Property (d) in Item 64 allows us to writewhere (262) follows from (255).To determine the region where the sphere-packing error exponent is infinite and show (257), first note that if , then because for any , the function in on the right side of (256) satisfieswhere (264) follows from the monotonicity of in we saw in (143). Conversely, if , there exists such that , which implies that in the minimizationwe may restrict to those such that , and consequently, . Therefore, to avoid a contradiction, we must have .The remaining case is . Again, the monotonicity of the Augustin–Csiszár mutual information implies that for all . So, (128) prescribes for any is such that . Therefore, for all , as we wanted to show. □Augustin [36] provided lower bounds on error probability for codes of type as a function of but did not state (256); neither did Csiszár in [32] as he was interested in a non-conventional parametrization (generalized cutoff rates) of the reliability function. As pointed out in p. 5605 of [64], the ingredients for the proof of (256) were already present in the hint of Problem 23 of Section II.5 of [24]. In the discrete case, an exponential lower bound on error probability for codes with constant composition is given as a function of in [44,64]. As in [64], Nakiboglu [65] gives (256) as the definition of the sphere-packing function and connects it with (254) in Lemma 3 therein, within the context of discrete input alphabets.
- 66.
- The critical rate, , is defined as the smallest abscissa at which the convex function meets its supporting line of slope . According to (256),
- 67.
- If and , the random-coding exponent function is (e.g., (10.15) of [48])with .
- 68.
- The random-coding error exponent function is determined by the sphere-packing error exponent function through the following relation, illustrated in Figure 1.Theorem 22.Proof.Identities (268) and (269) are well-known (e.g., Lemma 10.4 and Corollary 10.4 in [48]). To show (270), note that (256) expresses as the supremum of supporting lines parametrized by their slope . By definition of critical rate (for brevity, we do not show explicitly its dependence on ), if , then can be obtained by restricting the optimization in (256) to . In that segment of values of R, according to (269). Moreover, on the interval , we havewhere we have used (266) and (269). □The first explicit connection between and the Augustin–Csiszár mutual information was made by Poltyrev [35] although he used a different form for , as we discussed in (29).
- 69.
- The unconstrained maximizations over the input distribution of the sphere-packing and random coding error exponent functions are denoted, respectively, byCoding theorems [8,9,10,22,48] have shown that when these functions coincide they yield the reliability function (optimum speed at which the error probability vanishes with blocklength) as a function of the rate . The intuition is that, for the most favorable input distribution, errors occur when the channel behaves so atypically that codes of rate R are not reliable. There are many ways in which the channel may exhibit such behavior and they are all unlikely, but the most likely among them is the one that achieves (254).It follows from (187), (256) and (270) that (274) and (275) can be expressed asTherefore, we can sidestep working with the Augustin–Csiszár mutual information in the absence of cost constraints.
- 70.
- Shannon [1] showed that, operating at rates below maximal mutual information, it is possible to find codes whose error probability vanishes with blocklength; for the converse, instead of error probability, Shannon measured reliability by the conditional entropy of the message given the channel output. That alternative reliability measure, as well as its generalization to Arimoto-Rényi conditional entropy, is also useful analyzing the average performance over code ensembles. It turns out (see e.g., [28,68]) that, below capacity, those conditional entropies also vanish exponentially fast in much the same way as error probability with bounds that are governed by and thereby lending additional operational significance to those functions.
- 71.
- We now introduce a cost function and real scalar , and reexamine the optimizations in (274) and (275) allowing only those probability measures that satisfy With a patent, but unavoidable, abuse of notation we definewhere (279), (281) and (282) follow from (256), (208) and (206), respectively.
- 72.
- In parallel to (278)–(281),where (284) follows from (270). In particular, if we define the critical rate and the cutoff rate asrespectively, then it follows from (270) thatSummarizing, the evaluation of and can be accomplished by the method proposed in Section 8, at the heart of which is the maximization in (206) involving -mutual information instead of Augustin–Csiszár mutual information. In Section 11 and Section 12, we illustrate the evaluation of the error exponent functions with two important additive-noise examples.
11. Additive Independent Gaussian Noise; Input Power Constraint
- 73.
- Suppose , , and . We start by testing whether we can find such that its -response satisfies (230). Naturally, it makes sense to try for some yet to be determined . As we saw in Example 6, this choice implies that its -response is . Specializing Example 4, we obtainTherefore, (230) is indeed satisfied withwhere (292) follows if we choose the variance of the auxiliary input asIn (294) we have introduced an alternative, more convenient, parametrization for the Lagrange multiplierIn conclusion, with the choice in (293), attains the maximum in (206), and in view of (231), is given by the right side of (291) substituting by (293). Therefore, we havewhere we denotedIn accordance with Theorem 16 all that remains is to minimize (297) with respect to , or equivalently, with respect to . Differentiating (297) with respect to , the minimum is achieved at satisfyingwhose only valid root (obtained by solving a quadratic equation) iswith defined in (118). So, for , (208) becomesLetting , we obtainwith
- 74.
- Alternatively, it is instructive to apply Theorem 18 to the current Gaussian/quadratic cost setting. Suppose we let , where is to be determined. With the aid of the formulaswhere , and , (217) becomesupon substituting andLikewise (218) translates into (291) and (292) with , namely,Eliminating from (305) by means of (308) results in (299) and the same derivation that led to (300) shows that it is equal to .
- 75.
- Applying Theorem 17, we can readily find the input distribution, , that attains as well as its -response (recall the notation in Item 53). According to Example 2, , the -response to is Gaussian with zero mean and variancewhere (309) follows from (308) and (310) follows by using the expression for in (118). Note from Example 7 that is nothing but the -response to . We can easily verify from Theorem 17 that indeed since in this case (216) becomeswhich can only be satisfied by in view of (305). As an independent confirmation, we can verify, after some algebra, that the right sides of (127) and (300) are identical.In fact, in the current Gaussian setting, we could start by postulating that the distribution that maximizes the Augustin–Csiszár mutual information under the second moment constraint does not depend on and is given by . Its -response was already obtained in Example 7. Then, an alternative method to find , given in Section 6.2 of [43], is to follow the approach outlined in Item 53. To validate the choice of we must show that it maximizes (in the notation introduced in (199)) among the subset of which satisfies . This follows from the fact that is an affine function of .
- 76.
- Let’s now use the result in Item 73 to evaluate, with a novel parametrization, the error exponent functions for the Gaussian channel under an average power constraint.Theorem 23.Let , , and . Then, for ,The critical rate and cutoff rate are, respectively,Proof.Expression (315) for the cutoff rate follows by letting in (301) and (302). The supremum in (281) is attained by that satisfies (recall the concavity result in Theorem 9-(a))obtained after a dose of symbolic computation working with (301). In particular, letting , we obtain the critical rate in (314). Note that if in (302) we substitute , with given as a function of R, and by (317), we end up with an equation involving R, , and . We proceed to verify that that equation is, in fact, (312). By solving a quadratic equation, we can readily check that (302) is the positive root ofIf we particularize (318) to , with given by (317), namely,we obtainwhich is (313). Notice that the right side of (320) is monotonic increasing in ranging from 1 (for ) to (for ). Therefore, spans the whole gamut of values of R of interest.Assembling (281), (301) and (317), we obtainwhere (324) follows by substituting (313) on the left side. □Note that the parametric expression in (312) and (313) (shown in Figure 2) is, in fact, a closed-form expression for since we can invert (313) to obtainThe random coding error exponent iswith the critical rate and cutoff rate in (314) and (315), respectively. It can be checked that (326) coincides with the expression given by Gallager [9] (p. 340) where he optimizes (235) with respect to and r, but not , which he just assumes to be . The expression for in (314) can be found in (7.4.34) of [9]; in (314) is implicit in p. 340 of [9], and explicit in e.g., [69].
- 77.
- The expression for in Theorem 23 has more structure than meets the eye. The analysis in Item 73 has shown that is maximized over with second moment not exceeding by regardless of . The fact that we have found a closed-form expression for (254) when evaluated at such input probability measure and is indicative that the minimum therein is attained by a Gaussian random transformation . This is indeed the case: define the random transformationIn comparison with the nominal random transformation , this channel attenuates the input and contaminates it with a more powerful noise. Then,Furthermore, invoking (33), we getwhere (333) is (312). Therefore, does indeed achieve the minimum in (254) if and . So, the most likely error mechanism is the result of atypically large noise strength and an attenuated received signal. Both effects cannot be combined into additional noise variance: there is no such that achieves the minimum in (254).
12. Additive Independent Exponential Noise; Input-Mean Constraint
- 78.
- Suppose that , , andwhere N is exponentially distributed, independent of X, and . Therefore has densityTo determine , , we invoke Theorem 18. A sensible candidate for the auxiliary input distribution is a mixed random variable with densitywhere is yet to be determined. This is an attractive choice because its -response, , is particularly simple: exponential with mean , as we can verify using Laplace transforms. Then, if Z is exponential with unit mean, with the aid of Example 5, we can writeSo, (218) is satisfied withTo evaluate (217), it is useful to note that if , thenTherefore, the left side of (217) specializes to, with ,while the expectation on the right side of (217) is given byTherefore, (217) yieldswhose solution iswith . So, finally, (220), (344) and (345) give the closed-form expressionAs in Item 73, we can postulate an auxiliary distribution that satisfies (230) for every . This is identical to what we did in (341)–(343) except that now (344) and (345) hold for generic and . Then, (351) is the result of solving , which is, in fact, somewhat simpler than obtaining it through (217).
- 79.
- We proceed to get a very simple parametric expression for .Theorem 24.Let , , and , with N exponentially distributed, independent of X, and . Then, under the average cost constraint ,where .Proof.Rewriting (353), results inwhich is monotonically decreasing with . With , the counterpart of (317) is nowwhere the drastic simplification in (360) occurs because, with the current parametrization, (351) becomesNow we go ahead and express both and as functions of and R exclusively. We may rewrite (357)–(360) aswhich, when plugged in (361), results inwhere the inequalities in (363) and (364) follow from . So, in conclusion,where we have introducedEvidently, the left identity in (372) is the same as (355). □The critical rate and the cutoff rate are obtained by particularizing (360) and (356) to and , respectively. This yieldsAs in (326), the random coding error exponent iswith the critical rate and cutoff rate in (373) and (375), respectively. This function is shown along with in Figure 3 for .
- 80.
- In parallel to Item 77, we find the random transformation that explains the most likely mechanism to produce errors at every rate R, namely the minimizer of (254) when , the maximizer of the Augustin–Csiszár mutual information of order . In this case, is not as trivial to guess as in Section 11, but since we already found in (339) with , we can invoke Theorem 17 to show that the density of achieving the maximal order- Augustin–Csiszár mutual information iswhose mean is, as it should,Let be exponential with mean , and have densitywithand as defined in (372). Using Laplace transforms, we can verify that where is the probability measure with density in (377). Let Z be unit-mean exponentially distributed. Writing mutual information as the difference between the output differential entropy and the noise differential entropy we getin view of (363). Furthermore, using (335) and (379),where we have used (380) and (354). Therefore, we have shown that is indeed the minimizer of (254). In this case, the most likely mechanism for errors to happen is that the channel adds independent exponential noise with mean , instead of the nominal mean . In this respect, the behavior is reminiscent of that of the exponential timing channel for which the error exponent is dominated (at least above critical rate) by an exponential server which is slower than the nominal [72].
13. Recap
- 81.
- The analysis of the fundamental limits of noisy channels in the regime of vanishing error probability with blocklength growing without bound expresses channel capacity in terms of a basic information measure: the input–output mutual information maximized over the input distribution. In the regime of fixed nonzero error probability, the asymptotic fundamental limit is a function of not only capacity but channel dispersion [73], which is also expressible in terms of an information measure: the variance of the information density obtained with the capacity-achieving distribution. In the regime of exponentially decreasing error probability (at fixed rate below capacity) the analysis of the fundamental limits has gone through three distinct phases. No information measures were involved during the first phase and any optimization with respect to various auxiliary parameters and input distribution had to rely on standard convex optimization techniques, such as Karush-Kuhn-Tucker conditions, which not only are cumbersome to solve in this particular setting, but shed little light on the structure of the solution. The second phase firmly anchored the problem in a large deviations foundation, with the fundamental limits expressed in terms of conditional relative entropy as well as mutual information. Unfortunately, the associated maximinimization in (2) did not immediately lend itself to analytical progress. Thanks to Csiszár’s realization of the relevance of Rényi’s information measures to this problem, the third phase has found a way to, not only express the error exponent functions as a function of information measures, but to solve the associated optimization problems in a systematic way. While, in the absence of cost constraints, the problem reduces to finding the maximal -mutual information, cost constraints make the problem much more challenging because of the difficulty in determining the order- Augustin–Csiszár mutual information. Fortunately, thanks to the introduction of an auxiliary input distribution (the -adjunct of the distribution that maximizes ), we have shown that -mutual information also comes to the rescue in the maximization of the order- Augustin–Csiszár mutual information in the presence of average cost constraints. We have also finally ended the isolation of Gallager’s function with cost constraints from the representations in Phases 2 and 3. The pursuit of such a link is what motivated Augustin in 1978 to define a generalized mutual information measure. Overall, the analysis has given yet another instance of the benefits of variational representations of information measures, leading to solutions based on saddle points. However, we have steered clear of off-the-shelf minimax theorems and their associated topological constraints.We have worked out two channels/cost constraints (additive Gaussian noise with quadratic cost, and additive exponential noise with a linear cost) that admit closed-form error-exponent functions, most easily expressed in parametric form. Furthermore, in Items 77 and 80 we have illuminated the structure of those closed-form expressions by identifying the anomalous channel behavior responsible for most errors at every given rate. In the exponential noise case, the solution is simply a noisier exponential channel, while in the Gaussian case it is the result of both a noisier Gaussian channel and an attenuated input.These observations prompt the question of whether there might be an alternative general approach that eschews Rényi’s information measures to arrive at not only the most likely anomalous channel behavior, but the error exponent functions themselves.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
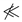 Q.
Q.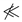 Q, i.e., that the expectation on the left side is , we invoke the Lebesgue decomposition theorem (e.g. p. 384 of [74]), which ensures that we can find , and , such that
Q, i.e., that the expectation on the left side is , we invoke the Lebesgue decomposition theorem (e.g. p. 384 of [74]), which ensures that we can find , and , such that
- (A8) ⟸ (A4).
References
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Rice, S.O. Communication in the Presence of Noise–Probability of Error for Two Encoding Schemes. Bell Syst. Tech. J. 1950, 29, 60–93. [Google Scholar] [CrossRef]
- Shannon, C.E. Probability of Error for Optimal Codes in a Gaussian Channel. Bell Syst. Tech. J. 1959, 38, 611–656. [Google Scholar] [CrossRef]
- Elias, P. Coding for Noisy Channels. IRE Conv. Rec. 1955, 4, 37–46. [Google Scholar]
- Feinstein, A. Error Bounds in Noisy Channels without Memory. IRE Trans. Inf. Theory 1955, 1, 13–14. [Google Scholar] [CrossRef]
- Shannon, C.E. Certain Results in Coding Theory for Noisy Channels. Inf. Control 1957, 1, 6–25. [Google Scholar] [CrossRef]
- Fano, R.M. Transmission of Information; Wiley: New York, NY, USA, 1961. [Google Scholar]
- Gallager, R.G. A Simple Derivation of the Coding Theorem and Some Applications. IEEE Trans. Inf. Theory 1965, 11, 3–18. [Google Scholar] [CrossRef]
- Gallager, R.G. Information Theory and Reliable Communication; Wiley: New York, NY, USA, 1968. [Google Scholar]
- Shannon, C.E.; Gallager, R.G.; Berlekamp, E. Lower Bounds to Error Probability for Coding on Discrete Memoryless Channels, I. Inf. Control 1967, 10, 65–103. [Google Scholar] [CrossRef]
- Shannon, C.E.; Gallager, R.G.; Berlekamp, E. Lower Bounds to Error Probability for Coding on Discrete Memoryless Channels, II. Inf. Control 1967, 10, 522–552. [Google Scholar] [CrossRef]
- Dobrushin, R.L. Asymptotic Estimates of the Error Probability for Transmission of Messages over a Discrete Memoryless Communication Channel with a Symmetric Transition Probability Matrix. Theory Probab. Appl. 1962, 7, 270–300. [Google Scholar] [CrossRef]
- Dobrushin, R.L. Optimal Binary Codes for Low Rates of Information Transmission. Theory Probab. Appl. 1962, 7, 208–213. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Graph Decomposition: A New Key to Coding Theorems. IEEE Trans. Inf. Theory 1981, 27, 5–11. [Google Scholar] [CrossRef]
- Barg, A.; Forney, G.D., Jr. Random codes: Minimum Distances and Error Exponents. IEEE Trans. Inf. Theory 2002, 48, 2568–2573. [Google Scholar] [CrossRef]
- Sason, I.; Shamai, S. Performance Analysis of Linear Codes under Maximum-likelihood Decoding: A Tutorial. Found. Trends Commun. Inf. Theory 2006, 3, 1–222. [Google Scholar] [CrossRef]
- Ashikhmin, A.E.; Barg, A.; Litsyn, S.N. A New Upper Bound on the Reliability Function of the Gaussian Channel. IEEE Trans. Inf. Theory 2000, 46, 1945–1961. [Google Scholar] [CrossRef]
- Haroutunian, E.A.; Haroutunian, M.E.; Harutyunyan, A.N. Reliability Criteria in Information Theory and in Statistical Hypothesis Testing. Found. Trends Commun. Inf. Theory 2007, 4, 97–263. [Google Scholar] [CrossRef]
- Scarlett, J.; Peng, L.; Merhav, N.; Martinez, A.; Guillén i Fàbregas, A. Expurgated Random-coding Ensembles: Exponents, Refinements, and Connections. IEEE Trans. Inf. Theory 2014, 60, 4449–4462. [Google Scholar] [CrossRef]
- Somekh-Baruch, A.; Scarlett, J.; Guillén i Fàbregas, A. A Recursive Cost-Constrained Construction that Attains the Expurgated Exponent. In Proceedings of the 2019 IEEE International Symposium on Information Theory, Paris, France, 7–12 July 2019; pp. 2938–2942. [Google Scholar]
- Haroutunian, E.A. Estimates of the Exponent of the Error Probability for a Semicontinuous Memoryless Channel. Probl. Inf. Transm. 1968, 4, 29–39. [Google Scholar]
- Blahut, R.E. Hypothesis Testing and Information Theory. IEEE Trans. Inf. Theory 1974, 20, 405–417. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems; Academic: New York, NY, USA, 1981. [Google Scholar]
- Rényi, A. On Measures of Information and Entropy. In Berkeley Symposium on Mathematical Statistics and Probability; Neyman, J., Ed.; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Campbell, L.L. A Coding Theorem and Rényi’s Entropy. Inf. Control 1965, 8, 423–429. [Google Scholar] [CrossRef]
- Arimoto, S. Information Measures and Capacity of Order α for Discrete Memoryless Channels. In Topics in Information Theory; Bolyai: Keszthely, Hungary, 1975; pp. 41–52. [Google Scholar]
- Sason, I.; Verdú, S. Arimoto-Rényi conditional entropy and Bayesian M-ary hypothesis testing. IEEE Trans. Inf. Theory 2018, 64, 4–25. [Google Scholar] [CrossRef]
- Fano, R.M. Class Notes for Course 6.574: Statistical Theory of Information; Massachusetts Institute of Technology: Cambridge, MA, USA, 1953. [Google Scholar]
- Csiszár, I. A Class of Measures of Informativity of Observation Channels. Period. Mat. Hung. 1972, 2, 191–213. [Google Scholar] [CrossRef]
- Sibson, R. Information Radius. Z. Wahrscheinlichkeitstheorie Und Verw. Geb. 1969, 14, 149–161. [Google Scholar] [CrossRef]
- Csiszár, I. Generalized Cutoff Rates and Rényi’s Information Measures. IEEE Trans. Inf. Theory 1995, 41, 26–34. [Google Scholar] [CrossRef]
- Arimoto, S. Computation of Random Coding Exponent Functions. IEEE Trans. Inf. Theory 1976, 22, 665–671. [Google Scholar] [CrossRef]
- Candan, C. Chebyshev Center Computation on Probability Simplex with α-divergence Measure. IEEE Signal Process. Lett. 2020, 27, 1515–1519. [Google Scholar] [CrossRef]
- Poltyrev, G.S. Random Coding Bounds for Discrete Memoryless Channels. Probl. Inf. Transm. 1982, 18, 9–21. [Google Scholar]
- Augustin, U. Noisy Channels. Ph.D. Thesis, Universität Erlangen-Nürnberg, Erlangen, Germany, 1978. [Google Scholar]
- Tomamichel, M.; Hayashi, M. Operational Interpretation of Rényi Information Measures via Composite Hypothesis Testing against Product and Markov Distributions. IEEE Trans. Inf. Theory 2018, 64, 1064–1082. [Google Scholar] [CrossRef]
- Polyanskiy, Y.; Verdú, S. Arimoto Channel Coding Converse and Rényi Divergence. In Proceedings of the 48th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 29 September–1 October 2010; pp. 1327–1333. [Google Scholar]
- Shayevitz, O. On Rényi Measures and Hypothesis Testing. In Proceedings of the 2011 IEEE International Symposium on Information Theory, St. Petersburg, Russia, 31 July–5 August 2011; pp. 894–898. [Google Scholar]
- Verdú, S. α-Mutual Information. In Proceedings of the 2015 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 1–6 February 2015. [Google Scholar]
- Ho, S.W.; Verdú, S. Convexity/Concavity of Rényi Entropy and α-Mutual Information. In Proceedings of the 2015 IEEE International Symposium on Information Theory, Hong Kong, China, 15–19 June 2015; pp. 745–749. [Google Scholar]
- Nakiboglu, B. The Rényi Capacity and Center. IEEE Trans. Inf. Theory 2019, 65, 841–860. [Google Scholar] [CrossRef]
- Nakiboglu, B. The Augustin Capacity and Center. arXiv 2018, arXiv:1803.07937. [Google Scholar] [CrossRef]
- Dalai, M. Some Remarks on Classical and Classical-Quantum Sphere Packing Bounds: Rényi vs. Kullback–Leibler. Entropy 2017, 19, 355. [Google Scholar] [CrossRef]
- Cai, C.; Verdú, S. Conditional Rényi Divergence Saddlepoint and the Maximization of α-Mutual Information. Entropy 2019, 21, 969. [Google Scholar] [CrossRef]
- Vázquez-Vilar, G.; Martinez, A.; Guillén i Fàbregas, A. A Derivation of the Cost-constrained Sphere-Packing Exponent. In Proceedings of the 2015 IEEE International Symposium on Information Theory, Hong Kong, China, 15–19 June 2015; pp. 929–933. [Google Scholar]
- Wyner, A.D. Capacity and Error Exponent for the Direct Detection Photon Channel. IEEE Trans. Inf. Theory 1988, 34, 1449–1471. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Rényi, A. On Measures of Dependence. Acta Math. Hung. 1959, 10, 441–451. [Google Scholar] [CrossRef]
- van Erven, T.; Harremoës, P. Rényi Divergence and Kullback-Leibler Divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
- Csiszár, I.; Matúš, F. Information Projections Revisited. IEEE Trans. Inf. Theory 2003, 49, 1474–1490. [Google Scholar] [CrossRef]
- Csiszár, I. Information-type Measures of Difference of Probability Distributions and Indirect Observations. Stud. Sci. Math. Hung. 1967, 2, 299–318. [Google Scholar]
- Nakiboglu, B. The Sphere Packing Bound via Augustin’s Method. IEEE Trans. Inf. Theory 2019, 65, 816–840. [Google Scholar] [CrossRef]
- Nakiboglu, B. The Augustin Capacity and Center. Probl. Inf. Transm. 2019, 55, 299–342. [Google Scholar] [CrossRef]
- Vázquez-Vilar, G. Error Probability Bounds for Gaussian Channels under Maximal and Average Power Constraints. arXiv 2019, arXiv:1907.03163. [Google Scholar]
- Shannon, C.E. Geometrische Deutung einiger Ergebnisse bei der Berechnung der Kanalkapazität. Nachrichtentechnische Z. 1957, 10, 1–4. [Google Scholar]
- Verdú, S.; Han, T.S. A General Formula for Channel Capacity. IEEE Trans. Inf. Theory 1994, 40, 1147–1157. [Google Scholar] [CrossRef]
- Kemperman, J.H.B. On the Shannon Capacity of an Arbitrary Channel. K. Ned. Akad. Van Wet. Indag. Math. 1974, 77, 101–115. [Google Scholar] [CrossRef]
- Aubin, J.P. Mathematical Methods of Game and Economic Theory; North-Holland: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Luenberger, D.G. Optimization by Vector Space Methods; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Gastpar, M.; Rimoldi, B.; Vetterli, M. To Code, or Not to Code: Lossy Source–Channel Communication Revisited. IEEE Trans. Inf. Theory 2003, 49, 1147–1158. [Google Scholar] [CrossRef]
- Arimoto, S. On the Converse to the Coding Theorem for Discrete Memoryless Channels. IEEE Trans. Inf. Theory 1973, 19, 357–359. [Google Scholar] [CrossRef]
- Sason, I. On the Rényi Divergence, Joint Range of Relative Entropies, Measures and a Channel Coding Theorem. IEEE Trans. Inf. Theory 2016, 62, 23–34. [Google Scholar] [CrossRef]
- Dalai, M.; Winter, A. Constant Compositions in the Sphere Packing Bound for Classical-quantum Channels. IEEE Trans. Inf. Theory 2017, 63, 5603–5617. [Google Scholar] [CrossRef][Green Version]
- Nakiboglu, B. The Sphere Packing Bound for Memoryless Channels. Probl. Inf. Transm. 2020, 56, 201–244. [Google Scholar] [CrossRef]
- Dalai, M. Lower Bounds on the Probability of Error for Classical and Classical-quantum Channels. IEEE Trans. Inf. Theory 2013, 59, 8027–8056. [Google Scholar] [CrossRef]
- Shannon, C.E. The Zero Error Capacity of a Noisy Channel. IRE Trans. Inf. Theory 1956, 2, 8–19. [Google Scholar] [CrossRef]
- Feder, M.; Merhav, N. Relations Between Entropy and Error Probability. IEEE Trans. Inf. Theory 1994, 40, 259–266. [Google Scholar] [CrossRef]
- Einarsson, G. Signal Design for the Amplitude-limited Gaussian Channel by Error Bound Optimization. IEEE Trans. Commun. 1979, 27, 152–158. [Google Scholar] [CrossRef]
- Anantharam, V.; Verdú, S. Bits through Queues. IEEE Trans. Inf. Theory 1996, 42, 4–18. [Google Scholar] [CrossRef]
- Verdú, S. The Exponential Distribution in Information Theory. Probl. Inf. Transm. 1996, 32, 86–95. [Google Scholar]
- Arikan, E. On the Reliability Exponent of the Exponential Timing Channel. IEEE Trans. Inf. Theory 1996, 48, 1681–1689. [Google Scholar] [CrossRef]
- Polyanskiy, Y.; Poor, H.V.; Verdú, S. Channel Coding Rate in the Finite Blocklength Regime. IEEE Trans. Inf. Theory 2010, 56, 2307–2359. [Google Scholar] [CrossRef]
- Royden, H.L.; Fitzpatrick, P. Real Analysis, 4th ed.; Prentice Hall: Boston, FL, USA, 2010. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verdú, S. Error Exponents and α-Mutual Information. Entropy 2021, 23, 199. https://doi.org/10.3390/e23020199
Verdú S. Error Exponents and α-Mutual Information. Entropy. 2021; 23(2):199. https://doi.org/10.3390/e23020199
Chicago/Turabian StyleVerdú, Sergio. 2021. "Error Exponents and α-Mutual Information" Entropy 23, no. 2: 199. https://doi.org/10.3390/e23020199
APA StyleVerdú, S. (2021). Error Exponents and α-Mutual Information. Entropy, 23(2), 199. https://doi.org/10.3390/e23020199