Elliptic Solutions of Dynamical Lucas Sequences
Abstract
1. Introduction
2. Elliptic Solution of a Level-Dependent Lucas System
3. Weight-Dependent Commutation Relations and Elliptic Weights
3.1. Noncommutative Weight-Dependent Binomial Theorem
3.2. Elliptic Weights
4. Noncommutative Fibonacci Polynomials
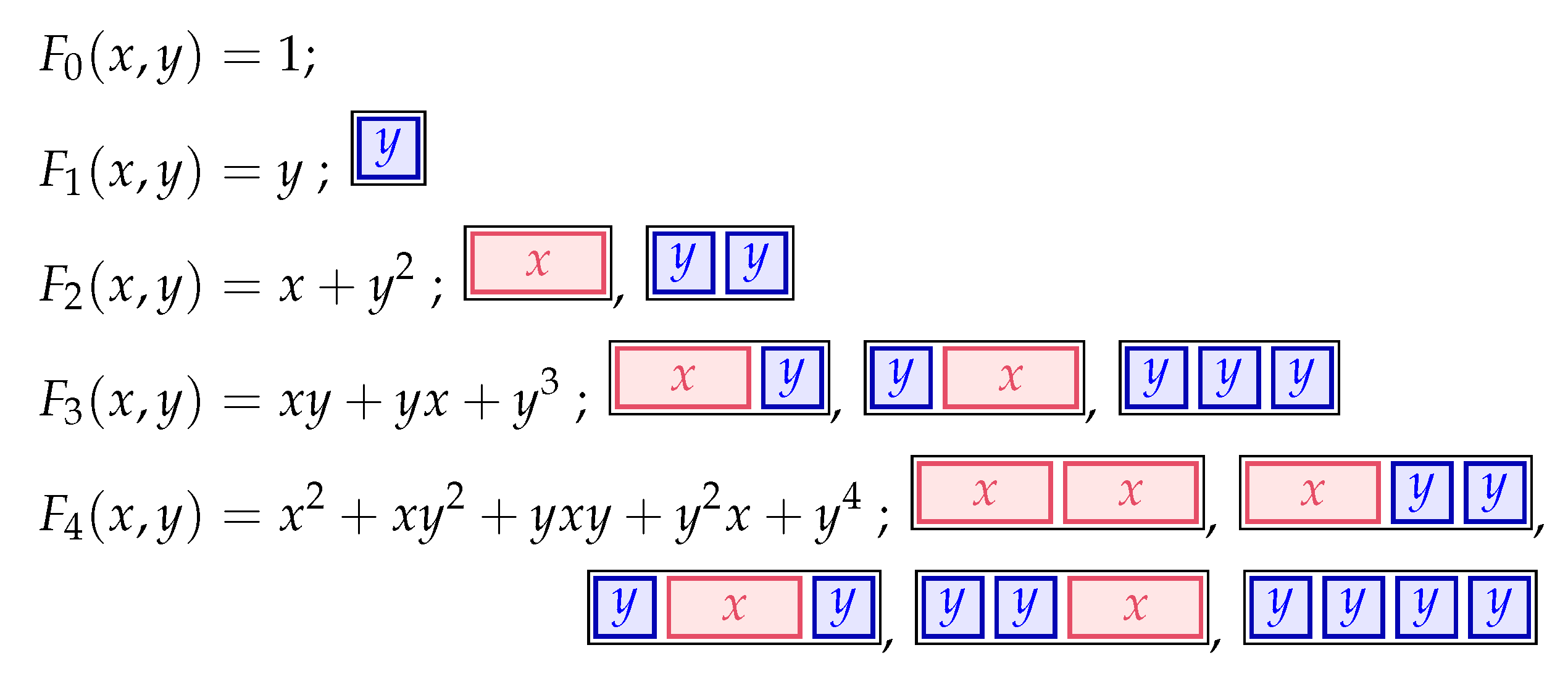
4.1. Noncommutative Weight-Dependent Fibonacci Polynomials
4.2. Noncommutative Elliptic Fibonacci Polynomials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lucas, E. Theorie des fonctions numeriques simplement periodique. Am. J. Math. 1878, 1, 184–196. [Google Scholar] [CrossRef]
- Lucas, E. Theorie des fonctions numeriques simplement periodique. Am. J. Math. 1878, 1, 197–240. [Google Scholar] [CrossRef]
- Lucas, E. Theorie des fonctions numeriques simplement periodique. Am. J. Math. 1878, 1, 289–321. [Google Scholar] [CrossRef]
- Weber, H. Elliptische Functionen und Algebraische Zahlen; Vieweg-Verlag: Braunschweig, Germany, 1897. [Google Scholar]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis, 4th ed.; Cambridge University Press: Cambridge, UK, 1962. [Google Scholar]
- Cigler, J. q-Fibonacci polynomials. Fibonacci Quart. 2003, 41, 31–40. [Google Scholar]
- Cigler, J. Some algebraic aspects of Morse code sequences. Discret. Math. Theor. Comp. Sci. 2003, 6, 55–68. [Google Scholar]
- Schlosser, M.J.; Yoo, M. Weight-dependent commutation relations and combinatorial identities. Discret. Math. 2018, 341, 2308–2325. [Google Scholar] [CrossRef]
- Bergeron, N.; Ceballos, C.; Küstner, J. Elliptic and q-analogs of the Fibonomial numbers. SIGMA 2020, 16, 76. [Google Scholar]
- Schlosser, M.J. A noncommutative weight-dependent generalization of the binomial theorem. Sém. Lothar. Combin. 2020, B81j, 24. [Google Scholar]
- Schlosser, M.J. Elliptic enumeration of nonintersecting lattice paths. J. Combin. Theory Ser. A 2007, 114, 505–521. [Google Scholar] [CrossRef]
- Gasper, G.; Rahman, M. Basic Hypergeometric Series (Encyclopedia of Mathematics and its Applications 96), 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schlosser, M.J.; Yoo, M. Elliptic Solutions of Dynamical Lucas Sequences. Entropy 2021, 23, 183. https://doi.org/10.3390/e23020183
Schlosser MJ, Yoo M. Elliptic Solutions of Dynamical Lucas Sequences. Entropy. 2021; 23(2):183. https://doi.org/10.3390/e23020183
Chicago/Turabian StyleSchlosser, Michael J., and Meesue Yoo. 2021. "Elliptic Solutions of Dynamical Lucas Sequences" Entropy 23, no. 2: 183. https://doi.org/10.3390/e23020183
APA StyleSchlosser, M. J., & Yoo, M. (2021). Elliptic Solutions of Dynamical Lucas Sequences. Entropy, 23(2), 183. https://doi.org/10.3390/e23020183





