U-Model-Based Two-Degree-of-Freedom Internal Model Control of Nonlinear Dynamic Systems
Abstract
:1. Introduction
- Design control systems in a universal procedure, separate two dynamic inversions, invariant controller implementation by inversing specified system performance in a feedback configuration and plant utilization by plant inversion. These two designs are parallel and separable;
- The difference in U-control between linear models and nonlinear models is the solution with the first-order or higher-order polynomial root-solving. The difference in U-control between polynomial models and state-space models is the one-layer or multi-layer polynomial root-solving;
- Propose a general U-model-based Two-Degree-of-Freedom IMC (UTDF-IMC) structure for controlling a class of open-loop stable polynomial/state-space modeled linear and nonlinear dynamic plants. The new control system structure accommodates both linear and nonlinear plants consistently and separate the tracking control filter design from robust control filter design.
- Tailor the UM-dynamic inversion platform [31] in conjunction with IMC, which removes the necessity of either linearizing the nonlinear model, or converting it to a quasi-linear parameter-varying (quasi-LPV) model in advance. This UM-dynamic inversion platform directly provides algorithms dealing with all types of inversions in IMC structured systems.
- Analyze the designed UTDF-IMC control system properties to provide a valid reference for future study expansions and applications.
- Verify the control system performance through benchmark tests of simulated case studies and illustrate application procedure from an industrial case demonstration.
2. Preliminaries
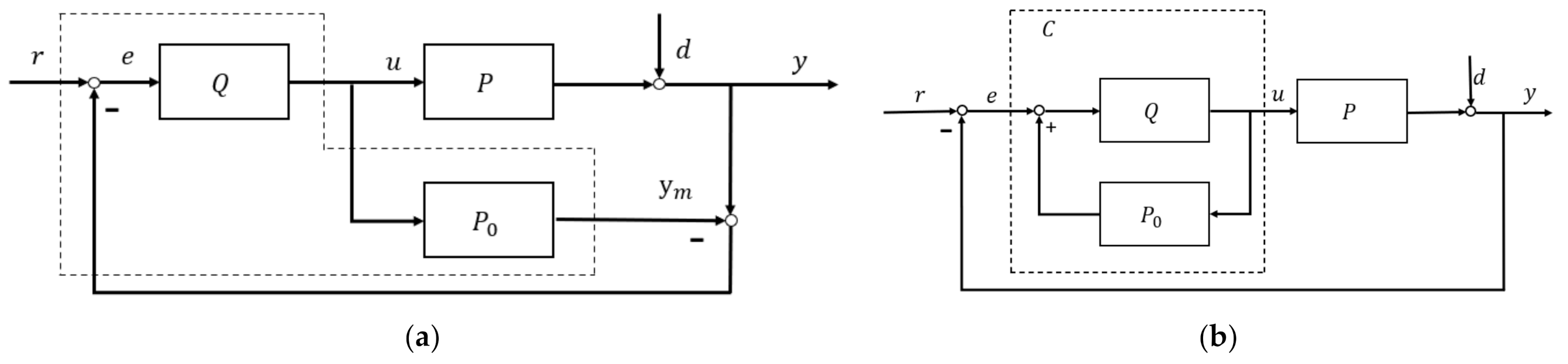
2.1. Internal Model Control (IMC)
- Dual stability: For and , and , the feedback error signal is obviously zero. IMC system becomes an open-loop structure and both controller and plant stable.
- Perfect control: This requests plant minimum-phase and invertible and controller as the model inverse . Accordingly (2) becomes:
- Augmented robust IMC is shown in Figure 2. It decomposes model and dynamic inversion by factorizing into and , namely: , where is the part containing pure delay and uncertain zero, and is the minimum-phase part. There are certain factorization techniques, such as simple factorization, all-pass factorization [32]. Hence, the controller is kept as the inverse of the plant/process model with invertible portion, i.e.,
2.2. U-Model-Based Control (U-Control)
2.2.1. U-Models
2.2.2. UM-Dynamic Inversion
2.2.3. U-Control
- Model of is invertible, i.e., exists
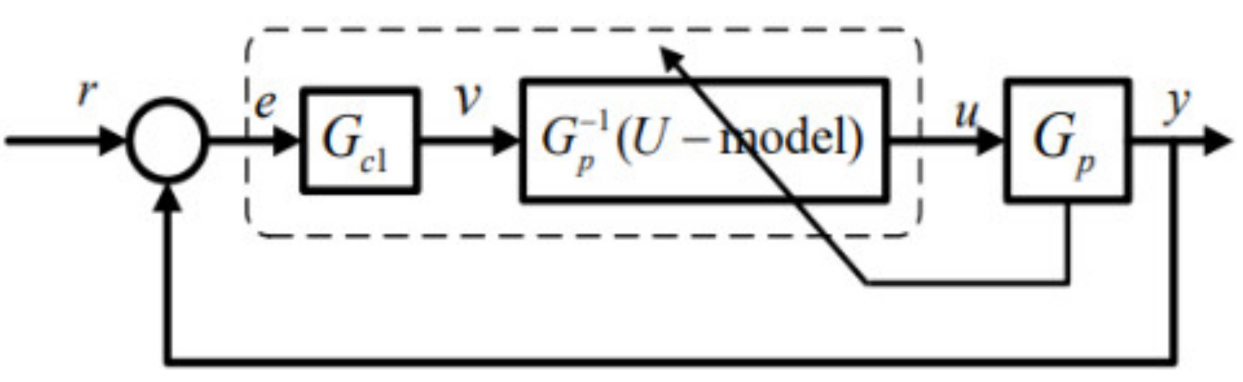
- Meet the continuity of Lipschitz, and its inverse are globally unified and diffeomorphic in , i.e.,where are the states while in the expression of state-space equation, and are the Lipschitz coefficients. This study takes SISO (input and output ) prototype in consideration. U-control system framework [25] is shown in Figure 3, in which is for U-control system structure, is a linear invariant controller to be designed, and is the inverter of the controlled plant to be designed as well. It is noted that U-control framework is applicable to various plants/processes when the dynamic inverse exist.
- Designed dynamic inverter to achieve . This gives
- Design invariant controller , which is a typically linear controller. Let the specified closed-loop performance in transfer function , in form of , which can be comfortably assigned using damping ratio and undamped natural frequency for linear system dynamic/steady-state response.
3. U-Model-Based Two-Degree-of-Freedom IMC (UTDF-IMC)
3.1. Classical Two-Degree-of-Freedom IMC (TDF-IMC) Structure
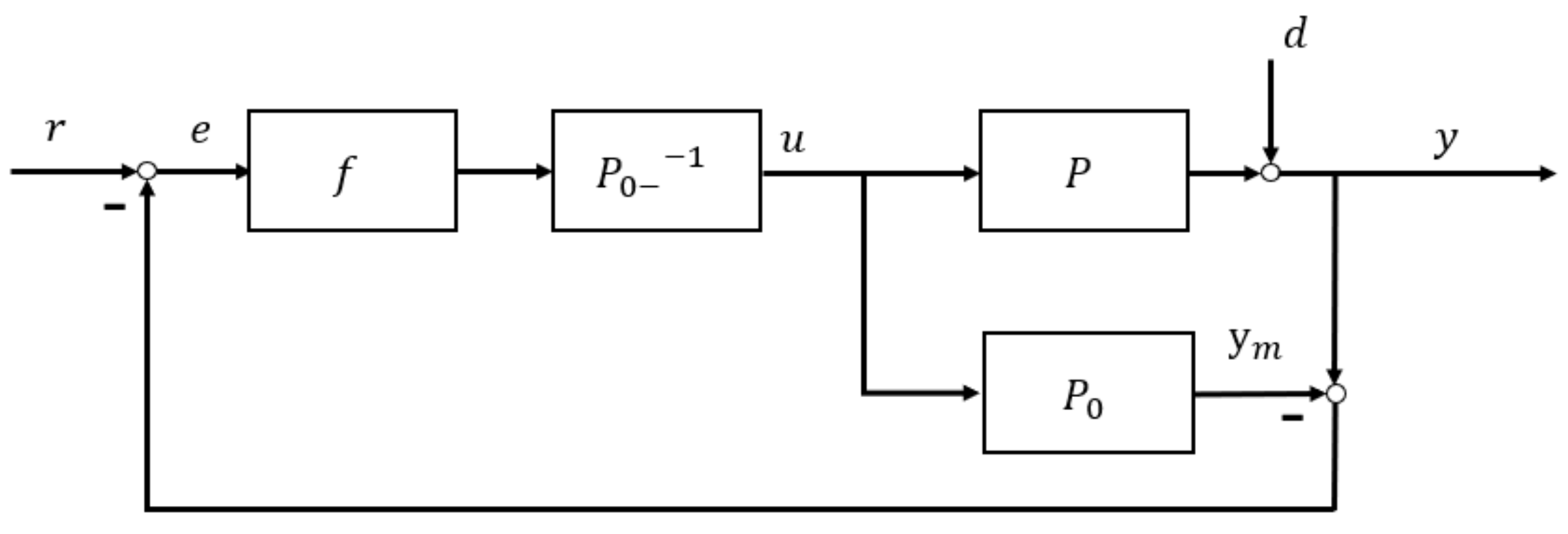
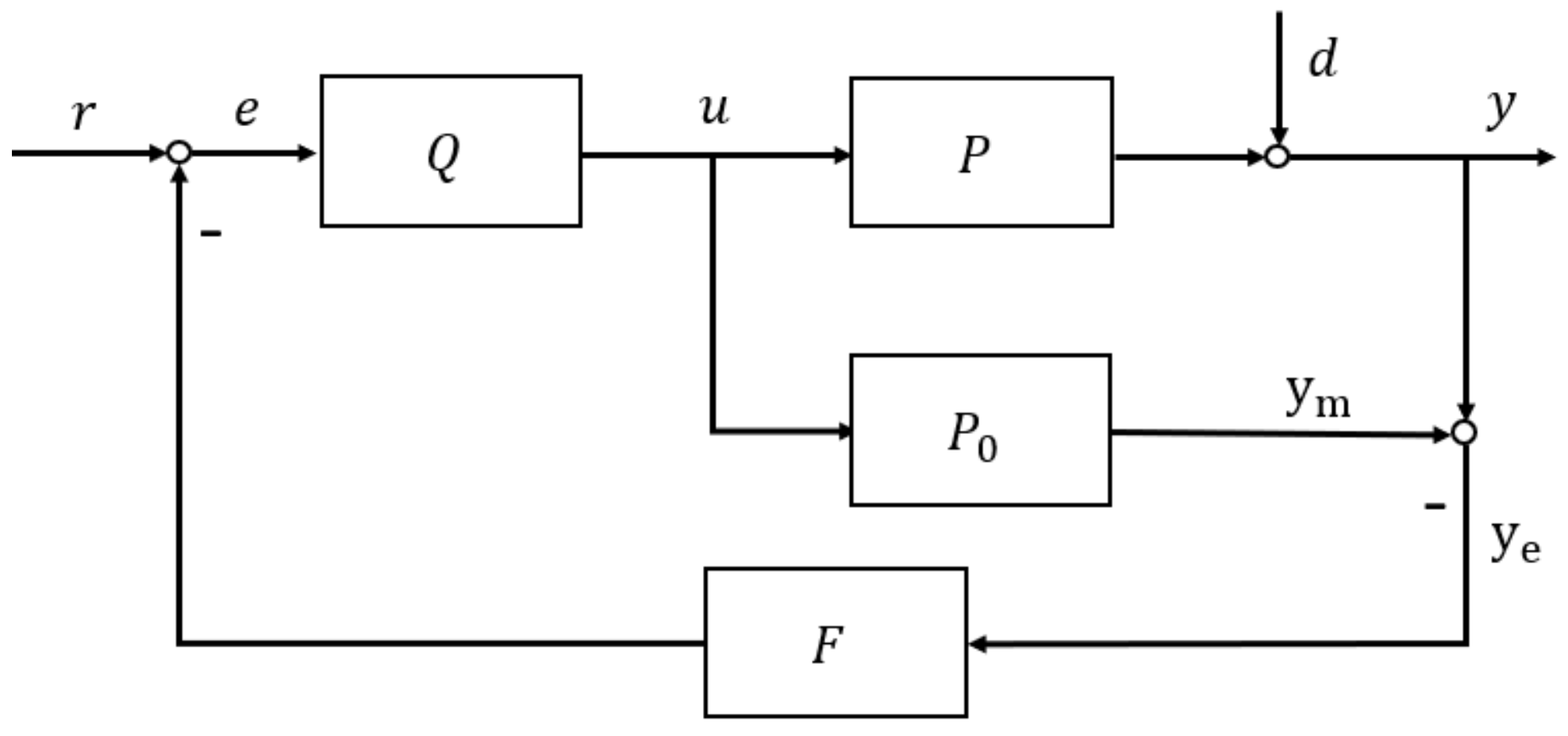
3.2. U-Model-Based Two-Degree-of-Freedom IMC (UTDF-IMC) Structure
3.3. UTDF-IMC Design Procedures
- Assume the controlled plant or process is stable and bounded, and its inverse exists. Use U-model to describe or convert the plant model into its U-realization . The specific U-modeling process can refer to Section 2.1. In contrast to the classical IMC or classical TDF-IMC, U-realization of the original model can comfortably cover nonlinear dynamics, therefore, remove linearization restrictions.
- Design filters and according to system control performance requirements, then re-optimize the parameters of the filters according to the controller output limit. The feedforward filter determines the system’s set-point tracking ability (response time) while the feedback filter determines the system’s robustness. Because the control system performance is completely designed according to the two filters independently, designers can select the appropriate filters according to performance requirements, hardware limitations, controller output limitations, etc.
3.4. Property Analysis
- Property 1 (Dual stability): Assume the plant model is perfectly matched () and system disturbance is absent , then from Table 1, the closed-loop stability is characterized by the stability of the plant () and the feedforward filter . In this case, the system output signal will be: .
- Property 2 (Perfect control): Assume that the dynamic inverter is satisfied with and stable, then the closed-loop system is stable and perfectly controlled. In this case, the system output is . The faster the response speed of feedback filter , the better the system robustness.
- Property 3 (Zero offset): Assume that the steady-state gain of the controller equals to steady-state gain of the inverse model, and this closed-loop system is input-output stable with this controller, then offset free control is obtained asymptotically to step or ramp type inputs and disturbances.
- Property 4: Separability of designing the tracking filter and the robust filter: This is shown in the tables, which UTDF-IMC has no product of the two filters .
- Classical TDF-IMC structure can make tracking ability and robustness be designed separately but not wholly independent due to the product of Ff in robustness specification. The UTDF-IMC overcomes this shortcoming without resorting to a more complex structure. Therefore, when the robustness performance of the system is determined, UTDF-IMC structure will have a faster response speed than the classical TDF-IMC structure.
- U-model is used to facilitate control system design, which can be easily to form an inversion of the plants to cancel both dynamic and nonlinearities. Accordingly, it converts the nonlinear control system into a linear model-based control with a nonlinear dynamic inverter.
- UM-dynamic inversion algorithm is used to design the inversion part in UTDF-IMC structure, which has a faster convergence speed and allows the inversion part exists alone properly without the feedforward filter.
- This structure where feedforward filter from outside the control loop allows the tracking ability and robustness performance to be completely independently designed.
- The improved control performance is not complicating the system structure and/or increasing the additional computation burden throughout the design process.
4. Simulation Demonstrations
4.1. Linear Internal Model (Also Called Nominal Model in the Study)
- Convert plant model (25) into its corresponding U-model:
- Design the inverter of the plant model :
- Design feedforward filter and feedback filter
4.2. Nonlinear Internal Model
- Convert plant model (29) into its corresponding U-model:
- Design the inverter of the plant model :
- 3.
- Design feedforward filter and feedback filter
4.3. Control of PMSM System
4.3.1. Modeling of PMSM System
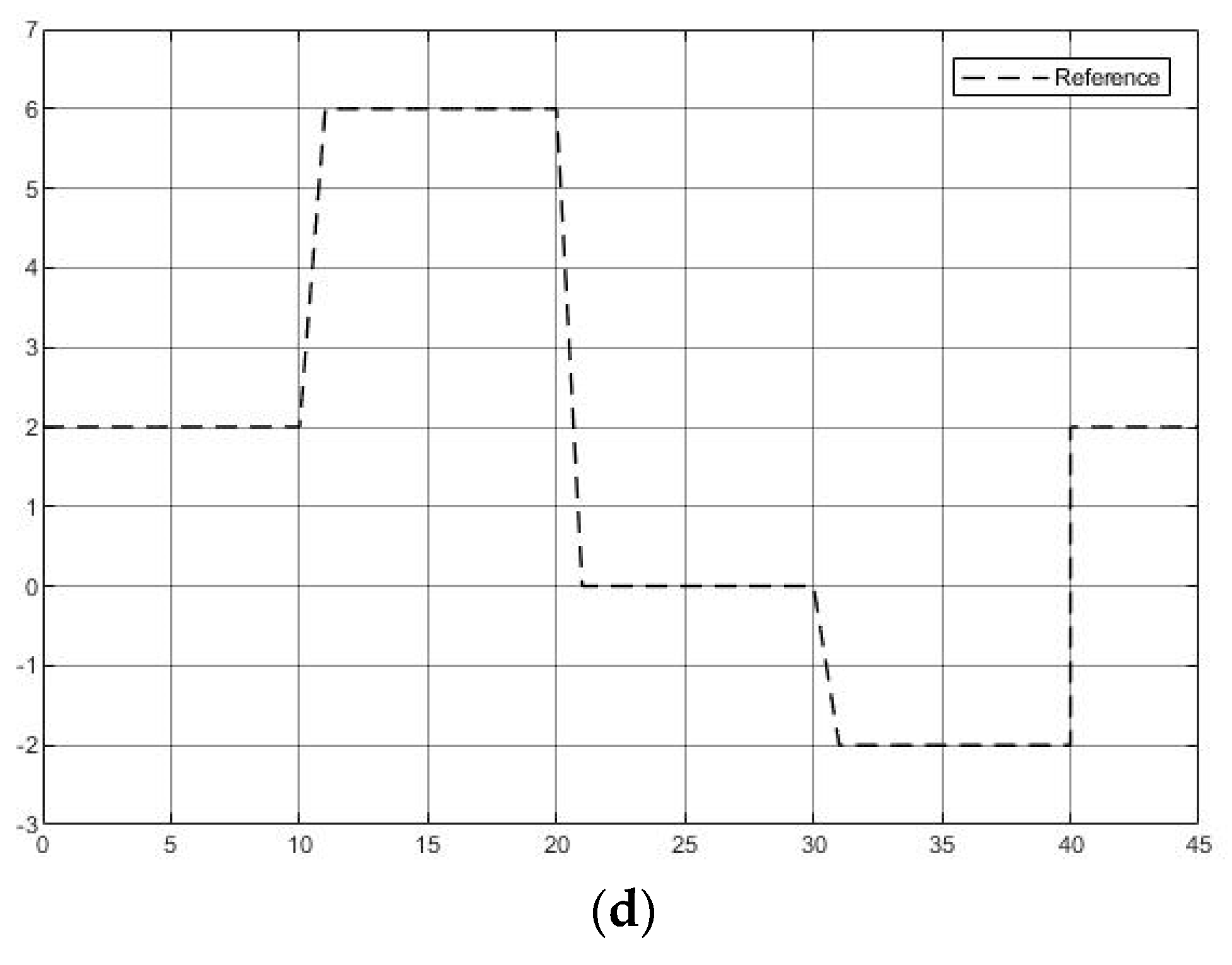
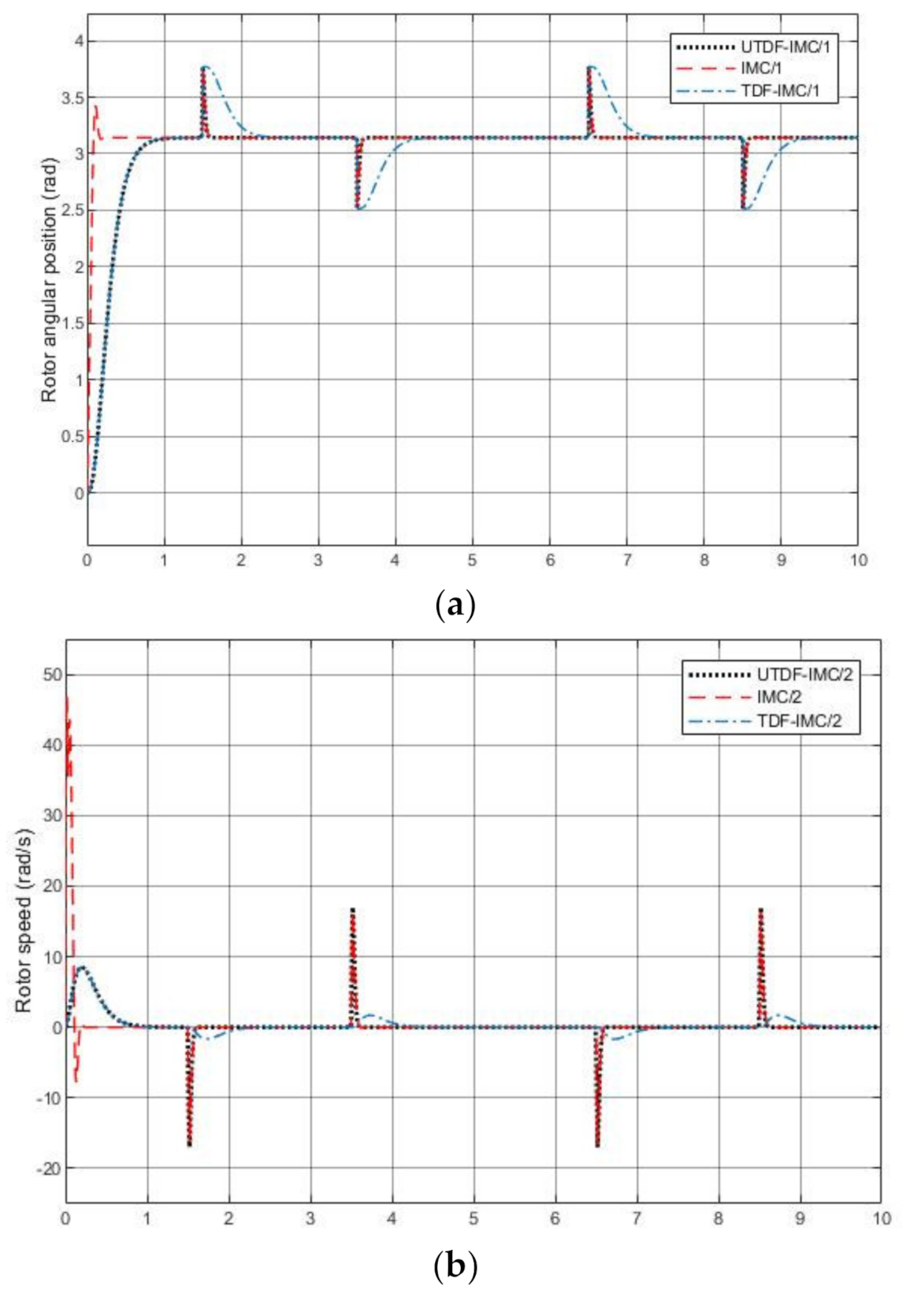
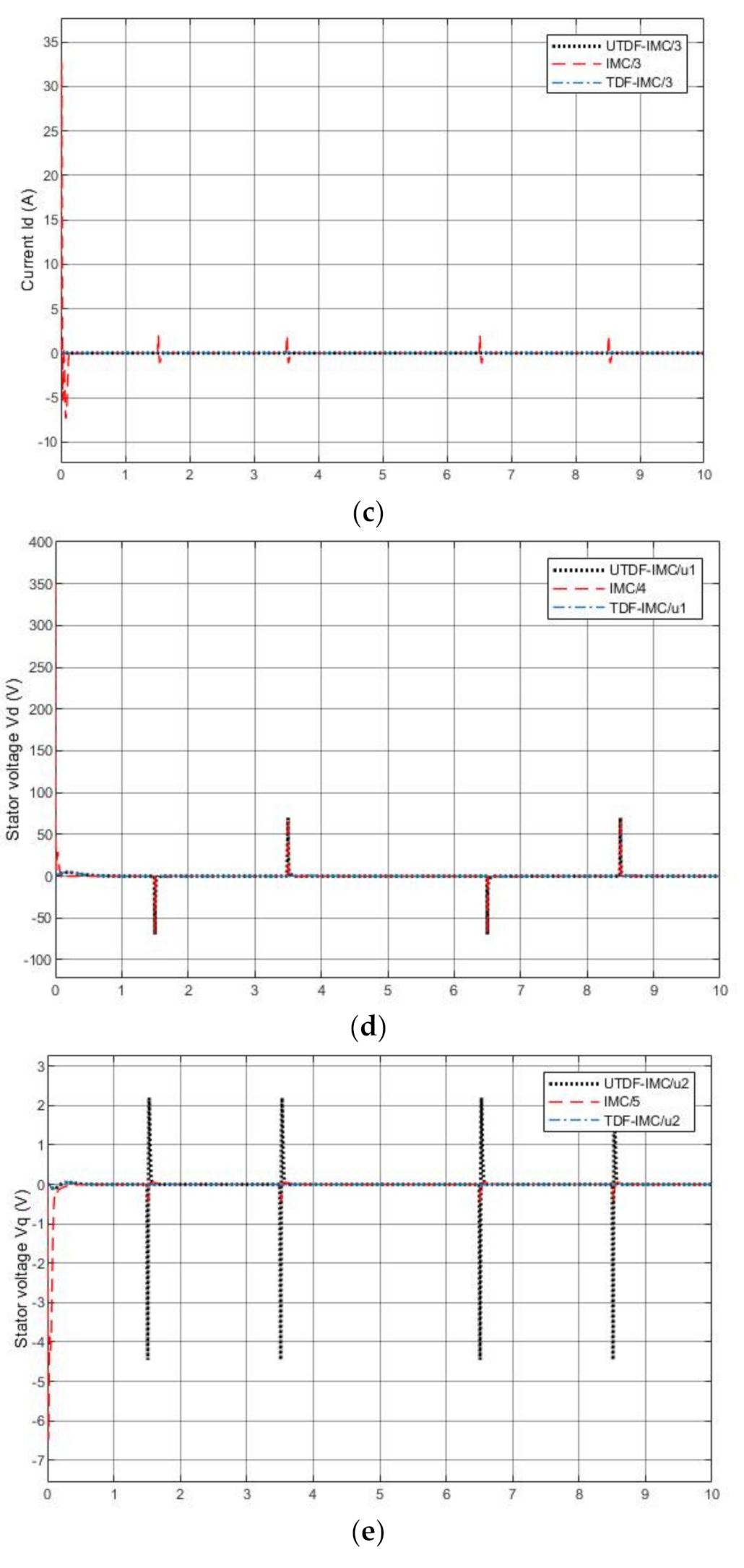
4.3.2. Simulation Test
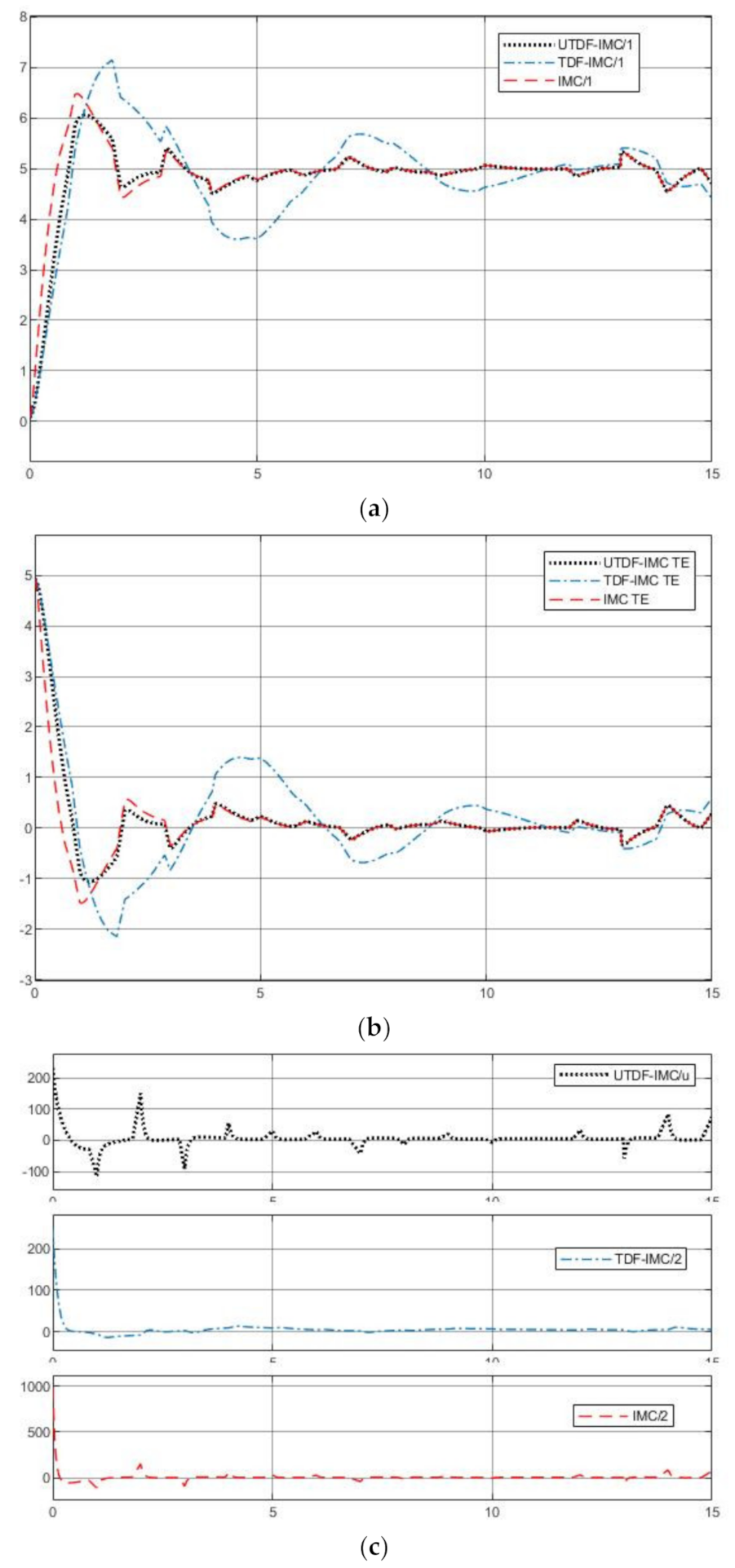
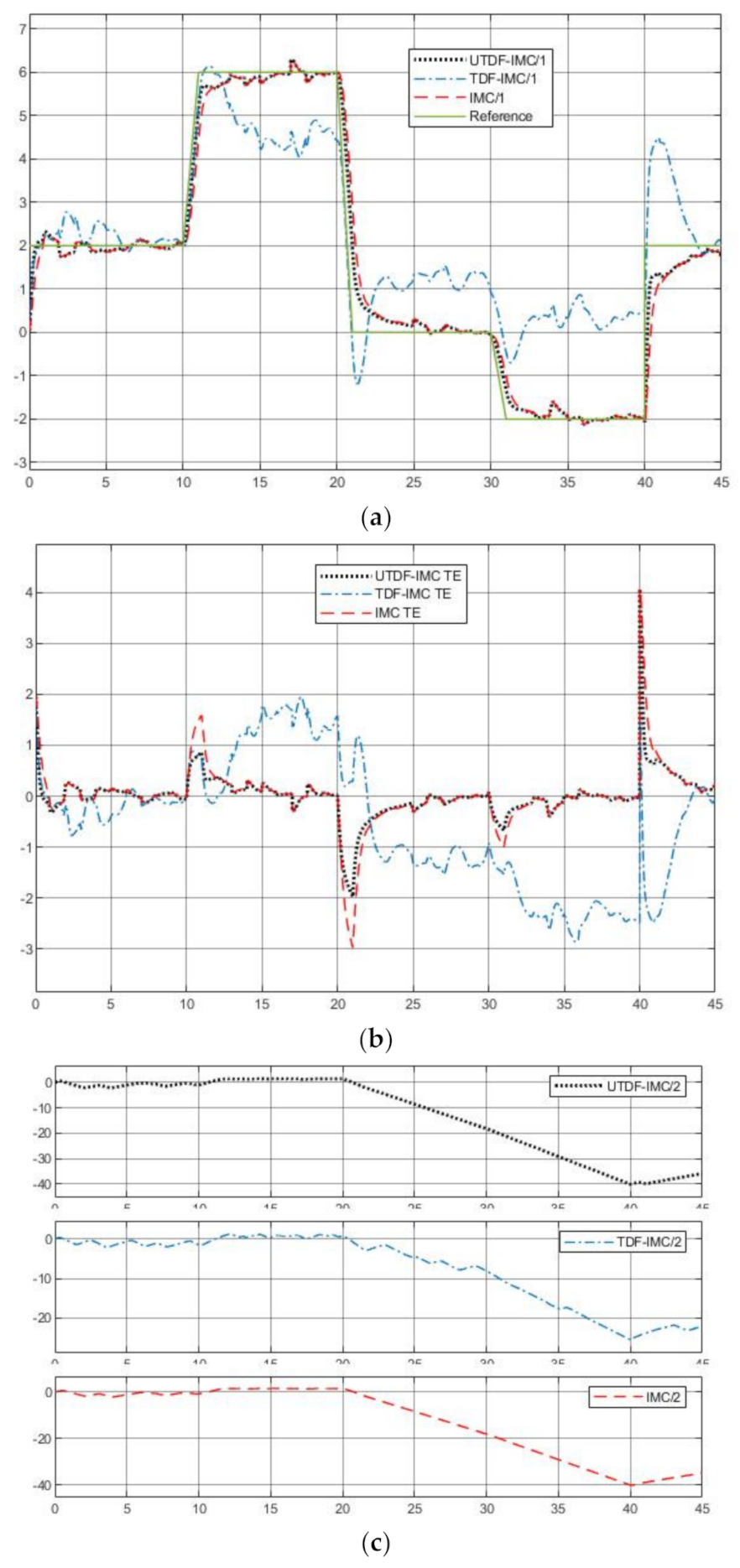
- IMC: The filter time parameter shown in equation (9) is chosen as , use linearization to approximate the inverse of PMSM.
- TDF-IMC: Based on the structure in Figure 4, the feedforward filter and feedback filter are chosen as , use UM-dynamic inversion to design the inverse of PMSM.
- UTPF-IMC: To test the performance of UTDF-IMC fairly, based on the structure in Figure 5, the feed forward filter and feedback filter are chosen as , use UM-dynamic inversion to design the inverse of PMSM.
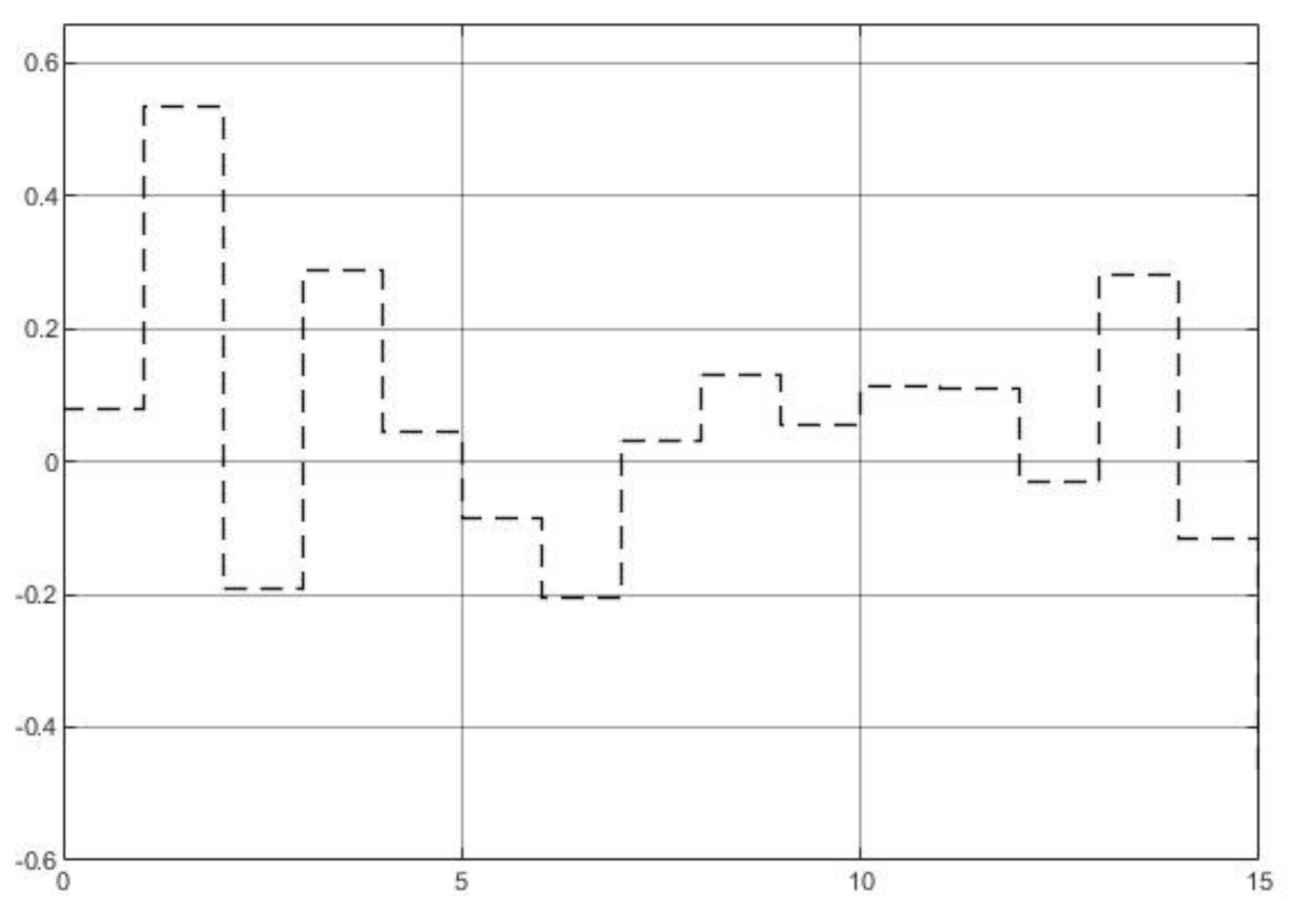
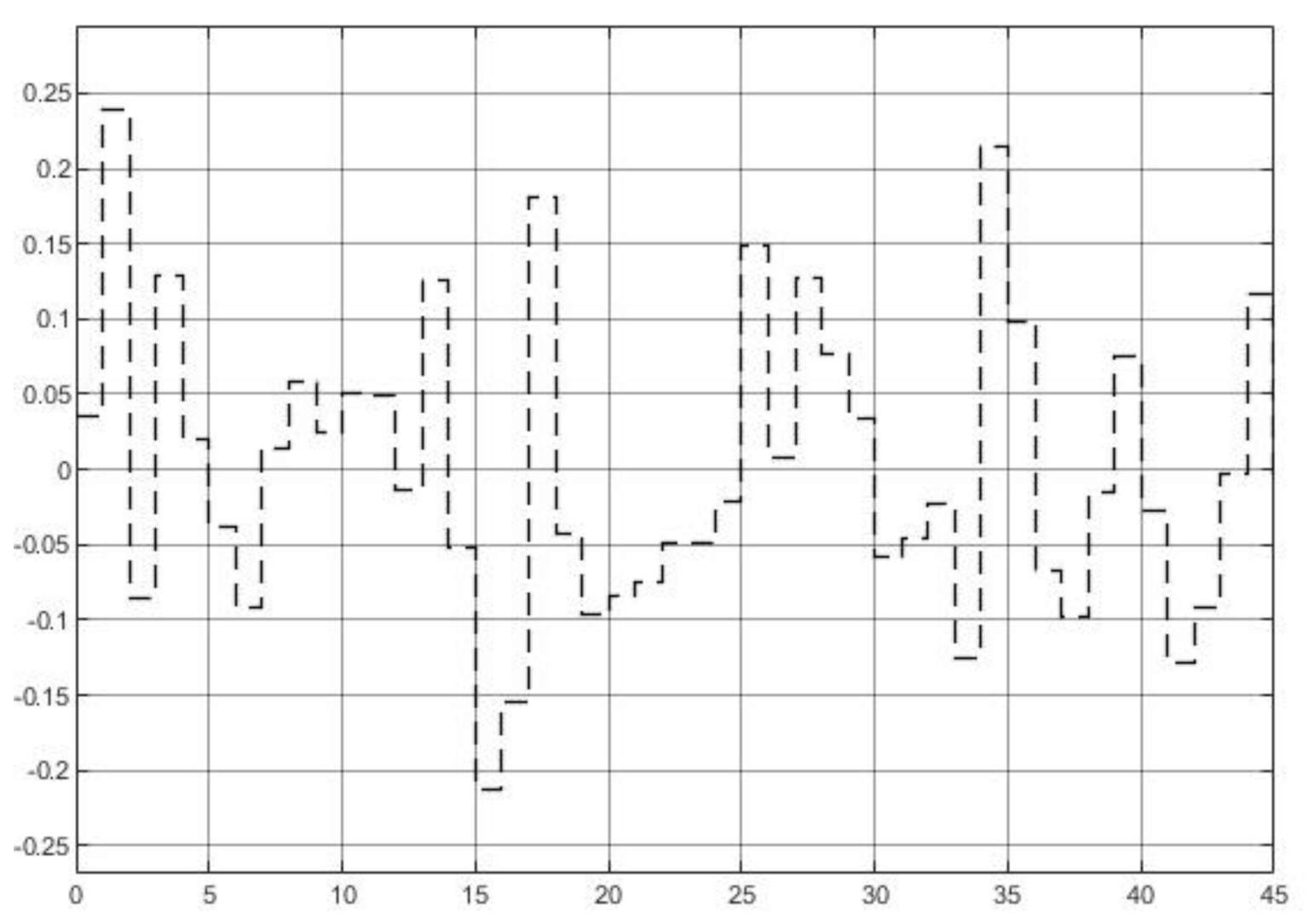
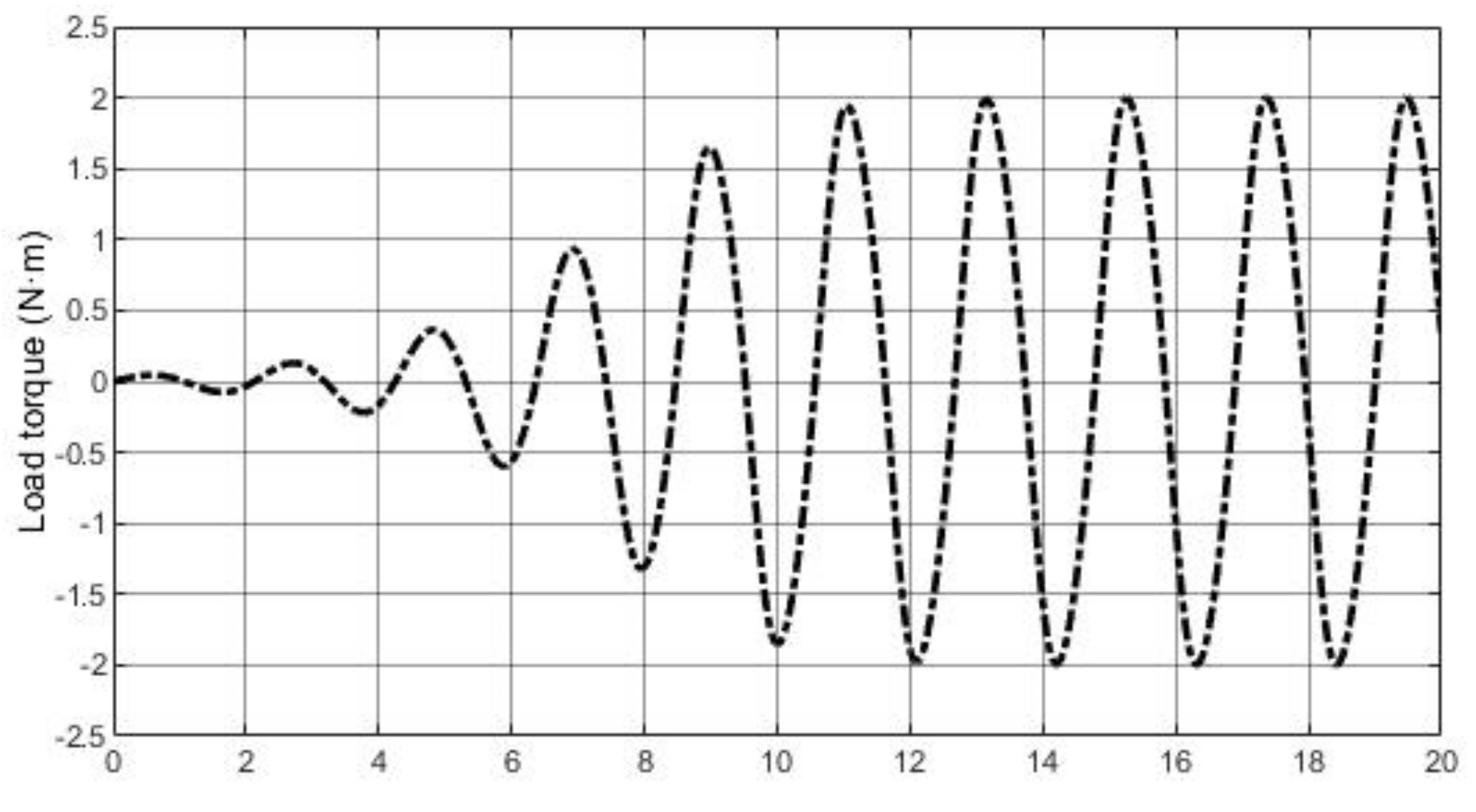
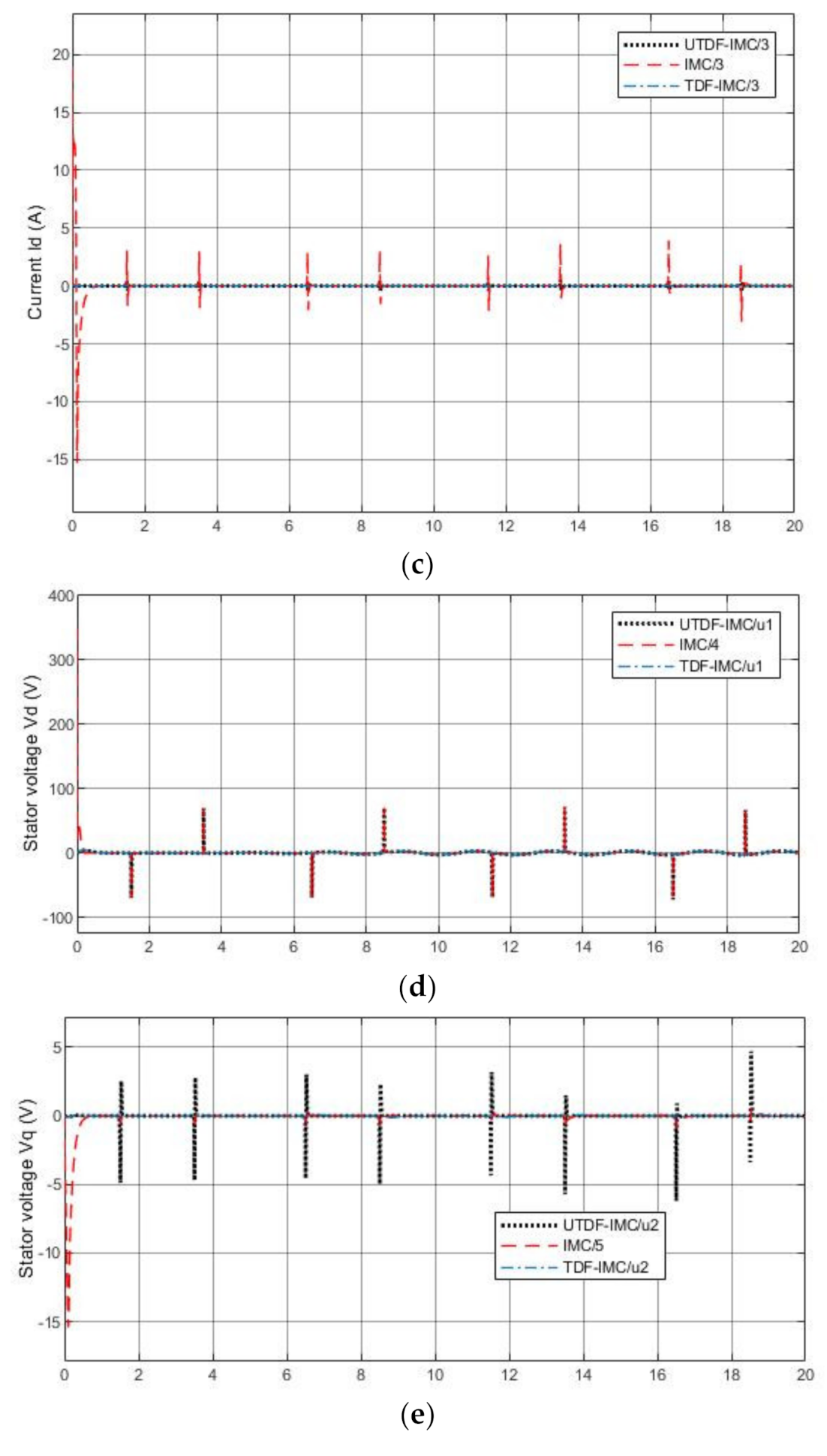
4.3.3. Matched Model with System Disturbance
4.3.4. Mismatched Model with System Disturbance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ElMaraghy, W.; ElMaraghy, H.; Tomiyama, T.; Monostori, L. Complexity in engineering design and manufacturing. CIRP Ann. 2012, 61, 793–814. [Google Scholar]
- Sari, N.N.; Jahanshahi, H.; Fakoor, M. Adaptive fuzzy PID control strategy for spacecraft attitude control. Int. J. Fuzzy Syst. 2019, 21, 769–781. [Google Scholar]
- Rosales, C.; Soria, C.M.; Rossomando, F.G. Identification and adaptive PID control of a hexacopter UAV based on neural networks. Int. J. Adapt. Control Signal Process. 2019, 33, 74–91. [Google Scholar]
- Kawan, C. Invariance Entropy for Deterministic Control Systems; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kawan, C. Special Issue, Entropy in Networked Control, Entropy. 2019. Available online: https://www.mdpi.com/journal/entropy/specialissues/control (accessed on 11 April 2019).
- Morari, M.; Zafiriou, E. Robust Process Control; PTR Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Garcia, C.E.; Morari, M. Internal model control. A unifying review and some new results. Ind. Eng. Chem. Process Des. Dev. 1982, 21, 308–323. [Google Scholar]
- Li, P.; Zhu, G.; Zhang, M. Linear Active Disturbance Rejection Control for Servo Motor Systems with Input Delay via Internal Model Control Rules. IEEE Trans. Ind. Electron. 2020, 68, 1077–1086. [Google Scholar]
- Liu, J.; Yin, Z.; Bai, C.; Du, N. Internal model control of induction motors based on extended state observer. J. Power Electron. 2020, 20, 163–175. [Google Scholar]
- Reddy, P.S.; Patwardhan, S.C.; Rani, K.Y. Robust trajectory tracking in a reactive batch distillation process using multirate nonlinear internal model control. Ind. Eng. Chem. Res. 2019, 58, 11364–11381. [Google Scholar]
- Saxena, S.; Hote, Y.V. Advances in internal model control technique: A review and future prospects. IETE Tech. Rev. 2012, 29, 461–472. [Google Scholar]
- Sonker, B.; Kumar, D.; Samuel, P. Design of two-degree-of-freedom-internal model control configuration for load frequency control using model approximation. Int. J. Model. Simul. 2019, 39, 27–37. [Google Scholar]
- Singh, J.; Chattterjee, K.; Vishwakarma, C.B. Two-degree-of-freedom internal model control-PID design for LFC of power systems via logarithmic approximations. ISA Trans. 2018, 72, 185–196. [Google Scholar]
- Zhu, Q.; Yin, Z.; Zhang, Y.; Niu, J.; Li, Y.; Zhong, Y. Research on two-degree-of-freedom internal model control strategy for induction motor based on immune algorithm. IEEE Trans. Ind. Electron. 2015, 63, 1981–1992. [Google Scholar]
- Qiu, Z.; Sun, J.; Jankovic, M.; Santillo, M. Nonlinear internal model controller design for wastegate control of a turbocharged gasoline engine. Control Eng. Pract. 2016, 46, 105–114. [Google Scholar]
- Economou, C.G.; Morari, M.; Palsson, B.O. Internal model control: Extension to nonlinear system. Ind. Eng. Chem. Process Des. Dev. 1986, 25, 403–411. [Google Scholar]
- Cirtoaje, V. A practical unified algorithm of P-IMC type. Processes 2020, 8, 165. [Google Scholar]
- Sun, X.; Chen, L.; Jiang, H.; Yang, Z.; Chen, J.; Zhang, W. High-performance control for a bearingless permanent-magnet synchronous motor using neural network inverse scheme plus internal model controllers. IEEE Trans. Ind. Electron. 2016, 63, 3479–3488. [Google Scholar]
- Rivals, I.; Personnaz, L. Nonlinear internal model control using neural networks: Application to processes with delay and design issues. IEEE Trans. Neural Netw. 2000, 11, 80–90. [Google Scholar]
- Zhang, X.; Hu, J.; Liu, Z. Fuzzy adaptive internal model control for a pneumatic muscle actuator. In Proceedings of the 2019 11th International Conference on Machine Learning and Computing, Zhuhai, China, 22–24 February 2019; pp. 546–550. [Google Scholar]
- Ahmed, I.B.C.; Othman, C.; Soudani, D. On the fuzzy adaptative internal model control of the discrete-time nonlinear systems. In Proceedings of the 2017 International Conference on Advanced Systems and Electric Technologies (IC_ASET), Hammamet, Tunisia, 14–17 January 2017; IEEE: Hammamet, Tunisia, 2017; pp. 395–400. [Google Scholar]
- Abbasbandy, S. Improving Newton–Raphson method for nonlinear equations by modified Adomian decomposition method. Appl. Math. Comput. 2003, 145, 887–893. [Google Scholar]
- Zhang, W.; Zhu, Q.; Mobayen, S.; Yan, H.; Qiu, J.; Narayan, P. U-Model and U-control methodology for nonlinear dynamic systems. Complexity 2020. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, Y.; Zhao, D.; Li, S.; Billings, S.A. Review of rational (total) nonlinear dynamic system modelling, identification, and control. Int. J. Syst. Sci. 2015, 46, 2122–2133. [Google Scholar]
- Zhu, Q.; Li, S.; Zhao, D. A universal U-model based control system design. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; IEEE: Nanjing, China, 2014; pp. 1839–1844. [Google Scholar]
- Zhu, Q.M.; Guo, L.Z. A pole placement controller for non-linear dynamic plants. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2002, 216, 467–476. [Google Scholar]
- Geng, X.; Zhu, Q.; Liu, T.; Na, J. U-model based predictive control for nonlinear processes with input delay. J. Process Control 2019, 75, 156–170. [Google Scholar]
- Zhu, Q.; Zhang, W.; Zhang, J.; Sun, B. U-neural network-enhanced control of nonlinear dynamic systems. Neurocomputing 2019, 352, 12–21. [Google Scholar]
- Hussain, N.A.A.; Ali, S.S.A.; Ovinis, M.; Arshad, M.R.; Al-Saggaf, U.M. Underactuated coupled nonlinear adaptive control synthesis using u-model for multivariable unmanned marine robotics. IEEE Access 2019, 8, 1851–1865. [Google Scholar]
- Shafiq, M.; Haseebuddin, M. U-model-based internal model control for non-linear dynamic plants. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2005, 219, 449–458. [Google Scholar]
- Li, R.; Zhu, Q.; Kiely, J.; Zhang, W. Algorithms for U-model-based dynamic inversion (UM-dynamic inversion) for continuous time control systems. Complexity 2020. [Google Scholar] [CrossRef]
- Hu, M.; Chen, S. One-Pass Incomplete Multi-View Clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3838–3845. [Google Scholar]
- Zhu, Q.; Zhang, W.; Na, J.; Sun, B. U-model based control design framework for continuous-time systems. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; IEEE: Guangzhou, China, 2019; pp. 106–111. [Google Scholar]
- Zhu, Q.M.; Warwick, K.; Douce, J.L. Adaptive general predictive controller for nonlinear systems. IEE Proc. D (Control Theory Appl.) 1991, 138, 33–40. [Google Scholar]
- Isidori, A. Nonlinear Control Systems; Springer Science Business Media: London, UK, 2000. [Google Scholar]
- Wang, H.; Li, S.; Yang, J.; Zhou, X. Continuous sliding mode control for permanent magnet synchronous motor speed regulation systems under time-varying disturbances. J. Power Electron. 2016, 16, 1324–1335. [Google Scholar]
- Sun, X.; Shi, Z.; Lei, G.; Guo, Y.; Zhu, J. Analysis and design optimization of a permanent magnet synchronous motor for a campus patrol electric vehicle. IEEE Trans. Veh. Technol. 2019, 68, 10535–10544. [Google Scholar]
- Zaihidee, F.M.; Mekhilef, S.; Mubin, M. Application of fractional order sliding mode control for speed control of permanent magnet synchronous motor. IEEE Access 2019, 7, 101765–101774. [Google Scholar]
- Fei, Q.; Deng, Y.; Li, H.; Liu, J.; Shao, M. Speed ripple minimization of permanent magnet synchronous motor based on model predictive and iterative learning controls. IEEE Access 2019, 7, 31791–31800. [Google Scholar]
- Wang, T.; Ping, Z.; Huang, Y.; Lu, J.G. Nonlinear internal model based two-step controller design for PMSM position servo system. In Proceedings of the 2019 IEEE 15th International Conference on Control and Automation (ICCA), Edinburgh, UK, 16–19 July 2019; IEEE: Edinburgh, UK, 2019; pp. 1264–1269. [Google Scholar]
- Pillay, P.; Krishnan, R. Modeling, simulation, and analysis of permanent-magnet motor drives. I. The permanent-magnet synchronous motor drive. IEEE Trans. Ind. Appl. 1989, 25, 265–273. [Google Scholar]



| IMC | ||
| TDF-IMC | ||
| UTDF-IMC | ||
| where is the U-realization of |
| IMC | |
| TDF-IMC | |
| UTDF-IMC |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Zhu, Q.; Narayan, P.; Yue, A.; Yao, Y.; Deng, M. U-Model-Based Two-Degree-of-Freedom Internal Model Control of Nonlinear Dynamic Systems. Entropy 2021, 23, 169. https://doi.org/10.3390/e23020169
Li R, Zhu Q, Narayan P, Yue A, Yao Y, Deng M. U-Model-Based Two-Degree-of-Freedom Internal Model Control of Nonlinear Dynamic Systems. Entropy. 2021; 23(2):169. https://doi.org/10.3390/e23020169
Chicago/Turabian StyleLi, Ruobing, Quanmin Zhu, Pritesh Narayan, Alex Yue, Yufeng Yao, and Mingcong Deng. 2021. "U-Model-Based Two-Degree-of-Freedom Internal Model Control of Nonlinear Dynamic Systems" Entropy 23, no. 2: 169. https://doi.org/10.3390/e23020169
APA StyleLi, R., Zhu, Q., Narayan, P., Yue, A., Yao, Y., & Deng, M. (2021). U-Model-Based Two-Degree-of-Freedom Internal Model Control of Nonlinear Dynamic Systems. Entropy, 23(2), 169. https://doi.org/10.3390/e23020169








