Figure 1.
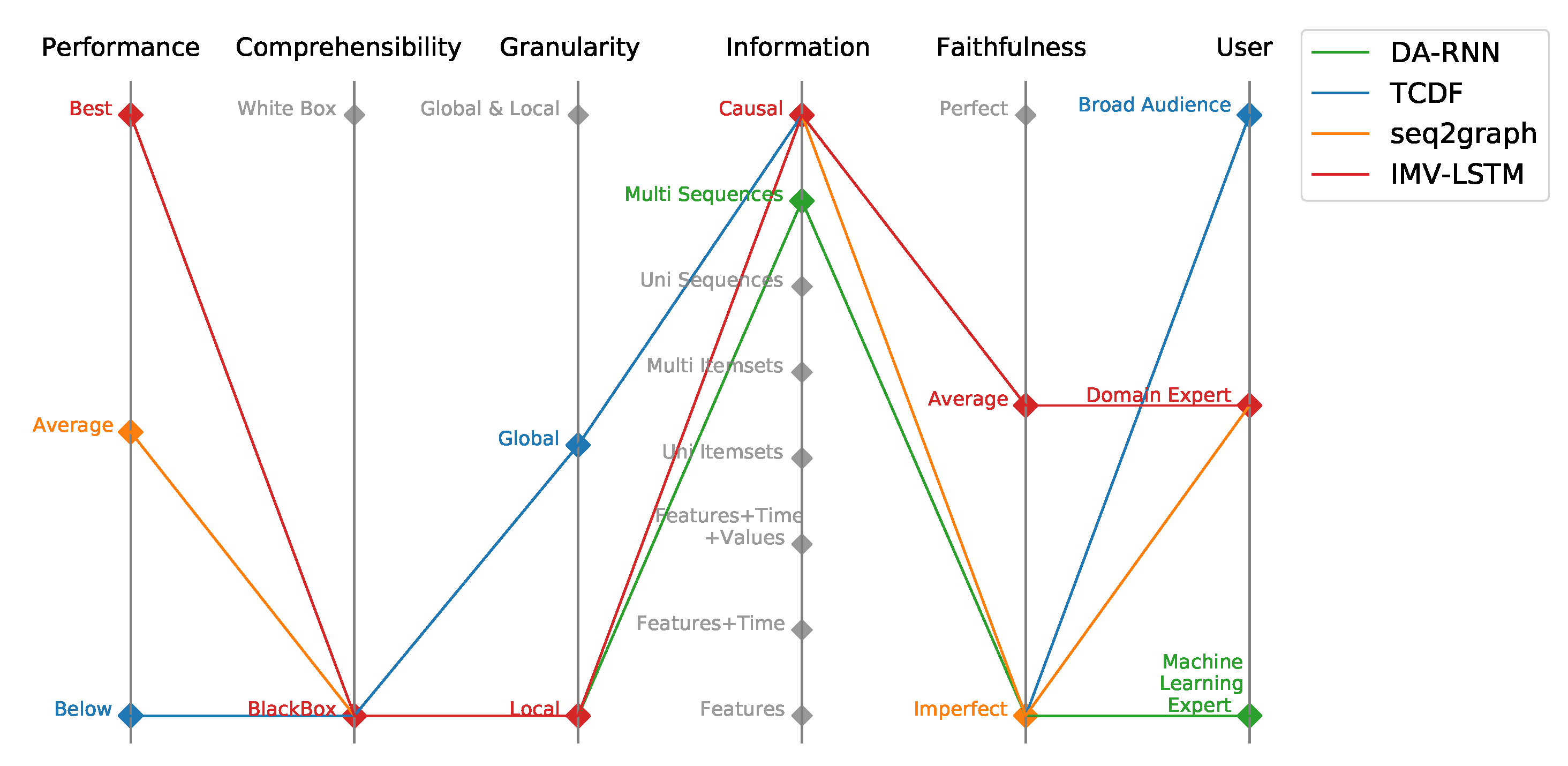
Parallel coordinates plot of evaluated models within Performance-Explainability Framework.
Figure 1.
Parallel coordinates plot of evaluated models within Performance-Explainability Framework.
Figure 2.
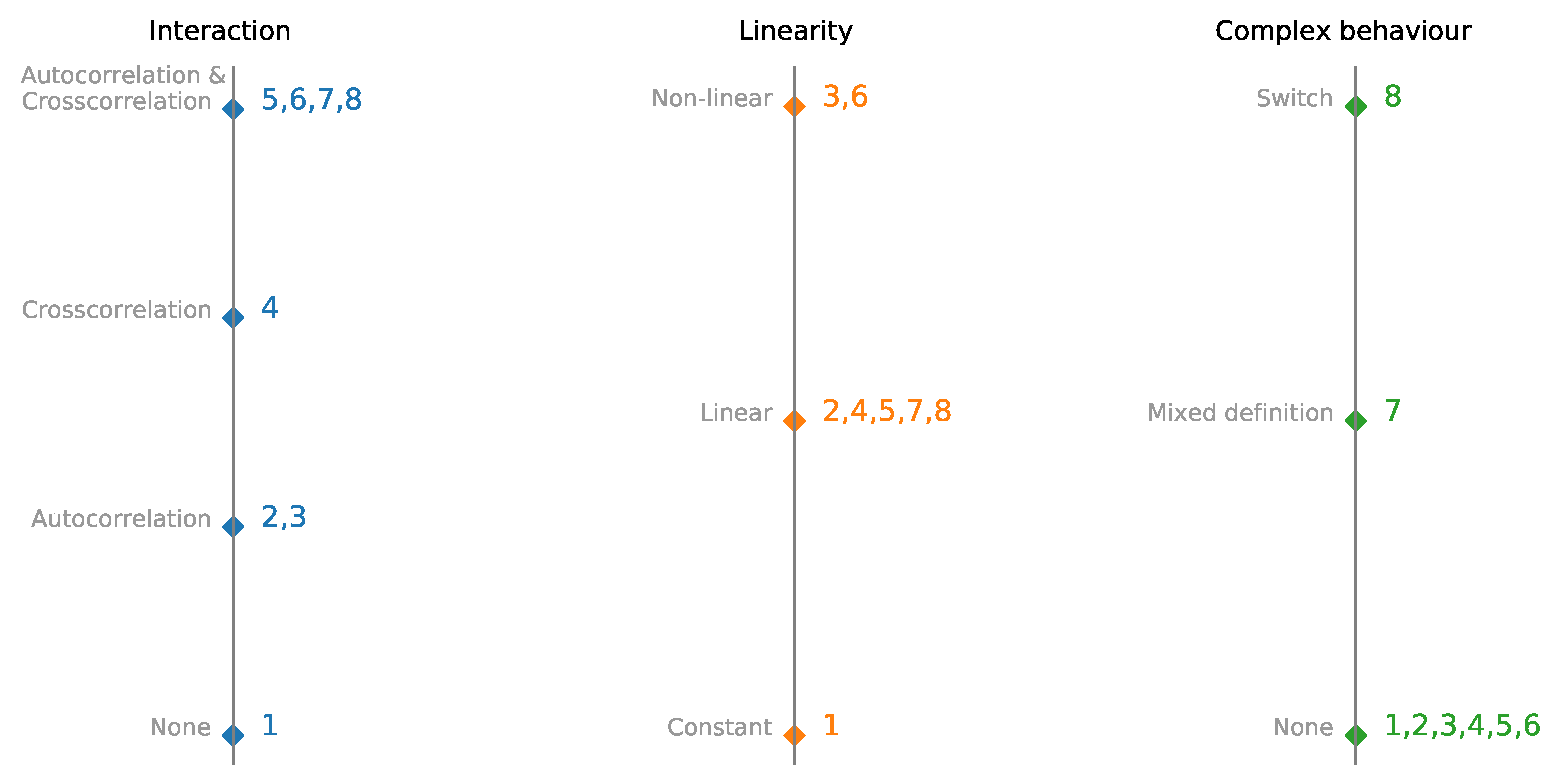
Parallel coordinates plot of multivariate time-series synthetic datasets with embedded interactions, linearity, and complexity. Datesets are presented in detail in
Table 1.
Figure 2.
Parallel coordinates plot of multivariate time-series synthetic datasets with embedded interactions, linearity, and complexity. Datesets are presented in detail in
Table 1.
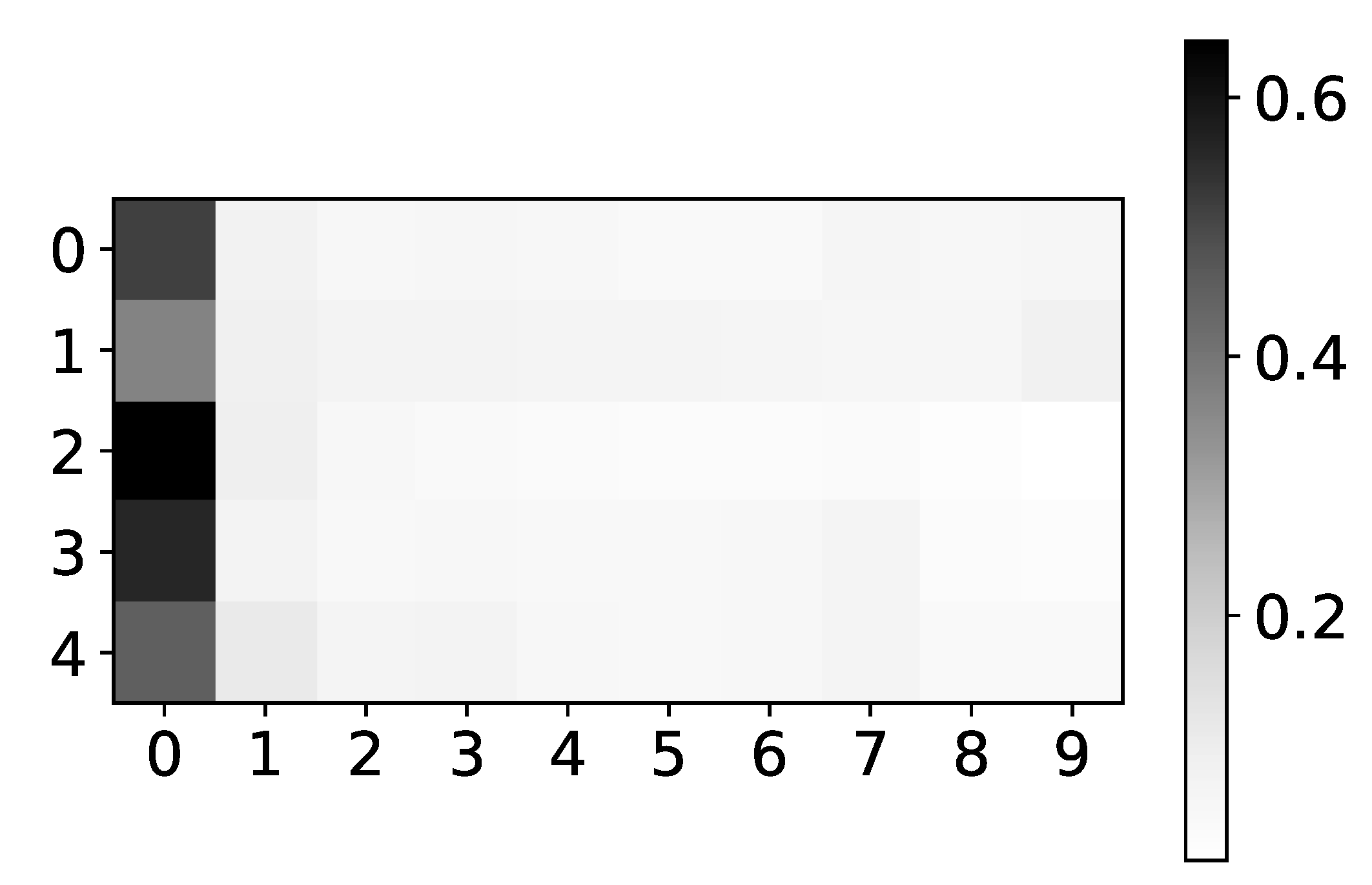
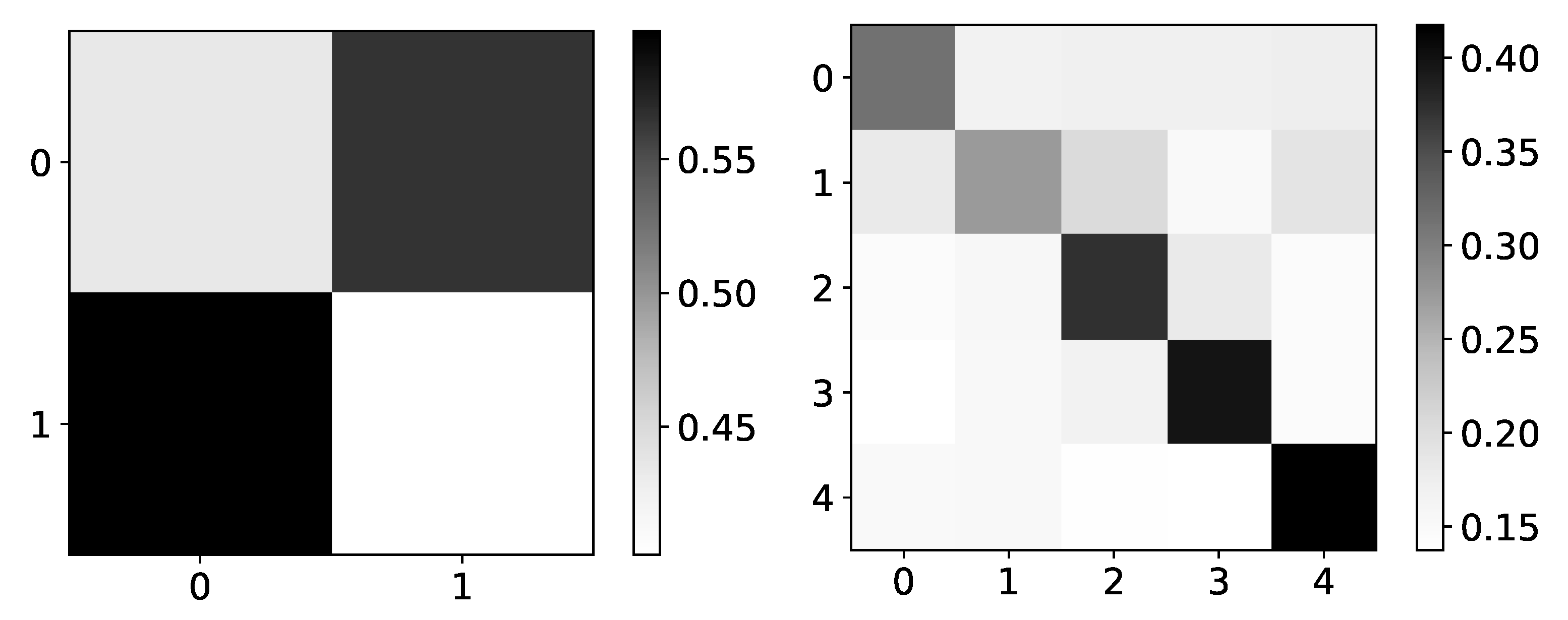
Figure 3.
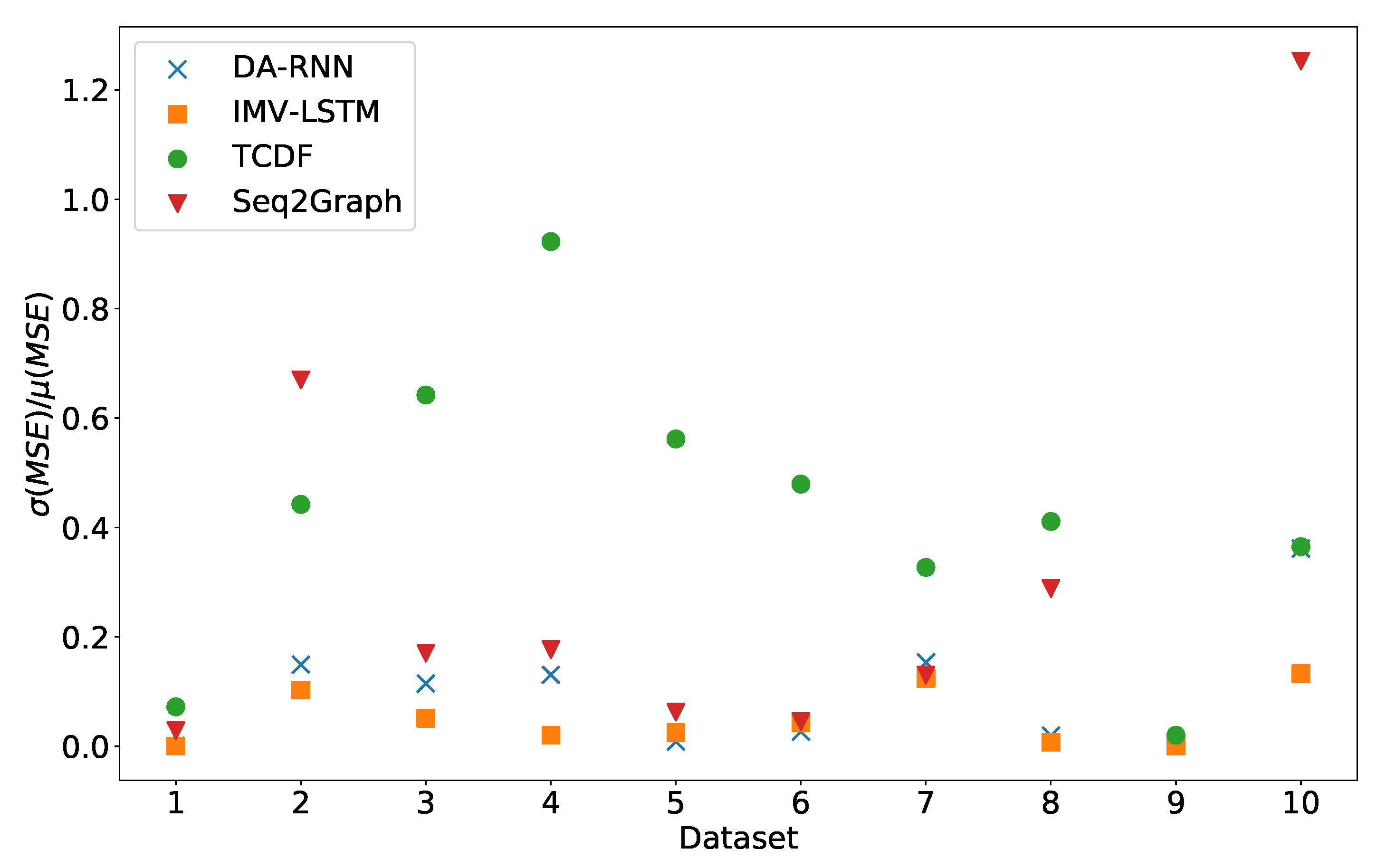
Stability of prediction performance by dataset. On y-axis we plot standard deviation of MSE divided by mean value of MSE. The x-axis corresponds to the index of dataset. As we can see TCDF model is the model with most unstable performance across most datasets, with seq2graph having worse performance on datasets 2 and 10. IMV-LSTM is the model with most stable performance.
Figure 3.
Stability of prediction performance by dataset. On y-axis we plot standard deviation of MSE divided by mean value of MSE. The x-axis corresponds to the index of dataset. As we can see TCDF model is the model with most unstable performance across most datasets, with seq2graph having worse performance on datasets 2 and 10. IMV-LSTM is the model with most stable performance.
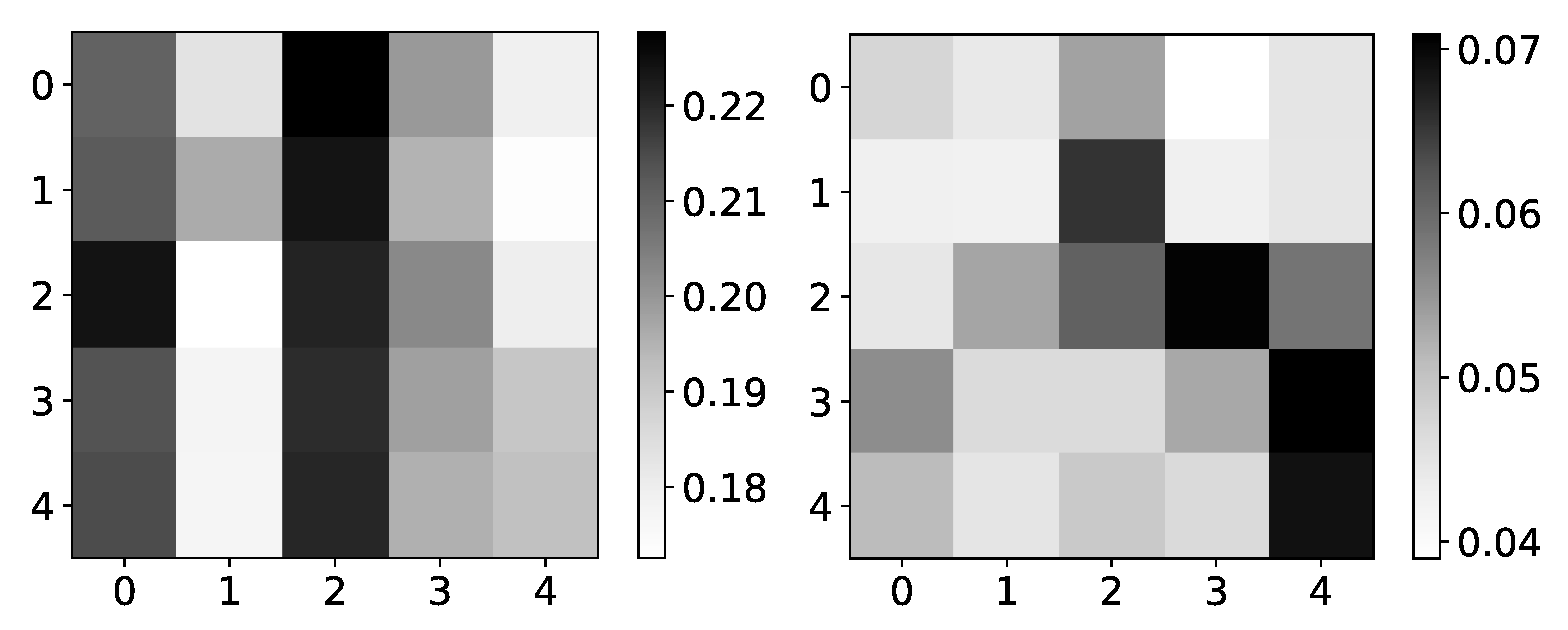
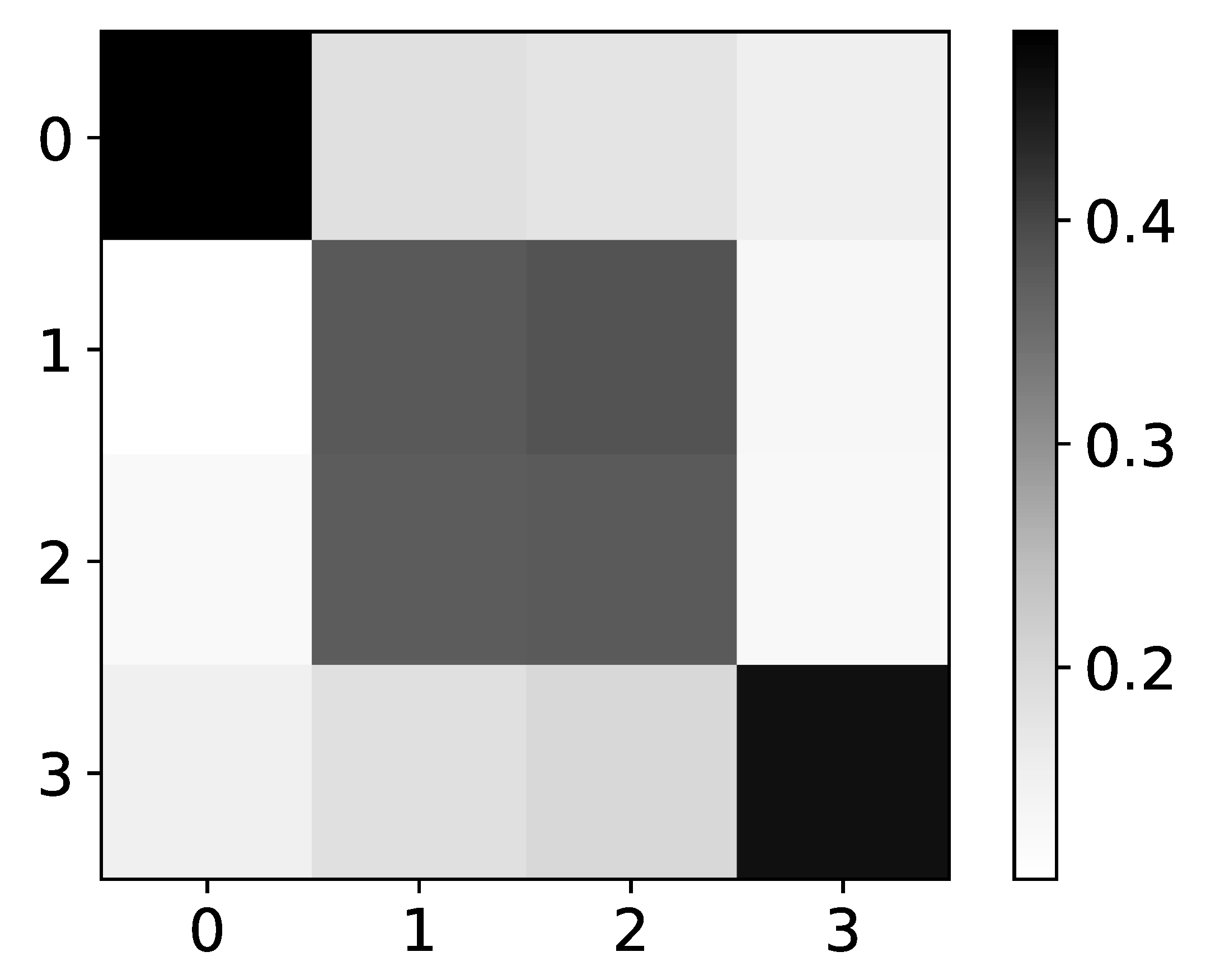
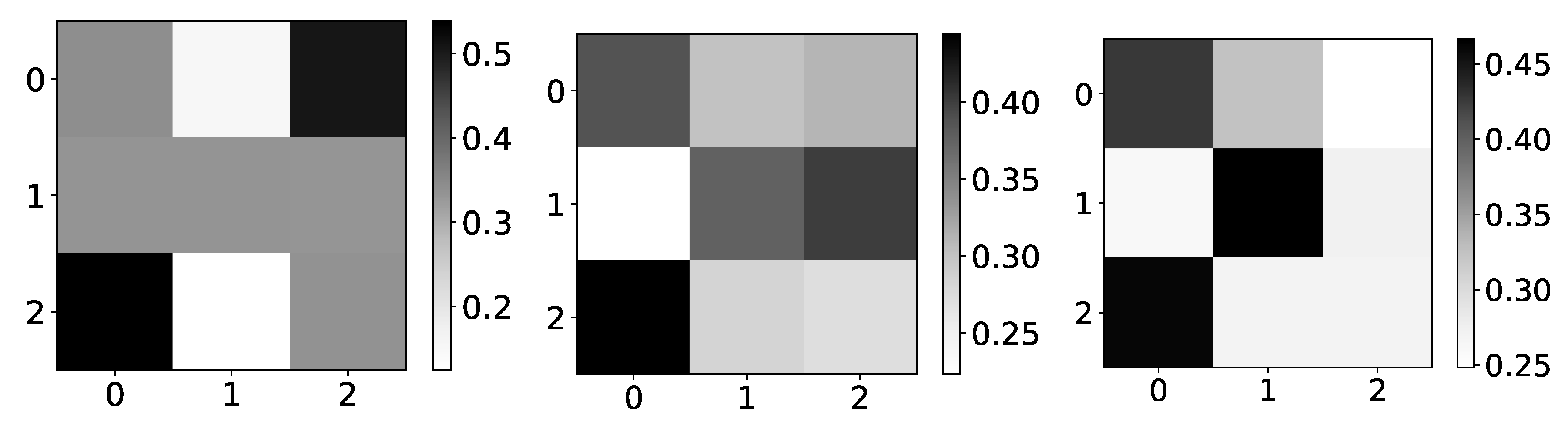
Figure 4.
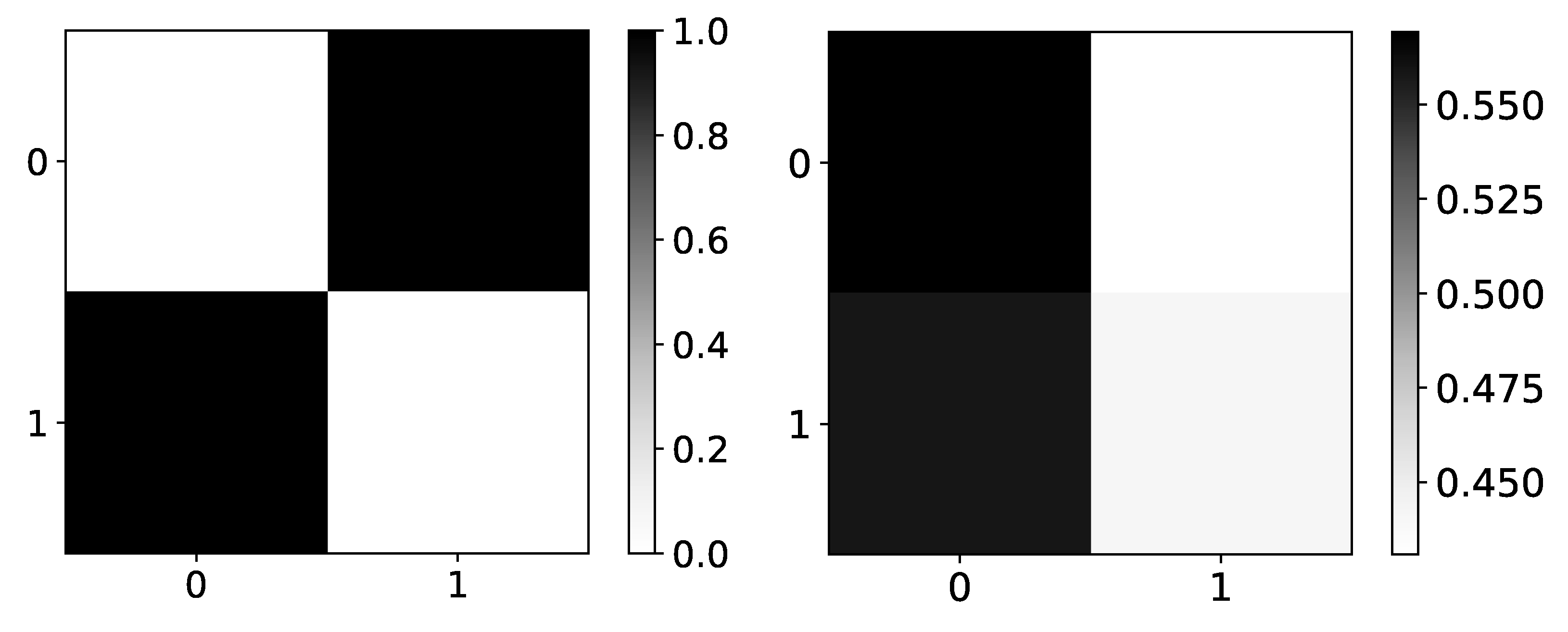
Ground truth (left panel) and mean values (right panel) from seq2graphs model for dataset 4. The y-axis corresponds to the target series index, and the x-axis corresponds to the index of series whose impact on selected target series we plot. This dataset consists of two time-series that are generated from each other without autoregression included. This is the reason we expect high values on antidiagonal. coefficients of seq2graph differ from what we expect, and they are biased towards time-series with index 0.
Figure 4.
Ground truth (left panel) and mean values (right panel) from seq2graphs model for dataset 4. The y-axis corresponds to the target series index, and the x-axis corresponds to the index of series whose impact on selected target series we plot. This dataset consists of two time-series that are generated from each other without autoregression included. This is the reason we expect high values on antidiagonal. coefficients of seq2graph differ from what we expect, and they are biased towards time-series with index 0.
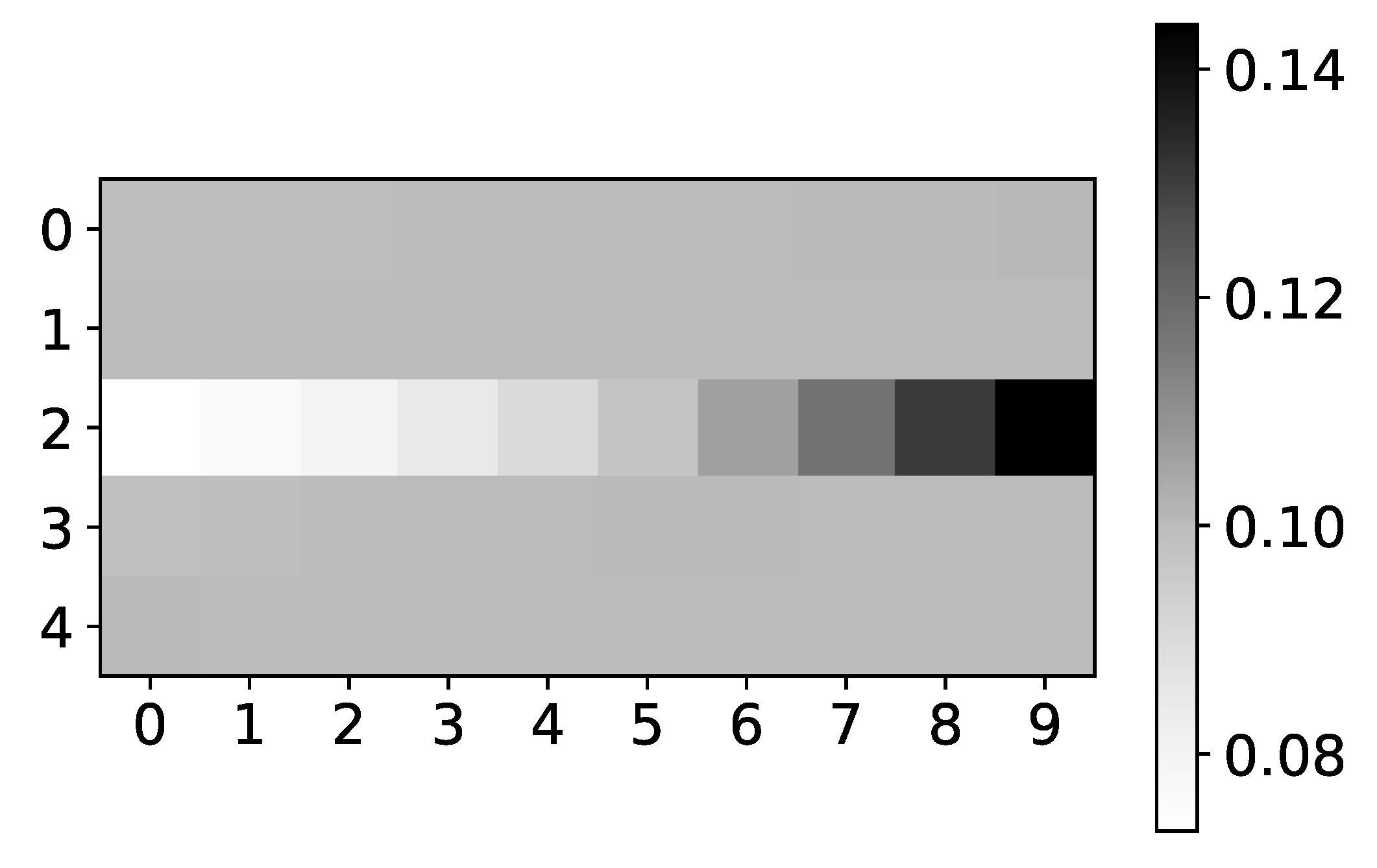
Figure 5.
The mean values of coefficients of seq2graph model for dataset 2. The y-axis corresponds to the index of target series and x-axis corresponds to the time lag whose impact on selected target series we plot. We can see seq2graph bias towards beginning of the window.
Figure 5.
The mean values of coefficients of seq2graph model for dataset 2. The y-axis corresponds to the index of target series and x-axis corresponds to the time lag whose impact on selected target series we plot. We can see seq2graph bias towards beginning of the window.
Figure 6.
Mean (left) and standard deviation (right) of
coefficients from seq2graphs model for dataset 2. The y-axis corresponds to the target series index, and the x-axis corresponds to the index of series whose impact on selected target series we plot. In the left panel, we plot the mean values of
coefficients of seq2graph model for dataset 2. Similar to the analysis on
Figure 4, we can see that seq2graph is biased to one time series. In this case, it is time series with index 2 and a lesser extent time series with index 0 (i.e., beginning of the window). We plot the standard deviation of
coefficients in the right panel, averaged across all experiments. High standard deviation with almost uniform mean values suggests low confidence in given interpretability.
Figure 6.
Mean (left) and standard deviation (right) of
coefficients from seq2graphs model for dataset 2. The y-axis corresponds to the target series index, and the x-axis corresponds to the index of series whose impact on selected target series we plot. In the left panel, we plot the mean values of
coefficients of seq2graph model for dataset 2. Similar to the analysis on
Figure 4, we can see that seq2graph is biased to one time series. In this case, it is time series with index 2 and a lesser extent time series with index 0 (i.e., beginning of the window). We plot the standard deviation of
coefficients in the right panel, averaged across all experiments. High standard deviation with almost uniform mean values suggests low confidence in given interpretability.
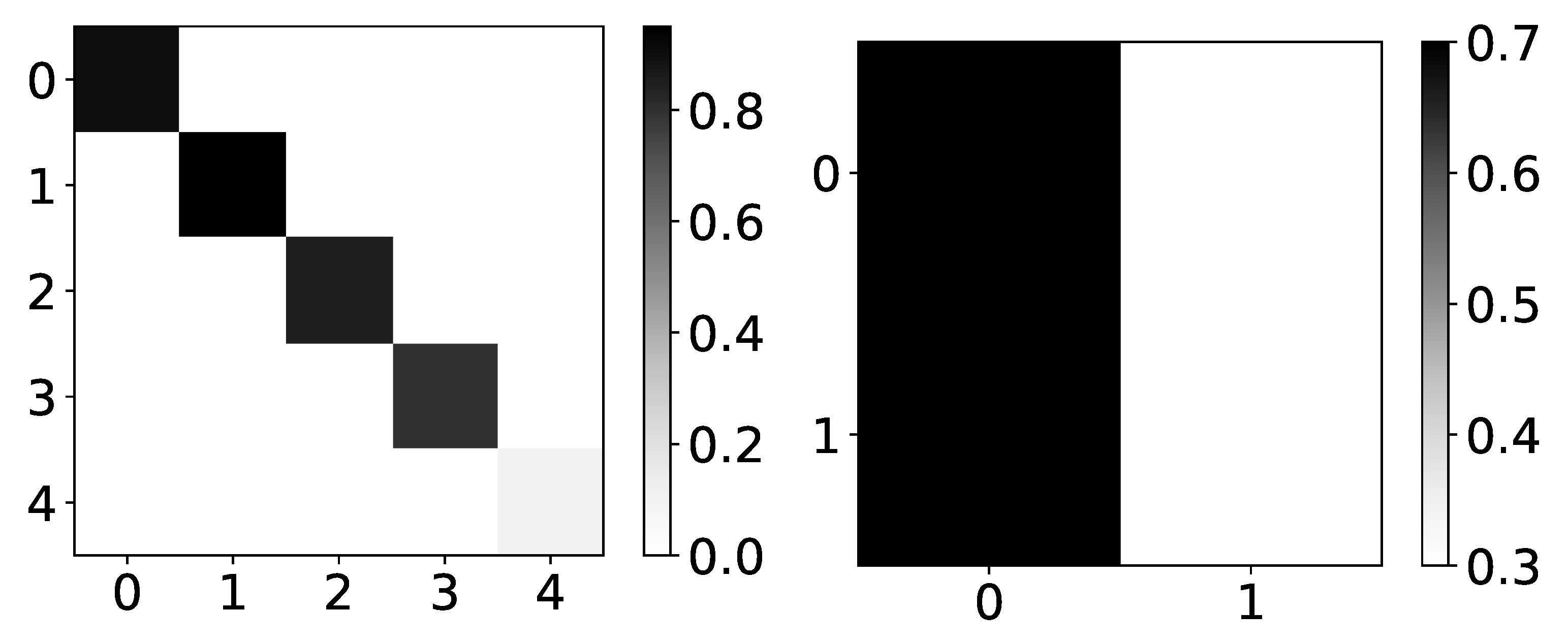
Figure 7.
Percentage of TCDF retrieved causality association within series in dataset 2 and 4. On the y-axis, we plot the target time series. The x-axis corresponds to the index of the series whose impact on the selected target series we count. Values in a single row do not need to sum to 1 for TCDF because there can be a case where TCDF did not find any causality for the targeted time series. These are not attention coefficients. In the left panel, we plot the percentage of experiments that TCDF did find causality for dataset 2. We can see that interpretability is correct for this dataset. However, for the last time series, it found causality in a small percentage of experiments. It is crucial to notice that TCDF never found incorrect causality in this dataset. In the right panel, we plot the percentage of experiments that TCDF did find causality for dataset 4. For this dataset, TCDF always says that a single time series is generating both of them. In the majority of experiments, it was time series with index 0.
Figure 7.
Percentage of TCDF retrieved causality association within series in dataset 2 and 4. On the y-axis, we plot the target time series. The x-axis corresponds to the index of the series whose impact on the selected target series we count. Values in a single row do not need to sum to 1 for TCDF because there can be a case where TCDF did not find any causality for the targeted time series. These are not attention coefficients. In the left panel, we plot the percentage of experiments that TCDF did find causality for dataset 2. We can see that interpretability is correct for this dataset. However, for the last time series, it found causality in a small percentage of experiments. It is crucial to notice that TCDF never found incorrect causality in this dataset. In the right panel, we plot the percentage of experiments that TCDF did find causality for dataset 4. For this dataset, TCDF always says that a single time series is generating both of them. In the majority of experiments, it was time series with index 0.
![Entropy 23 00143 g007 Entropy 23 00143 g007]()
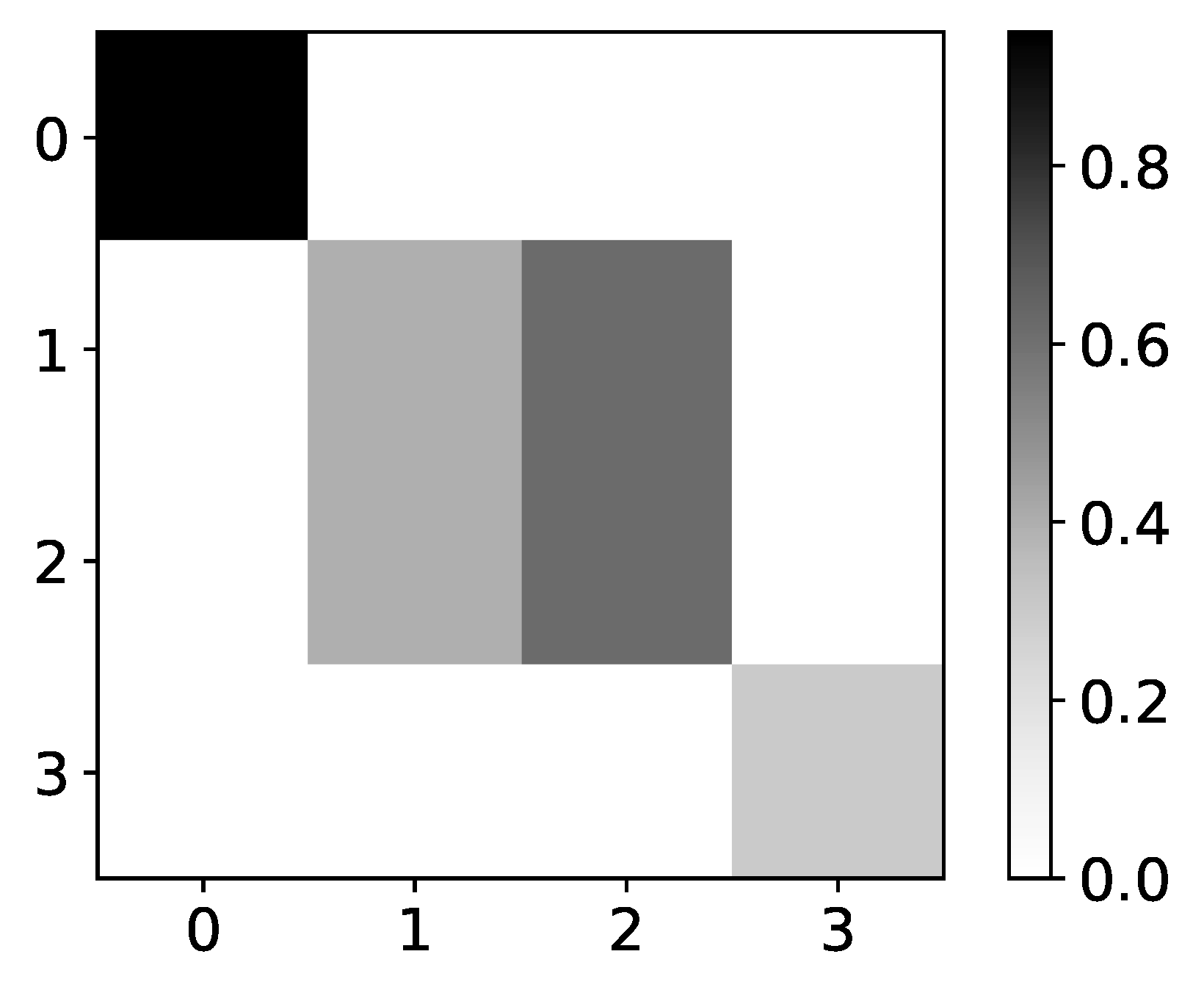
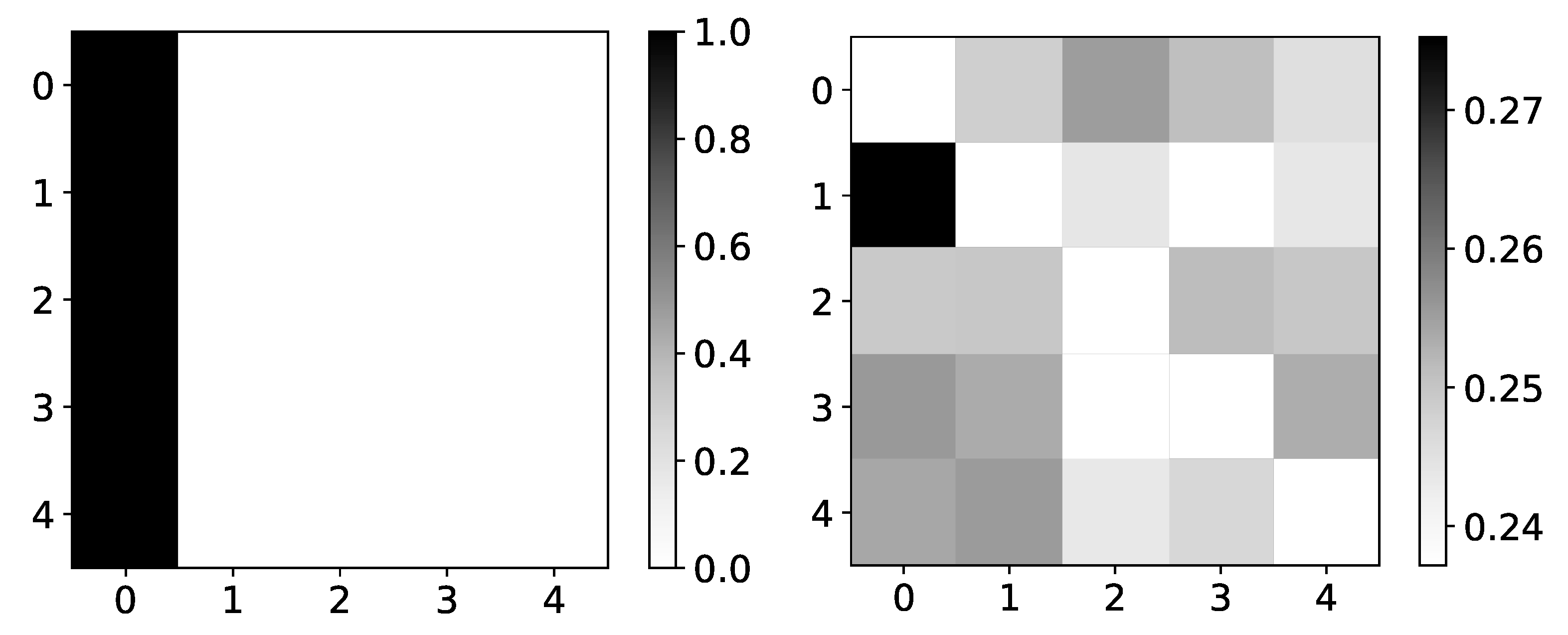
Figure 8.
Percentage of TCDF retrieved causality association within series in dataset 8. On y-axis we plot target time series. The x-axis corresponds to the index of series whose impact on selected target series we count. Values in single row do not need to sum to 1 for TCDF, because there can be an experiment where TCDF did not find any causality for targeted time series. In this figure we plot interpretability given by TCDF on dataset 8. We can see that TCDF gives correct interpretability for time series with index 0 and 3, whose behaviour is autoregressive. For time series with index 1 and 2, this model gives wrong interpretability. Furthermore, even though model gives correct interpretability for time series with index 3, it is only found in 40% of experiments.
Figure 8.
Percentage of TCDF retrieved causality association within series in dataset 8. On y-axis we plot target time series. The x-axis corresponds to the index of series whose impact on selected target series we count. Values in single row do not need to sum to 1 for TCDF, because there can be an experiment where TCDF did not find any causality for targeted time series. In this figure we plot interpretability given by TCDF on dataset 8. We can see that TCDF gives correct interpretability for time series with index 0 and 3, whose behaviour is autoregressive. For time series with index 1 and 2, this model gives wrong interpretability. Furthermore, even though model gives correct interpretability for time series with index 3, it is only found in 40% of experiments.
Figure 9.
The mean values of coefficients from IMV-LSTM model for dataset 4 and dataset 2. The y-axis corresponds to the target series index, and the x-axis corresponds to the index of series whose impact on selected target series we plot. left) In the left panel, we plot mean coefficients of IMV-LSTM model for dataset 4. We can see that IMV-LSTM model gives correct interpretability for this dataset, but with low confidence. In the right panel, we plot mean coefficients of IMV-LSTM for dataset 2. Again, IMV-LSTM model gives correct interpretability, but with high confidence on this dataset.
Figure 9.
The mean values of coefficients from IMV-LSTM model for dataset 4 and dataset 2. The y-axis corresponds to the target series index, and the x-axis corresponds to the index of series whose impact on selected target series we plot. left) In the left panel, we plot mean coefficients of IMV-LSTM model for dataset 4. We can see that IMV-LSTM model gives correct interpretability for this dataset, but with low confidence. In the right panel, we plot mean coefficients of IMV-LSTM for dataset 2. Again, IMV-LSTM model gives correct interpretability, but with high confidence on this dataset.
Figure 10.
The mean values of coefficients of IMV-LSTM model for dataset 2. The y-axis corresponds to the target series’s index, and the x-axis corresponds to the time lag whose impact on the selected target series we plot. We can see that IMV-LSTM is also biased towards the end of the window. However, it is crucial to notice that for time series which do not impact target series, coefficients are uniform.
Figure 10.
The mean values of coefficients of IMV-LSTM model for dataset 2. The y-axis corresponds to the target series’s index, and the x-axis corresponds to the time lag whose impact on the selected target series we plot. We can see that IMV-LSTM is also biased towards the end of the window. However, it is crucial to notice that for time series which do not impact target series, coefficients are uniform.
Figure 11.
The mean values of coefficients from IMV-LSTM model for dataset 8. The y axis corresponds to the index of target series and x axis corresponds to the index of series whose impact on selected target series we plot. We can see that IMV-LSTM gives correct interpretability for time series with index 0 and 3, whose behaviour is autoregressive. For time series with index 1 and 2, this model gives wrong interpretability.
Figure 11.
The mean values of coefficients from IMV-LSTM model for dataset 8. The y axis corresponds to the index of target series and x axis corresponds to the index of series whose impact on selected target series we plot. We can see that IMV-LSTM gives correct interpretability for time series with index 0 and 3, whose behaviour is autoregressive. For time series with index 1 and 2, this model gives wrong interpretability.
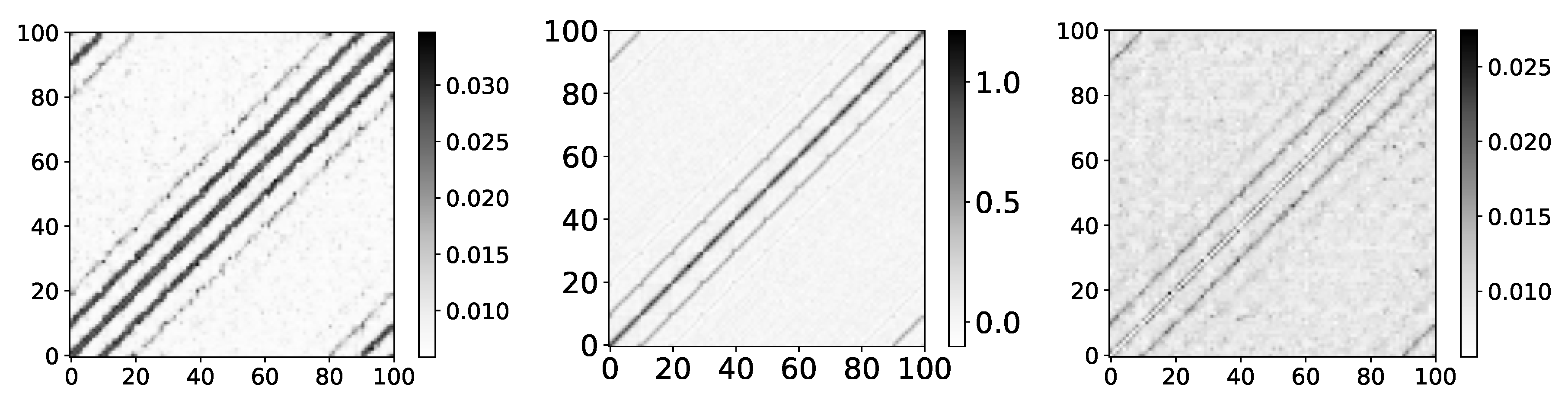
Figure 12.
Ground truth (left panel) and aggregated values (right panel) from the DA-RNN model for dataset 5. The y-axis corresponds to the target series index, and the x-axis corresponds to the index of series whose impact on selected target series we plot. This dataset consists of N = 5 time series that are generated from time series with index 0. This is the reason we expect high values in the first column. coefficients of DA-RNN differ from what we expect. Furthermore, the distribution of these coefficients is highly uniform.
Figure 12.
Ground truth (left panel) and aggregated values (right panel) from the DA-RNN model for dataset 5. The y-axis corresponds to the target series index, and the x-axis corresponds to the index of series whose impact on selected target series we plot. This dataset consists of N = 5 time series that are generated from time series with index 0. This is the reason we expect high values in the first column. coefficients of DA-RNN differ from what we expect. Furthermore, the distribution of these coefficients is highly uniform.
Figure 13.
The mean values of coefficients of the DA-RNN model for dataset 7 for time series with index 0. The y-axis corresponds to the index of feature in Encoder output, and the x-axis corresponds to the time lag whose impact on selected target series we plot. We can see that DA-RNN is biased towards the end of the window. The same behavior is seen with seq2graph and IMV-LSTM.
Figure 13.
The mean values of coefficients of the DA-RNN model for dataset 7 for time series with index 0. The y-axis corresponds to the index of feature in Encoder output, and the x-axis corresponds to the time lag whose impact on selected target series we plot. We can see that DA-RNN is biased towards the end of the window. The same behavior is seen with seq2graph and IMV-LSTM.
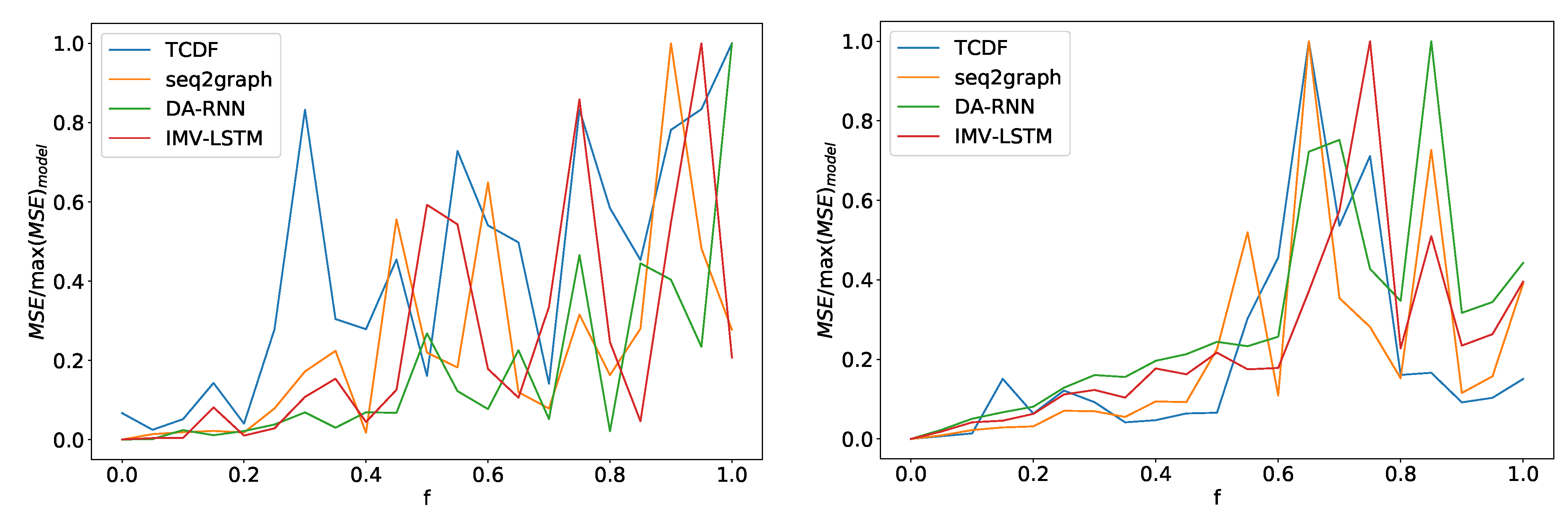
Figure 14.
In the left panel, we can see how the maximum error percentage for specific model changes with f for dataset 2. We observe a change in behavior at around . In the right panel, we can see results for dataset 7. Here we see a change in behavior around . All models show similar behavior with a slight deviation from the TCDF model on dataset 2.
Figure 14.
In the left panel, we can see how the maximum error percentage for specific model changes with f for dataset 2. We observe a change in behavior at around . In the right panel, we can see results for dataset 7. Here we see a change in behavior around . All models show similar behavior with a slight deviation from the TCDF model on dataset 2.
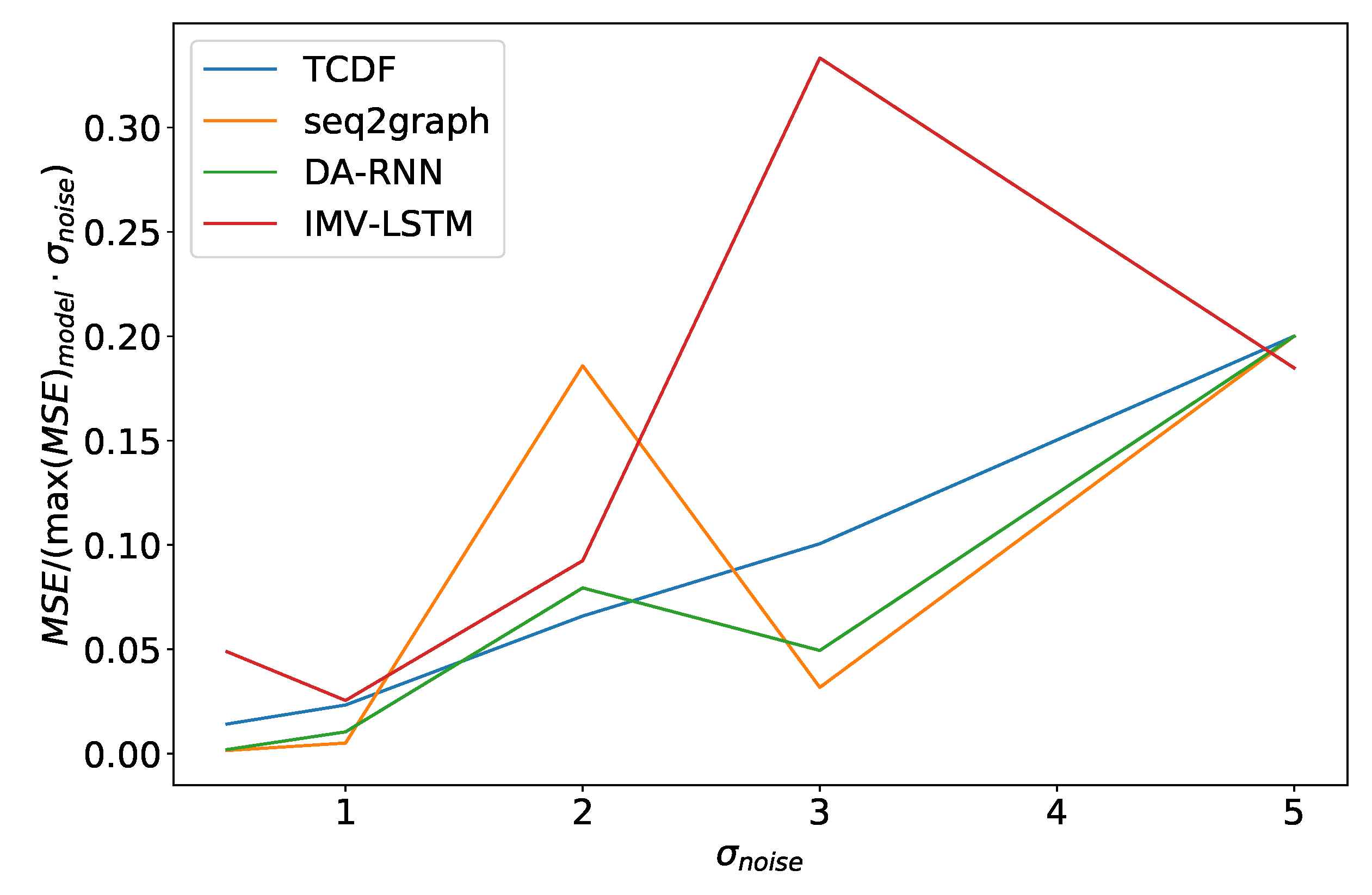
Figure 15.
Maximum error percentage divided by vs. for dataset 2. We see that models have an almost linear dependency on , with TCDF achieving almost perfect linearity.
Figure 15.
Maximum error percentage divided by vs. for dataset 2. We see that models have an almost linear dependency on , with TCDF achieving almost perfect linearity.
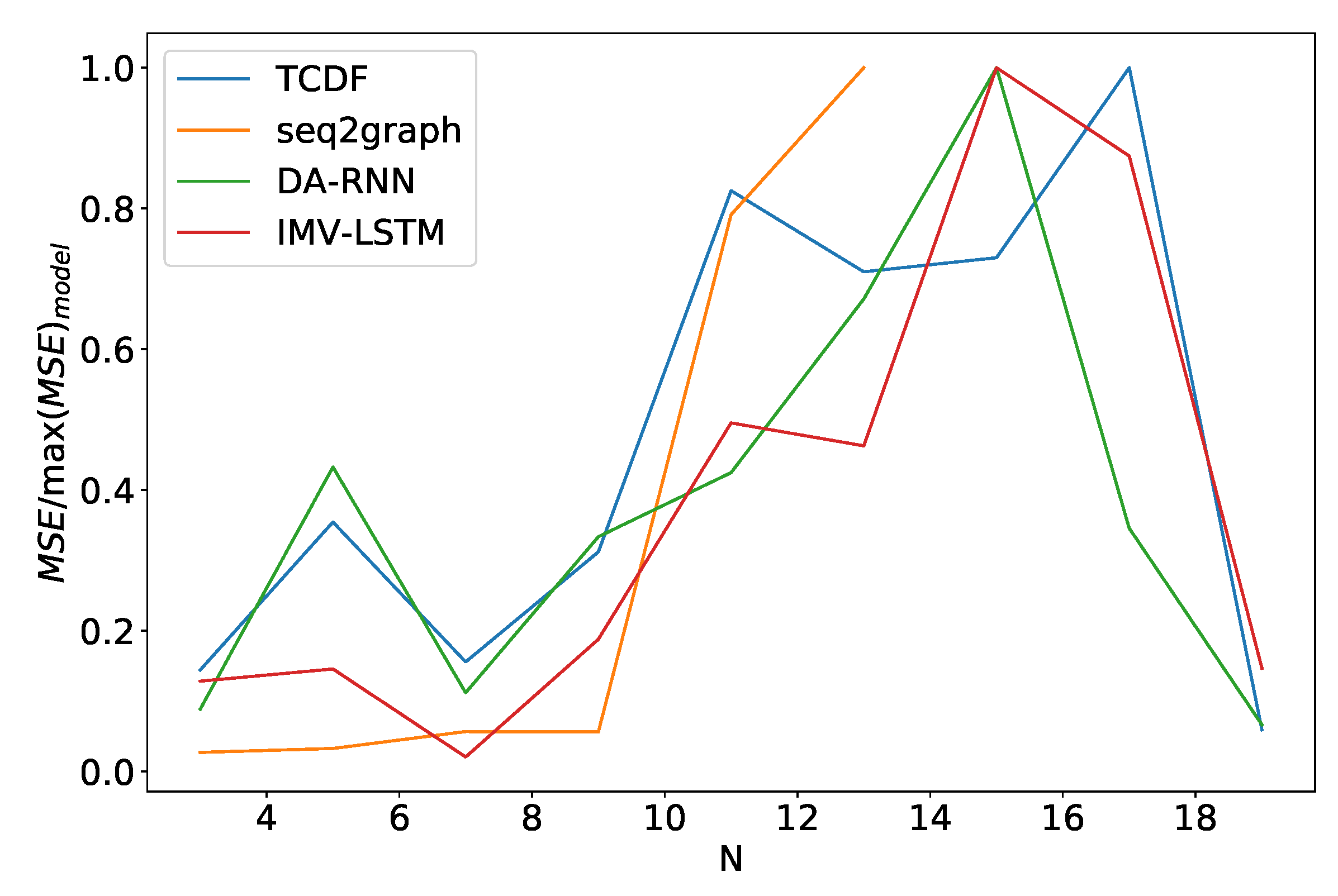
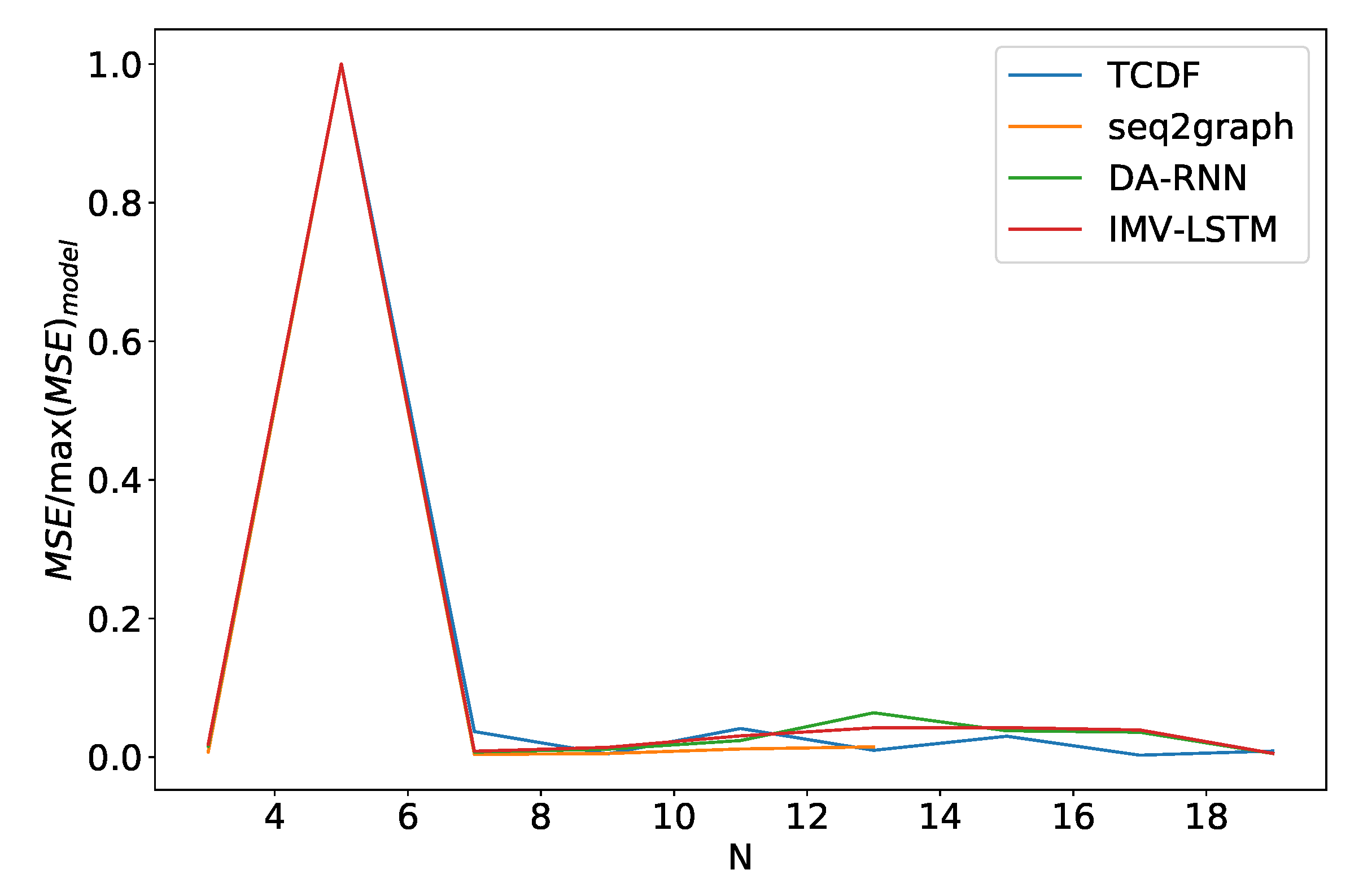
Figure 16.
Percentage of maximum model error vs. number of time series N for dataset 2. We can see a significant increase in error percentage at . Notice that seq2graph only goes to . For higher N, seq2graph model had memory problems.
Figure 16.
Percentage of maximum model error vs. number of time series N for dataset 2. We can see a significant increase in error percentage at . Notice that seq2graph only goes to . For higher N, seq2graph model had memory problems.
Figure 17.
Percentage of maximum model error vs. number of time series N for dataset 5. For this dataset percentage of the maximal model error is almost independent of N, and this behavior is almost identical for all models.
Figure 17.
Percentage of maximum model error vs. number of time series N for dataset 5. For this dataset percentage of the maximal model error is almost independent of N, and this behavior is almost identical for all models.
Figure 18.
The y axis corresponds to the index of target series and x axis corresponds to the index of series whose impact on selected target series we plot. On left image we plot mean values for dataset 9 for . Model shows that first neighbours have highest impact on targeted spin with diminishing impact for higher order neighbours. Spin correlation given by RMB approach. We can see high similarity between these values and values given by IMV-LSTM. Same graph as left, but with T = 2. At temperatures lower than critical, spins become frozen and we have long-range correlations. This long-range correlation is what makes this graph more blurry.
Figure 18.
The y axis corresponds to the index of target series and x axis corresponds to the index of series whose impact on selected target series we plot. On left image we plot mean values for dataset 9 for . Model shows that first neighbours have highest impact on targeted spin with diminishing impact for higher order neighbours. Spin correlation given by RMB approach. We can see high similarity between these values and values given by IMV-LSTM. Same graph as left, but with T = 2. At temperatures lower than critical, spins become frozen and we have long-range correlations. This long-range correlation is what makes this graph more blurry.
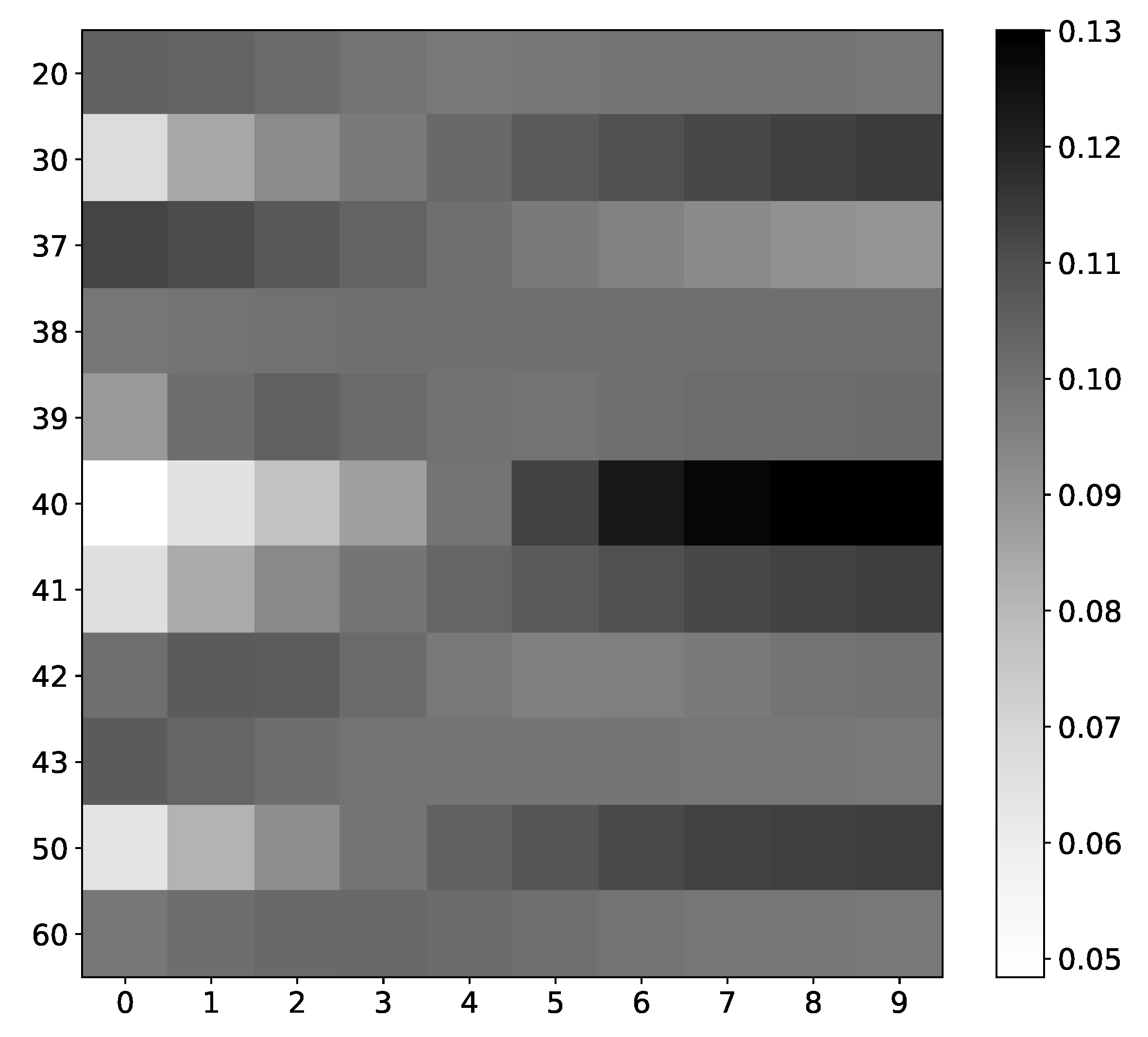
Figure 19.
IMV-LSTM mean coefficients for spin #40. The x-axis corresponds to the time lag, and the y-axis corresponds to the index of spin. We only show interaction with selected spins, as there are 100 of them. As we can see, spins that interact with our selected spin have the most diverse values. Spins that do not interact with spin #40, for instance, spin #20 or spin #37, have almost uniform values across all time stamps.
Figure 19.
IMV-LSTM mean coefficients for spin #40. The x-axis corresponds to the time lag, and the y-axis corresponds to the index of spin. We only show interaction with selected spins, as there are 100 of them. As we can see, spins that interact with our selected spin have the most diverse values. Spins that do not interact with spin #40, for instance, spin #20 or spin #37, have almost uniform values across all time stamps.
Figure 20.
The mean values of coefficients from IMV-LSTM model for dataset 10 for 3 different values of r: 1.5, 3.55 and 3.56996. The y-axis corresponds to the index of target series and x-axis corresponds to the index of series whose impact on selected target series we plot. left) In the left panel we plot mean values of coefficients for . As we can see, the interpretability is completely wrong, but in this regime, logistic map converges to single value. In the middle panel we plot mean values of coefficients for . As we can see, the interpretability is much closer to expected behaviour. In this regime, logistic map oscillates between several different values, so it is beneficial to model to learn correct interpretability. In the right panel we plot mean values of coefficients for . As we can see, the interpretability is almost correct with high confidence.
Figure 20.
The mean values of coefficients from IMV-LSTM model for dataset 10 for 3 different values of r: 1.5, 3.55 and 3.56996. The y-axis corresponds to the index of target series and x-axis corresponds to the index of series whose impact on selected target series we plot. left) In the left panel we plot mean values of coefficients for . As we can see, the interpretability is completely wrong, but in this regime, logistic map converges to single value. In the middle panel we plot mean values of coefficients for . As we can see, the interpretability is much closer to expected behaviour. In this regime, logistic map oscillates between several different values, so it is beneficial to model to learn correct interpretability. In the right panel we plot mean values of coefficients for . As we can see, the interpretability is almost correct with high confidence.
Table 1.
Models used for benchmarking, with each successive dataset model’s complexity is increased: constant time series (dataset 1) to autoregressive (dataset 2) and nonlinear autoregressive (dataset 3) with no interaction between time series, two interdependent time series without autoregression (dataset 4), first series is autoregressive (dataset 5) and nonlinear autoregressive (dataset 6) time series with all other time series calculated from first, custom vector autoregression model (dataset 7), switching time series (dataset 8). Additionally, we created two datasets from statistical and mechanistic models: The logistic map inspired model (dataset 9) and the Ising model on the first-order 2D square lattice (dataset 10).
Table 1.
Models used for benchmarking, with each successive dataset model’s complexity is increased: constant time series (dataset 1) to autoregressive (dataset 2) and nonlinear autoregressive (dataset 3) with no interaction between time series, two interdependent time series without autoregression (dataset 4), first series is autoregressive (dataset 5) and nonlinear autoregressive (dataset 6) time series with all other time series calculated from first, custom vector autoregression model (dataset 7), switching time series (dataset 8). Additionally, we created two datasets from statistical and mechanistic models: The logistic map inspired model (dataset 9) and the Ising model on the first-order 2D square lattice (dataset 10).
| Name | Formula | Parameters |
|---|
| Dataset 1 | | |
| Dataset 2 | | |
| Dataset 3 | | |
| Dataset 4 | | |
| Dataset 5 | |
|
| Dataset 6 | |
|
| Dataset 7 |
|
|
| Dataset 8 | if
else:
|
|
| Dataset 9 | | T = 2, Tc, 2.75 |
| Dataset 10 |
| r = 1.5, 2.5, 3.2, 3.55, 3.56996 |
Table 2.
Model prediction performance on all datasets. The average experiment MSE for each model is reported as a score. We do not report seq2graph results on dataset 9 because the model had memory problems. Dataset 9 consists of 100 series in our experiment, and seq2graph cannot model that many time series. ES-RNN model (the winner of the M4 competition) is added for comparison and evaluated only on datasets 1–8. ES-RNN is only used in quantitative analysis since it does not provide interpretability.
Table 2.
Model prediction performance on all datasets. The average experiment MSE for each model is reported as a score. We do not report seq2graph results on dataset 9 because the model had memory problems. Dataset 9 consists of 100 series in our experiment, and seq2graph cannot model that many time series. ES-RNN model (the winner of the M4 competition) is added for comparison and evaluated only on datasets 1–8. ES-RNN is only used in quantitative analysis since it does not provide interpretability.
| Dataset | DA-RNN | IMV-LSTM | seq2graph | TCDF | ES-RNN |
|---|
| 1 | 0.00293 ± 1 × 10−5 | 0.02905 ± 9 × 10−7 | 0.00303 ± 9 × 10−5 | 0.0033 ± 0.0002 | 0.003731 ± 1 × 10−6 |
| 2 | 0.00150 ± 6 × 10−5 | 0.0018 ± 0.0002 | 0.011 ± 0.007 | 0.02 ± 0.01 | 0.001496 ± 9 × 10−6 |
| 3 | 0.00013 ± 1 × 10−5 | 0.000125 ± 6 × 10−6 | 0.00001 ± 2 × 10−5 | 0.0006 ± 0.0004 | 0.000137 ± 1 × 10−6 |
| 4 | 0.000244 ± 2 × 10−6 | 0.000238 ± 5 × 10−6 | 0.00032 ± 6 × 10−6 | 0.002 ± 0.002 | 0.00045 ± 1 × 10−4 |
| 5 | 0.00229 ± 7 × 10−5 | 0.00138 ± 3 × 10−5 | 0.0020 ± 0.0001 | 0.005 ± 0.003 | 0.017833 ± 1 × 10−6 |
| 6 | 0.00210 ± 1 × 10−5 | 0.00143 ± 6 × 10−5 | 0.00213 ± 0.0001 | 0.005 ± 0.002 | 0.018541 ± 1 × 10−6 |
| 7 | 0.009 ± 0.001 | 0.0051 ± 0.0006 | 0.008 ± 0.001 | 0.021 ± 0.007 | 0.0120 ± 0.0002 |
| 8 | 0.286 ± 0.006 | 0.258 ± 0.002 | 0.18 ± 0.05 | 0.3 ± 0.1 | 0.250 ± 0.001 |
| 9 | 0.3353 ± 0.0005 | 0.2688 ± 0.0001 | - | 0.348 ± 0.007 | - |
| 10 | 0.002 ± 0.001 | (9 ± 1) × 10−5 | 0.006 ± 0.008 | 0.03 ± 0.01 | - |