An Entropy-Based Tool to Help the Interpretation of Common-Factor Spaces in Factor Analysis
Abstract
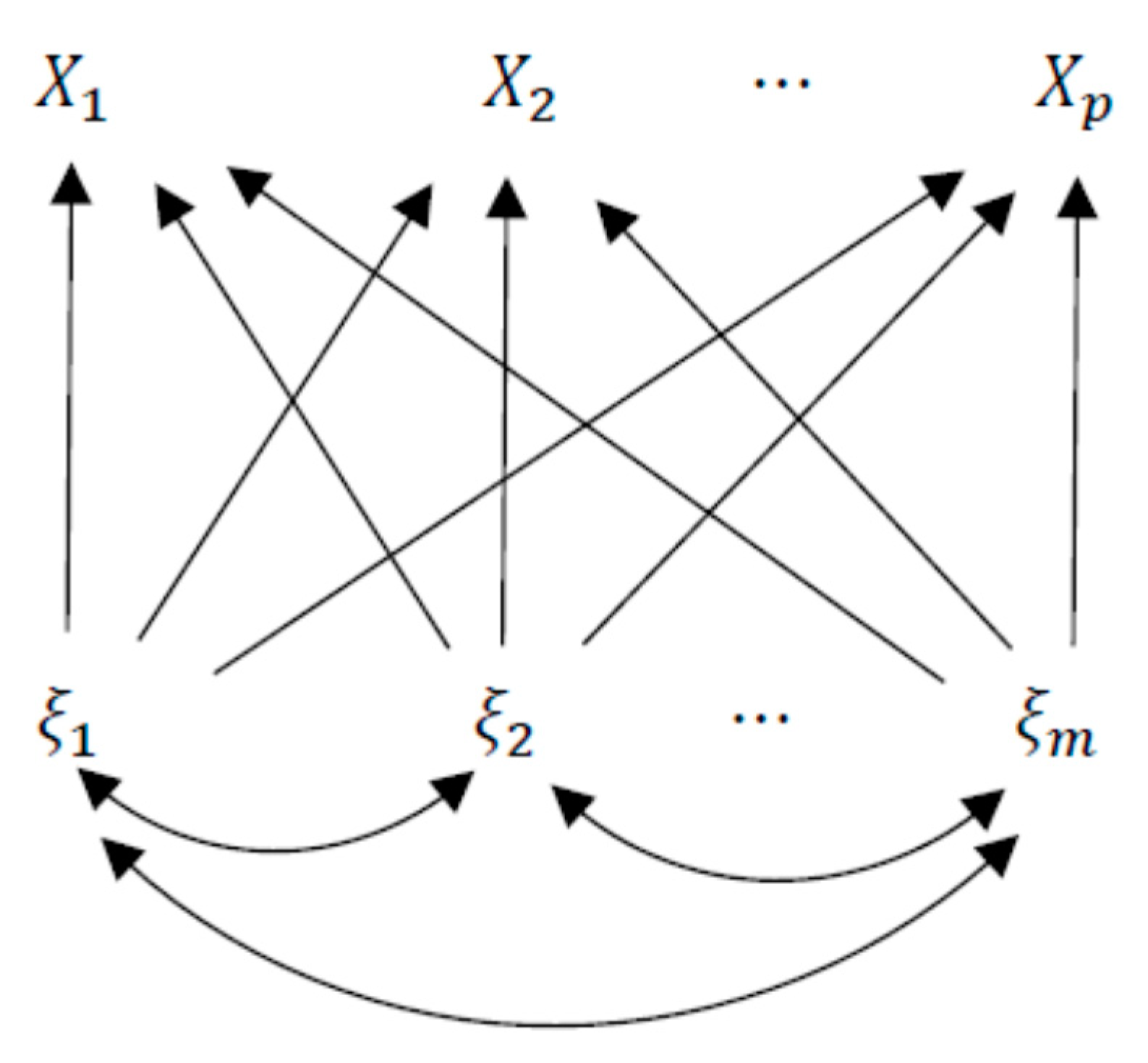
1. Introduction
2. Entropy-Based Method for Measuring Factor Contributions
3. Canonical Factor Analysis
Numerical Example 1
4. Deriving Important Common Factors Based on Decomposition of Manifest Variables into Subsets
4.1. Numerical Example 1 (Continued)
4.2. Numerical Example 2
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Ten Berge, J.M.F. A joint treatment of VARIMAX rotation and the problem of diagonalizing symmetric matrices simultaneously in the least-squares sense. Psychometrika 1984, 49, 347–358. [Google Scholar] [CrossRef]
- Jennrich, R.I.; Sampson, P.F. Rotation for simple loadings. Psychometrika 1966, 31, 313–323. [Google Scholar] [CrossRef] [PubMed]
- Harris, C.W.; Kaiser, H.F. Oblique factor analytic solutions by orthogonal transformation. Psychometrika 1964, 29, 347–362. [Google Scholar] [CrossRef]
- Thurstone, L.L. Vector of Mind: Multiple Factor Analysis for the Isolation of Primary Traits; University of Chicago Press: Chicago, IL, USA, 1935. [Google Scholar]
- Eshima, N.; Tabata, M.; Borroni, C.G. An entropy-based approach for measuring factor contributions in factor analysis models. Entropy 2018, 20, 634. [Google Scholar] [CrossRef] [PubMed]
- Nelder, J.A.; Wedderburn, R.W.M. Generalized linear model. J. R. Stat. Soc. A 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Eshima, N.; Tabata, M. Entropy coefficient of determination for generalized linear models. Comput. Stat. Data Anal. 2010, 54, 1381–1389. [Google Scholar] [CrossRef]
- Rao, C.R. Estimation and tests of significance in factor analysis. Psychometrika 1955, 20, 93–111. [Google Scholar] [CrossRef]
- Bartholomew, D.J. Latent Variable Models and Factor Analysis; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
| 0.60 | 0.75 | 0.65 | 0.32 | 0.00 | |
| 0.39 | 0.24 | 0.00 | 0.59 | 0.92 | |
| uniqueness | 0.50 | 0.38 | 0.58 | 0.55 | 0.16 |
| 0.62 | 0.80 | 0.70 | 0.31 | ||
| 0.19 | 0.49 | 0.94 | |||
| uniqueness | 0.50 | 0.38 | 0.58 | 0.55 | 0.16 |
| 0.64 | 0.34 | 0.46 | 0.25 | 0.97 | 0.82 | |
| 0.37 | 0.54 | 0.76 | 0.41 | |||
| uniqueness | 0.45 | 0.59 | 0.21 | 0.77 | 0.04 | 0.33 |
| 0.49 | 0.63 | 0.89 | 0.48 | 0.07 | ||
| 0.39 | 0.01 | 0.00 | 0.00 | 0.98 | ||
| uniqueness | 0.45 | 0.59 | 0.21 | 0.77 | 0.04 | 0.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eshima, N.; Borroni, C.G.; Tabata, M.; Kurosawa, T. An Entropy-Based Tool to Help the Interpretation of Common-Factor Spaces in Factor Analysis. Entropy 2021, 23, 140. https://doi.org/10.3390/e23020140
Eshima N, Borroni CG, Tabata M, Kurosawa T. An Entropy-Based Tool to Help the Interpretation of Common-Factor Spaces in Factor Analysis. Entropy. 2021; 23(2):140. https://doi.org/10.3390/e23020140
Chicago/Turabian StyleEshima, Nobuoki, Claudio Giovanni Borroni, Minoru Tabata, and Takeshi Kurosawa. 2021. "An Entropy-Based Tool to Help the Interpretation of Common-Factor Spaces in Factor Analysis" Entropy 23, no. 2: 140. https://doi.org/10.3390/e23020140
APA StyleEshima, N., Borroni, C. G., Tabata, M., & Kurosawa, T. (2021). An Entropy-Based Tool to Help the Interpretation of Common-Factor Spaces in Factor Analysis. Entropy, 23(2), 140. https://doi.org/10.3390/e23020140





