Super-Alarms with Diagnosis Proficiency Used as an Additional Layer of Protection Applied to an Oil Transport System
Abstract
1. Introduction
2. Research Method
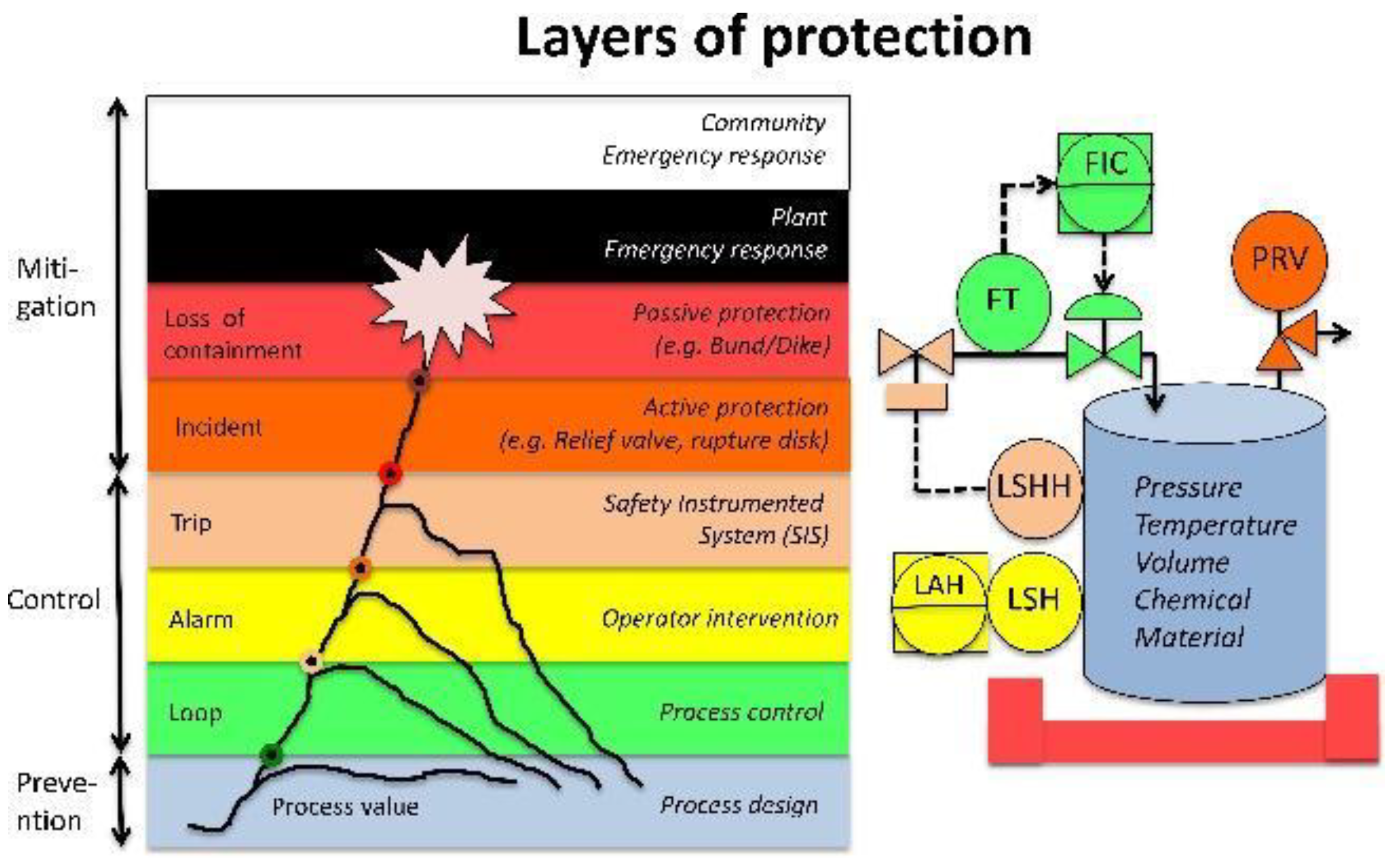
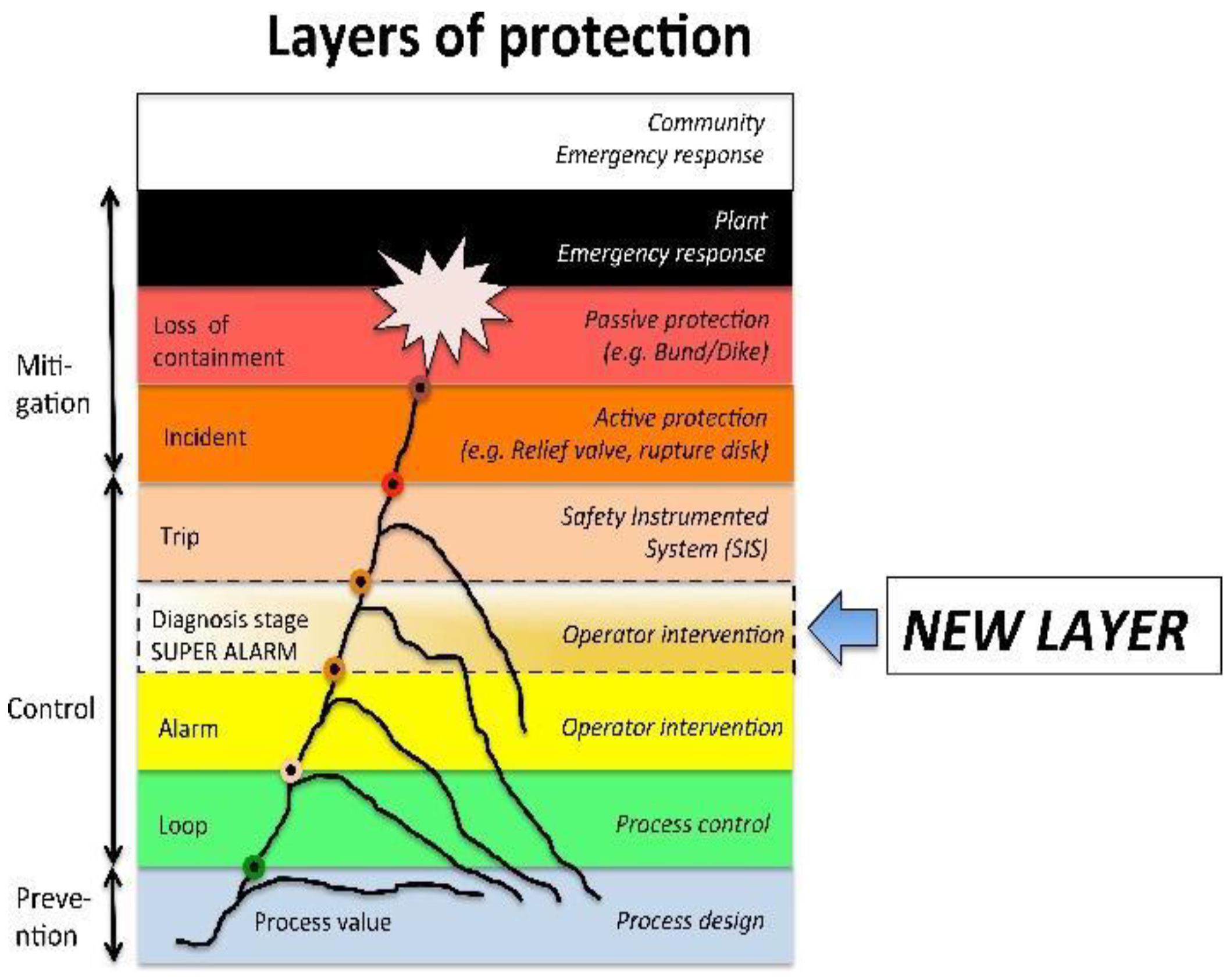
2.1. Layers of Protection and the Super-Alarm Layer
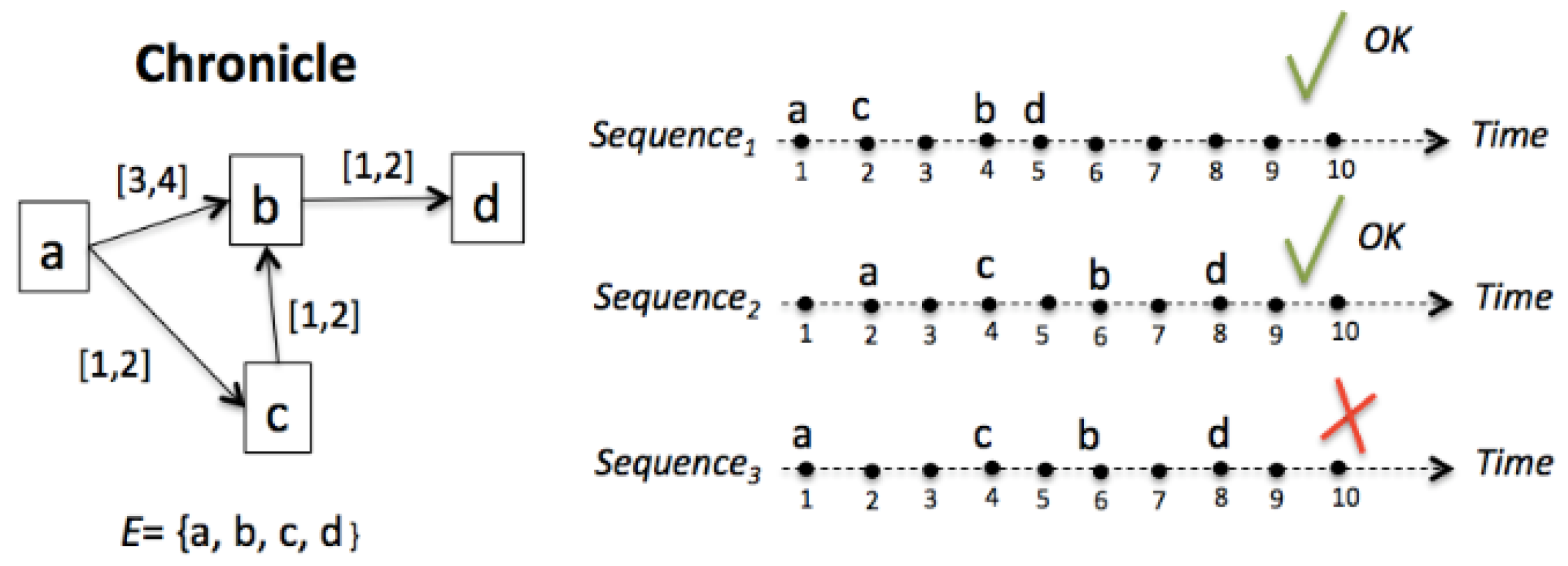
2.2. Chronicle Based Alarm Management Methodology
- Ψ is a set of indexed event types, i.e., a finite indexed family defined by ψ: H → E, in which H ⊏ N.
- A is a set of edges between the indexed event types; there is an edge (, ) ∈ A if and only if there is a time constraint between , and .
- V = {υi} is a set of continuous process variables which are functions of time.
- D is a set of discrete variables. D = Q⋃K⋃VQ, where:
- ○
- Q is a set of states qi of the transition system, which represents the system’s operation modes.
- ○
- The set of auxiliary discrete variables K = {Ki}, I = 1,2,3,….nc represents the system configuration in each mode qi, in which Ki indicates the discrete state of the active components.
- ○
- VQ is a set of qualitative variables whose values are obtained from the behavior of each continuous variable υi.
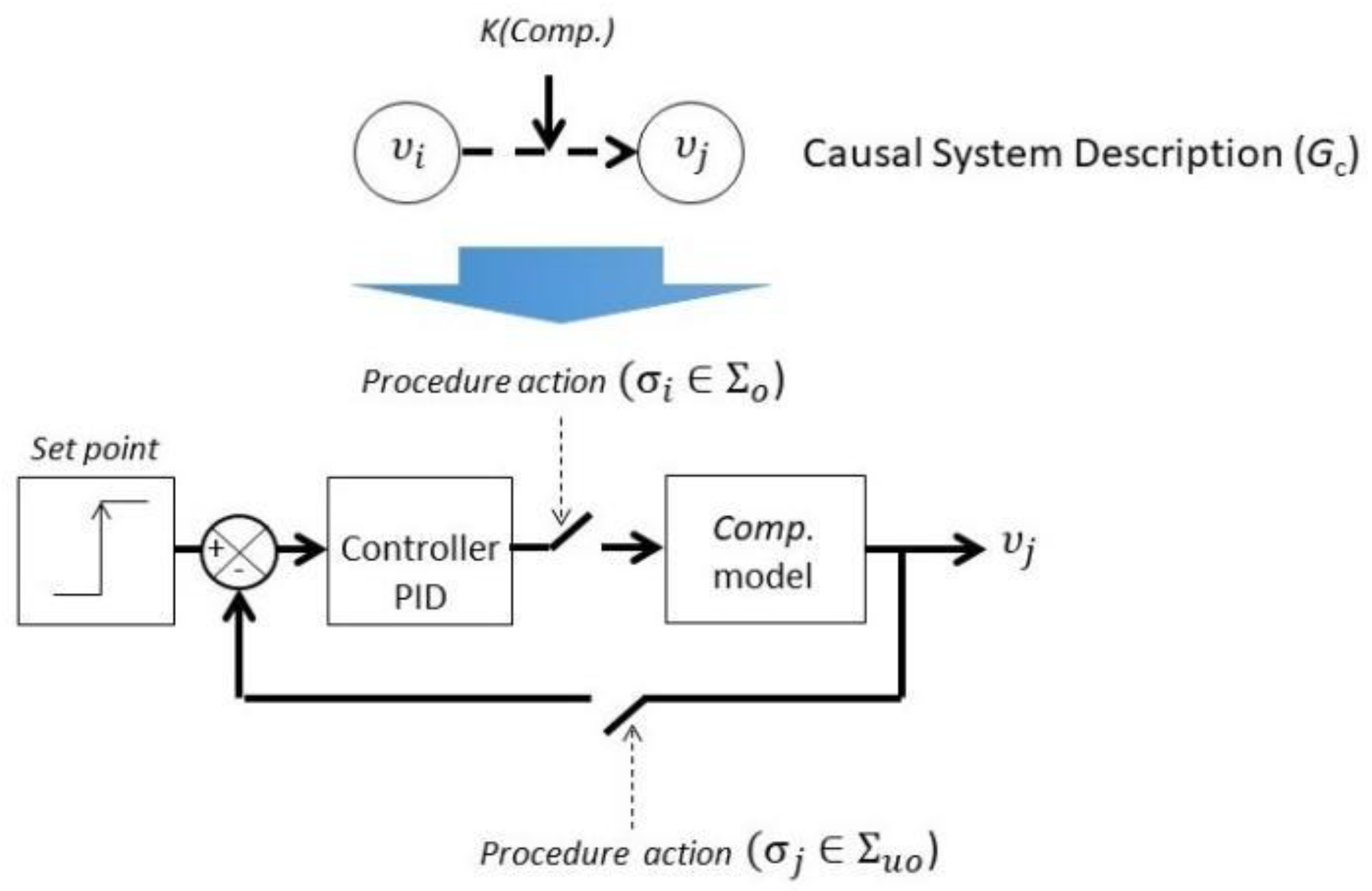
- E = Σ ⋃ Σc is a finite set of observables (Σo) and unobservable (Σuo) event types, in which Σ is the set of event type associated to the procedural actions, for example, in the start-up or shutdown stages, and Σc is the set of event types associated to the behavior of the continuous process variables.
- Tr:Q × Σ → Q is the transition function. The transition from mode qi to mode qj with associated event σ is noted (qi,σ,qj).
- CSD ⊇ ⋃iCSDi is the Causal System Description or the causal model used to represent the constraints underlying the continuous dynamics of the hybrid system.
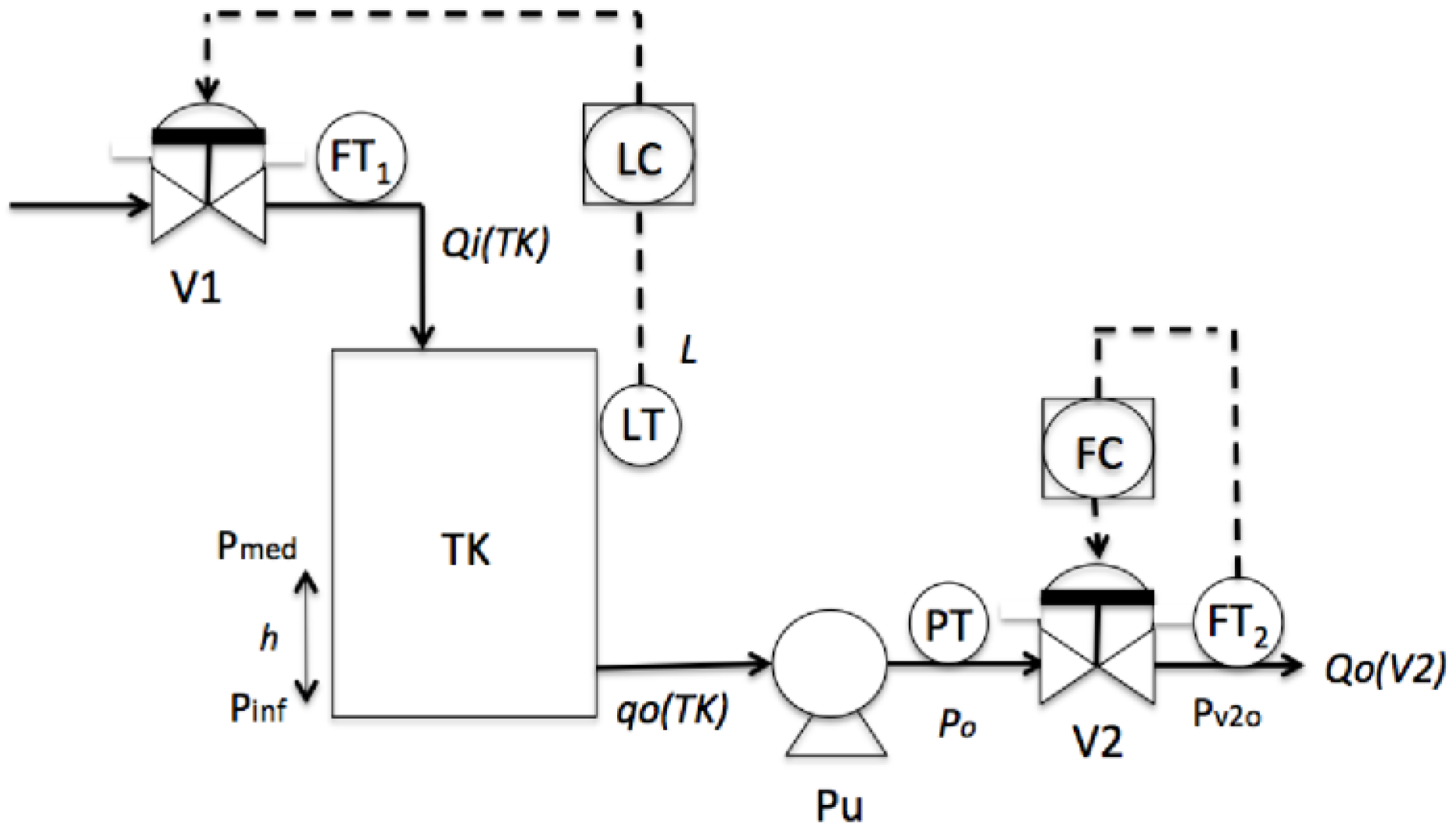
3. Results
3.1. Applying CBAM
3.1.1. STEP 1: Event Type Identification
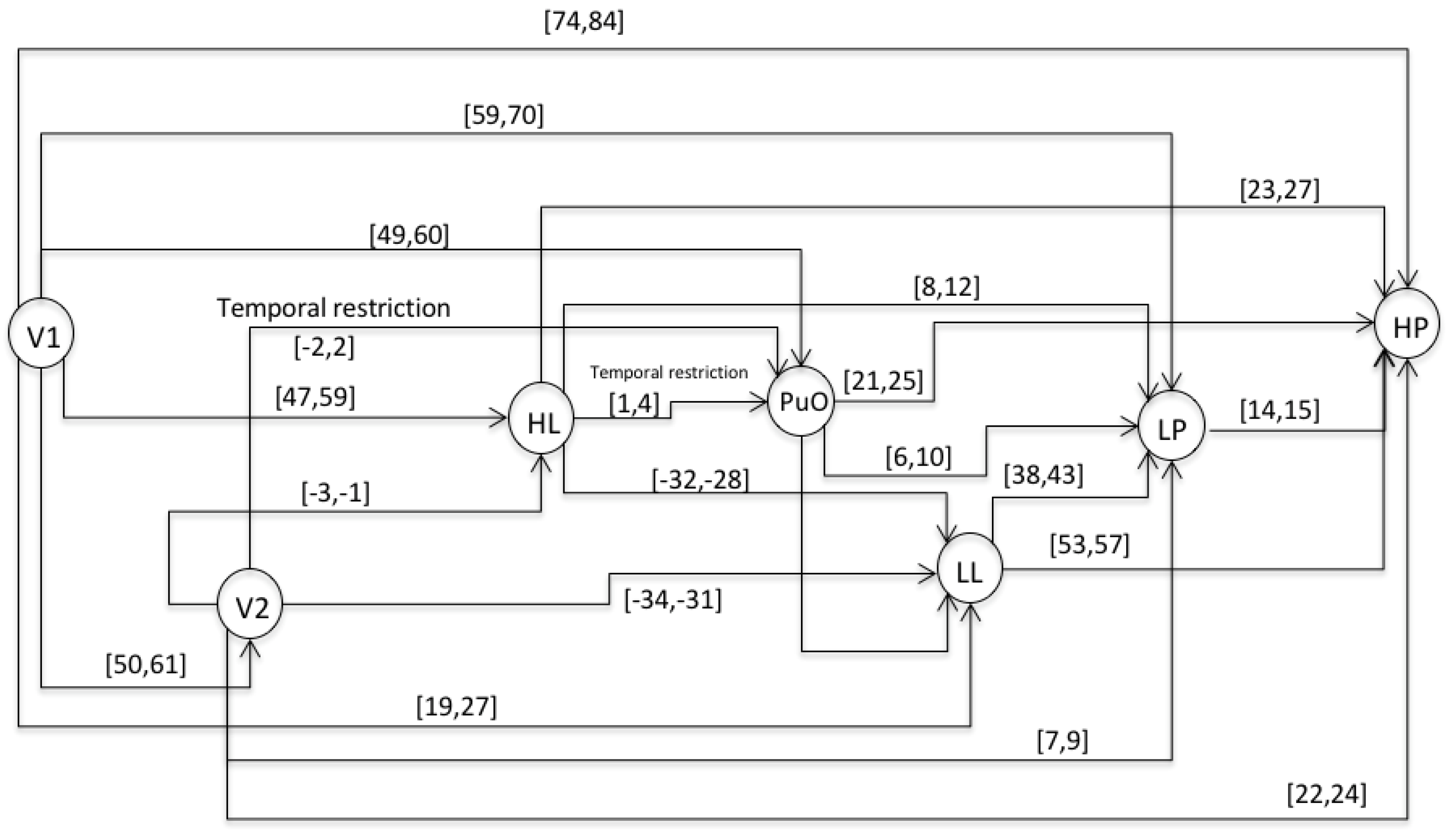
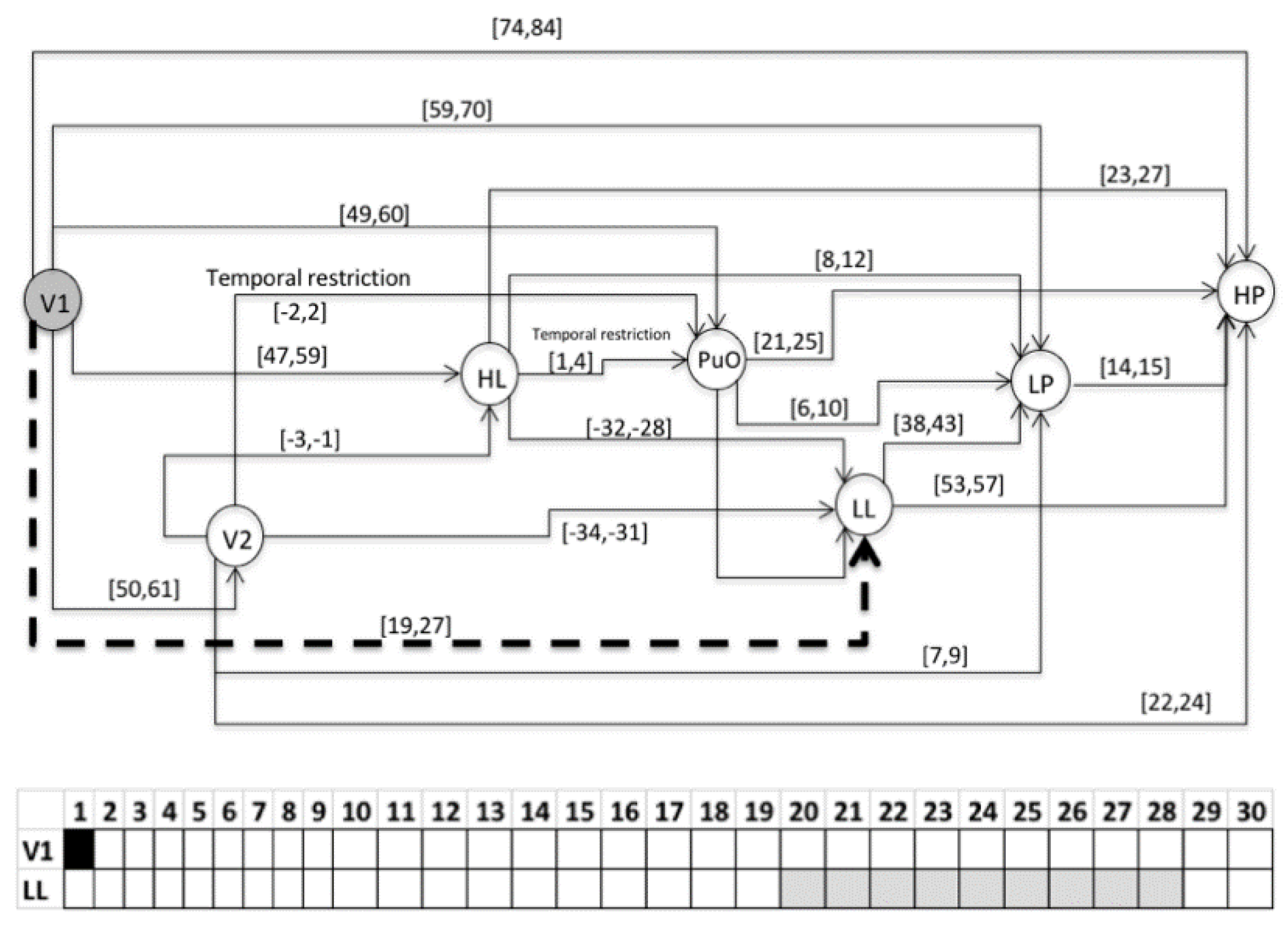
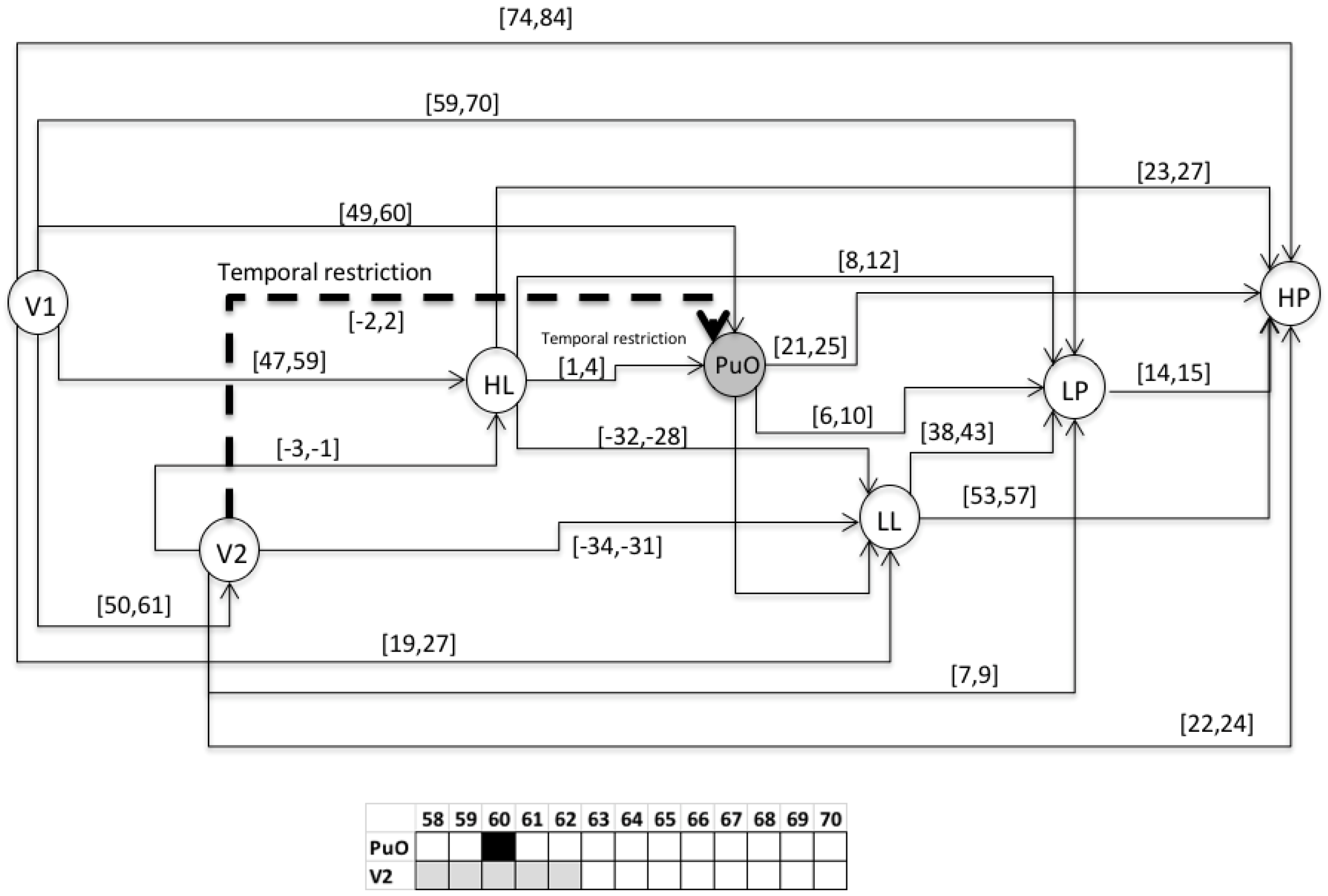
3.1.2. STEP 2: Event Sequence Generation
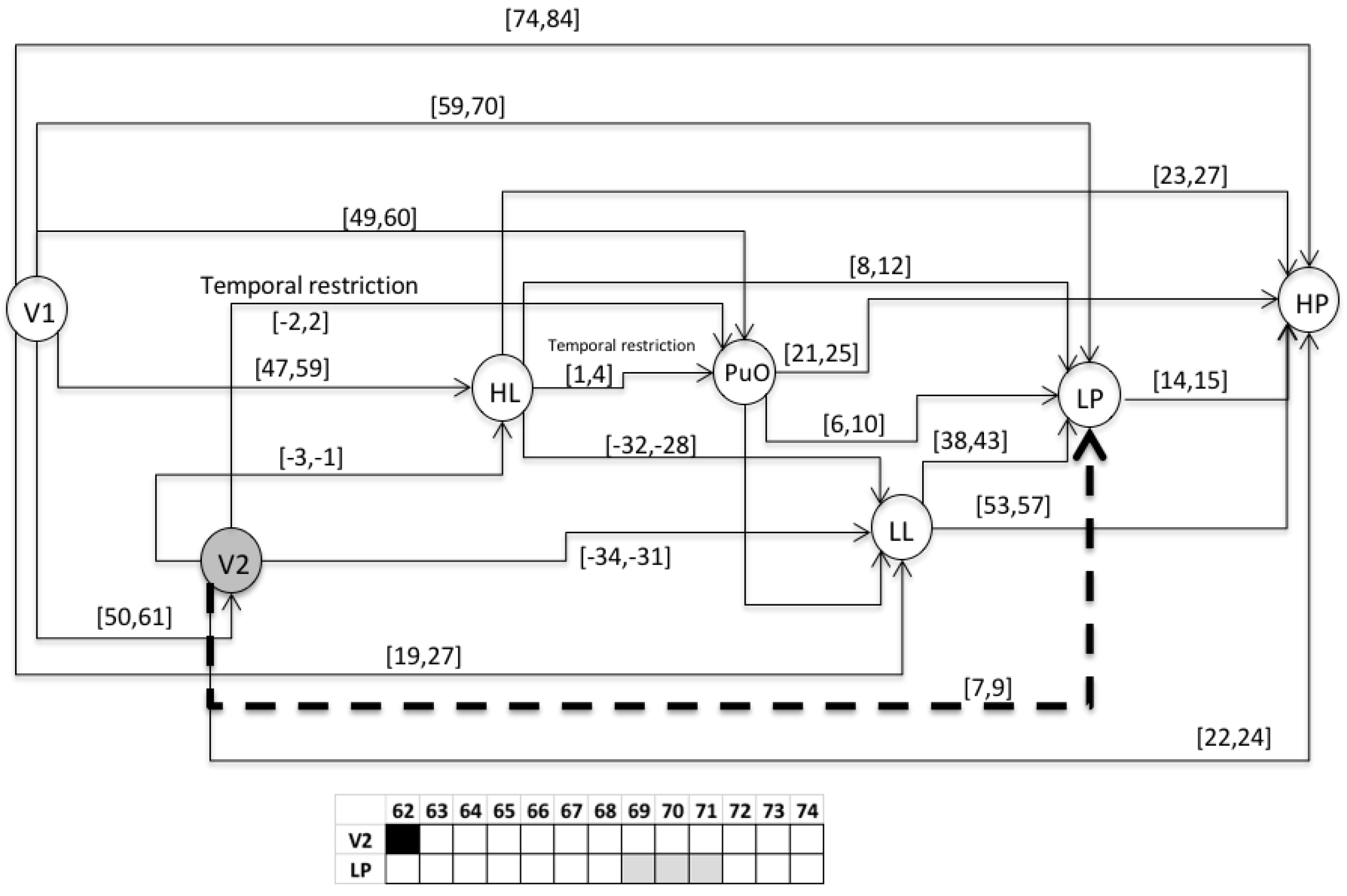
- S1 = 〈(V1,1); (L(L),21); (H(L),48); (PuO,50); (V2,51); (L(Po),60); (H(Po),75)〉
- S2 = 〈(V1,1); (L(L),25); (H(L),55); (V2,56); (PuO,57); (L((Po),63); (H(Po),78)〉
- S3 = 〈(V1,1); (L(L),28); (H(L),60); (PuO,61); (V2,62); (L(Po),71); (H(Po),85)〉
- For the variable of the level (L), the value of 0 corresponds to 0 m; each increase of 2 (vertical axis) corresponds to 2 m.
- For the variable of the pressure (Po), the value of 0 corresponds to 0 PSI; each increase of 2 (vertical axis) corresponds to 20 psi.
3.1.3. STEP 3: Chronicle Database Construction
3.2. Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brennan, R. Toward Real-Time Distributed Intelligent Control: A Survey of Research Themes and Applications. IEEE Trans. Syst. Man Cybern. 2007, 37, 744–765. [Google Scholar] [CrossRef]
- Zhang, J.; Khalgui, M.; Li, Z.; Frey, G.; Mosbahi, O.; Ben Salah, H. Reconfigurable Coordination of Distributed Discrete Event Control Systems. IEEE Trans. Control. Syst. Technol. 2014, 23, 323–330. [Google Scholar] [CrossRef]
- Reifer, D.J. Software Failure Modes and Effects Analysis. IEEE Trans. Reliab. 1979, 28, 247–249. [Google Scholar] [CrossRef]
- Morel, G.; Valckenaers, P.; Faure, J.-M.; Pereira, C.E.; Diedrich, C. Manufacturing Plant Control Challenges and Issues. Control. Eng. Pract. 2007, 15, 1321–1331. [Google Scholar] [CrossRef]
- Rodrigo, V.; Chioua, M.; Hagglund, T.; Hollender, M. Causal Analysis for Alarm Flood Reduction. IFAC-PapersOnLine 2016, 49, 723–728. [Google Scholar] [CrossRef]
- Bodsberg, L.; Hokstad, P. Alarm and Shutdown Frequencies in Offshore Production. IFAC Proc. Vol. 1988, 21, 19–25. [Google Scholar] [CrossRef]
- Agudelo, C.; Morant Anglada, F.; Quiles Cucarella, E.; Garca Moreno, E. Secuencias De Alarmas Para detección Y diagnóstico de fallos. Rev. Colomb. Comput. 2011, 12, 31–44. (In Spanish) [Google Scholar] [CrossRef]
- Izadi, I.; Shah, S.L.; Shook, D.S.; Chen, T. An Introduction to Alarm Analysis and Design. IFAC Proc. Vol. 2009, 42, 645–650. [Google Scholar] [CrossRef]
- Gómez, C.F.A. Integracion de Tecnicas y Las Secuencias de Alarmas Para la Deteccion y el Diagnostico de Fallos; Universitat Politecnica de Valencia: Valencia, Spain, 2016. [Google Scholar] [CrossRef][Green Version]
- Vásquez Capacho, J.W. Chronicle Based Alarm Management. Available online: https://hal.laas.fr/Tel-02059631 (accessed on 1 October 2017).
- Beebe, D.; Ferrer, S.; Logerot, D. The Connection of Peak Alarm Rates to Plant Incidents and What You Can Do to Minimize. Process. Saf. Prog. 2012, 32, 72–77. [Google Scholar] [CrossRef]
- Zhu, J.; Shu, Y.; Zhao, J.; Yang, F. A Dynamic Alarm Management Strategy for Chemical Process Transitions. J. Loss Prev. Process. Ind. 2014, 30, 207–218. [Google Scholar] [CrossRef]
- John, V.; Jorge, P.; Carlos, A.; Jose, J. Analysis of Alarm Management in Startups and Shutdowns for Oil Refining Processes. In Proceedings of the 2013 II International Congress of Engineering Mechatronics and Automation (CIIMA), Bogotá, Colombia, 23–25 October 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Willey, R.J. Layer of Protection Analysis. Procedia Eng. 2014, 84, 12–22. [Google Scholar] [CrossRef]
- Hokstad, P.; Corneliussen, K. Loss of Safety Assessment and the IEC 61508 Standard. Reliab. Eng. Syst. Saf. 2004, 83, 111–120. [Google Scholar] [CrossRef]
- Kościelny, J.; Bartyś, M. The Requirements for a New Layer in the Industrial Safety Systems. IFAC-PapersOnLine 2015, 48, 1333–1338. [Google Scholar] [CrossRef]
- Sklet, S. Safety Barriers: Definition, Classification, and Performance. J. Loss Prev. Process. Ind. 2006, 19, 494–506. [Google Scholar] [CrossRef]
- Dowell, A.M. Layer of Protection Analysis and Inherently Safer Processes. Process. Saf. Prog. 1999, 18, 214–220. [Google Scholar] [CrossRef]
- Vásquez, J.; Zuñiga, C.G.P.; Moriano, J.S.; Maldonado, Y.A.M.; Ospino, A. New Concept of Safeprocess Based on a Fault Detection Methodology: Super Alarms. IFAC-PapersOnLine 2019, 52, 231–236. [Google Scholar] [CrossRef]
- Vásquez Capacho, J.W.; Perez Zuñiga, C.G.; Muñoz Maldonado, Y.A.; Ospino Castro, A.J. An additional layer of protection through superalarms with diagnosis capability. CT&F Cienc. Tecnol. Futuro 2020, 10, 45–65. [Google Scholar] [CrossRef]
- Bayoudh, M.; Travé-Massuyès, L.; Olive, X. Hybrid Systems Diagnosis by Coupling Continuous and Discrete Event Techniques. IFAC Proc. Vol. 2008, 41, 7265–7270. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis with Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Vásquez, J.; Travé-Massuyès, L.; Subias, A.; Jimenez, F.; Agudelo, C. Alarm Management Based on Diagnosis. IFAC-PapersOnLine 2016, 49, 126–131. [Google Scholar] [CrossRef]
- Capacho, J.V.; Subias, A.; Travé-Massuyès, L.; Jimenez, F. Alarm Management via Temporal Pattern Learning. Eng. Appl. Artif. Intell. 2017, 65, 506–516. [Google Scholar] [CrossRef]
- Vásquez, J.W.; Travé-Massuyès, L.; Subias, A.; Jiménez, F.; Agudelo, C. Chronicle Based Alarm Management in Startup and Shutdown stages. In Proceedings of the 26th International Workshop on Principles of Diagnosis, Paris, France, 31 August–3 September 2015; pp. 277–280. Available online: https://hal.laas.fr/Hal-01847469 (accessed on 1 October 2017).
- Cordier, M.-O.; Dousson, C. Alarm Driven Monitoring Based on Chronicles. IFAC Proc. Vol. 2000, 33, 291–296. [Google Scholar] [CrossRef]
- Dousson, C. Suivi d’évolutions Et Reconnaissance De Chroniques. Ph.D. Thesis, Université de Toulouse, Toulouse, France, 1994. Available online: http://www.theses.fr/1994TOU30264 (accessed on 1 October 2017).
- Pons, R.; Subias, A.; Travé-Massuyès, L. Iterative Hybrid Causal Model Based Diagnosis: Application to Automotive Embedded Functions. Eng. Appl. Artif. Intell. 2015, 37, 319–335. [Google Scholar] [CrossRef]
- Vásquez, J.W.; Perez-Zuñiga, G.; Muñoz, Y.; Ospino, A. Simultaneous occurrences and false-positives analysis in discrete event dynamic systems. J. Comput. Sci. 2020, 44, 101162. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vásquez, J.W.; Pérez-Zuñiga, G.; Sotomayor-Moriano, J.; Ospino, A. Super-Alarms with Diagnosis Proficiency Used as an Additional Layer of Protection Applied to an Oil Transport System. Entropy 2021, 23, 139. https://doi.org/10.3390/e23020139
Vásquez JW, Pérez-Zuñiga G, Sotomayor-Moriano J, Ospino A. Super-Alarms with Diagnosis Proficiency Used as an Additional Layer of Protection Applied to an Oil Transport System. Entropy. 2021; 23(2):139. https://doi.org/10.3390/e23020139
Chicago/Turabian StyleVásquez, John W., Gustavo Pérez-Zuñiga, Javier Sotomayor-Moriano, and Adalberto Ospino. 2021. "Super-Alarms with Diagnosis Proficiency Used as an Additional Layer of Protection Applied to an Oil Transport System" Entropy 23, no. 2: 139. https://doi.org/10.3390/e23020139
APA StyleVásquez, J. W., Pérez-Zuñiga, G., Sotomayor-Moriano, J., & Ospino, A. (2021). Super-Alarms with Diagnosis Proficiency Used as an Additional Layer of Protection Applied to an Oil Transport System. Entropy, 23(2), 139. https://doi.org/10.3390/e23020139






