Electronic Wave-Packets in Integer Quantum Hall Edge Channels: Relaxation and Dissipative Effects
Abstract
1. Introduction
2. Model
2.1. “Strongly Interacting” Regime
2.2. “Moderately Interacting” Regime
3. Edge–Magnetoplasmon Scattering Matrix
- Injection region :In this region, one can assume , and the Hamiltonian density can be simply written asThe bosonic fields and propagate freely according to the equations of motion:By moving into a Fourier transform with respect to time, they becomewith field amplitudes in the frequency space defined as
- Interacting region :In this region, the Hamiltonian density is the one in Equation (1). According to the previous discussion, the bosonic fields and are no longer eigenstates of the Hamiltonian, and the system is diagonalized in terms of a charged and a dipole mode, indicated respectively with and , with the eigenvelocities and , as discussed above. In this case, the equations of motion arewhich, expressed in a Fourier transform with respect to time, becomeThe solution of the equations of motion in this region readswithand the (possibly frequency-dependent) amplitudes are achieved by imposing the continuity of the fields at (boundary between regions and ).
- Detection region :Analogously to what was discussed for region , also in this case, inter-channel interaction is negligible and the equations of motion are written as in Equation (11) . Here, imposing the continuity of the fields at (boundary between regions and ), we observe that the outgoing field amplitudes are related to the incoming ones through the relations
3.1. Dissipative Effects
3.2. General Form of the Scattering Matrix
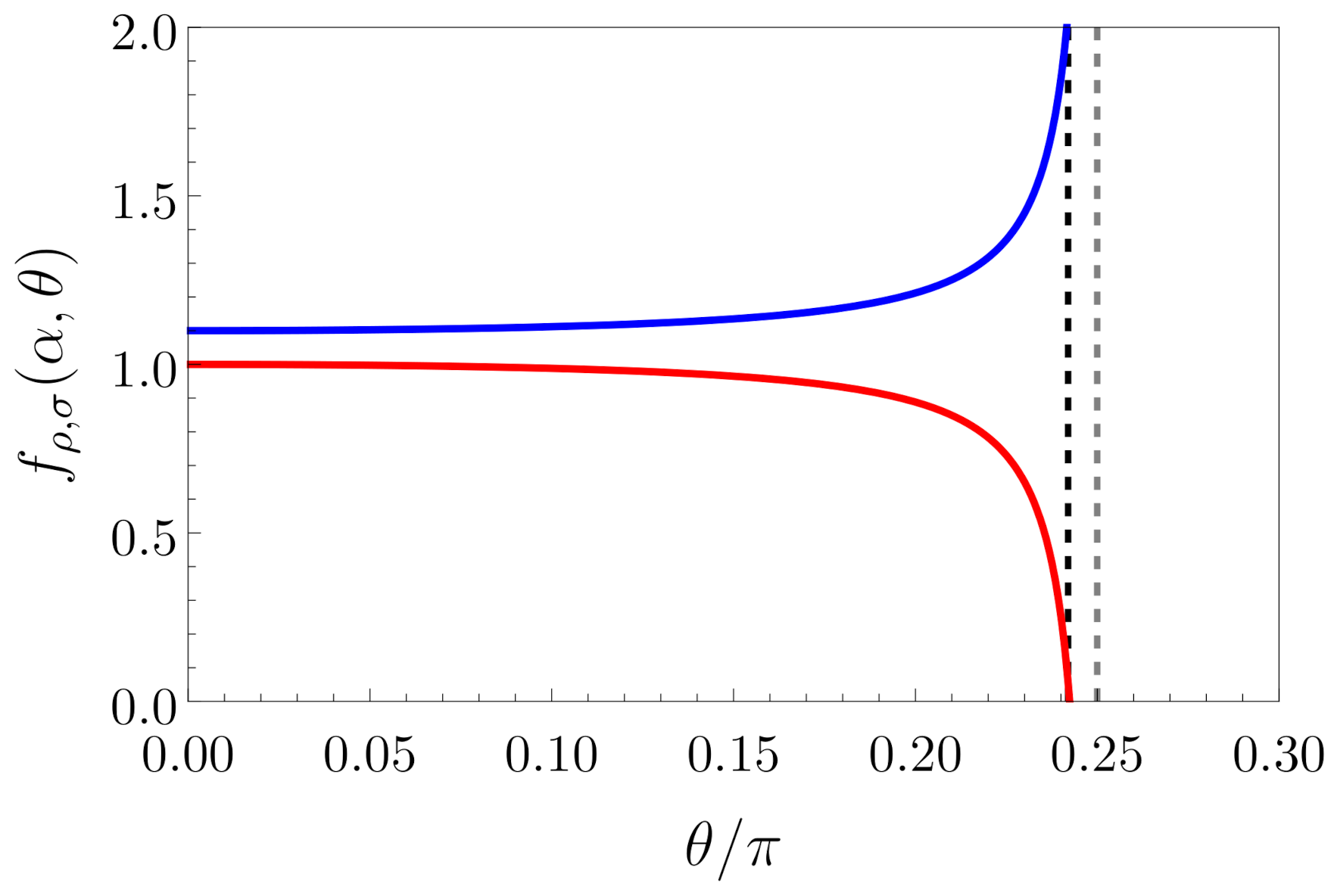
4. Elastic Scattering Amplitude
4.1. Non-Dissipative Case
4.2. Linear Dissipation
4.3. Quadratic Dissipation
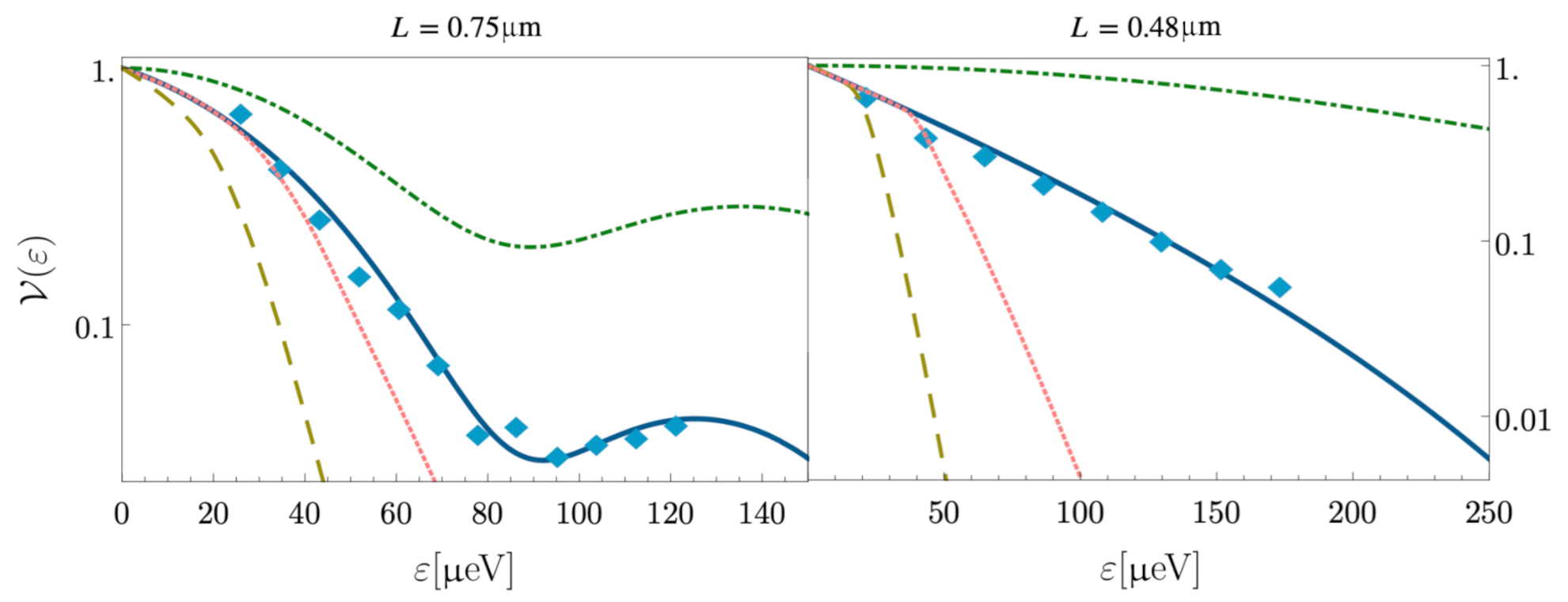
5. Comparison with Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QH | Quantum Hall |
| EQO | Electron Quantum Optics |
Appendix A. Calculation of the Elastic Scattering Amplitude
References
- Fève, G.; Mahé, A.; Berroir, J.-M.; Kontos, T.; Plaçais, B.; Glattli, D.C.; Cavanna, A.; Etienne, B.; Jin, Y. An on-demand coherent single-electron source. Science 2007, 316, 1169. [Google Scholar]
- Grenier, C.; Hervé, R.; Fève, G.; Degiovanni, P. Electron quantum optics in quantum Hall edge channels. Mod. Phys. Lett. B 2011, 25, 1053. [Google Scholar] [CrossRef]
- Bocquillon, E.; Freulon, V.; Parmentier, F.D.; Berroir, J.-M.; Plaçais, B.; Wahl, C.; Rech, J.; Jonckheere, T.; Martin, T.; Grenier, C.; et al. Electron quantum optics in ballistic chiral conductors. Ann. Phys. (Berl.) 2014, 526, 1. [Google Scholar] [CrossRef]
- Ferraro, D.; Jonckheere, T.; Rech, J.; Martin, T. Electronic quantum optics beyond the integer quantum Hall effect. Phys. Status Solidi B 2017, 254, 1600531. [Google Scholar] [CrossRef]
- Roussel, B.; Cabart, C.; Fève, G.; Thibierge, E.; Degiovanni, P. Electron quantum optics as quantum signal processing. Phys. Status Solidi B 2017, 254, 1600621. [Google Scholar] [CrossRef]
- Glattli, D.C.; Roulleau, P. Levitons for electron quantum optics. Phys. Status Solidi B 2017, 254, 1600650. [Google Scholar] [CrossRef]
- Bäuerle, C.; Glattli, D.C.; Meunier, T.; Portier, F.; Roche, P.; Roulleau, P.; Takada, S.; Waintal, X. Coherent control of single electrons: A review of current progress. Rep. Prog. Phys. 2018, 81, 056503. [Google Scholar] [CrossRef]
- Hanbury-Brown, R.; Twiss, R.Q. Correlation between photons in two coherent beams of light. Nature (Lond.) 1956, 177, 27. [Google Scholar] [CrossRef]
- Hong, C.K.; Ou, Z.Y.; Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 1987, 59, 2044. [Google Scholar] [CrossRef]
- Bocquillon, E.; Parmentier, F.D.; Grenier, C.; Berroir, J.-M.; Degiovanni, P.; Glattli, D.C.; Plaçais, B.; Cavanna, A.; Jin, Y.; Fève, G. Electron Quantum Optics: Partitioning Electrons One by One. Phys. Rev. Lett. 2012, 108, 196803. [Google Scholar] [CrossRef]
- Bocquillon, E.; Freulon, V.; Berroir, J.-M.; Degiovanni, P.; Plaçais, B.; Cavanna, A.; Jin, Y.; Fève, G. Coherence and Indistinguishability of Single Electrons Emitted by Independent Sources. Science 2013, 339, 1054. [Google Scholar] [CrossRef] [PubMed]
- Dubois, J.; Jullien, T.; Portier, F.; Roche, P.; Cavanna, A.; Jin, Y.; Wegscheider, W.; Roulleau, P.; Glattli, D.C. Minimal excitation states for electron quantum optics using levitons. Nature (Lond.) 2013, 502, 659. [Google Scholar] [CrossRef] [PubMed]
- Freulon, V.; Marguerite, A.; Berroir, J.-M.; Plaçais, B.; Cavanna, A.; Jin, Y.; Fève, G. Hong-Ou-Mandel experiment for temporal investigation of single-electron fractionalization. Nat. Comm. 2015, 6, 6854. [Google Scholar] [CrossRef] [PubMed]
- Marguerite, A.; Cabart, C.; Wahl, C.; Roussel, B.; Freulon, V.; Ferraro, D.; Grenier, C.; Berroir, J.-M.; Plaçais, B.; Jonckheere, T.; et al. Decoherence and relaxation of a single electron in a one-dimensional conductor. Phys. Rev. B 2016, 94, 115311. [Google Scholar] [CrossRef]
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys. Rev. Lett. 1982, 49, 405. [Google Scholar] [CrossRef]
- Yamamoto, M.; Takada, S.; Bäuerle, C.; Watanabe, K.; Wieck, A.D.; Tarucha, S. Electrical control of a solid-state flying qubit. Nat. Nanotechnol. 2012, 7, 247. [Google Scholar] [CrossRef]
- Bautze, T.; Süssmeier, C.; Takada, S.; Groth, C.; Meunier, T.; Yamamoto, M.; Tarucha, S.; Waintal, X.; Bäuerle, C. Theoretical, numerical, and experimental study of a flying qubit electronic interferometer. Phys. Rev. B 2014, 89, 125432. [Google Scholar] [CrossRef]
- Gaury, B.; Waintal, X. Dynamical control of interference using voltage pulses in the quantum regime. Nat. Commun. 2014, 5, 3844. [Google Scholar] [CrossRef]
- Di Vincenzo, D.P. The Physical Implementation of Quantum Computation. Fortschritte Der Phys. 2000, 48, 771. [Google Scholar] [CrossRef]
- Wahl, C.; Rech, J.; Jonckheere, T.; Martin, T. Interactions and Charge Fractionalization in an Electronic Hong-Ou-Mandel Interferometer. Phys. Rev. Lett. 2014, 112, 046802. [Google Scholar] [CrossRef]
- Ferraro, D.; Roussel, B.; Cabart, C.; Thibierge, E.; Fève, G.; Grenier, C.; Degiovanni, P. Real-Time Decoherence of Landau and Levitov Quasiparticles in Quantum Hall Edge Channels. Phys. Rev. Lett. 2014, 113, 166403. [Google Scholar] [CrossRef]
- Cabart, C.; Roussel, B.; Fève, G.; Degiovanni, P. Taming electronic decoherence in one-dimensional chiral ballistic quantum conductors. Phys. Rev. B 2018, 98, 155302. [Google Scholar] [CrossRef]
- Acciai, M.; Carrega, M.; Rech, J.; Jonckheere, T.; Martin, T.; Sassetti, M. Probing interactions via non-equilibrium momentum distribution and noise in integer quantum Hall systems at ν = 2. Phys. Rev. B 2018, 98, 035426. [Google Scholar] [CrossRef]
- Rebora, G.; Acciai, M.; Ferraro, D.; Sassetti, M. Collisional interferometry of levitons in quantum Hall edge channels at ν = 2. Phys. Rev. B 2020, 101, 245310. [Google Scholar] [CrossRef]
- Ferraro, D.; Rech, J.; Jonckheere, T.; Martin, T. Single quasiparticle and electron emitter in the fractional quantum Hall regime. Phys. Rev. B 2015, 91, 205409. [Google Scholar] [CrossRef]
- Rech, J.; Ferraro, D.; Jonckheere, T.; Vannucci, L.; Sassetti, M.; Martin, T. Minimal Excitations in the Fractional Quantum Hall Regime. Phys. Rev. Lett. 2017, 118, 076801. [Google Scholar] [CrossRef] [PubMed]
- Vannucci, L.; Ronetti, F.; Rech, J.; Ferraro, D.; Jonckheere, T.; Martin, T.; Sassetti, M. Minimal excitation states for heat transport in driven quantum Hall systems. Phys. Rev. B 2017, 95, 245415. [Google Scholar] [CrossRef]
- Ronetti, F.; Vannucci, L.; Ferraro, D.; Jonckheere, T.; Rech, J.; Martin, T.; Sassetti, M. Crystallization of levitons in the fractional quantum Hall regime. Phys. Rev. B 2018, 98, 075401. [Google Scholar] [CrossRef]
- Ferraro, D.; Ronetti, F.; Vannucci, L.; Acciai, M.; Rech, J.; Jockheere, T.; Martin, T.; Sassetti, M. Hong-Ou-Mandel characterization of multiply charged Levitons. Eur. Phys. J. Spec. Top. 2018, 227, 1345. [Google Scholar] [CrossRef]
- Ronetti, F.; Vannucci, L.; Ferraro, D.; Jonckheere, T.; Rech, J.; Martin, T.; Sassetti, M. Hong-Ou-Mandel heat noise in the quantum Hall regime. Phys. Rev. B 2019, 99, 205406. [Google Scholar] [CrossRef]
- Traverso Ziani, N.; Cavaliere, F.; Sassetti, M. Signatures of Wigner correlations in the conductance of a one-dimensional quantum dot coupled to an AFM tip. Phys. Rev. B 2012, 86, 125451. [Google Scholar] [CrossRef]
- Traverso Ziani, N.; Crepin, F.; Trauzettel, B. Fractional Wigner crystal in the Helical Luttinger Liquid. Phys. Rev. Lett. 2015, 115, 206402. [Google Scholar] [CrossRef] [PubMed]
- Kylänpää, I.; Cavaliere, F.; Traverso Ziani, N.; Sassetti, M.; Räsänen, E. Thermal effects on the Wigner localization and Friedel oscillations in many-electron nanowires. Phys. Rev. B 2016, 94, 115417. [Google Scholar] [CrossRef]
- Porta, S.; Gambetta, F.M.; Cavaliere, F.; Traverso Ziani, N.; Sassetti, M. Out-of-equilibrium density dynamics of a quenched fermionic system. Phys. Rev. B 2016, 94, 085122. [Google Scholar] [CrossRef]
- Dolcetto, G.; Sassetti, M.; Schmidt, T.L. Edge physics in two-dimensional topological insulators. Riv. Del Nuovo C. 2016, 39, 113. [Google Scholar]
- Fève, G.; Degiovanni, P.; Jolicoeur, T. Quantum detection of electronic flying qubits in the integer quantum Hall regime. Phys. Rev. B 2008, 77, 035308. [Google Scholar] [CrossRef]
- Jacak, J.E. Application of path-integral quantization to indistinguishable particle systems topologically confined by a magnetic field. Phys. Rev. A 2018, 97, 012108. [Google Scholar] [CrossRef]
- Altimiras, C.; Le Sueur, H.; Gennser, U.; Cavanna, A.; Mailly, D.; Pierre, F. Non-equilibrium edge-channel spectroscopy in the integer quantum Hall regime. Nat. Phys. 2009, 6, 34. [Google Scholar] [CrossRef]
- le Sueur, H.; Altimiras, C.; Gennser, U.; Cavanna, A.; Mailly, D.; Pierre, F. Energy Relaxation in the Integer Quantum Hall Regime. Phys. Rev. Lett. 2010, 105, 056803. [Google Scholar] [CrossRef]
- Degiovanni, P.; Grenier, C.; Fève, G.; Altimiras, C.; Le Sueur, H.; Pierre, F. Plasmon scattering approach to energy exchange and high-frequency noise in ν = 2 quantum Hall edge channels. Phys. Rev. B 2010, 81, 121302(R). [Google Scholar] [CrossRef]
- Lunde, A.M.; Nigg, S.E.; Büttiker, M. Interaction-induced edge channel equilibration. Phys. Rev. B 2010, 81, 041311(R). [Google Scholar] [CrossRef]
- Kovrizhin, D.L.; Chalker, J.T. Relaxation in Driven Integer Quantum Hall Edge States. Phys. Rev. Lett. 2012, 109, 106403. [Google Scholar] [CrossRef] [PubMed]
- Bocquillon, E.; Freulon, V.; Berroir, J.-M.; Degiovanni, P.; Plaçais, B.; Cavanna, A.; Jin, Y.; Fève, G. Separation of neutral and charge modes in one-dimensional chiral edge channels. Nat. Commun. 2013, 4, 1839. [Google Scholar] [CrossRef]
- Rodriguez, R.H.; Parmentier, F.D.; Ferraro, D.; Roulleau, P.; Gennser, U.; Cavanna, A.; Sassetti, M.; Portier, F.; Mailly, D.; Roche, P. Relaxation and revival of quasiparticles injected in an interacting quantum Hall liquid. Nat. Commun. 2020, 11, 2426. [Google Scholar] [CrossRef] [PubMed]
- Goremykina, A.S.; Borin, A.; Sukhorukov, E.V. Heat current in a dissipative quantum Hall edge. arXiv 2019, arXiv:1908.01213. [Google Scholar]
- Krähenmann, T.; Fischer, S.G.; Röösli, M.; Ihn, T.; Reichl, C.; Wegscheider, W.; Ensslin, K.; Gefen, Y.; Meir, Y. Auger-spectroscopy in quantum Hall edge channels and the missing energy problem. Nat. Commun. 2019, 10, 3915. [Google Scholar] [CrossRef]
- Wen, X.-G. Topological orders and edge excitations in fractional quantum Hall states. Adv. Phys. 1995, 44, 405. [Google Scholar] [CrossRef]
- Braggio, A.; Ferraro, D.; Carrega, M.; Magnoli, N.; Sassetti, M. Environmental induced renormalization effects in quantum Hall edge states. New J. Phys. 2012, 14, 093032. [Google Scholar] [CrossRef]
- Levkivskyi, I.P.; Sukhorukov, E.V. Dephasing in the electronic Mach-Zehnder interferometer at filling factor ν = 2. Phys. Rev. B 2008, 78, 045322. [Google Scholar] [CrossRef]
- Slobodeniuk, A.O.; Idrisov, E.G.; Sukhorukov, E.V. Relaxation of an electron wave packet at the quantum Hall edge at filling factor ν = 2. Phys. Rev. B 2016, 93, 035421. [Google Scholar] [CrossRef]
- Ferraro, D.; Sukhorukov, E.V. Interaction effects in a multi-channel Fabry-Perot interferometer in the Aharonov-Bohm regime. Sci. Post Phys. 2017, 3, 014. [Google Scholar] [CrossRef]
- Tewari, S.; Roulleau, P.; Grenier, C.; Portier, F.; Cavanna, A.; Gennser, U.; Mailly, D.; Roche, P. Robust quantum coherence above the Fermi sea. Phys. Rev. B 2016, 93, 035420. [Google Scholar] [CrossRef]
- Goremykina, A.S.; Sukhorukov, E.V. Coherence recovery mechanisms of quantum Hall edge states. Phys. Rev. B 2018, 97, 115418. [Google Scholar] [CrossRef]
- Degiovanni, P.; Grenier, C.; Fève, G. Decoherence and relaxation of single-electron excitations in quantum Hall edge channels. Phys. Rev. B 2009, 80, 241307(R). [Google Scholar] [CrossRef]
- Ferraro, D.; Braggio, A.; Magnoli, N.; Sassetti, M. Neutral modes’ edge state dynamics through quantum point contacts. New J. Phys. 2010, 12, 013012. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rebora, G.; Ferraro, D.; Rodriguez, R.H.; Parmentier, F.D.; Roche, P.; Sassetti, M. Electronic Wave-Packets in Integer Quantum Hall Edge Channels: Relaxation and Dissipative Effects. Entropy 2021, 23, 138. https://doi.org/10.3390/e23020138
Rebora G, Ferraro D, Rodriguez RH, Parmentier FD, Roche P, Sassetti M. Electronic Wave-Packets in Integer Quantum Hall Edge Channels: Relaxation and Dissipative Effects. Entropy. 2021; 23(2):138. https://doi.org/10.3390/e23020138
Chicago/Turabian StyleRebora, Giacomo, Dario Ferraro, Ramiro H. Rodriguez, François D. Parmentier, Patrice Roche, and Maura Sassetti. 2021. "Electronic Wave-Packets in Integer Quantum Hall Edge Channels: Relaxation and Dissipative Effects" Entropy 23, no. 2: 138. https://doi.org/10.3390/e23020138
APA StyleRebora, G., Ferraro, D., Rodriguez, R. H., Parmentier, F. D., Roche, P., & Sassetti, M. (2021). Electronic Wave-Packets in Integer Quantum Hall Edge Channels: Relaxation and Dissipative Effects. Entropy, 23(2), 138. https://doi.org/10.3390/e23020138






