An Improved Moth-Flame Optimization Algorithm with Adaptation Mechanism to Solve Numerical and Mechanical Engineering Problems
Abstract
:1. Introduction
2. Related Works
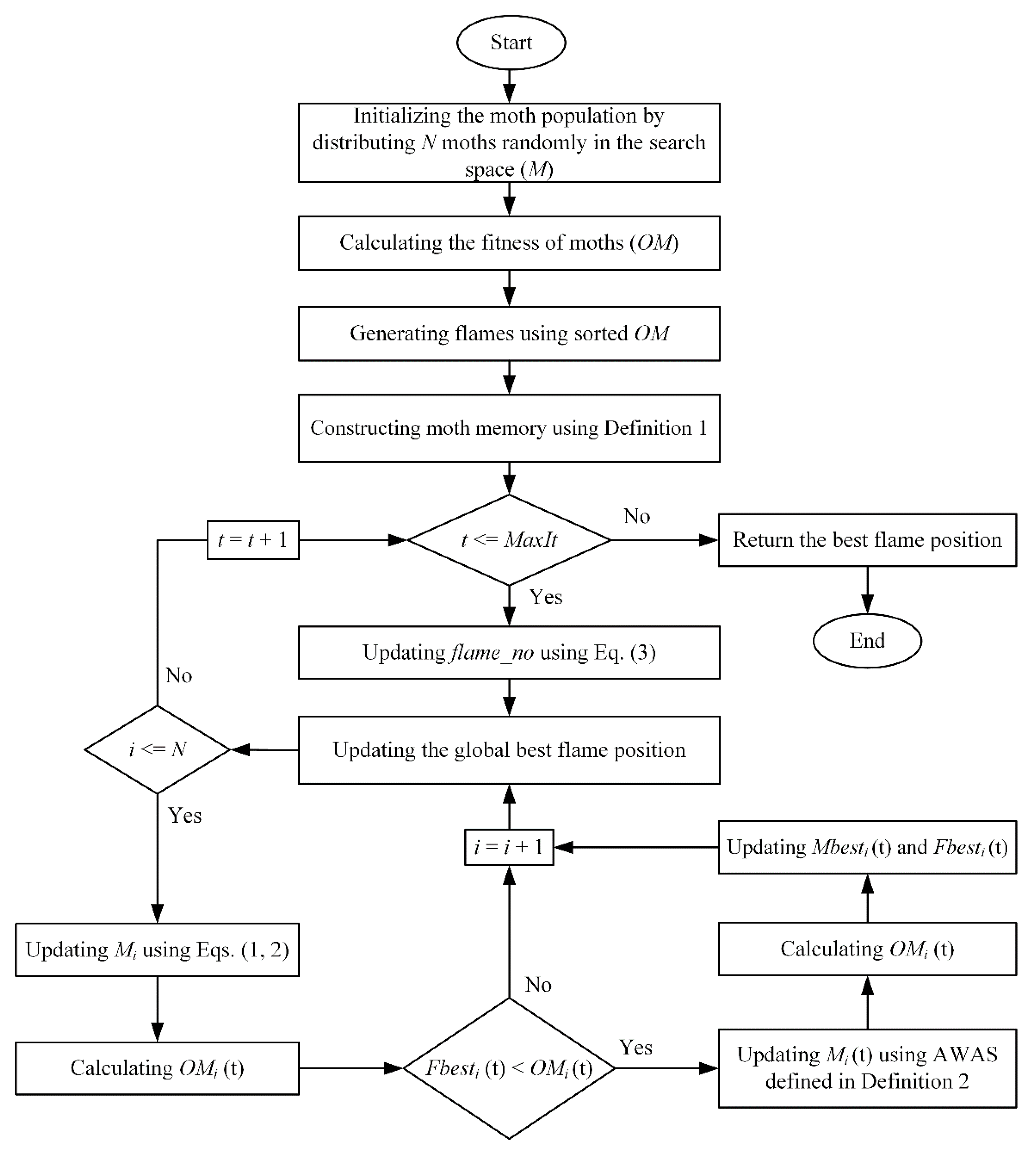
3. Proposed Algorithm
| Algorithm 1. The pseudo-code of I-MFO | |
| Algorithm of improved moth-flame optimization (I-MFO) | |
| Input: Maximum iterations (MaxIt), Number of moths (N), and Dimension size (D). | |
| Output: The best flame position and its fitness value. | |
| 1 | Begin |
| 2 | Randomly distributing M moths in the D-dimensional search space. |
| 3 | Calculating moths’ fitness (OM). |
| 4 | Set t = 1. |
| 5 | OF ← sort (OM). |
| 6 | F ← sort (M). |
| 7 | Defining the moth memory Mbest and Fbest using Definition 1. |
| 8 | While t ≤ MaxIt |
| 9 | Updating F and OF by the best N moths from F and current M. |
| 10 | Updating flame_no using Equation (3) |
| 11 | For i = 1: N |
| 12 | Computing the distance between moth Mi (t) and flame Fj (t) using Equation (2). |
| 13 | Updating the position of Mi (t) using Equation (1). |
| 14 | Computing the fitness value of Mi (t) and update OMi (t). |
| 15 | If Fbesti (t) < OMi (t) |
| 16 | Selecting a random moth Mr (t). |
| 17 | Updating the position of Mi (t) using AWAS defined in Definition 2. |
| 18 | Updating the fitness value OMi (t). |
| 19 | End if |
| 20 | Updating the moth memory Mi using Definition 1. |
| 21 | End for |
| 22 | Updating the position and fitness value of the global best flame. |
| 23 | t = t + 1. |
| 24 | End while |
4. Numerical Experiment and Analysis
4.1. Benchmark Test Functions and Experimental Environment
4.2. Exploitation and Exploration Analysis
4.3. Local Optima Avoidance Evaluation
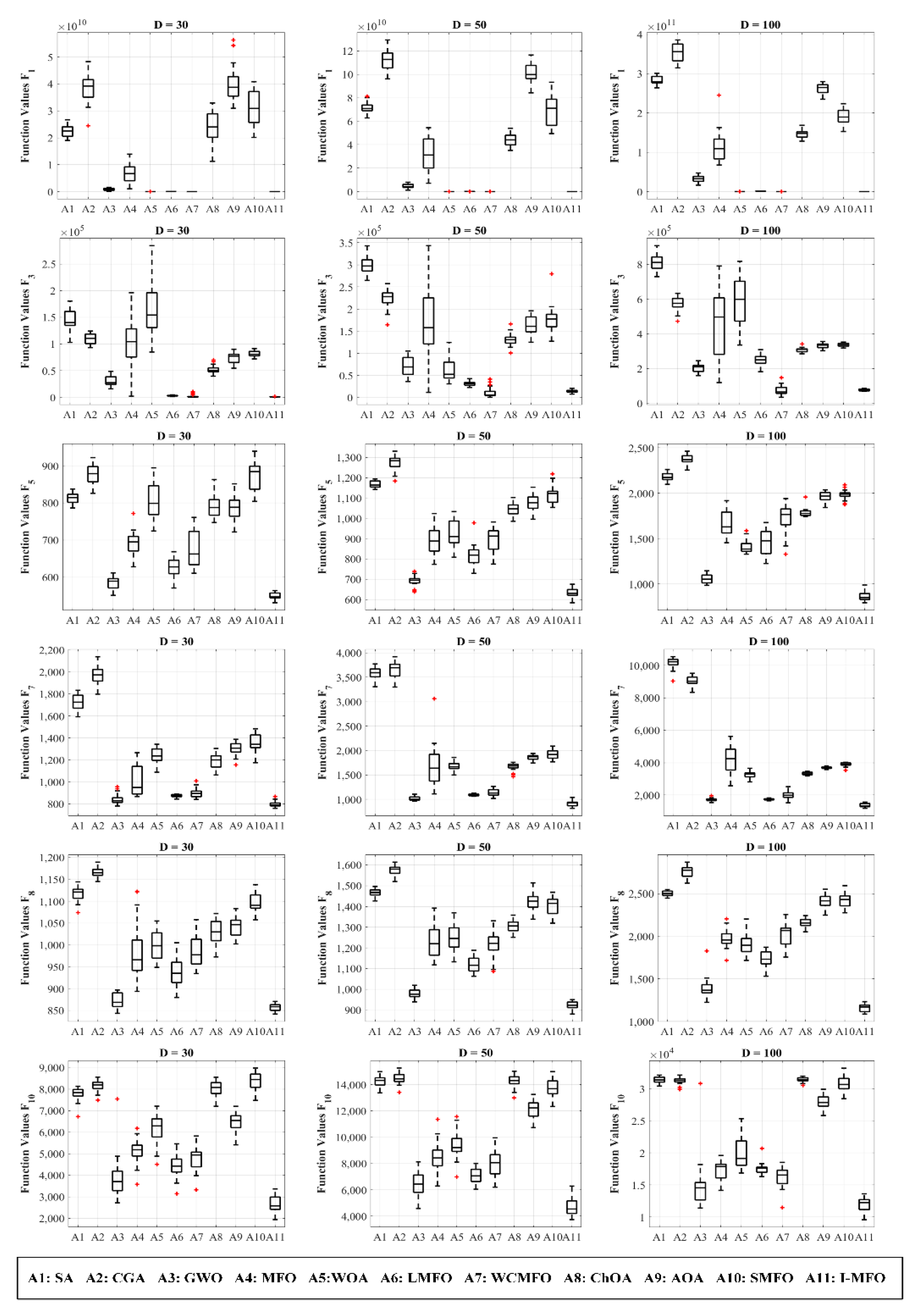
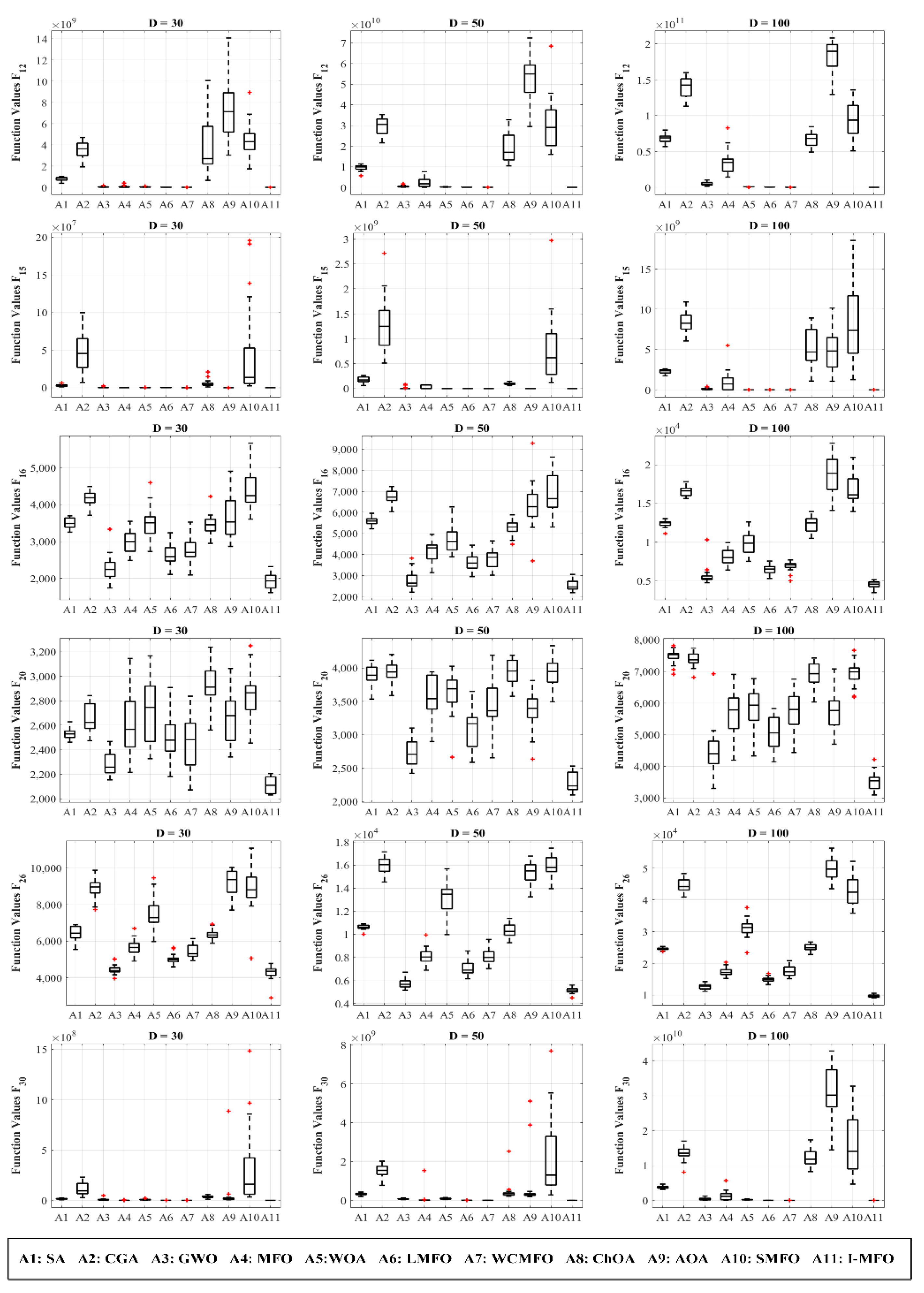
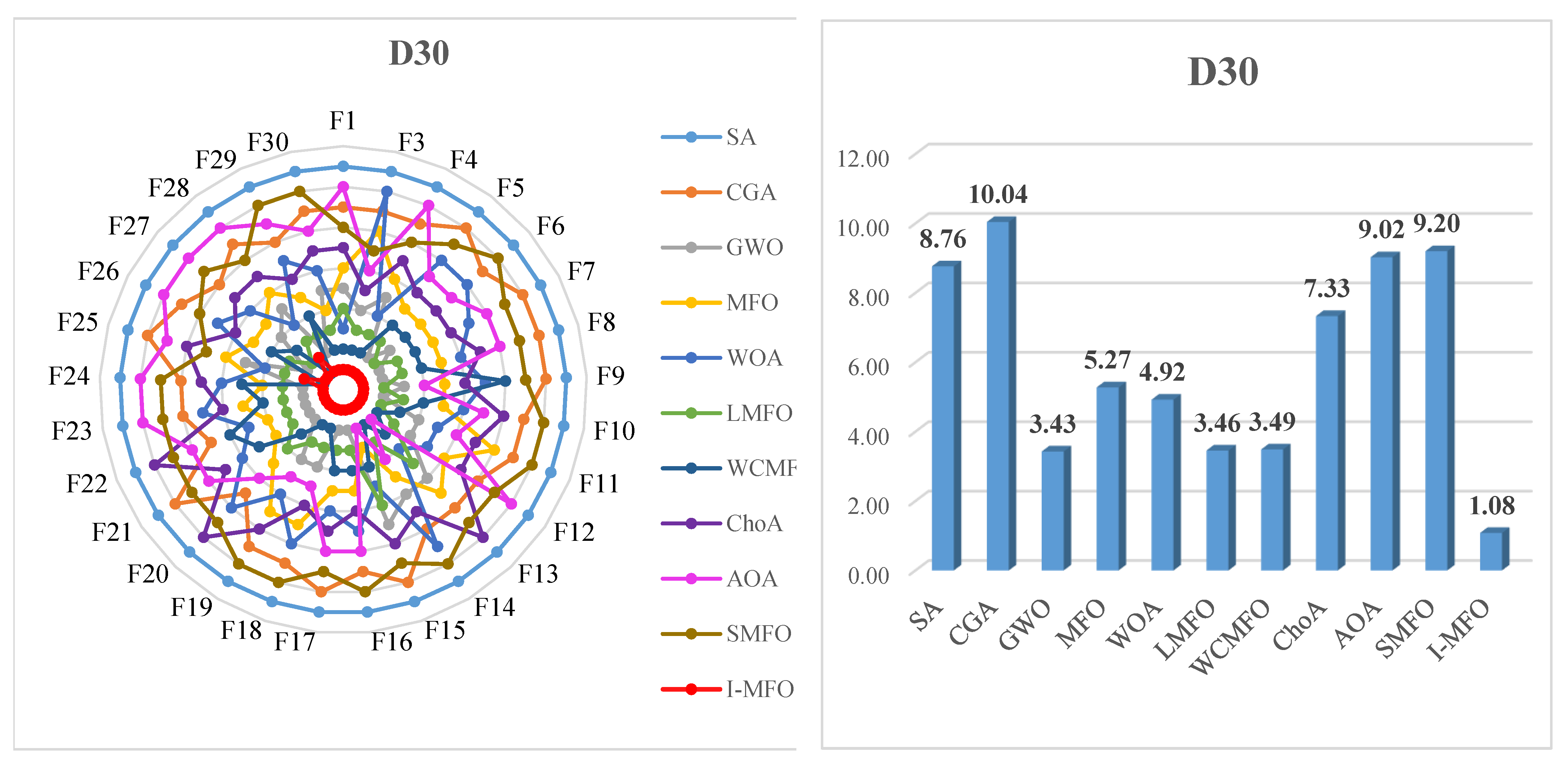
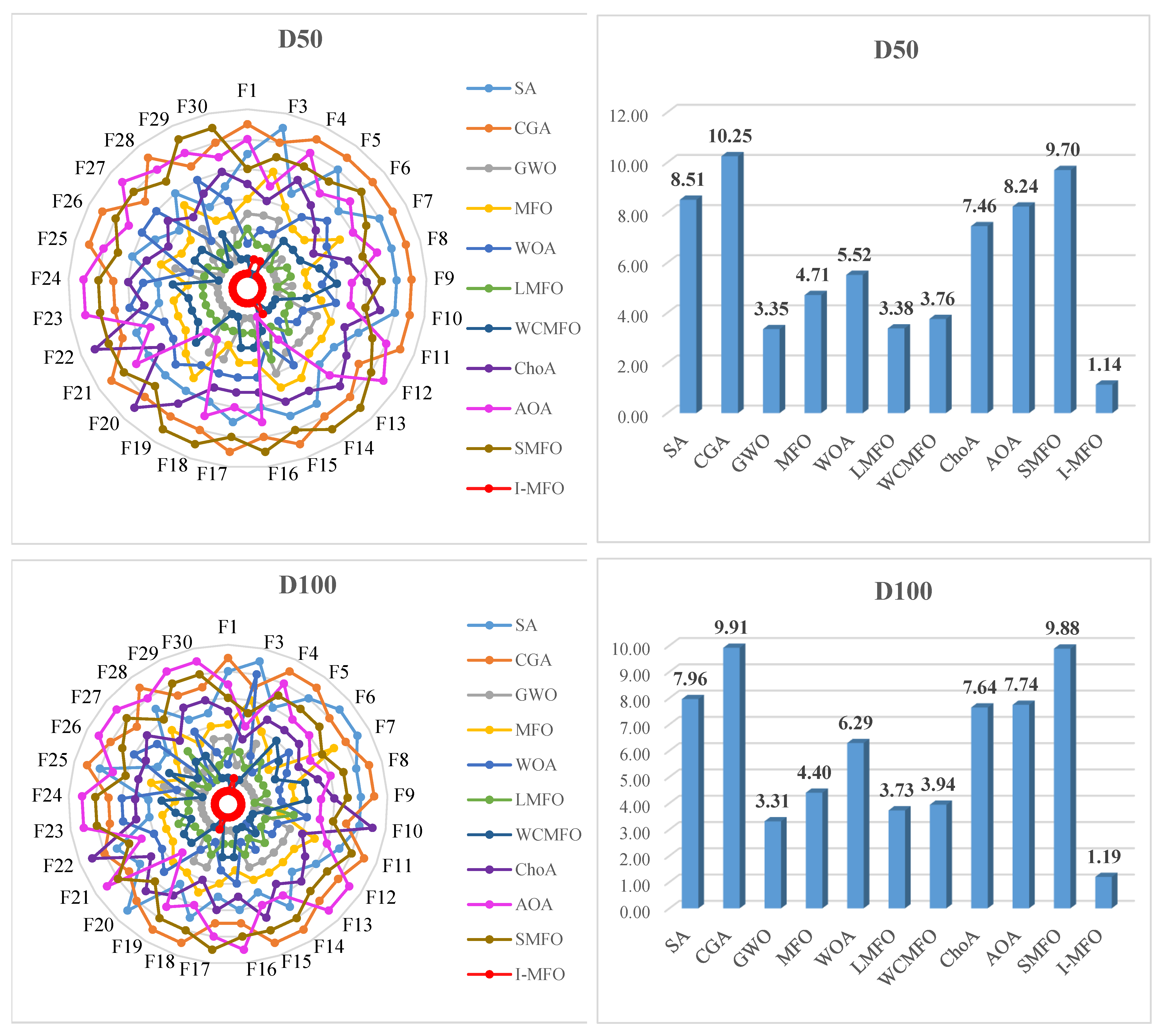
4.4. I-MFO Overall Effectiveness
4.5. Convergence Behavior Analysis
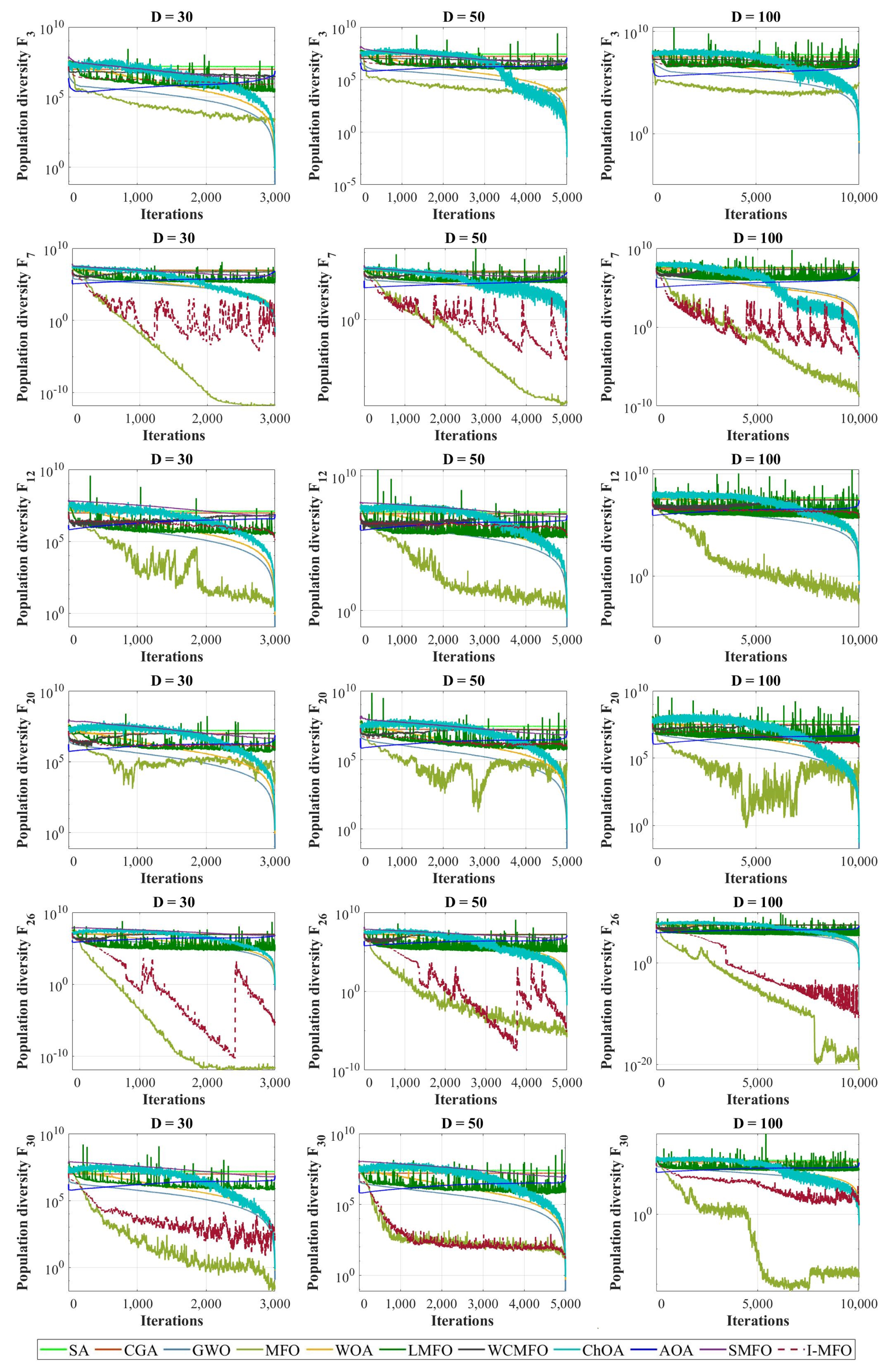
4.6. Population Diversity Analysis
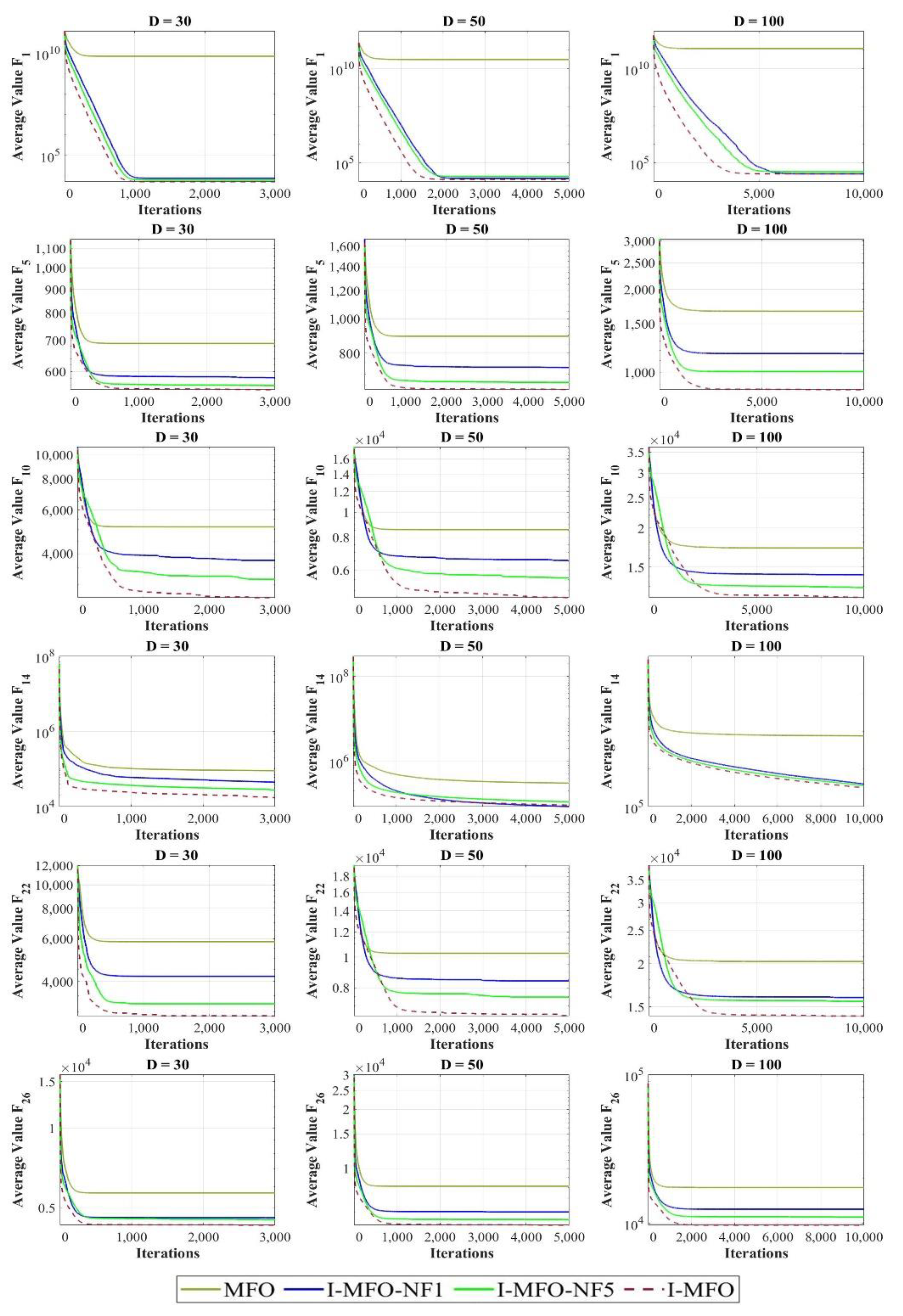
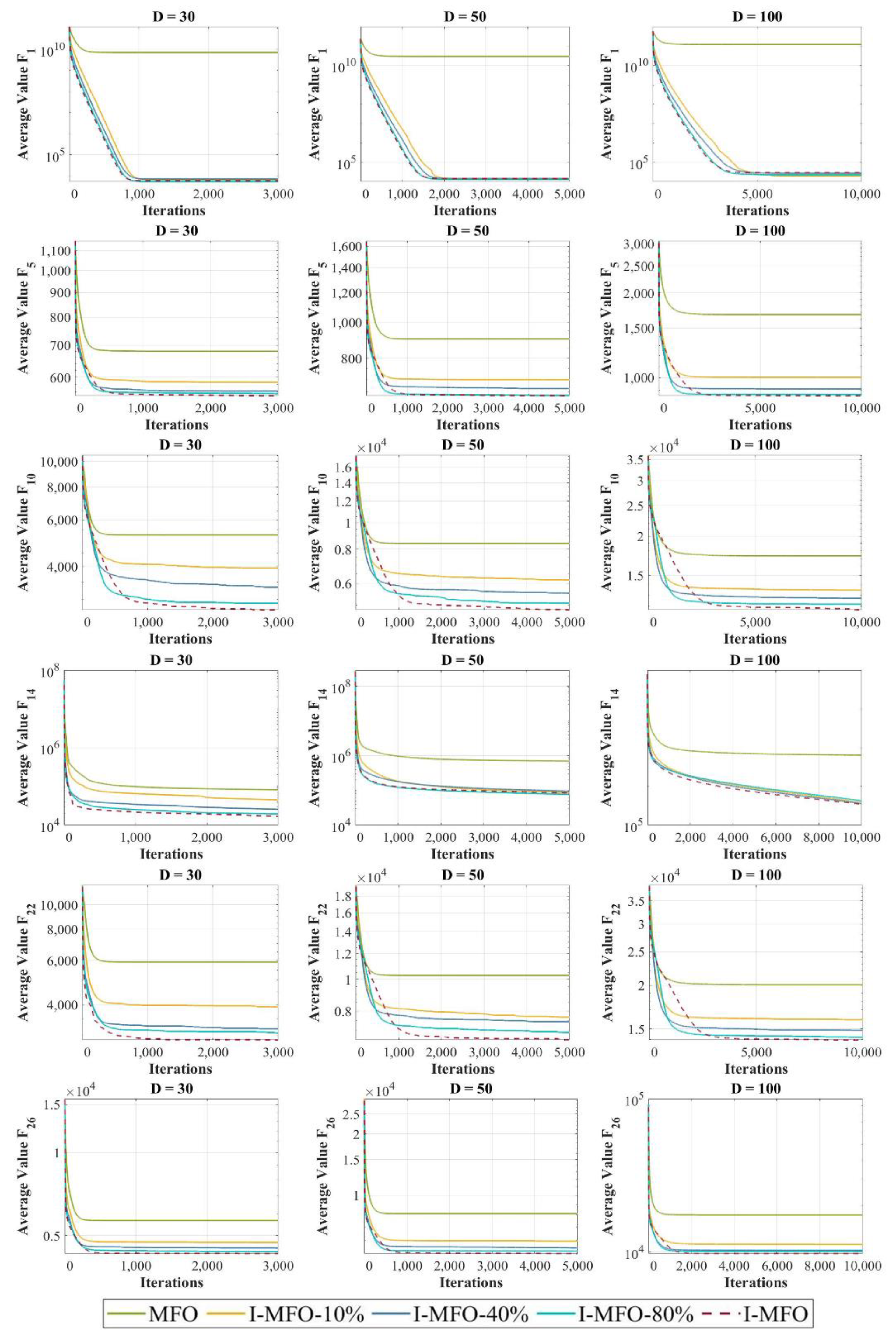
4.7. Sensitivity Analysis on the Number of Flight (NF) Parameter
4.8. Impact Analysis of Applying AWAS Strategy
5. Statistical Analysis
5.1. Non-Parametric Friedman Test
5.2. Post Hoc Analysis
6. Applicability of I-MFO Algorithm to Solve Mechanical Engineering Problems
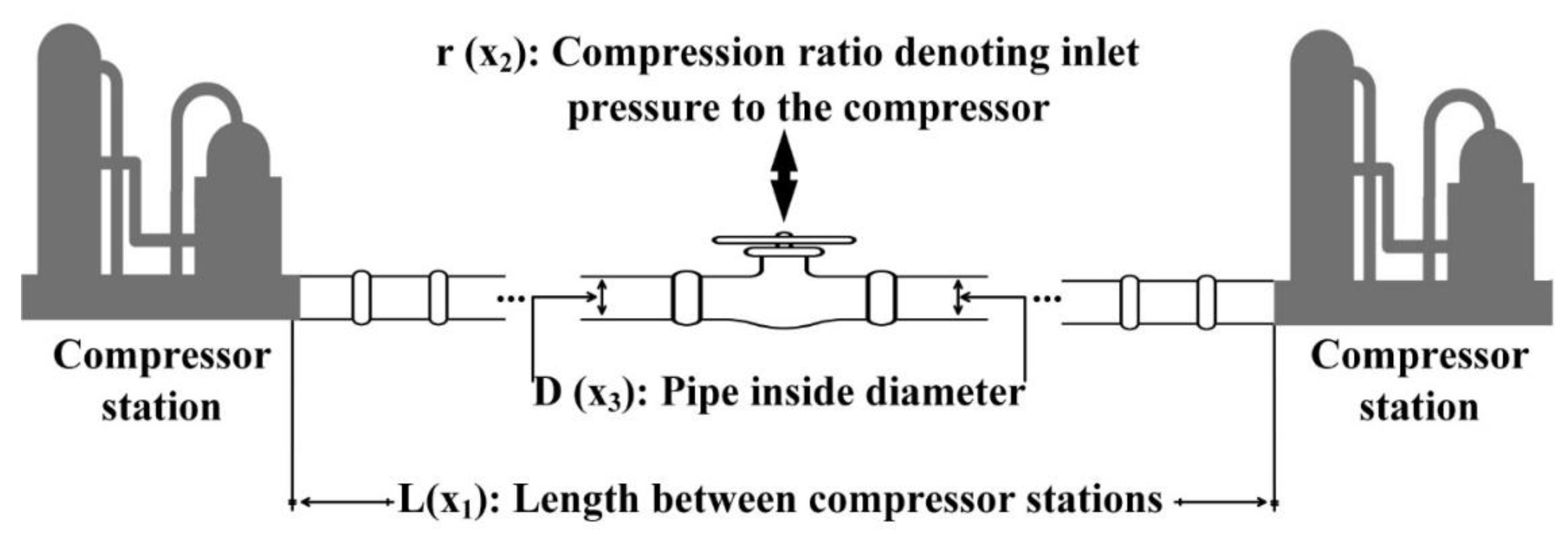
- P1: Gas transmission compressor design problem
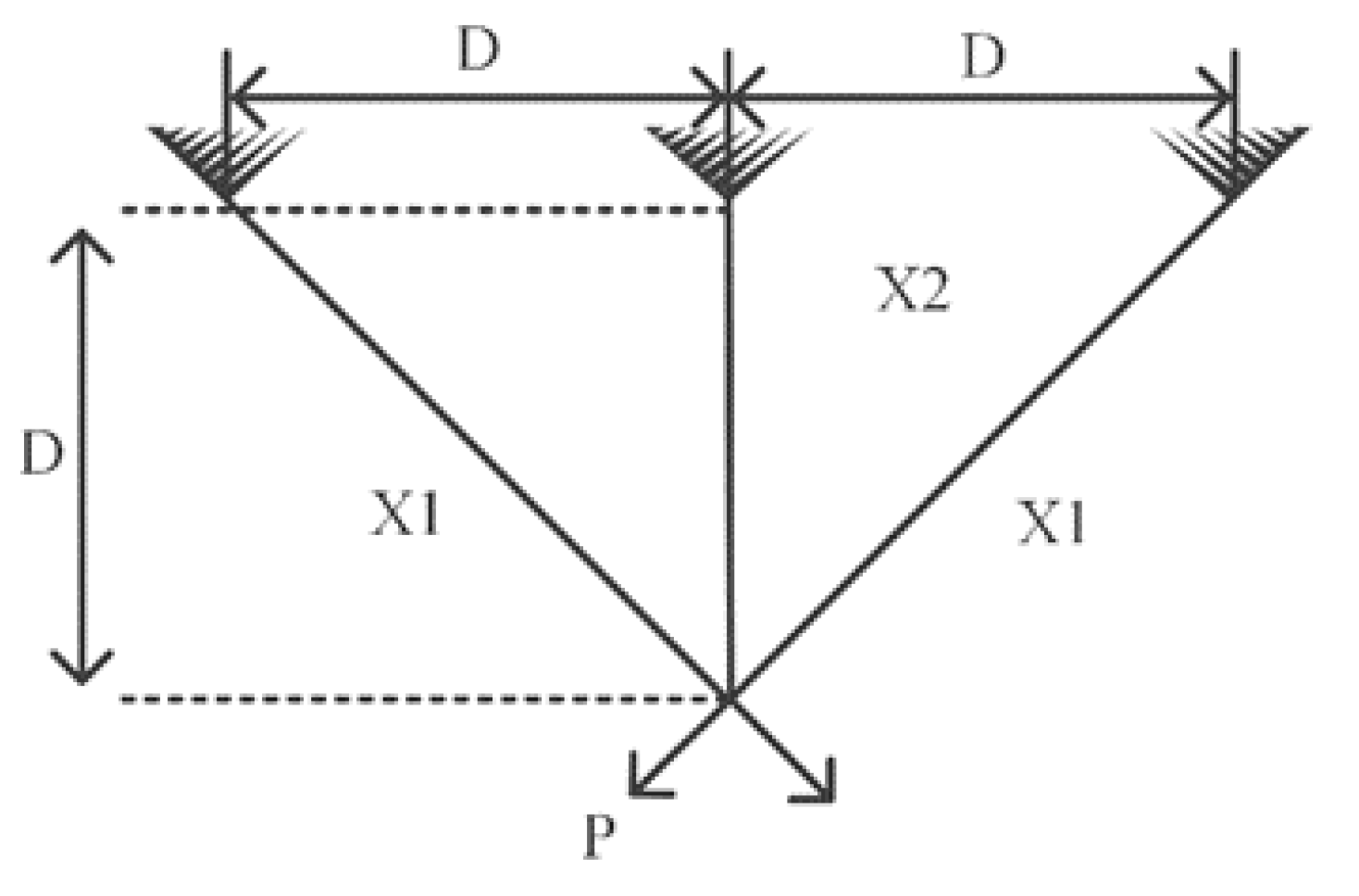
- P2: Three-bar truss problem
- P3: Tension/compression spring design problem
7. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Del Ser, J.; Osaba, E.; Molina, D.; Yang, X.; Salcedo-Sanz, S.; Camacho, D.; Das, S.; Suganthan, P.; Coello, C.C.; Herrera, F. Bio-inspired computation: Where we stand and what’s next. Swarm Evol. Comput 2019, 48, 220–250. [Google Scholar] [CrossRef]
- Talbi, E.-G. Metaheuristics: From Design to Implementation; John Wiley & Sons: New York, NY, USA, 2009; Volume 74. [Google Scholar]
- Kar, A.K. Bio inspired computing—A review of algorithms and scope of applications. Expert Syst. Appl. 2016, 59, 20–32. [Google Scholar] [CrossRef]
- Dezfouli, M.B.; Nadimi-Shahraki, M.H.; Zamani, H. A novel tour planning model using big data. In Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018; pp. 1–6. [Google Scholar]
- Zahrani, H.K.; Nadimi-Shahraki, M.H.; Sayarshad, H.R. An intelligent social-based method for rail-car fleet sizing problem. J. Rail Transp. Plan. Manag. 2021, 17, 100231. [Google Scholar] [CrossRef]
- Javadian, N.; Sayarshad, H.R.; Najafi, S. Using simulated annealing for determination of the capacity of yard stations in a railway industry. Appl. Soft Comput. 2011, 11, 1899–1907. [Google Scholar] [CrossRef]
- Sayarshad, H.R.; Javadian, N.; Tavakkoli-Moghaddam, R.; Forghani, N. Solving multi-objective optimization formulation for fleet planning in a railway industry. Ann. Oper. Res. 2010, 181, 185–197. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S. A multi-objective optimization algorithm for feature selection problems. Eng. Comput. 2021, 1–19. [Google Scholar] [CrossRef]
- Ewees, A.A.; Al-qaness, M.A.A.; Abualigah, L.; Oliva, D.; Algamal, Z.Y.; Anter, A.M.; Ali Ibrahim, R.; Ghoniem, R.M.; Abd Elaziz, M. Boosting Arithmetic Optimization Algorithm with Genetic Algorithm Operators for Feature Selection: Case Study on Cox Proportional Hazards Model. Mathematics 2021, 9, 2321. [Google Scholar] [CrossRef]
- Mienye, I.D.; Sun, Y. Improved Heart Disease Prediction Using Particle Swarm Optimization Based Stacked Sparse Autoencoder. Electronics 2021, 10, 2347. [Google Scholar] [CrossRef]
- Taghian, S.; Nadimi-Shahraki, M.H.; Zamani, H. Comparative analysis of transfer function-based binary Metaheuristic algorithms for feature selection. In Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018; pp. 1–6. [Google Scholar]
- Zamani, H.; Nadimi-Shahraki, M.H. Swarm intelligence approach for breast cancer diagnosis. Int. J. Comput. Appl. 2016, 151, 40–44. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H. Feature selection based on whale optimization algorithm for diseases diagnosis. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 1243. [Google Scholar]
- Ibrahim, R.A.; Abualigah, L.; Ewees, A.A.; Al-Qaness, M.A.; Yousri, D.; Alshathri, S.; Abd Elaziz, M. An Electric Fish-Based Arithmetic Optimization Algorithm for Feature Selection. Entropy 2021, 23, 1189. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Shi, R.; Dong, J. A Hybridization of Dragonfly Algorithm Optimization and Angle Modulation Mechanism for 0-1 Knapsack Problems. Entropy 2021, 23, 598. [Google Scholar] [CrossRef]
- Lee, J.; Park, J.; Kim, H.-C.; Kim, D.-W. Competitive Particle Swarm Optimization for Multi-Category Text Feature Selection. Entropy 2019, 21, 602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nadimi-Shahraki, M.H.; Moeini, E.; Taghian, S.; Mirjalili, S. DMFO-CD: A Discrete Moth-Flame Optimization Algorithm for Community Detection. Algorithms 2021, 14, 314. [Google Scholar] [CrossRef]
- Alsalibi, B.; Abualigah, L.; Khader, A.T. A novel bat algorithm with dynamic membrane structure for optimization problems. Appl. Intell. 2021, 51, 1992–2017. [Google Scholar] [CrossRef]
- Asghari, K.; Masdari, M.; Gharehchopogh, F.S.; Saneifard, R. A chaotic and hybrid gray wolf-whale algorithm for solving continuous optimization problems. Prog. Artif. Intell. 2021, 10, 349–374. [Google Scholar] [CrossRef]
- Goldanloo, M.J.; Gharehchopogh, F.S. A hybrid OBL-based firefly algorithm with symbiotic organisms search algorithm for solving continuous optimization problems. J. Supercomput. 2021, 1–34. [Google Scholar] [CrossRef]
- Zaman, H.R.R.; Gharehchopogh, F.S. An improved particle swarm optimization with backtracking search optimization algorithm for solving continuous optimization problems. Eng. Comput. 2021, 1–35. [Google Scholar] [CrossRef]
- Doumari, S.A.; Givi, H.; Dehghani, M.; Montazeri, Z.; Leiva, V.; Guerrero, J.M. A New Two-Stage Algorithm for Solving Optimization Problems. Entropy 2021, 23, 491. [Google Scholar] [CrossRef] [PubMed]
- Abd Elaziz, M.; Elsheikh, A.H.; Oliva, D.; Abualigah, L.; Lu, S.; Ewees, A.A. Advanced Metaheuristic Techniques for Mechanical Design Problems. Arch. Comput. Methods Eng. 2021, 1–22. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. Artificial bee colony algorithm for large-scale problems and engineering design optimization. J. Intell. Manuf. 2012, 23, 1001–1014. [Google Scholar] [CrossRef]
- Aloui, M.; Hamidi, F.; Jerbi, H.; Omri, M.; Popescu, D.; Abbassi, R. A Chaotic Krill Herd Optimization Algorithm for Global Numerical Estimation of the Attraction Domain for Nonlinear Systems. Mathematics 2021, 9, 1743. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Farnad, B.; Alizadeh, A. A farmland fertility algorithm for solving constrained engineering problems. Concurr. Comput. Pract. Exp. 2021, 33, e6310. [Google Scholar] [CrossRef]
- Ivanov, O.; Neagu, B.-C.; Grigoraș, G.; Scarlatache, F.; Gavrilaș, M. A Metaheuristic Algorithm for Flexible Energy Storage Management in Residential Electricity Distribution Grids. Mathematics 2021, 9, 2375. [Google Scholar] [CrossRef]
- Wang, S.; Jia, H.; Abualigah, L.; Liu, Q.; Zheng, R. An Improved Hybrid Aquila Optimizer and Harris Hawks Algorithm for Solving Industrial Engineering Optimization Problems. Processes 2021, 9, 1551. [Google Scholar] [CrossRef]
- Ziadeh, A.; Abualigah, L.; Abd Elaziz, M.; Şahin, C.B.; Almazroi, A.A.; Omari, M. Augmented grasshopper optimization algorithm by differential evolution: A power scheduling application in smart homes. Multimed. Tools Appl. 2021, 80, 31569–31597. [Google Scholar] [CrossRef]
- Varaee, H.; Ghasemi, M.R. Engineering optimization based on ideal gas molecular movement algorithm. Eng. Comput. 2017, 33, 71–93. [Google Scholar] [CrossRef]
- Ghasemi, M.R.; Varaee, H. A fast multi-objective optimization using an efficient ideal gas molecular movement algorithm. Eng. Comput. 2017, 33, 477–496. [Google Scholar] [CrossRef]
- Hua, Z.; Xiao, Y.; Cao, J. Misalignment Fault Prediction of Wind Turbines Based on Improved Artificial Fish Swarm Algorithm. Entropy 2021, 23, 692. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Q.; Liu, Y.; Jia, H.; Abualigah, L.; Zheng, R.; Wu, D. A Hybrid SSA and SMA with Mutation Opposition-Based Learning for Constrained Engineering Problems. Comput. Intell. Neurosci. 2021, 2021, 6379469. [Google Scholar] [CrossRef]
- Selvaraj, S.; Choi, E. Swarm Intelligence Algorithms in Text Document Clustering with Various Benchmarks. Sensors 2021, 21, 3196. [Google Scholar] [CrossRef]
- Bacanin, N.; Bezdan, T.; Venkatachalam, K.; Al-Turjman, F. Optimized convolutional neural network by firefly algorithm for magnetic resonance image classification of glioma brain tumor grade. J. Real-Time Image Process. 2021, 18, 1085–1098. [Google Scholar] [CrossRef]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M. Optimizing convolutional neural network hyperparameters by enhanced swarm intelligence metaheuristics. Algorithms 2020, 13, 67. [Google Scholar] [CrossRef] [Green Version]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Glover, F.; Laguna, M. Tabu search. In Handbook of Combinatorial Optimization; Springer: Boston, MA, USA, 1998; pp. 2093–2229. [Google Scholar]
- Hasançebi, O.; Azad, S.K. Adaptive dimensional search: A new metaheuristic algorithm for discrete truss sizing optimization. Comput. Struct. 2015, 154, 1–16. [Google Scholar] [CrossRef]
- Lourenço, H.R.; Martin, O.C.; Stützle, T. Iterated local search: Framework and applications. In Handbook of Metaheuristics; Springer: Cham, Switzerland, 2019; pp. 129–168. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Chelouah, R.; Siarry, P. A continuous genetic algorithm designed for the global optimization of multimodal functions. J. Heuristics 2000, 6, 191–213. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Beyer, H.-G.; Schwefel, H.-P. Evolution strategies—A comprehensive introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. QANA: Quantum-based avian navigation optimizer algorithm. Eng. Appl. Artif. Intell. 2021, 104, 104314. [Google Scholar] [CrossRef]
- Mallipeddi, R.; Suganthan, P.N.; Pan, Q.-K.; Tasgetiren, M.F. Differential evolution algorithm with ensemble of parameters and mutation strategies. Appl. Soft Comput. 2011, 11, 1679–1696. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N.; Wang, R.; Chen, H. Differential evolution with multi-population based ensemble of mutation strategies. Inf. Sci. 2016, 329, 329–345. [Google Scholar] [CrossRef]
- Wu, G.; Shen, X.; Li, H.; Chen, H.; Lin, A.; Suganthan, P.N. Ensemble of differential evolution variants. Inf. Sci. 2018, 423, 172–186. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S.; Faris, H. MTDE: An effective multi-trial vector-based differential evolution algorithm and its applications for engineering design problems. Appl. Soft Comput. 2020, 97, 106761. [Google Scholar] [CrossRef]
- Erol, O.K.; Eksin, I. A new optimization method: Big bang—Big crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. A novel heuristic optimization method: Charged system search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Kaveh, A.; Khayatazad, M. A new meta-heuristic method: Ray optimization. Comput. Struct. 2012, 112, 283–294. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl.-Based Syst. 2019, 163, 283–304. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Azizi, M. Atomic orbital search: A novel metaheuristic algorithm. Appl. Math. Model. 2021, 93, 657–683. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. CCSA: Conscious neighborhood-based crow search algorithm for solving global optimization problems. Appl. Soft Comput. 2019, 85, 105583. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Soleimanian Gharehchopogh, F.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Jia, H.; Sun, K.; Zhang, W.; Leng, X. An enhanced chimp optimization algorithm for continuous optimization domains. Complex Intell. Syst. 2021, 1–18. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, J.; Yu, H.; Wang, Y.; Zhou, X. An Improved Grey Wolf Optimizer Based on Differential Evolution and OTSU Algorithm. Appl. Sci. 2020, 10, 6343. [Google Scholar] [CrossRef]
- Chen, C.; Wang, X.; Chen, H.; Wu, C.; Mafarja, M.; Turabieh, H. Towards Precision Fertilization: Multi-Strategy Grey Wolf Optimizer Based Model Evaluation and Yield Estimation. Electronics 2021, 10, 2183. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Kaveh, A.; Farhoudi, N. A new optimization method: Dolphin echolocation. Adv. Eng. Softw. 2013, 59, 53–70. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Dorigo, M.; Di Caro, G. Ant colony optimization: A new meta-heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; pp. 1470–1477. [Google Scholar]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- James, J.; Li, V.O. A social spider algorithm for global optimization. Appl. Soft Comput. 2015, 30, 614–627. [Google Scholar]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization Algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Abd El Aziz, M.; Ewees, A.A.; Hassanien, A.E. Whale optimization algorithm and moth-flame optimization for multilevel thresholding image segmentation. Expert Syst. Appl. 2017, 83, 242–256. [Google Scholar] [CrossRef]
- Jia, H.; Ma, J.; Song, W. Multilevel thresholding segmentation for color image using modified moth-flame optimization. IEEE Access 2019, 7, 44097–44134. [Google Scholar] [CrossRef]
- Khan, M.A.; Sharif, M.; Akram, T.; Damaševičius, R.; Maskeliūnas, R. Skin Lesion Segmentation and Multiclass Classification Using Deep Learning Features and Improved Moth Flame Optimization. Diagnostics 2021, 11, 811. [Google Scholar] [CrossRef] [PubMed]
- Abd Elaziz, M.; Ewees, A.A.; Ibrahim, R.A.; Lu, S. Opposition-based moth-flame optimization improved by differential evolution for feature selection. Math. Comput. Simul. 2020, 168, 48–75. [Google Scholar] [CrossRef]
- Gupta, D.; Ahlawat, A.K.; Sharma, A.; Rodrigues, J.J. Feature selection and evaluation for software usability model using modified moth-flame optimization. Computing 2020, 102, 1503–1520. [Google Scholar] [CrossRef]
- Tumar, I.; Hassouneh, Y.; Turabieh, H.; Thaher, T. Enhanced binary moth flame optimization as a feature selection algorithm to predict software fault prediction. IEEE Access 2020, 8, 8041–8055. [Google Scholar] [CrossRef]
- Abu Khurmaa, R.; Aljarah, I.; Sharieh, A. An intelligent feature selection approach based on moth flame optimization for medical diagnosis. Neural Comput. Appl. 2021, 33, 7165–7204. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Banaie-Dezfouli, M.; Zamani, H.; Taghian, S.; Mirjalili, S. B-MFO: A Binary Moth-Flame Optimization for Feature Selection from Medical Datasets. Computers 2021, 10, 136. [Google Scholar] [CrossRef]
- Sarma, A.; Bhutani, A.; Goel, L. Hybridization of moth flame optimization and gravitational search algorithm and its application to detection of food quality. In Proceedings of the 2017 Intelligent Systems Conference (IntelliSys), London, UK, 7–8 September 2017; pp. 52–60. [Google Scholar]
- Hassanien, A.E.; Gaber, T.; Mokhtar, U.; Hefny, H. An improved moth flame optimization algorithm based on rough sets for tomato diseases detection. Comput. Electron. Agric. 2017, 136, 86–96. [Google Scholar] [CrossRef]
- Lei, X.; Fang, M.; Fujita, H. Moth–flame optimization-based algorithm with synthetic dynamic PPI networks for discovering protein complexes. Knowl.-Based Syst. 2019, 172, 76–85. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Liu, Y. A least squares support vector machine model optimized by moth-flame optimization algorithm for annual power load forecasting. Appl. Intell. 2016, 45, 1166–1178. [Google Scholar] [CrossRef]
- Mei, R.N.S.; Sulaiman, M.H.; Mustaffa, Z.; Daniyal, H. Optimal reactive power dispatch solution by loss minimization using moth-flame optimization technique. Appl. Soft Comput. 2017, 59, 210–222. [Google Scholar]
- Allam, D.; Yousri, D.; Eteiba, M. Parameters extraction of the three diode model for the multi-crystalline solar cell/module using Moth-Flame Optimization Algorithm. Energy Convers. Manag. 2016, 123, 535–548. [Google Scholar] [CrossRef]
- Ebrahim, M.A.; Becherif, M.; Abdelaziz, A.Y. Dynamic performance enhancement for wind energy conversion system using Moth-Flame Optimization based blade pitch controller. Sustain. Energy Technol. Assess. 2018, 27, 206–212. [Google Scholar] [CrossRef]
- Raju, K.; Madurai Elavarasan, R.; Mihet-Popa, L. An assessment of onshore and offshore wind energy potential in India using moth flame optimization. Energies 2020, 13, 3063. [Google Scholar] [CrossRef]
- Rezk, H.; Ali, Z.M.; Abdalla, O.; Younis, O.; Gomaa, M.R.; Hashim, M. Hybrid moth-flame optimization algorithm and incremental conductance for tracking maximum power of solar PV/thermoelectric system under different conditions. Mathematics 2019, 7, 875. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zhou, Y.; Zhang, S.; Song, J. Lévy-flight moth-flame algorithm for function optimization and engineering design problems. Math. Probl. Eng. 2016, 2016, 1423930. [Google Scholar] [CrossRef] [Green Version]
- Savsani, V.; Tawhid, M.A. Non-dominated sorting moth flame optimization (NS-MFO) for multi-objective problems. Eng. Appl. Artif. Intell. 2017, 63, 20–32. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.; Li, K.; Beng, G.H.; Jiang, Z.; Wang, C.; Liu, N. Enhanced moth-flame optimization based on cultural learning and Gaussian mutation. J. Bionic Eng. 2018, 15, 751–763. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Khalilpourazary, S. An efficient hybrid algorithm based on Water Cycle and Moth-Flame Optimization algorithms for solving numerical and constrained engineering optimization problems. Soft Comput. 2019, 23, 1699–1722. [Google Scholar] [CrossRef]
- Chen, C.; Wang, X.; Yu, H.; Wang, M.; Chen, H. Dealing with multi-modality using synthesis of Moth-flame optimizer with sine cosine mechanisms. Math. Comput. Simul. 2021, 188, 291–318. [Google Scholar] [CrossRef]
- Kaur, K.; Singh, U.; Salgotra, R. An enhanced moth flame optimization. Neural Comput. Appl. 2020, 32, 2315–2349. [Google Scholar] [CrossRef]
- Pelusi, D.; Mascella, R.; Tallini, L.; Nayak, J.; Naik, B.; Deng, Y. An Improved Moth-Flame Optimization algorithm with hybrid search phase. Knowl.-Based Syst. 2020, 191, 105277. [Google Scholar] [CrossRef]
- Hongwei, L.; Jianyong, L.; Liang, C.; Jingbo, B.; Yangyang, S.; Kai, L. Chaos-enhanced moth-flame optimization algorithm for global optimization. J. Syst. Eng. Electron. 2019, 30, 1144–1159. [Google Scholar]
- Xu, Y.; Chen, H.; Luo, J.; Zhang, Q.; Jiao, S.; Zhang, X. Enhanced Moth-flame optimizer with mutation strategy for global optimization. Inf. Sci. 2019, 492, 181–203. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, X.; Liu, J. An improved moth-flame optimization algorithm for engineering problems. Symmetry 2020, 12, 1234. [Google Scholar] [CrossRef]
- Awad, N.; Ali, M.; Liang, J.; Qu, B.; Suganthan, P. Problem definitions and evaluation criteria for the cec 2017 special sessionand competition on single objective bound constrained real-parameter numerical optimization. In Technical Report; Nanyang Technological University: Singapore, 2016. [Google Scholar]
- Kumar, A.; Wu, G.; Ali, M.Z.; Mallipeddi, R.; Suganthan, P.N.; Das, S. A test-suite of non-convex constrained optimization problems from the real-world and some baseline results. Swarm Evol. Comput. 2020, 56, 100693. [Google Scholar] [CrossRef]
- Hussien, A.G.; Amin, M.; Abd El Aziz, M. A comprehensive review of moth-flame optimisation: Variants, hybrids, and applications. J. Exp. Theor. Artif. Intell. 2020, 32, 705–725. [Google Scholar] [CrossRef]
- Mehne, S.H.H.; Mirjalili, S. Moth-flame optimization algorithm: Theory, literature review, and application in optimal nonlinear feedback control design. In Nature-Inspired Optimizers; Springer: Cham, Switzerland, 2020; pp. 143–166. [Google Scholar]
- Shehab, M.; Abualigah, L.; Al Hamad, H.; Alabool, H.; Alshinwan, M.; Khasawneh, A.M. Moth–flame optimization algorithm: Variants and applications. Neural Comput. Appl. 2020, 32, 9859–9884. [Google Scholar] [CrossRef]
- Apinantanakon, W.; Sunat, K. Omfo: A new opposition-based moth-flame optimization algorithm for solving unconstrained optimization problems. In Proceedings of the International Conference on Computing and Information Technology, Singapore, 27–29 December 2017; pp. 22–31. [Google Scholar]
- Sapre, S.; Mini, S. Opposition-based moth flame optimization with Cauchy mutation and evolutionary boundary constraint handling for global optimization. Soft Comput. 2019, 23, 6023–6041. [Google Scholar] [CrossRef]
- Yu, C.; Heidari, A.A.; Chen, H. A quantum-behaved simulated annealing algorithm-based moth-flame optimization method. Appl. Math. Model. 2020, 87, 1–19. [Google Scholar] [CrossRef]
- Bhesdadiya, R.; Trivedi, I.N.; Jangir, P.; Kumar, A.; Jangir, N.; Totlani, R. A novel hybrid approach particle swarm optimizer with moth-flame optimizer algorithm. In Advances in Computer and Computational Sciences; Springer: Singapore, 2017; pp. 569–577. [Google Scholar]
- Sayed, G.I.; Hassanien, A.E. A hybrid SA-MFO algorithm for function optimization and engineering design problems. Complex Intell. Syst. 2018, 4, 195–212. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.K.; Gangwar, S.; Singh, D.; Pathak, V.K. A novel hybridization of artificial neural network and moth-flame optimization (ANN–MFO) for multi-objective optimization in magnetic abrasive finishing of aluminium 6060. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 270. [Google Scholar] [CrossRef]
- Dang, M.P.; Le, H.G.; Chau, N.L.; Dao, T.-P. Optimization for a flexure hinge using an effective hybrid approach of fuzzy logic and moth-flame optimization algorithm. Math. Probl. Eng. 2021, 2021, 6622655. [Google Scholar] [CrossRef]
- Mittal, T. A hybrid moth flame optimization and variable neighbourhood search technique for optimal design of IIR filters. Neural Comput. Appl. 2021, 1–16. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Yousri, D.; Mirjalili, S. A hybrid Harris hawks-moth-flame optimization algorithm including fractional-order chaos maps and evolutionary population dynamics. Adv. Eng. Softw. 2021, 154, 102973. [Google Scholar] [CrossRef]
- Ahmed, O.H.; Lu, J.; Xu, Q.; Ahmed, A.M.; Rahmani, A.M.; Hosseinzadeh, M. Using differential evolution and Moth–Flame optimization for scientific workflow scheduling in fog computing. Appl. Soft Comput. 2021, 112, 107744. [Google Scholar] [CrossRef]
- Li, Z.; Zeng, J.; Chen, Y.; Ma, G.; Liu, G. Death mechanism-based moth–flame optimization with improved flame generation mechanism for global optimization tasks. Expert Syst. Appl. 2021, 183, 115436. [Google Scholar] [CrossRef]
- Blackiston, D.J.; Silva Casey, E.; Weiss, M.R. Retention of memory through metamorphosis: Can a moth remember what it learned as a caterpillar? PLoS ONE 2008, 3, e1736. [Google Scholar] [CrossRef] [Green Version]
- Morrison, R.W. Designing Evolutionary Algorithms for Dynamic Environments; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]




| Algorithms | Parameter Settings |
|---|---|
| SA | T0 = 10. |
| CGA | IPMut = 0.9, PXcross = 0.5. |
| GWO | The parameter a is linearly decreased from 2 to 0. |
| MFO | b = 1, a is decreased linearly from −1 to −2. |
| WOA | α variable decreases linearly from 2 to 0, b = 1. |
| LMFO | β = 1.5, µ and v are normal distributions, Γ is the gamma function. |
| WCMFO | The number of rivers and sea = 4. |
| ChOA | f decreases linearly from 2 to 0. |
| AOA | µ = 0.5, α = 5. |
| SMFO | r4 = random number between interval (0, 1). |
| I-MFO | δ1 = 2.02, δ2 = 1.08, NF = random number between 1 and D. |
| F | D | Metrics | SA (1983) | CGA (2000) | GWO (2014) | MFO (2015) | WOA (2016) | LMFO (2016) | WCMFO (2019) | ChOA (2020) | AOA (2021) | SMFO (2021) | I-MFO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 30 | Avg | 2.251 × 1010 | 3.794 × 1010 | 8.223 × 108 | 6.952 × 109 | 1.906 × 106 | 2.402 × 107 | 1.328 × 104 | 2.238 × 1010 | 3.943 × 1010 | 3.091 × 1010 | 5.859 × 103 |
| Min | 1.897 × 1010 | 2.437 × 1010 | 4.404 × 107 | 1.027 × 109 | 5.654 × 105 | 1.731 × 107 | 1.214 × 102 | 1.123 × 1010 | 2.791 × 1010 | 2.010 × 1010 | 1.488 × 102 | ||
| 50 | Avg | 7.170 × 1010 | 1.126 × 1011 | 4.522 × 109 | 3.099 × 1010 | 7.172 × 106 | 1.091 × 108 | 2.826 × 104 | 4.407 × 1010 | 9.968 × 1010 | 6.933 × 1010 | 1.430 × 104 | |
| Min | 6.279 × 1010 | 9.612 × 1010 | 1.231 × 109 | 7.095 × 109 | 1.980 × 106 | 7.284 × 107 | 6.883 × 102 | 3.201 × 1010 | 8.424 × 1010 | 4.945 × 1010 | 1.948 × 102 | ||
| 100 | Avg | 2.830 × 1011 | 3.547 × 1011 | 3.207 × 1010 | 1.173 × 1011 | 3.677 × 107 | 7.525 × 108 | 2.017 × 105 | 1.457 × 1011 | 2.617 × 1011 | 1.908 × 1011 | 2.881 × 104 | |
| Min | 2.638 × 1011 | 3.147 × 1011 | 1.634 × 1010 | 6.748 × 1010 | 1.409 × 107 | 6.332 × 108 | 1.093 × 104 | 1.282 × 1011 | 2.343 × 1011 | 1.527 × 1011 | 1.033 × 102 | ||
| F3 | 30 | Avg | 1.439 × 105 | 1.095 × 105 | 2.993 × 104 | 1.009 × 105 | 1.715 × 105 | 2.786 × 103 | 1.887 × 103 | 5.221 × 104 | 7.488 × 104 | 8.189 × 104 | 6.106 × 102 |
| Min | 1.029 × 105 | 9.312 × 104 | 1.576 × 104 | 1.920 × 103 | 8.481 × 104 | 1.424 × 103 | 3.092 × 102 | 3.954 × 104 | 5.445 × 104 | 7.186 × 104 | 3.388 × 102 | ||
| 50 | Avg | 2.994 × 105 | 2.241 × 105 | 7.147 × 104 | 1.650 × 105 | 6.180 × 104 | 3.151 × 104 | 1.150 × 104 | 1.306 × 105 | 1.648 × 105 | 1.775 × 105 | 1.460 × 104 | |
| Min | 2.647 × 105 | 1.648 × 105 | 3.628 × 104 | 1.176 × 104 | 3.098 × 104 | 2.291 × 104 | 7.428 × 102 | 1.006 × 105 | 1.249 × 105 | 1.273 × 105 | 7.827 × 103 | ||
| 100 | Avg | 8.110 × 105 | 5.742 × 105 | 2.023 × 105 | 4.556 × 105 | 5.928 × 105 | 2.495 × 105 | 7.361 × 104 | 3.071 × 105 | 3.330 × 105 | 3.366 × 105 | 7.625 × 104 | |
| Min | 7.298 × 105 | 4.725 × 105 | 1.595 × 105 | 1.191 × 105 | 3.355 × 105 | 1.819 × 105 | 3.430 × 104 | 2.701 × 105 | 3.027 × 105 | 3.182 × 105 | 6.767 × 104 | ||
| F4 | 30 | Avg | 1.587 × 103 | 7.327 × 103 | 5.441 × 102 | 9.082 × 102 | 5.476 × 102 | 4.928 × 102 | 4.886 × 102 | 2.971 × 103 | 8.808 × 103 | 5.977 × 103 | 4.868 × 102 |
| Min | 1.354 × 103 | 6.137 × 103 | 4.963 × 102 | 5.424 × 102 | 4.995 × 102 | 4.755 × 102 | 4.239 × 102 | 1.134 × 103 | 3.824 × 103 | 3.030 × 103 | 4.704 × 102 | ||
| 50 | Avg | 7.832 × 103 | 2.608 × 104 | 8.767 × 102 | 4.097 × 103 | 6.676 × 102 | 5.907 × 102 | 5.493 × 102 | 9.176 × 103 | 2.582 × 104 | 1.879 × 104 | 5.550 × 102 | |
| Min | 6.386 × 103 | 1.598 × 104 | 6.745 × 102 | 1.216 × 103 | 5.138 × 102 | 5.084 × 102 | 4.849 × 102 | 5.017 × 103 | 1.686 × 104 | 1.005 × 104 | 4.210 × 102 | ||
| 100 | Avg | 4.778 × 104 | 1.033 × 105 | 2.812 × 103 | 2.348 × 104 | 9.992 × 102 | 7.215 × 102 | 6.423 × 102 | 2.760 × 104 | 7.703 × 104 | 5.544 × 104 | 6.318 × 102 | |
| Min | 3.845 × 104 | 8.305 × 104 | 1.870 × 103 | 6.742 × 103 | 8.615 × 102 | 6.726 × 102 | 5.980 × 102 | 2.116 × 104 | 6.019 × 104 | 3.485 × 104 | 5.772 × 102 | ||
| F5 | 30 | Avg | 8.120 × 102 | 8.777 × 102 | 5.855 × 102 | 6.894 × 102 | 8.044 × 102 | 6.278 × 102 | 6.744 × 102 | 7.877 × 102 | 7.905 × 102 | 8.721 × 102 | 5.499 × 102 |
| Min | 7.865 × 102 | 8.259 × 102 | 5.508 × 102 | 6.280 × 102 | 7.242 × 102 | 5.707 × 102 | 6.104 × 102 | 7.471 × 102 | 7.217 × 102 | 8.041 × 102 | 5.308 × 102 | ||
| 50 | Avg | 1.167 × 103 | 1.273 × 103 | 6.892 × 102 | 8.934 × 102 | 9.209 × 102 | 8.152 × 102 | 8.940 × 102 | 1.037 × 103 | 1.078 × 103 | 1.118 × 103 | 6.348 × 102 | |
| Min | 1.142 × 103 | 1.184 × 103 | 6.379 × 102 | 7.731 × 102 | 8.081 × 102 | 7.287 × 102 | 7.743 × 102 | 9.853 × 102 | 9.951 × 102 | 1.053 × 103 | 5.836 × 102 | ||
| 100 | Avg | 2.180 × 103 | 2.374 × 103 | 1.058 × 103 | 1.666 × 103 | 1.413 × 103 | 1.456 × 103 | 1.726 × 103 | 1.789 × 103 | 1.955 × 103 | 1.985 × 103 | 8.613 × 102 | |
| Min | 2.098 × 103 | 2.255 × 103 | 9.864 × 102 | 1.455 × 103 | 1.329 × 103 | 1.226 × 103 | 1.328 × 103 | 1.724 × 103 | 1.842 × 103 | 1.875 × 103 | 7.885 × 102 | ||
| F6 | 30 | Avg | 6.582 × 102 | 6.734 × 102 | 6.043 × 102 | 6.267 × 102 | 6.671 × 102 | 6.038 × 102 | 6.225 × 102 | 6.604 × 102 | 6.655 × 102 | 6.830 × 102 | 6.000 × 102 |
| Min | 6.468 × 102 | 6.612 × 102 | 6.011 × 102 | 6.144 × 102 | 6.410 × 102 | 6.017 × 102 | 6.095 × 102 | 6.386 × 102 | 6.476 × 102 | 6.615 × 102 | 6.000 × 102 | ||
| 50 | Avg | 6.835 × 102 | 6.936 × 102 | 6.105 × 102 | 6.437 × 102 | 6.760 × 102 | 6.094 × 102 | 6.400 × 102 | 6.720 × 102 | 6.837 × 102 | 6.890 × 102 | 6.000 × 102 | |
| Min | 6.691 × 102 | 6.784 × 102 | 6.052 × 102 | 6.270 × 102 | 6.638 × 102 | 6.034 × 102 | 6.165 × 102 | 6.608 × 102 | 6.747 × 102 | 6.780 × 102 | 6.000 × 102 | ||
| 100 | Avg | 7.210 × 102 | 7.176 × 102 | 6.275 × 102 | 6.648 × 102 | 6.768 × 102 | 6.398 × 102 | 6.664 × 102 | 6.860 × 102 | 7.028 × 102 | 7.030 × 102 | 6.000 × 102 | |
| Min | 7.164 × 102 | 7.143 × 102 | 6.229 × 102 | 6.466 × 102 | 6.676 × 102 | 6.222 × 102 | 6.526 × 102 | 6.761 × 102 | 6.970 × 102 | 6.865 × 102 | 6.000 × 102 | ||
| F7 | 30 | Avg | 1.728 × 103 | 1.965 × 103 | 8.418 × 102 | 1.011 × 103 | 1.238 × 103 | 8.735 × 102 | 8.985 × 102 | 1.190 × 103 | 1.295 × 103 | 1.349 × 103 | 7.964 × 102 |
| Min | 1.593 × 103 | 1.798 × 103 | 7.801 × 102 | 8.671 × 102 | 1.089 × 103 | 8.438 × 102 | 8.402 × 102 | 1.063 × 103 | 1.154 × 103 | 1.175 × 103 | 7.595 × 102 | ||
| 50 | Avg | 3.572 × 103 | 3.656 × 103 | 1.015 × 103 | 1.701 × 103 | 1.684 × 103 | 1.092 × 103 | 1.141 × 103 | 1.663 × 103 | 1.860 × 103 | 1.919 × 103 | 9.208 × 102 | |
| Min | 3.305 × 103 | 3.300 × 103 | 9.654 × 102 | 1.113 × 103 | 1.500 × 103 | 1.065 × 103 | 1.020 × 103 | 1.464 × 103 | 1.744 × 103 | 1.769 × 103 | 8.168 × 102 | ||
| 100 | Avg | 1.014 × 104 | 9.052 × 103 | 1.710 × 103 | 4.169 × 103 | 3.250 × 103 | 1.736 × 103 | 1.988 × 103 | 3.320 × 103 | 3.712 × 103 | 3.891 × 103 | 1.356 × 103 | |
| Min | 9.035 × 103 | 8.338 × 103 | 1.542 × 103 | 2.576 × 103 | 2.814 × 103 | 1.649 × 103 | 1.531 × 103 | 3.127 × 103 | 3.579 × 103 | 3.536 × 103 | 1.140 × 103 | ||
| F8 | 30 | Avg | 1.116 × 103 | 1.166 × 103 | 8.713 × 102 | 9.790 × 102 | 1.000 × 103 | 9.379 × 102 | 9.841 × 102 | 1.032 × 103 | 1.041 × 103 | 1.096 × 103 | 8.574 × 102 |
| Min | 1.074 × 103 | 1.144 × 103 | 8.435 × 102 | 8.938 × 102 | 9.488 × 102 | 8.797 × 102 | 9.344 × 102 | 9.726 × 102 | 1.002 × 103 | 1.058 × 103 | 8.418 × 102 | ||
| 50 | Avg | 1.467 × 103 | 1.573 × 103 | 9.792 × 102 | 1.229 × 103 | 1.249 × 103 | 1.119 × 103 | 1.213 × 103 | 1.305 × 103 | 1.426 × 103 | 1.404 × 103 | 9.201 × 102 | |
| Min | 1.427 × 103 | 1.519 × 103 | 9.384 × 102 | 1.118 × 103 | 1.132 × 103 | 1.062 × 103 | 1.087 × 103 | 1.251 × 103 | 1.339 × 103 | 1.320 × 103 | 8.796 × 102 | ||
| 100 | Avg | 2.499 × 103 | 2.751 × 103 | 1.397 × 103 | 1.968 × 103 | 1.897 × 103 | 1.740 × 103 | 2.026 × 103 | 2.157 × 103 | 2.404 × 103 | 2.422 × 103 | 1.160 × 103 | |
| Min | 2.448 × 103 | 2.620 × 103 | 1.225 × 103 | 1.717 × 103 | 1.716 × 103 | 1.531 × 103 | 1.756 × 103 | 2.052 × 103 | 2.248 × 103 | 2.276 × 103 | 1.087 × 103 | ||
| F9 | 30 | Avg | 1.079 × 104 | 1.239 × 104 | 1.384 × 103 | 6.278 × 103 | 7.233 × 103 | 1.015 × 103 | 8.747 × 103 | 6.612 × 103 | 5.570 × 103 | 9.591 × 103 | 9.882 × 102 |
| Min | 9.017 × 103 | 8.805 × 103 | 1.025 × 103 | 4.471 × 103 | 4.425 × 103 | 9.056 × 102 | 5.118 × 103 | 4.627 × 103 | 4.101 × 103 | 7.754 × 103 | 9.065 × 102 | ||
| 50 | Avg | 3.302 × 104 | 4.335 × 104 | 4.571 × 103 | 1.644 × 104 | 1.783 × 104 | 1.306 × 103 | 2.195 × 104 | 2.591 × 104 | 2.277 × 104 | 3.066 × 104 | 1.305 × 103 | |
| Min | 2.622 × 104 | 3.603 × 104 | 2.135 × 103 | 8.748 × 103 | 1.187 × 104 | 9.481 × 102 | 1.190 × 104 | 1.969 × 104 | 1.804 × 104 | 1.925 × 104 | 9.853 × 102 | ||
| 100 | Avg | 1.197 × 105 | 1.243 × 105 | 2.638 × 104 | 4.507 × 104 | 3.820 × 104 | 1.421 × 104 | 5.208 × 104 | 6.813 × 104 | 5.374 × 104 | 6.959 × 104 | 7.081 × 103 | |
| Min | 1.034 × 105 | 1.079 × 105 | 1.102 × 104 | 3.679 × 104 | 2.557 × 104 | 3.037 × 103 | 3.986 × 104 | 5.806 × 104 | 4.673 × 104 | 5.852 × 104 | 4.038 × 103 | ||
| F10 | 30 | Avg | 7.764 × 103 | 8.149 × 103 | 3.909 × 103 | 5.130 × 103 | 6.156 × 103 | 4.422 × 103 | 4.808 × 103 | 8.037 × 103 | 6.487 × 103 | 8.363 × 103 | 2.745 × 103 |
| Min | 6.721 × 103 | 7.474 × 103 | 2.718 × 103 | 3.575 × 103 | 4.506 × 103 | 3.149 × 103 | 3.332 × 103 | 7.199 × 103 | 5.410 × 103 | 7.473 × 103 | 1.941 × 103 | ||
| 50 | Avg | 1.426 × 104 | 1.446 × 104 | 6.428 × 103 | 8.566 × 103 | 9.478 × 103 | 7.081 × 103 | 7.956 × 103 | 1.419 × 104 | 1.223 × 104 | 1.368 × 104 | 4.799 × 103 | |
| Min | 1.337 × 104 | 1.342 × 104 | 4.582 × 103 | 6.288 × 103 | 6.969 × 103 | 6.045 × 103 | 6.204 × 103 | 1.301 × 104 | 1.058 × 104 | 1.234 × 104 | 3.734 × 103 | ||
| 100 | Avg | 3.136 × 104 | 3.121 × 104 | 1.497 × 104 | 1.728 × 104 | 2.012 × 104 | 1.758 × 104 | 1.618 × 104 | 3.141 × 104 | 2.783 × 104 | 3.071 × 104 | 1.168 × 104 | |
| Min | 3.040 × 104 | 2.990 × 104 | 1.141 × 104 | 1.417 × 104 | 1.687 × 104 | 1.631 × 104 | 1.147 × 104 | 3.035 × 104 | 2.582 × 104 | 2.843 × 104 | 9.083 × 103 | ||
| Ranking | 30 | W|T|L | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 9/0/0 |
| 50 | W|T|L | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 2/0/7 | 0/0/9 | 0/0/9 | 0/0/9 | 7/0/2 | |
| 100 | W|T|L | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 0/0/9 | 1/0/8 | 0/0/9 | 0/0/9 | 0/0/9 | 8/0/1 |
| F | D | Metrics | SA (1983) | CGA (2000) | GWO (2014) | MFO (2015) | WOA (2016) | LMFO (2016) | WCMFO (2019) | ChOA (2020) | AOA (2021) | SMFO (2021) | I-MFO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F11 | 30 | Avg | 3.124 × 103 | 5.262 × 103 | 1.406 × 103 | 3.749 × 103 | 1.462 × 103 | 1.292 × 103 | 1.336 × 103 | 3.361 × 103 | 3.325 × 103 | 5.265 × 103 | 1.188 × 103 |
| Min | 2.512 × 103 | 3.284 × 103 | 1.271 × 103 | 1.363 × 103 | 1.282 × 103 | 1.177 × 103 | 1.254 × 103 | 1.731 × 103 | 1.739 × 103 | 2.547 × 103 | 1.119 × 103 | ||
| 50 | Avg | 1.128 × 104 | 1.978 × 104 | 3.078 × 103 | 7.297 × 103 | 1.591 × 103 | 1.532 × 103 | 1.491 × 103 | 8.609 × 103 | 1.605 × 104 | 1.426 × 104 | 1.326 × 103 | |
| Min | 9.143 × 103 | 1.250 × 104 | 1.480 × 103 | 1.574 × 103 | 1.421 × 103 | 1.380 × 103 | 1.344 × 103 | 6.220 × 103 | 9.287 × 103 | 8.985 × 103 | 1.212 × 103 | ||
| 100 | Avg | 1.883 × 105 | 2.174 × 105 | 3.531 × 104 | 1.257 × 105 | 7.762 × 103 | 3.319 × 103 | 2.191 × 103 | 7.211 × 104 | 1.625 × 105 | 2.086 × 105 | 1.776 × 103 | |
| Min | 1.465 × 105 | 1.629 × 105 | 1.647 × 104 | 2.137 × 104 | 4.463 × 103 | 2.955 × 103 | 1.840 × 103 | 6.100 × 104 | 1.167 × 105 | 1.399 × 105 | 1.464 × 103 | ||
| F12 | 30 | Avg | 7.895 × 108 | 3.540 × 109 | 3.900 × 107 | 6.158 × 107 | 3.770 × 107 | 5.460 × 106 | 1.254 × 106 | 3.360 × 109 | 7.828 × 109 | 4.462 × 109 | 2.499 × 105 |
| Min | 3.859 × 108 | 1.934 × 109 | 2.109 × 106 | 7.305 × 104 | 2.509 × 106 | 1.046 × 106 | 3.718 × 104 | 6.620 × 108 | 3.034 × 109 | 1.749 × 109 | 5.318 × 104 | ||
| 50 | Avg | 9.643 × 109 | 2.939 × 1010 | 4.764 × 108 | 2.475 × 109 | 1.861 × 108 | 4.882 × 107 | 7.229 × 106 | 1.887 × 1010 | 5.350 × 1010 | 3.075 × 1010 | 1.599 × 106 | |
| Min | 5.659 × 109 | 2.161 × 1010 | 7.558 × 107 | 1.646 × 107 | 5.114 × 107 | 2.169 × 107 | 1.549 × 106 | 1.045 × 1010 | 2.948 × 1010 | 1.600 × 1010 | 3.874 × 105 | ||
| 100 | Avg | 6.862 × 1010 | 1.398 × 1011 | 4.919 × 109 | 3.523 × 1010 | 6.875 × 108 | 3.370 × 108 | 3.428 × 107 | 6.764 × 1010 | 1.766 × 1011 | 9.544 × 1010 | 3.131 × 106 | |
| Min | 5.696 × 1010 | 1.132 × 1011 | 1.450 × 109 | 1.435 × 1010 | 2.918 × 108 | 2.296 × 108 | 3.806 × 106 | 4.928 × 1010 | 1.296 × 1011 | 5.096 × 1010 | 1.250 × 106 | ||
| F13 | 30 | Avg | 9.518 × 107 | 8.620 × 108 | 8.368 × 105 | 7.958 × 106 | 1.463 × 105 | 4.494 × 105 | 1.047 × 105 | 8.863 × 108 | 4.348 × 104 | 8.738 × 108 | 1.994 × 104 |
| Min | 4.048 × 107 | 3.361 × 108 | 1.991 × 104 | 1.122 × 104 | 2.283 × 104 | 2.705 × 105 | 1.436 × 104 | 3.327 × 107 | 2.158 × 104 | 2.189 × 108 | 1.396 × 103 | ||
| 50 | Avg | 1.722 × 109 | 8.709 × 109 | 1.532 × 108 | 2.427 × 108 | 1.657 × 105 | 2.510 × 106 | 8.895 × 104 | 5.260 × 109 | 3.917 × 109 | 1.288 × 1010 | 1.434 × 104 | |
| Min | 1.103 × 109 | 5.824 × 109 | 1.312 × 105 | 1.136 × 105 | 4.764 × 104 | 1.415 × 106 | 2.174 × 104 | 5.002 × 108 | 1.041 × 107 | 1.435 × 109 | 1.582 × 103 | ||
| 100 | Avg | 8.436 × 109 | 2.634 × 1010 | 4.163 × 108 | 4.053 × 109 | 8.423 × 104 | 1.168 × 107 | 1.378 × 105 | 1.915 × 1010 | 3.479 × 1010 | 1.965 × 1010 | 1.105 × 104 | |
| Min | 6.140 × 109 | 1.992 × 1010 | 1.579 × 106 | 2.629 × 108 | 3.701 × 104 | 9.896 × 106 | 3.658 × 104 | 1.137 × 1010 | 2.155 × 1010 | 1.073 × 1010 | 1.651 × 103 | ||
| F14 | 30 | Avg | 1.022 × 105 | 3.619 × 105 | 1.438 × 105 | 8.969 × 104 | 9.075 × 105 | 2.614 × 104 | 2.073 × 104 | 3.244 × 105 | 4.223 × 104 | 1.548 × 106 | 1.671 × 104 |
| Min | 3.932 × 104 | 7.165 × 104 | 3.679 × 103 | 2.197 × 103 | 1.364 × 105 | 2.724 × 103 | 6.252 × 103 | 4.503 × 104 | 2.213 × 103 | 7.879 × 104 | 5.615 × 103 | ||
| 50 | Avg | 1.285 × 106 | 5.160 × 106 | 4.016 × 105 | 3.086 × 105 | 6.358 × 105 | 1.086 × 105 | 8.151 × 104 | 1.206 × 106 | 3.933 × 105 | 2.634 × 107 | 8.426 × 104 | |
| Min | 8.972 × 105 | 2.700 × 106 | 4.749 × 104 | 1.071 × 104 | 9.639 × 104 | 2.360 × 104 | 1.194 × 104 | 5.706 × 105 | 4.727 × 104 | 8.185 × 105 | 8.798 × 103 | ||
| 100 | Avg | 2.710 × 107 | 6.024 × 107 | 3.480 × 106 | 7.558 × 106 | 1.876 × 106 | 1.207 × 106 | 3.627 × 105 | 7.928 × 106 | 2.267 × 107 | 3.200 × 107 | 3.439 × 105 | |
| Min | 2.008 × 107 | 3.524 × 107 | 1.056 × 106 | 3.097 × 105 | 6.461 × 105 | 1.938 × 105 | 1.387 × 105 | 4.302 × 106 | 4.241 × 106 | 7.455 × 106 | 1.557 × 105 | ||
| F15 | 30 | Avg | 2.966 × 106 | 4.746 × 107 | 3.637 × 105 | 3.412 × 104 | 8.683 × 104 | 9.006 × 104 | 3.448 × 104 | 5.434 × 106 | 2.498 × 104 | 4.469 × 107 | 1.983 × 104 |
| Min | 1.113 × 106 | 6.971 × 106 | 1.847 × 104 | 3.640 × 103 | 1.368 × 104 | 5.002 × 104 | 2.547 × 103 | 1.019 × 106 | 1.454 × 104 | 2.375 × 106 | 2.006 × 103 | ||
| 50 | Avg | 1.739 × 108 | 1.276 × 109 | 9.314 × 106 | 2.145 × 107 | 7.839 × 104 | 5.206 × 105 | 7.164 × 104 | 1.070 × 108 | 3.131 × 104 | 8.129 × 108 | 9.247 × 103 | |
| Min | 6.074 × 107 | 5.105 × 108 | 1.565 × 104 | 4.235 × 104 | 2.225 × 104 | 3.594 × 105 | 1.422 × 104 | 5.379 × 107 | 1.979 × 104 | 1.237 × 108 | 1.622 × 103 | ||
| 100 | Avg | 2.250 × 109 | 8.426 × 109 | 9.478 × 107 | 1.045 × 109 | 2.527 × 105 | 2.824 × 106 | 9.337 × 104 | 4.851 × 109 | 4.659 × 109 | 8.332 × 109 | 7.383 × 103 | |
| Min | 1.743 × 109 | 6.068 × 109 | 5.864 × 105 | 1.058 × 105 | 2.549 × 104 | 1.949 × 106 | 1.223 × 104 | 1.096 × 109 | 1.070 × 109 | 1.272 × 109 | 1.752 × 103 | ||
| F16 | 30 | Avg | 3.496 × 103 | 4.179 × 103 | 2.287 × 103 | 2.995 × 103 | 3.519 × 103 | 2.640 × 103 | 2.807 × 103 | 3.475 × 103 | 3.676 × 103 | 4.402 × 103 | 1.928 × 103 |
| Min | 3.252 × 103 | 3.709 × 103 | 1.744 × 103 | 2.487 × 103 | 2.728 × 103 | 2.110 × 103 | 2.095 × 103 | 2.940 × 103 | 2.867 × 103 | 3.607 × 103 | 1.617 × 103 | ||
| 50 | Avg | 5.575 × 103 | 6.744 × 103 | 2.791 × 103 | 4.150 × 103 | 4.689 × 103 | 3.621 × 103 | 3.778 × 103 | 5.240 × 103 | 6.261 × 103 | 6.930 × 103 | 2.546 × 103 | |
| Min | 5.216 × 103 | 6.027 × 103 | 2.209 × 103 | 3.133 × 103 | 3.895 × 103 | 2.949 × 103 | 3.014 × 103 | 4.488 × 103 | 3.693 × 103 | 5.302 × 103 | 2.186 × 103 | ||
| 100 | Avg | 1.236 × 104 | 1.660 × 104 | 5.610 × 103 | 8.085 × 103 | 9.811 × 103 | 6.439 × 103 | 6.869 × 103 | 1.231 × 104 | 1.814 × 104 | 1.679 × 104 | 4.533 × 103 | |
| Min | 1.111 × 104 | 1.563 × 104 | 4.748 × 103 | 6.389 × 103 | 7.512 × 103 | 5.301 × 103 | 4.978 × 103 | 1.047 × 104 | 1.301 × 104 | 1.394 × 104 | 3.471 × 103 | ||
| F17 | 30 | Avg | 2.410 × 103 | 2.789 × 103 | 1.956 × 103 | 2.411 × 103 | 2.520 × 103 | 2.203 × 103 | 2.315 × 103 | 2.598 × 103 | 2.620 × 103 | 2.752 × 103 | 1.875 × 103 |
| Min | 2.242 × 103 | 2.467 × 103 | 1.777 × 103 | 1.975 × 103 | 1.931 × 103 | 1.801 × 103 | 1.942 × 103 | 2.275 × 103 | 2.085 × 103 | 2.359 × 103 | 1.736 × 103 | ||
| 50 | Avg | 4.770 × 103 | 5.784 × 103 | 2.676 × 103 | 3.708 × 103 | 3.892 × 103 | 3.155 × 103 | 3.758 × 103 | 4.205 × 103 | 4.226 × 103 | 5.316 × 103 | 2.573 × 103 | |
| Min | 4.087 × 103 | 4.805 × 103 | 2.257 × 103 | 2.866 × 103 | 3.106 × 103 | 2.538 × 103 | 2.931 × 103 | 3.304 × 103 | 3.228 × 103 | 3.873 × 103 | 2.176 × 103 | ||
| 100 | Avg | 1.132 × 104 | 9.223 × 104 | 4.439 × 103 | 7.668 × 103 | 7.212 × 103 | 5.693 × 103 | 6.345 × 103 | 1.240 × 104 | 2.886 × 105 | 4.082 × 105 | 4.247 × 103 | |
| Min | 1.036 × 104 | 1.996 × 104 | 3.338 × 103 | 5.623 × 103 | 5.421 × 103 | 4.630 × 103 | 4.935 × 103 | 9.483 × 103 | 1.665 × 104 | 1.263 × 104 | 2.980 × 103 | ||
| F18 | 30 | Avg | 2.207 × 106 | 7.273 × 106 | 6.631 × 105 | 3.177 × 106 | 2.408 × 106 | 3.682 × 105 | 1.734 × 105 | 1.487 × 106 | 7.850 × 105 | 2.844 × 107 | 8.793 × 104 |
| Min | 1.112 × 106 | 1.967 × 106 | 8.000 × 104 | 3.737 × 104 | 1.933 × 105 | 8.629 × 104 | 3.793 × 104 | 4.340 × 105 | 1.205 × 105 | 2.007 × 106 | 3.279 × 103 | ||
| 50 | Avg | 1.242 × 107 | 4.494 × 107 | 3.300 × 106 | 3.443 × 106 | 4.272 × 106 | 7.009 × 105 | 4.064 × 105 | 8.349 × 106 | 2.081 × 107 | 7.061 × 107 | 3.192 × 105 | |
| Min | 5.637 × 106 | 1.275 × 107 | 2.968 × 105 | 1.807 × 105 | 1.009 × 106 | 3.224 × 105 | 1.508 × 105 | 3.517 × 106 | 8.364 × 105 | 1.412 × 107 | 3.532 × 104 | ||
| 100 | Avg | 5.093 × 107 | 1.121 × 108 | 4.158 × 106 | 1.162 × 107 | 2.020 × 106 | 2.306 × 106 | 8.326 × 105 | 1.088 × 107 | 3.135 × 107 | 5.663 × 107 | 1.164 × 106 | |
| Min | 3.392 × 107 | 6.823 × 107 | 7.431 × 105 | 4.881 × 105 | 8.476 × 105 | 1.032 × 106 | 3.782 × 105 | 5.042 × 106 | 9.728 × 106 | 9.819 × 106 | 2.003 × 105 | ||
| F19 | 30 | Avg | 1.278 × 107 | 9.064 × 107 | 2.913 × 105 | 4.071 × 106 | 2.647 × 106 | 6.193 × 104 | 3.223 × 104 | 4.950 × 107 | 1.071 × 106 | 1.072 × 108 | 2.012 × 104 |
| Min | 6.005 × 106 | 3.289 × 107 | 9.466 × 103 | 2.093 × 103 | 1.744 × 105 | 1.764 × 104 | 2.168 × 103 | 2.507 × 106 | 8.696 × 105 | 5.192 × 106 | 1.940 × 103 | ||
| 50 | Avg | 9.348 × 107 | 6.178 × 108 | 2.362 × 106 | 6.151 × 106 | 2.457 × 106 | 2.445 × 105 | 2.361 × 104 | 3.031 × 108 | 4.614 × 105 | 9.214 × 108 | 1.409 × 104 | |
| Min | 4.313 × 107 | 2.829 × 108 | 6.908 × 104 | 5.030 × 103 | 1.534 × 105 | 1.272 × 105 | 2.700 × 103 | 3.918 × 107 | 4.438 × 105 | 1.580 × 108 | 2.081 × 103 | ||
| 100 | Avg | 2.062 × 109 | 8.505 × 109 | 1.003 × 108 | 3.561 × 108 | 1.528 × 107 | 4.435 × 106 | 7.032 × 104 | 3.211 × 109 | 4.723 × 109 | 5.975 × 109 | 1.009 × 104 | |
| Min | 1.411 × 109 | 6.413 × 109 | 2.250 × 106 | 2.761 × 106 | 5.273 × 106 | 2.123 × 106 | 1.223 × 104 | 7.255 × 108 | 1.529 × 109 | 2.984 × 109 | 2.081 × 103 | ||
| F20 | 30 | Avg | 2.533 × 103 | 2.656 × 103 | 2.288 × 103 | 2.600 × 103 | 2.702 × 103 | 2.498 × 103 | 2.468 × 103 | 2.921 × 103 | 2.638 × 103 | 2.847 × 103 | 2.116 × 103 |
| Min | 2.461 × 103 | 2.473 × 103 | 2.154 × 103 | 2.215 × 103 | 2.327 × 103 | 2.180 × 103 | 2.072 × 103 | 2.560 × 103 | 2.327 × 103 | 2.454 × 103 | 2.018 × 103 | ||
| 50 | Avg | 3.891 × 103 | 3.930 × 103 | 2.736 × 103 | 3.557 × 103 | 3.628 × 103 | 3.060 × 103 | 3.431 × 103 | 3.932 × 103 | 3.346 × 103 | 3.929 × 103 | 2.297 × 103 | |
| Min | 3.535 × 103 | 3.587 × 103 | 2.422 × 103 | 2.897 × 103 | 2.664 × 103 | 2.586 × 103 | 2.655 × 103 | 3.576 × 103 | 2.634 × 103 | 3.493 × 103 | 2.097 × 103 | ||
| 100 | Avg | 7.466 × 103 | 7.382 × 103 | 4.469 × 103 | 5.692 × 103 | 5.875 × 103 | 5.054 × 103 | 5.740 × 103 | 6.931 × 103 | 5.751 × 103 | 6.923 × 103 | 3.566 × 103 | |
| Min | 6.910 × 103 | 6.809 × 103 | 3.301 × 103 | 4.194 × 103 | 4.326 × 103 | 4.139 × 103 | 4.438 × 103 | 6.030 × 103 | 4.700 × 103 | 6.187 × 103 | 3.093 × 103 | ||
| Ranking | 30 | W|T|L | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 10/0/0 |
| 50 | W|T|L | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 1/0/9 | 0/0/10 | 0/0/10 | 0/0/10 | 9/0/1 | |
| 100 | W|T|L | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 1/0/9 | 0/0/10 | 0/0/10 | 0/0/10 | 9/0/1 |
| F | D | Metrics | SA (1983) | CGA (2000) | GWO (2014) | MFO (2015) | WOA (2016) | LMFO (2016) | WCMFO (2019) | ChOA (2020) | AOA (2021) | SMFO (2021) | I-MFO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F21 | 30 | Avg | 2.593 × 103 | 2.655 × 103 | 2.383 × 103 | 2.476 × 103 | 2.558 × 103 | 2.439 × 103 | 2.493 × 103 | 2.565 × 103 | 2.604 × 103 | 2.653 × 103 | 2.363 × 103 |
| Min | 2.565 × 103 | 2.626 × 103 | 2.352 × 103 | 2.421 × 103 | 2.463 × 103 | 2.378 × 103 | 2.398 × 103 | 2.503 × 103 | 2.515 × 103 | 2.551 × 103 | 2.334 × 103 | ||
| 50 | Avg | 2.945 × 103 | 3.065 × 103 | 2.485 × 103 | 2.694 × 103 | 2.888 × 103 | 2.609 × 103 | 2.694 × 103 | 2.886 × 103 | 3.002 × 103 | 3.064 × 103 | 2.430 × 103 | |
| Min | 2.893 × 103 | 3.026 × 103 | 2.440 × 103 | 2.575 × 103 | 2.744 × 103 | 2.542 × 103 | 2.580 × 103 | 2.819 × 103 | 2.885 × 103 | 2.935 × 103 | 2.399 × 103 | ||
| 100 | Avg | 4.058 × 103 | 4.393 × 103 | 2.845 × 103 | 3.594 × 103 | 3.884 × 103 | 3.280 × 103 | 3.539 × 103 | 4.044 × 103 | 4.581 × 103 | 4.394 × 103 | 2.738 × 103 | |
| Min | 3.956 × 103 | 4.275 × 103 | 2.751 × 103 | 3.262 × 103 | 3.502 × 103 | 3.106 × 103 | 3.233 × 103 | 3.804 × 103 | 4.161 × 103 | 4.128 × 103 | 2.652 × 103 | ||
| F22 | 30 | Avg | 6.618 × 103 | 6.787 × 103 | 4.413 × 103 | 5.842 × 103 | 5.949 × 103 | 5.006 × 103 | 6.637 × 103 | 9.124 × 103 | 7.785 × 103 | 8.654 × 103 | 2.889 × 103 |
| Min | 4.837 × 103 | 5.363 × 103 | 2.420 × 103 | 3.150 × 103 | 2.315 × 103 | 2.325 × 103 | 5.330 × 103 | 8.503 × 103 | 5.492 × 103 | 5.677 × 103 | 2.300 × 103 | ||
| 50 | Avg | 1.569 × 104 | 1.600 × 104 | 8.634 × 103 | 1.029 × 104 | 1.208 × 104 | 8.858 × 103 | 1.001 × 104 | 1.655 × 104 | 1.468 × 104 | 1.616 × 104 | 6.525 × 103 | |
| Min | 1.464 × 104 | 1.489 × 104 | 7.065 × 103 | 7.958 × 103 | 8.721 × 103 | 7.176 × 103 | 8.609 × 103 | 1.554 × 104 | 1.304 × 104 | 1.529 × 104 | 5.551 × 103 | ||
| 100 | Avg | 3.336 × 104 | 3.346 × 104 | 1.777 × 104 | 2.032 × 104 | 2.397 × 104 | 1.948 × 104 | 1.943 × 104 | 3.374 × 104 | 3.092 × 104 | 3.277 × 104 | 1.393 × 104 | |
| Min | 3.264 × 104 | 3.169 × 104 | 1.413 × 104 | 1.778 × 104 | 2.087 × 104 | 1.791 × 104 | 1.671 × 104 | 3.233 × 104 | 2.790 × 104 | 3.043 × 104 | 1.189 × 104 | ||
| F23 | 30 | Avg | 2.916 × 103 | 3.149 × 103 | 2.731 × 103 | 2.801 × 103 | 3.032 × 103 | 2.759 × 103 | 2.785 × 103 | 3.011 × 103 | 3.312 × 103 | 3.283 × 103 | 2.700 × 103 |
| Min | 2.819 × 103 | 3.102 × 103 | 2.695 × 103 | 2.762 × 103 | 2.886 × 103 | 2.710 × 103 | 2.721 × 103 | 2.930 × 103 | 3.093 × 103 | 3.027 × 103 | 2.680 × 103 | ||
| 50 | Avg | 3.380 × 103 | 3.816 × 103 | 2.907 × 103 | 3.135 × 103 | 3.592 × 103 | 3.027 × 103 | 3.104 × 103 | 3.515 × 103 | 4.310 × 103 | 3.929 × 103 | 2.858 × 103 | |
| Min | 3.345 × 103 | 3.644 × 103 | 2.835 × 103 | 3.046 × 103 | 3.377 × 103 | 2.990 × 103 | 2.980 × 103 | 3.373 × 103 | 3.850 × 103 | 3.594 × 103 | 2.820 × 103 | ||
| 100 | Avg | 4.322 × 103 | 5.475 × 103 | 3.405 × 103 | 3.716 × 103 | 4.823 × 103 | 3.475 × 103 | 3.545 × 103 | 4.661 × 103 | 6.745 × 103 | 6.024 × 103 | 3.035 × 103 | |
| Min | 4.238 × 103 | 5.225 × 103 | 3.289 × 103 | 3.547 × 103 | 4.263 × 103 | 3.366 × 103 | 3.306 × 103 | 4.424 × 103 | 6.011 × 103 | 5.104 × 103 | 2.971 × 103 | ||
| F24 | 30 | Avg | 3.084 × 103 | 3.342 × 103 | 2.904 × 103 | 2.974 × 103 | 3.167 × 103 | 2.927 × 103 | 2.978 × 103 | 3.201 × 103 | 3.682 × 103 | 3.433 × 103 | 2.871 × 103 |
| Min | 3.063 × 103 | 3.270 × 103 | 2.855 × 103 | 2.910 × 103 | 3.021 × 103 | 2.897 × 103 | 2.928 × 103 | 3.128 × 103 | 3.473 × 103 | 3.217 × 103 | 2.852 × 103 | ||
| 50 | Avg | 3.459 × 103 | 4.039 × 103 | 3.087 × 103 | 3.227 × 103 | 3.733 × 103 | 3.136 × 103 | 3.231 × 103 | 3.713 × 103 | 4.749 × 103 | 4.359 × 103 | 3.008 × 103 | |
| Min | 3.416 × 103 | 3.856 × 103 | 3.000 × 103 | 3.152 × 103 | 3.545 × 103 | 3.071 × 103 | 3.135 × 103 | 3.588 × 103 | 4.340 × 103 | 3.875 × 103 | 2.964 × 103 | ||
| 100 | Avg | 5.059 × 103 | 8.073 × 103 | 3.962 × 103 | 4.272 × 103 | 5.854 × 103 | 4.086 × 103 | 4.293 × 103 | 5.913 × 103 | 1.065 × 104 | 8.875 × 103 | 3.651 × 103 | |
| Min | 4.961 × 103 | 7.435 × 103 | 3.819 × 103 | 4.124 × 103 | 5.238 × 103 | 3.976 × 103 | 4.048 × 103 | 5.524 × 103 | 8.928 × 103 | 6.869 × 103 | 3.556 × 103 | ||
| F25 | 30 | Avg | 4.148 × 103 | 5.436 × 103 | 2.957 × 103 | 3.107 × 103 | 2.945 × 103 | 2.889 × 103 | 2.887 × 103 | 4.099 × 103 | 4.426 × 103 | 3.940 × 103 | 2.888 × 103 |
| Min | 3.828 × 103 | 4.615 × 103 | 2.913 × 103 | 2.889 × 103 | 2.898 × 103 | 2.888 × 103 | 2.884 × 103 | 3.456 × 103 | 3.635 × 103 | 3.463 × 103 | 2.887 × 103 | ||
| 50 | Avg | 1.054 × 104 | 1.824 × 104 | 3.371 × 103 | 4.930 × 103 | 3.155 × 103 | 3.043 × 103 | 3.041 × 103 | 8.621 × 103 | 1.388 × 104 | 1.083 × 104 | 3.000 × 103 | |
| Min | 7.933 × 103 | 1.397 × 104 | 3.055 × 103 | 3.159 × 103 | 3.039 × 103 | 2.994 × 103 | 2.962 × 103 | 6.928 × 103 | 1.101 × 104 | 7.534 × 103 | 2.978 × 103 | ||
| 100 | Avg | 5.160 × 104 | 5.583 × 104 | 5.277 × 103 | 1.123 × 104 | 3.590 × 103 | 3.456 × 103 | 3.321 × 103 | 1.363 × 104 | 2.328 × 104 | 2.002 × 104 | 3.262 × 103 | |
| Min | 4.633 × 104 | 4.701 × 104 | 4.686 × 103 | 4.792 × 103 | 3.464 × 103 | 3.365 × 103 | 3.206 × 103 | 1.142 × 104 | 1.986 × 104 | 1.680 × 104 | 3.116 × 103 | ||
| F26 | 30 | Avg | 6.408 × 103 | 8.876 × 103 | 4.424 × 103 | 5.689 × 103 | 7.599 × 103 | 5.012 × 103 | 5.447 × 103 | 6.328 × 103 | 9.412 × 103 | 8.871 × 103 | 4.300 × 103 |
| Min | 5.542 × 103 | 7.735 × 103 | 3.954 × 103 | 4.921 × 103 | 5.975 × 103 | 4.607 × 103 | 4.955 × 103 | 5.882 × 103 | 7.702 × 103 | 5.057 × 103 | 2.900 × 103 | ||
| 50 | Avg | 1.063 × 104 | 1.594 × 104 | 5.735 × 103 | 8.121 × 103 | 1.306 × 104 | 7.041 × 103 | 8.059 × 103 | 1.028 × 104 | 1.546 × 104 | 1.587 × 104 | 5.179 × 103 | |
| Min | 1.002 × 104 | 1.454 × 104 | 5.192 × 103 | 6.910 × 103 | 9.977 × 103 | 6.161 × 103 | 7.062 × 103 | 9.047 × 103 | 1.326 × 104 | 1.396 × 104 | 4.512 × 103 | ||
| 100 | Avg | 2.452 × 104 | 4.461 × 104 | 1.263 × 104 | 1.741 × 104 | 3.111 × 104 | 1.493 × 104 | 1.752 × 104 | 2.492 × 104 | 4.995 × 104 | 4.315 × 104 | 9.748 × 103 | |
| Min | 2.363 × 104 | 4.099 × 104 | 1.124 × 104 | 1.526 × 104 | 2.326 × 104 | 1.333 × 104 | 1.518 × 104 | 2.276 × 104 | 4.219 × 104 | 3.583 × 104 | 9.123 × 103 | ||
| F27 | 30 | Avg | 3.279 × 103 | 3.667 × 103 | 3.229 × 103 | 3.236 × 103 | 3.346 × 103 | 3.221 × 103 | 3.228 × 103 | 3.493 × 103 | 4.286 × 103 | 3.688 × 103 | 3.213 × 103 |
| Min | 3.250 × 103 | 3.497 × 103 | 3.212 × 103 | 3.208 × 103 | 3.282 × 103 | 3.200 × 103 | 3.201 × 103 | 3.355 × 103 | 3.633 × 103 | 3.397 × 103 | 3.184 × 103 | ||
| 50 | Avg | 3.730 × 103 | 5.183 × 103 | 3.471 × 103 | 3.550 × 103 | 4.305 × 103 | 3.356 × 103 | 3.504 × 103 | 4.272 × 103 | 6.565 × 103 | 5.306 × 103 | 3.337 × 103 | |
| Min | 3.669 × 103 | 4.697 × 103 | 3.342 × 103 | 3.407 × 103 | 3.678 × 103 | 3.249 × 103 | 3.377 × 103 | 3.997 × 103 | 5.687 × 103 | 4.453 × 103 | 3.231 × 103 | ||
| 100 | Avg | 4.858 × 103 | 8.855 × 103 | 3.854 × 103 | 3.867 × 103 | 4.945 × 103 | 3.500 × 103 | 3.607 × 103 | 5.656 × 103 | 1.177 × 104 | 9.335 × 103 | 3.467 × 103 | |
| Min | 4.700 × 103 | 7.573 × 103 | 3.594 × 103 | 3.655 × 103 | 3.909 × 103 | 3.389 × 103 | 3.482 × 103 | 5.033 × 103 | 9.541 × 103 | 5.884 × 103 | 3.381 × 103 | ||
| F28 | 30 | Avg | 4.040 × 103 | 5.557 × 103 | 3.339 × 103 | 3.721 × 103 | 3.303 × 103 | 3.255 × 103 | 3.194 × 103 | 4.295 × 103 | 5.958 × 103 | 5.524 × 103 | 3.226 × 103 |
| Min | 3.927 × 103 | 4.829 × 103 | 3.269 × 103 | 3.318 × 103 | 3.269 × 103 | 3.209 × 103 | 3.100 × 103 | 3.565 × 103 | 4.603 × 103 | 4.419 × 103 | 3.155 × 103 | ||
| 50 | Avg | 8.098 × 103 | 1.147 × 104 | 3.873 × 103 | 8.080 × 103 | 3.424 × 103 | 3.316 × 103 | 3.298 × 103 | 6.101 × 103 | 1.102 × 104 | 9.557 × 103 | 3.278 × 103 | |
| Min | 6.921 × 103 | 8.816 × 103 | 3.653 × 103 | 5.324 × 103 | 3.344 × 103 | 3.274 × 103 | 3.259 × 103 | 5.216 × 103 | 9.574 × 103 | 8.008 × 103 | 3.259 × 103 | ||
| 100 | Avg | 2.499 × 104 | 3.958 × 104 | 6.692 × 103 | 1.749 × 104 | 3.721 × 103 | 1.149 × 104 | 7.644 × 103 | 1.204 × 104 | 2.938 × 104 | 2.320 × 104 | 3.357 × 103 | |
| Min | 2.393 × 104 | 3.584 × 104 | 4.771 × 103 | 1.485 × 104 | 3.598 × 103 | 3.439 × 103 | 3.333 × 103 | 9.983 × 103 | 2.587 × 104 | 1.831 × 104 | 3.321 × 103 | ||
| F29 | 30 | Avg | 4.387 × 103 | 5.321 × 103 | 3.645 × 103 | 4.003 × 103 | 4.751 × 103 | 3.785 × 103 | 3.965 × 103 | 4.348 × 103 | 5.689 × 103 | 5.698 × 103 | 3.465 × 103 |
| Min | 4.114 × 103 | 4.426 × 103 | 3.459 × 103 | 3.603 × 103 | 4.062 × 103 | 3.596 × 103 | 3.650 × 103 | 4.057 × 103 | 4.626 × 103 | 4.728 × 103 | 3.343 × 103 | ||
| 50 | Avg | 6.503 × 103 | 9.644 × 103 | 4.214 × 103 | 5.076 × 103 | 7.281 × 103 | 4.337 × 103 | 4.671 × 103 | 6.906 × 103 | 1.548 × 104 | 1.622 × 104 | 3.589 × 103 | |
| Min | 5.954 × 103 | 7.327 × 103 | 3.750 × 103 | 4.271 × 103 | 6.025 × 103 | 3.820 × 103 | 3.992 × 103 | 5.462 × 103 | 8.398 × 103 | 8.290 × 103 | 3.288 × 103 | ||
| 100 | Avg | 1.758 × 104 | 5.024 × 104 | 7.229 × 103 | 1.370 × 104 | 1.413 × 104 | 6.953 × 103 | 7.986 × 103 | 1.940 × 104 | 8.567 × 104 | 5.425 × 104 | 5.805 × 103 | |
| Min | 1.557 × 104 | 2.701 × 104 | 6.385 × 103 | 7.555 × 103 | 1.053 × 104 | 5.760 × 103 | 7.019 × 103 | 1.268 × 104 | 3.350 × 104 | 1.727 × 104 | 5.194 × 103 | ||
| F30 | 30 | Avg | 1.398 × 107 | 1.149 × 108 | 7.020 × 106 | 3.271 × 105 | 6.709 × 106 | 1.579 × 105 | 2.811 × 104 | 3.527 × 107 | 4.703 × 107 | 3.278 × 108 | 1.064 × 104 |
| Min | 4.880 × 106 | 2.608 × 107 | 8.829 × 105 | 1.393 × 104 | 4.463 × 105 | 4.934 × 104 | 1.582 × 104 | 1.030 × 107 | 1.875 × 106 | 3.212 × 107 | 5.336 × 103 | ||
| 50 | Avg | 3.257 × 108 | 1.521 × 109 | 6.713 × 107 | 8.852 × 107 | 8.101 × 107 | 5.293 × 106 | 2.475 × 106 | 5.299 × 108 | 5.682 × 108 | 2.207 × 109 | 1.323 × 106 | |
| Min | 1.906 × 108 | 7.735 × 108 | 3.536 × 107 | 2.389 × 106 | 4.041 × 107 | 3.797 × 106 | 1.155 × 106 | 1.890 × 108 | 1.863 × 108 | 2.782 × 108 | 7.972 × 105 | ||
| 100 | Avg | 3.841 × 109 | 1.351 × 1010 | 3.958 × 108 | 1.283 × 109 | 1.922 × 108 | 1.283 × 107 | 1.932 × 106 | 1.185 × 1010 | 3.055 × 1010 | 1.581 × 1010 | 7.578 × 103 | |
| Min | 3.148 × 109 | 8.053 × 109 | 5.455 × 107 | 3.821 × 107 | 7.264 × 107 | 7.913 × 106 | 3.637 × 105 | 8.263 × 109 | 1.450 × 1010 | 4.669 × 109 | 5.286 × 103 | ||
| 30 | W|T|L | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 2/0/8 | 0/0/10 | 0/0/10 | 0/0/10 | 8/0/2 | |
| Ranking | 50 | W|T|L | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 10/0/0 |
| 100 | W|T|L | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 0/0/10 | 10/0/0 |
| Algorithms | SA (W/T/L) | CGA (W/T/L) | GWO (W/T/L) | MFO (W/T/L) | WOA (W/T/L) | LMFO (W/T/L) | WCMFO (W/T/L) | ChOA (W/T/L) | AOA (W/T/L) | SMFO (W/T/L) | I-MFO (W/T/L) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| D = 30 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 2/0/27 | 0/0/29 | 0/0/29 | 0/0/29 | 27/0/2 |
| D = 50 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 3/0/26 | 0/0/29 | 0/0/29 | 0/0/29 | 26/0/3 |
| D = 100 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 0/0/29 | 2/0/27 | 0/0/29 | 0/0/29 | 0/0/29 | 27/0/2 |
| Total | 0/0/87 | 0/0/87 | 0/0/87 | 0/0/87 | 0/0/87 | 0/0/87 | 7/0/80 | 0/0/87 | 0/0/87 | 0/0/87 | 80/0/7 |
| OE | 0% | 0% | 0% | 0% | 0% | 0% | 8% | 0% | 0% | 0% | 92% |
| Functions | Unimodal Functions | Multimodal Functions | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dimensions | 30 | 50 | 100 | 30 | 50 | 100 | ||||||
| Algorithms | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank |
| SA | 9.22 | 10 | 9.77 | 10 | 10.50 | 11 | 8.67 | 9 | 9.45 | 10 | 10.15 | 10 |
| CGA | 9.75 | 11 | 10.42 | 11 | 10.25 | 10 | 10.49 | 11 | 10.74 | 11 | 10.29 | 11 |
| GWO | 4.57 | 4 | 5.12 | 5 | 4.12 | 3 | 2.52 | 2 | 2.66 | 2 | 2.578 | 2 |
| MFO | 6.30 | 6 | 6.07 | 6 | 6.30 | 7 | 4.65 | 5 | 4.67 | 5 | 5.26 | 6 |
| WOA | 6.70 | 7 | 3.60 | 4 | 6.10 | 5 | 6.21 | 6 | 5.45 | 6 | 4.53 | 4 |
| LMFO | 3.45 | 3 | 3.57 | 3 | 4.15 | 4 | 2.99 | 3 | 2.85 | 3 | 3.29 | 3 |
| WCMFO | 1.77 | 2 | 1.62 | 2 | 1.70 | 2 | 4.61 | 4 | 4.52 | 4 | 4.67 | 5 |
| ChOA | 6.17 | 5 | 6.70 | 7 | 6.17 | 6 | 7.19 | 7 | 7.27 | 7 | 7.34 | 7 |
| AOA | 8.12 | 8 | 9.02 | 9 | 7.80 | 9 | 7.67 | 8 | 8.04 | 8 | 7.98 | 8 |
| SMFO | 8.57 | 9 | 8.57 | 8 | 7.57 | 8 | 9.75 | 10 | 9.14 | 9 | 8.82 | 9 |
| I-MFO | 1.35 | 1 | 1.50 | 1 | 1.32 | 1 | 1.20 | 1 | 1.17 | 1 | 1.06 | 1 |
| Functions | Hybrid Functions | Composition Functions | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dimensions | 30 | 50 | 100 | 30 | 50 | 100 | ||||||
| Algorithms | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank | Avg. Rank | Overall Rank |
| SA | 7.96 | 8 | 8.74 | 9 | 8.52 | 8 | 7.20 | 7 | 8.74 | 9 | 7.68 | 8 |
| CGA | 9.94 | 10 | 10.19 | 11 | 10.20 | 11 | 9.50 | 9 | 10.19 | 11 | 9.65 | 10 |
| GWO | 3.79 | 2 | 3.79 | 3 | 4.17 | 5 | 3.12 | 2 | 3.795 | 3 | 3.14 | 2 |
| MFO | 3.87 | 4 | 4.56 | 5 | 5.4 | 6 | 4.36 | 5 | 4.56 | 5 | 4.95 | 5 |
| WOA | 6.49 | 7 | 5.14 | 6 | 4.04 | 4 | 6.05 | 6 | 5.14 | 6 | 5.83 | 6 |
| LMFO | 4.63 | 5 | 4.06 | 4 | 3.65 | 3 | 3.39 | 3 | 4.06 | 4 | 3.23 | 3 |
| WCMFO | 3.86 | 3 | 3.57 | 2 | 2.95 | 2 | 3.99 | 4 | 3.57 | 2 | 3.55 | 4 |
| ChOA | 8.18 | 9 | 7.74 | 8 | 7.48 | 7 | 7.70 | 8 | 7.74 | 8 | 7.4 | 7 |
| AOA | 5.81 | 6 | 6.96 | 7 | 8.8 | 9 | 9.64 | 10 | 6.96 | 7 | 10.15 | 11 |
| SMFO | 10.21 | 11 | 10.12 | 10 | 9.62 | 10 | 9.90 | 11 | 10.12 | 10 | 9.36 | 9 |
| I-MFO | 1.23 | 1 | 1.10 | 1 | 1.09 | 1 | 1.12 | 1 | 1.10 | 1 | 1.03 | 1 |
| Dimensions | 30 | 50 | 100 | |||
|---|---|---|---|---|---|---|
| Algorithms | Bonferroni p-Value | Tukey p-Value | Bonferroni p-Value | Tukey p-Value | Bonferroni p-Value | Tukey p-Value |
| SA | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10-08 |
| CGA | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 |
| GWO | 5.337 × 10−7 | 5.338 × 10−7 | 5.337 × 10−7 | 5.338 × 10−7 | 7.238 × 10−8 | 7.247 × 10−8 |
| MFO | 5.337 × 10−7 | 5.338 × 10−7 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 |
| WOA | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 |
| LMFO | 3.444 × 10−6 | 3.444 × 10−6 | 5.337 × 10−7 | 5.338 × 10−7 | 5.337 × 10−7 | 5.338 × 10−7 |
| WCMFO | 1.595 × 10−3 | 1.595 × 10−3 | 3.444 × 10−6 | 3.444 × 10−6 | 3.444 × 10−6 | 3.444 × 10−6 |
| ChOA | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 |
| AOA | 5.337 × 10−7 | 5.338 × 10−7 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 |
| SMFO | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 | 7.238 × 10−8 | 7.247 × 10−8 |
| Algorithms | Optimal Values for Variables | Optimal Cost | |||
|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | ||
| SA | 46.76 | 1.62 | 25.79 | 0.55 | 4.390311 × 106 |
| CGA | 49.97 | 20.01 | 31.47 | 49.83 | 1.735023 × 107 |
| GWO | 20.00 | 7.81 | 20.00 | 60.00 | 2.964974 × 106 |
| MFO | 50.00 | 1.18 | 24.57 | 0.39 | 2.964902 × 106 |
| WOA | 50.00 | 1.18 | 24.86 | 0.39 | 2.965002 × 106 |
| LMFO | 49.46 | 1.18 | 24.64 | 0.39 | 2.965456 × 106 |
| WCMFO | 50.00 | 1.18 | 24.61 | 0.39 | 2.964897 × 106 |
| ChOA | 50.00 | 1.19 | 24.24 | 0.41 | 2.966828 × 106 |
| AOA | 50.00 | 1.23 | 20.00 | 0.51 | 3.014615 × 106 |
| SMFO | 23.66 | 1.09 | 23.66 | 0.19 | 3.052254 × 106 |
| I-MFO | 50.00 | 1.18 | 24.60 | 0.39 | 2.964896 × 106 |
| Algorithms | Optimal Values for Variables | Optimal Weight | |
|---|---|---|---|
| x1 | x2 | ||
| SA | 0.768630 | 0.474232 | 2.6482456 × 102 |
| CGA | 0.792428 | 0.397752 | 2.6390770 × 102 |
| GWO | 0.787771 | 0.410872 | 2.6389619 × 102 |
| MFO | 0.789186 | 0.406806 | 2.6389603 × 102 |
| WOA | 0.787713 | 0.410977 | 2.6389653 × 102 |
| LMFO | 0.791713 | 0.399909 | 2.6392114 × 102 |
| WCMFO | 0.788472 | 0.408822 | 2.6389589 × 102 |
| ChOA | 0.787802 | 0.410724 | 2.6389653 × 102 |
| AOA | 0.792789 | 0.396906 | 2.6392526 × 102 |
| SMFO | 0.792044 | 0.398859 | 2.6390973 × 102 |
| I-MFO | 0.788792 | 0.407919 | 2.6389585 × 102 |
| Algorithms | Optimal Values for Variables | Optimum Weight | ||
|---|---|---|---|---|
| d | D | N | ||
| SA | 0.075935 | 0.993094 | 3.879891 | 0.033670 |
| CGA | 0.071031 | 1.019975 | 1.726076 | 0.019749 |
| GWO | 0.051231 | 0.345699 | 11.970135 | 0.012676 |
| MFO | 0.053064 | 0.390718 | 9.542437 | 0.012699 |
| WOA | 0.050451 | 0.327675 | 13.219341 | 0.012694 |
| LMFO | 0.050000 | 0.317154 | 14.107156 | 0.012771 |
| WCMFO | 0.051509 | 0.352411 | 11.545969 | 0.012666 |
| ChOA | 0.051069 | 0.341746 | 12.251078 | 0.012702 |
| AOA | 0.050000 | 0.310475 | 15.000000 | 0.013195 |
| SMFO | 0.050000 | 0.314692 | 14.696505 | 0.013136 |
| I-MFO | 0.051710 | 0.357217 | 11.259785 | 0.012665 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nadimi-Shahraki, M.H.; Fatahi, A.; Zamani, H.; Mirjalili, S.; Abualigah, L. An Improved Moth-Flame Optimization Algorithm with Adaptation Mechanism to Solve Numerical and Mechanical Engineering Problems. Entropy 2021, 23, 1637. https://doi.org/10.3390/e23121637
Nadimi-Shahraki MH, Fatahi A, Zamani H, Mirjalili S, Abualigah L. An Improved Moth-Flame Optimization Algorithm with Adaptation Mechanism to Solve Numerical and Mechanical Engineering Problems. Entropy. 2021; 23(12):1637. https://doi.org/10.3390/e23121637
Chicago/Turabian StyleNadimi-Shahraki, Mohammad H., Ali Fatahi, Hoda Zamani, Seyedali Mirjalili, and Laith Abualigah. 2021. "An Improved Moth-Flame Optimization Algorithm with Adaptation Mechanism to Solve Numerical and Mechanical Engineering Problems" Entropy 23, no. 12: 1637. https://doi.org/10.3390/e23121637
APA StyleNadimi-Shahraki, M. H., Fatahi, A., Zamani, H., Mirjalili, S., & Abualigah, L. (2021). An Improved Moth-Flame Optimization Algorithm with Adaptation Mechanism to Solve Numerical and Mechanical Engineering Problems. Entropy, 23(12), 1637. https://doi.org/10.3390/e23121637










