Gradient Regularization as Approximate Variational Inference
Abstract
:1. Introduction
2. Background
2.1. Variational Inference (VI) for Bayesian Neural Networks
2.2. Laplace’s Method
3. Related Work
4. Methods
4.1. Pathological Optima When Using the Hessian
4.2. Avoiding Pathologies with the Fisher
4.3. Constraints on the Network Architecture
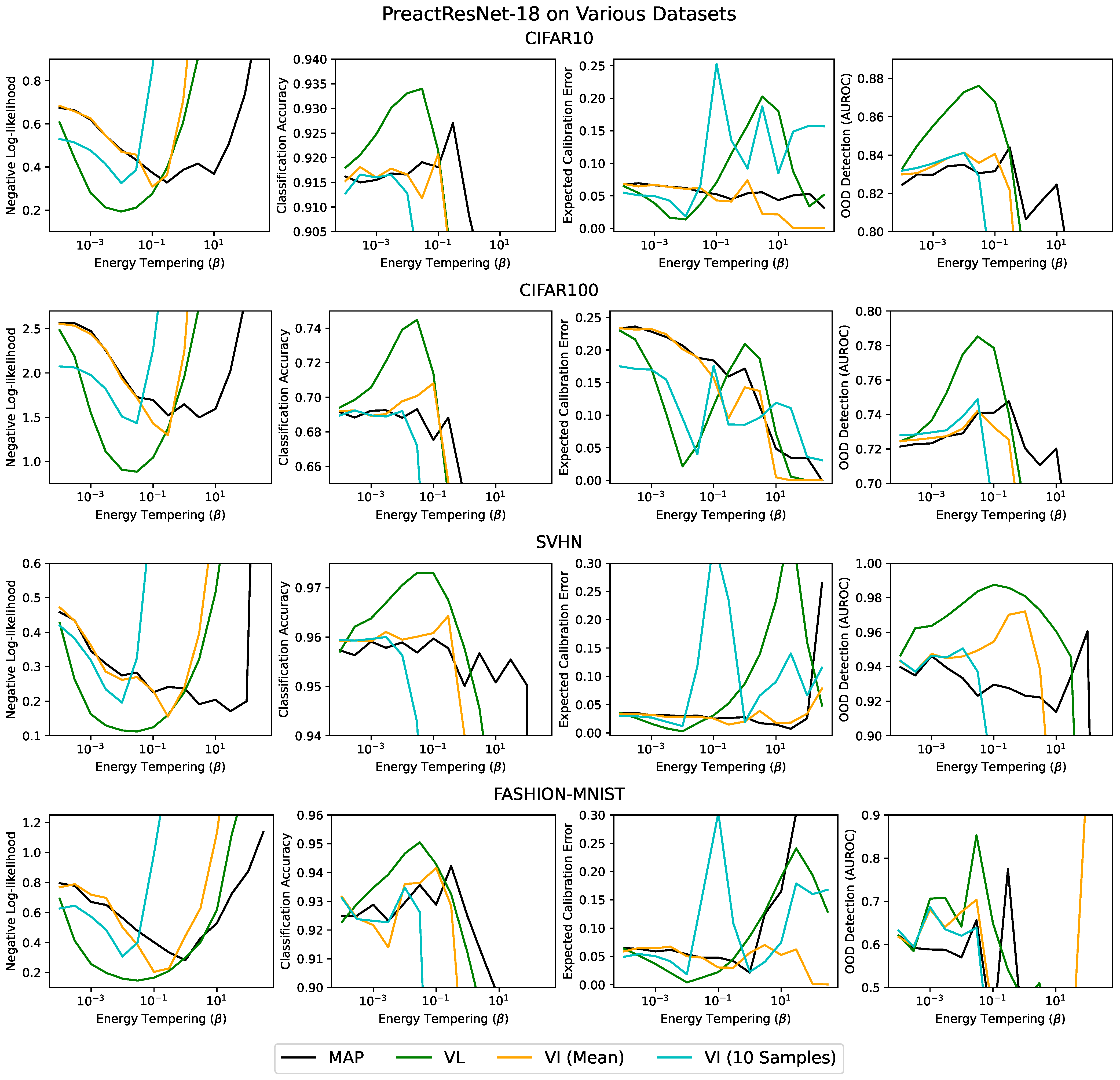
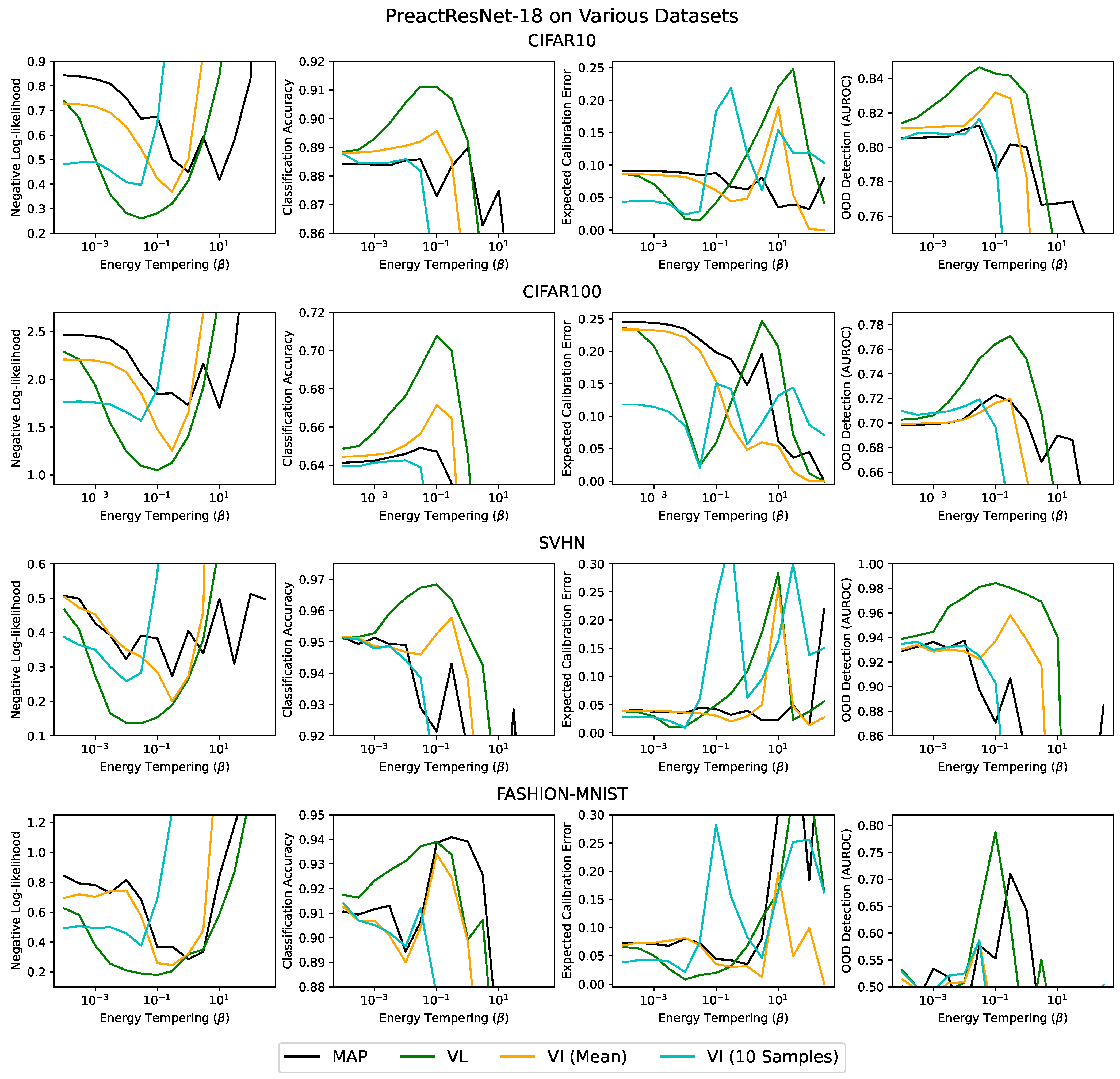
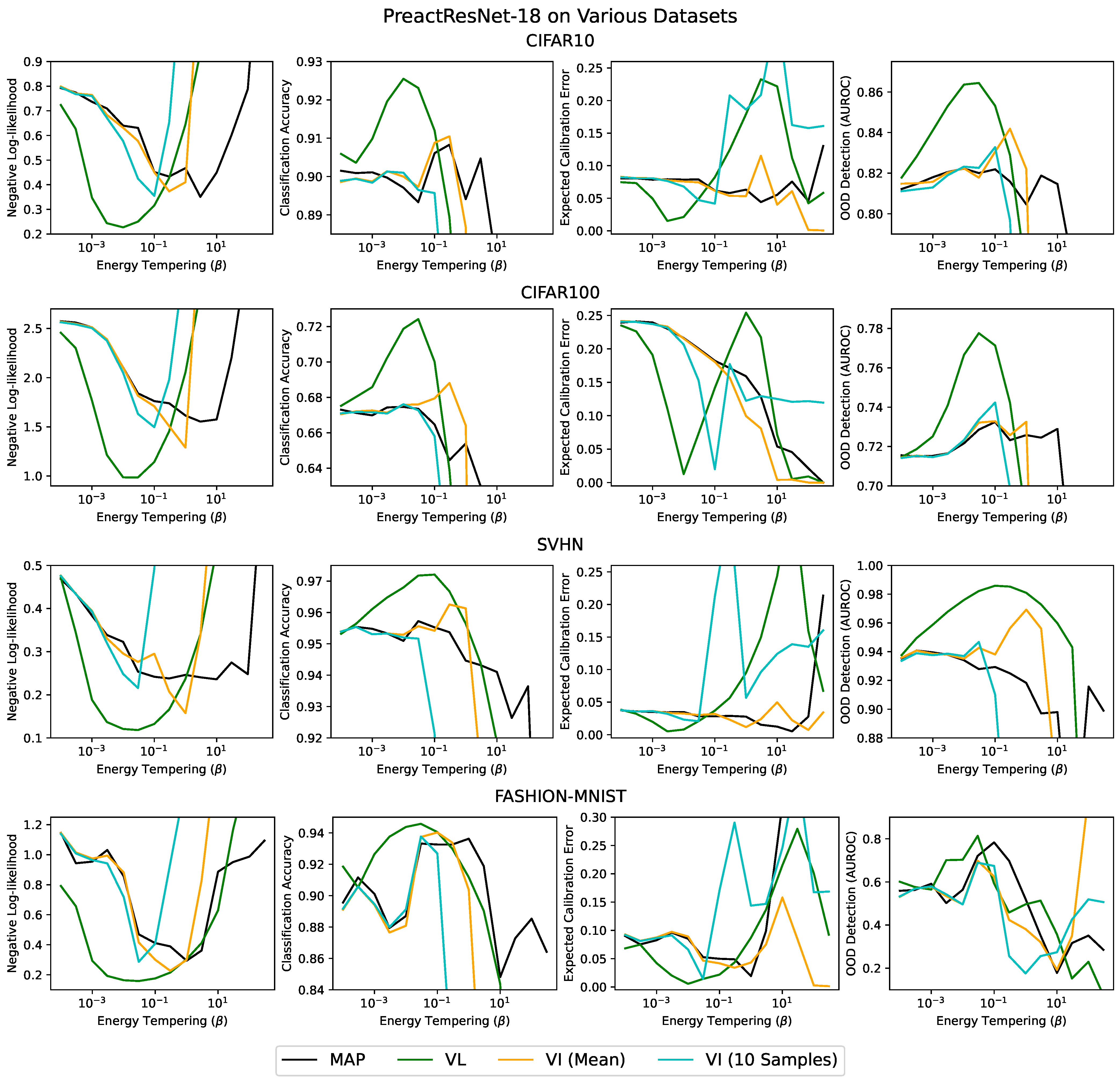
5. Results
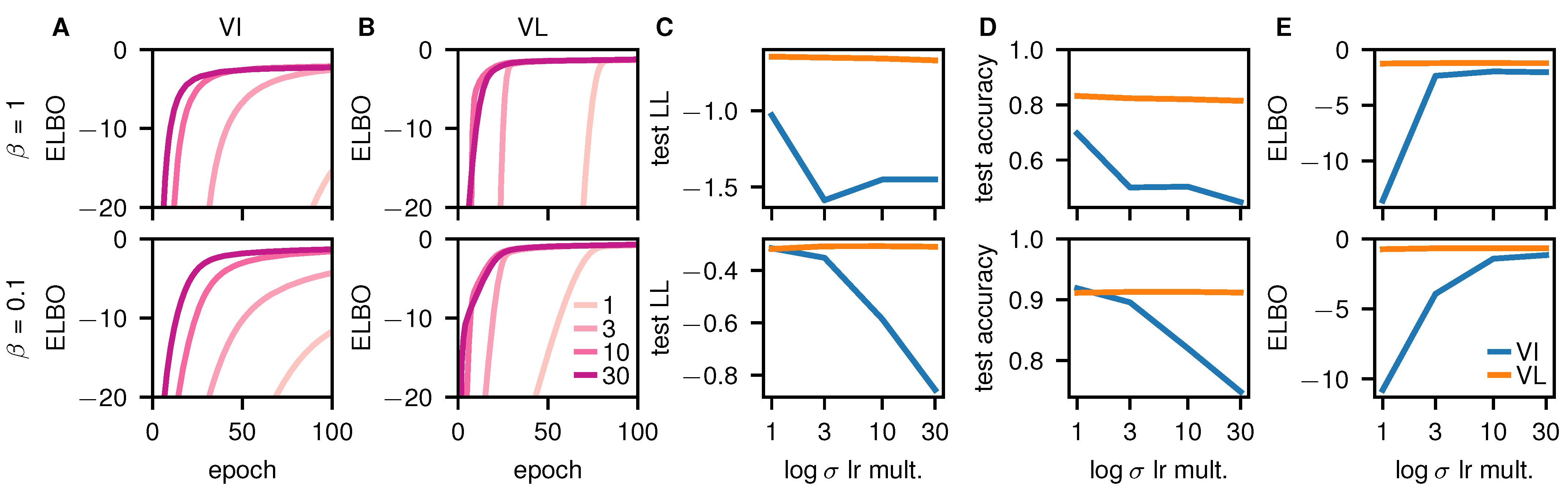
Early-Stopping and Poor Performance in VI
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Stationary Distribution of SGD
Appendix B. Varying the Batch Size
References
- Bojarski, M.; Del Testa, D.; Dworakowski, D.; Firner, B.; Flepp, B.; Goyal, P.; Jackel, L.D.; Monfort, M.; Muller, U.; Zhang, J.; et al. End to end learning for self-driving cars. arXiv 2016, arXiv:1604.07316. [Google Scholar]
- Amato, F.; López, A.; Peña-Méndez, E.M.; Vanhara, P.; Hampl, A.; Havel, J. Artificial neural networks in medical diagnosis. J. Appl. Biomed. 2013, 11, 47–58. [Google Scholar] [CrossRef]
- McAllister, R.; Gal, Y.; Kendall, A.; Van Der Wilk, M.; Shah, A.; Cipolla, R.; Weller, A. Concrete problems for autonomous vehicle safety: Advantages of bayesian deep learning. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017. [Google Scholar]
- Welling, M.; Teh, Y.W. Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 681–688. [Google Scholar]
- Azevedo-Filho, A.; Shachter, R.D. Laplace’s Method Approximations for Probabilistic Inference in Belief Networks with Continuous Variables. In Uncertainty Proceedings 1994; Elsevier: Amsterdam, The Netherlands, 1994; pp. 28–36. [Google Scholar]
- MacKay, D.J. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Ritter, H.; Botev, A.; Barber, D. A scalable laplace approximation for neural networks. In Proceedings of the 6th International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 30 April–3 May 2018; Volume 6. [Google Scholar]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight uncertainty in neural networks. arXiv 2015, arXiv:1505.05424. [Google Scholar]
- Ober, S.W.; Aitchison, L. Global inducing point variational posteriors for Bayesian neural networks and deep Gaussian processes. arXiv 2020, arXiv:2005.08140. [Google Scholar]
- Wainwright, M.J.; Jordan, M.I. Graphical Models, Exponential Families, and Variational Inference; Now Publishers Inc.: Delft, The Netherlands, 2008. [Google Scholar]
- Neyshabur, B.; Bhojanapalli, S.; McAllester, D.; Srebro, N. Exploring generalization in deep learning. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 5947–5956. [Google Scholar]
- Barrett, D.G.; Dherin, B. Implicit Gradient Regularization. arXiv 2020, arXiv:2009.11162. [Google Scholar]
- Geiping, J.; Goldblum, M.; Pope, P.E.; Moeller, M.; Goldstein, T. Stochastic training is not necessary for generalization. arXiv 2021, arXiv:2109.14119. [Google Scholar]
- Hinton, G.E.; Van Camp, D. Keeping the neural networks simple by minimizing the description length of the weights. In Proceedings of the Sixth Annual Conference on Computational Learning Theory, Santa Cruz, CA, USA, 26–28 July 1993; pp. 5–13. [Google Scholar]
- Huang, C.W.; Tan, S.; Lacoste, A.; Courville, A.C. Improving explorability in variational inference with annealed variational objectives. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2018; pp. 9701–9711. [Google Scholar]
- Wenzel, F.; Roth, K.; Veeling, B.S.; Swiatkowski, J.; Tran, L.; Mandt, S.; Snoek, J.; Salimans, T.; Jenatton, R.; Nowozin, S. How Good is the Bayes Posterior in Deep Neural Networks Really? arXiv 2020, arXiv:2002.02405. [Google Scholar]
- Aitchison, L. A statistical theory of cold posteriors in deep neural networks. arXiv 2020, arXiv:2008.05912. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Rezende, D.J.; Mohamed, S.; Wierstra, D. Stochastic backpropagation and approximate inference in deep generative models. arXiv 2014, arXiv:1401.4082. [Google Scholar]
- Friston, K.; Mattout, J.; Trujillo-Barreto, N.; Ashburner, J.; Penny, W. Variational free energy and the Laplace approximation. NeuroImage 2007, 34, 220–234. [Google Scholar] [CrossRef]
- Daunizeau, J.; Friston, K.J.; Kiebel, S.J. Variational Bayesian identification and prediction of stochastic nonlinear dynamic causal models. Phys. D Nonlinear Phenom. 2009, 238, 2089–2118. [Google Scholar] [CrossRef] [Green Version]
- Daunizeau, J. The Variational Laplace approach to approximate Bayesian inference. arXiv 2017, arXiv:1703.02089. [Google Scholar]
- Wu, A.; Nowozin, S.; Meeds, E.; Turner, R.E.; Hernández-Lobato, J.M.; Gaunt, A.L. Deterministic variational inference for robust bayesian neural networks. arXiv 2018, arXiv:1810.03958. [Google Scholar]
- Haußmann, M.; Hamprecht, F.A.; Kandemir, M. Sampling-free variational inference of bayesian neural networks by variance backpropagation. In Proceedings of the 35th Uncertainty in Artificial Intelligence Conference, Tel Aviv, Israel, 22–25 July 2019; pp. 563–573. [Google Scholar]
- MacKay, D.J. A practical Bayesian framework for backpropagation networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Smith, S.L.; Dherin, B.; Barrett, D.G.; De, S. On the Origin of Implicit Regularization in Stochastic Gradient Descent. arXiv 2021, arXiv:2101.12176. [Google Scholar]
- Kunstner, F.; Hennig, P.; Balles, L. Limitations of the empirical Fisher approximation for natural gradient descent. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 4156–4167. [Google Scholar]
- Khan, M.E.; Immer, A.; Abedi, E.; Korzepa, M. Approximate inference turns deep networks into gaussian processes. arXiv 2019, arXiv:1906.01930. [Google Scholar]
- Kuok, S.C.; Yuen, K.V. Broad Bayesian learning (BBL) for nonparametric probabilistic modeling with optimized architecture configuration. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 1270–1287. [Google Scholar] [CrossRef]
- Yao, J.; Pan, W.; Ghosh, S.; Doshi-Velez, F. Quality of uncertainty quantification for Bayesian neural network inference. arXiv 2019, arXiv:1906.09686. [Google Scholar]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On calibration of modern neural networks. In Proceedings of the 34th International Conference on Machine Learning (ICML 2017), Sydney, NSW, Australia, 6–11 August 2017; pp. 1321–1330. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading digits in natural images with unsupervised feature learning. In Proceedings of the NIPS 2011 Workshop on Deep Learning and Unsupervised Feature Learning, Granada, Spain, 16–17 December 2011. [Google Scholar]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 630–645. [Google Scholar]
- Naeini, M.P.; Cooper, G.; Hauskrecht, M. Obtaining well calibrated probabilities using bayesian binning. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Chrabaszcz, P.; Loshchilov, I.; Hutter, F. A Downsampled Variant of ImageNet as an Alternative to the CIFAR datasets. arXiv 2017, arXiv:1707.08819. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Mandt, S.; Hoffman, M.D.; Blei, D.M. Stochastic gradient descent as approximate bayesian inference. J. Mach. Learn. Res. 2017, 18, 4873–4907. [Google Scholar]
| Dataset | Method | Test NLL | Test Acc. | ECE |
|---|---|---|---|---|
| CIFAR-10 | VL | 0.23 | 92.4% | 0.017 |
| VI (Mean) | 0.37 | 91.1% | 0.053 | |
| VI (10 Samples) | 0.35 | 90.2% | 0.044 | |
| MAP | 0.43 | 90.8% | 0.058 | |
| CIFAR-100 | VL | 1.00 | 71.4% | 0.024 |
| VI (Mean) | 1.29 | 68.8% | 0.100 | |
| VI (10 Samples) | 1.49 | 67.3% | 0.026 | |
| MAP | 1.61 | 67.5% | 0.159 | |
| SVHN | VL | 0.14 | 97.1% | 0.009 |
| VI (Mean) | 0.16 | 96.3% | 0.012 | |
| VI (10 Samples) | 0.22 | 95.5% | 0.022 | |
| MAP | 0.24 | 95.7% | 0.028 | |
| Fashion MNIST | VL | 0.16 | 94.6% | 0.010 |
| VI (Mean) | 0.23 | 94.0% | 0.034 | |
| VI (10 Samples) | 0.29 | 93.6% | 0.016 | |
| MAP | 0.29 | 93.6% | 0.096 |
| Method | Time per Epoch (s) |
|---|---|
| VL | 114.9 |
| VI | 43.2 |
| MAP | 41.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unlu, A.; Aitchison, L. Gradient Regularization as Approximate Variational Inference. Entropy 2021, 23, 1629. https://doi.org/10.3390/e23121629
Unlu A, Aitchison L. Gradient Regularization as Approximate Variational Inference. Entropy. 2021; 23(12):1629. https://doi.org/10.3390/e23121629
Chicago/Turabian StyleUnlu, Ali, and Laurence Aitchison. 2021. "Gradient Regularization as Approximate Variational Inference" Entropy 23, no. 12: 1629. https://doi.org/10.3390/e23121629
APA StyleUnlu, A., & Aitchison, L. (2021). Gradient Regularization as Approximate Variational Inference. Entropy, 23(12), 1629. https://doi.org/10.3390/e23121629





