Perfect Density Models Cannot Guarantee Anomaly Detection
Abstract
:1. Introduction
- Similar to classification, we propose in Section 3 a principle of invariance to formalize the underlying assumptions behind the current practice of (deep) density-based methods.
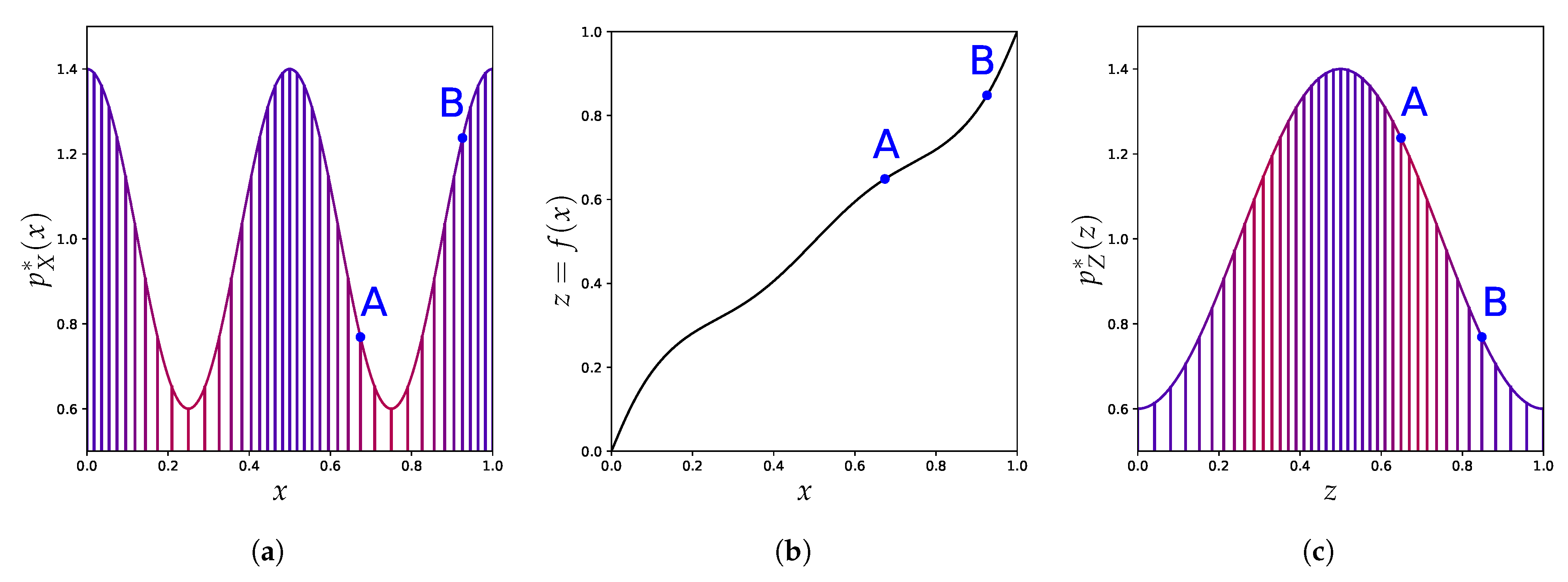
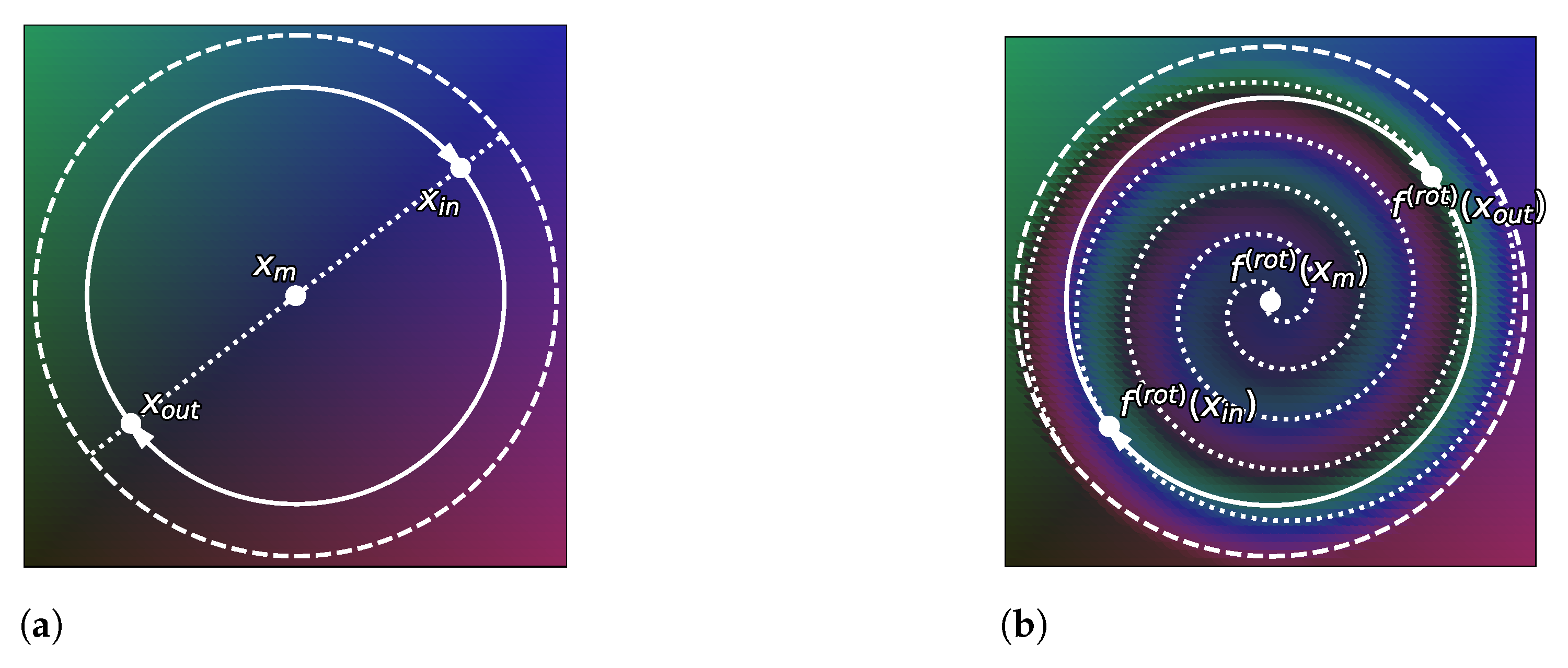
- We use the well-known change of variables formula for probability density to show in Section 4 how these density-based methods are not invariant to reparametrization (see Figure 1) and contradict this principle. We demonstrate the extent of the issues with current practices by building adversarial cases, even under strong distributional constraints.
- Given the resulting tension between the use of these anomaly detection methods and their lack of invariance, we focus in Section 5 on the importance of explicitly incorporating prior knowledge into (density-based) anomaly detection methods as a more promising avenue to reconcile this tension.
2. Density-Based Anomaly Detection
2.1. Unsupervised Anomaly Detection: Problem Statement
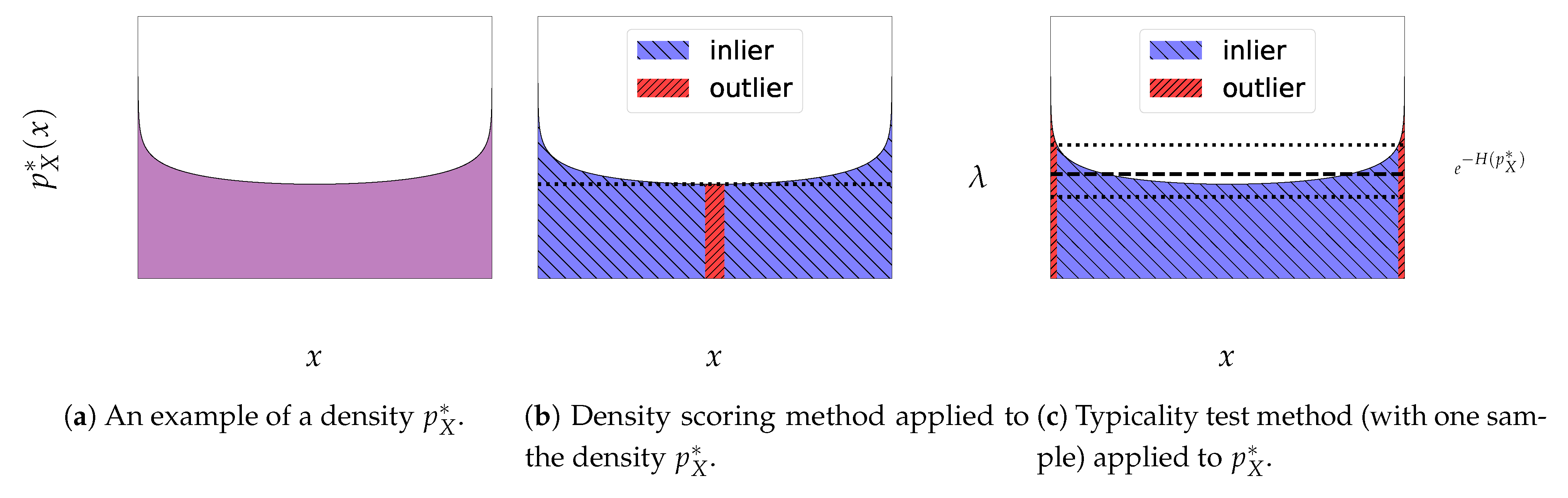
2.2. Density Scoring Method
2.3. Typicality Test Method
3. The Role of Reparametrization
3.1. A Binary Classification Analogy
3.2. A Principle for Anomaly Detection Methods
4. Leveraging the Change of Variables Formula
4.1. Uniformization
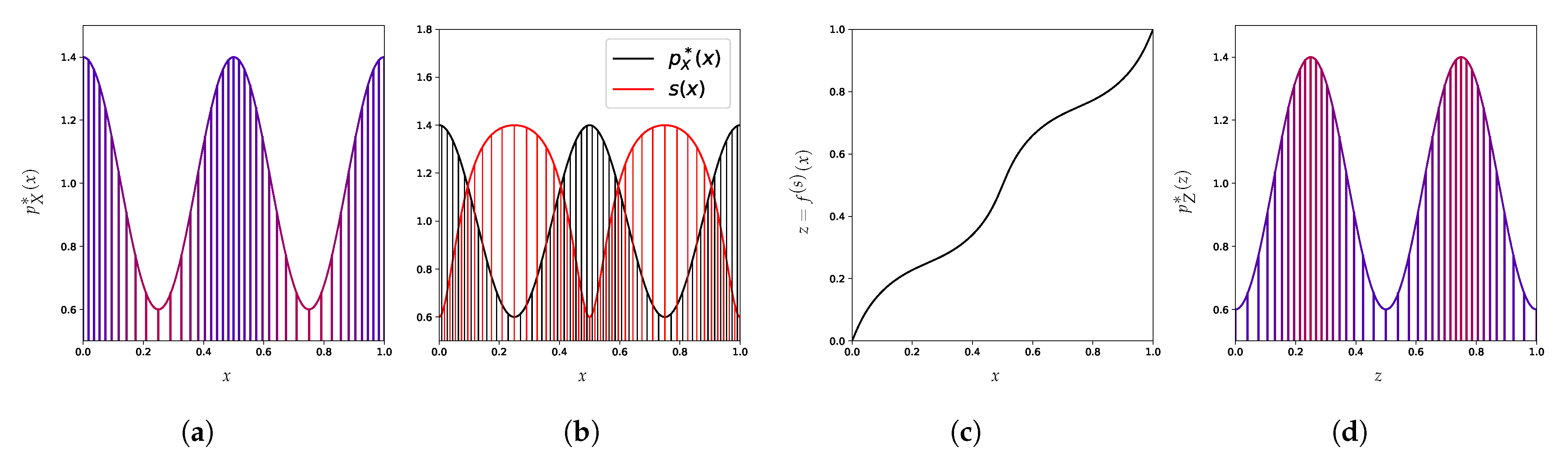
4.2. Arbitrary Scoring
4.3. Canonical Distribution
4.4. Practical Consequences for Anomaly Detection
4.4.1. Learning a Representation by Applying Explicit Transformations f
4.4.2. Arbitrary Input Representation Result from Implicit Transformations f
5. Promising Avenues for Unsupervised Density-Based Anomaly Detection
6. Discussion and Limitations
7. Broader Impact
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Proposition 2
References
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.J.; Fergus, R. Intriguing properties of neural networks. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Carlini, N.; Wagner, D. Adversarial examples are not easily detected: Bypassing ten detection methods. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, Dallas, TX, USA, 3 November 2017; pp. 3–14. [Google Scholar]
- Hendrycks, D.; Dietterich, T. Benchmarking Neural Network Robustness to Common Corruptions and Perturbations. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Zhao, R.; Tresp, V. Curiosity-driven experience prioritization via density estimation. arXiv 2019, arXiv:1902.08039. [Google Scholar]
- Fu, J.; Co-Reyes, J.; Levine, S. Ex2: Exploration with exemplar models for deep reinforcement learning. arXiv 2017, arXiv:1703.01260. [Google Scholar]
- Lee, K.; Lee, K.; Lee, H.; Shin, J. A simple unified framework for detecting out-of-distribution samples and adversarial attacks. Adv. Neural Inf. Process. Syst. 2018, 31, 7167–7177. [Google Scholar]
- Filos, A.; Tigkas, P.; Mcallister, R.; Rhinehart, N.; Levine, S.; Gal, Y. Can Autonomous Vehicles Identify, Recover From, and Adapt to Distribution Shifts? In Proceedings of the 37th International Conference on Machine Learning, Online, 13–18 July 2020; Volume 119, pp. 3145–3153. [Google Scholar]
- Grubbs, F.E. Procedures for detecting outlying observations in samples. Technometrics 1969, 11, 1–21. [Google Scholar] [CrossRef]
- Barnett, V.; Lewis, T. Outliers in statistical data. In Wiley Series in Probability and Mathematical Statistics. Applied Probability and Statistics; John Wiley & Sons: Chichester, UK, 1984. [Google Scholar]
- Hodge, V.; Austin, J. A survey of outlier detection methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef] [Green Version]
- Pimentel, M.A.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A review of novelty detection. Signal Process. 2014, 99, 215–249. [Google Scholar] [CrossRef]
- Ruff, L.; Kauffmann, J.R.; Vandermeulen, R.A.; Montavon, G.; Samek, W.; Kloft, M.; Dietterich, T.G.; Müller, K.R. A unifying review of deep and shallow anomaly detection. Proc. IEEE 2021. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Rezende, D.J.; Mohamed, S.; Wierstra, D. Stochastic backpropagation and approximate inference in deep generative models. In Proceedings of the International Conference on Machine Learning 2014, Beijing, China, 21–26 June 2014. [Google Scholar]
- Vahdat, A.; Kautz, J. NVAE: A Deep Hierarchical Variational Autoencoder. arXiv 2020, arXiv:2007.03898. [Google Scholar]
- Uria, B.; Murray, I.; Larochelle, H. A deep and tractable density estimator. In Proceedings of the International Conference on Machine Learning 2014, Beijing, China, 21–26 June 2014; pp. 467–475. [Google Scholar]
- van den Oord, A.; Kalchbrenner, N.; Kavukcuoglu, K. Pixel Recurrent Neural Networks. In Proceedings of the International Conference on Machine Learning 2014, Beijing, China, 21–26 June 2014; pp. 1747–1756. [Google Scholar]
- van den Oord, A.; Kalchbrenner, N.; Espeholt, L.; Vinyals, O.; Graves, A. Conditional image generation with pixelcnn decoders. arXiv 2016, arXiv:1606.05328. [Google Scholar]
- Dinh, L.; Krueger, D.; Bengio, Y. Nice: Non-linear independent components estimation. arXiv 2014, arXiv:1410.8516. [Google Scholar]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using real nvp. arXiv 2016, arXiv:1605.08803. [Google Scholar]
- Kingma, D.P.; Dhariwal, P. Glow: Generative flow with invertible 1x1 convolutions. arXiv 2018, arXiv:1807.03039. [Google Scholar]
- Ho, J.; Chen, X.; Srinivas, A.; Duan, Y.; Abbeel, P. Flow++: Improving Flow-Based Generative Models with Variational Dequantization and Architecture Design. In Proceedings of the International Conference on Machine Learning, Beach, CA, USA, 9–15 June 2019; pp. 2722–2730. [Google Scholar]
- Kobyzev, I.; Prince, S.; Brubaker, M. Normalizing flows: An introduction and review of current methods. IEEE Trans. Pattern Anal. Mach. Intell. 2020. [Google Scholar] [CrossRef]
- Papamakarios, G.; Nalisnick, E.; Rezende, D.J.; Mohamed, S.; Lakshminarayanan, B. Normalizing Flows for Probabilistic Modeling and Inference. J. Mach. Learn. Res. 2021, 22, 1–64. [Google Scholar]
- Bishop, C.M. Novelty detection and neural network validation. IEE Proc. Vision Image Signal Process. 1994, 141, 217–222. [Google Scholar] [CrossRef]
- Choi, H.; Jang, E.; Alemi, A.A. Waic, but why? generative ensembles for robust anomaly detection. arXiv 2018, arXiv:1810.01392. [Google Scholar]
- Nalisnick, E.; Matsukawa, A.; Teh, Y.W.; Gorur, D.; Lakshminarayanan, B. Do Deep Generative Models Know What They Don’t Know? In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Hendrycks, D.; Mazeika, M.; Dietterich, T. Deep Anomaly Detection with Outlier Exposure. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 8 April 2009).
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading Digits in Natural Images with Unsupervised Feature Learning; NIPS Workshop: Grenada, Spain, 2011. [Google Scholar]
- Nalisnick, E.; Matsukawa, A.; Teh, Y.W.; Lakshminarayanan, B. Detecting Out-of-Distribution Inputs to Deep Generative Models Using Typicality. arXiv 2019, arXiv:1906.02994. [Google Scholar]
- Just, J.; Ghosal, S. Deep Generative Models Strike Back! Improving Understanding and Evaluation in Light of Unmet Expectations for OoD Data. arXiv 2019, arXiv:1911.04699. [Google Scholar]
- Fetaya, E.; Jacobsen, J.H.; Grathwohl, W.; Zemel, R. Understanding the Limitations of Conditional Generative Models. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Kirichenko, P.; Izmailov, P.; Wilson, A.G. Why Normalizing Flows Fail to Detect Out-of-Distribution Data. In Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Nice, France, 2020; Volume 33, pp. 20578–20589. [Google Scholar]
- Zhang, H.; Li, A.; Guo, J.; Guo, Y. Hybrid Models for Open Set Recognition. In Proceedings of the Computer Vision—ECCV 2020—16th European Conference, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J., Eds.; Springer: New York, NY, USA, 2020; Volume 12348, pp. 102–117. [Google Scholar] [CrossRef]
- Wang, Z.; Dai, B.; Wipf, D.; Zhu, J. Further Analysis of Outlier Detection with Deep Generative Models. Adv. Neural Inf. Process. Syst. 2020, 33. Available online: http://proceedings.mlr.press/v137/wang20a.html (accessed on 12 December 2021).
- Bottou, L.; Bousquet, O. The tradeoffs of large scale learning. Adv. Neural Inf. Process. Syst. 2008, 351, 161–168. [Google Scholar]
- Moya, M.M.; Koch, M.W.; Hostetler, L.D. One-class classifier networks for target recognition applications. STIN 1993, 93, 24043. [Google Scholar]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef]
- Steinwart, I.; Hush, D.; Scovel, C. A Classification Framework for Anomaly Detection. J. Mach. Learn. Res. 2005, 6, 211–232. [Google Scholar]
- Blei, D.; Heller, K.; Salimans, T.; Welling, M.; Ghahramani, Z. Presented at Panel: On the Foundations and Future of Approximate Inference. In Proceedings of the Advances in Approximate Bayesian Inference, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Rudolph, M.; Wandt, B.; Rosenhahn, B. Same Same but DifferNet: Semi-Supervised Defect Detection With Normalizing Flows. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 5–9 January 2021; pp. 1907–1916. [Google Scholar]
- Liu, W.; Wang, X.; Owens, J.; Li, Y. Energy-based Out-of-distribution Detection. arXiv 2020, arXiv:2010.03759. [Google Scholar]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
- Parmar, N.; Vaswani, A.; Uszkoreit, J.; Kaiser, L.; Shazeer, N.; Ku, A.; Tran, D. Image Transformer. In Proceedings of the Machine Learning Research 2018, Stockholm, Sweden, 6–9 July 2018; pp. 4055–4064. [Google Scholar]
- Blum, A.; Hopcroft, J.; Kannan, R. Foundations of data science. Vorabversion Eines Lehrbuchs 2016, 5, 21–23. [Google Scholar]
- Vershynin, R. High-Dimensional Probability: An Introduction with Applications in Data Science (Cambridge Series in Statistical and Probabilistic Mathematics); Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Morningstar, W.; Ham, C.; Gallagher, A.; Lakshminarayanan, B.; Alemi, A.; Dillon, J. Density of States Estimation for Out of Distribution Detection. In Proceedings of the 24th International Conference on Artificial Intelligence and Statistics, online, 13–15 April 2021; Volume 130, pp. 3232–3240. [Google Scholar]
- Dieleman, S. Musings on Typicality. 2020. Available online: https://benanne.github.io/2020/09/01/typicality.html (accessed on 12 December 2021).
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Magritte, R. La trahison des images. Oil Canvas Paint. 1929, 63, 93. [Google Scholar]
- Korzybski, A. Science and Sanity: An Introduction to Non-Aristotelian Systems and General Semantics; Institute of GS: New York, NY, USA, 1958. [Google Scholar]
- Hanna, A.; Park, T.M. Against Scale: Provocations and Resistances to Scale Thinking. arXiv 2020, arXiv:2010.08850. [Google Scholar]
- Sermanet, P.; Eigen, D.; Zhang, X.; Mathieu, M.; Fergus, R.; LeCun, Y. Overfeat: Integrated recognition, localization and detection using convolutional networks. In Proceedings of the 2nd International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Gueguen, L.; Sergeev, A.; Kadlec, B.; Liu, R.; Yosinski, J. Faster neural networks straight from jpeg. Adv. Neural Inf. Process. Syst. 2018, 31, 3933–3944. [Google Scholar]
- Xie, P.; Bilenko, M.; Finley, T.; Gilad-Bachrach, R.; Lauter, K.; Naehrig, M. Crypto-nets: Neural networks over encrypted data. arXiv 2014, arXiv:1412.6181. [Google Scholar]
- Gilad-Bachrach, R.; Dowlin, N.; Laine, K.; Lauter, K.; Naehrig, M.; Wernsing, J. Cryptonets: Applying neural networks to encrypted data with high throughput and accuracy. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 201–210. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Pinkus, A. Approximation theory of the MLP model in neural networks. Acta Numer. 1999, 8, 143–195. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press Cambridge: Cambridge, MA, USA, 2016. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Krusinga, R.; Shah, S.; Zwicker, M.; Goldstein, T.; Jacobs, D. Understanding the (un) interpretability of natural image distributions using generative models. arXiv 2019, arXiv:1901.01499. [Google Scholar]
- Winkens, J.; Bunel, R.; Roy, A.G.; Stanforth, R.; Natarajan, V.; Ledsam, J.R.; MacWilliams, P.; Kohli, P.; Karthikesalingam, A.; Kohl, S. Contrastive Training for Improved Out-of-Distribution Detection. arXiv 2020, arXiv:2007.05566. [Google Scholar]
- Behrmann, J.; Vicol, P.; Wang, K.C.; Grosse, R.; Jacobsen, J.H. Understanding and Mitigating Exploding Inverses in Invertible Neural Networks. In Proceedings of the 24th International Conference on Artificial Intelligence and Statistics, online, 13–15 April 2021; Volume 130, pp. 1792–1800. [Google Scholar]
- Kaplan, W. Advanced Calculus; Pearson Education India: London, UK, 1952. [Google Scholar]
- Tabak, E.G.; Turner, C.V. A family of nonparametric density estimation algorithms. Commun. Pure Appl. Math. 2013, 66, 145–164. [Google Scholar] [CrossRef] [Green Version]
- Rezende, D.; Mohamed, S. Variational Inference with Normalizing Flows. In Proceedings of the Machine Learning Research, Cambridge, MA, USA, 16–18 November 2015. [Google Scholar]
- Hyvärinen, A.; Pajunen, P. Nonlinear independent component analysis: Existence and uniqueness results. Neural Netw. 1999, 12, 429–439. [Google Scholar] [CrossRef]
- Devroye, L. Sample-based non-uniform random variate generation. In Proceedings of the 18th Conference on Winter Simulation, Washington, DC, USA, 8–10 December 1986; pp. 260–265. [Google Scholar]
- Rosenblatt, M. Remarks on a multivariate transformation. Ann. Math. Stat. 1952, 23, 470–472. [Google Scholar] [CrossRef]
- Knothe, H. Contributions to the theory of convex bodies. Mich. Math. J. 1957, 4, 39–52. [Google Scholar] [CrossRef]
- Chen, S.S.; Gopinath, R.A. Gaussianization. In Advances in Neural Information Processing Systems 13; Leen, T.K., Dietterich, T.G., Tresp, V., Eds.; MIT Press: Cambridge, MA, USA, 2001; pp. 423–429. [Google Scholar]
- Locatello, F.; Bauer, S.; Lucic, M.; Raetsch, G.; Gelly, S.; Schölkopf, B.; Bachem, O. Challenging common assumptions in the unsupervised learning of disentangled representations. In Proceedings of the International Conference on Machine Learning, Beach, CA, USA, 9–15 June 2019; pp. 4114–4124. [Google Scholar]
- Roth, L. Looking at Shirley, the ultimate norm: Colour balance, image technologies, and cognitive equity. Can. J. Commun. 2009, 34. Available online: https://pdfs.semanticscholar.org/e5e1/3351c49ae30baffe7339d085ed870b022e75.pdf (accessed on 12 December 2021). [CrossRef] [Green Version]
- Buolamwini, J.; Gebru, T. Gender shades: Intersectional accuracy disparities in commercial gender classification. In Proceedings of the Conference on Fairness, Accountability and Transparency, New York, NY, USA, 23–24 February 2018; pp. 77–91. [Google Scholar]
- Reinhard, E.; Heidrich, W.; Debevec, P.; Pattanaik, S.; Ward, G.; Myszkowski, K. High Dynamic Range Imaging: Acquisition, Display, and Image-Based Lighting; Morgan Kaufmann: Burlington, MA, USA, 2010. [Google Scholar]
- Torralba, A.; Fergus, R.; Freeman, W.T. 80 million tiny images: A large data set for nonparametric object and scene recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1958–1970. [Google Scholar] [CrossRef] [PubMed]
- Theis, L.; van den Oord, A.; Bethge, M. A note on the evaluation of generative models. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Raji, D.I.; Denton, E.; Hanna, A.; Bender, E.M.; Paullada, A. AI and the Everything in the Whole Wide World Benchmark. In NeurIPS 2020 Workshop: ML-Retrospectives; Surveys & Meta-Analyses: Vancouver, BC, Canada, 2020. [Google Scholar]
- Griffiths, T.L.; Tenenbaum, J.B. From mere coincidences to meaningful discoveries. Cognition 2007, 103, 180–226. [Google Scholar] [CrossRef]
- Zhang, L.; Goldstein, M.; Ranganath, R. Understanding Failures in Out-of-Distribution Detection with Deep Generative Models. In Proceedings of the International Conference on Machine Learning, Shenzhen, China, 18–21 July 2021; pp. 12427–12436. [Google Scholar]
- Ren, J.; Liu, P.J.; Fertig, E.; Snoek, J.; Poplin, R.; Depristo, M.; Dillon, J.; Lakshminarayanan, B. Likelihood ratios for out-of-distribution detection. arXiv 2019, arXiv:1906.02845. [Google Scholar]
- Serrà, J.; Álvarez, D.; Gómez, V.; Slizovskaia, O.; Núñez, J.F.; Luque, J. Input Complexity and Out-of-distribution Detection with Likelihood-based Generative Models. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Schirrmeister, R.T.; Zhou, Y.; Ball, T.; Zhang, D. Understanding Anomaly Detection with Deep Invertible Networks through Hierarchies of Distributions and Features. arXiv 2020, arXiv:2006.10848. [Google Scholar]
- Houthooft, R.; Chen, X.; Chen, X.; Duan, Y.; Schulman, J.; De Turck, F.; Abbeel, P. VIME: Variational Information Maximizing Exploration. In Advances in Neural Information Processing Systems; Lee, D., Sugiyama, M., Luxburg, U., Guyon, I., Garnett, R., Eds.; Curran Associates, Inc.: Nice, France, 2016; Volume 29. [Google Scholar]
- Bellemare, M.G.; Srinivasan, S.; Ostrovski, G.; Schaul, T.; Saxton, D.; Munos, R. Unifying count-based exploration and intrinsic motivation. arXiv 2016, arXiv:1606.01868. [Google Scholar]
- Hanna, A.; Denton, E.; Smart, A.; Smith-Loud, J. Towards a critical race methodology in algorithmic fairness. In Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, Barcelona, Spain, 27–30 January 2020; pp. 501–512. [Google Scholar]
- Wang, C.; Cho, K.; Gu, J. Neural machine translation with byte-level subwords. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 9154–9160. [Google Scholar]
- de Vries, T.; Misra, I.; Wang, C.; van der Maaten, L. Does object recognition work for everyone? In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019; pp. 52–59. [Google Scholar]
- Du, Y.; Mordatch, I. Implicit generation and modeling with energy based models. Adv. Neural Inf. Process. Syst. 2019, 3608–3618. Available online: https://openreview.net/forum?id=S1laPVSxIS (accessed on 12 December 2021).
- Grathwohl, W.; Wang, K.C.; Jacobsen, J.H.; Duvenaud, D.; Norouzi, M.; Swersky, K. Your classifier is secretly an energy based model and you should treat it like one. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Liu, H.; Abbeel, P. Hybrid Discriminative-Generative Training via Contrastive Learning. arXiv 2020, arXiv:2007.09070. [Google Scholar]
- Kurenkov, A. Lessons from the PULSE Model and Discussion. Gradient 2020, 11. [Google Scholar]
- Birhane, A.; Prabhu, V.U. Large Image Datasets: A Pyrrhic Win for Computer Vision? In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikola, HI, USA, 5–9 January 2021; pp. 1537–1547. [Google Scholar]
- Paullada, A.; Raji, I.D.; Bender, E.M.; Denton, E.; Hanna, A. Data and its (dis) contents: A survey of dataset development and use in machine learning research. arXiv 2020, arXiv:2012.05345. [Google Scholar] [CrossRef] [PubMed]
- Van Rossum, G.; Drake, F.L., Jr. Python Reference Manual; Centrum voor Wiskunde en Informatica: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Oliphant, T.E. Python for scientific computing. Comput. Sci. Eng. 2007, 9, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Oliphant, T.E. A guide to NumPy; Trelgol Publishing: Spanish Fork, UT, USA, 2006. [Google Scholar]
- Walt, S.V.d.; Colbert, S.C.; Varoquaux, G. The NumPy array: A structure for efficient numerical computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Lan, C.; Dinh, L. Perfect Density Models Cannot Guarantee Anomaly Detection. Entropy 2021, 23, 1690. https://doi.org/10.3390/e23121690
Le Lan C, Dinh L. Perfect Density Models Cannot Guarantee Anomaly Detection. Entropy. 2021; 23(12):1690. https://doi.org/10.3390/e23121690
Chicago/Turabian StyleLe Lan, Charline, and Laurent Dinh. 2021. "Perfect Density Models Cannot Guarantee Anomaly Detection" Entropy 23, no. 12: 1690. https://doi.org/10.3390/e23121690
APA StyleLe Lan, C., & Dinh, L. (2021). Perfect Density Models Cannot Guarantee Anomaly Detection. Entropy, 23(12), 1690. https://doi.org/10.3390/e23121690




