Quantifying Decoherence via Increases in Classicality
Abstract
1. Introduction
- (1)
- Decoherence of which (state)?
- (2)
- Decoherence relative to which (basis, or more generally, channel)?
- (3)
- Decoherence caused by which (environment or observation)?
2. Preliminaries
2.1. Classicality in Terms of the Jordan Product
- (a)
- Moreover, if and only if for all i.
- (b)
- is concave in
- (c)
- is covariant in the sense thatfor any unitary operator U on the system Hilbert space. Here
2.2. Classicality in Terms of Uncertainty
- (a)
- (b)
- is concave in
- (c)
- is covariant in the sense thatfor any unitary operator U on the system Hilbert space. Here the channel is defined as
3. Quantifying Decoherence of System Induced by Environment
- (a)
- Moreover, if (proportional to the identity operator on the i-th sub-environment for all i).
- (b)
- is convex in
4. Influence on Environment Caused by System
5. Illustrating Decoherence in Interferometry
6. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dirac, P.A.M. The Principles of Quantum Mechanics, 4th ed.; Clarendon Press: Oxford, UK, 1958. [Google Scholar]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Ficek, Z.; Swain, S. Quantum Interference and Coherence: Theory and Experiments; Springer: Berlin, Germany, 2005. [Google Scholar]
- Landau, L.D. The damping problem in wave mechanics. Z. Phys. 1927, 45, 430–441. [Google Scholar] [CrossRef]
- Mott, N.F. The wave mechanics of α-ray tracks. Proc. R. Soc. Lond. A 1929, 126, 79–84. [Google Scholar]
- Zeh, H.D. On the interpretation of measurement in quantum theory. Found. Phys. 1970, 1, 69–76. [Google Scholar] [CrossRef]
- Zeh, H.D. Toward a quantum theory of observation. Found. Phys. 1973, 3, 109–116. [Google Scholar] [CrossRef]
- Zurek, W.H. Pointer basis of quantum apparatus: Into what mixture does the wave packet collapse? Phys. Rev. D 1981, 24, 1516. [Google Scholar] [CrossRef]
- Zurek, W.H. Environment-induced superselection rules. Phys. Rev. D 1982, 26, 1862. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence and the transition from quantum to classical. Phys. Today 1991, 44, 36–44. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambrideg University Press: Cambridge, UK, 2000. [Google Scholar]
- Joos, E.; Zeh, H.D. The emergence of classical properties through interaction with the environment. Z. Phys. B 1985, 59, 223–243. [Google Scholar] [CrossRef]
- Giulini, D.; Joos, E.; Kiefer, C.; Kupsch, J.; Stamatescu, I.-O.; Zeh, H.D. Decoherence and the Appearance of a Classical World in Quantum Theory; Springer: Berlin, Germany, 1996. [Google Scholar]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherence, the measurement problem and interpretations of quantum mechanics. Rev. Mod. Phys. 2004, 76, 1267. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherence and the Quantum-to-Classical Transition; Springer: Berlin, Germany, 2007. [Google Scholar]
- Schlosshauer, M. Quantum decoherence. Phys. Rep. 2019, 831, 1–57. [Google Scholar] [CrossRef]
- Duplantier, B.; Raimond, J.M.; Rivasseau, V. Quantum Decoherence. In Poincaré Seminar 2005; Springer: Berlin, Germany, 2007. [Google Scholar]
- Zeh, H.D. The Physical Basis of The Direction of Time; Springer: Berlin, Germany, 2007. [Google Scholar]
- Ollivier, H.; Poulin, D.; Zurek, W.H. Objective properties from subjective quantum states: Environment as a witness. Phys. Rev. Lett. 2004, 93, 220401. [Google Scholar] [CrossRef] [PubMed]
- Blume-Kohout, R.; Zurek, W.H. Quantum Darwinism: Entanglement, branches, and the emergent classicality of redundantly stored quantum information. Phys. Rev. A 2006, 73, 062310. [Google Scholar] [CrossRef]
- Zurek, W.H. Quantum Darwinism. Nat. Phys. 2009, 5, 181–188. [Google Scholar] [CrossRef]
- Zwolak, M.; Quan, H.T.; Zurek, W.H. Quantum Darwinism in a hazy environment. Phys. Rev. Lett. 2009, 103, 110402. [Google Scholar] [CrossRef] [PubMed]
- Riedel, C.J.; Zurek, W.H.; Zwolak, M. The rise and fall of redundancy in decoherence and quantum Darwinism. New J. Phys. 2012, 14, 083010. [Google Scholar] [CrossRef]
- Korbicz, J.K.; Horodecki, P.; Horodecki, R. Objectivity in the photonic environment through state information broadcasting. Phys. Rev. Lett. 2014, 112, 120402. [Google Scholar] [CrossRef]
- Horodecki, R.; Korbicz, J.K.; Horodecki, P. Quantum origins of objectivity. Phys. Rev. A 2015, 91, 032122. [Google Scholar] [CrossRef]
- Brandaö, F.G.S.L.; Piani, M.; Horodecki, P. Generic emergence of classical features in quantum Darwinism. Nat. Commun. 2015, 6, 7908. [Google Scholar] [CrossRef]
- Knott, P.A.; Tufarelli, T.; Piani, M.; Adesso, G. Generic emergence of objectivity of observables in infinite dimensions. Phys. Rev. Lett. 2018, 121, 160401. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H. Quantum theory of the classical: Quantum jumps, Born’s rule and objective classical reality via quantum Darwinism. Philos. Trans. R. Soc. A 2018, 376, 20180107. [Google Scholar] [CrossRef]
- Le, T.P.; Olaya-Castro, A. Strong quantum darwinism and strong independence are equivalent to spectrum broadcast structure. Phys. Rev. Lett. 2019, 122, 010403. [Google Scholar] [CrossRef] [PubMed]
- Wootters, W.K.; Zurek, W.H. Complementarity in the double-slit experiment: Quantum nonseparability and a quantitative statement of Bohr’s principle. Phys. Rev. D 1979, 19, 473. [Google Scholar] [CrossRef]
- Greenberger, D.M.; Yasin, A. Simultaneous wave and particle knowledge in a neutron interferometer. Phys. Lett. A 1988, 128, 391–394. [Google Scholar] [CrossRef]
- Scully, M.O.; Englert, B.G.; Walther, H. Quantum optical tests of complementarity. Nature 1991, 351, 111–116. [Google Scholar] [CrossRef]
- Englert, B.-G. Fringe visibility and which-way information: An inequality. Phys. Rev. Lett. 1996, 77, 2154. [Google Scholar] [CrossRef] [PubMed]
- Dürr, S. Quantitative wave-particle duality in multibeam interferometers. Phys. Rev. A 2001, 64, 042113. [Google Scholar] [CrossRef]
- Englert, B.-G.; Kaszlikowsk, D.; Kwek, L.C.; Chee, W.H. Wave-particle duality in multi-path interferometers: General concepts and three-path interferometers. Int. J. Quantum Inf. 2008, 06, 129–157. [Google Scholar] [CrossRef]
- Luo, S. From quantum no-cloning to wave-packet collapse. Phys. Lett. A 2010, 374, 1350–1353. [Google Scholar] [CrossRef]
- Zurek, W.H. Wave-packet collapse and the core quantum postulates: Discreteness of quantum jumps from unitarity, repeatability, and actionable information. Phys. Rev. A 2013, 87, 052111. [Google Scholar] [CrossRef]
- Janssens, B.; Maassen, H. Information transfer implies state collapse. J. Phys. A 2006, 39, 9845–9860. [Google Scholar] [CrossRef][Green Version]
- Janssens, B. Unifying decoherence and the Heisenberg principle. Lett. Math. Phys. 2017, 107, 1557–1579. [Google Scholar] [CrossRef]
- Wu, Z.; Zhu, C.; Luo, S.; Wang, J. Information transfer in generalized probabilistic theories. Phys. Lett. A 2015, 379, 2694–2697. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Barnum, H.; Caves, C.M.; Fuchs, C.A.; Jozsa, R.; Schumacher, B. Noncommuting mixed states cannot be broadcast. Phys. Rev. Lett. 1996, 76, 2818. [Google Scholar] [CrossRef]
- Chiribella, G.; D’Ariano, G.M. Quantum information becomes classical when distributed to many users. Phys. Rev. Lett. 2006, 97, 250503. [Google Scholar] [CrossRef]
- Piani, M.; Horodecki, P.; Horodecki, R. No-local-broadcasting theorem for multipartite quantum correlations. Phys. Rev. Lett. 2008, 100, 090502. [Google Scholar] [CrossRef]
- Luo, S.; Sun, W. Decomposition of bipartite states with applications to quantum no-broadcasting theorems. Phys. Rev. A 2010, 82, 012338. [Google Scholar] [CrossRef]
- Scandolo, C.M.; Salazar, R.; Korbicz, J.K.; Horodecki, P. Universal structure of objective states in all fundamental causal theories. Phys. Rev. Res. 2021, 3, 033148. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef]
- Henderson, L.; Vedral, V. Classical, quantum and total correlations. J. Phys. A 2001, 34, 6899–6905. [Google Scholar] [CrossRef]
- Luo, S. Quantum discord for two-qubit systems. Phys. Rev. A 2008, 77, 042303. [Google Scholar] [CrossRef]
- Luo, S.; Fu, S. Geometric measure of quantum discord. Phys. Rev. A 2010, 82, 034302. [Google Scholar] [CrossRef]
- Modi, K.; Brodutch, A.; Cable, H.; Paterek, T.; Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 2012, 84, 1655. [Google Scholar] [CrossRef]
- Chang, L.; Luo, S. Remedying the local ancilla problem with geometric discord. Phys. Rev. A 2013, 87, 062303. [Google Scholar] [CrossRef]
- Streltsov, A.; Zurek, W.H. Quantum discord cannot be shared. Phys. Rev. Lett. 2013, 111, 040401. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, R.B. Consistent histories and the interpretation of quantum mechanics. J. Stat. Phys. 1984, 36, 219–272. [Google Scholar] [CrossRef]
- Paz, J.P.; Zurek, W.H. Environment-induced decoherence, classicality and consistency of quantum histories. Phys. Rev. D 1993, 48, 2728. [Google Scholar] [CrossRef]
- Griffiths, R.B. Consistent histories and quantum reasoning. Phys. Rev. A 1996, 54, 2759. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, R.B. Consistent Quantum Theory; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Riedel, C.J.; Zurek, W.H.; Zwolak, M. Objective past of a quantum universe: Redundant records of consistent histories. Phys. Rev. A 2016, 93, 032126. [Google Scholar] [CrossRef]
- Fuchs, C.A. Just two nonorthogonal quantum states. arXiv 1998, arXiv:quant-ph/9810032. [Google Scholar]
- Fuchs, C.A.; Sasaki, M. The quantumness of a set of quantum states. arXiv 2003, arXiv:quant-ph/0302108. [Google Scholar]
- Fuchs, C.A.; Sasaki, M. Squeezing quantum information through a classical channel: Measuring the “quantumness” of a set of quantum states. Quantum Inf. Comput. 2003, 3, 377–404. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Horodecki, R.; Piani, M. Quantumness of ensemble from nobroadcasting principle. Int. J. Quantum Inf. 2006, 4, 105–118. [Google Scholar] [CrossRef]
- Alicki, R.; Van Ryn, N. A simple test of quantumness for a single system. J. Phys. A 2008, 41, 062001. [Google Scholar] [CrossRef]
- Alicki, R.; Piani, M.; Van Ryn, N. Quantumness witnesses. J. Phys. A 2008, 41, 495303. [Google Scholar] [CrossRef]
- Brida, G.; Degiovanni, I.P.; Genovese, M.; Schettini, V.; Polyakov, S.V.; Migdall, A. Experimental test of nonclassicality for a single particle. Opt. Express 2008, 16, 11750. [Google Scholar] [CrossRef]
- Brida, G.; Degiovanni, I.P.; Genovese, M.; Piacentini, F.; Schettini, V.; Gisin, N.; Polyakov, S.V.; Migdall, A. Improved implementation of the Alicki-Van Ryn nonclassicality test for a single particle using Si detectors. Phys. Rev. A 2009, 79, 044102. [Google Scholar] [CrossRef]
- Luo, S.; Li, N.; Sun, W. How quantum is a quantum ensemble. Quantum Inf. Process. 2010, 9, 711–726. [Google Scholar] [CrossRef]
- Luo, S.; Li, N.; Fu, S. Quantumness of quantum ensembles. Theor. Math. Phys. 2011, 169, 1724–1739. [Google Scholar] [CrossRef]
- Facchi, P.; Ferro, L.; Marmo, G.; Pascazio, S. Defining quantumness via the Jordan product. J. Phys. A 2014, 47, 035301. [Google Scholar] [CrossRef][Green Version]
- Li, N.; Luo, S.; Mao, Y. Quantifying the quantumness of quantum ensembles. Phys. Rev. A 2017, 96, 022132. [Google Scholar] [CrossRef]
- Ferro, L.; Fazio, R.; Illuminati, F.; Marmo, G.; Pascazio, S.; Vedral, V. Measuring quantumness: From theory to observability in interferometric setups. Eur. Phys. J. D 2018, 72, 219. [Google Scholar] [CrossRef]
- Herbut, F. A quantum measure of coherence and incompatibility. J. Phys. A 2005, 38, 2959–2974. [Google Scholar] [CrossRef]
- Åberg, J. Quantifying superposition. arXiv 2016, arXiv:Quant-ph/0612146. [Google Scholar]
- Levi, F.; Mintert, F. A quantitative theory of coherent delocalization. New J. Phys. 2014, 16, 033007. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef]
- Streltsov, A.; Singh, U.; Dhar, H.S.; Bera, M.N.; Adesso, G. Measuring quantum coherence with entanglement. Phys. Rev. Lett. 2015, 115, 020403. [Google Scholar] [CrossRef]
- Yuan, X.; Zhou, H.; Cao, Z.; Ma, X. Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 2015, 92, 022124. [Google Scholar] [CrossRef]
- Winter, A.; Yang, D. Operational resource theory of coherence. Phys. Rev. Lett. 2016, 116, 120404. [Google Scholar] [CrossRef]
- Streltsov, A.; Adesso, G.; Plenio, M.B. Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef]
- Luo, S.; Sun, Y. Partial coherence with application to the monotonicity problem of coherence involving skew information. Phys. Rev. A 2017, 96, 022136. [Google Scholar] [CrossRef]
- Luo, S.; Sun, Y. Quantum coherence versus quantum uncertainty. Phys. Rev. A 2017, 96, 022130. [Google Scholar] [CrossRef]
- Sun, Y.; Mao, Y.; Luo, S. From quantum coherence to quantum correlations. Europhys. Lett. 2017, 118, 60007. [Google Scholar] [CrossRef]
- Luo, S.; Sun, Y. Coherence and complementarity in state-channel interaction. Phys. Rev. 2018, 98, 012113. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, S. Quantum states as observables: Their variance and nonclassicality. Phys. Rev. A 2020, 102, 062211. [Google Scholar] [CrossRef]
- Sun, Y.; Luo, S. Coherence as uncertainty. Phys. Rev. A 2021, 103, 042423. [Google Scholar] [CrossRef]
- Kraus, B. States, Effects, and Operations: Fundamental Notions of Quantum Theory; Springer: Berlin, Germany, 1983. [Google Scholar]
- Wigner, E.P.; Yanase, M.M. Information contents of distributions. Proc. Natl. Acad. Sci. USA 1963, 49, 910–918. [Google Scholar] [CrossRef]
- Luo, S. Wigner-Yanase skew information and uncertainty relations. Phys. Rev. Lett. 2003, 91, 180403. [Google Scholar] [CrossRef]
- Luo, S. Winger-Yanase skew information versus quantum Fisher information. Proc. Am. Math. Soc. 2003, 132, 885–890. [Google Scholar] [CrossRef]
- Luo, S. Heisenberg uncertainty relation for mixed states. Phys. Rev. A 2005, 72, 042110. [Google Scholar] [CrossRef]
- Luo, S. Quantum versus classical uncertainty. Theor. Math. Phys. 2005, 143, 681–688. [Google Scholar] [CrossRef]
- Luo, S.; Fu, S.; Oh, C.H. Quantifying correlations via the Wigner-Yanase skew information. Phys. Rev. A 2012, 85, 032117. [Google Scholar] [CrossRef]
- Marvian, I.; Spekkens, R.W. Extending Noether’s theorem by quantifying the asymmetry of quantum states. Nat. Commun. 2014, 5, 3821. [Google Scholar] [CrossRef]
- Girolami, D. Observable measure of quantum coherence in finite dimensional systems. Phys. Rev. Lett. 2014, 113, 170401. [Google Scholar] [CrossRef] [PubMed]
- Lostaglio, M.; Korzekwa, K.; Jennings, D.; Rudolph, T. Quantum coherence, time-translation symmetry, and thermodynamics. Phys. Rev. X 2015, 5, 021001. [Google Scholar] [CrossRef]
- Marvian, I.; Spekkens, R.W.; Zanardi, P. Quantum speed limits, coherence and asymmetry. Phys. Rev. A 2016, 93, 052331. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, Q. Skew information decreases under quantum measurements. Theor. Math. Phys. 2007, 151, 529–538. [Google Scholar] [CrossRef]
- Li, W. Monotonicity of skew information and its applications in quantum resource theory. Quantum Inf. Process. 2019, 18, 166. [Google Scholar] [CrossRef]
- Lieb, E.H. Convex trace functions and the Wigner-Yanase-Dyson conjecture. Adv. Math. 1973, 11, 267–288. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, Y. Detecting nonclassicality of light via Lieb’s concavity. Phys. Lett. A 2019, 383, 125836. [Google Scholar] [CrossRef]
- Horn, R.A. Topics in Matrix Analysis; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Marshall, A.W. Inequalities: Theory of Majorization and Its Applications; Springer: New York, NY, USA, 2011. [Google Scholar]
- Bhatia, R. Matrix Analysis; Springer: Berlin, Germany, 2013. [Google Scholar]
- Hadamard, J. Résolution d’une question relative aux determinants. Bull. Sci. Math. 1893, 17, 240–246. [Google Scholar]
- Luo, S.; Fu, S.; Li, N. Decorrelating capabilities of operations with application to decoherence. Phys. Rev. A 2010, 82, 052122. [Google Scholar] [CrossRef]
- Luo, S.; Li, N. Decoherence and measurement-induced correlations. Phys. Rev. A 2011, 84, 052309. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of n-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Laine, E.-M.; Piilo, J. Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Fu, S.; Song, H. Quantifying non-Markovianity via correlations. Phys. Rev. 2012, 86, 044101. [Google Scholar] [CrossRef]
- Jiang, M.; Luo, S. Comparing quantum Markovianities: Distinguishability versus correlations. Phys. Rev. A 2013, 88, 034101. [Google Scholar] [CrossRef]
- Rivas, Á.; Huelga, S.F.; Plenio, M.B. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 09400. [Google Scholar] [CrossRef]
- Song, H.; Luo, S.; Hong, Y. Quantum non-Markovianity based on the Fisher information matrix. Phys. Rev. A 2015, 91, 042110. [Google Scholar] [CrossRef]
- Li, L.; Hall, M.J.W.; Wiseman, H.M. Concepts of quantum non-Markovianity: A hierarchy. Phys. Rep. 2018, 759, 1–51. [Google Scholar] [CrossRef]
- Wu, K.-D.; Hou, Z.; Xiang, G.-Y.; Li, C.-F.; Guo, G.-C.; Dong, D.; Nori, F. Detecting non-Markovianity via quantified coherence: Theory and experiments. NPJ Quantum Inf. 2020, 6, 55. [Google Scholar] [CrossRef]

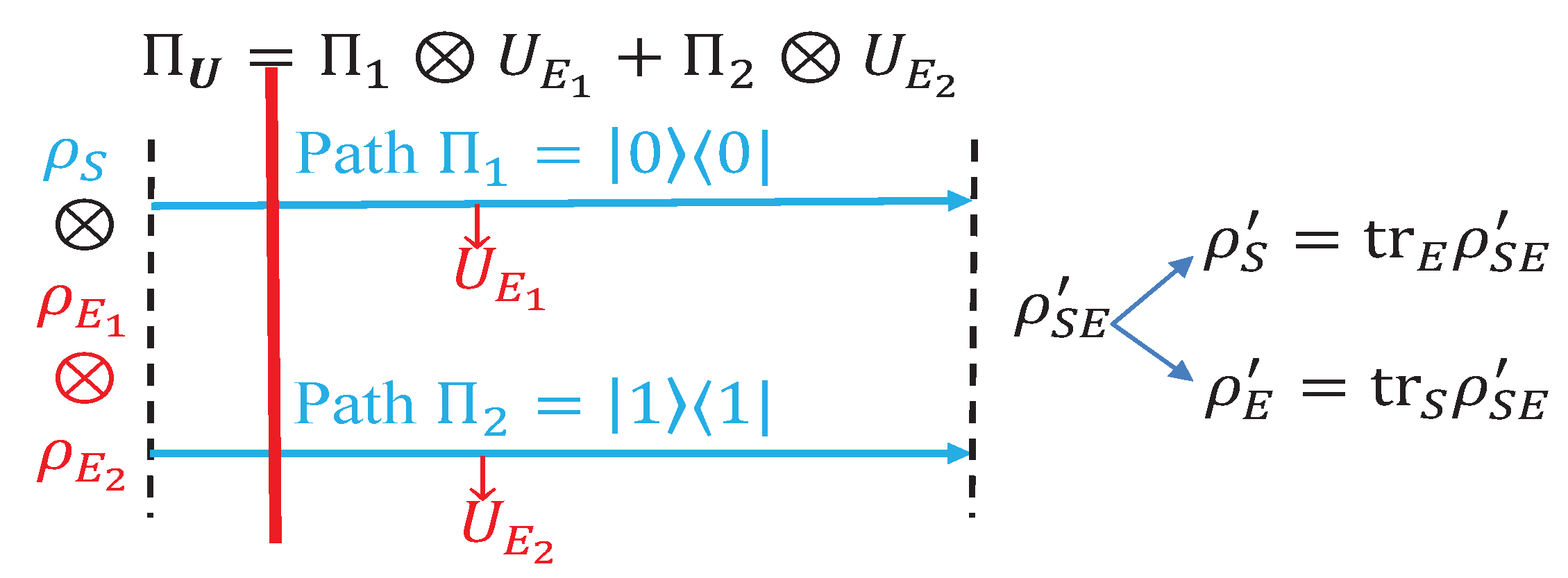
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, S.; Luo, S. Quantifying Decoherence via Increases in Classicality. Entropy 2021, 23, 1594. https://doi.org/10.3390/e23121594
Fu S, Luo S. Quantifying Decoherence via Increases in Classicality. Entropy. 2021; 23(12):1594. https://doi.org/10.3390/e23121594
Chicago/Turabian StyleFu, Shuangshuang, and Shunlong Luo. 2021. "Quantifying Decoherence via Increases in Classicality" Entropy 23, no. 12: 1594. https://doi.org/10.3390/e23121594
APA StyleFu, S., & Luo, S. (2021). Quantifying Decoherence via Increases in Classicality. Entropy, 23(12), 1594. https://doi.org/10.3390/e23121594





