Limits to Perception by Quantum Monitoring with Finite Efficiency
Abstract
:1. Quantum Limits to Perception
2. Transition to Complete Descriptions
3. Illustrations
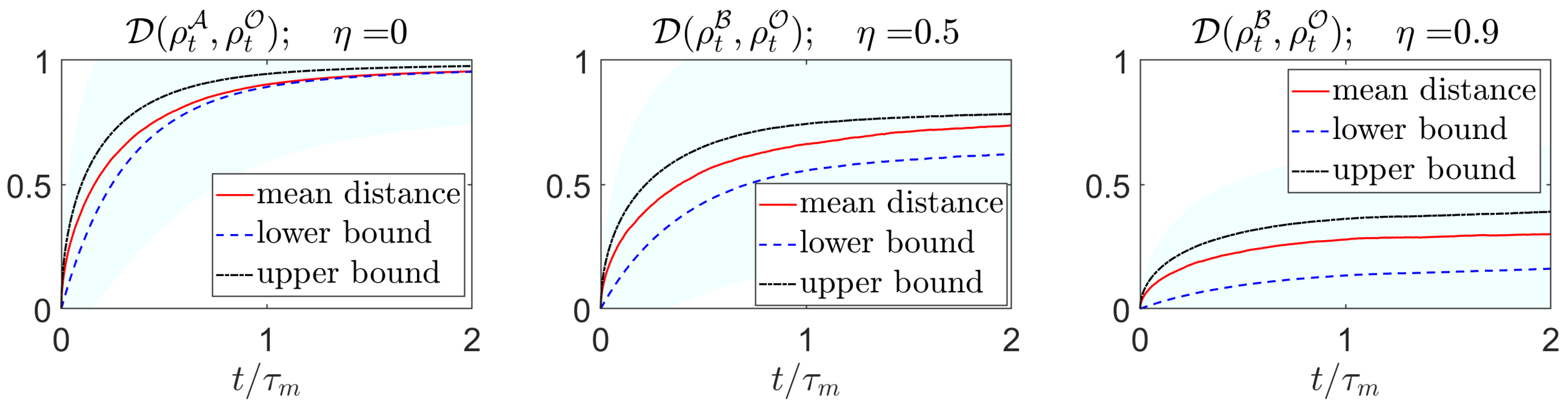
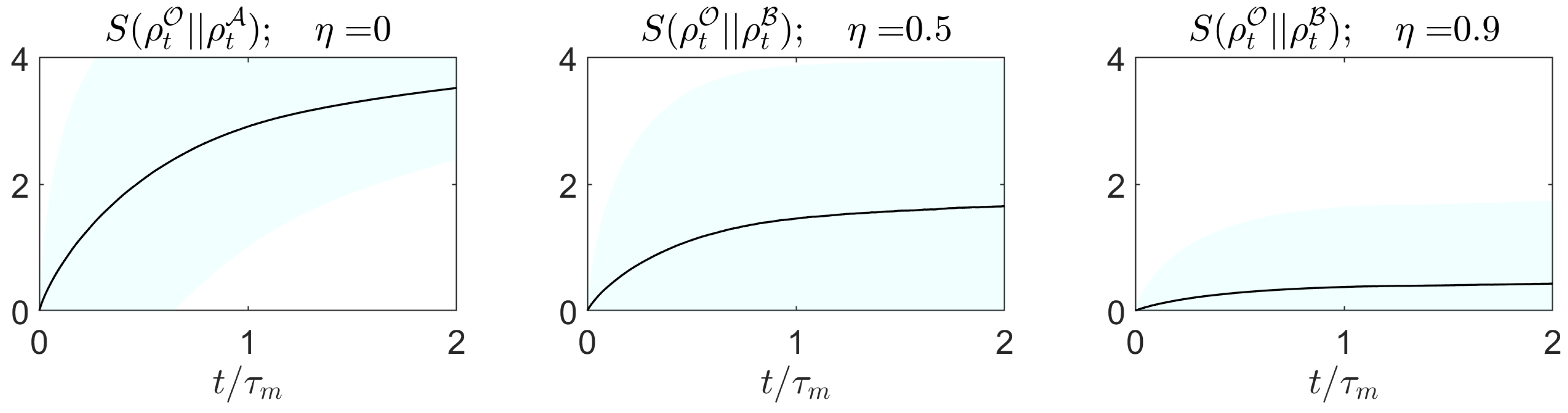
3.1. Evolution of the Limits to Perception
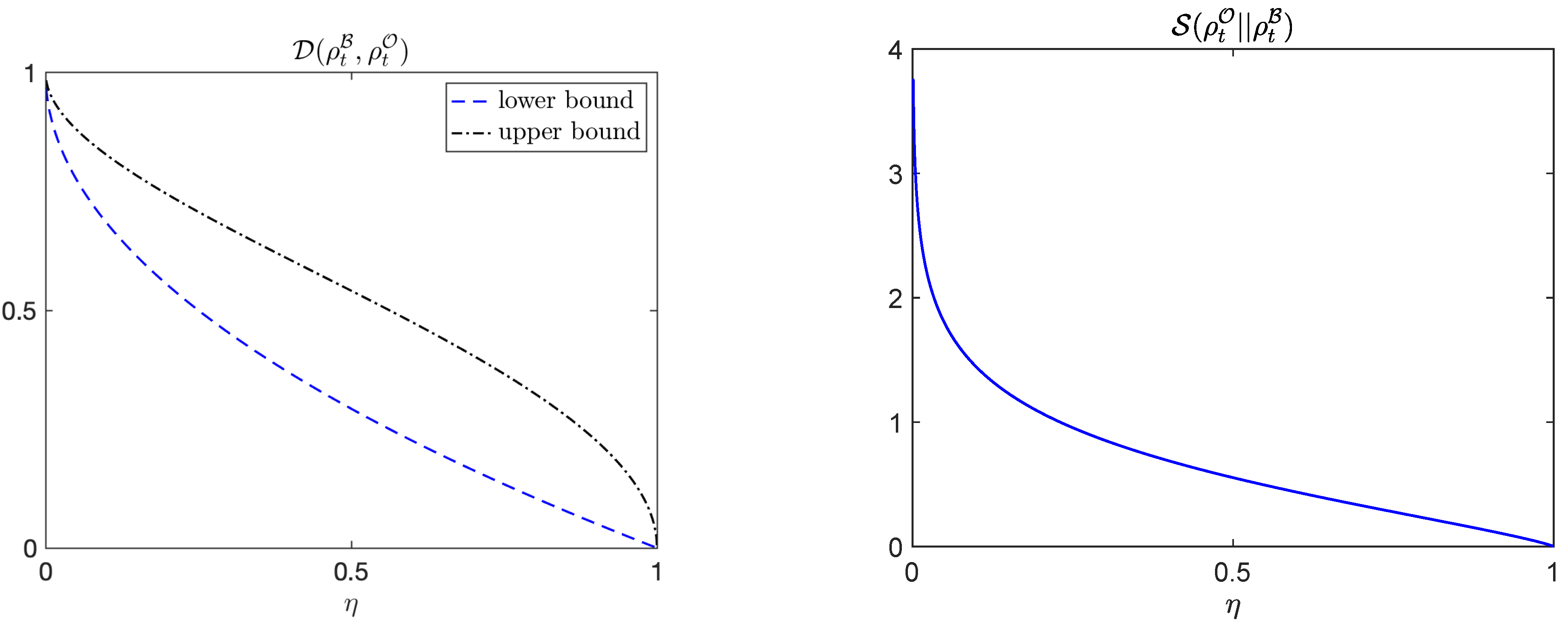
3.2. Transition to Complete Descriptions
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Derivation of Bounds to Average Trace Distance
Appendix A.2. Derivation of the Average and Variance of the Quantum Relative Entropy
Appendix A.3. Bounds to the Difference between Perceptions of Multiple Agents
Appendix A.4. Illustration—Evolution of Limits to Perception
Appendix A.5. Illustration—Transition to Complete Descriptions
References
- Jacobs, K.; Steck, D. A straightforward introduction to continuous quantum measurement. Contemp. Phys. 2006, 47, 279–303. [Google Scholar] [CrossRef] [Green Version]
- Wiseman, H.M.; Milburn, G.J. Quantum Measurement and Control; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Jacobs, K. Quantum Measurement Theory and Its Applications; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Murch, K.W.; Weber, S.J.; Macklin, C.; Siddiqi, I. Observing single quantum trajectories of a superconducting quantum bit. Nature 2013, 502, 211–214. [Google Scholar] [CrossRef] [Green Version]
- Devoret, M.H.; Schoelkopf, R.J. Superconducting Circuits for Quantum Information: An Outlook. Science 2013, 339, 1169–1174. [Google Scholar] [CrossRef] [Green Version]
- Weber, S.J.; Chantasri, A.; Dressel, J.; Jordan, A.N.; Murch, K.W.; Siddiqi, I. Mapping the optimal route between two quantum states. Nature 2014, 511, 570. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef] [Green Version]
- Wilde, M.M. Quantum Information Theory; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef] [Green Version]
- Watrous, J. The Theory of Quantum Information; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef] [Green Version]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Hiai, F.; Petz, D. The proper formula for relative entropy and its asymptotics in quantum probability. Commun. Math. Phys. 1991, 143, 99–114. [Google Scholar] [CrossRef]
- Ogawa, T.; Nagaoka, H. Strong converse and Stein’s lemma in quantum hypothesis testing. In Asymptotic Theory of Quantum Statistical Inference: Selected Papers; World Scientific: Singapore, 2005; pp. 28–42. [Google Scholar] [CrossRef] [Green Version]
- Schumacher, B.; Westmoreland, M.D. Relative entropy in quantum information theory. Contemp. Math. 2002, 305, 265–290. [Google Scholar] [CrossRef]
- Vedral, V. The role of relative entropy in quantum information theory. Rev. Mod. Phys. 2002, 74, 197–234. [Google Scholar] [CrossRef] [Green Version]
- Chenu, A.; Beau, M.; Cao, J.; del Campo, A. Quantum Simulation of Generic Many-Body Open System Dynamics Using Classical Noise. Phys. Rev. Lett. 2017, 118, 140403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beau, M.; Kiukas, J.; Egusquiza, I.L.; del Campo, A. Nonexponential Quantum Decay under Environmental Decoherence. Phys. Rev. Lett. 2017, 119, 130401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barchielli, A. Entropy and information gain in quantum continual measurements. In Quantum Communication, Computing, and Measurement 3; Springer: Berlin/Heidelberg, Germany, 2002; pp. 49–57. [Google Scholar] [CrossRef] [Green Version]
- Barchielli, A.; Gregoratti, M. Quantum Trajectories and Measurements in Continuous Time: The Diffusive Case; Springer: Berlin/Heidelberg, Germany, 2009; Volume 782. [Google Scholar] [CrossRef] [Green Version]
- Zurek, W.H. Decoherence and the Transition from Quantum to Classical. Phys. Today 1991, 44, 36–44. [Google Scholar] [CrossRef]
- Schlosshauer, M.A. Decoherence: And the Quantum-to-Classical Transition; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef] [Green Version]
- Doherty, A.C.; Jacobs, K. Feedback control of quantum systems using continuous state estimation. Phys. Rev. A 1999, 60, 2700–2711. [Google Scholar] [CrossRef] [Green Version]
- Paris, M.G.A.; Illuminati, F.; Serafini, A.; De Siena, S. Purity of Gaussian states: Measurement schemes and time evolution in noisy channels. Phys. Rev. A 2003, 68, 012314. [Google Scholar] [CrossRef] [Green Version]
- Ferraro, A.; Olivares, S.; Paris, M. Gaussian States in Quantum Information; Napoli Series on physics and Astrophysics; Bibliopolis: Pittsburgh, PA, USA, 2005. [Google Scholar]
- Wang, X.B.; Hiroshima, T.; Tomita, A.; Hayashi, M. Quantum information with Gaussian states. Phys. Rep. 2007, 448, 1–111. [Google Scholar] [CrossRef] [Green Version]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621–669. [Google Scholar] [CrossRef]
- Adesso, G.; Ragy, S.; Lee, A.R. Continuous variable quantum information: Gaussian states and beyond. Open Syst. Inf. Dyn. 2014, 21, 1440001. [Google Scholar] [CrossRef] [Green Version]
- Laverick, K.T.; Chantasri, A.; Wiseman, H.M. Quantum State Smoothing for Linear Gaussian Systems. Phys. Rev. Lett. 2019, 122, 190402. [Google Scholar] [CrossRef] [Green Version]
- Schlosshauer, M. Decoherence, the measurement problem, and interpretations of quantum mechanics. Rev. Mod. Phys. 2005, 76, 1267–1305. [Google Scholar] [CrossRef] [Green Version]
- Zurek, W.H. Quantum darwinism. Nat. Phys. 2009, 5, 181. [Google Scholar] [CrossRef]
- Zwolak, M.; Quan, H.T.; Zurek, W.H. Redundant imprinting of information in nonideal environments: Objective reality via a noisy channel. Phys. Rev. A 2010, 81, 062110. [Google Scholar] [CrossRef] [Green Version]
- Jess Riedel, C.; Zurek, W.H.; Zwolak, M. The rise and fall of redundancy in decoherence and quantum Darwinism. New J. Phys. 2012, 14, 083010. [Google Scholar] [CrossRef]
- Zwolak, M.; Zurek, W.H. Complementarity of quantum discord and classically accessible information. Sci. Rep. 2013, 3, 1729. [Google Scholar] [CrossRef]
- Brandão, F.G.S.L.; Piani, M.; Horodecki, P. Generic emergence of classical features in quantum Darwinism. Nat. Commun. 2015, 6, 7908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Horodecki, R.; Korbicz, J.K.; Horodecki, P. Quantum origins of objectivity. Phys. Rev. A 2015, 91, 032122. [Google Scholar] [CrossRef] [Green Version]
- Le, T.P.; Olaya-Castro, A. Strong Quantum Darwinism and Strong Independence are Equivalent to Spectrum Broadcast Structure. Phys. Rev. Lett. 2019, 122, 010403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ciampini, M.A.; Pinna, G.; Mataloni, P.; Paternostro, M. Experimental signature of quantum Darwinism in photonic cluster states. Phys. Rev. A 2018, 98, 020101. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.C.; Zhong, H.S.; Li, Y.; Wu, D.; Wang, X.L.; Li, L.; Liu, N.L.; Lu, C.Y.; Pan, J.W. Emergence of classical objectivity of quantum Darwinism in a photonic quantum simulator. Sci. Bull. 2019, 64, 580–585. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Pintos, L.P.; del Campo, A. Limits to Perception by Quantum Monitoring with Finite Efficiency. Entropy 2021, 23, 1527. https://doi.org/10.3390/e23111527
García-Pintos LP, del Campo A. Limits to Perception by Quantum Monitoring with Finite Efficiency. Entropy. 2021; 23(11):1527. https://doi.org/10.3390/e23111527
Chicago/Turabian StyleGarcía-Pintos, Luis Pedro, and Adolfo del Campo. 2021. "Limits to Perception by Quantum Monitoring with Finite Efficiency" Entropy 23, no. 11: 1527. https://doi.org/10.3390/e23111527
APA StyleGarcía-Pintos, L. P., & del Campo, A. (2021). Limits to Perception by Quantum Monitoring with Finite Efficiency. Entropy, 23(11), 1527. https://doi.org/10.3390/e23111527






