Statistical Physics of Evolving Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. The State Equation
2.2. The Evolutionary Equation
2.3. The Continuous Equation of Motion
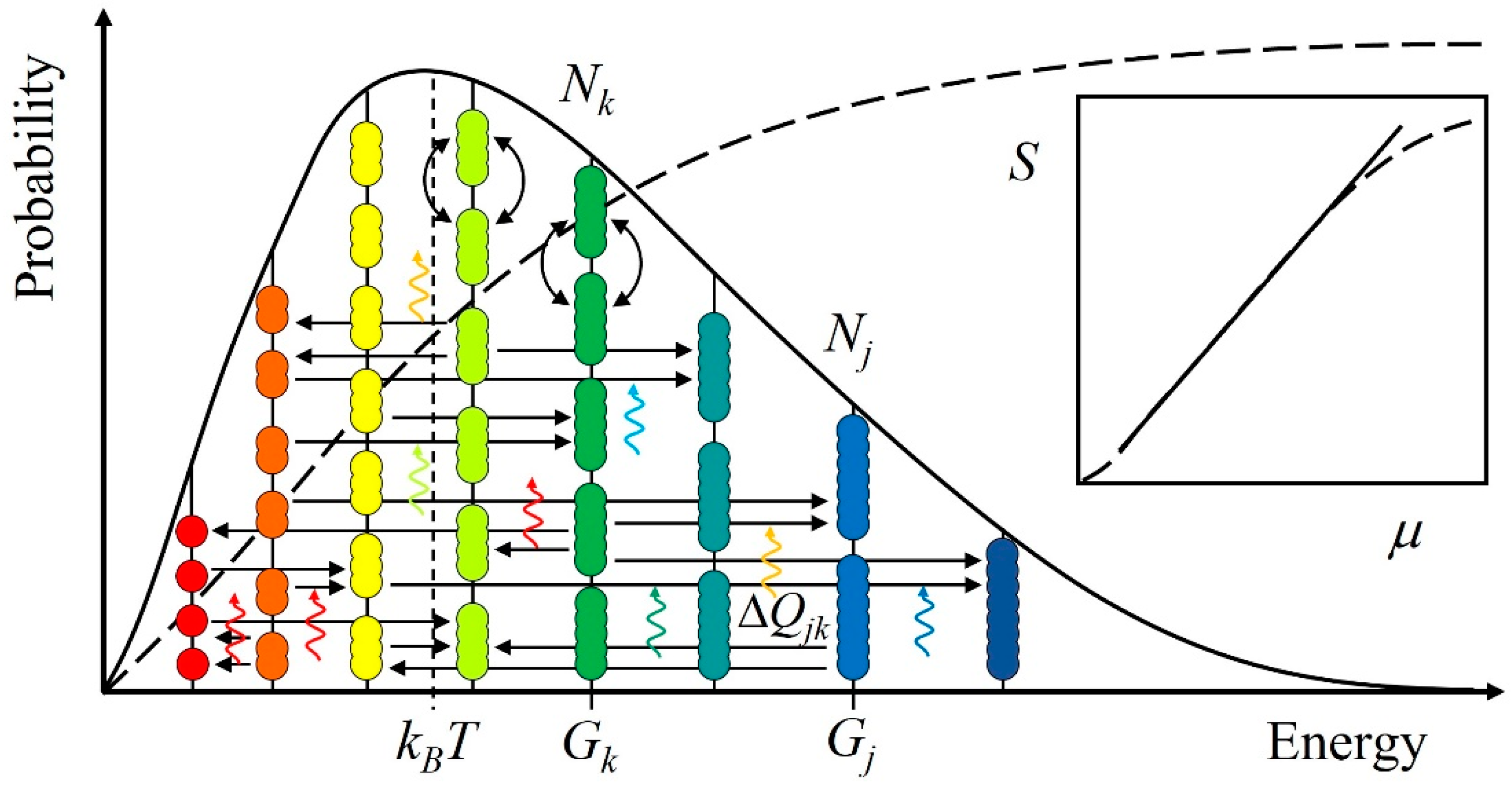
3. Results
3.1. The Ubiquitous Patterns
3.2. Non-Deterministic Motion
4. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boltzmann, L. The Second Law of Thermodynamics; D. Reidel: Dordrecht, Holland, 1974. [Google Scholar]
- Demetrius, L. Thermodynamics and Evolution. J. Theor. Biol. 2000, 206, 1–16. [Google Scholar] [CrossRef]
- Annila, A.; Salthe, S. Physical foundations of evolutionary theory. J. Non-Equil. Therm. 2010, 35, 301–321. [Google Scholar] [CrossRef]
- Roach, T.N.F. Use and Abuse of Entropy in Biology: A Case for Caliber. Entropy 2020, 22, 1335. [Google Scholar] [CrossRef]
- Styer, D. Entropy as Disorder: History of a Misconception. Phys. Teach. 2019, 57, 454–458. [Google Scholar] [CrossRef]
- Schrödinger, E. What is Life—The Physical Aspect of the Living Cell; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Boltzmann, L. Populäre Schriften; Barth: Leipzig, Germany, 1905. [Google Scholar]
- Loschmidt, J. Uber den Zustand des Warmegleichgewichtes eines Systems von Korpern mit Rücksicht auf die Schwerkraft. Wien. Ber. 1876, 73, 28–142. [Google Scholar]
- Zermelo, E. On the mechanical explanation of irreversible processes. Ann. Phys. 1896, 59, 793–801. [Google Scholar] [CrossRef]
- Lucia, U. Second law considerations on the third law: From Boltzmann and Loschmidt paradox to non equilibrium temperature. Phys. A Stat. Mech. Its Appl. 2016, 444, 121–128. [Google Scholar] [CrossRef]
- Vilar, J.M.G.; Rubí, J.M. Thermodynamics “beyond” local equilibrium. Proc. Natl. Acad. Sci. USA 2001, 98, 11081–11084. [Google Scholar] [CrossRef]
- Kondepudi, D.K.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Onsager, L. Reciprocal Relations in Irreversible Processes. I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Edwards, A.W.F. Mathematizing Darwin. Behav. Ecol. Sociobiol. 2011, 65, 421–430. [Google Scholar] [CrossRef]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publications: New York, NY, USA, 2013. [Google Scholar]
- Popper, K.R. The Logic of Scientific Discovery; Routledge: New York, NY, USA, 2002. [Google Scholar]
- Schmidt-Nielsen, K. Scaling: Why is Animal Size So Important? Cambridge University Press: Cambridge, UK, 1984; p. 241. [Google Scholar]
- Snell, O. Die Abhängigkeit des Hirngewichts von dem Körpergewicht und den geistigen Fähigkeiten. Arch. Psychiatr. 1892, 23, 436–446. [Google Scholar] [CrossRef]
- Thompson, D.A.W. On Growth and Form; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Huxley, J.S. Problems of Relative Growth, 2nd ed.; Dover: New York, NY, USA, 1972. [Google Scholar]
- Pinto, C.M.A.; Mendes Lopes, A.; Machado, J.A.T. A review of power laws in real life phenomena. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3558–3578. [Google Scholar] [CrossRef]
- West, G. Scale: The Universal Laws of Life, Growth, and Death in Organisms, Cities, and Companies; Penguin Publishing Group: New York, NY, USA, 2017. [Google Scholar]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef]
- Demetrius, L. Quantum statistics and allometric scaling of organisms. Phys. A Stat. Mech. Its Appl. 2003, 322, 477–490. [Google Scholar] [CrossRef]
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Limpert, E.; Stahel, W.; Abbt, M. Lognormal Distributions Across the Sciences: Keys and Clues. Bioscience 2001, 51, 341–352. [Google Scholar] [CrossRef]
- Annila, A.; Kuismanen, E. Natural hierarchy emerges from energy dispersal. Biosystems 2009, 95, 227–233. [Google Scholar] [CrossRef]
- Newton, I. Opticks: Or, a Treatise of the Reflexions, Refractions, Inflexions and Colours of Light, 4th ed.; William Innys: St. Paul’s, MN, USA, 1703; p. 382. [Google Scholar]
- Lewis, G.N. The Conservation of Photons. Nature 1926, 118, 874–875. [Google Scholar] [CrossRef]
- Annila, A. All in Action. Entropy 2010, 12, 2333–2358. [Google Scholar] [CrossRef]
- Grahn, P.; Annila, A.; Kolehmainen, E. On the carrier of inertia. AIP Adv. 2018, 8, 035028. [Google Scholar] [CrossRef]
- Wilson, C.M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J.R.; Duty, T.; Nori, F.; Delsing, P. Observation of the Dynamical Casimir Effect in a Superconducting Circuit. Nature 2011, 479, 376. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. Lett. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Sharma, V.; Annila, A. Natural process—Natural selection. Biophys. Chem. 2007, 127, 123–128. [Google Scholar] [CrossRef] [PubMed]
- Annila, A. Natural thermodynamics. Phys. A 2016, 444, 843–852. [Google Scholar] [CrossRef]
- Michaelian, K.; Santamaria-Holek, I. Invalid Microstate Densities for Model Systems Lead to Apparent Violation of Thermodynamic Law. Entropy 2017, 19, 314. [Google Scholar] [CrossRef]
- Gibbs, J.W. Elementary Principles in Statistical Mechanics: Developed with Especial Reference to the Rational Foundation of Thermodynamics; Charles Scribner’s Sons: New York, NY, USA, 1902. [Google Scholar] [CrossRef]
- Falcon, A. Aristotle on Causality. In The Stanford Encyclopedia of Philosophy, Spring 2021 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2019. [Google Scholar]
- Michaelian, K. Microscopic dissipative structuring and proliferation at the origin of life. Heliyon 2017, 3, e00424. [Google Scholar] [CrossRef]
- Michaelian, K. The Dissipative Photochemical Origin of Life: UVC Abiogenesis of Adenine. Entropy 2021, 23, 217. [Google Scholar] [CrossRef] [PubMed]
- Annila, A.; Annila, E. Why did life emerge? Int. J. Astrobiol. 2008, 7, 293–300. [Google Scholar] [CrossRef]
- Karnani, M.; Annila, A. Gaia again. Biosystems 2009, 95, 82–87. [Google Scholar] [CrossRef]
- Jaakkola, S.; Sharma, V.; Annila, A. Cause of Chirality Consensus. Curr. Chem. Biol. 2008, 2, 153–158. [Google Scholar] [CrossRef]
- Würtz, P.; Annila, A. Roots of diversity relations. J. Biophys. 2008, 2008, 654672. [Google Scholar] [CrossRef] [PubMed]
- De Maupertuis, P.-L.M. Les loix du mouvement et du repos déduites d’un principe métaphysique. Hist. l’Académie R. Sci. Belles Lett. 1748, 1746, 267–294. [Google Scholar]
- Chatterjee, A. Thermodynamics of Action and Organization in a System. Complexity 2016, 21, 307–317. [Google Scholar] [CrossRef]
- Kuchling, F.; Friston, K.; Georgiev, G.; Levin, M. Morphogenesis as Bayesian inference: A variational approach to pattern formation and control in complex biological systems. Phys. Life Rev. 2020, 33, 88–108. [Google Scholar] [CrossRef]
- Riek, R.; Chatterjee, A. Causality in Discrete Time Physics Derived from Maupertuis Reduced Action Principle. Entropy 2021, 23, 1212. [Google Scholar] [CrossRef]
- Chatterjee, A.; Iannacchione, G. Time and thermodynamics extended discussion on “Time & clocks: A thermodynamic approach”. Results Phys. 2020, 17, 103165. [Google Scholar] [CrossRef]
- Simon, H.A. On a Class of Skew Distribution Functions. Biometrika 1955, 42, 425–440. [Google Scholar] [CrossRef]
- Mäkelä, T.; Annila, A. Natural patterns of energy dispersal. Phys. Life Rev. 2010, 7, 477–498. [Google Scholar] [CrossRef]
- Georgiev, G.Y.; Chatterjee, A.; Iannacchione, G. Exponential Self-Organization and Moore’s Law: Measures and Mechanisms. Complexity 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef]
- Aitchison, J.; Brown, J.A.C. The Lognormal Distribution with Special Reference to Its Uses in Economics; Cambridge University Press: Cambridge, UK, 1963. [Google Scholar]
- Gaddum, J.H. Lognormal Distributions. Nature 1945, 156, 463–466. [Google Scholar] [CrossRef]
- Tsuji, K.; Müller, S.C. Spirals and Vortices: In Culture, Nature, and Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Annila, A. Physical portrayal of computational complexity. ISRN Comp. Math. 2012, 321372, 15. [Google Scholar] [CrossRef][Green Version]
- Lucia, U.; Grisolia, G. Irreversible Thermodynamics and Bioeconomy: Toward a Human-Oriented Sustainability. FrPhy 2021, 9, 154. [Google Scholar] [CrossRef]
- Kuhn, T.S. The Essential Tension: Selected Studies in Scientific Tradition and Change; Chicago University Press: Chicago, IL, USA, 1977; p. 366. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: New York, NY, USA, 2018. [Google Scholar]
- Bacon, F. Novum Organum; Cambridge University Press: Cambridge, UK, 2000; p. 252. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Annila, A. Statistical Physics of Evolving Systems. Entropy 2021, 23, 1590. https://doi.org/10.3390/e23121590
Annila A. Statistical Physics of Evolving Systems. Entropy. 2021; 23(12):1590. https://doi.org/10.3390/e23121590
Chicago/Turabian StyleAnnila, Arto. 2021. "Statistical Physics of Evolving Systems" Entropy 23, no. 12: 1590. https://doi.org/10.3390/e23121590
APA StyleAnnila, A. (2021). Statistical Physics of Evolving Systems. Entropy, 23(12), 1590. https://doi.org/10.3390/e23121590





