Hidden Hypergraphs, Error-Correcting Codes, and Critical Learning in Hopfield Networks
Abstract
:1. Introduction
2. Applications
2.1. Unsupervised Clustering
2.2. Natural Signal Modeling
2.3. Error-Correcting Codes
2.4. Computational Graph Theory
2.5. Theory of Learning
3. Background
3.1. Hopfield Networks
3.2. Robust Capacity
3.3. Learning Networks
3.4. Minimum Energy Flow
3.5. Properties
3.6. Minimizing Energy Flow Is Biologically Plausible
3.7. Extensions
4. Results
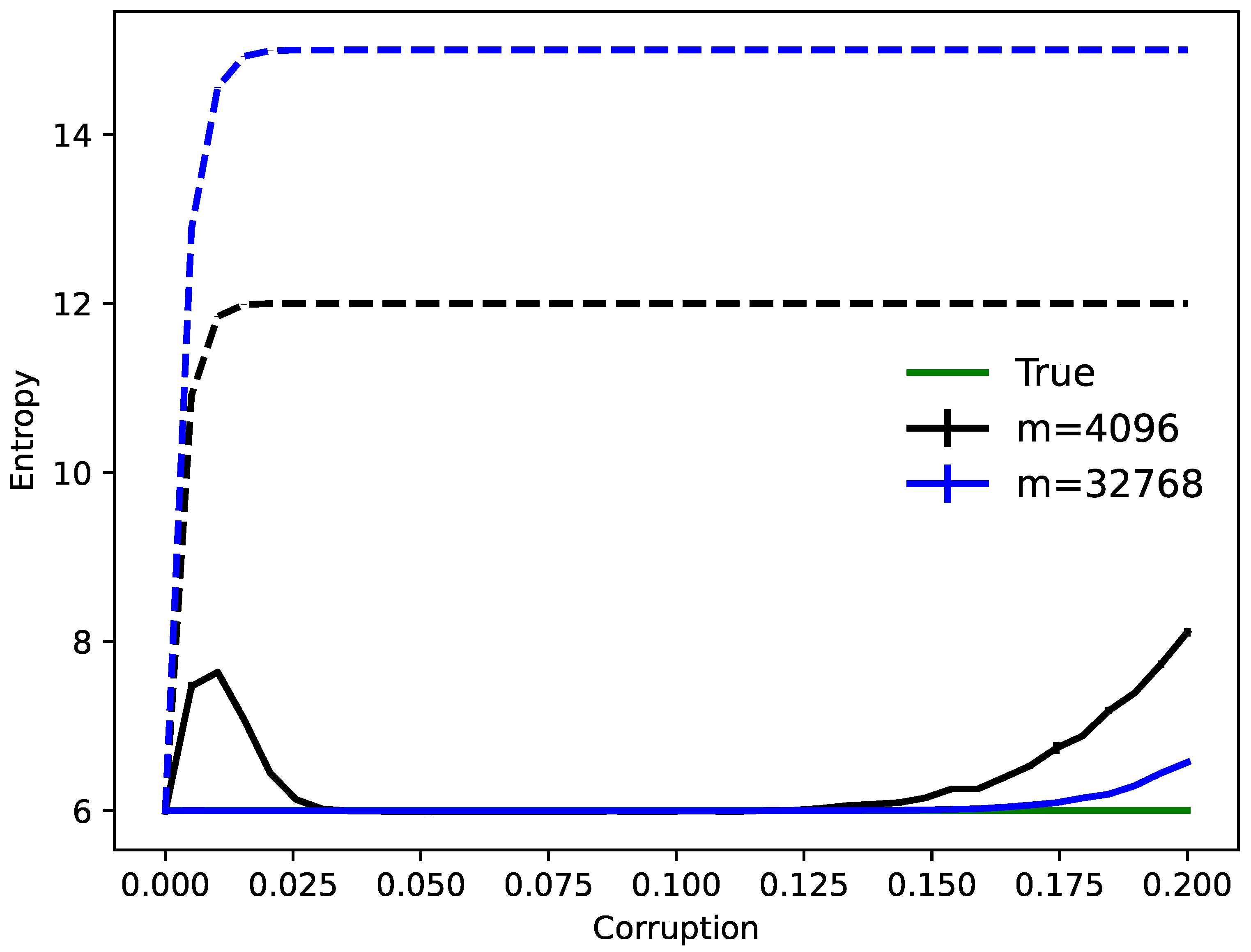
4.1. Experimental Neuroscience
4.2. Hypergraph Codes
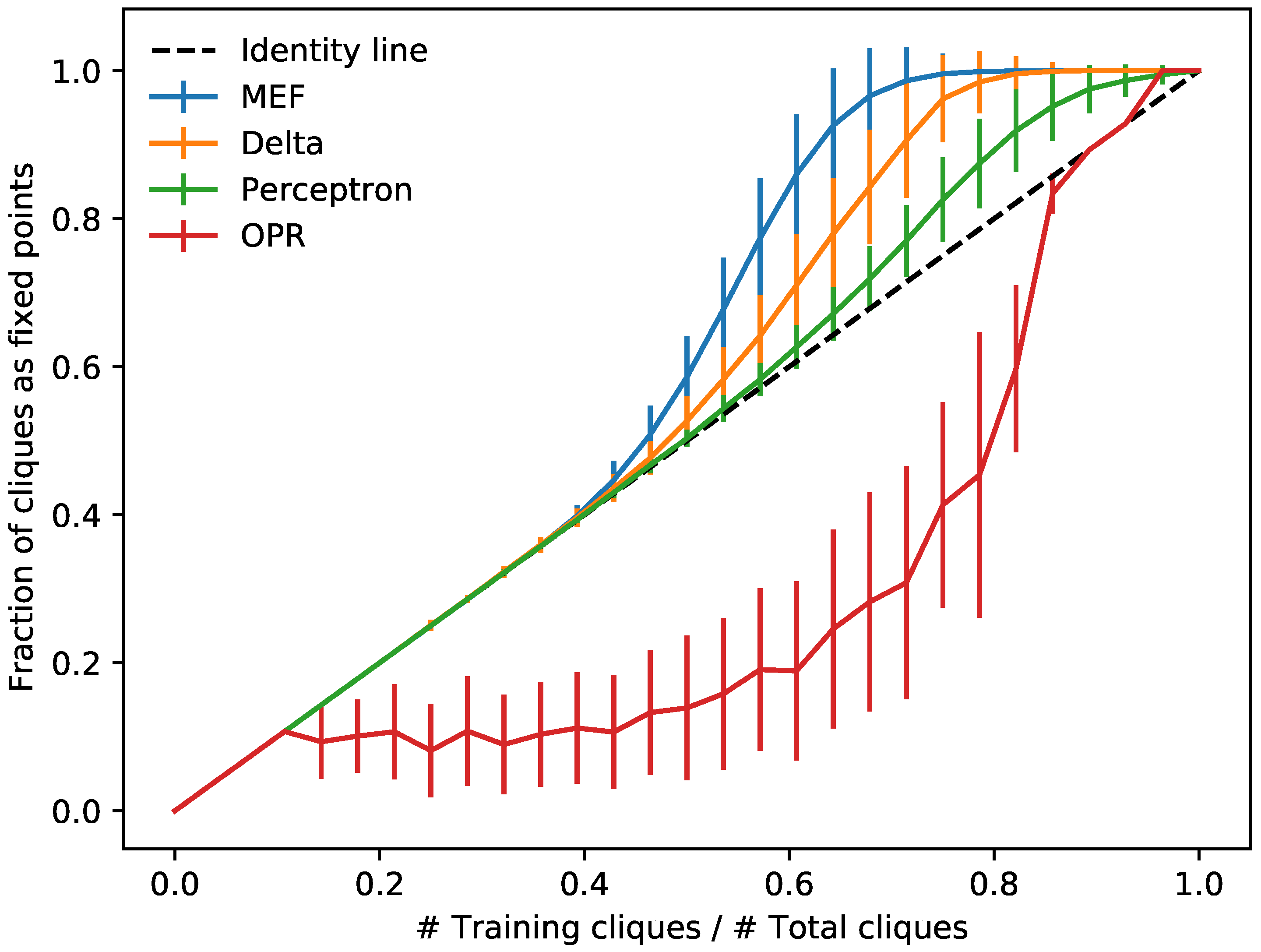
4.3. Critical Learning
5. Proofs
5.1. MEF Inequality
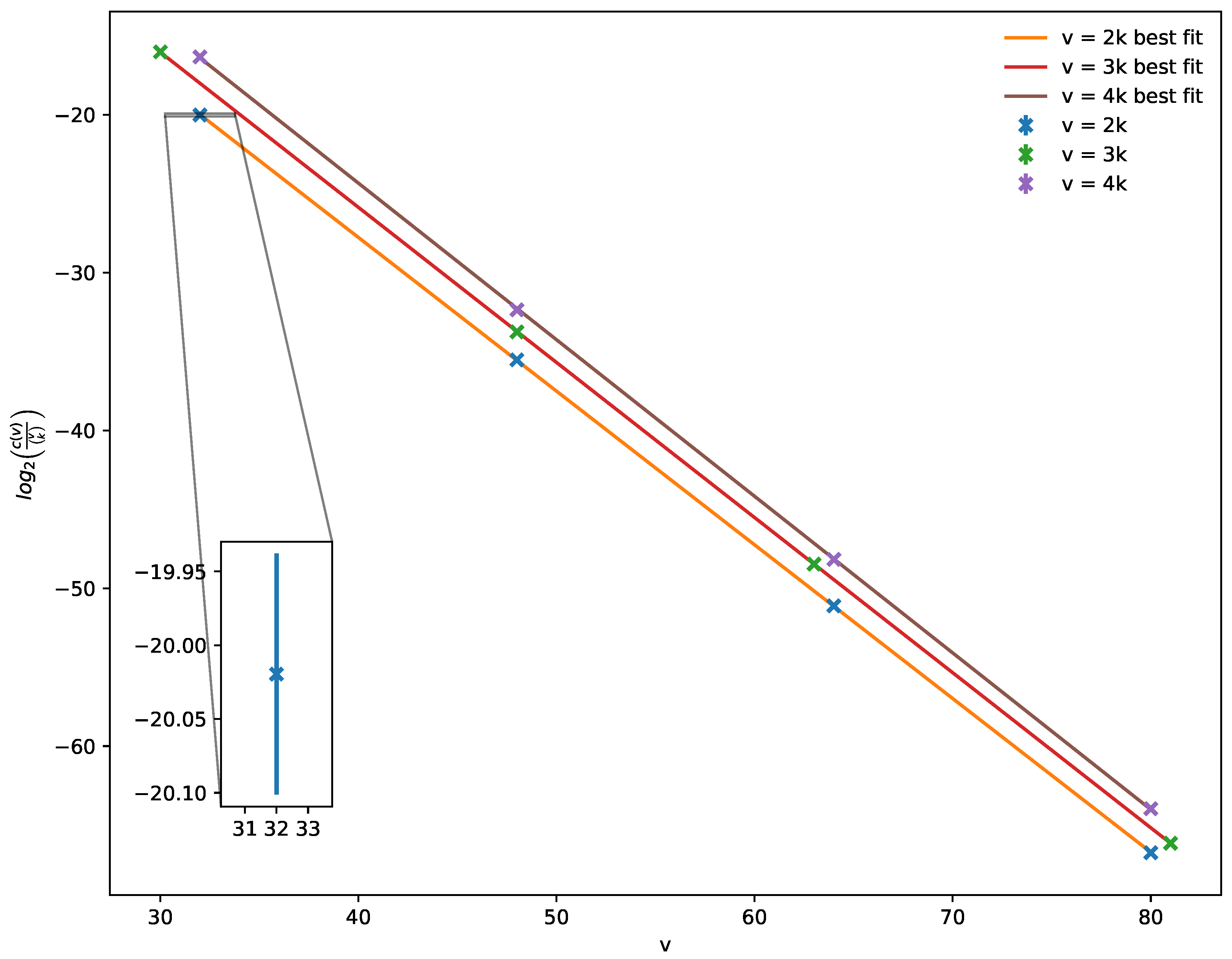
5.2. Hyperclique Theorem
- If i is complete,
- If i is incomplete,
- The number of complete i is
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MEF | minimum energy flow |
| MLE | maximum likelihood estimation |
| OPR | outer product rule |
| DRNN | discrete recurrent neural network |
References
- McCulloch, W.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Piccinini, G. The First computational theory of mind and brain: A close look at McCulloch and Pitts’s “A logical calculus of ideas immanent in nervous activity”. Synthese 2004, 141, 175–215. [Google Scholar] [CrossRef]
- Von Neumann, J. First draft of a report on the EDVAC. IEEE Ann. Hist. Comput. 1993, 15, 27–75. [Google Scholar] [CrossRef]
- Hopfield, J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Little, W. The existence of persistent states in the brain. Math. Biosci. 1974, 19, 101–120. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. Imagenet classification with deep convolutional neural networks. In Proceedings of the Twenty-Sixth Annual Conference on Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–6 December 2021; pp. 1106–1114. [Google Scholar]
- Ba, J.; Caruana, R. Do deep nets really need to be deep? Adv. Neural Inform. Process. Syst. 2014, 27, 1–9. [Google Scholar]
- Ramsauer, H.; Schäfl, B.; Lehner, J.; Seidl, P.; Widrich, M.; Adler, T.; Gruber, L.; Holzleitner, M.; Pavlović, M.; Sandve, G.K.; et al. Hopfield networks is all you need. arXiv 2021, arXiv:2008.02217. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Kar, K.; Kubilius, J.; Schmidt, K.; Issa, E.B.; DiCarlo, J.J. Evidence that recurrent circuits are critical to the ventral stream’s execution of core object recognition behavior. Nat. Neurosci. 2019, 22, 974–983. [Google Scholar] [CrossRef] [Green Version]
- Kietzmann, T.C.; Spoerer, C.J.; Sörensen, L.K.; Cichy, R.M.; Hauk, O.; Kriegeskorte, N. Recurrence is required to capture the representational dynamics of the human visual system. Proc. Natl. Acad. Sci. USA 2019, 116, 21854–21863. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Martino, A.; De Martino, D. An introduction to the maximum entropy approach and its application to inference problems in biology. Heliyon 2018, 4, e00596. [Google Scholar] [CrossRef] [Green Version]
- Schneidman, E.; Berry, M.; Segev, R.; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007–1012. [Google Scholar] [CrossRef] [Green Version]
- Shlens, J.; Field, G.; Gauthier, J.; Greschner, M.; Sher, A.; Litke, A.; Chichilnisky, E. The structure of large-scale synchronized firing in primate retina. J. Neurosci. 2009, 29, 5022. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ising, E. Beitrag zur Theorie des Ferromagnetismus. Z. Phys. 1925, 31, 253–258. [Google Scholar] [CrossRef]
- Fiete, I.; Schwab, D.J.; Tran, N.M. A binary Hopfield network with 1/log(n) information rate and applications to grid cell decoding. arXiv 2014, arXiv:1407.6029. [Google Scholar]
- Chaudhuri, R.; Fiete, I. Associative content-addressable networks with exponentially many robust stable states. arXiv 2017, arXiv:1704.02019. [Google Scholar]
- Hillar, C.J.; Tran, N.M. Robust exponential memory in Hopfield networks. J. Math. Neurosci. 2018, 8, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Chaudhuri, R.; Fiete, I. Bipartite expander Hopfield networks as self-decoding high-capacity error correcting codes. Adv. Neural Inform. Process. Syst. 2019, 32, 1–12. [Google Scholar]
- Hillar, C.; Sohl-Dickstein, J.; Koepsell, K. Efficient and optimal binary Hopfield associative memory storage using minimum probability flow. arXiv 2012, arXiv:1204.2916. [Google Scholar]
- Still, S.; Bialek, W. How many clusters? An information-theoretic perspective. Neural Comput. 2004, 16, 2483–2506. [Google Scholar] [CrossRef]
- Li, Y.; Hu, P.; Liu, Z.; Peng, D.; Zhou, J.T.; Peng, X. Contrastive clustering. In Proceedings of the 2021 AAAI Conference on Artificial Intelligence (AAAI), Vancouver, BC, Canada, 2–9 February 2021. [Google Scholar]
- Coviello, E.; Chan, A.B.; Lanckriet, G.R. Clustering hidden Markov models with variational HEM. J. Mach. Learn. Res. 2014, 15, 697–747. [Google Scholar]
- Lan, H.; Liu, Z.; Hsiao, J.H.; Yu, D.; Chan, A.B. Clustering hidden Markov models with variational Bayesian hierarchical EM. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Andriyanov, N. Methods for preventing visual attacks in convolutional neural networks based on data discard and dimensionality reduction. Appl. Sci. 2021, 11, 5235. [Google Scholar] [CrossRef]
- Andriyanov, N.; Andriyanov, D. Intelligent processing of voice messages in civil aviation: Message recognition and the emotional state of the speaker analysis. In Proceedings of the 2021 International Siberian Conference on Control and Communications (SIBCON), Kazan, Russia, 13–15 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Shannon, C. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Naillon, M.; Theeten, J.B. Neural approach for TV image compression using a Hopfield type network. Adv. Neural Inform. Process. Syst. 1989, 1, 264–271. [Google Scholar]
- Hillar, C.; Mehta, R.; Koepsell, K. A Hopfield recurrent neural network trained on natural images performs state-of-the-art image compression. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 4092–4096. [Google Scholar]
- Hillar, C.; Marzen, S. Revisiting perceptual distortion for natural images: Mean discrete structural similarity index. In Proceedings of the 2017 Data Compression Conference (DCC), Snowbird, UT, USA, 4–7 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 241–249. [Google Scholar]
- Mehta, R.; Marzen, S.; Hillar, C. Exploring discrete approaches to lossy compression schemes for natural image patches. In Proceedings of the 2015 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2236–2240. [Google Scholar]
- Hillar, C.J.; Marzen, S.E. Neural network coding of natural images with applications to pure mathematics. In Contemporary Mathematics; American Mathematical Sociecty: Providence, RI, USA, 2017; Volume 685, pp. 189–222. [Google Scholar]
- Hillar, C.; Effenberger, F. Robust discovery of temporal structure in multi-neuron recordings using Hopfield networks. Procedia Comput. Sci. 2015, 53, 365–374. [Google Scholar] [CrossRef] [Green Version]
- Effenberger, F.; Hillar, C. Discovery of salient low-dimensional dynamical structure in neuronal population activity using Hopfield networks. In Proceedings of the International Workshop on Similarity-Based Pattern Recognition, Copenhagen, Denmark, 12–14 October 2015; Springer: Berlin, Germany, 2015; pp. 199–208. [Google Scholar]
- Hillar, C.; Effenberger, F. hdnet—A Python Package for Parallel Spike Train Analysis. 2015. Available online: https://github.com/team-hdnet/hdnet (accessed on 15 July 2015).
- Hopfield, J.J.; Tank, D.W. “Neural” computation of decisions in optimization problems. Biol. Cybern. 1985, 52, 141–152. [Google Scholar]
- Lucas, A. Ising formulations of many NP problems. Front. Phys. 2014, 2, 5. [Google Scholar] [CrossRef] [Green Version]
- Boothby, K.; Bunyk, P.; Raymond, J.; Roy, A. Next-generation topology of d-wave quantum processors. arXiv 2020, arXiv:2003.00133. [Google Scholar]
- Dekel, Y.; Gurel-Gurevich, O.; Peres, Y. Finding hidden cliques in linear time with high probability. Comb. Probab. Comput. 2014, 23, 29–49. [Google Scholar] [CrossRef] [Green Version]
- Hebb, D. The Organization of Behavior; Wiley: New York, NY, USA, 1949. [Google Scholar]
- Amari, S.I. Learning patterns and pattern sequences by self-organizing nets of threshold elements. IEEE Trans. Comput. 1972, 100, 1197–1206. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef] [Green Version]
- Widrow, B.; Hoff, M.E. Adaptive Switching Circuits; Technical Report; Stanford University Ca Stanford Electronics Labs: Stanford, CA, USA, 1960. [Google Scholar]
- Rescorla, R.A.; Wagner, A.R. A theory of Pavlovian conditioning: Variations on the effectiveness of reinforcement and non-reinforcement. In Classical Conditioning II: Current Research and Theory; Black, A.H., Prokasy, W.F., Eds.; Appleton-Century-Crofts: New York, NY, USA, 1972; pp. 64–99. [Google Scholar]
- Hinton, G.; Sejnowski, T. Learning and relearning in Boltzmann machines. Parallel Distrib. Process. Explor. Microstruct. Cogn. 1986, 1, 282–317. [Google Scholar]
- Cover, T.; Thomas, J. Elements of Information Theory, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 721–741. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, S.; Diaconis, P.; Sly, A. Random graphs with a given degree sequence. Ann. Appl. Probab. 2011, 21, 1400–1435. [Google Scholar] [CrossRef] [Green Version]
- Hillar, C.; Wibisono, A. Maximum entropy distributions on graphs. arXiv 2013, arXiv:1301.3321. [Google Scholar]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Hazan, E.; Agarwal, A.; Kale, S. Logarithmic regret algorithms for online convex optimization. Mach. Learn. 2007, 69, 169–192. [Google Scholar] [CrossRef]
- Turrigiano, G.G.; Leslie, K.R.; Desai, N.S.; Rutherford, L.C.; Nelson, S.B. Activity-dependent scaling of quantal amplitude in neocortical neurons. Nature 1998, 391, 892–896. [Google Scholar] [CrossRef]
- Potts, R.B. Some generalized order-disorder transformations. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1952; Volume 48, pp. 106–109. [Google Scholar]
- Sohl-Dickstein, J.; Battaglino, P.B.; DeWeese, M.R. New method for parameter estimation in probabilistic models: Minimum probability flow. Phys. Rev. Lett. 2011, 107, 220601. [Google Scholar] [CrossRef]
- Blanche, T.; Spacek, M.; Hetke, J.; Swindale, N. Polytrodes: High-density silicon electrode arrays for large-scale multiunit recording. J. Neurophysiol. 2005, 93, 2987–3000. [Google Scholar] [CrossRef]
- Grossberger, L.; Battaglia, F.P.; Vinck, M. Unsupervised clustering of temporal patterns in high-dimensional neuronal ensembles using a novel dissimilarity measure. PLoS Comput. Biol. 2018, 14, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Hoeffding, W. Probability inequalities for sums of bounded random variables. J. Am. Stat. Assoc. 1963, 58, 13–30. [Google Scholar] [CrossRef]
- Azuma, K. Weighted sums of certain dependent random variables. Tohoku Math. J. Second. Ser. 1967, 19, 357–367. [Google Scholar] [CrossRef]
- Liu, Z.; Chotibut, T.; Hillar, C.; Lin, S. Biologically plausible sequence learning with spiking neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 1316–1323. [Google Scholar]
- Valiant, L.G. A theory of the learnable. Commun. ACM 1984, 27, 1134–1142. [Google Scholar] [CrossRef] [Green Version]
- Mora, T.; Bialek, W. Are biological systems poised at criticality? J. Stat. Phys. 2011, 144, 268–302. [Google Scholar] [CrossRef] [Green Version]
- Del Papa, B.; Priesemann, V.; Triesch, J. Criticality meets learning: Criticality signatures in a self-organizing recurrent neural network. PLoS ONE 2017, 12, e0178683. [Google Scholar] [CrossRef] [PubMed]


| Learning Rule | Principle |
|---|---|
| Outer-product (OPR) | Hebb’s rule sets weights to be correlation |
| Perceptron | Supervised pattern memorization |
| Delta | Least mean square objective function |
| Contrastive divergence | Maximum likelihood estimation by sampling |
| Minimum energy flow (MEF) | Approximate maximum likelihood estimation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hillar, C.; Chan, T.; Taubman, R.; Rolnick, D. Hidden Hypergraphs, Error-Correcting Codes, and Critical Learning in Hopfield Networks. Entropy 2021, 23, 1494. https://doi.org/10.3390/e23111494
Hillar C, Chan T, Taubman R, Rolnick D. Hidden Hypergraphs, Error-Correcting Codes, and Critical Learning in Hopfield Networks. Entropy. 2021; 23(11):1494. https://doi.org/10.3390/e23111494
Chicago/Turabian StyleHillar, Christopher, Tenzin Chan, Rachel Taubman, and David Rolnick. 2021. "Hidden Hypergraphs, Error-Correcting Codes, and Critical Learning in Hopfield Networks" Entropy 23, no. 11: 1494. https://doi.org/10.3390/e23111494
APA StyleHillar, C., Chan, T., Taubman, R., & Rolnick, D. (2021). Hidden Hypergraphs, Error-Correcting Codes, and Critical Learning in Hopfield Networks. Entropy, 23(11), 1494. https://doi.org/10.3390/e23111494





