Measurement of the Temperature Using the Tomographic Representation of Thermal States for Quadratic Hamiltonians
Abstract
1. Introduction
2. Wigner and Tomographic Representations of Unimodal Thermal States
3. Tomographic Representation of Two-Mode Thermal States
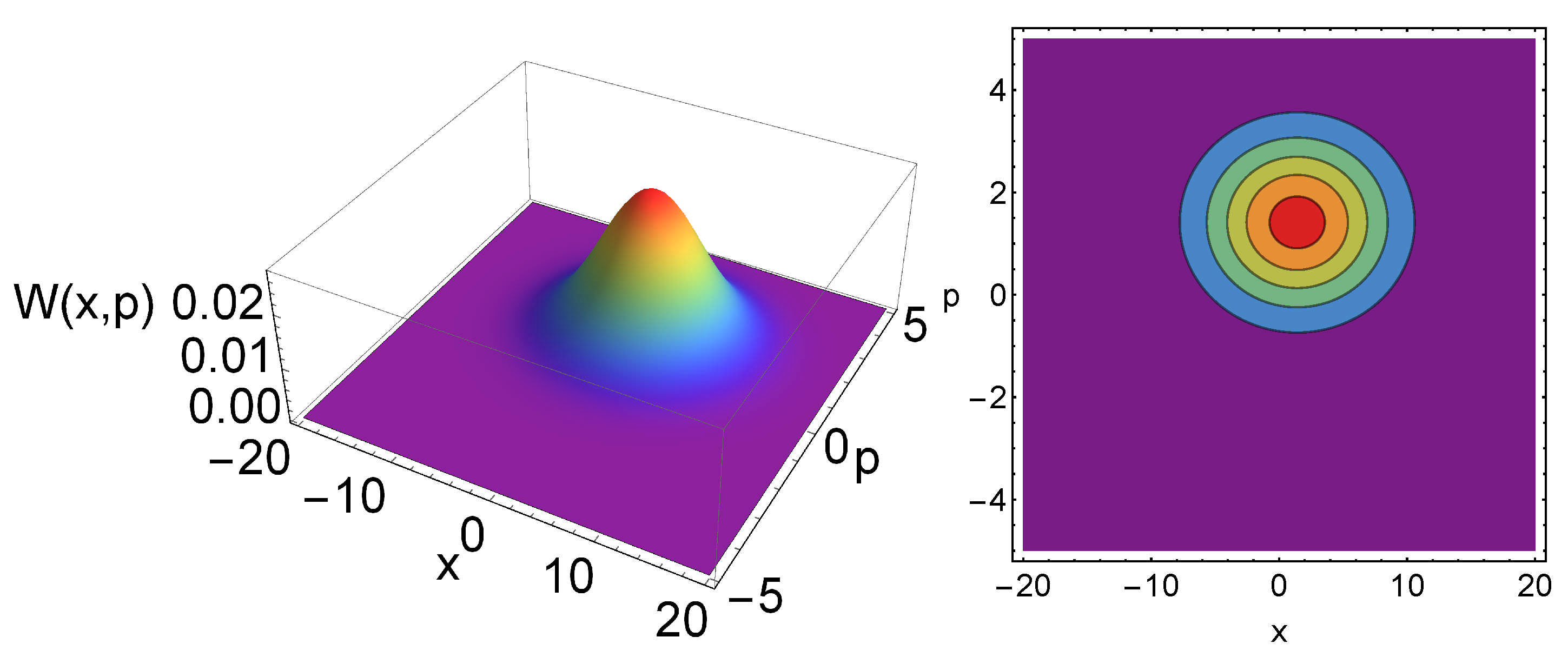
Example
Two Coupled Harmonic Oscillators
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, 2nd ed.; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- Schrödinger, E. Quantisierung als Eigenwertproblem (Zweite Mitteilung). Ann. Phys. 1926, 384. [Google Scholar] [CrossRef]
- Landau, L. Das Dämpfungsproblem in der Wellenmechanik. Z. Phys. 1927, 45, 430. [Google Scholar] [CrossRef]
- Von Neumann, J. Wahrscheinlichkeitstheoretischer Aufbau der Quantenmechanik. Mathematisch-Physikalische Klasse 1927, 1927, 245–272. [Google Scholar]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Kossakowski, A. On quantum statistical mechanics of non-Hamiltonian systems. Rep. Math. Phys. 1972, 3, 247. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive semigroups of N-level systems. J. Math. Phys. 1976, 17, 821. [Google Scholar] [CrossRef]
- Wigner, E.P. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749. [Google Scholar] [CrossRef]
- Husimi, K. Some Formal Properties of the Density Matrix. Proc. Phys. Math. Soc. Jpn. 1940, 22, 264. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and incoherent states of the radiation field. Phys. Rev. 1963, 131, 2766. [Google Scholar] [CrossRef]
- Sudarshan, E.C.G. Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams. Phys. Rev. Lett. 1963, 10, 277. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172. [Google Scholar] [CrossRef]
- Mancini, S.; Man’ko, V.I.; Tombesi, P. Symplectic Tomography as Classical Approach to Quantum Systems. Phys. Lett. A 1996, 213, 1–6. [Google Scholar] [CrossRef]
- Radon, J. On the determination of functions from their integral values along certain manifolds. IEEE Trans. Med. Imaging 1986, 5, 170. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Man’ko, V.I. Invariants and the evolution of nonstationary quantum systems. In Proceedings of the Lebedev Physical Institute; Nova Science Publishers: New York, NY, USA, 1989; Volume 183. [Google Scholar]
- Pitaevskii, L.; Stringari, S. Bose–Einstein Condensation and Superfluidity; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Weinbub, J.; Ferry, D.K. Recent advances in Wigner function approaches. Appl. Phys. Rev. 2018, 5, 041104. [Google Scholar] [CrossRef]
- Man’ko, V.I.; Marmo, G.; Porzio, A.; Solimeno, S.; Ventriglia, F. Homodyne estimation of quantum states purity by exploiting covariant uncertainty relation. arXiv 2010, arXiv:1012.3297v2. [Google Scholar] [CrossRef]
- Man’ko, V.I.; Marmo, G.; Simoni, A.; Ventriglia, F. A possible experimental check of the uncertainty relations by means of homodyne measuring field quadrature. Adv. Sci. Lett. 2009, 2, 517. [Google Scholar] [CrossRef]
- Schleich, W.P. Quantum Optics in Phase Space; Wiley-VCH Verlag: Berlin, Germany, 2001. [Google Scholar]
- Dodonov, V.V.; Malkin, I.A.; Man’ko, V.I. The Green function and thermodynamical properties of quadratic systems. J. Phys. A 1975, 8, L19. [Google Scholar] [CrossRef]
- Akhundova, E.A.; Dodonov, V.V.; Man’ko, V.I. Wigner functions of quadratic systems. Physica A 1982, 115, 215. [Google Scholar] [CrossRef][Green Version]
- Dodonov, V.V. Invariant Quantum States of Quadratic Hamiltonians. Entropy 2021, 23, 634. [Google Scholar] [CrossRef]
- López-Saldívar, J.A.; Man’ko, M.A.; Man’ko, V.I. Differential parametric formalism for the evolution of Gaussian states: Nonunitary evolution and invariant states. Entropy 2020, 22, 586. [Google Scholar] [CrossRef]
- López-Saldívar, J.A.; Man’ko, M.A.; Man’ko, V.I. Nonlinear differential equations of Gaussian states. AIP Conf. Proc. 2021, 2362, 040007. [Google Scholar] [CrossRef]
- Duan, L.M.; Giedke, G.; Cirac, J.I.; Zoller, P. Inseparability Criterion for Continuous Variable Systems. Phys. Rev. Lett. 2000, 84, 2722. [Google Scholar] [CrossRef] [PubMed]
- Simon, R. Peres–Horodecki Separability Criterion for Continuous Variable Systems. Phys. Rev. Lett. 2000, 84, 2726. [Google Scholar] [CrossRef]
- Urzúa, A.R.; Ramos-Prieto, I.; Fernández-Guasti, M.; Moya-Cessa, H.M. Solution to the time-dependent coupled harmonic oscillators Hamiltonian with arbitrary interactions. Quantum Rep. 2019, 1, 82–90. [Google Scholar] [CrossRef]
- Ramos-Prieto, I.; Récamier, J.; Moya-Cessa, H.M. Time-dependent coupled harmonic oscillators: Classical and quantum solutions. Int. J. Mod. Phys. E 2020, 29, 2075001. [Google Scholar] [CrossRef]
- Makarov, D.N. Coupled harmonic oscillators and their quantum entanglement. Phys. Rev. E 2018, 97, 042203. [Google Scholar] [CrossRef]
- Makarov, D.N. Quantum entanglement and reflection coefficient for coupled harmonic oscillators. Phys. Rev. E 2020, 102, 052213. [Google Scholar] [CrossRef]
- Zhou, J.Y.; Zhou, Y.H.; Yin, X.L.; Huang, J.F.; Liao, J.Q. Quantum entanglement maintained by virtual excitations in an ultrastrongly coupled oscillator system. Sci. Rep. 2020, 10, 12557. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Saldívar, J.A.; Man’ko, M.A.; Man’ko, V.I. Measurement of the Temperature Using the Tomographic Representation of Thermal States for Quadratic Hamiltonians. Entropy 2021, 23, 1445. https://doi.org/10.3390/e23111445
López-Saldívar JA, Man’ko MA, Man’ko VI. Measurement of the Temperature Using the Tomographic Representation of Thermal States for Quadratic Hamiltonians. Entropy. 2021; 23(11):1445. https://doi.org/10.3390/e23111445
Chicago/Turabian StyleLópez-Saldívar, Julio A., Margarita A. Man’ko, and Vladimir I. Man’ko. 2021. "Measurement of the Temperature Using the Tomographic Representation of Thermal States for Quadratic Hamiltonians" Entropy 23, no. 11: 1445. https://doi.org/10.3390/e23111445
APA StyleLópez-Saldívar, J. A., Man’ko, M. A., & Man’ko, V. I. (2021). Measurement of the Temperature Using the Tomographic Representation of Thermal States for Quadratic Hamiltonians. Entropy, 23(11), 1445. https://doi.org/10.3390/e23111445







