This article introduces the concept and mathematical formulation of model unity in the field of mathematical consciousness science (MCS). Importantly, several example applications of model unity are provided and give a demonstration of its agreement with intuition. Model unity is a related and yet different concept to the usual concept of the unity of consciousness. When people talk of the unity of consciousness, or integration, they are usually referring to the somewhat loosely characterized concept called phenomenal unity. In [
1], Bayne and Chalmers consider two conscious states as being phenomenally unified “if there is something it is like for the subject to be in both conscious states simultaneously”. In [
2], Tononi, Oizumi and Albantakis characterize integration by the following “each experience is (strongly) irreducible to non-interdependent components. Thus, experiencing the word ‘SONO’ written in the middle of a blank page is irreducible to an experience of the word ‘SO’ at the right border of a half-page, plus an experience of the word ‘NO’ on the left border of another half page—the experience is whole. Similarly, seeing a red triangle is irreducible to seeing a triangle but no red color, plus a red patch but no triangle”.
By definition, see more formally below, a given system has model unity if one can do no better than a single relational model stretched across the whole system. Such relational models provide an interpretation of the states of the system. However, for some systems, the model that best fits is not given by one relational model stretched across the whole system but is instead given by the system as a collection of subsystems each having their own individualized and tailored relational model. More complex systems may then have higher levels that span lower subsystems where the lower subsystems together do not have model unity but the higher levels do. Therefore, a given level within a system may not have model unity and in theory the different relational models may relate to different aspects of consciousness. For example, the relational model in visual experience will be a different relational model to that for auditory experience. So model unity is a different and yet connected concept to the normal idea of the unity of consciousness and appeals to Wiese’s observations.
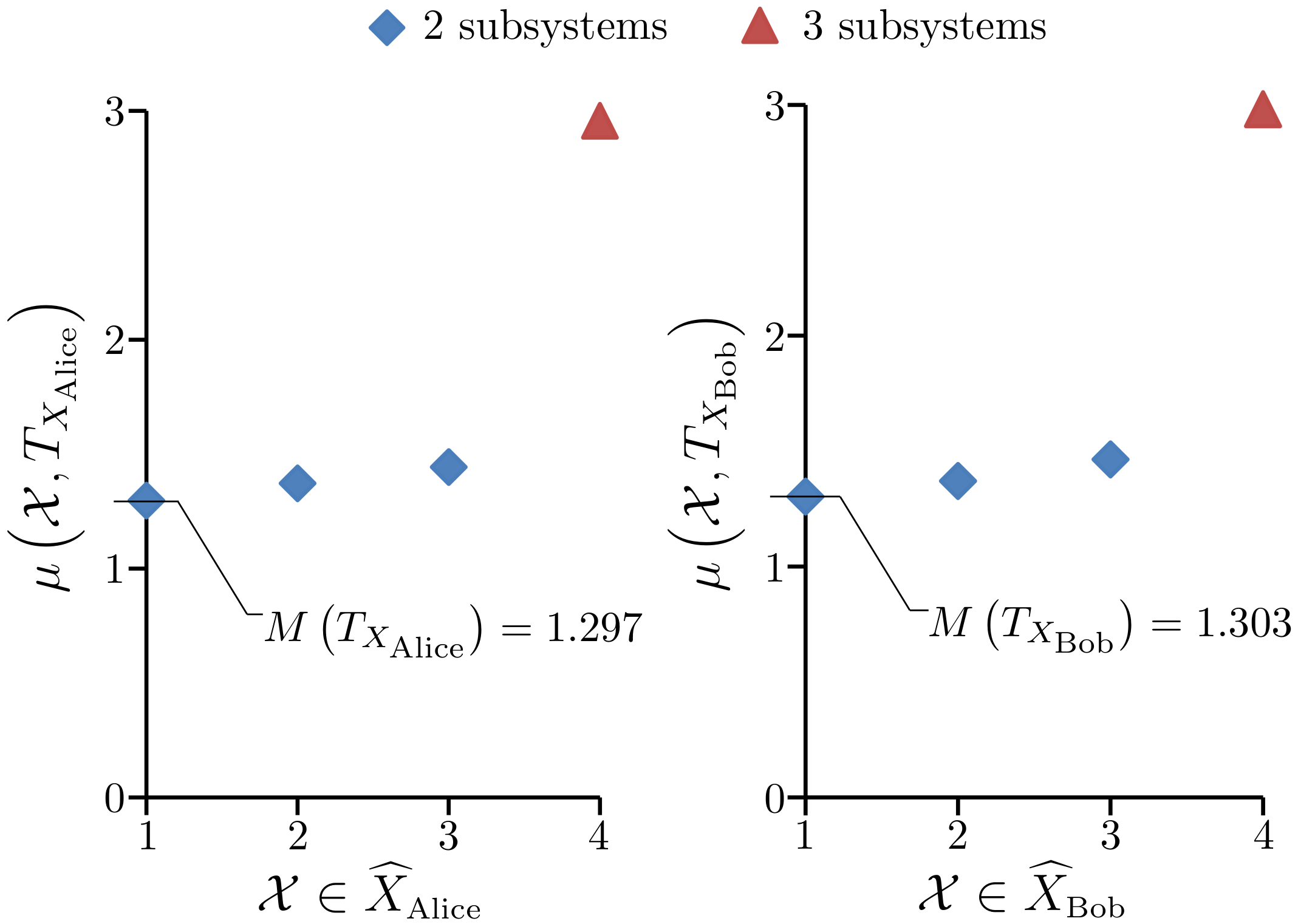
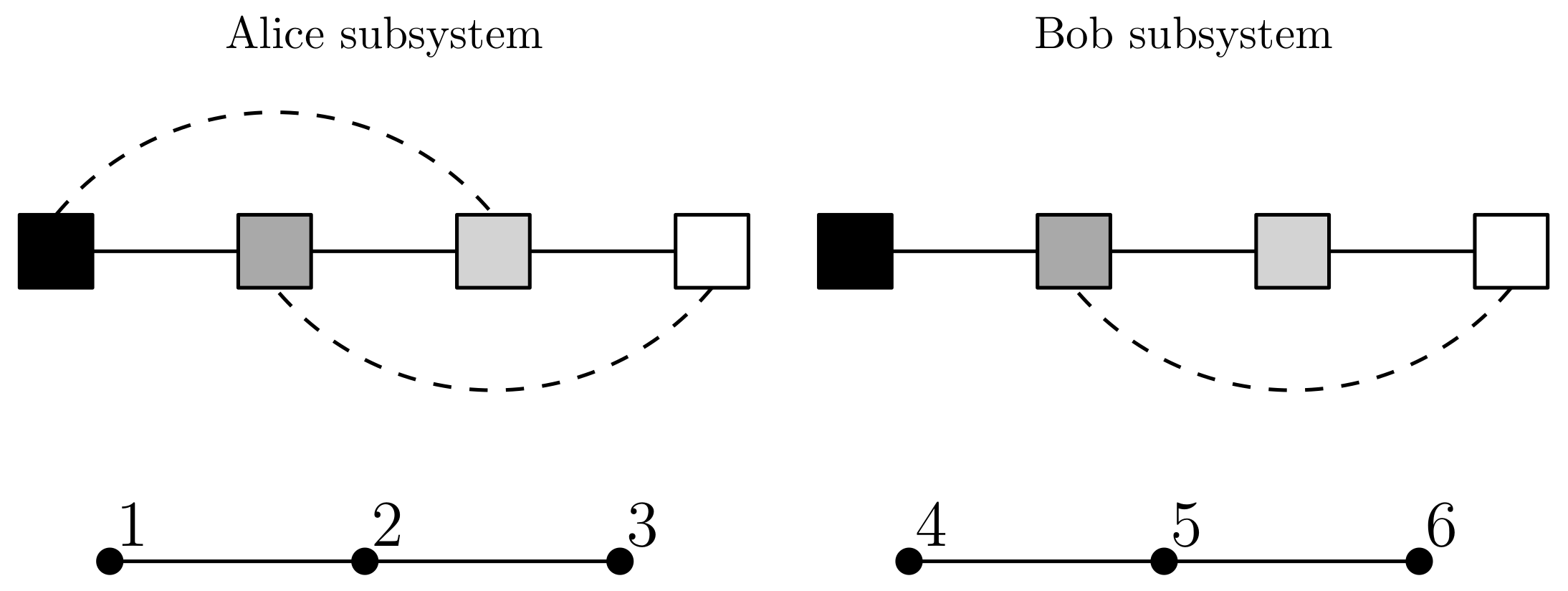
Moreover, due to the objectivity that mathematical methods afford, we should also talk about the disunity of consciousness. We tend not to think of different individuals as being part of the same system but mathematically it’s informative to consider the application of theory to say the “Alice and Bob system” where Alice and Bob are two different people. Initially it might seem ridiculous to suggest we need a theory to show that Alice and Bob have separate conscious experiences. However, what if Alice and Bob’s brains are conjoined perhaps just by one or two synapses or perhaps by millions of connections. How many connections are enough and which connections are the right connections for there to be phenomenal unity involving both brains? Of course the brain itself is in fact two brains as highlighted by the case of Christina Santhouse, see [
4], who had a hemispherectomy at age eight but later earned a master’s degree and started a family. Therefore, a normal brain is formed of two interconnected brains, each partly conditioned by the other, which together have phenomenal unity. Consideration of model unity may also be helpful here since a lack of model unity aught to indicate disunity of consciousness unless the unity is coming from some higher system level and model. In such cases the separate models determined can be very different or virtually identical if the lack of overall model unity is only due to the independence of the subsystems involved rather than the subsystems being very different. For example, this article provides strong evidence that for a given layer within Alice and Bob’s visual cortices, when taken together, there would not be model unity. And yet there is also some evidence to suggest that the same layer within Bob’s left and right visual cortices together would have model unity. The example experiments are only preliminary and do not use actual brain data but nevertheless show that model unity gives the right (anticipated) results in these tests. Of course, more experiments and research is needed if model unity is to gain a substantive foothold within MCS.
1.1. The Fundamental Postulate of EFE Minimisation
Model unity extends the theory of expected float entropy minimisation (EFE) which first appeared in the literature in 2012; see [
5,
6,
7,
8]. EFE minimisation is a mathematical formulation of a largely overlooked and yet arguably fundamental property of consciousness. Put simply, it is the property that consciousness is very smooth, as continuous as possible and free of unnecessary abrupt transitions, pops and crackles etc. In more scientific terms we state the following helpful postulate. It should be noted that the use of the word “interpretation” in the postulate will mean relational model when transferred to the mathematical domain. The relational model creates a context relative to which the system states are meaningful.
Postulate 1 (The fundamental postulate of EFE minimisation). If we suppose that consciousness is given by an interpretation or representation of system states then, notwithstanding the possibility that a system may need to satisfy a number of requirements to be conscious, among the infinitely many possible interpretations, consciousness is given by some form of minimum expected entropy interpretation of system states that yields an experience free of unnecessary discontinuities whilst exhibiting the intrinsic structural regularities of probable system states.
The postulate mentions “minimum expected entropy interpretation of system states”. The word “expected” is important here. It is not that the interpretation treats each system stare in isolation such that each system state has as few discontinuities as possible. That clearly would not correspond to conscious experience since when we look at a Jackson Pollock painting the geometry of the field of view does not jump to some new geometry relative to which the painting is almost free of abrupt discontinuities. Instead, we mean that the interpretation, i.e. relational model in the mathematical domain, is the same, or at least very stable whilst the system’s bias is stable, for whatever the current system state is. And, given that the system is biased toward being in certain system states over other system states due to a long history of conditioning by sensory inputs, the interpretation is the one for which the more probable system states have minimal abrupt discontinuities while improbable system states are likely to be full of such abrupt artifacts.
For those who like the idea of consciousness being given by some form of interpretation of system states there is the explanatory gap of why consciousness is given by one interpretation rather than another. In science it is often the case that a boundary point, limit point or stationary point is important, often referred to as the principle of least action. In the present theory we argue that the interpretation involved is special because it is a limit or boundary point of the set of all possible interpretations of system states since giving the minimum possible expected entropy.
Figure 1 provides a visual illustration of the fundamental postulate of EFE minimisation. Note the possibility of auditory analogs of
Figure 1 involving abrupt crackles and pops. In
Figure 1, while interpretation
is completely free of discontinuities it is actually a maximum expected entropy interpretation not a minimum. That might come as a surprise to some but to understand why we need to understand something of the notion of entropy being used. An analogy to the common understanding of Boltzmann entropy may help here. Boltzmann entropy is proportional to the log of the number of microstates that satisfy some macroscopic condition. In our case, to calculate the float entropy of a system state
relative to a particular relational model we first measure the discontinuity (in some suitable sense) of
given the relationships in the model. That discontinuity measurement is taken as our macroscopic condition and the float entropy of
is then the log of the number of other system states
with discontinuity measure less than or equal to that of
for the given relational model. We see then that a relational model where all of the relationships are identical (that is there are no relational distinctions) will result in the discontinuity measurement being the same for all system states and therefore, every system state will have maximum float entropy. Accordingly the system will have maximum expected float entropy for such a relational model as in the case for
in
Figure 1.
It is hoped that the reader does not find the postulate to be outlandish and that in time consideration may be given to the possibility of the postulate being a point of fact. It is likely that the property of consciousness outlined by the postulate has been largely overlooked because people take the minimal expected entropy aspect of experience for granted, perhaps because we assume that’s how the world outside of our brain is. But, from the author’s experience, a majority of researchers in the field of MCS, and consciousness science in general, think consciousness is most likely to be a property of the brain rather than a property of the brain and the world outside of the brain together. Of course sensory information from the world outside greatly influences brain activity and conditions the brain but we dream with our eyes closed and sometimes of places we have never see. Therefore, if we think that consciousness is a property internal to the brain then clearly the property of consciousness outlined by the postulate is striking and a significant aspect of experience.
Note that consciousness having minimal expected entropy is missing from the list of IIT axioms and postulates (see [
2]) even though it is clearly a fundamental aspect of consciousness and, at least on first inspection, does not appear to be implicitly given by the IIT axioms. The postulate is also a useful example of how mathematical consciousness science makes available concepts that aren’t immediately obvious without mathematics.
1.2. Expected Float Entropy Minimisation
Before delving into the mathematical details of EFE, it may be helpful to mention a couple of points to kept in mind. Firstly, what follows only involves relational models for the primary relationships that a system may determine. As mentioned earlier in the introduction, many systems will determine a hierarchy of relational models. In particular, secondary models and higher may involve relationships between features such as edges and objects, for example, that are present when system states are interpreted in the context of a primary relational model that a system determines. Accordingly, the mathematical details of EFE below, involving primary relational models, generalise to multi-relational EFE involving higher models. Little work has been undertaken on multi-relational EFE but initial definitions can be found in [
5,
6]. Secondly, the following talks about the nodes of a system. In the case of the brain, it is important not to immediately assume that a system node is an individual neuron. It is reasonable for a node to be a tuple of neurons in a somewhat analogous way to bytes being the nodes within a synthetic digital representation of sound rather than individual bits. Initial investigations into how systems may determine such a node base are given in [
5] and the present article provides a short discussion in
Section 4.3.
In the following, we recall the mathematical details of EFE minimisation before giving the mathematical definition of model unity. It will help us with the latter if we slightly simplify the notation used in [
5,
6] in a similar way to that given in [
8].
A system, such as the brain and its subsystems, is assumed to be made up of a finite number of nodes. We denote the set of such system nodes by
S and take
. The range
of states that the nodes can be in is also assumed to be finite. Given
S and
V, a system state is equivalent to a mapping,
and in this article we denote the set of all such maps by
, where
, and refer to such maps as system states. Informally, the probability of finding the system in system state
is given by a probability distribution
determined by the system. In practice,
P is usually unknown and instead a finite set
T of numbered observations of the system is used. In this case the observations are handled using a function
so that for the
ith observation we have
for some
. Note that
need not be injective. In order to move from the above particulars about systems to relational models that such systems may determine we use weighted relations. For any given set
S, a weighted relation on
S is a map
We say that
R is reflexive and symmetric if
and
,
respectively. All of the weighted relations used in this article are reflexive and symmetric and we denote the set of all such relations on a set
S by
. For notes on the use of reflexive and symmetric relations, see [
5,
6]. A primary relational model on a system with set of noses
S, as described above, involves a pair of weighted relations
and
. Of course, we are looking for a particular pair
R and
U that minimise expected float entropy, but to do this requires the following composition. For all
and
we have the composition
and note that
. Then, for all such
f,
U, and
, we use the composition to determine the following subset of
where
is usually taken as the
metric on the set of all weighted relations on
S. We can now give the definition of float entropy and expected float entropy as follows. For a system with probability distribution
, let
T be a finite set of numbered observations of the system, let
and
. The float entropy of a system state
, the expected float entropy of the system, and the approximation of the expected float entropy using
T, all relative to
R and
U, are defined as
respectively. The primary relational model that a system determines (up to a certain resolution) under EFE minimisation is then
In practice we replace
in (
5) with
. At this point it may be helpful to add the following note of clarification. We are not saying that a system itself is calculating EFE values and preforming such a minimisation, but instead that, due to the system’s bias, such a minimum solution, when able to be determined, is associated with the system as an emergent property. It is worth noting however that EFE minimisation is a form of machine learning and therefore the system’s bias might be the result of some form of distributed approximate analog to EFE minimisation happening within the system; see [
6].
Finally, we should link the obtained primary model in (
5) back to the fundamental postulate; Postulate 1. The model provides an interpretation of system states that exhibits the required minimum expected entropy property of consciousness mentioned in the postulate; see [
5]. For example, an appropriate application of the theory to the visual system may result in
giving the relationships between points in our perception of the field of view, giving the perceived geometry of the field of view, and
giving the perceived relationships between colours. Of course, as mentioned earlier in the introduction, the primary model is just that “primary” and consciousness is vastly richer requiring many more relational models to be involved in the interpretation of system states. We can now introduce the mathematics behind model unite.
1.3. Model Unity
The definition of model unity requires the introduction of two functions
and
M. We also require some additional notation. Let
S be the set of nodes of a system with probability distribution
. We will call
a subsystem of
S. We can view
S as a collection of subsystems and denote the set of all such possible collections by
Mathematically speaking,
is the set of all nontrivial partitions of
S but it is important to avoid confusion here with ideas in IIT. An element
is just
S viewed as a collection of subsystems and no structural changes have been made to the system. We are instead interested in whether it is best to use a single relational model across the whole of a system or whether using a number of individualized models for
S viewed as a collection of subsystems is better.
Now, the notation introduced in
Section 1.2 can be extended. For
a subsystem of
S, an element of
is denoted by
and
denotes the marginal probability distribution for the subsystem
X obtained from the distribution
. That is we have
where the sum is taken over all
and
is the restriction of
f to
X. A point to be aware of is that in theory it is possible to have
This would imply that for the subsystem
X we should perhaps replace the node range
V with a smaller range
resulting in a smaller set of possible subsystem states
when calculating EFE values. However, for systems with comparable nodes, this is a rather contrived situation and usually in practice, as is the case for all subsystems in all of the examples in this article, we do have
. This should also be kept in mind when denoting the weighted relations in our primary models for subsystems. In particular,
denotes an element of
and
denotes an element of
but in the usual case where
the notation
is just a way of showing that
and
form part of the same primary model.
We can now extend the above notation to definitions (
1)–(
4) above. We have,
where
is the restriction of
to
X. This is all straightforward and allows us to finally give the definitions of the functions
and
M. Let
, then
where, with reference to (
5), each term is individually minimized with respect to the choice of primary models used and the last term is the minimum EFE for the whole system. In practice we use
. Furthermore, define
We can now give the definition of model unity.
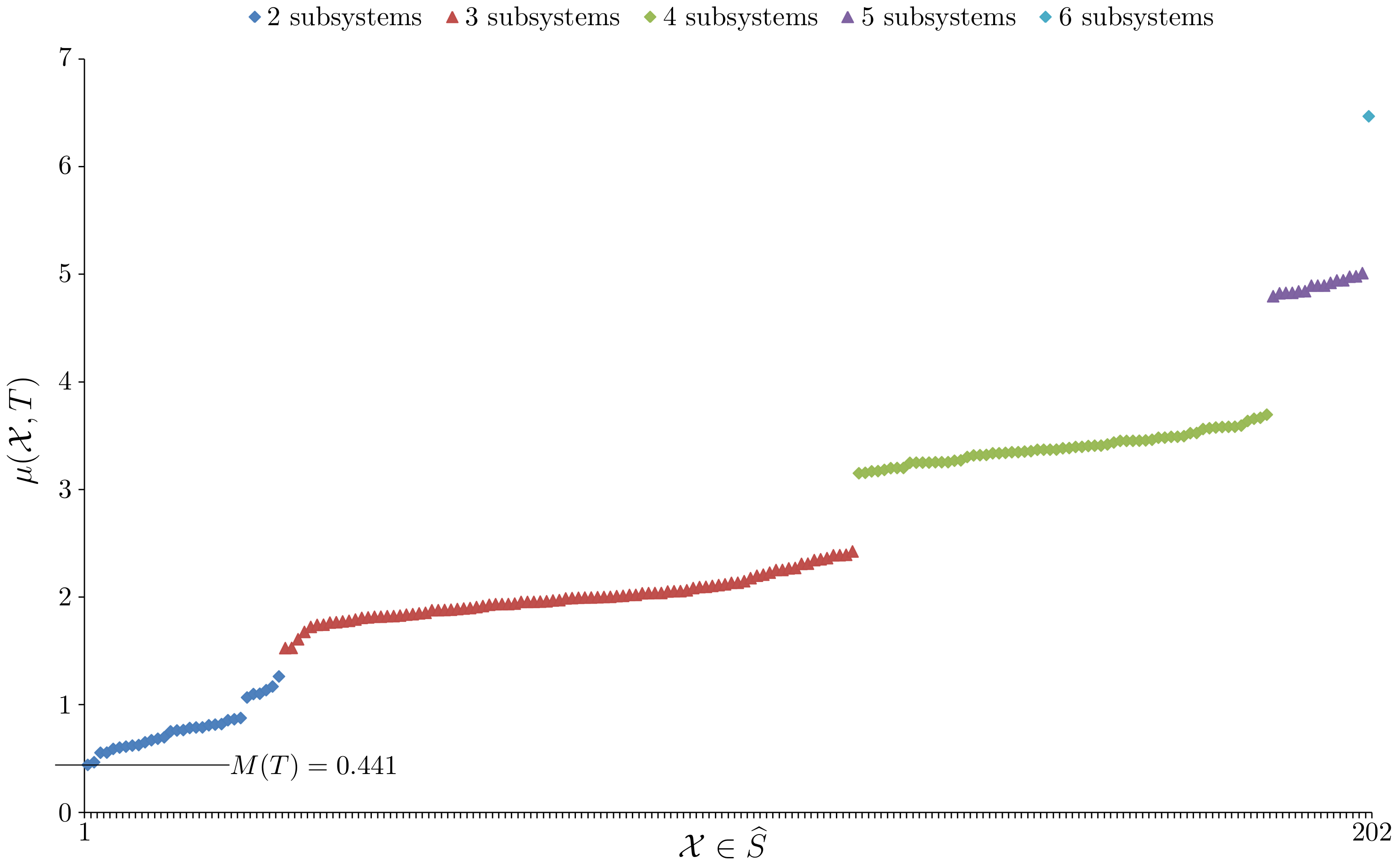
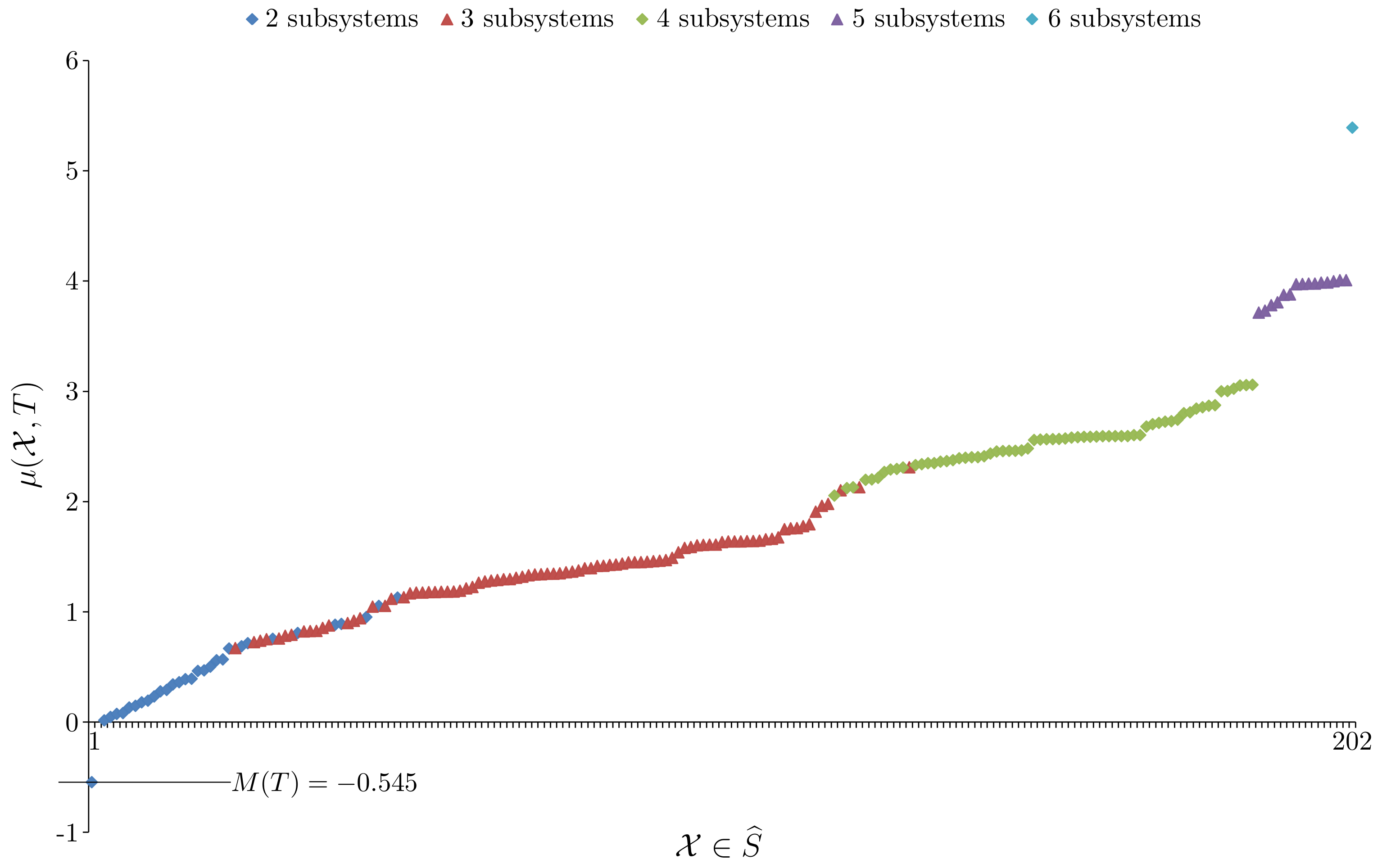
Definition 1 (Model unity). A system, with probability distribution giving the probability of finding the system in any given state, has model unity if and only if .
Superficially, it is easy to see why the definition of model unity makes sense. When an optimal single model stretched across the whole system gives equal or lower EFE than that given by a number of optimal individualized models when S is viewed as any nontrivial collection of subsystems. In other words, we can do no better than to use a single model. However, we should look at M and more closely.
The intended interpretation of
M is rather literal and should not be confused with that of
in IIT; see [
2]. For a given system with
, we interpret
as quantifying the strength of the system’s model unity, while recalling that the model gives an interpretation of system states. For systems without model unity,
, Lemma 1 can be applied. Relevant details are also given in
Section 4.2.
Lemma 1 (First lemma of model unity).
For a system having a probability distribution , defineor let be any such minimum argument if not unique. Then each subsystem with has model unity, that is . When and is unique, every subsystem that is a union of subsystems from the collection does not have model unity. Proof. The proof is almost immediate. Suppose, towards a contradiction, there is subsystem with and . Then, applying the definition of to the subsystem, we can replace X with some nontrivial partition of X giving a new partition of S with . This contradicts the definition of . The second part of the lemma follows in a similar way. □
When a system does not have model unity Lemma 1 and Postulate 1 suggest what to do. At the level of primary models the system S should be viewed as the collection of subsystems defined in Lemma 1. Each subsystem has its own minimum EFE value and the sum of these individual EFE values (which is the bracketed summation in the definition of ) gives a collective minimum EFE value for S when viewed as the collection of subsystems . Each subsystem has its own individualised optimal primary model (when determined) giving an interpretation of the states of the subsystem. Finally, each subsystem has its own model unity value and has model unity by Lemma 1. The second part of the lemma tells us that we cannot build larger subsystems with model unity out of the subsystems in . Of course this is still assuming .
Turning our attention to
, we note that the value of the summation in (
6) over the partition
falls within a comparable range to that of the final term which is the minimum EFE for the system as a whole. To show this, we need to express the summation in a different form, which will also reveals another identity for
. We have,
The product in the last equality can be expressed as
which, with reference to (
1), confirms that the value of the summation in (
6) falls within a comparable range to that of the final term in (
6). With respect to giving another identity for
, define
The identity for
is then
where
is just another notation for
, recalling that
is the primary model that minimises the EFE of the system when taken as a whole.
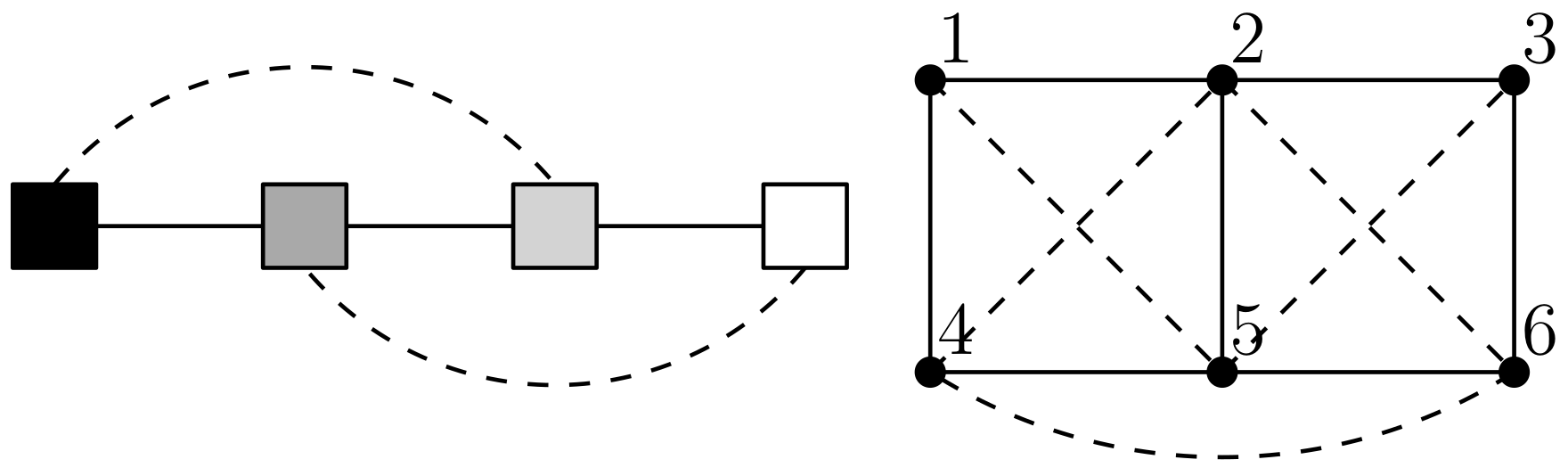
Before moving on to the Materials and Methods Section, it may be helpful to consider, all be it very informally, something of why, with regard to primary models, some systems have model unity and others do not. When a system has two or more subsystems that, in some suitable sense, are doing different things or are independent then giving each subsystem its own individualised optimal model will likely be best because (1) the individualised models will fit well whilst a single optimal model stretched across the whole system may fit some subsystems well but possibly not others, and (2) having relational parameters between nodes in the different, possibly independent, subsystems may actually result in a poorer single model. On the other hand, if there is some dependence and some form of regularity of activity across a system then having a single model that stretches across the whole system is likely best because the model benefits from having more parameters; namely the relationship parameters between the subsystems rather than just those within the subsystems. Indeed, very early work on model unity first appeared in Subsection 3.2 of [
5] but these initial results involved systems that were too small,
. In this case we usually have
because the primary models of nontrivial subsystems have very few parameters in them resulting in very weak models. Having slightly larger systems,
, makes a big difference and in this case the theory agrees well with intuition, as shown by the results in this article. Future research will be needed to look at still larger systems.