1. Introduction
Kullback and Leibler [
1] showed that minimizing a divergence
between the truth,
f, and a parametric model density,
, is necessary and sufficient for making accurate predictions about data using the model defined by
. Recent work [
2] on Berk–Nash equilibria has shown the central role that KL divergence plays in game theoretic choice models such as multi-armed bandits and stochastic multi-party games. KL divergence thus plays a leading role in machine learning and neuroscience, with several inferential approaches developed in the information theory literature. Such approaches for minimizing KL divergence employ a range of methods, including data partitioning, Bayesian indirect inference and M-estimation [
3,
4,
5]. These approaches are quite distinct from the standard penalized loss minimization framework and, as such, are non-trivial to combine with supervised learning methods such as neural networks.
It is well known that maximum likelihood estimation (MLE) introduces an asymptotic bias in the KL divergence minimizer which is problematic for both model estimation and model selection. For many models, where the parameters
are themselves important, this may be investigated as parameter bias and parameter variance. However, for models common in modern machine learning, the parameters themselves do not have any easily interpreted meaning. For these models, the parameters themselves are irrelevant and only the accuracy (in terms of KL divergence) of the model predictions matter. Within the information theory literature, this has often been referred to simply as bias (e.g.,
from [
6]). To distinguish it from parameter bias, one might refer to it as “prediction bias” or “generalization error”. Generalization error is the more common terminology (see, for example, Equation 1.1.6 [
7]) and will be used here.
Before the widespread use of machine learning, most models had interpretable parameters, and thus there is a large literature focused on reducing parameter bias. For instance, the jackknife [
8] (leave-one-out cross-validation) estimator is an early example. More relevant to this paper is the approach of Firth [
9] and later Kosmidis [
10,
11]. More recently, Pagui, Salvan, and Sartori [
12] proposed a parameter bias reducing estimation methodology. An extensive review of the literature around this point can be found in [
13]. Unfortunately, these approaches do not consider the impact on KL divergence-based generalization error and thus are not applicable to the field of machine learning where the parameters themselves are devoid of meaning. Heskes [
14] shows that classifiers do have a notion of bias-variance decomposition for generalization error, but it is not computable from parameter bias and parameter variance. Therefore, parameter bias reducing formulations are not useful within machine learning unless it can be shown that they also reduce generalization error.
In fact, to seat the approach taken in this paper to generalization error, we recall much earlier and seminal work at the intersection of statistics and information theory. Akaike [
15], and later Takeuchi [
16], proposed information criteria (AIC and TIC, respectively) for model selection designed explicitly to reduce generalization error. Konishi and Kitagawa [
6] extended the approach of Takeuchi to cases where MLE was not used to fit the underlying model, but still restricted themselves to the question of model selection. Stone [
17] proved that Akaike’s Information Criterion (AIC) is asymptotically equivalent to jackknifing when the estimator is finite. Takeuchi himself showed that TIC is an extension of AIC with fewer restrictions, and thus it too is equivalent to jackknifing whenever AIC would be valid.
For highly parameterized models, as are common in machine learning, model selection such as this is of limited utility. The parameter count may necessarily be very large, and thus none of the models fit using MLE may be acceptable. Then, merely choosing among them is unlikely to produce acceptable results. Within this field, typically
or similar regularization is used to reduce generalization error. See Section 11.5.2 [
18], for a typical example. For a more recent innovation, refer to [
19]. Note that regularization schemes such as this often increase parameter bias while decreasing generalization error. Golub, Heath, and Wahba [
20] showed that
regularization is asymptotically equivalent to cross-validation for linear models, subject to certain assumptions. For nonlinear models, it has long been known that
regularization is not always valid, and it is trivial to construct example models (See
Section 4.1 for one such example) where this approach is always harmful in expectation.
Therefore, it is important to develop a method to reduce generalization error in model estimation analogous to the way that regularization would commonly be used for a highly parameterized model, but having applicability for a wider family of models, especially those for which regularization is not applicable. It is not the goal of this paper to perform a wide survey of generalization error reducing approaches, but we will rather propose an additional approach, investigate its properties, and show that it has superior performance when compared against regularization, which is currently the dominant generalization error reducing estimation procedure within the field of machine learning.
To this end, this paper introduces a generalization error reducing estimation approach referred to as Information Corrected Estimation (ICE). This estimator is proven to have a generalization error of only instead of as is the case for MLE, and is shown to be valid within a neighborhood around the MLE parameter estimate. Optimizing over this ICE objective function instead of the negative log likelihood thus produces parameters with superior out of sample performance.
Takeuchi’s TIC and Firth’s approach have never seen widespread use due to the computational and numerical issues that arise from the computation of this adjustment [
21], and the ICE estimator in its raw form would have similar problems. Therefore, this paper also proposes an efficient approximation of this correction term, and shows through numerical experiments that the approximation is effective at improving model performance across a range of models.
2. Preliminaries
Let us assume that we have data generated from an unknown joint density function of . Where necessary, we define to denote a second sample drawn from , independent of , and is the observed realization of . We consider a model given by a parametric family of densities , for some compact Euclidean parameter space , which is misspecified and hence excludes the truth f. Henceforth, the distribution over x identified by may be referred to as where it is notationally convenient to do so.
Suppose that
is the quasi-true parameter of model
, and
is the random variable representing the MLE of
fit on a dataset,
. The negative log-likelihood of
under the distribution
is
where
is written including a
to make the expectation of this quantity
and asymptotically independent of
n. Similarly, the minus sign is incorporated because
is a strictly non-negative quantity if
is a probability. The MLE,
, minimizes the negative log likelihood of the data set with respect to the model:
The expectation of
is the cross entropy between
f and
:
Here, the expectation is a function only of
and of the distribution
f that generated the data
. As a function of the distribution
f, this value is
, but could be large for poorly conditioned
f. The quasi-true parameter
is
Generalization Error in KL Divergence Based Loss Functions
Kullback and Leibler [
1] viewed “information” as discriminating the sample data drawn from one distribution against another, and defined the KL-divergence
between distributions in terms of the ability to make predictions about one by knowing the other. Here,
This value is in general unknowable, but given a sample
from
f,
will converge asymptotically to
plus an additive constant that depends only on
f. The convergence relies on White’s regularity conditions [
22].
A well known result by Stone [
17] shows that the MLE is a biased estimator of the minimum KL-divergence:
because it is evaluated on the data
which was used to fit
. Cross-validation was developed as a model selection technique to select a model from a group that actually minimizes
and not merely
in the limit of large
n. Takeuchi [
16] and Akaike [
15] explicitly modeled this bias (generalization error) of an estimation procedure
as
Our goal is to obtain an estimate, , of the generalization error b without using the MLE. We will then add this term to the objective function to develop the estimator so as to cancel the lower order terms of the generalization error. This estimator will then minimize more effectively than MLE, and potentially would in turn produce improved predictions from the model fitted over finite training sets.
Remark 1. We note that under MLE, [16]. Equivalently, one could say that a particular realization of the generalization error is itself . Here, is used to indicate that the quantity is a random variable with finite variance, whose mean is . 3. Information Corrected Estimation (ICE)
We propose the following penalized likelihood function:
Definition 1 (ICE Objective).
where is the negative expected Hessian and is the Fisher Information matrix with , being their estimates over the data.Let denote the minimizer of (8). The trace term in Equation (
8) will be familiar from Takeuchi [
16]. However, Takeuchi showed only that this was the leading order of the bias for the MLE estimate
, and therefore the proof found there is not sufficient to justify a new estimator that will itself be the target of optimization, and is required to be valid away from
. As in Takeuchi, because
I and
J are unknowable, we will substitute their approximations computed from the training data,
and
during the actual computation of this objective. The numerical impact of this approximation will be examined in
Section 4.2.1.
Remark 2. Though AIC was developed before TIC, it is easily reproduced as a special case of TIC. Subject to certain conditions (guaranteed by the requirements of [15]), at least in expectation, . Thus, the quantity within the TIC trace term, , is the identity matrix. Therefore, its trace is equal to p, the parameter count of the model, recovering AIC. TIC itself can be derived using a proof that is similar to, though somewhat simpler than, the one we include in (A2), of which Takeuchi’s proof is a special case that is valid only at the MLE estimate . We also define to be the negative hessian of rather than , and similarly for , with expectations written as and . Analogously, is the expectation of and is the minimizer of , while is the minimizer of .
We refer to the estimation of , by minimization of this corrected likelihood function as Information-Corrected Estimation (ICE). As the terminology suggests, we depart from the corrective approach used in Information Criterion, by directly minimizing the bias corrected likelihood function. Note that unlike regularization, the correction term is parameter-free and thus would not require cross validation to estimate a hyperparameter such as the used by .
General properties of this estimator are proved, and a set of regularity conditions are provided such that the estimator is asymptotically normal, and produces a bias that is instead of the usual . Though this adds only a half-order to the bias correction, for most problems with reasonably large n, any increase in order is likely to greatly reduce bias. Experimental results demonstrate superior properties of ICE for linear models compared to MLE with and without regularization.
Remark 3. For models satisfying White’s regularity conditions (See [22]), it is known that is positive definite (thus non-singular) and continuous, and also that is continuous with respect to θ. Therefore, would always be well defined in an open region around . Similarly, the solution would be expected to have the same properties, and hence (for large enough n) the estimate would be well defined when computed using the estimates and . Remark 4. N.B: Though is an estimator of accurate to within , that does not mean that is reduced by any particular amount relative to . We expect that using this corrected objective will always (if it can be calculated accurately) generate some improvement by virtue of more accurately representing the true performance of the model out of sample, but there is no proof that this level of improvement has any particular form or asymptotic behavior.
Our approach preserves the linear complexity of training with respect to
n. However, the computation of
at each iteration of the numerical solver requires the inversion of a symmetric positive definite matrix with a complexity of
. Hence the approach is not suitable for high dimensional datasets without adjustment. See
Section 5 for optimized approximations that are viable for larger parameter counts. Further exploration of large models based on this approach are beyond the scope of the present work.
Remark 5. It is clear from inspection that if is strictly convex, then so too is for large enough n.
We first provide a proof of asymptotic convergence of
under certain regularity conditions. With this convergence result in place, we then show that minimizing (
8) leads to an
bias term, an improvement over the
term produced by MLE.
Local Behavior of the ICE Objective
Suppose the following conditions hold:
satisfies White’s regularity conditions A1–A6 (see
Appendix A.1 or [
22]).
is a global minimum of in the compact space defined in A2.
There exists a such that for all other local minima .
For the derivative exists, is continuous, and bounded on an open set around .
For , the variance as on an open set around .
Then for sufficiently large n there exists a compact subset containing such that:
For the derivative exists, is continuous, and bounded on U, almost surely.
For , as on U, almost surely.
as almost surely.
almost surely.
almost surely.
Items (1–3) follow from Lemma A1 (see
Appendix A.2). These are additional regularity conditions that are prerequisites for later theorems.
Item (4) follows from Theorem A1 in
Appendix A.3. This states that the estimate
is asymtotically normal in a way that is analogous to classical asymptotic normality results for MLE. It is only true almost surely because results (1–3) upon which it relies are only true almost surely.
Item (5) follows from Theorem A2 in
Appendix A.4. This item establishes the superior accuracy of the ICE objective compared to the MLE objective function in predicting out of sample errors. Like item (4) this is only true almost surely because intermediate results on which it relies are only true almost surely.
The reduction in generalization error seen arises from the optimization over the superior ICE objective function, analogous to the way that regularization is used for this purpose.
Remark 6. The regularity conditions described here are only slightly more strict than the conditions described by White [22]. In particular, models having three continuous derivatives as required by White, but not 5 as needed here are thought to be very rare. Requirement (2) is just the definition of , which White labels differently, and requirement (3) excludes a pathological corner case, the further study of which is beyond the scope of this paper. Remark 7. Note that as is convex in the neighborhood of , so too is for large enough n because . Thus it can be concluded that the local behavior of in the neighborhood of is not appreciably worse than the behavior of if the problem is not too ill conditioned.
4. Direct Computation Results
The following experiments have been designed to compare MLE, MLE with regularization, and ICE for regression. Each experiment involves simulation of training and test sets and is implemented in R. See the attached code to run each experiment.
Each of these experiments has been performed using the raw formula for ICE provided in Equation (
8) with minimal adjustments. All gradients are computed using R’s default finite difference approach. This means that for a model with
p parameters, the objective function is dominated by the inversion of
J, which costs
time and
space. The use of finite difference gradients further increases the time complexity to
, compounding the problem. This approach is therefore viable for small models with few parameters, but not realistic for larger models. Optimizations to overcome this limitation will be considered in upcoming
Section 5. The use of finite difference derivatives was not found to produce appreciable numerical differences in the final output, so analytic derivatives were not used for this analysis.
The code and results for this section is provided in [
23]. Throughout this section, the following estimators will be compared.
4.1. Gaussian Error Model
We begin by considering the simplest case of univariate linear regression with Gaussian residuals. The advantage of this simple model is that the exact form of the correction term can be derived analytically and aids therefore in building intuition on its behavior. For such a toy model,
and, for simplicity, the following example will consider
to be a constant, but it is equally applicable if
. Consider the parameters of the model to therefore be
with their optimal values being
. The the probability density function is
It is known a priori that regularization cannot improve this model, as if , any decrease in the magnitude of is likely to be systematically harmful. Similarly, a decrease in below results in a decrease in model distribution entropy, and hence would be generally making overfitting worse, and would generate a correspondingly higher KL-divergence than the MLE estimate. Consequently, we would expect any computed through cross-validation to be statistically indistinguishable from zero, and regularization to be generally harmful whenever .
Generalization Error Analysis
The Gaussian model described was generated with , , and . For each of , 500 independent simulations of the data were performed, and then the parameters were fit from that data. In each simulation, was computed using MLE, MLE with regularization, and ICE. The parameter for regularization was computed using 2-way cross-validation on the available data, and as expected, none of the computed values of were statistically different from zero.
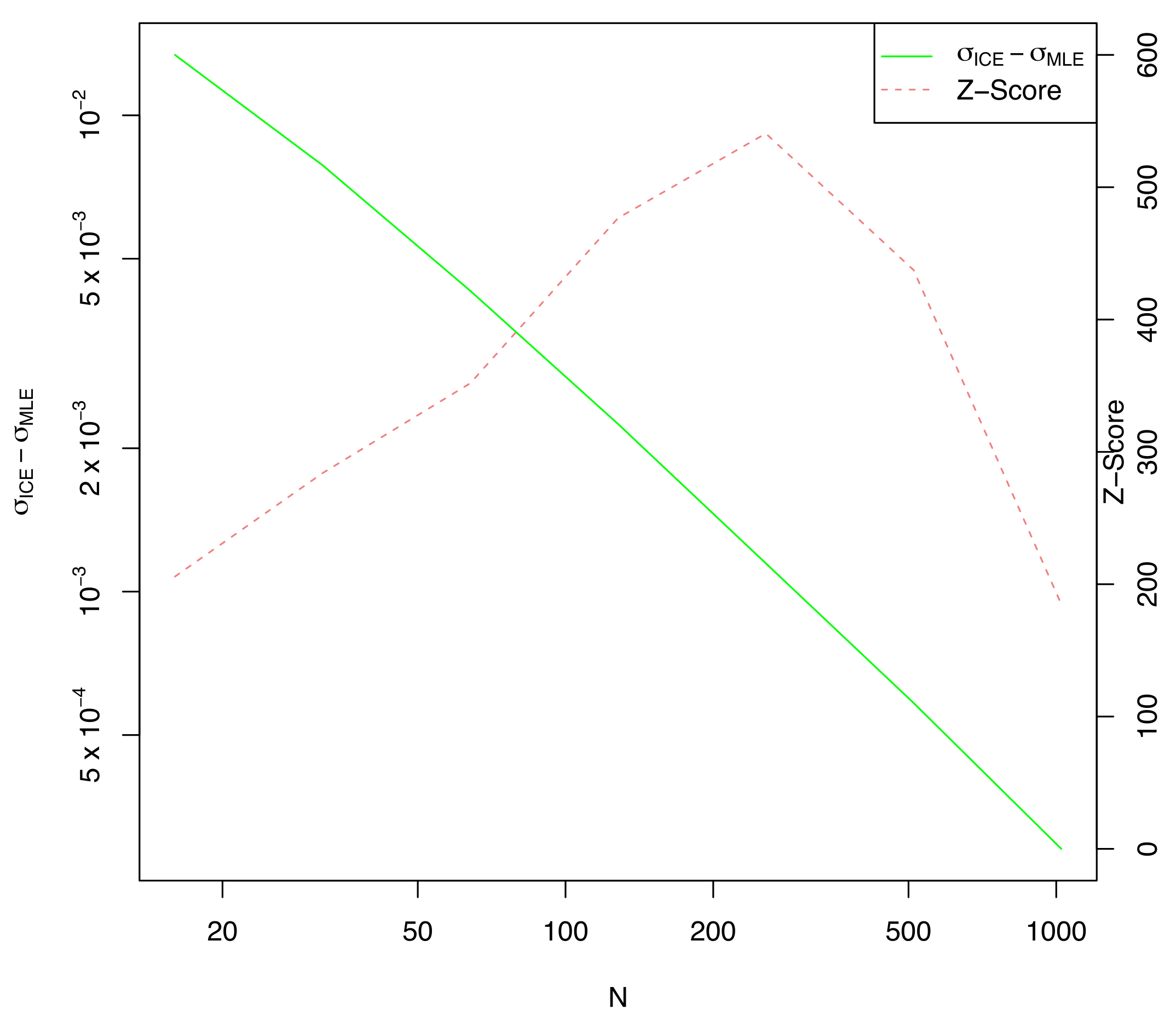
For each estimate of , the KL-divergence was computed (using the known value of ), and the results were compared. The ICE parameter estimation method showed statistically significant improvement over MLE at the 5-sigma level out to , and was improved by just under 1-sigma at .
The KL-divergence results graphed against
n on a log-log scale are shown in
Figure 1. Every value of
n is normalized by the average KL divergence of the MLE methodology to improve legibility. The
series is statistically indifferent from the MLE series at 2 standard deviations beyond
, and the two are not materially different for any
n. The ICE series is at least
standard deviations below the MLE series until
.
Remark 8. In addition to the series shown in Figure 1, a series was computed using the true value of J, estimated from a much larger sample n = 1024 from the underlying distribution, and this series was indistinguishable from the series computed using for every n, thus it was not graphed. This validates Takeuchi’s approach of approximating J with in this instance. As expected, the difference in
between ICE and MLE is not statistically significant (at three standard deviations) for any
n, but the ICE computed value of
(shown in
Figure 2) is considerably larger than the MLE estimate, especially for small values of
n. This explains the greatly reduced KL-divergence noted in
Figure 1.
Note that the difference in estimated is always statistically significant when compared to the MLE value. This is because both MLE and ICE are fit on the same data, so ICE would always have a larger than MLE regardless of the actual data chosen from the distribution f. This is the cause of the large z-scores shown, always exceeding 200. We know from elementary statistics that correlation between the mean and std. deviation causes the MLE estimate of to be systematically low by a factor of . Indeed, the ICE estimate of is closely tracking whereas is closely tracking as expected. This is one example where reducing generalization error also reduces parameter bias as a side effect.
4.2. Friedman’s Test Case
We now extend the example from
Section 4.1 to the case where
is no longer constants. For this example, we chose a standard regression test set, which is nonlinear in the features, based on
Section 4.3 of [
24]:
where the Friedman model is
The random features, , are i.i.d. uniform random and the parameter values are fixed. The true parameter set, , reserves the last parameter () for the value of .
Note that here must be treated as an unknown parameter. To do otherwise implies that the modeler knows the amount of noise expected in the data. In the case of a known noise term, overfitting is impossible since overfitting arises when a model reduces the projected noise below its actual value, which can never arise when the noise level is known.
The model probability density
of
y is given by
Recall that in
Section 4.1, the value of
was considered to be a constant. This example is a natural extension of
Section 4.1, and was chosen due to the well-explored difficulty of Friedman’s problem.
We simulate 500 batches of equally sized training sets of length . The test set is always of length 1024 to ensure accuracy for the smaller values of n. The starting point of the optimization is generated by adding a random perturbation, , to each parameter. As before, the KL-divergence is computed between the distribution represented by the parameters and the true distribution, and these values are compared between estimation methods.
For each test sample, the KL divergence is computed using numerical integration with a increment of over the interval containing for both the true and model distributions. The computed probabilities are verified to numerically sum to unity within an error of .
In each simulation, is computed using MLE, MLE with regularization, and ICE. The parameter for regularization is computed using 4-way cross validation on each batch of the training data.
As shown in
Figure 3 and
Table 1,
is not effective for any value of
n, and is is completely inactivated for
. Where regularization is used (i.e.,
), it generally underperforms MLE. ICE is effective across the entire data range, outperforming MLE for every
n, and always by a statistically significant margin of at least 5 sigma.
4.2.1. Impact of Approximation
It was noted previously that Takeuchi used
(and likewise,
) in place of the true value of
J, and we do so here as well. Though there is no realistic way to avoid this approximation in the real world, and the optimized approach discussed in
Section 5 has an entirely different set of approximations, the impact of this approximation will be briefly characterized here.
In
Table 2, we revisit
Table 1, but now drop the
regualarization column, and add a new column where the ICE objective is allowed to use a much better approximated value of
J, in this case approximated from 1024 independently drawn samples regardless of
n.
As can be seen from
Table 2, using the true value of
J is at most marginally helpful. In fact, for most values of
n it displays slightly better average results, but slightly higher std. deviation of those results, and thus reduced T-statistics. Thus, we conclude that the Takeuchi’s approximation, replacing
J with
is reasonable. The same conclusion was reached in
Section 4.1, see the remark there. We note also that the ICE estimator using
exhibits substantially better performance for very low sample sizes, but further investigation of this phenomenon is beyond the scope of the current paper.
In
Table 3, we show the average matrix norms of
J,
, and also of the diagonal of
, referred to as the matrix
D. The matrix
D will be examined further in
Section 5, and is included here for completeness. We also show the norms of several matrix differences.
We note that the ICE objective values themselves exhibit much lower variation than the matrix norms show in
Table 3. In particular though the matrix
D is not actually converging to
J as
n increases, we see from the correction term it generates that this difference does not appear to have a material impact for larger
n. We thus conclude that the major eigenvectors of
and
are very nearly orthogonal to the gradient vectors used to construct
for large
n.
It is not clear from examining the trace terms in
Table 3 that
D is a worse approximation of
J than
is, even for small
n where the impact of the ICE approach is most significant. A more complete investigation of the spectrum of these matrices is beyond the scope of the present work.
4.3. Multivariate Logistic Regression
The previous experiment is based on a well-known test case. In this second experiment, we assess the general performance of ICE under (i) varying dimensionality of the true data distribution, (ii) increasing misspecification, and (iii) increasing training set sizes. To achieve this goal, we generate a more exhaustive set of data from a more complex data generation process.
4.3.1. Data Generation Process
The synthetic data are designed to exhibit a number of characteristics needed to broadly evaluate the efficacy of ICE. First, the regressors should be sufficiently correlated so as to ensure that model selection is representative of typical datasets. However, we avoid multi-collinearity by ensuring the smallest eigenvalue is above a certain threshold. We additionally control the condition number of the covariance matrix
by randomly generating a symmetric positive definite covariance matrix
using the eigen-decomposition
where
U is an orthogonal random matrix with elements
and
D is diagonal matrix of positive eigenvalues. The eigenvalues are uniformly distributed over the interval
so that the condition number of
is
and the eigenvalues are kept distinct. Here,
a is chosen to be
and
b is chosen to be 0.1.
Using a Cholesky decomposition
and the random mean vector
, we generate correlated gaussian vectors of dimension
p with the properties
The data
are generated under a logistic regression
A key challenge in assessing the efficacy of bias reduction is to avoid generating excessively low entropy distributions. In such cases, bias reduction will have marginal effect as the parameters are all nearly zero. To avoid such scenarios, the intercept parameter of the true model is adjusted a-posterior until the following conditions are met:
where , , and . If these conditions can not be met, then the replication is discarded.
4.3.2. Model Performance Comparison
As in prior sections, KL divergence is computed between the estimated model and the true model for each of the estimation methods. The T-statistics of the difference with the corresponding MLE KL divergence are computed, with negative T-statistics showing that an approach is performing better than the MLE approach. For regularization in this section, the value of is computed via cross-validation, using two folds, on the provided fitting set.
Table 4 compares the KL divergences
from the true distribution to the model distributions produced using various estimation approaches applied to misspecified data. Here
m denotes the number of regressors that are not predictive, i.e.,
contains
m zeros. The experiment is replicated 300 times using the data generation process described above and the test set is fixed at 100,000 observations.
We observe that the t-statistic for is most significant for relatively small sample sizes, particularly . For these small sizes, the improvement over MLE is greater, though noisier. There is uniform decay in improvement over as n grows, until for and the largest sizes are no longer statistically significant. This is expected, as both the MLE and ICE estimates are converging towards the true value of , and for large enough sample sizes the ICE correction would be dominated by numerical error, particularly the ill conditioning of J.
The estimate improves for small values of p, but then becomes progressively worse for large values of p. We observe that for dimensionality above , the regularization described here is no longer effective in reducing the KL-divergence. For low values of p the value of has comparatively low variance, and thus the logistic function is reasonably locally approximated as linear. For higher p this approximation is less realistic and the performance of regularization degrades.
For the ICE estimates, larger values of p show fluctuations that are often not statistically significant. It is apparent that larger p is increasing the variance of the ICE divergences, probably due to numerical errors and ill conditioning. Larger values of n reduce the absolute size of the divergence improvement whereas larger values of p seem to increase it.
Note that though the t-statistics are degrading for large n, the absolute magnitude of the differences is asymptotically small. For these sizes, the results are insignificant, but more importantly, immaterial.
4.3.3. Convergence Analysis for Large n
For 10 randomly chosen example problems, under which the model coefficients are now fixed, the convergence behavior for large
n, the training set size, is explored. Note that the test set remains fixed at 100,000 observations for each problem.
Table 5 compares the KL divergence (averaged over all 10 problems) under MLE (
),
regularization, and ICE for progressively larger sample sizes. The divergences
and
converge to zero as
, as does
.
Generally the estimates are seen to converge slightly faster than the estimates. The regularization in is observed to be beneficial for very small sample sizes, but then becomes marginally detrimental for large n.
5. Optimized Computation Results
For any model satisfying White’s Regularity Criteria, it is known that the matrix J is positive definite near the MLE optimum . This implies that J is diagonally dominated, and indeed considering just its diagonal elements D, it is known that . Indeed differs strongly from most strongly for models with strong regressor interactions. Therefore, using finite difference gradients, consider the following approximations for the ICE objective function:
: J is computed directly, ICE is implemented as written.
: J is taken to be constant w.r.t. : ().
: J is taken to be diagonal: ().
: J is taken to be the identity: ().
Clearly, we expect that
above is the least accurate approximation, and items
and
have varying levels of accuracy depending on the problem at hand. The cost comparison of these approaches is shown in
Table 6.
Remark 9. When computing gradients for use in a solver, often approximation error will have only a marginal impact on the final result, though it may increase the number of iterations needed for convergence. Broyden’s method [25] is a typical example of this approach in action. Efficient approximations of might similarly have only a minor effect on accuracy and iteration count. The construction of approximate analytical derivatives is beyond the scope of the present work. These approximations were computed and compared for the Friedman (see
Section 4.2) problem, and the results are shown in
Table 6 below.
From
Table 7, it is apparent that approach
, taking
is not effective. This is not surprising as the actual
J matrix has dramatic differences in scale between regressors. Approximation
, taking
is accurate enough that it cannot be statistically distinguished from the direct computation of ICE by the test above. Approximation
tends to underperform approximation (3).
Therefore, we propose taking as a more numerically stable approximation of the ICE objective.