Population Risk Improvement with Model Compression: An Information-Theoretic Approach †
Abstract
:1. Introduction
1.1. Contributions
1.2. Related Works
2. Preliminaries
2.1. Review of Rate Distortion Theory
2.2. Generalization Error
3. Compression Can Improve Generalization
4. Generalization Error and Model Distortion
4.1. Distortion Metric in Model Compression
4.2. Population Risk Improvement
5. Example: Linear Regression
5.1. Information-Theoretic Generalization Bounds for Compressed Linear Model
5.2. Distortion-Rate Function for Linear Model
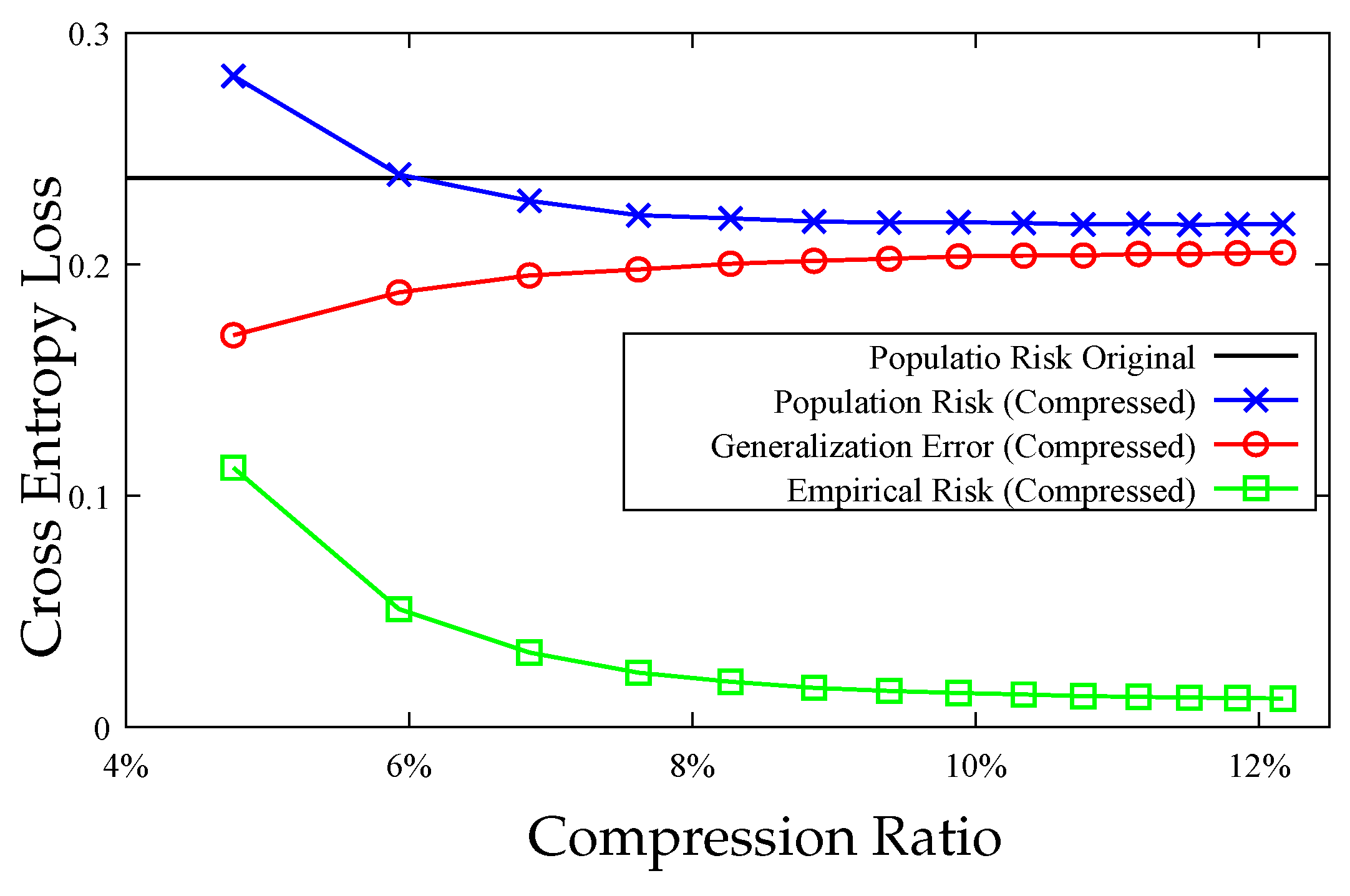
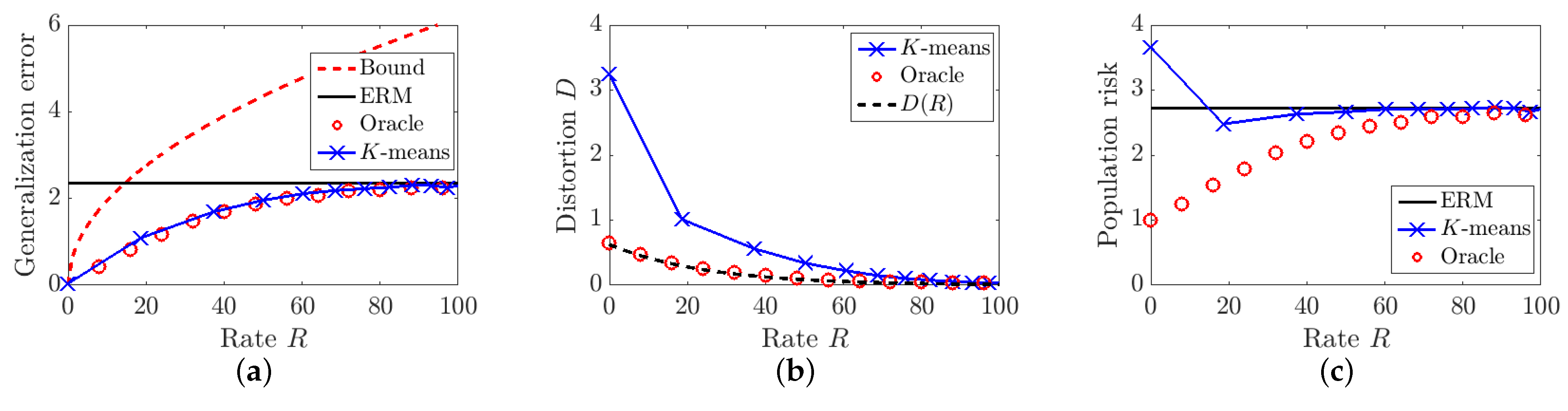
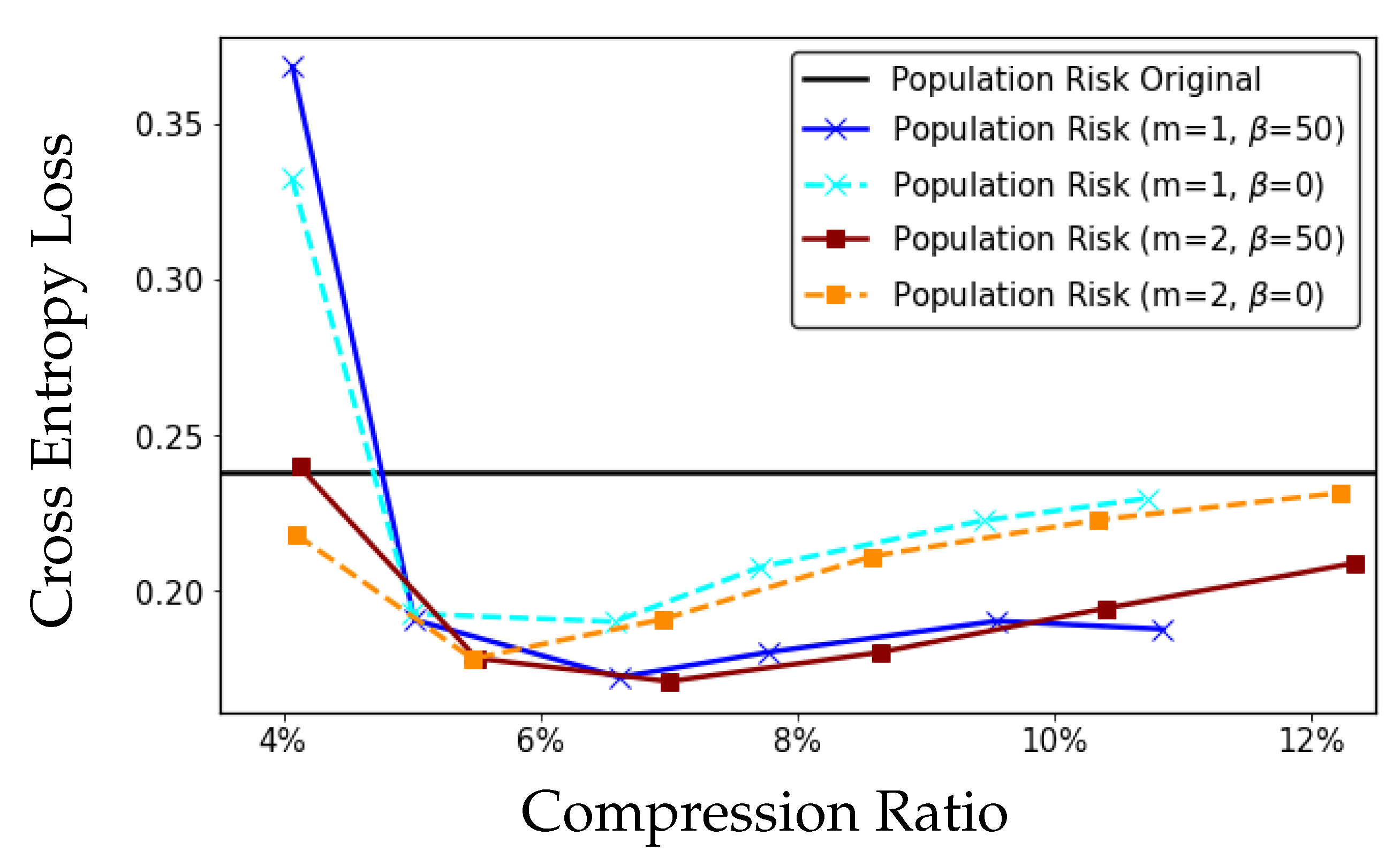
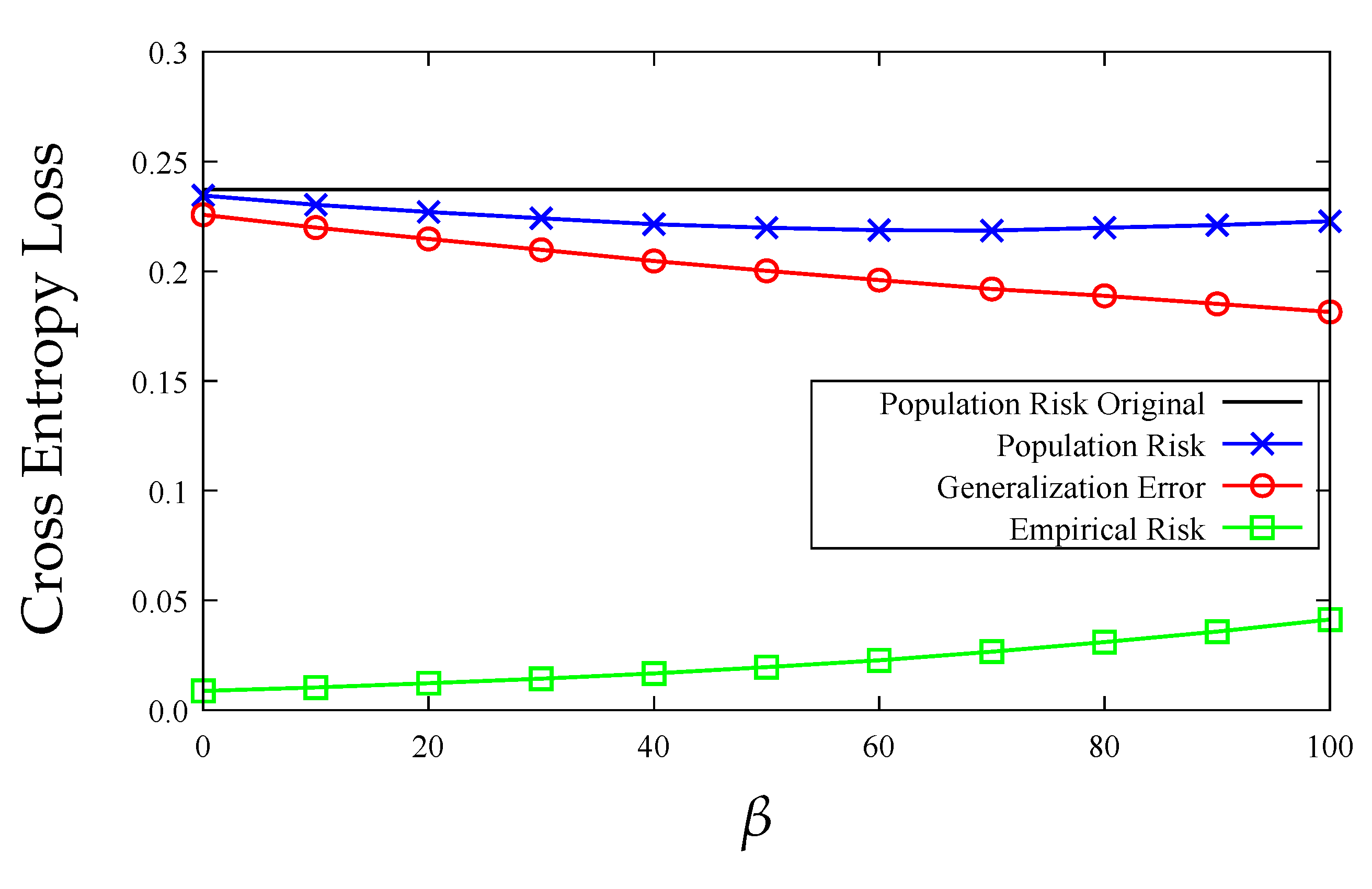
5.3. Evaluation and Visualization
6. Clustering Algorithm Minimizing
6.1. Hessian-Weighted K-Means Clustering
6.2. Diameter Regularization
| Algorithm 1 Diameter-regularized Hessian weighted K-means in vector case |
|
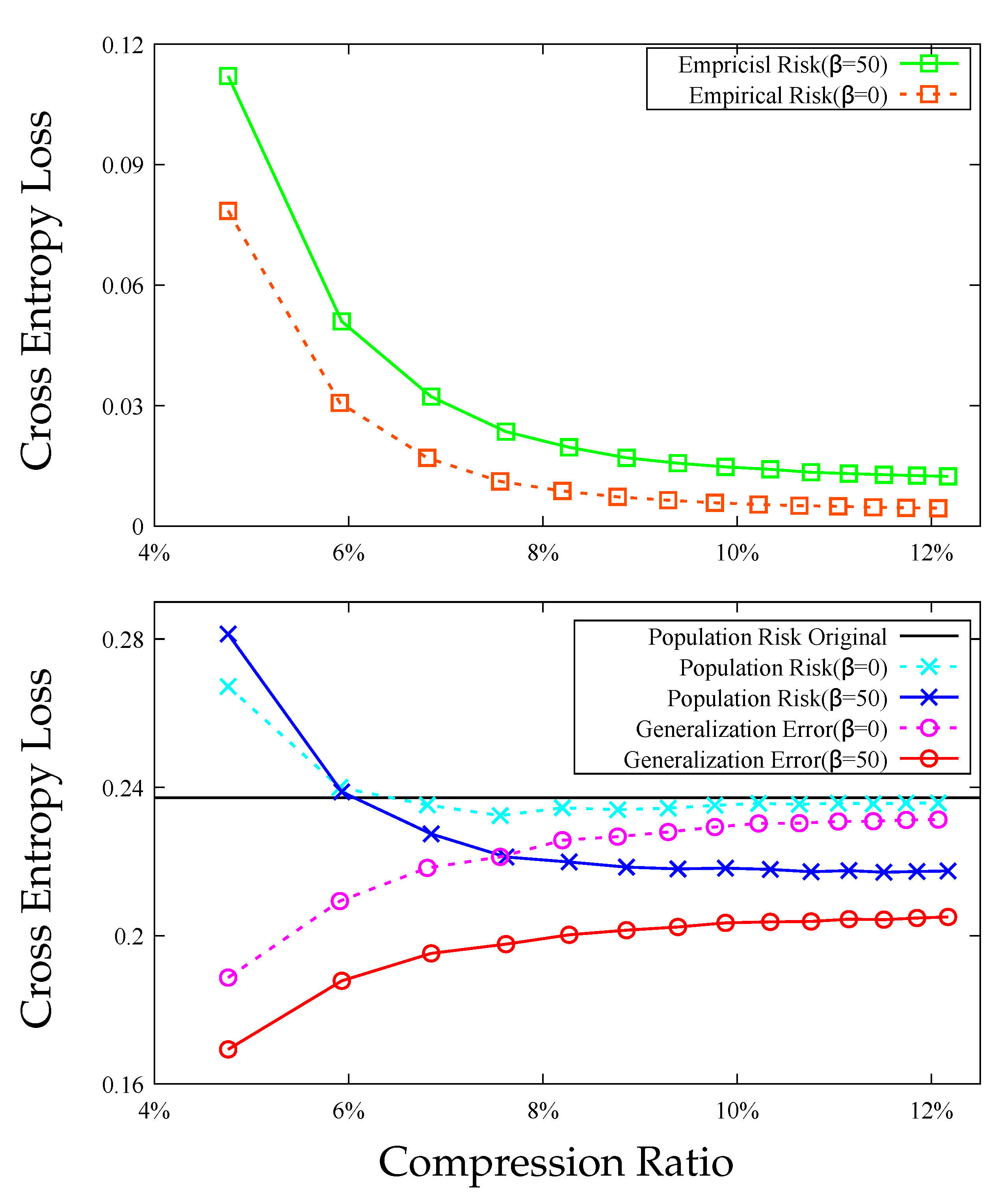
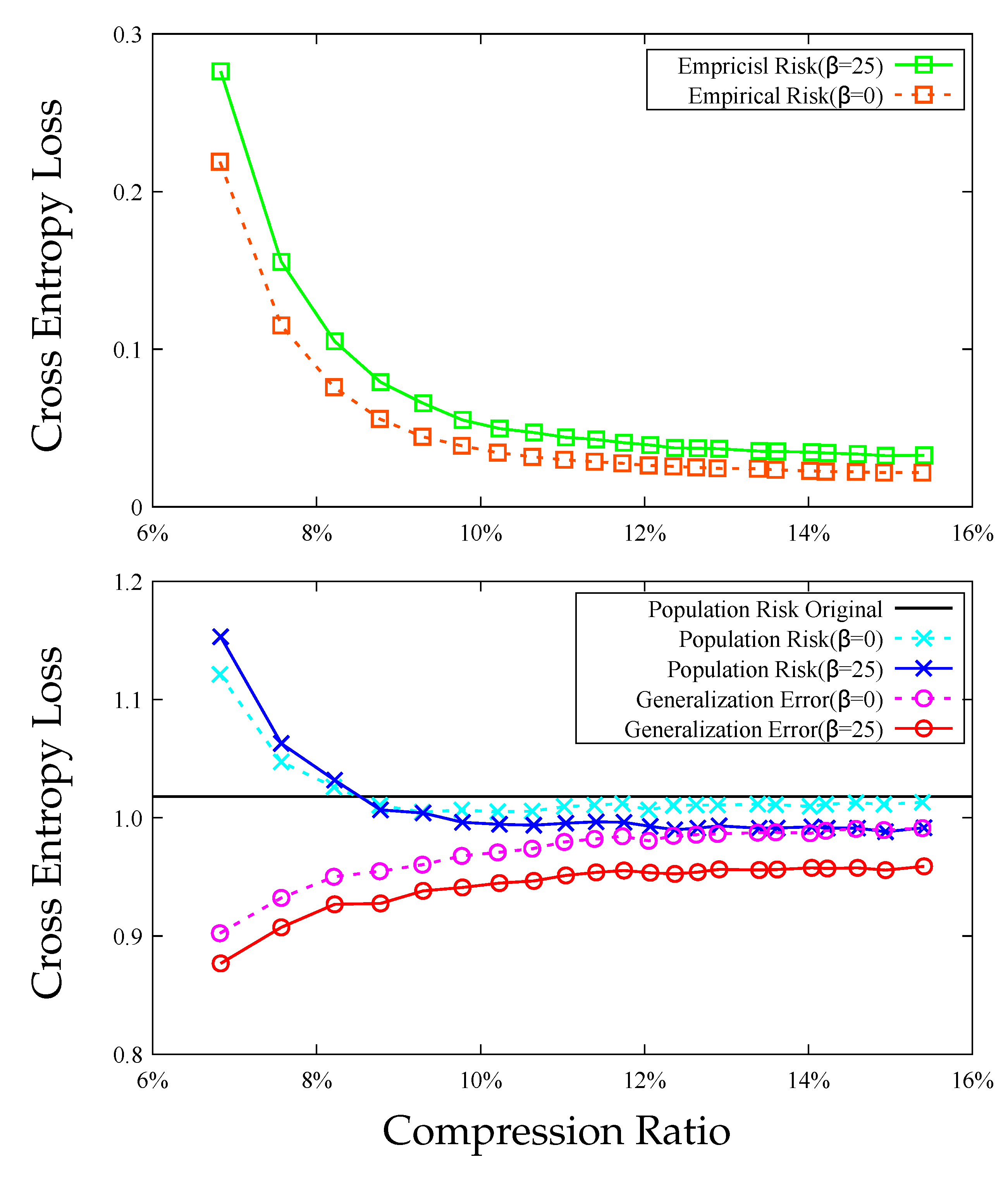
7. Experiments
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Lemma 3
Appendix B. Proof of Proposition 1
Appendix C. Proof of Proposition 2
Appendix D. Discussion of Remark 2
References
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, UK, 2016; Volume 1. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354. [Google Scholar] [CrossRef]
- Huval, B.; Wang, T.; Tandon, S.; Kiske, J.; Song, W.; Pazhayampallil, J.; Andriluka, M.; Rajpurkar, P.; Migimatsu, T.; Cheng-Yue, R. An empirical evaluation of deep learning on highway driving. arXiv 2015, arXiv:1504.01716. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Cheng, Y.; Wang, D.; Zhou, P.; Zhang, T. A survey of model compression and acceleration for deep neural networks. arXiv 2017, arXiv:1710.09282. [Google Scholar]
- Krishnamoorthi, R. Quantizing deep convolutional networks for efficient inference: A whitepaper. arXiv 2018, arXiv:1806.08342. [Google Scholar]
- Guo, Y. A survey on methods and theories of quantized neural networks. arXiv 2018, arXiv:1808.04752. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv 2015, arXiv:1510.00149. [Google Scholar]
- Zhu, C.; Han, S.; Mao, H.; Dally, W.J. Trained ternary quantization. arXiv 2016, arXiv:1612.01064. [Google Scholar]
- Choi, Y.; El-Khamy, M.; Lee, J. Towards the limit of network quantization. arXiv 2016, arXiv:1612.01543. [Google Scholar]
- Lin, Y.; Han, S.; Mao, H.; Wang, Y.; Dally, W.J. Deep gradient compression: Reducing the communication bandwidth for distributed training. arXiv 2017, arXiv:1712.01887. [Google Scholar]
- Xu, A.; Raginsky, M. Information-theoretic analysis of generalization capability of learning algorithms. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 2524–2533. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Gupta, S.; Agrawal, A.; Gopalakrishnan, K.; Narayanan, P. Deep learning with limited numerical precision. In Proceedings of the International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015; pp. 1737–1746. [Google Scholar]
- Courbariaux, M.; Bengio, Y.; David, J.P. Binaryconnect: Training deep neural networks with binary weights during propagations. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 7–12 December 2015; pp. 3123–3131. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. Xnor-net: Imagenet classification using binary convolutional neural networks. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 525–542. [Google Scholar]
- Mozer, M.C.; Smolensky, P. Skeletonization: A technique for trimming the fat from a network via relevance assessment. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Denver, CO, USA, 27–30 November 1989; pp. 107–115. [Google Scholar]
- LeCun, Y.; Denker, J.S.; Solla, S.A. Optimal brain damage. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Denver, CO, USA, 26–29 November 1990; pp. 598–605. [Google Scholar]
- Hassibi, B.; Stork, D.G. Second order derivatives for network pruning: Optimal brain surgeon. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), San Francisco, CA, USA, 30 November–3 December 1992; pp. 164–171. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both weights and connections for efficient neural network. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 7–12 December 2015; pp. 1135–1143. [Google Scholar]
- Gong, Y.; Liu, L.; Yang, M.; Bourdev, L. Compressing deep convolutional networks using vector quantization. arXiv 2014, arXiv:1412.6115. [Google Scholar]
- Ullrich, K.; Meeds, E.; Welling, M. Soft weight-sharing for neural network compression. arXiv 2017, arXiv:1702.04008. [Google Scholar]
- Louizos, C.; Ullrich, K.; Welling, M. Bayesian compression for deep learning. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 3288–3298. [Google Scholar]
- Lin, D.; Talathi, S.; Annapureddy, S. Fixed point quantization of deep convolutional networks. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 19–24 June 2016; pp. 2849–2858. [Google Scholar]
- Young, S.; Wang, Z.; Taubman, D.; Girod, B. Transform Quantization for CNN Compression. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 1. [Google Scholar] [CrossRef] [PubMed]
- Denton, E.L.; Zaremba, W.; Bruna, J.; LeCun, Y.; Fergus, R. Exploiting linear structure within convolutional networks for efficient evaluation. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 1269–1277. [Google Scholar]
- Tai, C.; Xiao, T.; Zhang, Y.; Wang, X. Convolutional neural networks with low-rank regularization. arXiv 2017, arXiv:1511.06067. [Google Scholar]
- Novikov, A.; Podoprikhin, D.; Osokin, A.; Vetrov, D.P. Tensorizing neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 7–12 December 2015; pp. 442–450. [Google Scholar]
- Gao, W.; Liu, Y.H.; Wang, C.; Oh, S. Rate distortion for model compression: From theory to practice. In Proceedings of the International Conference on Machine Learning (ICML), PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 2102–2111. [Google Scholar]
- Dziugaite, G.K.; Roy, D.M. Computing nonvacuous generalization bounds for deep (stochastic) neural networks with many more parameters than training data. arXiv 2017, arXiv:1703.11008. [Google Scholar]
- Neyshabur, B.; Bhojanapalli, S.; McAllester, D.; Srebro, N. Exploring generalization in deep learning. arXiv 2017, arXiv:1706.08947. [Google Scholar]
- Zhou, W.; Veitch, V.; Austern, M.; Adams, R.P.; Orbanz, P. Non-vacuous generalization bounds at the imagenet scale: A PAC-bayesian compression approach. arXiv 2018, arXiv:1804.05862. [Google Scholar]
- Russo, D.; Zou, J. Controlling bias in adaptive data analysis using information theory. In Proceedings of the International Conference on Artifical Intelligence and Statistics (AISTATS), Cadiz, Spain, 9–11 May 2016; pp. 1232–1240. [Google Scholar]
- Shannon, C.E. Coding theorems for a discrete source with a fidelity criterion. IRE Nat. Conv. Rec 1959, 4, 142–163. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Grønlund, A.; Kamma, L.; Larsen, K.G.; Mathiasen, A.; Nelson, J. Margin-Based Generalization Lower Bounds for Boosted Classifiers. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; pp. 11940–11949. [Google Scholar]
- Vershynin, R. Introduction to the non-asymptotic analysis of random matrices. arXiv 2010, arXiv:1011.3027. [Google Scholar]
- Linder, T.; Lugosi, G.; Zeger, K. Rates of convergence in the source coding theorem, in empirical quantizer design, and in universal lossy source coding. IEEE Trans. Inf. Theory 1994, 40, 1728–1740. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; Technical Report; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Basu, D.; Data, D.; Karakus, C.; Diggavi, S. Qsparse-local-SGD: Distributed SGD with Quantization, Sparsification and Local Computations. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; pp. 14668–14679. [Google Scholar]
- Bu, Y.; Zou, S.; Veeravalli, V.V. Tightening Mutual Information-Based Bounds on Generalization Error. IEEE J. Sel. Areas Inf. Theory 2020, 1, 121–130. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, Y.; Gao, W.; Zou, S.; Veeravalli, V.V. Population Risk Improvement with Model Compression: An Information-Theoretic Approach. Entropy 2021, 23, 1255. https://doi.org/10.3390/e23101255
Bu Y, Gao W, Zou S, Veeravalli VV. Population Risk Improvement with Model Compression: An Information-Theoretic Approach. Entropy. 2021; 23(10):1255. https://doi.org/10.3390/e23101255
Chicago/Turabian StyleBu, Yuheng, Weihao Gao, Shaofeng Zou, and Venugopal V. Veeravalli. 2021. "Population Risk Improvement with Model Compression: An Information-Theoretic Approach" Entropy 23, no. 10: 1255. https://doi.org/10.3390/e23101255
APA StyleBu, Y., Gao, W., Zou, S., & Veeravalli, V. V. (2021). Population Risk Improvement with Model Compression: An Information-Theoretic Approach. Entropy, 23(10), 1255. https://doi.org/10.3390/e23101255







