Abstract
In this paper, we consider the thermal bath Lindblad master equation to describe the quantum nonunitary dynamics of quantum states in a multi-mode bosonic system. For the two-mode bosonic system interacting with an environment, we analyse how both the coupling between the modes and the coupling with the environment characterised by the frequency and the relaxation rate vectors affect dynamics of the entanglement. We discuss how the revivals of entanglement can be induced by the dynamic coupling between the different modes. For the system, initially prepared in a two-mode squeezed state, we find the logarithmic negativity as defined by the magnitude and orientation of the frequency and the relaxation rate vectors. We show that, in the regime of finite-time disentanglement, reorientation of the relaxation rate vector may significantly increase the time of disentanglement.
1. Introduction
The theory of open quantum systems is very important for describing the transfer and storage of quantum information. In quantum information theory, these processes are generally described in terms of completely positive trace-preserving maps known as the quantum channels (see, e.g., [1,2,3,4,5] for analysis of the mathematical structures related to the quantum channels). There is also a variety of master equations for the reduced density matrix derived using different assumptions and approximations [6,7,8,9,10,11].
In particular, within the Markov approximation, master equations can often be cast into the well-known Lindblad form [12,13,14] which preserves complete positivity of the dynamics. This equation is also sometimes referred to as the Gorini–Kossakowski–Sudarshan–Lindblad (GKSL) equation.
Though the general physics behind Lindblad-type master equations has been extensively discussed (see, e.g., References [15,16,17,18]), the mathematical techniques developed for the analysis of bosonic systems are mostly applicable to the single-mode Lindblad equation [19,20,21,22,23,24,25] and cannot be employed to treat its multi-mode generalizations (the most general form of the multi-mode Lindblad equation is described, e.g., in [26]).
In a recent paper [27], Fock-like eigenstates of a Lindbladian are constructed using Lie algebras induced by the master equation for a linear chain of coupled harmonic oscillators. The special case of two coupled oscillators presents a family of models that has been the subject of intense studies [28,29,30,31,32,33,34,35,36,37] dealing with the dynamics of entanglement in open continuous-variable systems (see, e.g., [38] for a review).
Typically, this model assumes that there is no interaction between the centre-of-mass and relative-distance modes in the course of relaxation, so that the relaxation part of the Lindbladian is a sum of two commuting relaxation superoperators. By contrast to mechanical systems, in photonic systems with quantised polarisation modes interacting with an optically anisotropic environment, both the dynamical and environment-induced intermode couplings can be important as they manifest themselves in the birefringence and dichroism of absorption [39,40,41]. In this paper, we shall relax this assumption to explore the effects induced by intermode couplings arising from the interaction between the system and the environment. The effects related to the dynamics of entanglement will be our primary concern.
Entanglement is known to be a resource of vital importance for rapidly developing quantum technologies, such as quantum communications and quantum computations [42,43], and its dynamics have been extensively studied during the last two decades (a recent review can be found in [44]). For the cases of discrete and continuous variables, which are typically represented by two interacting oscillators and qubits in the pioneering papers [45,46], it was found that the decay time of entanglement (the time of disentanglement) may be shorter than the time of decoherence and, under certain conditions, revivals of entanglement may occur. Finite-time disentanglement, commonly known as the “sudden death of entanglement”, is another important effect [47,48,49,50,51,52].
The structure of this paper is as follows: In Section 2, after introducing the GKSL master equation for the multi-mode bosonic system interacting with the thermal bath, in Section 2.1, we derive dynamical equations for the mean values of operators that preserve their normal ordering. In Section 2.2, the method of characteristics is utilised to solve the dynamical equation for the normally ordered characteristic function, . In Section 3, the general theoretical results are applied to the important special case of a two-mode bosonic system in the thermal bath. This system can be regarded as a model describing the propagation of quantised polarisation modes in an optical fibre [41]. In Section 3.1, we derive the analytical results needed to evaluate time dependence of the averages that entre the elements of the covariance matrix. The logarithmic negativity of the Gaussian states introduced in Section 3.2 is numerically studied in Section 3.3. Finally, in Section 4, we discuss the results and make some concluding remarks.
2. Lindblad Dynamics
2.1. Master Equation
The starting point of our analysis is the Markovian thermal bath version of the Lindblad equation for the density matrix of an N-mode bosonic system:
written in terms of two superoperators given by
where the dagger denotes Hermitian conjugation, is the density matrix representing the quantum state; () is the creation (annihilation) operator of the nth mode; stands for the commutator; () is the element of the frequency (relaxation) matrix, (); is the dimensionless inverse temperature parameter given by
where is the bare frequency, ℏ is the reduced Planck constant, is the Boltzmann constant and T is the temperature of the environment. The frequency and relaxation matrices are both Hermitian: and . The relaxation matrix with elements giving the rates of thermalization is also positive definite: .
Note that the system (1) is conveniently rewritten in the following alternative form:
where the operators
are determined by the frequency and relaxation matrices, and , through the Jordan mapping that maps a Hermitian matrix J to the quadratic boson operator as follows:
Our next step is to deduce the dynamic equation for the mean value of an operator : . From Equation (1) combined with the algebraic identities
we have
where and is the mean number of thermal photons.
An important point is that, for a normally ordered operator with , the algebraic operations that entre the averages on the right hand side of Equation (10) preserve normal ordering.
2.2. Characteristic Function
In this section, we concentrate on the normally ordered characteristic function given by
where
and an asterisk will indicate complex conjugation.
The temporal evolution of the characteristic function is governed by the dynamical Equation (13) supplemented with the initial condition
where
and is expressed in terms of the Glauber–Sudarshan P function (quasidistribution), , related to the P-representation of the density matrix as follows:
We can now employ the method of characteristics [53] to solve the above initial value problem. According to this method, we begin with the system of characteristic equations
and its solution written in the matrix form as follows:
where . It is not difficult to obtain the solution along the characteristic curves (21) given by
3. Two-Mode System
In this section, we focus our attention on the task of computing the time dependence of the averages that can be regarded as one-point correlation functions. One of the approaches to this important problem is to derive and solve dynamical equations for the averaged operators. For example, Equation (10) and the algebraic identities for the bosonic bilinear forms (7)
can be utilised to deduce the equation for the mean value given by
where denotes the anticommutator.
For illustrative purposes, in what follows, we consider a photonic system with two orthogonally polarised quantised modes [40,41,54], thus restricting our analysis to the special case of the two-mode bosonic system with . Then, the above general result can be applied to the so-called Stokes operators that can be expressed in terms of the Pauli matrices
as follows [55]:
where and is the identity matrix. The mean values of these operators are known as the Stokes parameters and describe the state of polarization of the photonic system (dynamical regimes of the Stokes parameters are studied in [54]). These parameters, however, appear to be insufficient for complete characterization of the quantum states that generally requires the knowledge of higher order moments of the Stokes operators [55]. For such moments, the approach based on dynamical equations quickly becomes rather involved and unnecessarily complicated.
3.1. Exact Dynamics of Averages and Covariance Matrix
An alternative method is to use a formula for the characteristic Function (24). The derivatives of this function can be easily evaluated, giving the expressions for the mean values of normally ordered operators. In particular, the second order moments are computed as follows:
These moments determine the elements of the covariance matrix of our two-mode photonic system [56] and the relations (30) and (31) yield the starting point of our analysis in the subsequent section.
For the two-mode system, the frequency and relaxation matrices can be written as a linear combination of the Pauli matrices
where ; and are the frequency and the relaxation rate vector, respectively; and it is rather straightforward to obtain the matrix exponential for in the following explicit form:
where
We can now use Formulas (30)–(34) to evaluate the covariance matrix, , of our two-mode bosonic system. This matrix can be defined in terms of the quadrature operators (quadratures), and , expressed in terms of the annihilation and creation operators, and , as follows (see, e.g., references [38,56]):
In our case, the block structure of the covariance matrix is given by
where the diagonal and off-diagonal block matrices
are expressed in terms of the averages: and .
3.2. Symplectic Eigenvalues and Logarithmic Negativity
In what follows, we shall restrict our analysis to the important special case of the Gaussian states. These states are characterised by the symplectic eigenvalues of the covariance matrix (36) that can be computed using the relations [38,56]:
where is known as the “seralian” invariant.
The separability and entanglement criteria for bipartite continuous variable systems formulated in terms of the covariance matrix [29,57,58] and more general criteria [59,60] involving higher-order correlators provide a number of entanglement witnesses. For example, such witnesses are used for the analysis of the experimental data presented in [61] and the coherent state quantum key distribution suggested in [62,63].
For two-mode Gaussian states, different measures of entanglement have been proposed. These include the entanglement of formation, the Bures distance and the Gaussian measures of entanglement [64,65,66]. In this work, we deploy the logarithmic negativity [56] as a useful quantifier of bipartite entanglement in Gaussian states given by
where stands for the trace norm and is the partial transpose of . The right-hand side of Equation (40) gives the expression for in terms of the lowest symplectic eigenvalue of the partially transposed density matrix, , with the symplectic eigenvalues given by
where . The logarithmic negativity being an entanglement monotone (a quantity which cannot be increased using local operations and classical communication) is known to bound the distillable entanglement contained in [67]. Note that, recently, the link between the logarithmic negativity and the quadrature coherence scale introduced as a nonclassicality measure was studied in [68].
3.3. Numerical Results
We assume that the system is initially prepared in the two-mode squeezed state
where r is the squeezing parameter, () is the raising (lowering) generator of the Lie algebra, with the covariance matrix given by
According to Equation (33), the frequency and the relaxation rate vectors, and , describe the dynamical and environment mediated intermode couplings, respectively. These vectors determine the regime of the dissipative dynamics and will be parametrised using the angular representation:
In order to investigate the effects of the intermode couplings in the dynamics of entanglement, we have computed the time dependencies of the logarithmic negativity for differently oriented vectors and . The list of parameters used in our calculations is as follows: , , and . At these parameters, we have the initial values of the symplectic eigenvalues , and giving the corresponding value for the logarithmic negativity, .
For the dynamics governed by the thermal bath Lindblad Equation (1), in the long time limit with , the density matrix approaches the equilibrium state with the covariance matrix given by
The equilibrium density matrix, , is the disentangled mixed Gaussian state with and .
In Figure 1, we present the results on the temporal evolution of the logarithmic negativity computed at for different values of the angle . The curves clearly indicate the regime of finite-time disentanglement known as the “sudden death of entanglement”. In this regime, vanishes at , where is the time of disentanglement.
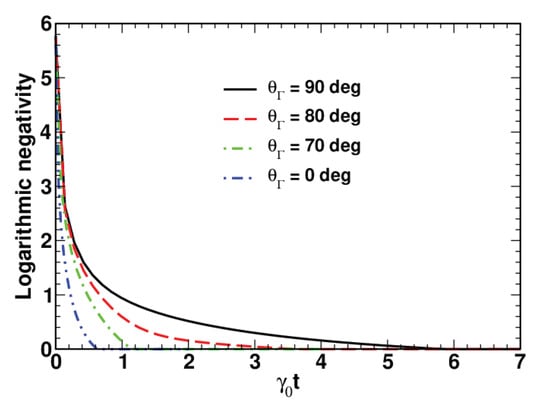
Figure 1.
Time dependence of the logarithmic negativity computed at different angles with for , , , and .
Figure 2 shows the disentanglement time calculated as a function of . It can be seen that is sensitive to orientation of the relaxation rate vector describing the intermode coupling induced by the interaction between the bosonic system and the environment.
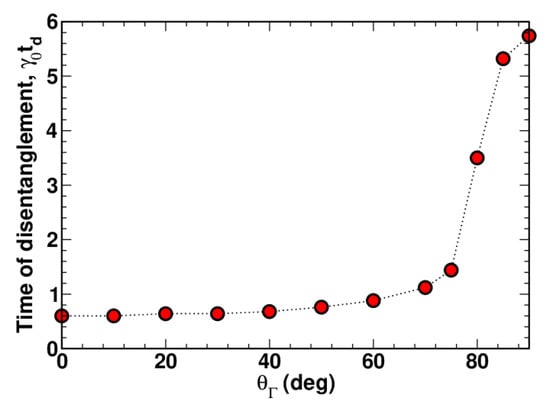
Figure 2.
Time of disentanglement as a function of the angle computed at , and (other parameters are listed in the caption of Figure 1).
The curves plotted in Figure 3 are computed at different values of the angle that specify the orientation of the frequency vector with and illustrate the effect of the dynamical intermode coupling on entanglement dynamics. It is seen that oscillatory behaviour of the logarithmic negativity at translates into sudden revivals of entanglement as the angle decreases.
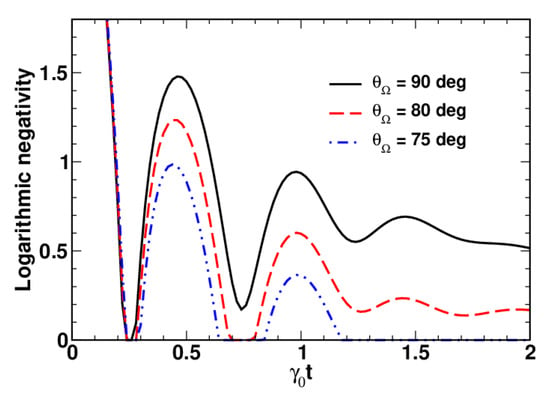
Figure 3.
Time dependence of the logarithmic negativity computed at different angles with for , , , , and .
4. Conclusions
In this paper, we have studied the dynamics of a multi-mode bosonic system governed by the thermal bath Lindblad master equation. Our general approach is based on an exact solution for the characteristic function obtained using the method of characteristics.
We have applied this approach to the special case of the two-mode bosonic system. In this case, the dynamics are determined by the intermode couplings that entre the dynamical and relaxation parts of the Lindblad superoperator (see Equation (1)) and can be described in terms of the frequency and the relaxation rate vectors (see Equation (32)). We have focussed our attention on the effects of the intermode couplings in the dynamics of entanglement and have presented a number of the numerical results on time dependence of the logarithmic negativity.
It is found that, for a vanishing frequency vector with , the logarithmic negativity of the system initially prepared in the two-mode squeezed state monotonically decays, reaching zero at the disentanglement point in time, . In this regime of finite-time disentanglement, the disentanglement time appears to be dependent on the orientation of the relaxation rate vector. We have also shown that the presence of the dynamical intermode coupling with complicates the dynamics of the logarithmic negativity, and its nonmonotonic behaviour results in revivals of entanglement.
Our theoretical considerations were motivated by the model describing mixed polarisation quantum states propagating in an optically anisotropic lossy environment [40,41]. Interestingly, our results are formulated in terms of the covariance matrix that can, in principle, be extracted from experimental data measured using either optical homodyne or heterodyne detection techniques [69]. Qualitatively, our results on the regime of finite-time disentanglement and revivals of entanglement are in agreement with the predictions for oscillators interacting with the thermal bath previously published in [28,29,32,33]. It turns out that the values of the disentaglement time reported in [29] and obtained in the limit of negligible relaxation anisotropy where are close to our estimate evaluated at .
Our findings provide further insights about the protection techniques of entangled states from the detrimental effects of surrounding environments by suitably manipulating the intermode interaction. Generally, revivals of quantum correlations in composite quantum systems are a useful dynamical feature against these effects [70,71,72,73]. Different experimental methods and theoretical approaches to protect quantum resources have been put forward in [74,75,76,77,78,79,80,81].
We conclude with the remark that our analytical approach can be readily extended to study a number of problems, such as Gaussian Einstein–Podolsky–Rosen steering for two-mode squeezed states transmitted in lossy quantum communication channels [82] and the problems related to controlled quantum dynamics in a realistic setup involving open environments. Quantum navigation is an important class of controlled quantum dynamics whereby the objective is to transport one quantum state into another, or to generate quantum gates, in the shortest possible time under the influence of an uncontrollable external field. Problems of this kind can be thought of as representing the quantum counterpart of the classical Zermelo navigation problem of finding the time-optimal control that takes a ship from one location to another, under the influence of external wind or currents [83,84,85]. In a forthcoming publication, we will apply our results to the Zermelo navigation problem for open multi-mode bosonic systems.
Author Contributions
Research, A.D.K., R.A. and A.V.R.; writing—original draft preparation, A.D.K. and R.A.; writing—review and editing, A.D.K. and A.V.R. All authors have read and agreed to the published version of the manuscript.
Funding
The work of A.D.K. and A.V.R. was supported by the Russian Science Foundation under grant No. 20-11-20226.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stinespring, W.F. Positive functions on C*-algebras. Proc. Am. Math. Soc. 1955, 6, 211–216. [Google Scholar]
- Choi, M.D. Completely positive linear maps on complex matrices. Linear Algebra Its Appl. 1975, 10, 285–290. [Google Scholar] [CrossRef]
- Kraus, K. States, Effects, and Operations: Fundamental Notions of Quantum Theory; Lecture Notes in Physics; Springer: Heidelberg/Berlin, Germany, 1983; Volume 190. [Google Scholar]
- Holevo, A.S. On the mathematical theory of quantum communication channels. Probl. Peredachi Informatsii 1972, 8, 62–71. [Google Scholar] [CrossRef]
- Caruso, F.; Giovannetti, V.; Lupo, C.; Mancini, S. Quantum channels and memory effects. Rev. Mod. Phys. 2014, 86, 1203. [Google Scholar] [CrossRef]
- Carmichael, H. An Open Systems Approach to Quantum Optics; Springer: Heidelberg/Berlin, Germany, 1993. [Google Scholar]
- Omnès, R. General theory of the decoherence effect in quantum mechanics. Phys. Rev. A 1997, 56, 3383. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Rivas, A.; Huelga, S.F. Open Quantum Systems: An Introduction; SpringerBriefs in Physics; Springer: Heidelberg/Berlin, Germany, 2012. [Google Scholar]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef]
- de Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Kossakowski, A. On quantum statistical mechanics of non-Hamiltonian systems. Rep. Math. Phys. 1972, 3, 247–274. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Pearle, P. Simple derivation of the Lindblad equation. Eur. J. Phys. 2012, 33, 805. [Google Scholar] [CrossRef]
- Albash, T.; Boixo, S.; Lidar, D.A.; Zanardi, P. Quantum adiabatic Markovian master equations. New J. Phys. 2012, 14, 123016. [Google Scholar] [CrossRef]
- McCauley, G.; Cruikshank, B.; Bondar, D.I.; Jacobs, K. Accurate Lindblad-form master equation for weakly damped quantum systems across all regimes. Npj Quantum Inf. 2020, 6, 74. [Google Scholar] [CrossRef]
- Manzano, D. A short introduction to the Lindblad master equation. Aip Adv. 2020, 10, 025106. [Google Scholar] [CrossRef]
- Arévalo-Aguilar, L.M.; Moya-Cessa, H. Solution to the master equation for a quantized cavity mode. Quantum Semiclassical Opt. J. Eur. Opt. Soc. Part B 1998, 10, 671. [Google Scholar] [CrossRef]
- Klimov, A.B.; Romero, J.L. An algebraic solution of Lindblad-type master equations. J. Opt. B Quantum Semiclassical Opt. 2003, 5, S316. [Google Scholar] [CrossRef]
- Lu, H.X.; Yang, J.; Zhang, Y.D.; Chen, Z.B. Algebraic approach to master equations with superoperator generators of su(1, 1) and su(2) Lie algebras. Phys. Rev. A 2003, 67, 024101. [Google Scholar] [CrossRef]
- Tay, B.A.; Petrosky, T. Biorthonormal eigenbasis of a Markovian master equation for the quantum Brownian motion. J. Math. Phys. 2008, 49, 113301. [Google Scholar] [CrossRef]
- Honda, D.; Nakazato, H.; Yoshida, M. Spectral resolution of the Liouvillian of the Lindblad master equation for a harmonic oscillator. J. Math. Phys. 2010, 51, 072107. [Google Scholar] [CrossRef]
- Tay, B.A. Eigenvalues of the Liouvillians of quantum master equation for a harmonic oscillator. Phys. A 2020, 556, 124768. [Google Scholar] [CrossRef]
- Shishkov, V.Y.; Andrianov, E.S.; Pukhov, A.A.; Vinogradov, A.P.; Lisyansky, A.A. Perturbation theory for Lindblad superoperators for interacting open quantum systems. Phys. Rev. A 2020, 102, 032207. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R. Entangling oscillators through environment noise. J. Phys. A Math. Gen. 2006, 39, 2689. [Google Scholar] [CrossRef]
- Teuber, L.; Scheel, S. Solving the quantum master equation of coupled harmonic oscillators with Lie-algebra methods. Phys. Rev. A 2020, 101, 042124. [Google Scholar] [CrossRef]
- Hiroshima, T. Decoherence and entanglement in two-mode squeezed vacuum states. Phys. Rev. A 2004, 63, 022305. [Google Scholar] [CrossRef]
- Serafini, A.; Illuminati, F.; Paris, M.G.A.; De Siena, S. Entanglement and purity of two-mode Gaussian states in noisy channels. Phys. Rev. A 2004, 69, 022318. [Google Scholar] [CrossRef]
- de Castro, A.; Siqueira, R.; Dodonov, V. Effect of dissipation and reservoir temperature on squeezing exchange and emergence of entanglement between two coupled bosonic modes. Phys. Lett. A 2008, 372, 367–374. [Google Scholar] [CrossRef]
- Chou, C.H.; Yu, T.; Hu, B.L. Exact master equation and quantum decoherence of two coupled harmonic oscillators in a general environment. Phys. Rev. E 2008, 77, 011112. [Google Scholar] [CrossRef]
- Paz, J.P.; Roncaglia, A.J. Dynamics of the entanglement between two oscillators in the same environment. Phys. Rev. Lett. 2008, 100, 220401. [Google Scholar] [CrossRef]
- Paz, J.P.; Roncaglia, A.J. Dynamical phases for the evolution of the entanglement between two oscillators coupled to the same environment. Phys. Rev. A 2009, 79, 032102. [Google Scholar] [CrossRef]
- Barbosa, F.A.S.; de Faria, A.J.; Coelho, A.S.; Cassemiro, K.N.; Villar, A.S.; Nussenzveig, P.; Martinelli, M. Disentanglement in bipartite continuous-variable systems. Phys. Rev. A 2011, 84, 052330. [Google Scholar] [CrossRef]
- Figueiredo, E.; Linhares, C.; Malbouisson, A.; Malbouisson, J. Time evolution of entanglement in a cavity at finite temperature. Phys. A Stat. Mech. Its Appl. 2016, 462, 1261–1272. [Google Scholar] [CrossRef]
- Linowski, T.; Gneiting, C.; Rudnicki, L. Stabilizing entanglement in two-mode Gaussian states. Phys. Rev. A 2020, 102, 042405. [Google Scholar] [CrossRef]
- Vendromin, C.; Dignam, M.M. Continuous-variable entanglement in a two-mode lossy cavity: An analytic solution. Phys. Rev. A 2021, 103, 022418. [Google Scholar] [CrossRef]
- Adesso, G.; Illuminati, F. Entanglement in continuous-variable systems: Recent advances and current perspectives. J. Phys. A Math. Theor. 2007, 40, 7821. [Google Scholar] [CrossRef]
- Miroshnichenko, G.P.; Kiselev, A.D.; Trifanov, A.L.; Gleim, A.V. Algebraic approach to electro-optic modulation of light: Exactly solvable multimode quantum model. J. Opt. Soc. Am. B 2017, 34, 1177–1190. [Google Scholar] [CrossRef]
- Kozubov, A.; Gaidash, A.; Miroshnichenko, G. Quantum model of decoherence in the polarization domain for the fiber channel. Phys. Rev. A 2019, 99, 053842. [Google Scholar] [CrossRef]
- Gaidash, A.; Kozubov, A.; Miroshnichenko, G. Dissipative dynamics of quantum states in the fiber channel. Phys. Rev. A 2020, 102, 023711. [Google Scholar] [CrossRef]
- Mintert, F.; Carvalho, A.R.; Kuś, M.; Buchleitner, A. Measures and dynamics of entangled states. Phys. Rep. 2005, 415, 207–259. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Aolita, L.; de Melo, F.; Davidovich, L. Open-system dynamics of entanglement: A key issues review. Rep. Prog. Phys. 2015, 78, 042001. [Google Scholar] [CrossRef]
- Rajagopal, A.K.; Rendell, R.W. Decoherence, correlation, and entanglement in a pair of coupled quantum dissipative oscillators. Phys. Rev. A 2001, 63, 022116. [Google Scholar] [CrossRef]
- Życzkowski, K.; Horodecki, P.; Horodecki, M.; Horodecki, R. Dynamics of quantum entanglement. Phys. Rev. A 2001, 65, 012101. [Google Scholar] [CrossRef]
- Dodd, P.J.; Halliwell, J.J. Disentanglement and decoherence by open system dynamics. Phys. Rev. A 2004, 69, 052105. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Finite-time disentanglement via spontaneous emission. Phys. Rev. Lett. 2004, 93, 140404. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Quantum open system theory: Bipartite aspects. Phys. Rev. Lett. 2006, 97, 140403. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Eberly, J.H. Sudden death of entanglement. Science 2009, 323, 598–601. [Google Scholar] [CrossRef] [PubMed]
- Passos, M.H.M.; Balthazar, W.F.; Khoury, A.Z.; Hor-Meyll, M.; Davidovich, L.; Huguenin, J.A.O. Experimental investigation of environment-induced entanglement using an all-optical setup. Phys. Rev. A 2018, 97, 022321. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sarma, A.K. Delayed sudden death of entanglement at exceptional points. Phys. Rev. A 2019, 100, 063846. [Google Scholar] [CrossRef]
- Shearer, M.; Levy, R. Partial Differential Equations: An Introduction to Theory and Applications; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Kozubov, A.V.; Gaidash, A.A.; Miroshnichenko, G.P.; Kiselev, A.D. Quantum dynamics of mixed polarization states: Effects of environment-mediated intermode coupling. J. Opt. Soc. Am. B 2021, 38, 2603–2611. [Google Scholar]
- Goldberg, A.Z.; e la Hoz, P.; Björk, G.; Klimov, A.B.; Grassl, M.; Leuchs, G.; Sánchez-Soto, L.L. Quantum concepts in optical polarization. Adv. Opt. Photon. 2021, 13, 1–73. [Google Scholar] [CrossRef]
- Serafini, A. Quantum Continuous Variables: A Primer of Theoretical Methods; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Simon, R. Peres-Horodecki separability criterion for continuous variable systems. Phys. Rev. Lett. 2000, 84, 2726. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.M.; Giedke, G.; Cirac, J.L.; Zoller, P. Inseparability criterion for continuous variable systems. Phys. Rev. Lett. 2000, 84, 2722. [Google Scholar] [CrossRef]
- Shchukin, E.; Vogel, W. Inseparability criteria for continuous bipartite quantum states. Phys. Rev. Lett. 2005, 95, 230502. [Google Scholar] [CrossRef]
- Gessner, M.; Pezzè, L.; Smerzi, A. Efficient entanglement criteria for discrete, continuous, and hybrid variables. Phys. Rev. A 2016, 94, 020101. [Google Scholar] [CrossRef]
- Bowen, W.P.; Schnabel, R.; Lam, P.K.; Ralph, T.C. Experimental characterization of continuous-variable entanglement. Phys. Rev. A 2004, 69, 012304. [Google Scholar] [CrossRef]
- Simon, D.S.; Jaeger, G.; Sergienko, A.V. Entangled-coherent-state quantum key distribution with entanglement witnessing. Phys. Rev. A 2014, 89, 012315. [Google Scholar] [CrossRef]
- Jaeger, G.; Simon, D.; Sergienko, A.V. Coherent state quantum key distribution based on entanglement sudden death. Quantum Inf. Process. 2016, 15, 1117–1133. [Google Scholar] [CrossRef]
- Adesso, G.; Illuminati, F. Gaussian measures of entanglement versus negativities: Ordering of two-mode Gaussian states. Phys. Rev. A 2005, 72, 032334. [Google Scholar] [CrossRef]
- Marian, P.; Marian, T.A. Bures distance as a measure of entanglement for symmetric two-mode Gaussian states. Phys. Rev. A 2008, 77, 062319. [Google Scholar] [CrossRef]
- Marian, P.; Marian, T.A. Entanglement of formation for an arbitrary two-mode Gaussian state. Phys. Rev. Lett. 2008, 101, 220403. [Google Scholar] [CrossRef]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef]
- Hertz, A.; Cerf, N.J.; De Bièvre, S. Relating the entanglement and optical nonclassicality of multimode states of a bosonic quantum field. Phys. Rev. A 2020, 102, 032413. [Google Scholar] [CrossRef]
- Lvovsky, A.I.; Raymer, M.G. Continuous-variable optical quantum-state tomography. Rev. Mod. Phys. 2009, 81, 299. [Google Scholar] [CrossRef]
- Joshi, C.; Jonson, M.; Öhberg, P.; Andersson, E. Constructive role of dissipation for driven coupled bosonic modes. Phys. Rev. A 2013, 87, 062304. [Google Scholar] [CrossRef]
- Xu, J.S.; Sun, K.; Li, C.F.; Xu, X.Y.; Guo, G.C.; Andersson, E.; Lo Franco, R.; Compagno, G. Experimental recovery of quantum correlations in absence of system-environment back-action. Nat. Commun. 2013, 4, 2851. [Google Scholar] [CrossRef]
- Shen, L.T.; Shi, Z.C.; Wu, H.Z.; Yang, Z.B. Dynamics of entanglement in jaynes–cummings nodes with nonidentical qubit-field coupling strengths. Entropy 2017, 19, 331. [Google Scholar] [CrossRef]
- Shen, L.T.; Shi, Z.C.; Yang, Z.B. Coherent state control to recover quantum entanglement and coherence. Entropy 2019, 21, 917. [Google Scholar] [CrossRef]
- Bellomo, B.; Lo Franco, R.; Compagno, G. Long-time preservation of nonlocal entanglement. Adv. Sci. Lett. 2009, 2, 459–462. [Google Scholar] [CrossRef][Green Version]
- Mortezapour, A.; Lo Franco, R. Protecting quantum resources via frequency modulation of qubits in leaky cavities. Sci. Rep. 2018, 8, 4304. [Google Scholar] [CrossRef] [PubMed]
- Man, Z.Y.; Xia, Y.J.; Lo Franco, R. Cavity-based architecture to preserve quantum coherence and entanglement. Sci. Rep. 2015, 5, 13843. [Google Scholar] [CrossRef]
- Nosrati, F.; Mortezapour, A.; Lo Franco, R. Validating and controlling quantum enhancement against noise by the motion of a qubit. Phys. Rev. A 2020, 101, 012331. [Google Scholar] [CrossRef]
- Ghiu, I.; Grimaudo, R.; Mihaescu, T.; Isar, A.; Messina, A. Quantum correlation dynamics in controlled two-coupled-qubit systems. Entropy 2020, 22, 785. [Google Scholar] [CrossRef] [PubMed]
- Nosrati, F.; Castellini, A.; Compagno, G.; Lo Franco, R. Robust entanglement preparation against noise by controlling spatial indistinguishability. Npj Quantum Inf. 2020, 6, 39. [Google Scholar] [CrossRef]
- Nosrati, F.; Castellini, A.; Compagno, G.; Lo Franco, R. Dynamics of spatially indistinguishable particles and quantum entanglement protection. Phys. Rev. A 2020, 102, 062429. [Google Scholar] [CrossRef]
- Piccolini, M.; Nosrati, F.; Compagno, G.; Livreri, P.; Morandotti, R.; Lo Franco, R. Entanglement robustness via spatial deformation of identical particle wave functions. Entropy 2021, 23, 708. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Liu, Y.; Wang, M.; Su, X.; Peng, K. Sudden death and revival of Gaussian Einstein–Podolsky–Rosen steering in noisy channels. Npj Quantum Inf. 2021, 7, 65. [Google Scholar] [CrossRef]
- Brody, D.C.; Graefe, E.M. Mixed-state evolution in the presence of gain and loss. Phys. Rev. Lett. 2012, 109, 230405. [Google Scholar] [CrossRef]
- Brody, D.C.; Gibbons, G.W.; Meier, D.M. Time-optimal navigation through quantum wind. New J. Phys. 2015, 17, 033048. [Google Scholar] [CrossRef]
- Brody, D.C.; Longstaff, B. Evolution speed of open quantum dynamics. Phys. Rev. Res. 2019, 1, 033127. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).