Numerical Prediction of Two-Phase Flow through a Tube Bundle Based on Reduced-Order Model and a Void Fraction Correlation
Abstract
:1. Introduction
2. Cross-Flow through a Horizontal Tube Bundle
2.1. Governing Equations of the Two-Phase Flow
2.2. Rewriting of the Slip Velocity
2.2.1. Hibiki’s Correlation (2017)
2.2.2. Feenstra’s Correlation (2000)
2.3. Definition of the Darcy–Forchheimer Term
3. Reduced Ordel Model on the REV to Compute the Forchheimer Term
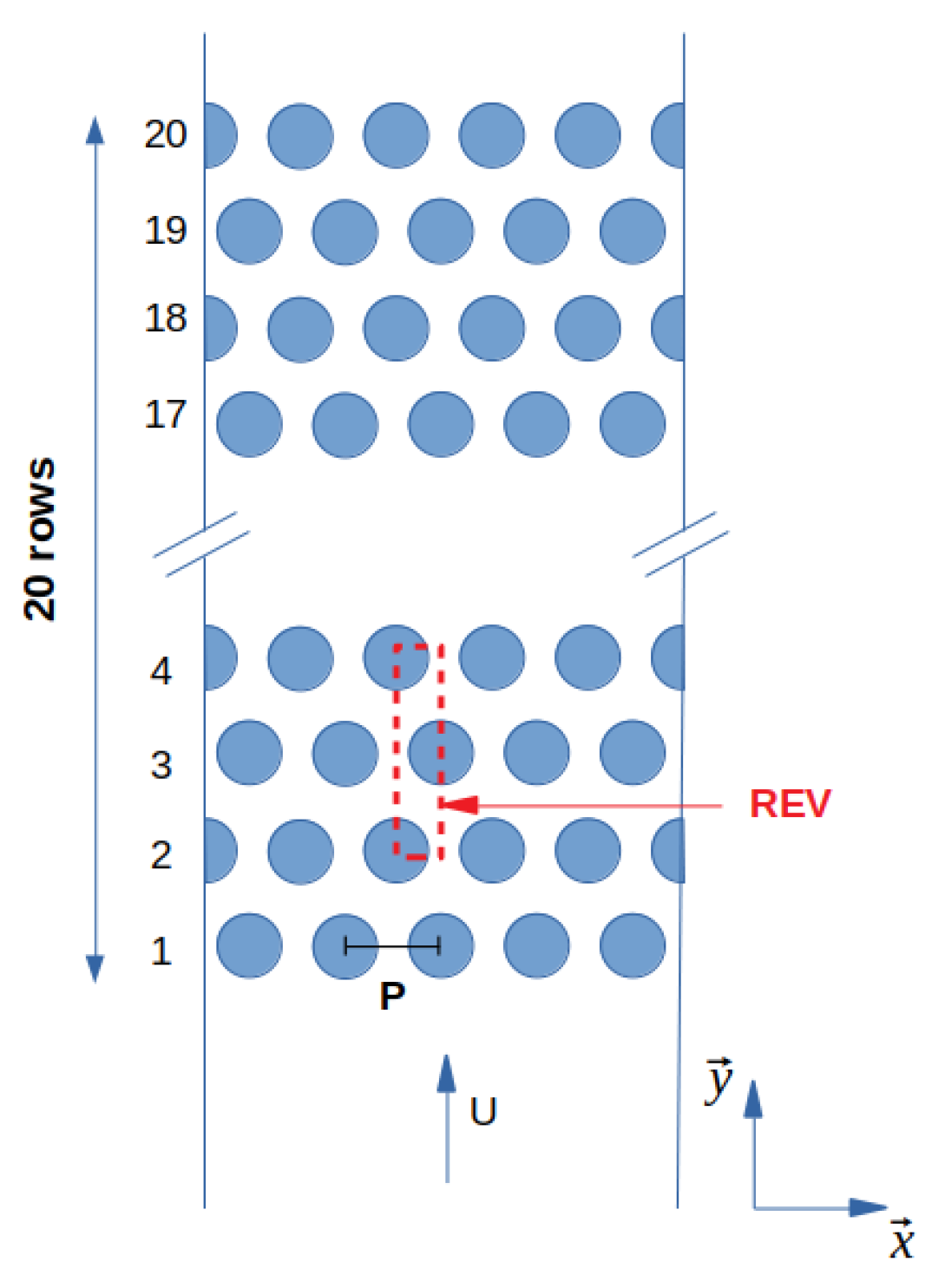
3.1. Representative Elementary Volume
3.2. Definition of Reduced Bases
3.3. Description of the Bi-CITSGM Method
4. Validation of the Using of the Modified Mixture Model on the Dowlati’s Experiment
4.1. Study Configuration
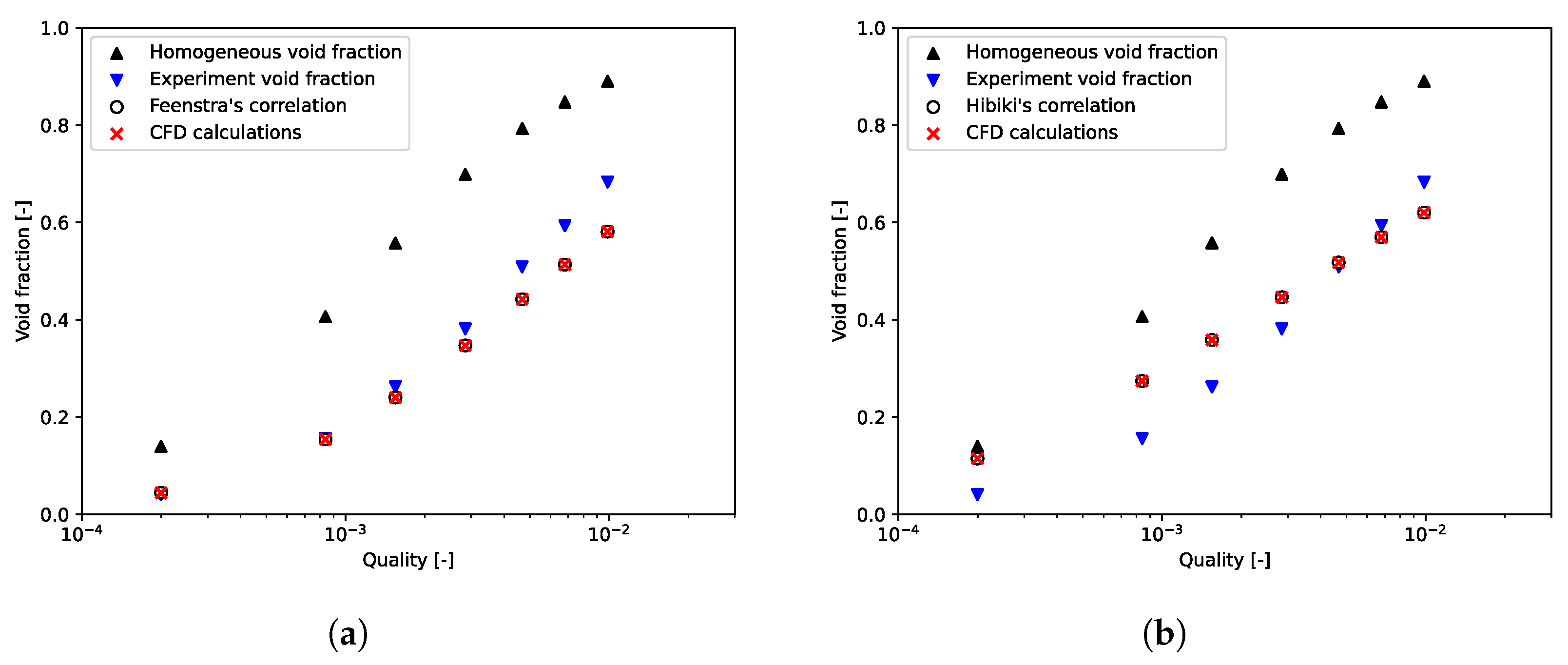
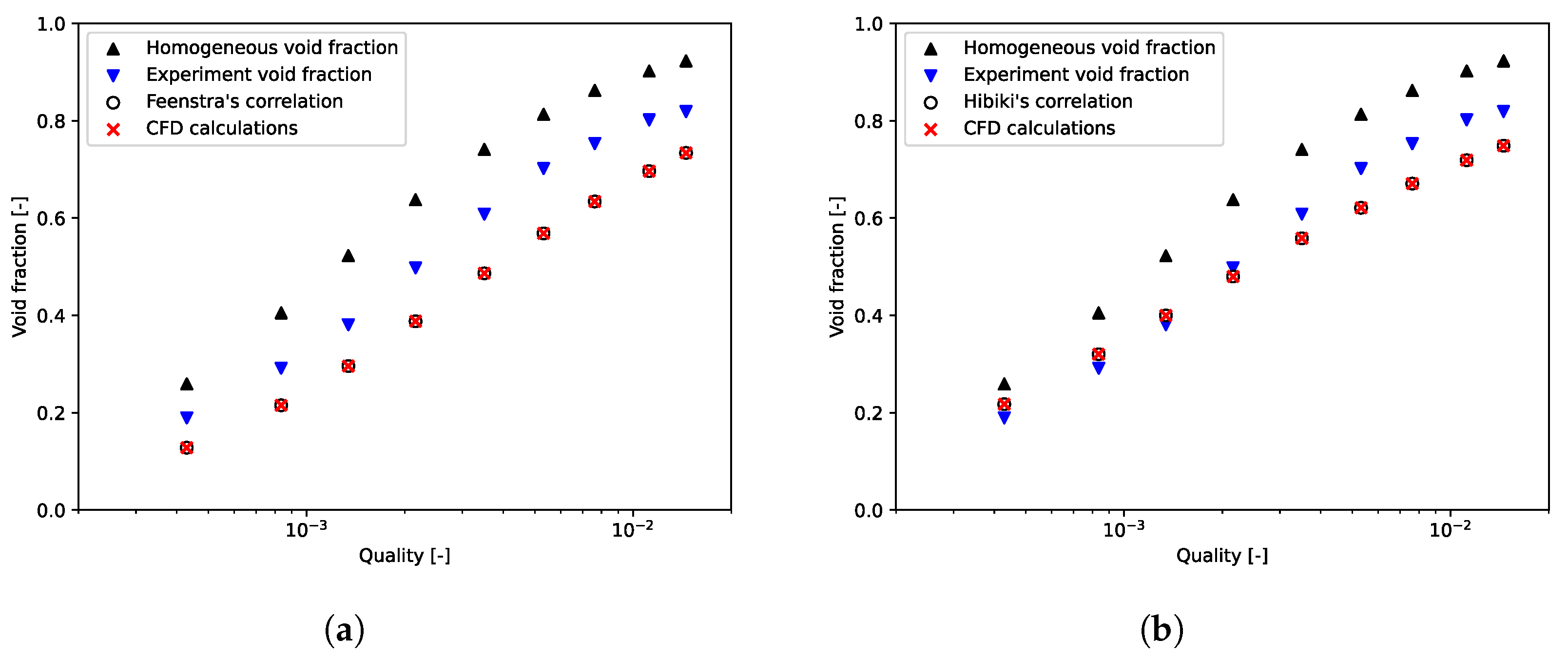
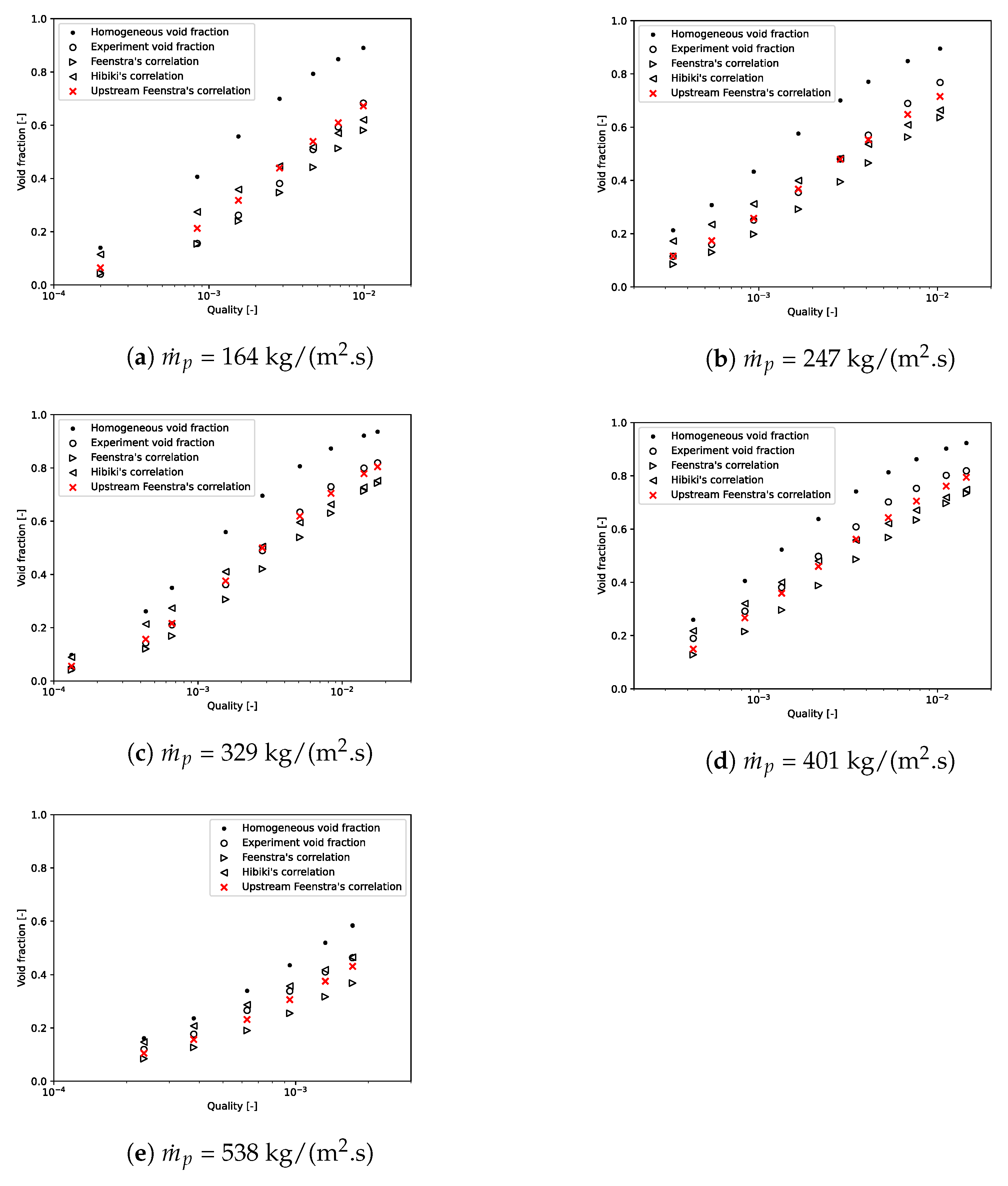
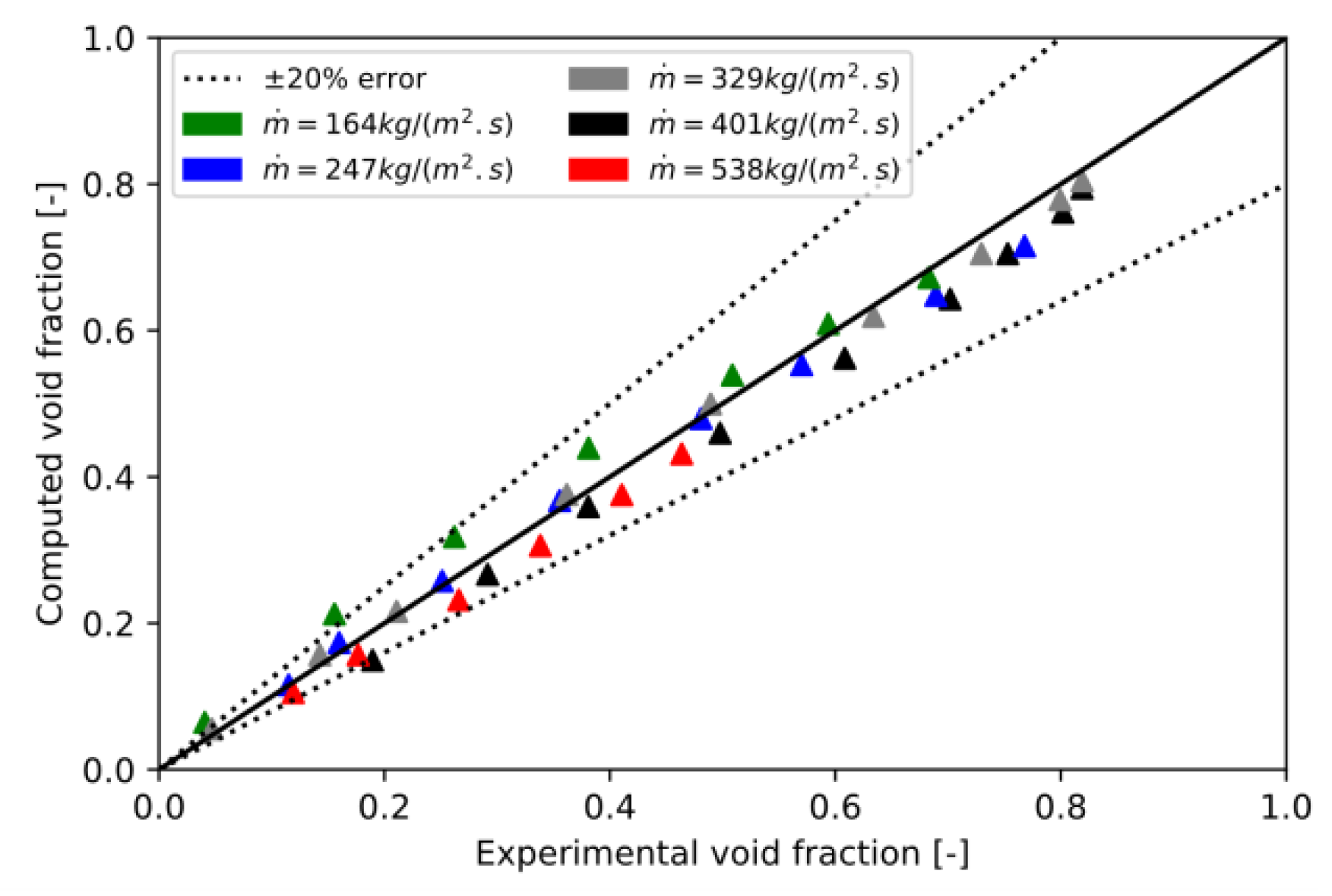
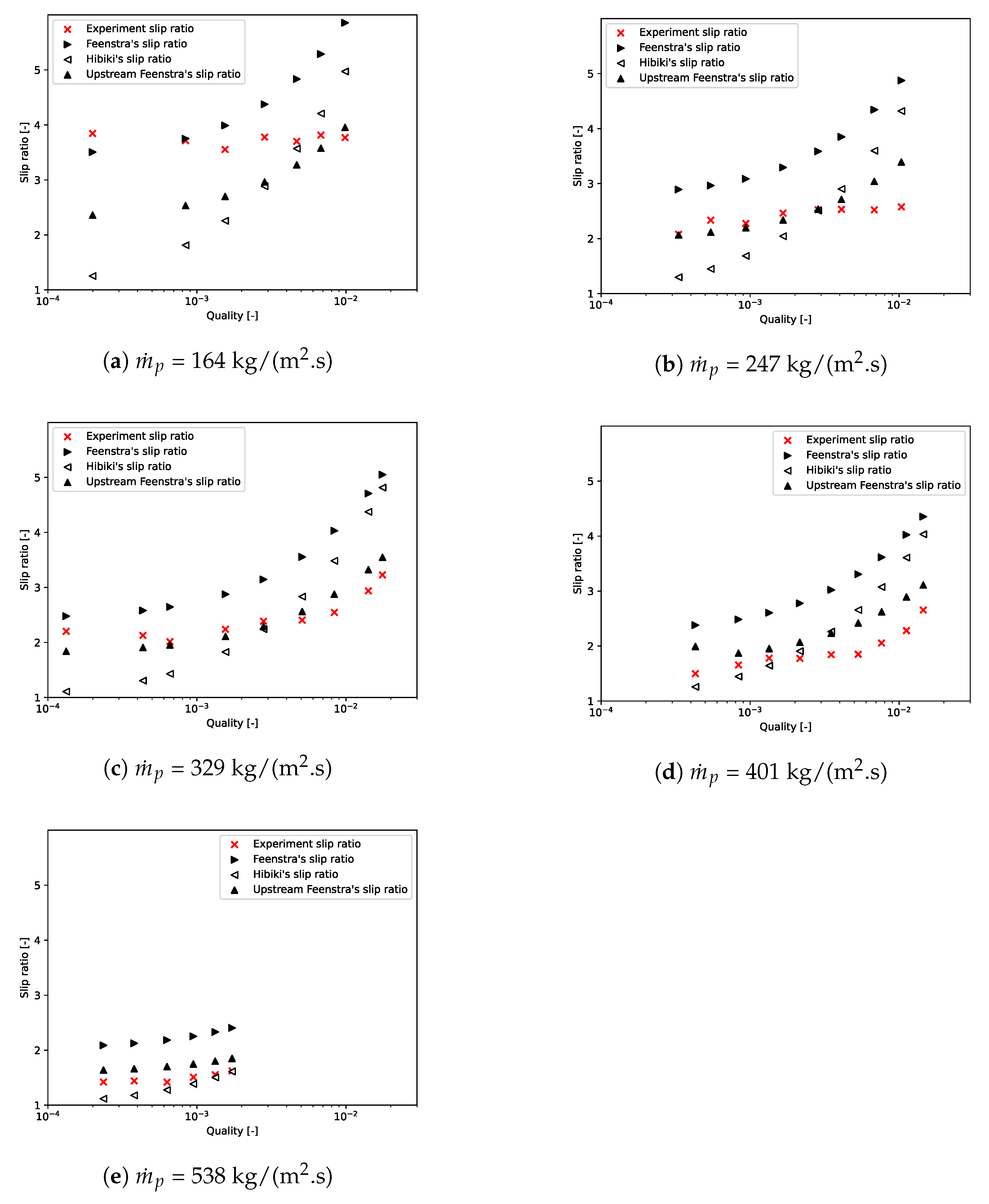
4.2. Influence of the Slip Model on the Void Fraction Prediction
5. Computation of the Pressure Drop in Tube Bundles by Using POD-ROM on an REV
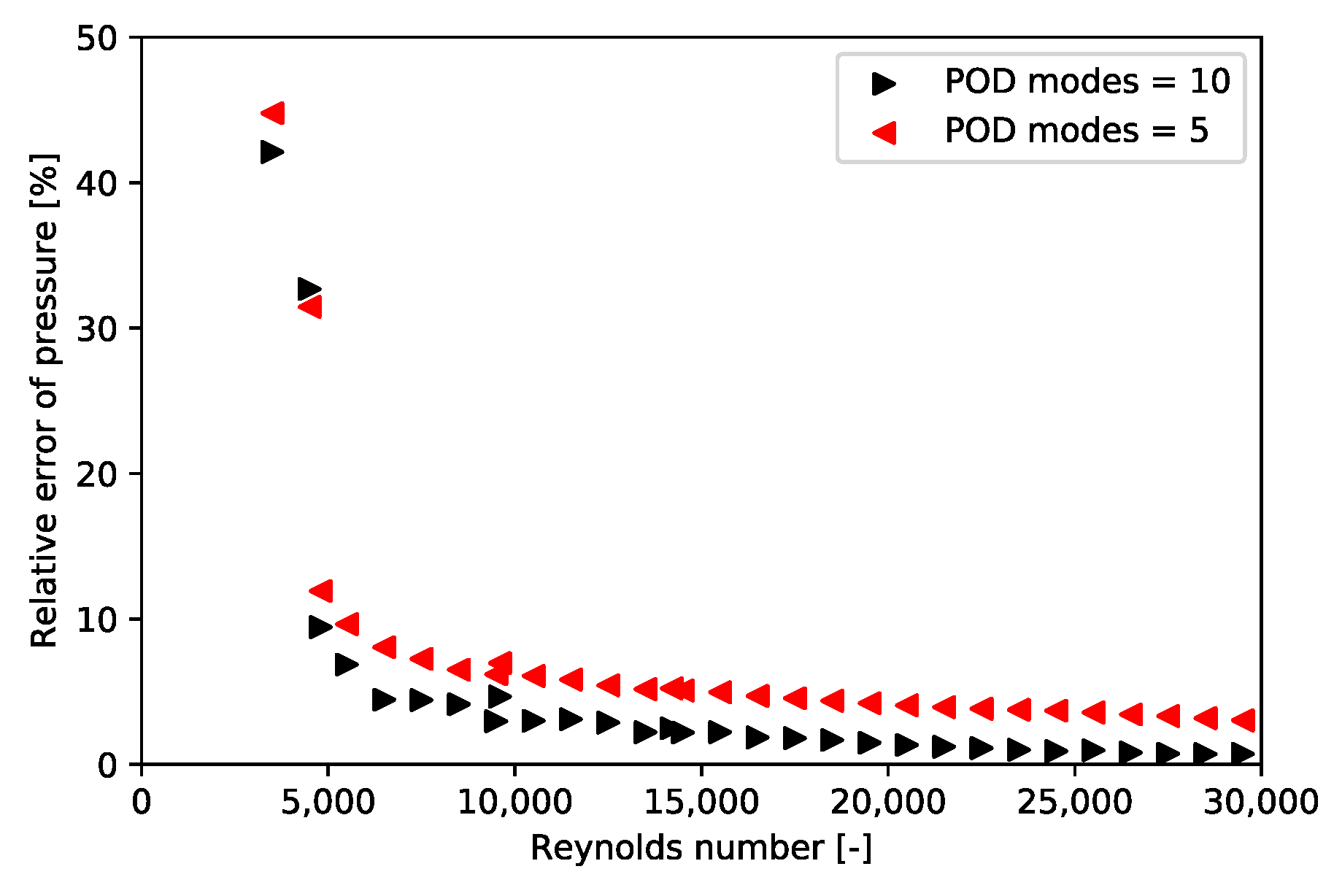
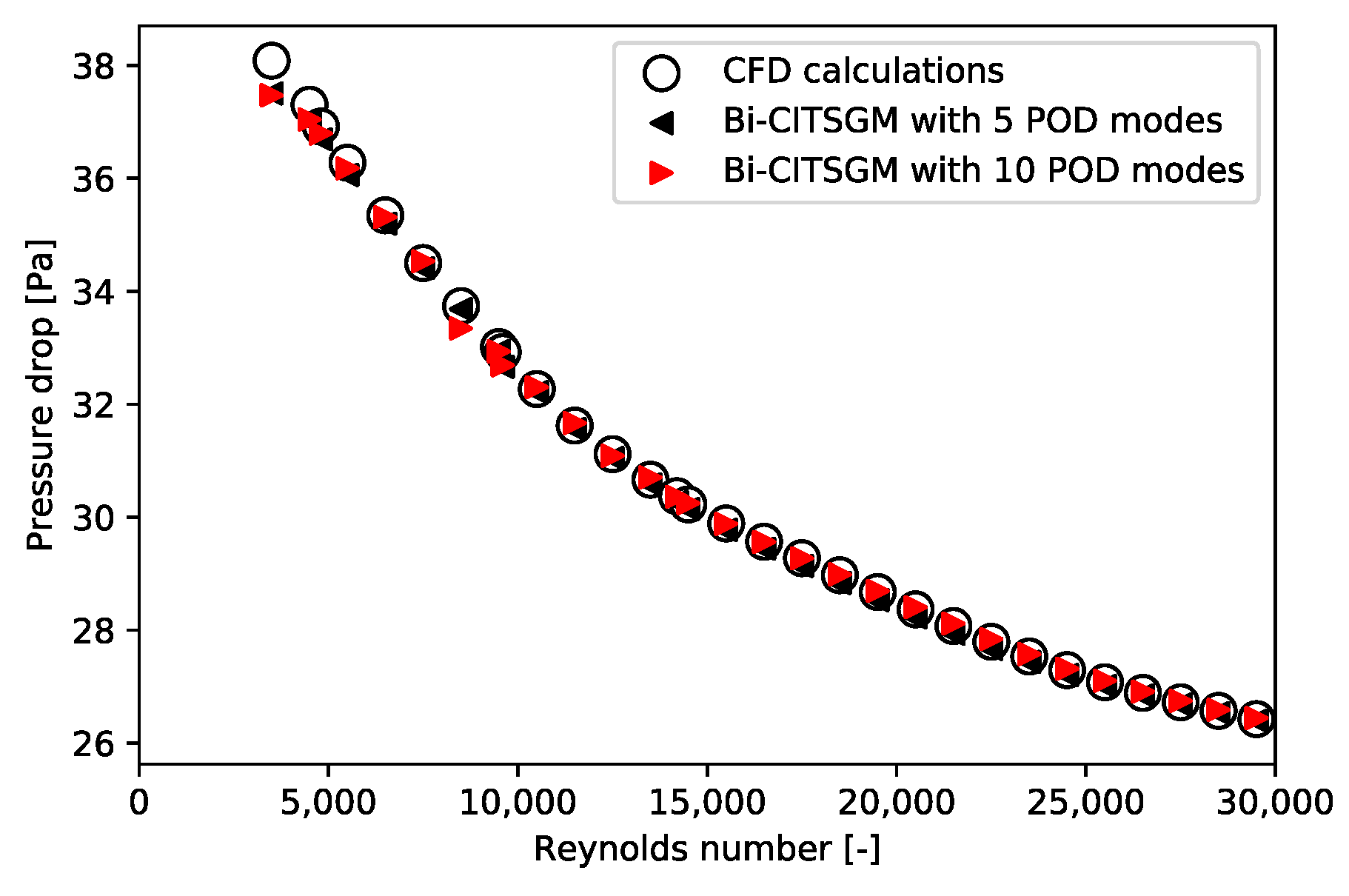
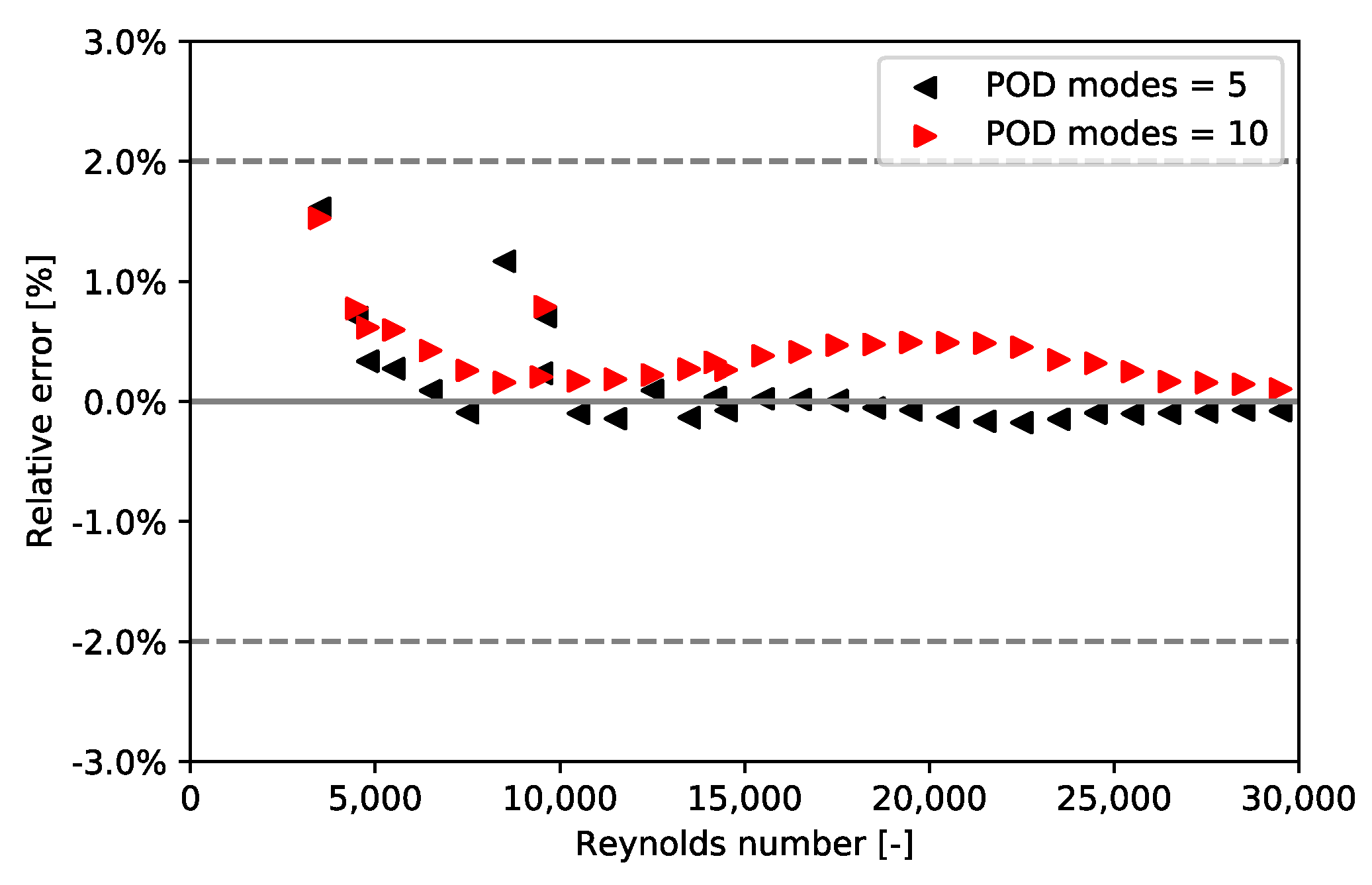
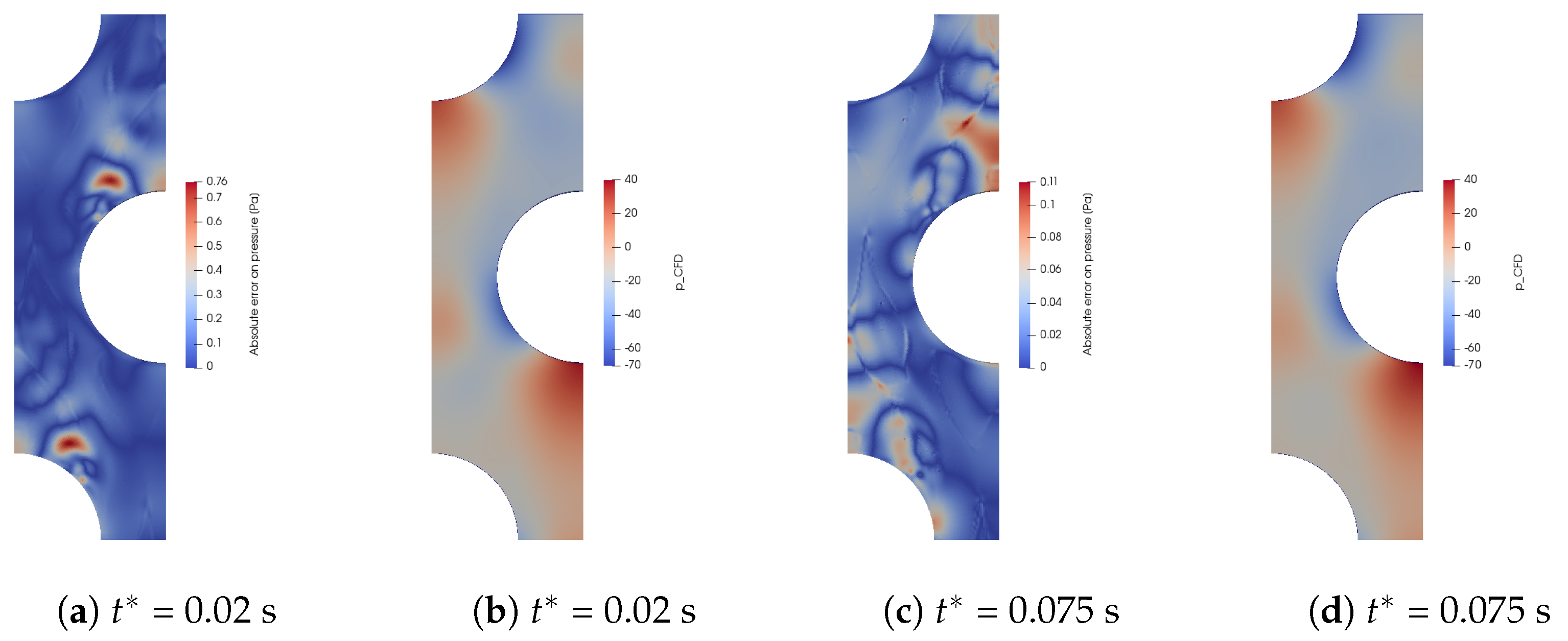
5.1. Validation of the Bi-CITSGM Method on the REV
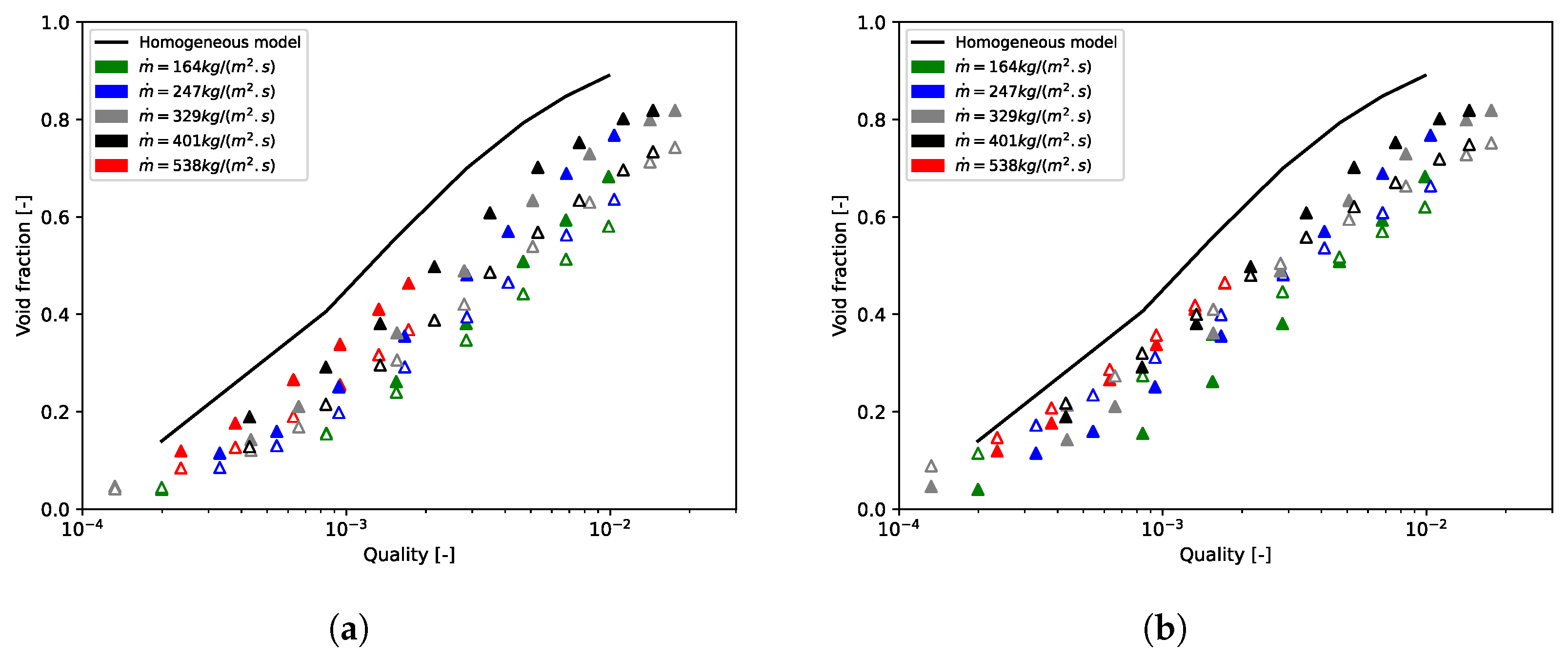
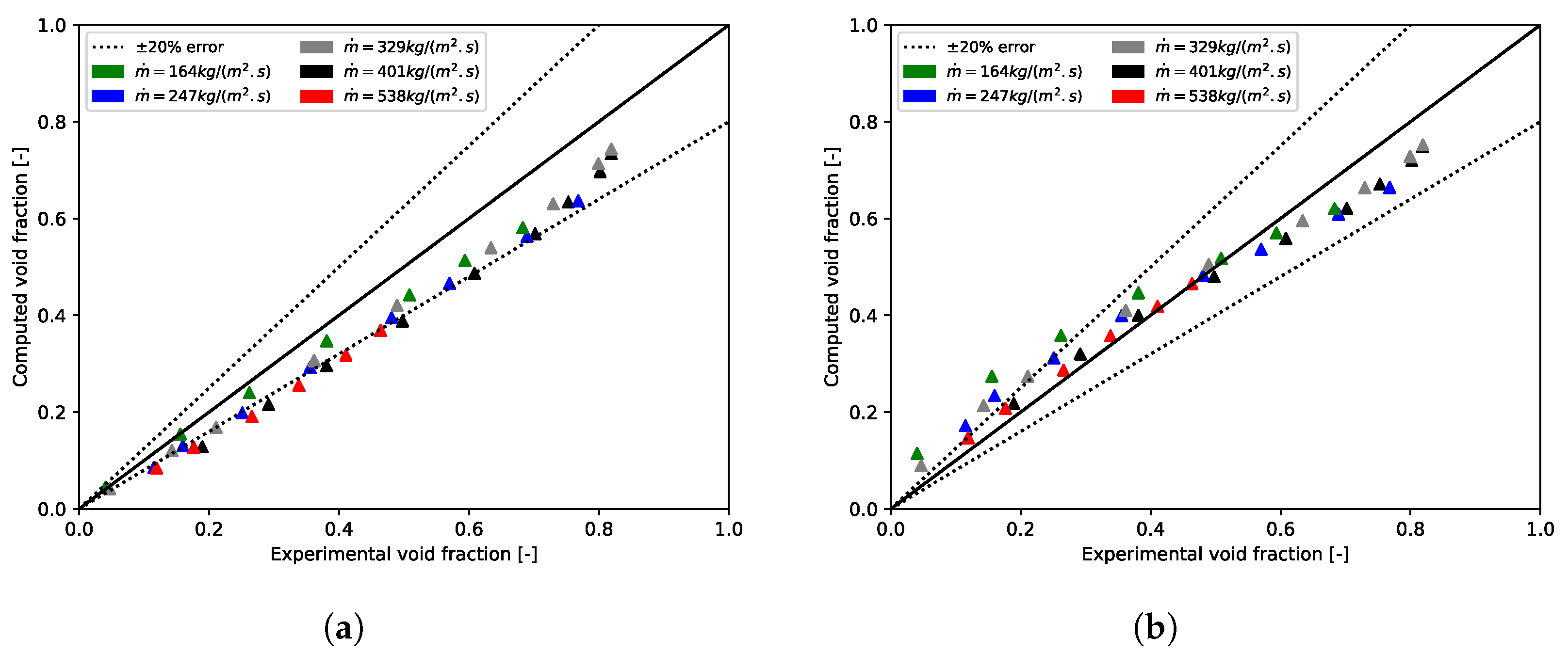
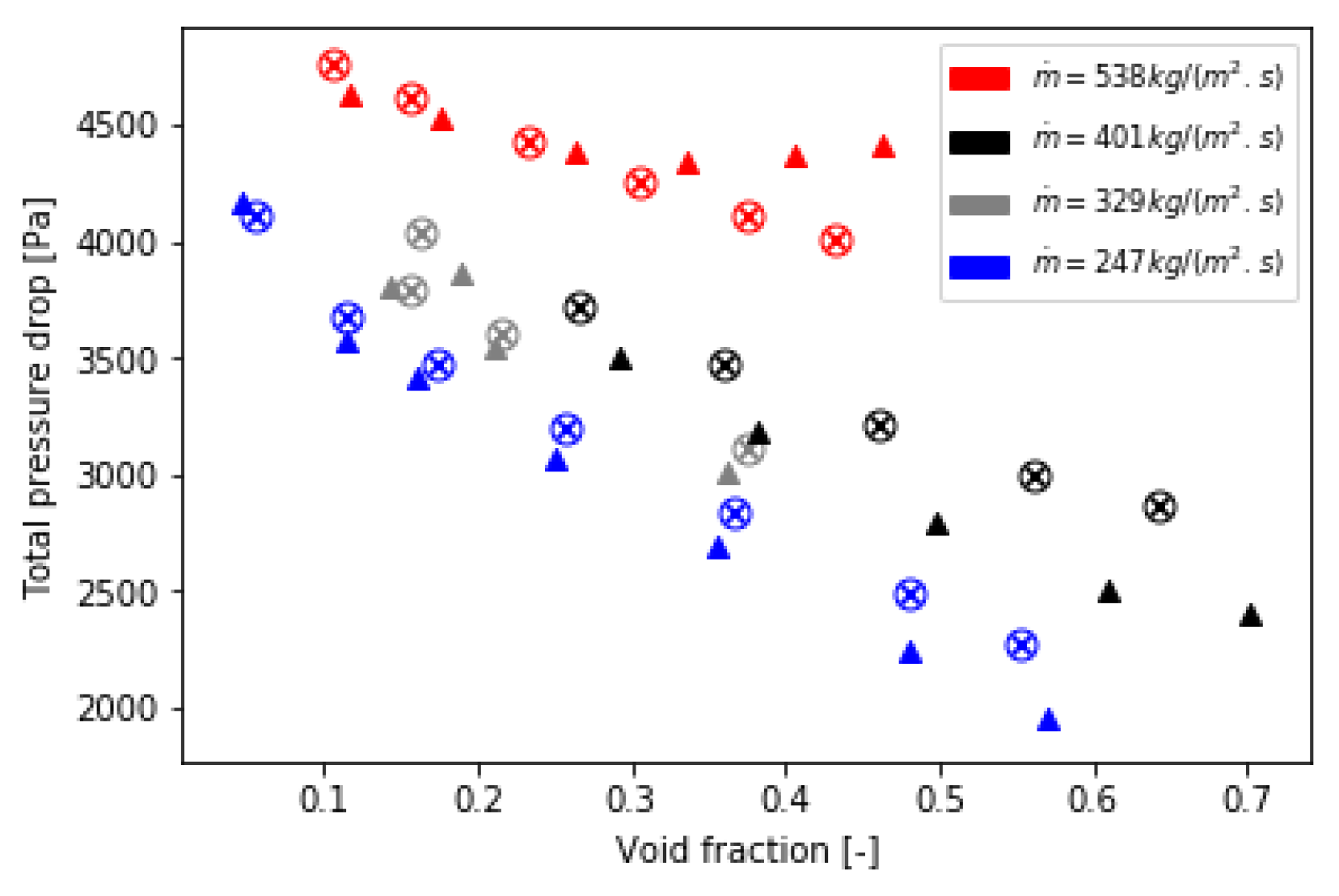
5.2. Validation of the Implementation of the Bi-CITSGM Method on the Dowlati’s Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamic |
| POD | Proper Orthogonal Decomposition |
| ROM | Reduced-order model |
| REV | Representative Elementary Volume |
| ITSGM | Interpolation on the Tangent Subspace of the Grassmann Manifold |
| Bi-CITSGM | Bi Calibrated Interpolation on the Tangent Subspace of the Grassmann Manifold |
| RBF | Radial Basis Function |
| IDW | Inverse Distance Weighting |
Appendix A. Algorithm of the ITSGM Method
| Algorithm A1 ITSGM Algorithm. |
|
Appendix B. Algorithm of the Bi-CITSGM Method
| Algorithm A2 Bi-CITSGM Algorithm. |
Offline step (do this step only once):
|
References
- Carver, M.B.; Carlucci, L.N.; Inch, W.W.R. Thermal-Hydraulics in Recirculating Steam Generators—THIRST Code User’s Manual; Atomic Energy of Canada Limited: Chalk River, ON, Canada, 1981. [Google Scholar]
- Tincq, D.; David, F. THYC, un code 3D de thermohydraulique pour les générateurs de vapeur, les échangeurs de chaleur et les condenseurs. Rev. Générale De Therm. 1995, 34, 141–153. [Google Scholar]
- Zuber, N.; Findlay, J.A. Average Volumetric Concentration in Two-Phase Flow Systems. J. Heat Transf. 1965, 87, 453–468. [Google Scholar] [CrossRef]
- Ozaki, T.; Suzuki, R.; Mashiko, H.; Hibiki, T. Development of drift flux model based on 8x8 BWR rod bundle geometry experiments under prototypic temperature and pressure conditions. J. Nucl. Sci. Technol. 2013, 50, 563–580. [Google Scholar] [CrossRef]
- Lellouche, G.S.; Zolotar, B.A. Mechanistic Model for Predicting Two-Phase Void Fraction for Water in Vertical Tubes, Channels, and Rod Bundles; No. EPRI-NP-2246-SR; Electric Power Research Inst.: Palo Alto, CA, USA, 1982. [Google Scholar]
- Armand, A.A. The resistance during the movement of a two-phase system in horizontal pipes. At. Energy Res. Establ. 1959, 1, 16–23. [Google Scholar]
- Massena, W.A. Steam-Water Pressure Drop and Critical Discharge Flow—A Digital Computer Program; No. HW-65706; General Electric Co. Hanford Atomic Products Operation: Richland, WA, USA, 1960. [Google Scholar]
- Mao, K.; Hibiki, T. Drift-Flux Model Upward Two-Phase Cross-Flow Horiz. Tube Bundles. Int. J. Multiph. Flow 2017, 91, 170–183. [Google Scholar] [CrossRef]
- Stosic, Z.V.; Stevanovic, V.D. Advanced Three-Dimensional Two-Fluid Porous Media Method for Transient Two-Phase Flow Thermal-Hydraulics in Complex Geometries. Numer. Heat Transf. B. 2002, 41, 263–289. [Google Scholar] [CrossRef]
- Ishii, M.; Zuber, N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows. AIChE J. 1979, 25, 843–855. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, A. Fundamental calculations in gravitational processing. Z. Des Vereines Dtsch. Ingenieure 1933, 77, 318–320. [Google Scholar]
- Tomiyama, A.; Kataoka, I.; Zun, I.; Sakaguchi, T. Drag Coefficients of Single Bubbles under Normal and Micro Gravity Conditions. JSME Int. J. Ser. B 1998, 41, 472–479. [Google Scholar] [CrossRef]
- Morsi, S.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Ozaki, T.; Hibiki, T.; Miwa, S.; Mori, M. Code performance with improved two-group interfacial area concentration correlation for one-dimensional forced convective two-phase flow simulation. J. Nucl. Sci. Technol. 2018, 55, 911–930. [Google Scholar] [CrossRef]
- Feenstra, P.; Weaver, D.; Judd, R. An improved void fraction model for two-phase cross-flow in horizontal tube bundles. Int. J. Multiph. Flow 2000, 26, 1851–1857. [Google Scholar] [CrossRef]
- Hibiki, T.; Mao, K.; Ozaki, T. Development of void fraction-quality correlation for two-phase flow in horizontal and vertical tube bundles. Prog. Nucl. Energy 2017, 97, 38–52. [Google Scholar] [CrossRef]
- Smith, S.L. Void fractions in two-phase flow: A correlation based upon an equal velocity head model. Proc. Inst. Mech. Eng. 1969, 184, 647–664. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la ville de Dijon; Victor Dalmont: Paris, France, 1856. [Google Scholar]
- Forchheimer, P. Wasserbewegung durch Boden. Z. Ver. Dtsch. Ing. 1901, 45, 1782–1788. [Google Scholar]
- Zukauskas, A.; Ulinskas, R. Banks of plain and finned tubes. In Heat Exchanger Design Handbook; Schlunder, E.U., Ed.; Hemisphere Publishing Corporation: Irvine, CA, USA, 1983; pp. 1–17. [Google Scholar]
- Rhodes, D.B.; Carlucci, L.N. Predicted and measured velocity distribution in a model heat exchanger. In Proceedings of the International Conference on Numerical Methods in Nuclear Engineering, Montreal, QC, Canada, 6–9 September 1983. AECL-8271. [Google Scholar]
- Oulghelou, M.; Allery, C. Non-intrusive method for parametric model order reduction using a bi-calibrated interpolation on the grassmann manifold. J. Comput. Phys 2021, 426, 109924. [Google Scholar] [CrossRef]
- Oulghelou, M.; Allery, C. Hyper bi-calibrated interpolation on the Grassmann manifold for near real time flow control using genetic algorithm. arXiv 2019, arXiv:1901.03177. [Google Scholar]
- Amsallem, D.; Farhat, C. Interpolation Method for Adapting Reduced-Order Models and Application to Aeroelasticity. AIAA J. 2008, 46, 1803–1813. [Google Scholar] [CrossRef] [Green Version]
- Dowlati, R.; Chan, A.M.C.; Kawaji, M. Hydrodynamics of two-phase flow across horizontal in-line and staggered rod bundles. J. Fluids Eng. 1992, 114, 450–456. [Google Scholar] [CrossRef]
- Manninen, M.; Taivassalo, V. On the mixture model for multiphase flow. VTT Publ. 1996, 288, 1–67. [Google Scholar]
- Woldesemayat, M.A.; Ghajar, A.J. Comparison of void fraction correlations for different flow patterns in horizontal and upward inclined pipes. Int. J. Multiph. Flow 2007, 33, 347–370. [Google Scholar] [CrossRef]
- Godbole, P.V.; Tang, C.C.; Ghajar, A.J. Comparison of Void Fraction Correlations for Different Flow Patterns in Upward Vertical Two-Phase Flow. Heat Transf. Eng. 2011, 32, 843–860. [Google Scholar] [CrossRef]
- Consolini, L.; Robinson, D.; Thome, J.R. Void fraction and two-phase pressure drops for evaporating flow over horizontal tube bundles. Heat Transf. Eng. 2006, 27, 5–21. [Google Scholar] [CrossRef]
- Ishihara, K.; Palen, J.W.; Taborek, J. Critical review of correlations for predicting two-phase flow pressure drop across tube banks. Heat Transf. Eng. 1980, 1, 23–32. [Google Scholar] [CrossRef]
- Lockhart, R.W.; Martinelli, R.C. Proposed correlation of data for isothermal two-phase, two-component flow in pipes. Chem. Eng. Prog. 1949, 45, 39–48. [Google Scholar]
- Abu-Hamdeh, H.N.; Bantan, R.A.R.; Alimoradi, A. Thermal and hydraulic performance of the twisted tube bank as a new arrangement and its comparison with other common arrangements. Chem. Eng. Res. Des. 2020, 157, 46–57. [Google Scholar] [CrossRef]
- Wu, C.C.; Chen, C.K.; Yang, Y.T.; Huang, K.H. Numerical simulation of turbulent flow forced convection in a twisted elliptical tube. Int. J. Therm. Sci. 2018, 132, 199–208. [Google Scholar] [CrossRef]
- Tan, X.; Zhu, D.S.; Zhou, G.Y. Heat transfer and pressure drop performance of twisted oval tube heat exchanger. Appl. Therm. Eng. 2013, 50, 374–383. [Google Scholar] [CrossRef]
- Patankar, S.V.; Liu, C.H.; Sparrow, E.M. Fully Developed Flow and Heat Transfer in Ducts Having Streamwise-Periodic Variations of Cross-Sectional Area. J. Heat Transf. 1977, 99, 180–186. [Google Scholar] [CrossRef]
- Stalio, E.; Piller, M. Direct Numerical Simulation of Heat Transfer in Converging-Diverging Wavy Channels. J. Heat Transf. 2007, 129, 769–778. [Google Scholar] [CrossRef]
- Sahamifar, S.; Kowsary, F.; Mazlaghani, M.H. Generalized optimization of cross-flow staggered tube banks using a subscale model. Int. Commun. Heat Mass Transf. 2019, 105, 46–57. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures, Part 1: Coherent structures. Part 2: Symmetries and transformations. Part 3: Dynamics and scaling. Q. J. Mech. Appl. Math. 1987, 45, 561–590. [Google Scholar]
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Amsallem, D.; Cordial, J.; Carlberg, K.; Farhat, C. A method for interpolating on manifolds structural dynamics reduced-order models. Int. J. Numer. Methods Eng. 2009, 80, 1241–1258. [Google Scholar] [CrossRef]
- Mosquera, M.R.; Hamdouni, A.; El Hamidi, A.; Allery, C. POD basis interpolation via Inverse Distance Weighting on Grassmann manifolds. Discret. Contin. Dyn.-Syst.-S 2018, 12, 1743–1759. [Google Scholar] [CrossRef] [Green Version]
- Mosquera, R.; El Hamidi, A.; Hamdouni, A.; Falaize, A. Generalization of the Neville–Aitken interpolation algorithm on Grassmann manifolds: Applications to reduced order model. Int. J. Numer. Methods Eng. 2021, 93, 2421–2442. [Google Scholar] [CrossRef]
- Oulghelou, M.; Allery, C. A fast and robust sub-optimal control approach using reduced order model adaptation techniques. Appl. Math. Comput. 2018, 333, 416–434. [Google Scholar] [CrossRef]
- Oulghelou, M.; Allery, C. Non-intrusive reduced genetic algorithm for near-real time flow optimal control. Int. J. Numer. Methods Fluids 2020, 92, 1118–1134. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Roser, R. Modélisation Thermique de Bouilleurs à Tubes Horizontaux. Etude Numérique et Validation ExpéRimentale. Ph.D. Thesis, Université de Provence Aix-Marseille 1, Marseille, France, 1999. [Google Scholar]

| Value | |
|---|---|
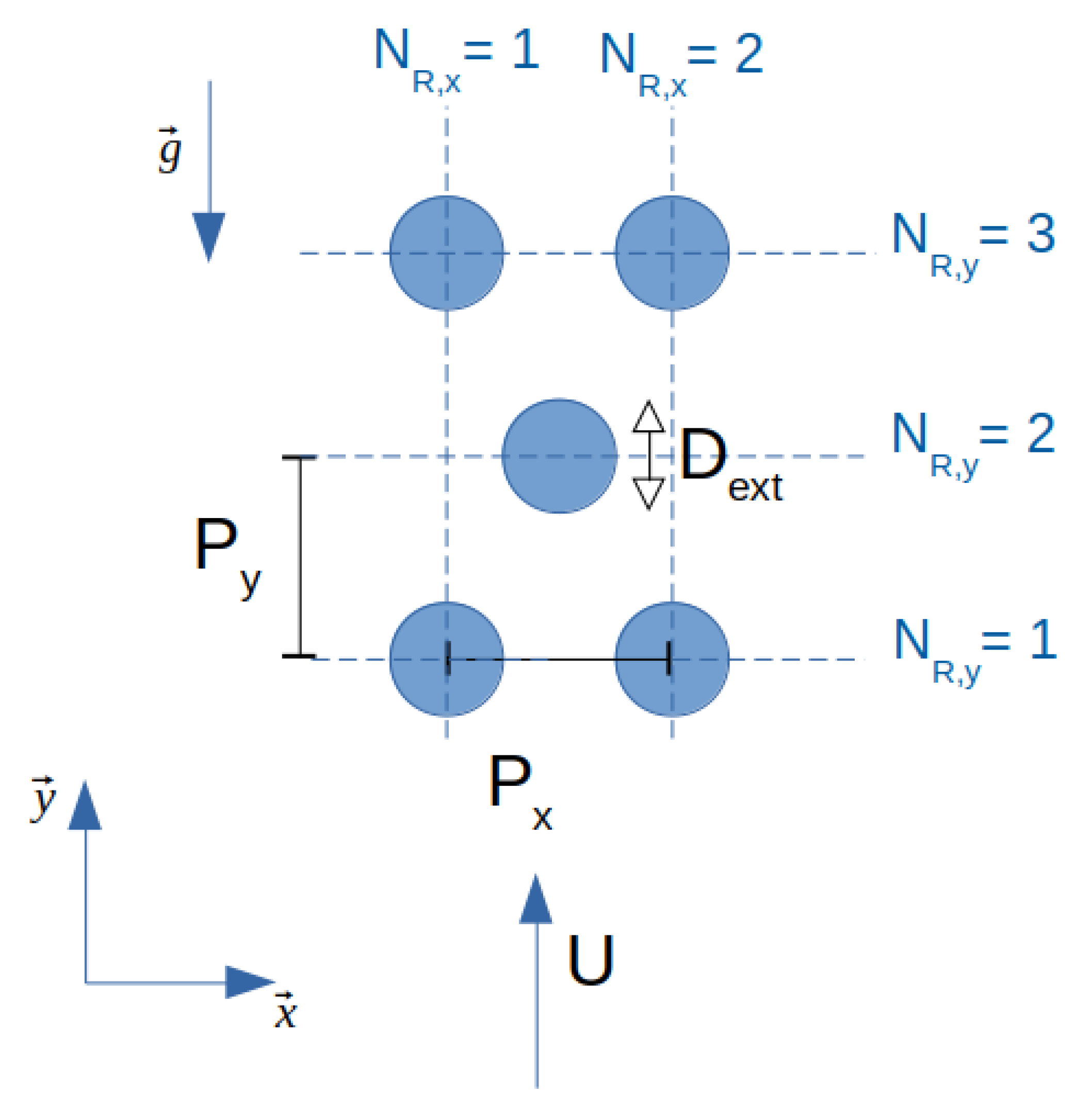
| Outer diameter of a tube [mm] | |
| Ratio [-] | |
| Pitch [mm] | |
| Pitch [mm] | |
| Width [mm] | |
| Height [mm] | 385 |
| Parameter | Uncertainty |
|---|---|
| Quality | |
| Void fraction | |
| Mass flux | |
| Frictional two-phase pressure drop |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubot, C.; Allery, C.; Melot, V.; Béghein, C.; Oulghelou, M.; Bonneau, C. Numerical Prediction of Two-Phase Flow through a Tube Bundle Based on Reduced-Order Model and a Void Fraction Correlation. Entropy 2021, 23, 1355. https://doi.org/10.3390/e23101355
Dubot C, Allery C, Melot V, Béghein C, Oulghelou M, Bonneau C. Numerical Prediction of Two-Phase Flow through a Tube Bundle Based on Reduced-Order Model and a Void Fraction Correlation. Entropy. 2021; 23(10):1355. https://doi.org/10.3390/e23101355
Chicago/Turabian StyleDubot, Claire, Cyrille Allery, Vincent Melot, Claudine Béghein, Mourad Oulghelou, and Clément Bonneau. 2021. "Numerical Prediction of Two-Phase Flow through a Tube Bundle Based on Reduced-Order Model and a Void Fraction Correlation" Entropy 23, no. 10: 1355. https://doi.org/10.3390/e23101355
APA StyleDubot, C., Allery, C., Melot, V., Béghein, C., Oulghelou, M., & Bonneau, C. (2021). Numerical Prediction of Two-Phase Flow through a Tube Bundle Based on Reduced-Order Model and a Void Fraction Correlation. Entropy, 23(10), 1355. https://doi.org/10.3390/e23101355





