Constraints on Non-Flat Starobinsky f(R) Dark Energy Model
Abstract
1. Introduction
2. Starobinsky f(R) Gravity in the Non-Flat Universe
3. Numerical Results
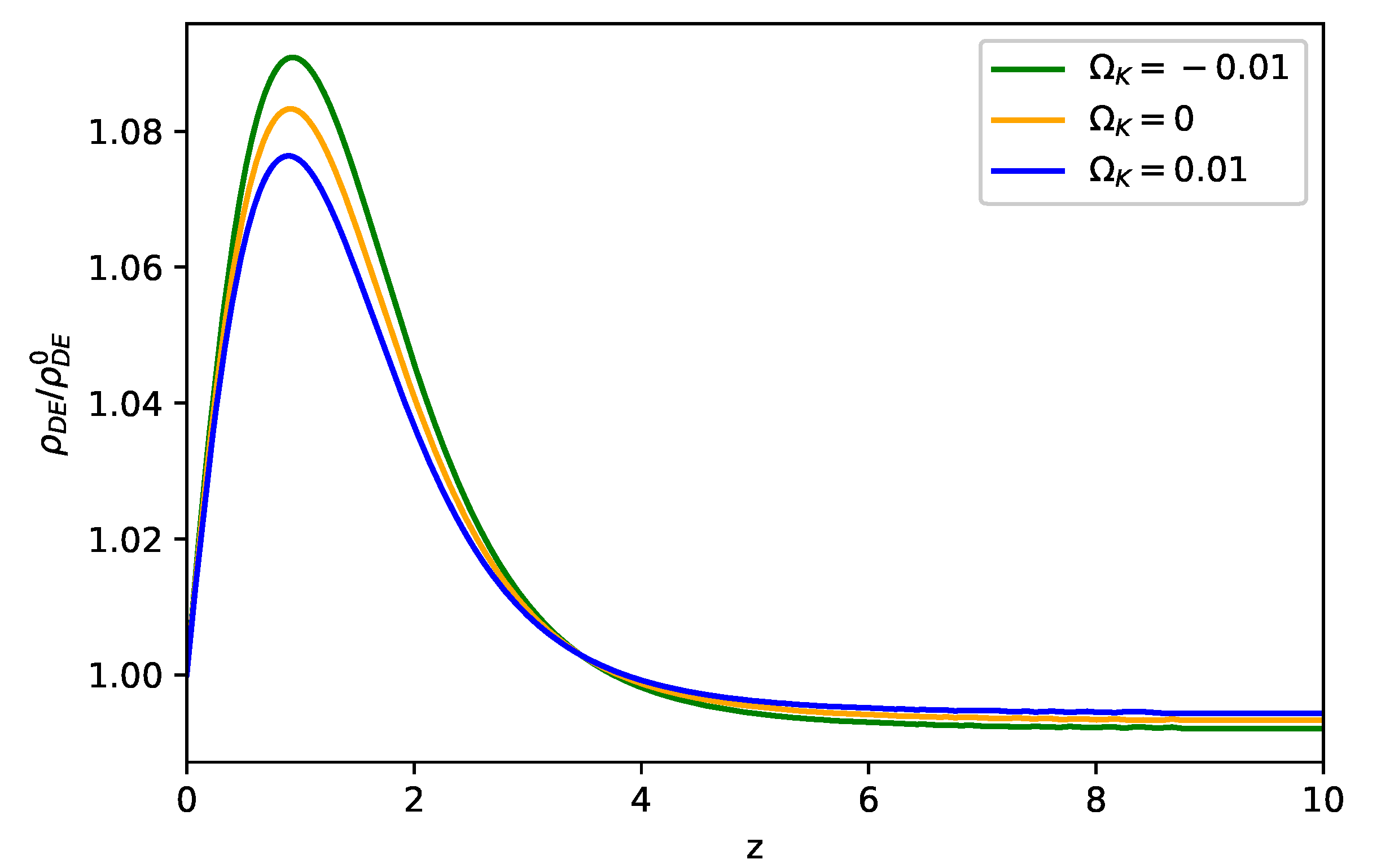
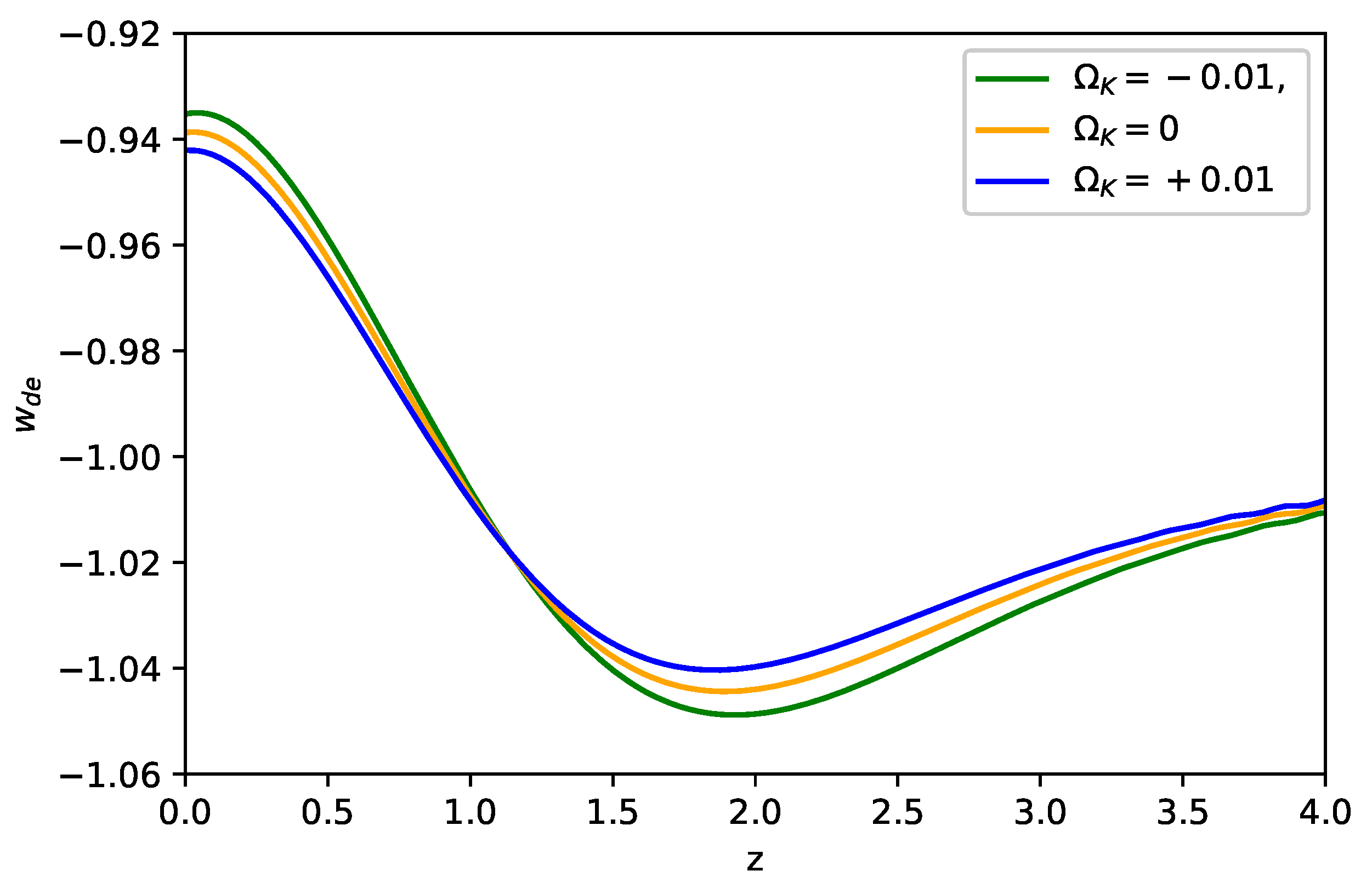
3.1. Cosmological Evolutions
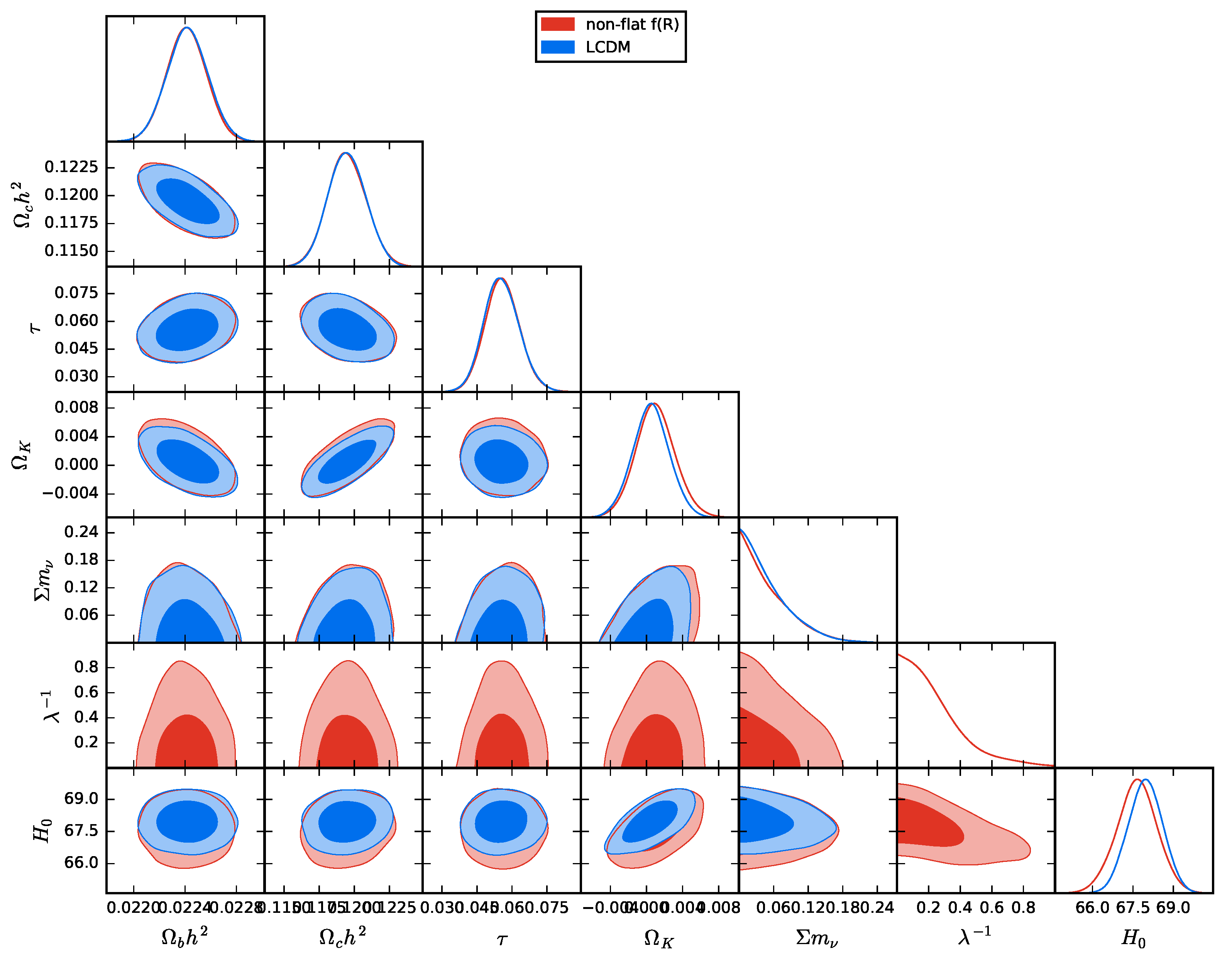
3.2. Global Fitting Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astron. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S. Planck 2018 results. V. CMB power spectra and likelihoods. Astron. Astrophys. 2020, 641, A5. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S. Planck 2018 results. VIII. Gravitational lensing. Astron. Astrophys. 2020, 641, A8. [Google Scholar]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S. Planck 2018 results. IX. Constraints on primordial non-Gaussianity. Astron. Astrophys. 2020, 641, A9. [Google Scholar]
- Beutler, F.; Blake, C.; Colless, M.; Heath Jones, D.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Baryon Acoustic Oscillations and the Local Hubble Constant. Mon. Not. R. Astron. Soc. 2011, 416, 3017–3032. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Shamir, M.F. Dark-energy cosmological models in f(G) gravity. J. Exp. Theor. Phys. 2016, 123, 607–616. [Google Scholar] [CrossRef]
- Munyeshyaka, A.; Ntahompagaze, J.; Mutabazi, T. Cosmological perturbations in f(G) gravity. Int. J. Mod. Phys. D 2021, 30, 2150053. [Google Scholar] [CrossRef]
- Silva, M.V.d.; Rodrigues, M.E. Regular black holes in f(G) gravity. Eur. Phys. J. C 2018, 78, 638. [Google Scholar] [CrossRef]
- Koch, B.; Reyes, I.A.; Rincón, Á. A scale dependent black hole in three-dimensional space–time. Class. Quant. Grav. 2016, 33, 225010. [Google Scholar] [CrossRef]
- Alvarez, P.D.; Koch, B.; Laporte, C.; Rincón, Á. Can scale-dependent cosmology alleviate the H0 tension? J. Cosmol. Astropart. Phys. 2021, 2021, 19. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, Á. Growth of structures and redshift-space distortion data in scale-dependent gravity. Eur. Phys. J. Plus 2021, 136, 622. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. Black holes in scalar-tensor gravity. Phys. Rev. Lett. 2012, 108, 081103. [Google Scholar] [CrossRef] [PubMed]
- Faraoni, V. de Sitter space and the equivalence between f(R) and scalar-tensor gravity. Phys. Rev. D 2007, 75, 067302. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Faraoni, V. A Bird’s eye view of f(R)-gravity. Open Astron. J. 2010, 3, 49. [Google Scholar] [CrossRef]
- Faraoni, V. f(R) gravity: Successes and challenges. arXiv 2008, arXiv:0810.2602. [Google Scholar]
- Nunez, A.; Solganik, S. The Content of f(R) gravity. arXiv 2004, arXiv:0403159. [Google Scholar]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, S0370157317301527. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. JETP Lett. 2007, 86, 157–163. [Google Scholar] [CrossRef]
- Kobayashi, T.; Maeda, K.-I. Relativistic stars in f(R) gravity, and absence thereof. Phys. Rev. D 2008, 78, 064019. [Google Scholar] [CrossRef]
- Frolov, A.V. A Singularity Problem with f(R) Dark Energy. Phys. Rev. Lett. 2008, 101, 061103. [Google Scholar] [CrossRef] [PubMed]
- Appleby, S.A.; Battye, R.A.; Starobinsky, A.A. Curing singularities in cosmological evolution of F(R) gravity. J. Cosmol. Astropart. Phys. 2010, 2010, 005. [Google Scholar] [CrossRef]
- Bamba, K.; Lopez-Revelles, A.; Myrzakulov, R.; Odintsov, S.D.; Sebastiani, L. Cosmic history of viable exponential gravity: Equation of state oscillations and growth index from inflation to dark energy era. Class. Quant. Grav. 2013, 30, 015008. [Google Scholar] [CrossRef]
- Bamba, K.; Nojiri, S.; Odintsov, S.D. Time-dependent matter instability and star singularity in F(R) gravity. Phys. Lett. B 2011, 698, 451–456. [Google Scholar] [CrossRef]
- Lee, C.C.; Geng, C.Q.; Yang, L. Singularity phenomena in viable f(R) gravity. Prog. Theor. Phys. 2012, 128, 415–427. [Google Scholar] [CrossRef][Green Version]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Planck evidence for a closed Universe and a possible crisis for cosmology. Nat. Astron. 2019, 4, 196–203. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Models of f(R) Cosmic Acceleration that Evade Solar-System Tests. Phys. Rev. D 2007, 76, 064004. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Rescaled Einstein-Hilbert Gravity from f(R) Gravity: Inflation, Dark Energy and the Swampland Criteria. Phys. Rev. D 2021, 103, 124028. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Unifying inflation with early and late dark energy epochs in axion F(R) gravity. Phys. Rev. D 2021, 103, 044036. [Google Scholar] [CrossRef]
- Lewis, A.; Challinor, A.; Lasenby, A. Efficient computation of CMB anisotropies in closed FRW models. Astrophys. J. 2000, 538, 473. [Google Scholar] [CrossRef]
- Lewis, A.; Bridle, S. Cosmological parameters from CMB and other data: A Monte Carlo approach. Phys. Rev. D 2002, 66, 103511. [Google Scholar] [CrossRef]
- Hojjati, A.; Pogosian, L.; Zhao, G.B. Testing gravity with CAMB and CosmoMC. J. Cosmol. Astropart. Phys. 2011, 08, 005. [Google Scholar] [CrossRef]
- Chen, Y.C.; Geng, C.Q.; Lee, C.C.; Yu, H. Matter Power Spectra in Viable f(R) Gravity Models with Dynamical Background. Eur. Phys. J. C 2019, 79, 93. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A.; Yokoyama, J. Future Oscillations around Phantom Divide in f(R) Gravity. J. Cosmol. Astropart. Phys. 2011, 2011, 006. [Google Scholar] [CrossRef]
- Efstathiou, G.; Bond, J.R. Cosmic confusion: Degeneracies among cosmological parameters derived from measurements of microwave background anisotropies. Mon. Not. R. Astron. Soc. 1999, 304, 75. [Google Scholar] [CrossRef]
- Howlett, C.; Lewis, A.; Hall, A.; Challinor, A. CMB power spectrum parameter degeneracies in the era of precision cosmology. J. Cosmol. Astropart. Phys. 2012, 1204, 027. [Google Scholar] [CrossRef]
- Ross, A.J.; Samushia, L.; Howlett, C.; Percival, W.J.; Burden, A.; Manera, M. The clustering of the SDSS DR7 main Galaxy sample—I. A 4 per cent distance measure at z = 0.15. Mon. Not. R. Astron. Soc. 2015, 449, 835. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.-H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Rezaei, M.; Malekjani, M. Comparison between different methods of model selection in cosmology. Eur. Phys. J. Plus 2021, 136, 219. [Google Scholar] [CrossRef]
- Liddle, A.R. Information criteria for astrophysical model selection. Mon. Not. R. Astron. Soc. 2007, 377, L74. [Google Scholar] [CrossRef]
| Parameter | Prior |
|---|---|
| model parameter | |
| Curvature parameter | |
| Baryon density | |
| CDM density | |
| Optical depth | |
| Neutrino mass sum | eV |
| Scalar power spectrum amplitude | |
| Spectral index |
| Parameter | Starobinsky | CDM |
|---|---|---|
| eV | eV | |
| − | ||
| Model | AIC | AIC | BIC | BIC | DIC | DIC | |
|---|---|---|---|---|---|---|---|
| CDM | 0 | 0 | 0 | ||||
| Starobinsky |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, C.-Q.; Hsu, Y.-T.; Lu, J.-R. Constraints on Non-Flat Starobinsky f(R) Dark Energy Model. Entropy 2021, 23, 1320. https://doi.org/10.3390/e23101320
Geng C-Q, Hsu Y-T, Lu J-R. Constraints on Non-Flat Starobinsky f(R) Dark Energy Model. Entropy. 2021; 23(10):1320. https://doi.org/10.3390/e23101320
Chicago/Turabian StyleGeng, Chao-Qiang, Yan-Ting Hsu, and Jhih-Rong Lu. 2021. "Constraints on Non-Flat Starobinsky f(R) Dark Energy Model" Entropy 23, no. 10: 1320. https://doi.org/10.3390/e23101320
APA StyleGeng, C.-Q., Hsu, Y.-T., & Lu, J.-R. (2021). Constraints on Non-Flat Starobinsky f(R) Dark Energy Model. Entropy, 23(10), 1320. https://doi.org/10.3390/e23101320






