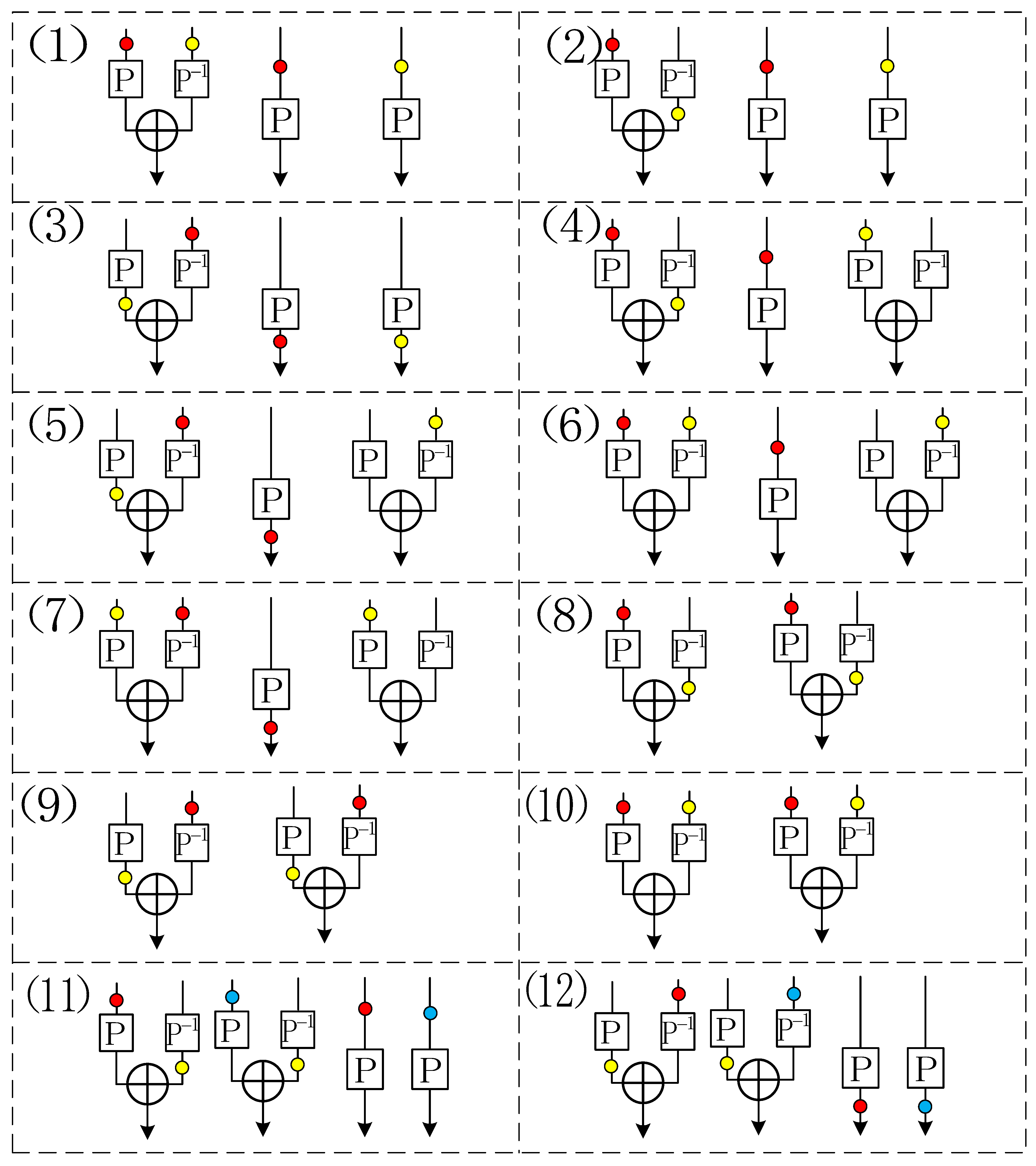
Proof. Given a good transcript
, we define the following probability
By a simple combinatorial argument, it holds that
We first introduce some subsets of
as follows:
Note that
,
, and
has been defined in (C-17). In fact, these sets form a partition of
.
Proposition 2. Let be a good transcript. Then defined above are pairwise disjoint.
Proof. By the definition of these five subsets, it holds that , , and . Since does not satisfy (C-1), one has . Besides, (resp. ) holds since does not satisfy (C-6) (resp. (C-7)). Finally, since . □
We use
,
,
,
, and
to denote the events
, and
, respectively. Note that
is equivalent to
. Therefore, it holds that
where
and
The next goal is to lower bound and .
. Conditioned on
,
P is fixed on exactly
p input-output pairs from
U to
V. For each
, there exists a unique
satisfying
. Hence,
. Then we define two sets:
All values in
(resp.
) are distinct since
does not satisfy (C-11) (resp. (C-6)). Moreover, since
and
, one has
and
respectively.
For each
, there exists a unique
satisfying
. In this case,
. Then we can define two sets:
All elements in
(resp.
) are distinct since
does not satisfy (C-7) (resp. (C-12)). Due to the fact
and
, one has
and
, respectively. Moreover,
(resp.
) since
(resp.
). Besides, it holds that
and
. Therefore, one can obtain that
Now, we can define two disjoint collections and . In this case, P is fixed on exactly input-output pairs from to .
. When conditioned on
, we next lower bound the number of all possible “new” and distinct input-output pairs of
P such that the event
happens. First, one can define some multi-sets associated to
and
as follows:
Let
,
,
, and
. For convenience, we rewrite these sets as:
Let
,
,
, and
. These sets can be written more clearly as:
Recall that
and
. Then, we get
Similarly, it also holds that
and
. Since
, there exists no repeated items in
and
. Hence, one can conclude that
and
. Now we define two multi-sets associated to
as
By the definition of
, there exists no repeated items in
and
. Based on these two sets, one can define two corresponding sets as:
Set and as two set collections. Then we can conclude the following proposition.
Proposition 3. With notations as above, one has
- (i)
All sets in (resp. ) are disjoint, i.e., , , and (resp. , , and ).
- (ii)
is inner disjoint with , and is inner disjoint with .
Proof. We first prove (i). From the fact , we have . By the definition of and , one can conclude that . holds due to the fact , and the disjoint property of and . We can conclude that , , and in a similar way.
Next we prove (ii) by enumerating all possible cases. For , the definition of means that ; comes from the fact ; holds due to the disjoint property between and , and the fact . For , comes from the fact , and the definition of ; comes from the fact ; By the disjoint property between and , and the fact , we have . For , the definition of means ; comes from the fact that ; By the disjoint property between and , and the fact , we has .
For , comes from the fact , and the definition of ; can be derived from the disjoint property between and , and the fact ; The fact means . For , holds from definition of ; comes from the definition of , and the fact ; The fact means . For , comes from definition of ; holds due to the disjoint property between and , and the fact ; Finally the fact means . □
Now we define two disjoint union sets (which equals to in (C-17)), and (which equals to in (C-17)).
Let
(actually,
) and
. Then it holds that
if
. Next we try to sample “new” values for
and
by allowing that there exist many construction queries
such that
or
holds. In the first case, we can obtain three maps like
In the second case, we have
If
and
, or
and
, then the above permutation maps are compatible with
and
. Intuitively, when we consider the above “collision” maps, there would be as many permutations chosen to be compatible with
and
as possible so that our construction can achieve BBB security.
Conditioned on , we next describe all possible permutations satisfying , and finally compute and lower bound .
For each
, we define the following set
where for each
, one has
(resp.
) for some query
and
(resp.
) for another query
.
Definition 2. We say a “good” set if the following four conditions are all satisfied
- (1)
,
- (2)
,
- (3)
, for any ,
- (4)
, for any .
The next lemma shows that for each , the number of all possible “good” sets derived from is close to .
Lemma 7. Assume that and . Let α be an integer with . Let be the number of all “good” sets derived from . Then we havewhere . Proof. We count all possible pairs in a “good” set step by step as follows. First, we decide all possible pairs for . There are possible pairs to be chosen for . Since , there are at most pairs not satisfying the first two conditions in Definition 2. Then we can choose at least possible pairs for .
After choosing
, we decide all possible
in the following way. We first choose
from the remaining
possible pairs, and then choose the corresponding pair
outside of
,
, and
to satisfy all four conditions in Definition 2. To satisfy the last two conditions
and
in Definition 2,
and
should chosen such that
In this case, from the definition of
and the fact
, it excludes at most 3 possibilities to be chosen for
. Then there are at least
possibilities to be chosen for
, when we only consider the last two conditions in Definition 2. Finally, from the fact
, there are at most
pairs to be removed for all possibilities
if we want them to satisfy the first two conditions
and
in Definition 2. Overall, there are at least
possible pairs to be chosen for
.
After choosing pairs , …, , there are at least possible pairs to be chosen for by repeating the above step.
When we finish the choice of all possible cases for
,
satisfying all four conditions in Definition 2, one can conclude that
where the term
appears because the set
S is unordered.
Furthermore,
can be lower bounded as follows
where (i) follows as
, (ii) follows as
, (iii) follows as
, and (iv) follows as
if
. □
For a fixed
with
and a corresponding “good” set
the following assignment (34) for
P is well-defined by the definition of
S:
Furthermore, based on the “good” set
S, we define two subsets of
and
as
Besides, we can also denote two additional sets as
where
(resp.
) and all items in
(resp.
) are distinct. After the assignment (34) for
P,
P is fixed on
input-ouput pairs from
to
. In addition, we can define the corresponding co-subset of
and
as
and
, respectively.
Until now, the random permutation P is fixed on p input-output pairs from U to V, input-output pairs from to , input-output pairs from to , and input-output pairs from to . Based on these facts, the next work is to choose all other possible compatible items for , , , , and to extend the fixed input-output pairs of P.
Note that once the items in are fixed, the corresponding items in are uniquely determined since these two sets are both derived from . Similarly, the items in (resp. ) uniquely determine the items in (resp. ). Then we sample all possible items for these sets through three steps.
.
Let and . The size of is , and the size of is . Recall that and . Let be the number of distinct tuples in such that the following two conditions are satisfied
- (i)
, for each where , .
- (ii)
with , for each , should be satisfied for each .
Now we count the number of all possible distinct tuples
satisfying these two conditions. First, one has
. The first condition can remove at most
items for each
k, and the second condition can exclude at most
values for each choice of
. By the choice of
above, we obtain that
Let and . The first condition ensures that is disjoint with . Items in are distinct due to the second condition and the fact . This fact tells us that for each and , it holds that but , which means that . Moreover, items in are distinct, and is disjoint with by the choice of . Let , and . The size of is , and the size of is .
.
Recall that . Let be the number of all distinct tuples in satisfying the following two conditions:
- (i)
, for each , .
- (ii)
with , for each , should be satisfied for each .
Now we count the number of all possible distinct tuples
satisfying these two conditions. Similarly, one has
. The first condition can remove at most
values for each
k, and the second condition can exclude at most
items for each choice of
. By the choice of
, we obtain that
Let , and . It holds that items in are distinct. Furthermore, is disjoint with by the choice of . Let , and . The size of is , and the size of is .
.
Let
(
). Let
m be the number of all distinct tweaks appearing in
, and then we use
to denote these
m distinct tweaks. We denote
and
. In this case, it holds that
. For convenience to count, we denote
and rewrite the items in
indexed by the
m distinct tweaks as
For
and
, denote
For convenience, and can be written as and , respectively. Let be all possible different tuples in such that the following two conditions are satisfied.
- (i)
For each and , .
- (ii)
For each and , is distinct from the values for and . Furthermore, should be distinct from the values for with .
Except these two conditions, each
must be different from each other. By a simple computation, one has
, where
and
. So
. Now we bound the number of all possible distinct tuples
satisfying these two conditions. The first condition excludes at most
values, and the second condition excludes at most
values for each choice of
. Furthermore,
should not be same as any one of previous
items. By combining these facts, one can conclude that
Overall, by combining (
33), (
35), (
36), and (
37), one has
By combining (
32) and (
38), we have
Recall that
By combining (
39) and (
40), we conclude that
where
follows as
.
Lower bounds on
,
, and
are given in
Appendix D, and the results are showed as follows:
where
,
, and
.
Putting (
42), (
43), and (
44) into (
41), we obtain
The last term in (45) can be bounded as
where
follows as Markov’s inequality and
follows as
which comes from the assumption
and the fact
. Let
. Then we can write (
45) as
Combing all these facts together, the proof of Lemma 6 is finished. □