Abstract
Many image encryption schemes based on compressed sensing have the problem of poor quality of decrypted images. To deal with this problem, this paper develops an image encryption scheme by multiscale block compressed sensing. The image is decomposed by a three-level wavelet transform, and the sampling rates of coefficient matrices at all levels are calculated according to multiscale block compressed sensing theory and the given compression ratio. The first round of permutation is performed on the internal elements of the coefficient matrices at all levels. Then the coefficient matrix is compressed and combined. The second round of permutation is performed on the combined matrix based on the state transition matrix. Independent diffusion and forward-backward diffusion between pixels are used to obtain the final cipher image. Different sampling rates are set by considering the difference of information between an image’s low- and high-frequency parts. Therefore, the reconstruction quality of the decrypted image is better than that of other schemes, which set one sampling rate on an entire image. The proposed scheme takes full advantage of the randomness of the Markov model and shows an excellent encryption effect to resist various attacks.
1. Introduction
With the rapid development of internet technology, digital images are widely used in all walks of life. As images can intuitively display information, they are widely used in banking, the military, medicine, finance, and other fields. Once images containing important information spread on the internet, they are likely to be attacked and cracked by hackers. To make meaningful images meaningless through encryption can effectively protect the security of private information in transmission and storage.
Technology applied to image encryption includes chaotic systems [1,2,3,4,5,6,7,8], cellular automatons [9,10,11], substitution boxes [12,13,14], DNA encoding [15,16,17,18,19,20], elliptic curves [21,22,23,24], finite-precision error [25], Galois field [26] and quantum computing [27,28]. The chaotic system is most popular in the field of image encryption and is continuously improved, such as symmetric chaotic maps [29] and adaptive chaotic maps [30,31]. In particular, the improvement of the traditional one-dimensional chaotic system [1,2,3,12,32] enhances the encryption effect. Therefore, we choose several chaotic systems with excellent encryption effects to generate chaotic sequences.
The combination of compressed sensing (CS) theory and image encryption algorithms, by which an image is simultaneously compressed and encrypted, has seen much research. The most special advantage of compressed sensing is that it can reduce data redundancy. Before data transmission, if the cipher image can be further compressed, it will not only improve the transmission efficiency but also be more suitable for transmission channels with limited bandwidth. Moreover, because the sampling process of compressed sensing is a linear random projection process, in the presence of noise, the target sparse signal can be reconstructed with high probability through a greedy algorithm or an optimized algorithm. This not only protects the security of information but saves bandwidth, time, and storage space. There are both one-dimensional (1D) [33,34,35,36] and two-dimensional (2D) compressed sensing [37], and encryption schemes for both single [33,38] and multiple images [39,40]. Chai et al. [39] proposed a scheme to compress and encrypt two color images at the same time through parallel operations on their RGB components, which improves efficiency and enhances security. To further reduce the bandwidth and computing load, Fan et al. [41] proposed an algorithm combined with vector quantization (VQ) and CS, distinguishing important and secondary information. Important data are extracted by a VQ compression algorithm, and the secondary data are compressed by a CS algorithm, so as to achieve higher compression efficiency. However, many encryption schemes are generated based on traditional compressed sensing theory, using one sampling rate for the whole image and a single measurement matrix to measure it, which is neither efficient nor safe enough [33,34,35,36,38,42]. Additionally, when the compression ratio is low, the reconstructed image after decryption has a poor visual effect.
Many effective encryption schemes with improved efficiency have been proposed. Wang et al. [43] proposed a scheme based on parallel compressive sensing (PCS) combined with count mode, where the measurement matrix is updated by continuously updating the key values. At the same time, the sampling object is reduced from the whole image matrix to a single column vector. Therefore, this scheme cannot only improve the efficiency but can effectively resist the chosen plain attack (CPA). Wen et al. [40] reduced the scale of single sampling by applying the semi-tensor product (STP) to the process of compressed sensing, employing the STP strategy for the sparse matrix of the plain image and measurement matrix, and cascading multiple images after compression into the main image for image encryption, reducing the storage scale of the measurement matrix and data transmission. To reduce the computation scale and improve security, Zhu et al. [44] designed the BCS-CRP framework, which divides the image coefficient matrices obtained by wavelet transform into blocks, using the coefficient random permutation (CRP) strategy to confuse each coefficient vector, with a good encryption effect according to simulation results.
The quality of a reconstructed image is improved mainly from two aspects. One aspect is to change the method of wavelet decomposition and image reconstruction. Chai et al. [33] designed a contrast experiment by combining different wavelet decomposition methods two-dimensional discrete cosine transform (DCT2), discrete wavelet transform (DWT) and different reconstruction algorithms smoothed l0 norm (SL0), orthogonal matching pursuit (OMP) to encrypt and decrypt an image. Experimental results showed that the adoption of DWT was more helpful for decryption. The other aspect is to optimize the measurement matrix through singular value decomposition (SVD) and optimization. The modified measurement matrix can satisfy the RIP condition of compressed sensing theory with high probability, which greatly improves the reconstruction quality of the decrypted image. Chai et al. [39] designed an algorithm to optimize the measurement matrix by SVD, and verified by simulation experiments that using the optimized measurement matrix to measure the image, the final decrypted image quality is better than without optimization.
Many encryption schemes fail to fully consider the information distribution characteristics of natural images, resulting in poor reconstruction quality of decrypted images. Gan et al. [10] used a circular matrix to construct the measurement matrix, with only one sample rate set for sampling the whole image matrix in each encryption process. From their experimental results, the values of the peak signal to noise ratio (PSNR) between the plain images and corresponding decrypted images at different sampling rates were not high enough, and as the sampling rate increased, the increase in PSNR was not large. Luo et al. [28] decomposed the image matrix into four coefficient matrices firstly, then retained the low-frequency matrix and used two measurement matrices generated by two different sampling rates to compress the remaining coefficient matrices separately. Their proposed scheme obtained the decrypted image with higher reconstruction quality under the same compression ratio. Based on the premise that different sampling rates should be set for coefficient matrices of different frequencies, we apply the theory of multiscale block compressed sensing to the design of an image encryption scheme. The low-frequency coefficient matrix of an image is fully sampled, and different sampling rates are set for the remaining coefficient matrices according to the amount of information they carry. There is a significant improvement in the reconstructed image after decryption. Different from the traditional encryption algorithms like DNA coding [15,16], cellular automata [9,10], and substitution box [12,13] that follow generally known rules to carry out the subsequent work, this paper introduces the Markov model in machine learning, and the scrambling process is carried out according to the information of the plain image and chaotic sequences. Experimental results show that the proposed scheme achieves a good encryption effect.
Our contributions are as follows.
- An encryption architecture of permutation, compression, secondary scrambling, and diffusion is designed, which shows good compression performance and guarantees security;
- A transition probability matrix in a Markov model is introduced to scramble the image and define the state space according to the characteristics of image pixel values in the encryption process. The state transition probability matrix is constructed based on the distribution of pixel values. The process achieves good randomness, so it is difficult to predict;
- Information about plain images and chaotic sequences is used in the encryption process, giving the scheme high plain sensitivity to resist known-plaintext attacks (KPAs) and chosen-plaintext attacks (CPAs);
- Multiscale block compressed sensing theory is introduced, sampling rates of images are set by a more reasonable approach, and the reconstruction quality of decrypted images is greatly improved.
2. Materials and Methods
2.1. Multiscale Block Compressed Sensing
Fowler et al. [45] proposed a multiscale block compressed sensing algorithm based on a wavelet domain. The MS-BCS-SPL algorithm divides the image into blocks based on the BCS algorithm and samples each image sub-block with a different matrix. The original image is decomposed by a multilayer wavelet transform, and the wavelet coefficients of each layer are divided into blocks whose size varies with the number of layers. A measurement matrix, determined by the sampling rate of each layer, is used for measurement. Since the different levels of wavelet decomposition have different importance to the final image reconstruction quality, each layer corresponds to a different sampling rate. The smooth projection Landweber method is used to reconstruct each image block; thus, the complete reconstructed image can be obtained.
As the main information of an image is concentrated in the low-frequency coefficient after wavelet decomposition, its details are concentrated in high-frequency coefficients. To improve the reconstruction quality of an image requires one to keep the low-frequency part of the image and abandon the high-frequency part as much as possible. The measurement matrix A of the original image is decomposed into multiscale transformation matrix and multiscale measurement matrix , and A is represented by , so the compression process can be expressed as
The multiscale transformation matrix is decomposed by an L-level wavelet transform to form L measurement operators, which constitute the multiscale block measurement matrix . The wavelet decomposition process of the original image x can be expressed as
The s-th sub-band of is cut into sub-blocks of size , each sampled by a sampling matrix of corresponding size. For example, the process of compressing the j-th sub block can be expressed as
After the original image is decomposed, the influence of the decomposition block of each layer on the image reconstruction is different. To improve the reconstruction quality of the image, it is necessary to set the corresponding sampling rate for each wavelet decomposition layer. Let the baseband sampling rate of wavelet decomposition be 1, so , and the wavelet decomposition sub-rate of each layer can be expressed as
where is the weight of each layer after wavelet decomposition in the whole image, i.e.,
For the whole image, the sampling rate can be expressed as
If the sampling rate S of the whole image and the weight of each wavelet decomposition layer are known, then the total sampling rate can be calculated by Equation (6). The sampling rate of the l-th level wavelet decomposition coefficient can be obtained by substituting in Equation (4). When solving for the sampling rate of each layer after wavelet decomposition, there will be multiple solutions greater than 1. In practice, the sampling rate of each layer should not be greater than 1, so such solutions should be set to 1. In this case, the sampling rate is expressed as
We recalculate from Equation (7). The above process is repeated for the wavelet decomposition of each layer , and we check for to ensure that in each layer.
2.2. Chaotic Systems
The tent-logistic-tent system (TLTS) and tent-sine-tent system (TSTS) are, respectively, obtained as [32]
where is the control parameter of the TLT and TST chaotic systems. When r is greater than 1.05, the LE value of the chaotic system is positive, i.e., the system is in a chaotic state.
The hybrid chaotic system [12] is defined as
where is the control parameter of the hybrid chaotic map. When r is greater than 1.1, the LE value of the chaotic system is positive, i.e., the system is in a chaotic state.
We use the three chaotic systems to generate three measurement matrices, respectively.
A new chaotic system-improved sine-exponent-logistic(ISEL) is obtained as [46]
where , , are the control parameters of the ISEL system. We use this system to generate chaotic sequences for diffusion.
2.3. Markov Model
The Markov model can be used to simulate random processes [47]. In our scheme, a Markov chain is used to construct the state transition matrix for scrambling the image matrix.
2.3.1. State Space
In the Markov chain, every variable has several possible values, and the set of all these is called the state space. To generate this, numbers are divided into four categories in our scheme:
If the integer part of a number is positive and odd, then it is a positive-odd (po-od) number;
If the integer part of a number is negative and odd, then it is a negative-odd (ne-od) number;
If the integer part of a number is positive and even, then it is a positive-even (po-ev) number;
If the integer part of a number is negative and even, then it is a negative-even (ne-ev) number.
2.3.2. Markov State Transition Matrix
Obviously, since there is more than one state at each time, there are several cases of transferring from the previous to the current state. All conditional probabilities form a transition probability matrix, as shown in Table 1. Here, is the state at the previous time, is the state at the current time, and is the conditional probability from to .

Table 1.
Transition probability matrix.
According to the above definition, the header of the state transition matrix is constructed.
Next, we initialize a matrix f of size 4 × 4, which is used to record the frequency of state transition. For each column vector of the matrix to be measured, we first determine the type of the first element, i.e., the row coordinate of the state transition matrix. Then the type of the next element is determined, i.e., the column coordinate of the state transition matrix. The position in the matrix f corresponding to the coordinate point is incremented by 1 to obtain the updated matrix f. For example, the matrix to record the frequency of state transition is shown in Table 2. We calculate the sum of four frequencies in each row of the matrix f, respectively, which means the total frequency of transitions from one type of number to other types of number. Each element is divided by the sum of the corresponding row to get a probability, which means the transition probability from one type of number to another type of number. After all probabilities are calculated, the row-based state transition probability matrix (RSTPM) is obtained, as shown in Table 3. The generation process of the column-based state transition probability matrix (CSTPM) is similar to that of RSTPM, where we get a row vector instead of a column vector of the matrix.

Table 2.
State transition frequency matrix.

Table 3.
State transition probability matrix.
For RSTPM, we find all positions of the probabilities greater than 0.25 of the matrix shown in Table 3. The row coordinates indicate whether odd- or even-column vectors are to be selected, and whether the direction of movement is up or down. If the row coordinate is odd (even), then odd (even)-column vectors are selected; if the row coordinate is positive (negative), then all selected elements move up (down). Specifically, if the row coordinate is a po-od (ne-od) number, then all odd-column vectors move up (down), and if the row coordinate is a po-ev (ne-ev) number, then all even-column vectors move up (down). The column coordinates indicate the number of cyclic shifts, whose values are generated by the chaotic map.
For CSTPM, we find all positions of the probabilities greater than 0.25 of the matrix like Table 3. The row coordinates indicate whether odd- or even-row vectors are to be selected, and whether the direction of movement is left or right. If the row coordinate is odd (even), then the odd (even)-row vectors are selected, and if the row coordinate is positive (negative), then all selected elements move left (right). Specifically, if the row coordinate is a po-od (ne-od) number, then all odd-row vectors move left (right), and if the row coordinate is a po-ev (ne-ev) number, then all even-row vectors move left (right). The column coordinates indicate the number of cyclic shifts, whose values are generated by the chaotic map.
3. Scheme Based on Multiscale Block Compressed Sensing
The proposed encryption scheme is shown in Figure 1. The image is decomposed by discrete wavelet transform to get the coefficient matrices, and each coefficient matrix is scrambled for the first time and measured by the corresponding measurement matrix. After compression, all matrices of measurement values are merged, and that matrix is scrambled by state transition matrices. The final cipher image is obtained by diffusion.
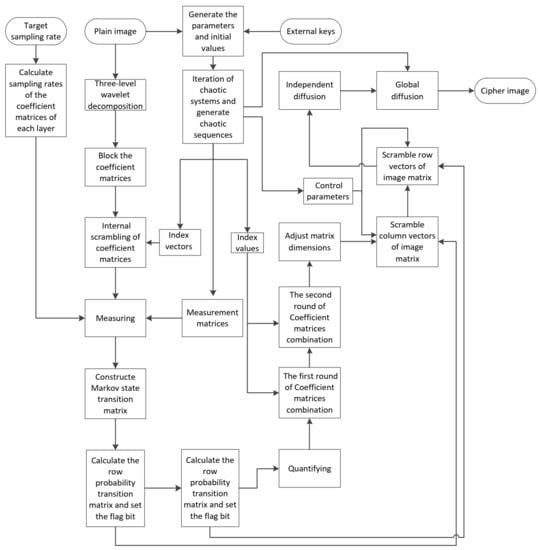
Figure 1.
Flowchart of image encryption process.
3.1. Encryption Process
3.1.1. Generating Parameters and Initial Values for Chaotic System
The encryption process should be closely related to plain information to make it resistant to known- and chosen-plaintext attacks. The hash value K of the plain image is generated by the SHA256 function. K is converted to binary numbers, and 32 groups of these are generated by dividing every eight bits into a group,
We count the number of zeros, number L of ones, length of the longest continuous zero sequence, and length of the longest continuous ones sequence in the hash value K as , , , and , respectively, and
We construct
and find their Kronecker product,
where represents the Kronecker product operator,
represents rounding down, and represents the i-th element of matrix .
3.1.2. Calculating Sampling Rates Based on Multiscale Block Compressed Sensing Theory
Given the target sampling rate, the sampling rate sequences of the coefficient matrices of each layer after wavelet decomposition are calculated according to Equations (4)–(7), and denoted as subrates. In this paper, the image is decomposed by three-level wavelet transform, and there are three sampling rates.
3.1.3. Generating the Measurement Matrix
In Section 3.1.1, all parameters and initial values of chaotic maps were generated, then and were brought into Equation (9), with iterations; and were brought into Equation (8), with iterations; and were brought into Equation (10), with iterations. The sinusoidal value of the initial value is multiplied by a small coefficient every 2000 iterations to disturb the initial value of the next iteration, and three chaotic sequences are finally generated after the first t numbers are discarded. , , and are one-dimensional vectors of length , , and , respectively, where are determined by the block sizes given in advance. To enhance the randomness of chaotic sequences, the generated chaotic sequences are further processed as
The generated chaotic sequences are transformed to matrix form,
and the corresponding orthogonal bases of , respectively, are used as redundant measurement matrices. The new row dimensions are obtained by multiplying the row dimensions of the redundant measurement matrices by the corresponding sampling rates. The first rows of are extracted as formal measurement matrices .
3.1.4. Encrypting the Plain Image
Step 1: After discrete wavelet decomposition of the original image, a low-frequency coefficient and nine high-frequency coefficients in horizontal, vertical, and diagonal directions are obtained. After three-layer wavelet decomposition, the ratio of the original image size to the block size of each layer is . The three-level wavelet decomposition is shown in Figure 2.
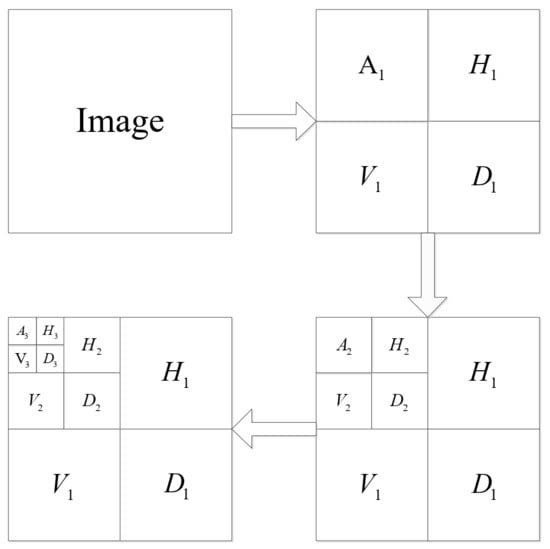
Figure 2.
Diagram of three-level wavelet decomposition.
Step 2: Given an array of length 3, the values of elements represent the block sizes. The third-, second-, and first-level wavelet decomposition coefficient matrices , , and are divided into blocks of , , and , respectively. Each block matrix is expanded to a column vector after partitioning. In this way, each block matrix in the third-, second-, and third-level wavelet decomposition coefficient matrices is transformed to a column vector of length , , and , respectively, and nine new coefficient matrices are constructed by merging the corresponding column vectors.
Step 3: The three chaotic sequences generated in Section 3.1.3 are sorted in ascending order to obtain the corresponding index sequences . The coefficient matrices , , and of the third-, second-, and first-level wavelet decomposition, respectively, are scrambled with , , and , respectively, to obtain , , and . For example, if is a matrix of size , we expand it to a sequence of length , i is the index of the i-th element in the sequence, and
where is the scrambled sequence of .
Step 4: The coefficient matrix remains unchanged. We compress the coefficient matrices , , and with , , and , respectively, to obtain corresponding measurement matrice s, , and , calculated by Equation (3).
Step 5: Coefficient matrices with the frequency of the three-level wavelet decomposition are combined to form the matrix to be measured,
To enhance the randomness, T is processed according to the information obtained in Section 3.1.1 to obtain
Step 6: According to the method proposed in Section 2.3.2, RSTPM and CSTPM are constructed according to the element information of matrix .
Step 7: The maximum and minimum values of nine coefficient matrices,, after wavelet decomposition, are obtained. The coefficient matrices are quantized to the interval [0,255],
where min and max are the minimum and maximum values, respectively, of M. The coefficient matrices are quantized to obtain corresponding matrices . The low-frequency coefficient matrix is decomposed by SVD to obtain three sub-matrices u,s,v of the same dimension, whose maximum and minimum values are obtained. The sub-matrices are quantized to the interval [0,255] by Equation (24) to obtain corresponding matrices U, S, VT.
Step 8: We combine the high frequency coefficients of each layer into groups in the same direction: are in the first group, are in the second group, and are in the third group. The index values are obtained using the chaotic sequences generated in Section 3.1.3,
That is, the index values , , and of the first through third groups, respectively, are determined by the last, penultimate, and antepenultimate elements of . The three index values are mapped to the interval [1,6], which indicates that there are six possible permutations for each group,
The first through third groups after sorting are being recorded as , , and , respectively, whose internal three block matrices are recorded as , , and .
Step 9: The quantization matrices U, S, and VT obtained from Step 7 are inserted in the first through third groups of matrices, respectively, after the first round of combination. The index values are obtained using the three chaotic sequences generated in Section 3.1.3,
That is, the index values , , and of the first through third groups, respectively, are determined by the first through third elements, respectively, of . At the same time, the three index values are mapped to the interval [1,4], which indicates that there are four possible permutations for each group: the top, the gaps between two adjacent block matrices, and the bottom,
We mark the first through third group matrices after combination as , , and , respectively, and combine them as
Step 10: The dimension of the matrix should be adjusted to prevent attackers from obtaining the information of the encryption scheme through the dimension of cipher images. Suppose the dimension of the merged matrix is . We find two factors and of such that , minimize , and adjust the dimension of the matrix to , obtaining the matrix information
Step 11: The parameters a, b, c and initial value generated in Section 3.1.1 are brought into Equation (11), iterating times, and the sinusoidal value of the initial state is multiplied by a small coefficient every 2000 iterations to disturb the initial value of the next iteration. The chaotic sequence V is generated after the first t numbers are discarded. To enhance the randomness, we determine the chaotic sequence
according to which we generate sub-sequences ,
The control parameters of the scrambling process are generated according to as
where are used for subsequent shift operations, fix is a function that rounds toward zero, and and are the largest prime factors of and , respectively.
Step 12: The scrambling operations are based on RSTPM, as generated in Step 6. The shift numbers are – when column coordinates are the po-od, po-ev, ne-od, and ne-ev numbers, respectively. The scrambling operations are shown in Table 4. The up arrow means move up, the down arrow means move down. We record the scrambled matrix as and set the initial transition flag bit matrix and all element values to zero. If the element of a position is shifted, then the flag bits of the corresponding position change from 0 to 1. Taking the state transition probability matrix generated in Table 3 as an example, the positions with probability values greater than 0.25 are in the ne-od number and po-ev number columns. That is, the probability values of the two middle columns are selected. Therefore, the flag bits of these two columns are set to 1.

Table 4.
Rule of column vector scrambling.
Step 13: The scrambling operations are based on CSTPM, as generated in Step 6. The shift numbers are , , , and , if the column coordinates are the po-od, ne-od, po-ev, and ne-ev numbers, respectively. We record the scrambled matrix as . We set the state transition flag bits in the same way. If the element of a position is shifted, then the flag bits of the corresponding position change from 0 to 1.
Step 14: The chaotic sequence generated in Step 11 is quantized to the interval [0,255] to get the new matrix . The matrix information and obtained in Step 10 is used to generate the chaotic sequences, is sampled at an interval of to obtain sequence , and is sampled at an interval of to obtain sequence ,
We take the position of the last element of sequence as the start position, and take the consecutive elements from sequence and record them as sequence ,
We perform an XOR operation between matrix and sequence ,
and denote as A.
Step 15: The matrix A is changed with front addition and a modular operation to obtain the matrix B, using the sequence generated in Step 14. We perform a cyclic left shift on B to obtain , i.e., and the definition of BitCircShift is shown in Algorithm 1.
is changed through back addition and a modular operation to get C, using the sequence generated in Step 14. We perform a cyclic left shift on C to obtain , i.e.,
At this point, the final cipher image is obtained.
| Algorithm 1. The BitCircShift Operation |
| Input: The number to be shifted x and the shift number k. Output: The number after shift y. |
| 1: if abs(k)>7 || k==0 then 2: yx 3: end if 4: if k>0 then 5: y1 mod 256 6: y2 floor() 7: else 8: y1 floor() 6: y2(x mod )× 9: end if 10: yy1 + y2 11: end |
3.2. Decryption Process
The image decryption scheme is the reverse of image encryption. The process is controlled by the key, including the initial values of chaotic systems, state transition flag bit matrix, and maximum and minimum of matrices, as received by the sender. The process is shown in Figure 3.
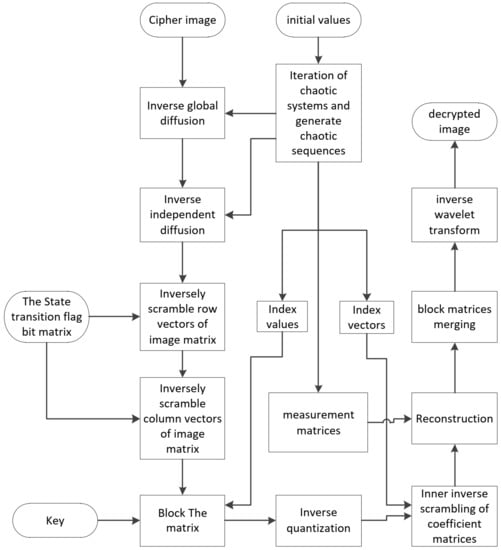
Figure 3.
Flowchart of image decryption process.
Step 1: The cipher image matrix is expanded to a sequence C, and then we perform a cyclic right shift operation on C to obtain D, which is changed with inverse back addition and a modular operation to get the sequence , using the sequence generated before,
We perform a cyclic right shift operation on to obtain E, which is changed with inverse front addition and a modular operation to get the sequence by using the sequence generated before,
Step 2: We perform an XOR operation between sequences and to obtain sequence ,
and transform to a matrix of size .
Step 3: is inversely scrambled according to the previously generated transition flag bit matrix, and we find the positions of its elements whose values are 1. We inversely scramble the matrix according to the rule described in Section 2.3.2. The matrix is recorded as after inversely scrambling row vectors, and that matrix’s column vectors are inversely scrambled to obtain .
Step 4: Find the positions of the U, S, VT and coefficient matrices in matrix according to and , then we divide the matrix into blocks to obtain them. The sub-matrices of low-frequency coefficient matrices U,S,VT are inversely quantized to obtain corresponding matrices , and the coefficient matrices are obtained by inverse quantization of corresponding matrices , where quantization is expressed as
where max and min are the maximum and minimum values, respectively, of M. The low-frequency coefficient matrix is obtained by calculating the product of the three sub-matrices,
Step 5: We first generate index vectors . Coefficient matrices , , and are inversely scrambled with , , and , respectively. For example, we expand of size to a sequence of length , whose i-th element is
where is the scrambled sequence of .
Step 6: We reconstruct the image with the SPL algorithm. The column vectors of the reconstructed coefficient matrices of each layer are restored to block matrices according to the corresponding block size. Block matrices of size , , and are, respectively, combined into third-, second-, and first-level wavelet decomposition coefficient matrices , , and , which are combined into a new matrix according to Figure 2.
Step 7: The matrix after inverse wavelet transform is the final decrypted image.
4. Simulation Results
4.1. Encryption and Decryption Results
Simulation experiments were carried out on a laptop computer with an Intel Core i5-6200U CPU at 2.3 GHz and 4 GB RAM, on the MATLAB R2015a platform. Images of size 512 × 512, including Lena, Goldhill, Cameraman, Peppers, Barbara, and Jet, were selected as test images. The external keys were . The array block_size, which determines the block sizes of the image matrix, was set to [8,16,32], i.e.,. The target sampling rate was 0.25. The experimental results of plain, cipher, and decrypted images are shown in Figure 4. The cipher images were meaningless and unrecognizable noise-like images with little connection to the plain images. Valid information about the original images cannot be obtained from the corresponding cipher images. The encryption scheme adjusted the dimensions of cipher images to 288 × 256, which further hid the information of the plain image and the encryption method. The decrypted images were meaningful images that could be clearly identified and were quite similar to the original images. Hence, the proposed scheme had good encryption and decryption effects.


Figure 4.
Experimental results: (a–f) plain images Lena, Goldhill, Cameraman, Peppers, Barbara, Jet; (g–l) corresponding cipher images; (m–r) corresponding decrypted images.
4.2. PSNR between Plain and Decrypted Images under Different Sampling Rates
The peak signal to noise ratio (PSNR) is used to objectively judge the quality of a decrypted image. A larger PSNR indicates a smaller difference between plain and decrypted images, and higher reconstruction accuracy. For gray images,
where M and N are the row dimension and column dimension of the image, and and are the pixel values of the plain image X and decrypted image Y, respectively, at position .
In this experiment, 512 × 512 images, including Lena, Cameraman, Peppers, and Couple, were selected as test images, and PSNR values between plain and decrypted images were measured at different sampling rates. Table 5 compares partial experimental results with those in Gan et al. [10]. The scheme of Gan et al. [10] adopts traditional compressed sensing theory, using one sampling rate for the whole image, which reveals that the distribution differences of image information between low- and high-frequency coefficients are not fully considered, and the resulting decrypted image does not have high reconstruction quality. The image reconstruction effect of the proposed scheme is better than that of the scheme in Gan et al. [10]. Table 6 compares some experimental results with those in Luo et al. [28]. In the latter, the plain image is first decomposed into approximate and detail components by discrete wavelet transform (DWT). All pixels in the approximate component are retained, and the remaining detailed components are measured by measurement matrices. A lower sampling rate is adapted to the horizontal direction decomposition coefficient (LH) and diagonal direction decomposition coefficient (HH), and a larger sampling rate is adapted to the vertical direction decomposition coefficient (HL). The reconstruction quality of the decrypted image is improved. However, there are some limitations because the sampling rates are set artificially. From Table 6, it can be seen that the proposed algorithm can better improve the reconstruction quality of the decrypted images.

Table 5.
PSNR (dB) of decrypted images at different sampling rates compared with another scheme.

Table 6.
Comparison of decrypted image quality of similar scheme at the sampling rate of 0.5.
4.3. Influence of Wavelet Basis on Image Reconstruction Effect (PSNR)
In this experiment, 12 images were decomposed by DWT in different wavelet bases, including the commonly used Symlets8, Haar, and CDF9/7. The PSNR values of the decrypted images were measured, with results as shown in Table 7. The experimental results show that the CDF9/7 wavelet base performs better in most cases; hence, this was chosen as the wavelet base.

Table 7.
Influence of different wavelet bases on image reconstruction effect (PSNR: dB).
4.4. Time Complexity Analysis
An algorithm should have fast encryption and decryption speeds to meet real-time needs. In this experiment, the plain image Lena with size of 512 × 512 was used as a test image, the sampling rate was set to 0.25, and the running time of each process of the scheme was measured. The results are shown in Table 8. In addition, the running times of the whole encryption process and decryption process at different sampling rates were also measured and the results are shown in Table 9. We can learn from the experimental result that the processes of iteration of chaotic systems and image reconstruction consume most of the time in the algorithm. Additionally, as the sampling rate increases, the encryption time also increases, but the decryption time is basically the same. More concretely, in encryption algorithm illustrated in Section 3.1, iteration of chaos includes Section 3.1.3 and Step 11 in Section 3.1.4, the compression process is Step 4 in Section 3.1.4, the first round of permutation is Step 3 in Section 3.1.4, the second round of permutation is Step 12 and Step 13 in Section 3.1.4, and the diffusion includes Step 14 and Step 15. The decryption process illustrated in Section 3.2 is the inverse process of the encryption process, and the compression process is replaced by the reconstruction process.

Table 8.
Runtime statistics of main processes at the sampling rate of 0.25.

Table 9.
Runtime statistics of encryption process and decryption process at different sampling rates.
In what follows, we analyzed the time complexity of our encryption algorithm in Section 3.1 in detail. Assume the size of plain image is , the block sizes of the third-, second-, and first-level wavelet decomposition coefficient matrices are , respectively, and the target sampling rate is CR. Section 3.1.3 is to generate three chaotic sequences for scrambling, and time complexity is .Step 11 in Section 3.1.4 is to generate the chaotic sequence for diffusion, and time complexity is . Step 3 in Section 3.1.4 is to scramble the coefficient matrices with index sequences, and time complexity is . Step 6 in Section 3.1.4 is to generate the RSTPM and CSTPM, and time complexity is . Step 12 and Step 13 in Section 3.1.4 are to scramble the matrix of measurement values after CS with RSTPM and CSTPM, and time complexity is . Step 14 and Step 15 in Section 3.1.4 are to diffuse the matrix after scrambling, and time complexity is . For the computational cost of the proposed method determined in other steps, the time complexity is about . From the result shown in Table 8, the total time complexity is approximately equal to . Comparing with the encryption algorithms in [49,50] listed in Table 10, our scheme has a smaller time complexity. However, the time complexity of our scheme is equal to that of [10].

Table 10.
Comparison results on time complexity of Encryption algorithm.
5. Security Analysis
5.1. Key Space
To withstand a brute-force attack, an encryption scheme should have a large key space. If the calculation accuracy of the computer is , the external key is , accounted for key space. Table 11 compares the proposed scheme and other schemes. Since the ideal key space is suggested to be at least for a good cryptosystem [9], the result illustrates that the key space of the proposed scheme is large enough to resist all kinds of attacks.

Table 11.
Key space comparison.
5.2. Histogram Analysis
A histogram is an effective index to evaluate the distribution of pixel values. With an effective image encryption scheme, the histogram of a cipher image should be evenly distributed, so as to effectively resist statistical attacks. In this experiment, the histograms of the images in Figure 4 were drawn, with results as shown in Figure 5, from which it can be seen that the pixels of cipher images are uniformly distributed, and are quite different from those of the original images, making it impossible to obtain useful information. The histograms of the reconstructed images are similar to those of the corresponding plain images, which indicates that the reconstruction effect of decrypted images is good. All in all, attackers can obtain no useful information about plain images through statistical attacks when the proposed scheme is used.
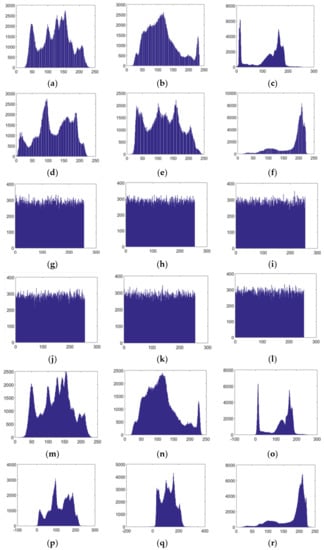
Figure 5.
Histograms of (a–f) plain images Lena, Goldhill, Cameraman, Peppers, Barbara, Jet; (g–l) corresponding cipher images; (m–r) corresponding decrypted images.
5.3. Sensitivity Analysis
Key sensitivity and plain sensitivity are important metrics to evaluate cryptosystems. Weak sensitivity enables the easy attack of a cryptosystem. We tested the key sensitivity and plain sensitivity of our scheme.
5.3.1. Plain Sensitivity
In a differential attack, the attacker encrypts an original and modified plain image with the same key and determines the relationship between the plain and encrypted images by comparing the corresponding cipher images. To resist such attacks, an encryption algorithm should have strong plain sensitivity, i.e., two plain images with small differences should have significant differences after encryption. The main indicators to measure the difference between two images include number of pixels change rate (NPCR) and unified average changing intensity (UACI) [51], which respectively reflect the proportion of the number of different pixels to the size of the image and the average ratio of the differences between pixels at corresponding positions and 255. These are expressed as
where sgn(·) is the sign function,
and
The critical values of NPCR and UACI of the two random images were 99.6094% and 33.4635%, respectively. For NPCR, the more the critical value is exceeded, the stronger the plain sensitivity of the encryption scheme. For UACI, the closer to the critical value, the stronger the plain image sensitivity of the encryption scheme. In the experiment, one pixel in plain image was randomly selected and the change of its pixel value was set to 1 to obtain the modified plain image . Cipher images and were obtained by encrypting plain images and , respectively, with the same key, and NPCR and UACI were calculated, as shown in Table 12. The experimental results show that NPCR exceeded the critical value for all images except Peppers, and UACI was close to the critical value for all images. Hence, the proposed encryption scheme has a strong resistance to differential attacks.

Table 12.
Calculation results of NPCR and UACI.
5.3.2. Key Sensitivity
An encryption scheme should have high sensitivity to the secret key in both the encryption and decryption processes [9], i.e., a small change of the secret key should produce a completely different cipher image. Similarly, in decryption, the plain image should not be recovered by a decryption key differing slightly from the encryption key. We tested the key sensitivity from the aspects of sensitivity in both encryption and decryption. The initial values of the four chaotic systems used in this paper were changed slightly from to , , , and . The Lena image was encrypted with the correct and wrong keys, with results as shown in Figure 6. From the experimental results, it can be seen that a small change in the key can cause a huge change in the cipher image but will not reveal information related to the plain image. To quantify the differences between cipher images obtained from the same plain image, NPCR and UACI were calculated using the correct and wrong keys to encrypt images, with results as shown in Table 13. It can be seen that NPCI and UACI are all close to the theoretical values, and more than 99.5% of pixels were modified, which implies that the encryption process is highly sensitive to the secret key.

Figure 6.
Experimental results of key sensitivity in encryption process: (a) cipher image using correct key K; (b,d,f,h) cipher images using wrong keys K1–K4, respectively; (c,e,g,i) differential images between (a,b), (a,d), (a,f), (a,h), respectively.

Table 13.
NPCR and UACI of cipher images with the correct key and different wrong keys.
Next, a cipher image was decrypted with both the correct and wrong keys, with results as shown in Figure 7, from which it can be seen that only through the correct key can we get the correct decrypted image. Even a slight key change produces a visually meaningless image. Table 14 lists the values of NPCR from Figure 7b–f. When the key has a tiny change, more than 99.8% of pixels are altered, which indicates that the decryption process is highly sensitive to the secret key.
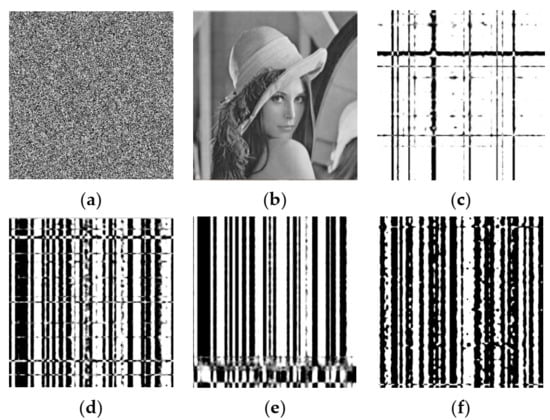
Figure 7.
Experimental results of key sensitivity in decryption process: (a) cipher image using correct key K; (b–f) decrypted images of (a) obtained using K, K1, K2, K3, K4, respectively.

Table 14.
NPCR of decrypted images with the correct key and different wrong keys.
5.4. Correlation Coefficients
Strong correlations, close to 1, exist between the pixels of natural images. The correlation coefficient reflects the linear relationship between adjacent pixels and is an important index to evaluate image encryption schemes. For a good encryption algorithm, correlations between adjacent pixels of cipher images should be very weak, tending to zero, which means that the correlation between pixels is largely eliminated. The correlation coefficient of u and v is calculated as [52]
where N is the number of adjacent pixel pairs from the image, and is the gray value of a pair.
In this experiment, 512 × 512 images Lena, Goldhill, and Peppers were selected as test images, and 5000, 6000 or 8000 pairs of adjacent pixels were randomly selected from the cipher images in the horizontal, vertical and diagonal directions for calculation. To reduce randomness, each calculation was carried out 100 times, the final result was taken as the average value, and this was compared with other schemes. The experimental results are shown in Table 15, and show that the correlations between adjacent pixels of the cipher images were small. We also determined adjacent pixel distributions for plain and cipher images, with results as shown in Figure 8, showing that adjacent pixels of the plain images were basically linearly distributed. However, there were weak correlations between adjacent pixels of the compressed cipher images, with correlation coefficients close to 0, showing that the proposed scheme has a good encryption effect.

Table 15.
Correlation coefficients of adjacent pixels in cipher images.
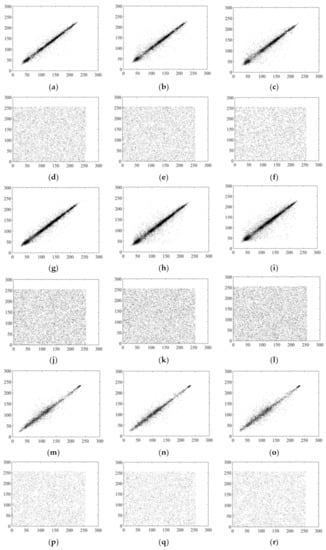
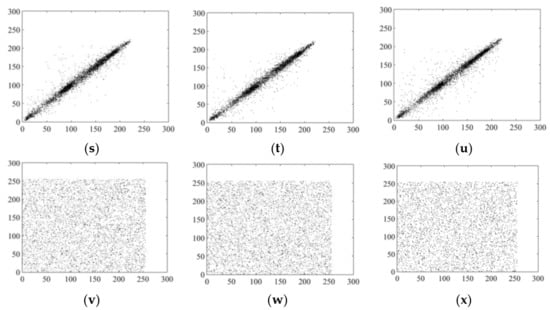
Figure 8.
Histogram analysis. Horizontal, vertical, and diagonal pixel distributions of (a–c) 5000 pairs of adjacent pixels in plain image Lena at sampling rate of 0.75; (d–f) corresponding cipher image; (g–i) 8000 pairs of adjacent pixels in plain image Lena at sampling rate of 0.25; (j–l) corresponding cipher image; (m–o) plain image Goldhill; (p–r) corresponding cipher image; (s–u) plain image Peppers; (v–x) corresponding cipher image.
5.5. Information Entropy
Information entropy reflects the randomness of the distribution of image pixels and is calculated as [37]
where is the probability of the i-th pixel value of image p, and n is its total number of digits. For an 8-bit grayscale image, its cipher image should have information entropy near 8 bits. In this experiment, the 512 × 512 images Lena, Peppers, Cameraman, Barbara, and Jet were selected as test images. The experiment was carried out at sampling rates of 0.5 and 0.25, with results as shown in Table 16, from which it can be seen that the information entropies of cipher images were all greater than 7.99. The results show the encryption effect of the proposed scheme was better than that of comparison schemes [10,40,43], which indicates that our scheme has better randomness than other schemes based on compressed sensing. Besides, compared to the algorithm proposed by Brindha et al. [53], our scheme can achieve higher information entropy. It shows that although our lossy compression algorithm using compressed sensing cannot fully restore the original image from the cipher image, it can obtain more secure cipher images than the lossless compression algorithm. What is more, it can be seen that the cipher images generated from our encryption scheme have greater information entropies than those of schemes based on substitution box [14] and quantum key image [28] in most instances, which means our scheme is more resistant to entropy attack than some encryption schemes based on non-chaotic techniques.

Table 16.
Comparison of information entropy of cipher images.
5.6. Robustness Analysis
During the transmission process, cipher images can be contaminated by noises and data loss, making it hard to decrypt them and recover the corresponding plain images. In this experiment, noise and crop attacks were utilized to test the robustness of the proposed scheme.
5.6.1. Noise Attack
Common types of noise include Gaussian noise (GN), speckle noise (SN), and salt-and-pepper noise (SPN). To evaluate the robustness of the proposed scheme to noise attacks, Lena was encrypted as the test image, different levels of three noises were added, and decrypted images were obtained, with experimental results as shown in Figure 9 from which it can be seen that the proposed scheme has a stronger resistance to speckle noise and salt-and-pepper noise than Gaussian noise.


Figure 9.
(a–c) Cipher images contaminated by Gaussian noise; (d–f) corresponding decrypted images; (g–i) cipher images contaminated by speckle noise; (j–l) corresponding decrypted images; (m–o) cipher images contaminated by salt-and-pepper noise; (p–r) corresponding decrypted images.
5.6.2. Crop Attack
Different areas of cipher images were randomly selected after encrypting Lena, cutting image blocks of size , , , , to obtain cipher images with some data loss, along with corresponding decrypted images. The results are shown in Figure 10, and numerical quantization results of decrypted images are shown in Table 17. From the results, although a crop attack will worsen the visual effect of decrypted images, the proposed scheme still retains most information of the image, i.e., the scheme has a certain robustness to crop attacks.

Figure 10.
(a–e) Cipher images after cutting blocks of size 16 × 16, 32 × 32, 64 × 64, 288 × 16, 16 × 256, respectively; (f–j) corresponding decrypted images.

Table 17.
Influence of different data loss on image reconstruction effect (PSNR).
6. Conclusions
An image encryption scheme based on multiscale block compressed sensing theory was proposed. In the scheme, considering that different information is carried by the low- and high-frequency coefficients of an image, different sampling rates were set for the low-and high-frequency coefficients of the image, so as to improve the reconstruction quality of decrypted images. Our scheme was experimentally compared with a scheme using the traditional compressed sensing theory and setting a sampling rate in each encryption process. Under the same compression ratio, the PSNR values between natural images and corresponding decrypted images of our scheme were better by more than 8 dB and were better by about 3–5 dB over a scheme that sets different sampling rates. Therefore, the proposed encryption scheme is suitable for natural image transmission with complex structures and large amounts of information. The safety of images is ensured, image information can be better preserved, and better visual effects can be obtained. With the combination of chaotic systems and a Markov model, the image is scrambled inside each coefficient matrix and is then scrambled among the coefficient matrices, and the encryption is completed by the strategies of independent and global diffusion. Experimental results show that the proposed scheme has a large key space, high plain sensitivity, and high key sensitivity in both the encryption and decryption processes. In particular, compared with an encryption scheme designed for problems of low entropy, the experimental scheme in this paper has a certain increase in information entropy values of most natural images, which shows the Markov probability model has certain advantages over traditional scrambling methods in simulating random processes. Therefore, the scheme has a certain guiding role for our future research work. At the same time, the scheme can effectively resist brute-force, differential, and statistical attacks. It also has a certain robustness to noise and crop attacks. However, high-intensity attacks cause large information loss, resulting in a poor visual effect. Hence, the design of a more robust encryption scheme warrants further study. Due to the use of multiscale block compressed sensing theory that better suits images, this scheme is suitable for mass image data transmission and can effectively save transmission space. To be honest, the times of the encryption and decryption processes in our scheme are long. Therefore, it remains to study the replacement of existing methods by more efficient chaotic systems and reconstruction methods while maintaining good encryption and decryption effects.
Author Contributions
Conceptualization, Y.S. and B.W.; methodology, Y.S.; software, Y.S.; validation, Y.S., Y.H. and B.W.; formal analysis, Y.H.; investigation, Y.H.; resources, B.W.; data curation, Y.S.; writing—original draft preparation, Y.S.; writing—review and editing, Y.S.; visualization, Y.S.; supervision, B.W.; project administration, Y.H. and B.W.; funding acquisition, B.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Technology R&D Program of China (No. 2018YFC0910500), the National Natural Science Foundation of China (Nos. 61425002, 61751203, 61772100, 61972266, 61802040), LiaoNing Revitalization Talents Program (No. XLYC2008017), the Innovation and Entrepreneurship Team of Dalian University (No. XQN202008), Natural Science Foundation of Liaoning Province (No. 2021-MS-344).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available upon reasonable request. Additional data (beyond those included in the main text) are available from the corresponding author upon request. The data are not publicly available due to [the data also forms part of an ongoing study].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hu, G.; Li, B. Coupling chaotic system based on unit transform and its applications in image encryption. Signal Process. 2021, 178, 107790. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Inf. Sci. 2019, 480, 403–419. [Google Scholar] [CrossRef]
- Mansouri, A.; Wang, X. A novel one-dimensional sine powered chaotic map and its application in a new image encryption scheme. Inf. Sci. 2020, 520, 46–62. [Google Scholar] [CrossRef]
- Pak, C.; Huang, L. A new color image encryption using combination of the 1D chaotic map. Signal Process. 2017, 138, 129–137. [Google Scholar] [CrossRef]
- Tsafack, N.; Kengne, J.; Abd-El-Atty, B.; Iliyasu, A.M.; Hirota, K.; Abd El-Latif, A.A. Design and implementation of a simple dynamical 4-D chaotic circuit with applications in image encryption. Inf. Sci. 2020, 515, 191–217. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Zhang, L.Y.; Zhu, H. A novel chaotic map constructed by geometric operations and its application. Nonlinear Dyn. 2020, 102, 2843–2858. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, C. A novel image encryption scheme based on conservative hyperchaotic system and closed-loop diffusion between blocks. Signal Process. 2020, 171, 107484. [Google Scholar] [CrossRef]
- Yu, J.; Li, C.; Song, X.; Guo, S.; Wang, E. Parallel Mixed Image Encryption and Extraction Algorithm Based on Compressed Sensing. Entropy 2021, 23, 278. [Google Scholar] [CrossRef]
- Chai, X.; Fu, X.; Gan, Z.; Zhang, Y.; Lu, Y.; Chen, Y. An efficient chaos-based image compression and encryption scheme using block compressive sensing and elementary cellular automata. Neural Comput. Appl. 2018, 32, 4961–4988. [Google Scholar] [CrossRef]
- Gan, Z.; Chai, X.; Zhang, J.; Zhang, Y.; Chen, Y. An effective image compression–encryption scheme based on compressive sensing (CS) and game of life (GOL). Neural Comput. Appl. 2020, 32, 14113–14141. [Google Scholar] [CrossRef]
- Naskar, P.K.; Bhattacharyya, S.; Nandy, D.; Chaudhuri, A. A robust image encryption scheme using chaotic tent map and cellular automata. Nonlinear Dyn. 2020, 100, 2877–2898. [Google Scholar] [CrossRef]
- Farah, M.A.B.; Farah, A.; Farah, T. An image encryption scheme based on a new hybrid chaotic map and optimized substitution box. Nonlinear Dyn. 2019, 99, 3041–3064. [Google Scholar] [CrossRef]
- Zhang, Y. The fast image encryption algorithm based on lifting scheme and chaos. Inf. Sci. 2020, 520, 177–194. [Google Scholar] [CrossRef]
- Azam, N.A.; Hayat, U.; Ayub, M. A substitution box generator, its analysis, and applications in image encryption. Signal Process. 2021, 187, 108144. [Google Scholar] [CrossRef]
- Enayatifar, R.; Abdullah, A.H.; Isnin, I.F. Chaos-based image encryption using a hybrid genetic algorithm and a DNA sequence. Opt. Lasers Eng. 2014, 56, 83–93. [Google Scholar] [CrossRef]
- Wu, X.; Wang, K.; Wang, X.; Kan, H.; Kurths, J. Color image DNA encryption using NCA map-based CML and one-time keys. Signal Process. 2018, 148, 272–287. [Google Scholar] [CrossRef]
- Cao, B.; Li, X.; Zhang, X.; Wang, B.; Wei, X. Designing Uncorrelated Address Constrain for DNA Storage by DMVO Algorithm. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 1, 15. [Google Scholar] [CrossRef]
- Cao, B.; Zhang, X.; Wu, J.; Wang, B.; Wei, X. Minimum free energy coding for DNA storage. IEEE Trans. NanoBiosci. 2021, 20, 212–222. [Google Scholar] [CrossRef]
- Zhou, S. A real-time one-time pad DNA-chaos image encryption algorithm based on multiple keys. Opt. Laser Technol. 2021, 143, 107359. [Google Scholar] [CrossRef]
- Zhou, S.; He, P.; Kasabov, N. A Dynamic DNA Color Image Encryption Method Based on SHA-512. Entropy 2020, 22, 1091. [Google Scholar] [CrossRef]
- Azam, N.A.; Ullah, I.; Hayat, U. A fast and secure public-key image encryption scheme based on Mordell elliptic curves. Opt. Lasers Eng. 2021, 137, 106371. [Google Scholar] [CrossRef]
- Hayat, U.; Azam, N.A. A novel image encryption scheme based on an elliptic curve. Signal Process. 2019, 155, 391–402. [Google Scholar] [CrossRef]
- Luo, Y.; Ouyang, X.; Liu, J.; Cao, L. An Image Encryption Method Based on Elliptic Curve Elgamal Encryption and Chaotic Systems. IEEE Access 2019, 7, 38507–38522. [Google Scholar] [CrossRef]
- Toughi, S.; Fathi, M.H.; Sekhavat, Y.A. An image encryption scheme based on elliptic curve pseudo random and Advanced Encryption System. Signal Process. 2017, 141, 217–227. [Google Scholar] [CrossRef]
- Nardo, L.G.; Nepomuceno, E.G.; Arias-Garcia, J.; Butusov, D.N. Image encryption using finite-precision error. Chaos Solitons Fractals 2019, 123, 69–78. [Google Scholar] [CrossRef]
- Nardo, L.G.; Nepomuceno, E.G.; Bastos, G.T.; Santos, T.A.; Butusov, D.N.; Arias-Garcia, J. A reliable chaos-based cryptography using Galois field. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 091101. [Google Scholar] [CrossRef]
- Abd-El-Atty, B.; Iliyasu, A.M.; Alanezi, A.; Abd El-latif, A.A. Optical image encryption based on quantum walks. Opt. Lasers Eng. 2021, 138, 106403. [Google Scholar] [CrossRef]
- Wang, J.; Geng, Y.-C.; Han, L.; Liu, J.-Q. Quantum Image Encryption Algorithm Based on Quantum Key Image. Int. J. Theor. Phys. 2018, 58, 308–322. [Google Scholar] [CrossRef]
- Li, X.; Zhang, G.; Zhang, X. Image encryption algorithm with compound chaotic maps. J. Ambient. Intell. Humaniz. Comput. 2014, 6, 563–570. [Google Scholar] [CrossRef]
- Tutueva, A.V.; Karimov, A.I.; Moysis, L.; Volos, C.; Butusov, D.N. Construction of one-way hash functions with increased key space using adaptive chaotic maps. Chaos Solitons Fractals 2020, 141, 110344. [Google Scholar] [CrossRef]
- Tutueva, A.V.; Nepomuceno, E.G.; Karimov, A.I.; Andreev, V.S.; Butusov, D.N. Adaptive chaotic maps and their application to pseudo-random numbers generation. Chaos Solitons Fractals 2020, 133, 109615. [Google Scholar] [CrossRef]
- Alawida, M.; Samsudin, A.; Teh, J.S.; Alkhawaldeh, R.S. A new hybrid digital chaotic system with applications in image encryption. Signal Process. 2019, 160, 45–58. [Google Scholar] [CrossRef]
- Chai, X.; Wu, H.; Gan, Z.; Zhang, Y.; Chen, Y.; Nixon, K.W. An efficient visually meaningful image compression and encryption scheme based on compressive sensing and dynamic LSB embedding. Opt. Lasers Eng. 2020, 124, 105837. [Google Scholar] [CrossRef]
- Dou, Y.; Li, M. An Image Encryption Algorithm Based on Compressive Sensing and M Sequence. IEEE Access 2020, 8, 220646–220657. [Google Scholar] [CrossRef]
- Huang, W.; Jiang, D.; An, Y.; Liu, L.; Wang, X. A Novel Double-Image Encryption Algorithm Based on Rossler Hyperchaotic System and Compressive Sensing. IEEE Access 2021, 9, 41704–41716. [Google Scholar] [CrossRef]
- Shi, M.; Guo, S.; Song, X.; Zhou, Y.; Wang, E. Visual Secure Image Encryption Scheme Based on Compressed Sensing and Regional Energy. Entropy 2021, 23, 570. [Google Scholar] [CrossRef]
- Chai, X.; Wu, H.; Gan, Z.; Zhang, Y.; Chen, Y. Hiding cipher-images generated by 2-D compressive sensing with a multi-embedding strategy. Signal Process. 2020, 171, 107525. [Google Scholar] [CrossRef]
- Ye, G.; Pan, C.; Dong, Y.; Shi, Y.; Huang, X. Image encryption and hiding algorithm based on compressive sensing and random numbers insertion. Signal Process. 2020, 172, 107563. [Google Scholar] [CrossRef]
- Chai, X.; Wu, H.; Gan, Z.; Han, D.; Zhang, Y.; Chen, Y. An efficient approach for encrypting double color images into a visually meaningful cipher image using 2D compressive sensing. Inf. Sci. 2021, 556, 305–340. [Google Scholar] [CrossRef]
- Wen, W.; Hong, Y.; Fang, Y.; Li, M.; Li, M. A visually secure image encryption scheme based on semi-tensor product compressed sensing. Signal Process. 2020, 173, 107580. [Google Scholar] [CrossRef]
- Fan, H.; Zhou, K.; Zhang, E.; Wen, W.; Li, M. Subdata image encryption scheme based on compressive sensing and vector quantization. Neural Comput. Appl. 2020, 32, 12771–12787. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Tan, W.; Li, L. An Efficient Plaintext-Related Chaotic Image Encryption Scheme Based on Compressive Sensing. Sensors 2021, 21, 758. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Xiao, D.; Li, M.; Xiang, Y.; Li, X. A visually secure image encryption scheme based on parallel compressive sensing. Signal Process. 2019, 155, 218–232. [Google Scholar] [CrossRef]
- Zhu, L.; Song, H.; Zhang, X.; Yan, M.; Zhang, T.; Wang, X.; Xu, J. A robust meaningful image encryption scheme based on block compressive sensing and SVD embedding. Signal Process. 2020, 175, 107629. [Google Scholar] [CrossRef]
- James, E.F.; Sungkwang, M.; Eric, W.T. Multiscale block compressed sensing with smoothed projected Landweber reconstruction. In Proceedings of the 19th European Signal Processing Conference, Barcelona, Spain, 29 August–2 September2011; pp. 564–568. [Google Scholar]
- Tan, Y.; Zhang, C.; Qin, J.; Xiang, X. Image encryption algorithm based on exponential compound chaotic system. J. Huazhong Univ. Sci. Tech. 2021, 49, 122–126. [Google Scholar] [CrossRef]
- Sarich, M.; Prinz, J.H.; Schutte, C. Markov Model Theory. In Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation; Bowman, G.R., Pande, V.S., Noe, F., Eds.; Advances in Experimental Medicine and Biology: Berlin/Heidelberg, Germany, 2014; Volume 797, pp. 23–44. [Google Scholar]
- Luo, Y.; Lin, J.; Liu, J.; Wei, D.; Cao, L.; Zhou, R.; Cao, Y.; Ding, X. A robust image encryption algorithm based on Chua’s circuit and compressive sensing. Signal Process. 2019, 161, 227–247. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.-D.; Zhang, W.; Yu, H.; Zhu, Z.-l. An image encryption scheme using self-adaptive selective permutation and inter-intra-block feedback diffusion. Signal Process. 2018, 151, 130–143. [Google Scholar] [CrossRef]
- Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Opt. Lasers Eng. 2016, 78, 17–25. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, A.; Tang, Y.; Dang, J.; Wang, G. Plaintext-related image encryption algorithm based on perceptron-like network. Inf. Sci. 2020, 526, 180–202. [Google Scholar] [CrossRef]
- Tang, Y.; Zhao, M.; Li, L.; Xu, L. Secure and Efficient Image Compression-Encryption Scheme Using New Chaotic Structure and Compressive Sensing. Secur. Commun. Netw. 2020, 2020, 6665702. [Google Scholar] [CrossRef]
- Brindha, M.; Gounden, N.A. A chaos based image encryption and lossless compression algorithm using hash table and Chinese Remainder Theorem. Appl. Soft Comput. 2016, 40, 379–390. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).