Quantum Walk on the Generalized Birkhoff Polytope Graph
Abstract
1. Introduction
2. Linear Programming Problems, Polytopes, and Polytope Graphs
3. TLP, the Generalized Birkhoff Polytope, and GBPG
4. Classical and Quantum Walk, and Their Mixing Times
4.1. RW on GBPG
4.2. QW on GBPG
4.2.1. QW
4.2.2. Limiting Distribution and Mixing Time
5. Simulation and Numerical Results for RW and QW on GBPG
5.1. Computational Platform and Instance Generation
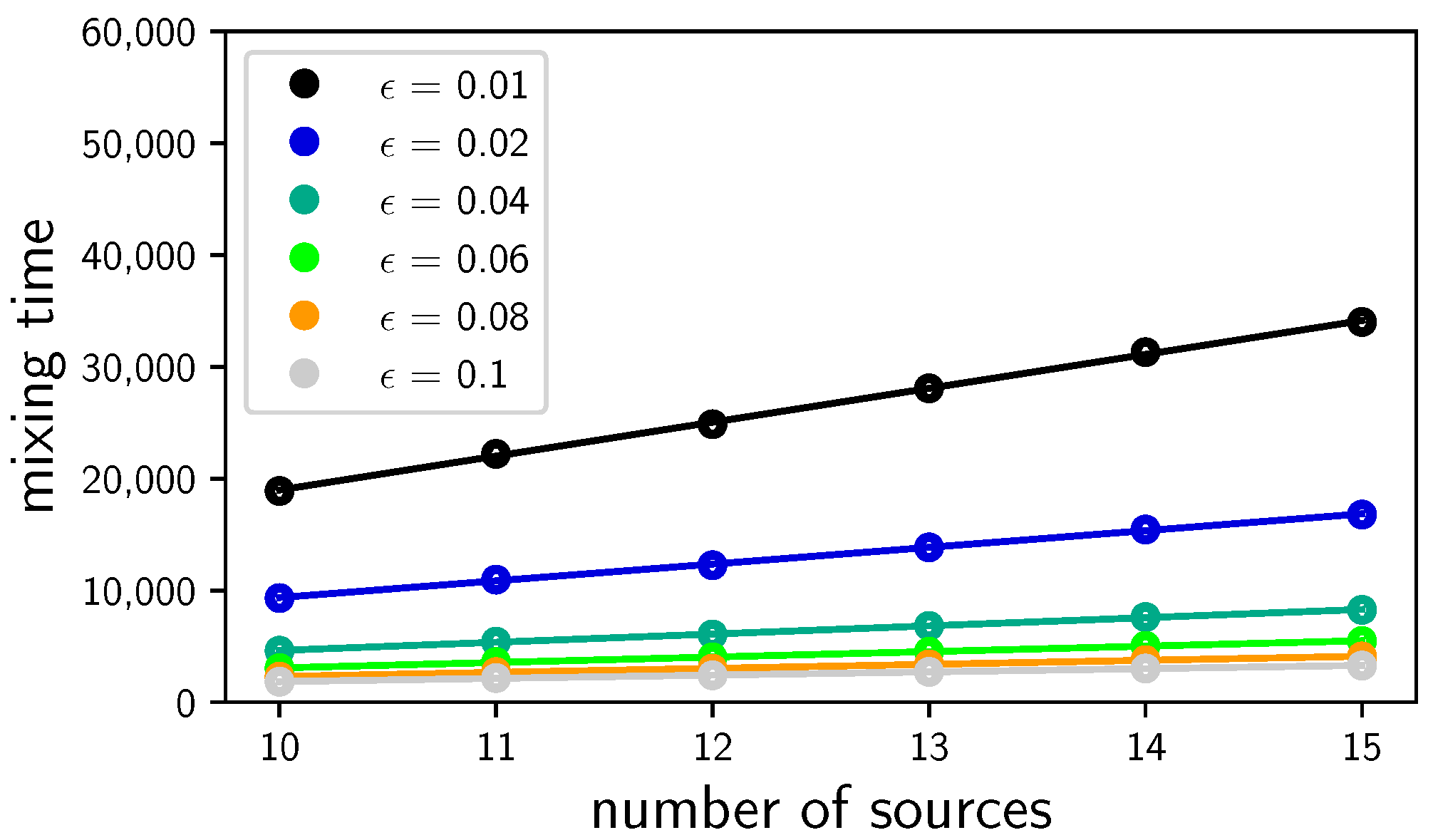
5.2. Classical Mixing Time
5.3. Limiting Probability Distribution (Quantum Case)
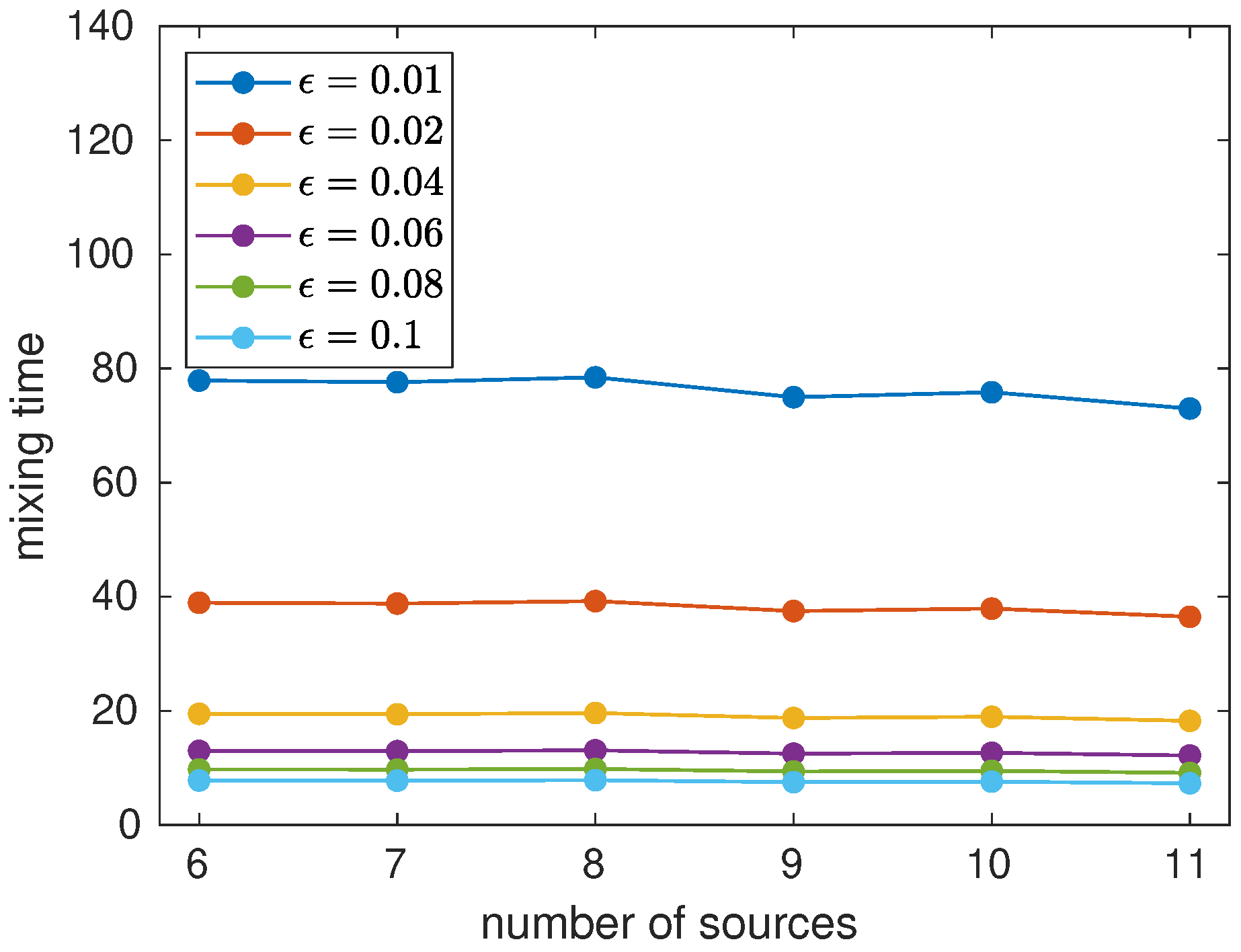
5.4. Quantum Mixing Time
6. Conclusions and Directions for Further Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nemhauser, G.; Wolsey, L. Integer and Combinatorial Optimization; Wiley: Hoboken, NJ, USA, 1988. [Google Scholar]
- Orlin, J. A Polynomial Time Primal Network Simplex Algorithm for Minimum Cost Flows. Math. Program. 1997, 8, 109–129. [Google Scholar] [CrossRef]
- Bertsimas, D.; Vempala, S. Solving convex programs by random walks. J. ACM 2004, 51, 540–556. [Google Scholar] [CrossRef]
- Cryan, M.; Dyer, M.; Müller, H.; Stougie, L. Random Walks on the Vertices of Transportation Polytopes with Constant Number of Sources. Random Struct. Algorithms 2008, 33, 333–355. [Google Scholar] [CrossRef]
- Aharonov, D.; Ambainis, A.; Kempe, J.; Vazirani, U. Quantum walks on graphs. In Proceedings of the Thirty-Third annual ACM Symposium on Theory of Computing, Crete, Greece, 6–8 July 2001; ACM: New York, NY, USA, 2001; pp. 50–59. [Google Scholar]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef]
- Wu, Y.; Bao, W.S.; Cao, S.; Chen, F.; Chen, M.C.; Chen, X.; Chung, T.H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong quantum computational advantage using a superconducting quantum processor. arXiv 2021, arXiv:2106.14734. [Google Scholar]
- Portugal, R. Quantum Walks and Search Algorithms; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Acasiete, F.; Agostini, F.P.; Moqadam, J.K.; Portugal, R. Implementation of quantum walks on IBM quantum computers. Quantum Inf. Process. 2020, 19, 426. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. arXiv 2018, arXiv:1801.00862. [Google Scholar] [CrossRef]
- de Loera, J.; Kim, E. Combinatorics and Geometry of Transportation Polytopes: An Update. Contemp. Math. 2014, 625, 37–76. [Google Scholar]
- Lovász, L. Random walks on graphs: A survey. Combinatorics 1993, 2, 1–46. [Google Scholar]
- Chvátal, V. Linear Programming; W.H. Freeman and Company: New York, NY, USA, 1980. [Google Scholar]
- Bondy, J.; Murty, U. Graph Theory with Applications; North-Holland: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Liu, F. Perturbation of Transportation Polytopes. J. Comb. Theory A 2013, 120, 1539–1561. [Google Scholar] [CrossRef]
- Bolker, E. Transportation Polytopes. J. Comb. Theory B 1972, 13, 251–262. [Google Scholar] [CrossRef][Green Version]
- Hitchcock, F. The Distribution of a Product from Several Sources to Numerous Locations. J. Math. Phys. 1941, 20, 224–230. [Google Scholar] [CrossRef]
- Koopmans, T. Optimum Utilization of the Transportation System. Econometrica 1947, 17, 136–146. [Google Scholar] [CrossRef]
- Ahrens, J.; Finke, G. Primal transportation and transshipment algorithms. Z. Oper. Res. 1980, 24, 1–32. [Google Scholar] [CrossRef]
- Baiöu, M.; Balinski, M. The stable allocation (or ordinal transportation) problem. Math. Oper. Res. 2002, 27, 485–503. [Google Scholar] [CrossRef]
- Barnes, E.; Hoffman, A. On Transportation Problems with Upper Bounds on Leading Rectangles. SIAM J. Algebr. Discret. Methods 1985, 6, 721–730. [Google Scholar] [CrossRef]
- De Loera, J.; Kim, E.; Onn, S.; Santos, F. Graphs of Transportation Polytopes. J. Comb. Theory A 2009, 116, 1306–1325. [Google Scholar] [CrossRef]
- Klee, V.; Witzgall, C. Facets and Vertices of Transportation Polytopes. In Mathematics of the Decision Sciences, Part 1; Dantzig, G., Veinott, A., Eds.; AMS: Providence, RI, USA, 1968; pp. 257–282. [Google Scholar]
- Pak, I. Four Questions on the Birkhoff Polytope. Ann. Comb. 2000, 2, 83–90. [Google Scholar] [CrossRef]
- Dyer, M. The Complexity of Vertex Enumeration Methods. Math. Oper. Res. 1983, 8, 381–402. [Google Scholar] [CrossRef]
- Diaconis, P.; Graham, R.; Morrison, J. Asymptotic Analysis of a Random Walk on a Hyper-Cube with Many Dimensions. Random Struct. Algorithms 1990, 1, 51–72. [Google Scholar] [CrossRef]
- Morris, B.; Sinclair, A. Random Walks on Truncated Cubes and Sampling 0–1 Knapsack Solutions. SIAM J. Comput. 2004, 34, 195–226. [Google Scholar] [CrossRef]
- Moore, C.; Russell, A. Quantum Walks on the Hypercube. In Proceedings of the 6th International Workshop on Randomization and Approximation Techniques RANDOM, Cambridge, MA, USA, 13–15 September 2002; Springer: Berlin, Germany, 2002; pp. 164–178. [Google Scholar]
- Marquezino, F.L.; Portugal, R.; Abal, G.; Donangelo, R. Mixing times in quantum walks on the hypercube. Phys. Rev. A 2008, 77, 042312. [Google Scholar] [CrossRef]
- Marquezino, F.L.; Portugal, R.; Abal, G. Mixing times in quantum walks on two-dimensional grids. Phys. Rev. A 2010, 82, 042341. [Google Scholar] [CrossRef]
- Kargin, V. Bounds for mixing time of quantum walks on finite graphs. J. Phys. A Math. Theor. 2010, 43, 335302. [Google Scholar] [CrossRef]
- Chakraborty, S.; Luh, K.; Roland, J. How Fast Do Quantum Walks Mix? Phys. Rev. Lett. 2020, 124, 050501. [Google Scholar] [CrossRef]
- Chakraborty, S.; Luh, K.; Roland, J. Analog quantum algorithms for the mixing of Markov chains. Phys. Rev. A 2020, 102, 022423. [Google Scholar] [CrossRef]
- Apers, S.; Sarlette, A.; Ticozzi, F. Simulation of quantum walks and fast mixing with classical processes. Phys. Rev. A 2018, 98, 032115. [Google Scholar] [CrossRef]
- Dervovic, D. Quantum Computation, Markov Chains and Combinatorial Optimisation. Ph.D. Thesis, University College London, London, UK, 2020. [Google Scholar]
- Christof, T.; Loebel, A. PORTA: POlyhedron Representation Transformation Algorithm, v. 1.4.1. 2015. Available online: http://porta.zib.de (accessed on 5 August 2021).
- Levin, D.; Peres, Y. Markov Chains and Mixing Times, 2nd ed.; AMS: Providence, RI, USA, 2017. [Google Scholar]
- Guruswami, V. Rapidly Mixing Markov Chains: A Comparison of Techniques (A Survey). arXiv 2016, arXiv:1603.01512. [Google Scholar]
- Daz, N.; Donangelo, R.; Portugal, R.; Romanelli, A. Transient temperature and mixing times of quantum walks on cycles. Phys. Rev. A 2016, 94, 012305. [Google Scholar] [CrossRef]





| Instance | m | N | Diam. | |
|---|---|---|---|---|
| 1 | 2 | 2 | 1 | 2 |
| 2 | 3 | 6 | 3 | |
| 3 | 4 | 12 | 3 | |
| 4 | 5 | 30 | 5 | |
| 5 | 6 | 60 | 5 | |
| 6 | 7 | 140 | 7 | |
| 7 | 8 | 280 | 7 | |
| 8 | 9 | 630 | 9 | |
| 9 | 10 | 1260 | 9 | |
| 10 | 11 | 2772 | 11 | |
| 11 | 12 | 5544 | 11 | |
| 12 | 13 | 12,012 | 13 | |
| 13 | 14 | 24,024 | 13 | − |
| 14 | 15 | 51,480 | 15 | − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cação, R.; Cortez, L.; de Farias, I.; Kozyreff, E.; Khatibi Moqadam, J.; Portugal, R. Quantum Walk on the Generalized Birkhoff Polytope Graph. Entropy 2021, 23, 1239. https://doi.org/10.3390/e23101239
Cação R, Cortez L, de Farias I, Kozyreff E, Khatibi Moqadam J, Portugal R. Quantum Walk on the Generalized Birkhoff Polytope Graph. Entropy. 2021; 23(10):1239. https://doi.org/10.3390/e23101239
Chicago/Turabian StyleCação, Rafael, Lucas Cortez, Ismael de Farias, Ernee Kozyreff, Jalil Khatibi Moqadam, and Renato Portugal. 2021. "Quantum Walk on the Generalized Birkhoff Polytope Graph" Entropy 23, no. 10: 1239. https://doi.org/10.3390/e23101239
APA StyleCação, R., Cortez, L., de Farias, I., Kozyreff, E., Khatibi Moqadam, J., & Portugal, R. (2021). Quantum Walk on the Generalized Birkhoff Polytope Graph. Entropy, 23(10), 1239. https://doi.org/10.3390/e23101239






