1. Introduction
Since the HP laboratory [
1] confirmed memristors’ physical existence in 2008, the memristors [
2] have received extensive attention from the academic community. Memristor [
3] is a kind of nonlinear resistor with memory function. The memristor has been investigated and applied in non-volatile memory [
3], artificial neural network [
4], confidential communication [
5], analog circuit [
6], an artificial intelligence computer [
4,
6], biological behavior simulation [
7], etc., showing great potential.
Although two-terminal memristors have proved the basic principle of neurons, the synapses of one neuron are far more than one, so it is necessary to study multi-terminal memristors. The three-terminal Widrow-Hoff memristor [
8] has carried out this kind of attempt by adding a control terminal to realize a three-terminal chemical memristor. A new floating gate silicon MOS (MOSFET) transistor [
9] was similarly proposed, and Lai proposed field-effect transistors with nano ionic gates [
10]. Mouttet proposed the basic definition of the three-terminal memristor [
11] based on the two-terminal memristor passive nonlinear system [
12] by Chua. Recently, using monolayer molybdenum disulfide, three-terminal [
13], six-terminal, or even more synapses’ memristors were realized.
Chaos exists in mathematical models [
14] and other aspects such as the macroeconomic model [
15], the breaking of topological supersymmetry [
16], etc. Chaotic systems are divided into the conservative system and dissipative system [
17]. The Lyapunov dimensions of dissipative chaotic systems are fractional; for instance, if the system’s full dimension is three, the Lyapunov dimension is slightly higher than two. The divergence of the dissipative chaotic system is less than zero leading to the phase volume converging to zero with the exponential rate of the divergence. Hence, the passing trajectories of the dissipative system are not ergodic in the 3D space as the chaotic attractor looks like, but occupies zero space of the fractional dimension. The system orbits cannot traverse the entire space given by the initial value, and even most of the spatial range cannot be experienced. The poor ergodicity caused by the fractional dimension is the disadvantage in chaos-based encryption. It is easy to obtain exhaustive attacks when used in encryption systems [
17,
18]. However, the conservative chaos has a full dimension in phase volume, and encryption based on conservative systems is better than dissipative systems in anti-attack [
17,
18,
19]. Constructing a memristor-based conservative chaotic system is helpful to the encryption of information and provides better security about information-theory.
A conservative chaotic system is a system in which the phase volume space remains unchanged [
17,
18,
19], so the dimension is an integer [
20], and the orbit can traverse and occupy the entire space given by the initial value. Compared with dissipative chaotic systems, conservative chaotic systems are scarce, and conservative chaos can be divided into two types: Hamiltonian conservative (energy conservative) and phase volume conservative [
17]. Recently, Qi [
17,
18] first established the four-dimensional (4D) Euler equations. The 4D Euler equation modeling is essential in mathematics, rigid-body dynamics, and the structure of symplectic manifolds and fluid dynamics [
17,
18]. Based on this, a 4D conservative chaotic system was constructed, which is strictly conservative chaos.
Nowadays, most of the research on memristors is based on dissipative chaos [
7,
14]. There are two research routes of two-terminal memristor chaotic systems based on dissipative system: (1) The memristor is used to replace nonlinear components such as the Chua circuits [
14,
21], oscillator circuits [
22], etc. The hidden attractor, multistability [
23], hyperchaotic and fractional-order form [
24] were proposed. (2) The memristor is used as a feedback term to couple into a neuron model such as the Hindmarsh-Rose (HR) neuron model [
7], etc. Some recent research methods on memristors, such as Chua’s periodic table [
16,
25,
26] and the multidimensional scaling [
27], have not explained the causes of chaos from the perspective of Hamiltonian energy.
Only a few two-terminal memristor systems are driven by piecewise function [
28] or sine function [
29,
30] to obtain conservative chaotic systems. However, the values of positive Lyapunov exponent (
LE) of these systems in [
28,
29,
30] are too small. The system [
29] just satisfies that the sum of
LEs is zero, but the system does not analytically meet zero divergence requirements. More importantly, to our best knowledge, no conservative chaos based on three-terminal memristor has been studied. A memristor-based conservative chaotic system is more complicated with more parameters, which increases the keyspace of the chaos generator. Besides, a memristor-based conservative chaotic system with a high positive Lyapunov exponent is necessary for chaos-based encryption to generate the pseudo-random number.
We consider designing a conservative three-terminal memristor chaotic system based on the 4D Euler equation given in [
18]. The 4D Euler equation is a very delicate ordinary differential equation based on mathematics, which is strictly conservative in both energy and divergence, but it just produces the periodic orbit instead of the chaos. By coupling the Euler equation with a three-terminal memristor, the energy conservation is broken, but the phase-volume conservation (divergence being zero) is still kept. Therefore, this paper constructs a three-terminal-memristor-based conservative chaotic system, and gives its energy function, pointing out the cause of its chaos. A large positive Lyapunov exponent is produced, which is advantageous over existing dissipative chaos and conservative chaos. An analog circuit is designed to prove the theory’s feasibility, and verify the existence of the non-Hamiltonian conservative chaotic system, which overcomes the challenge that a little bias will lead to the disappearance of conservative chaos.
This paper is organized as follows:
Section 2 proposes the three-terminal memristor and constructs the circuit to implement it.
Section 3 proposes the conservative chaotic system based on a three-terminal memristor from a strict conservative system [
18].
Section 4 gives the characteristics of equilibria of the three-terminal memristor conservative system.
Section 5 gives the dynamical analysis, and the cause of dynamical changing of the system in different levels and the impact of Hamiltonian on the system are investigated. Analog circuit implementation is provided in
Section 6.
Section 7 summarizes the paper.
2. Modeling of Three-Terminal Memristor
The memristor predicted by Chua is a two-port device [
31]. It also has three significant features: the hysteresis loop passes the origin, the hysteresis loop is the shape of eight, and the area of the hysteresis curve decreases with increasing signal frequency. Here, we choose the cubic smooth memductance nonlinearity model [
14,
32]. The memristor model is described in the following form
According to the magnetic controlled three-terminal memristor model proposed in the memristive systems analysis [
11], the following results are obtained
Here
represent the input voltages,
represent the output currents,
donates an n-dimensional state variable of the system,
are defined as continuous function, and
is an n-dimensional continuous function. The memristor model in Equation (1) is appropriately deformed. By changing it to the model of single-port input and dual-port output, the model is transformed as
where
is the input voltage of the model,
is the magnetic flux that controls the state of the model,
represents the memductance, and
are the two current outputs.
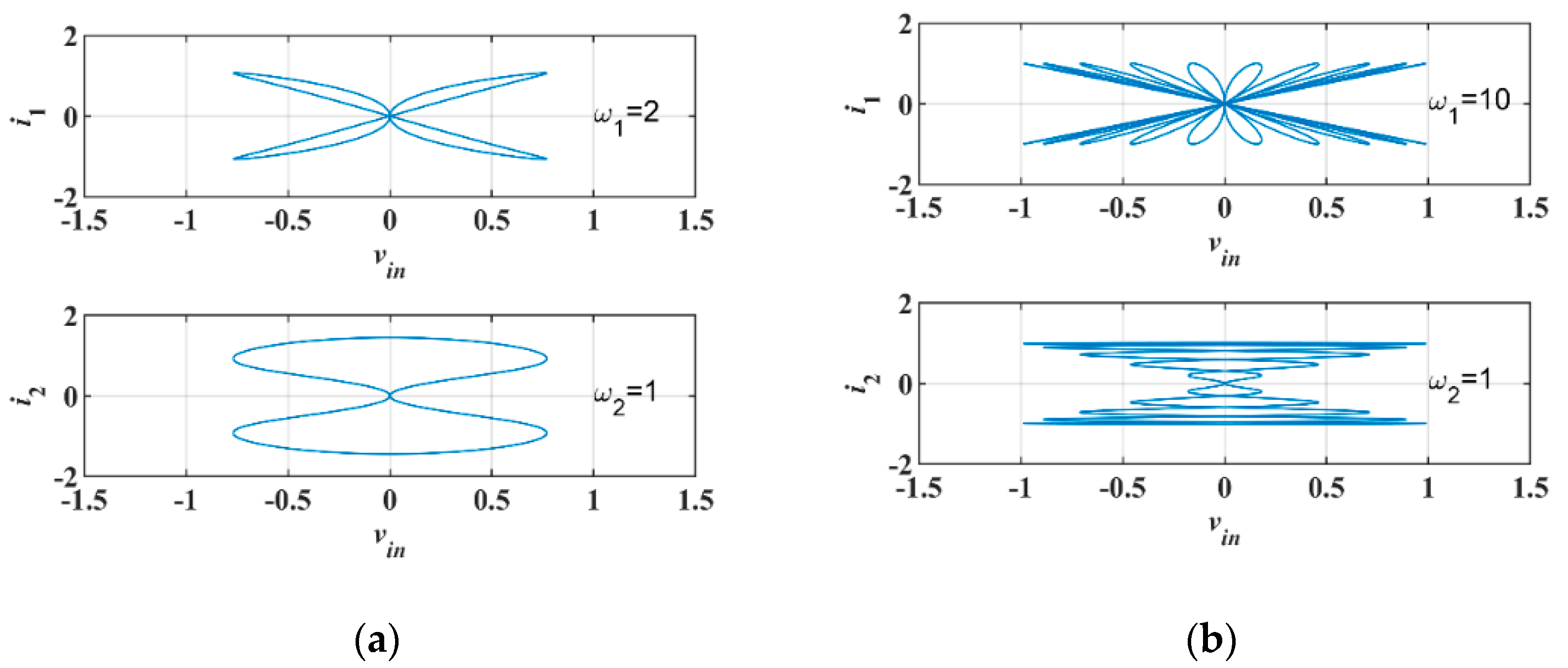
To verify the feature of the model Equation (3), we used Matlab for numerical simulation, as shown in
Figure 1, The product of
and
is the input of this device with parameters
, and
in
Figure 1a and
Figure 1b. We found that the hysteresis curve does not converge to a single-valued function, but a multi-valued resistance with the frequency increasing, which means this model has a complex resistance value. The three-terminal memristor can be implemented by the circuit shown in
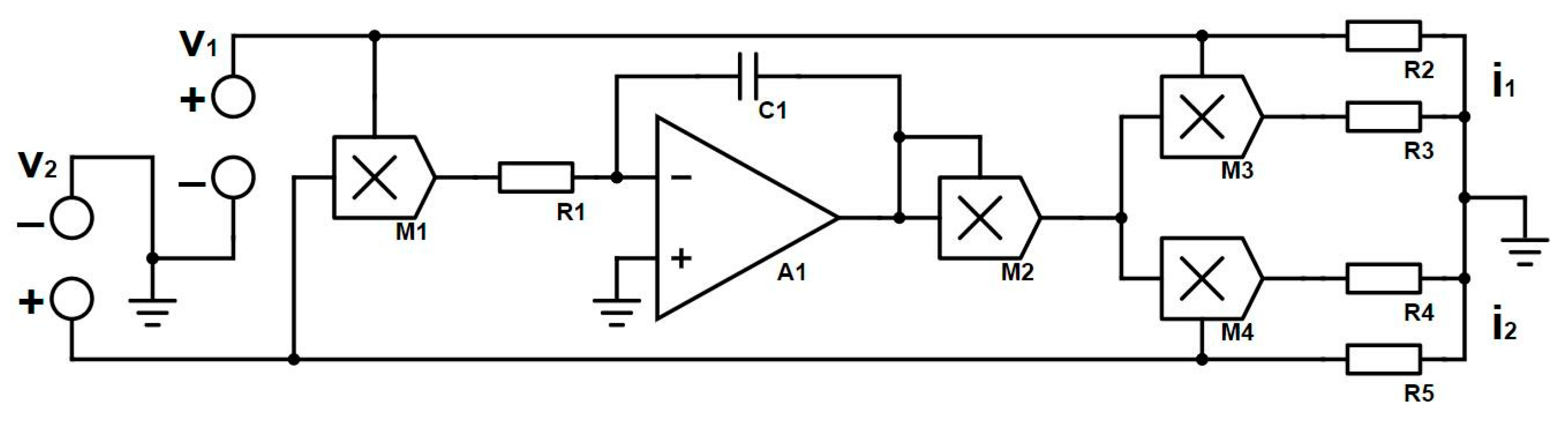
Figure 2.
In
Figure 2,
are input voltages of the model,
to
multipliers,
to
resistors,
a capacitor, and
output currents, respectively. The analytical mathematical model is given as
form the integrated circuit, and the remaining four resistors match the output coefficients. Using Multisim to simulate the model, input voltages are consistent with Matlab numerical simulation. The circuit simulation results received are shown in
Figure 3.
It was found that the simulation results of the circuit model are consistent with the simulation of the mathematical model, so the model can be used to build the actual hardware circuit.
3. Modeling of Conservative Chaotic System Based on Three-Terminal Memristor
Qi proposed a 4D Euler rigid body equation with a Hamiltonian vector field form [
18]
where
with
The system can be written as
The divergence of the 4D Euler equation is
Therefore, Equation (8) is a phase-volume conservative system. Because
in Equation (6) is a skew-symmetric matrix, we have
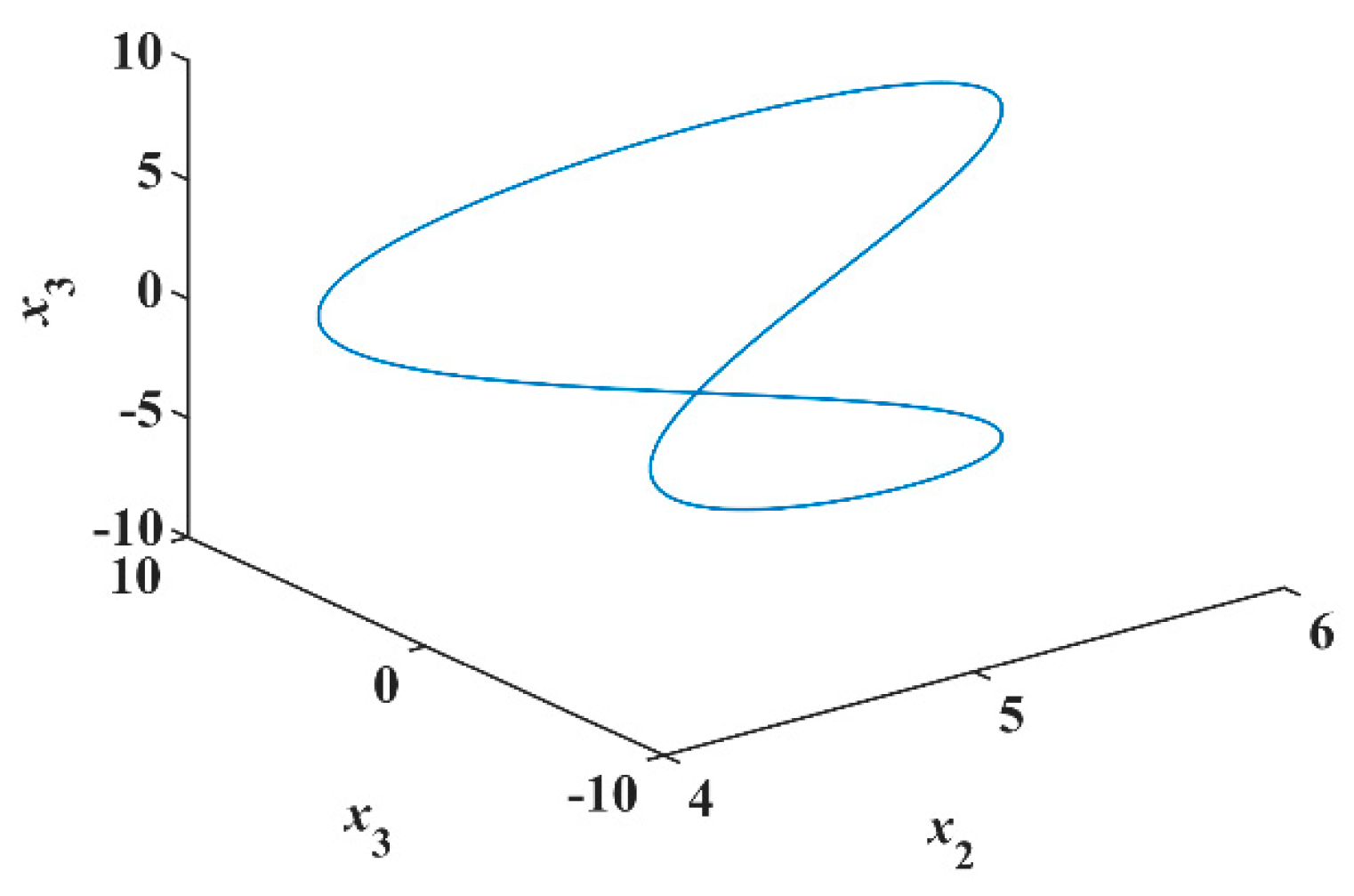
Thus, the system of Equation (8) is a Hamiltonian conservative system. Therefore, it preserves both the phase-volume and Hamiltonian. Using Matlab for numerical simulation, take parameters
, initial conditions
, and sampling time
s. Since the conservation of both phase-volume and Hamiltonian, this system only produces periodic orbit [
17,
18,
19], as shown in
Figure 4.
The 4-D Hamiltonian conservative system only produces a periodic orbit because of the conservation of both phase volume and Hamiltonian energy. Does it generate conservative chaos by breaking one of the conservations, like the Hamiltonian energy? Qi [
17] proposed a Hamiltonian conservative chaotic system by changing the Casimir conservation and keeping the Hamiltonian constant. Only one parameter was changed. So far, to our best knowledge, no memristor has been applied in all the conservative chaotic systems generation.
To generate chaos, we should break the conservation of Hamiltonian by adding a pair of constants
and
in the symplectic matrix
in Equation (6), and then Equation (5) can be written as
where
For simplification, the system parameters are fixed as
Then Equation (11) becomes
with
Because the main diagonal of Equation (12) is zero as Equation (6), the phase volume is still conservative.
However, for the Hamiltonian energy, we have
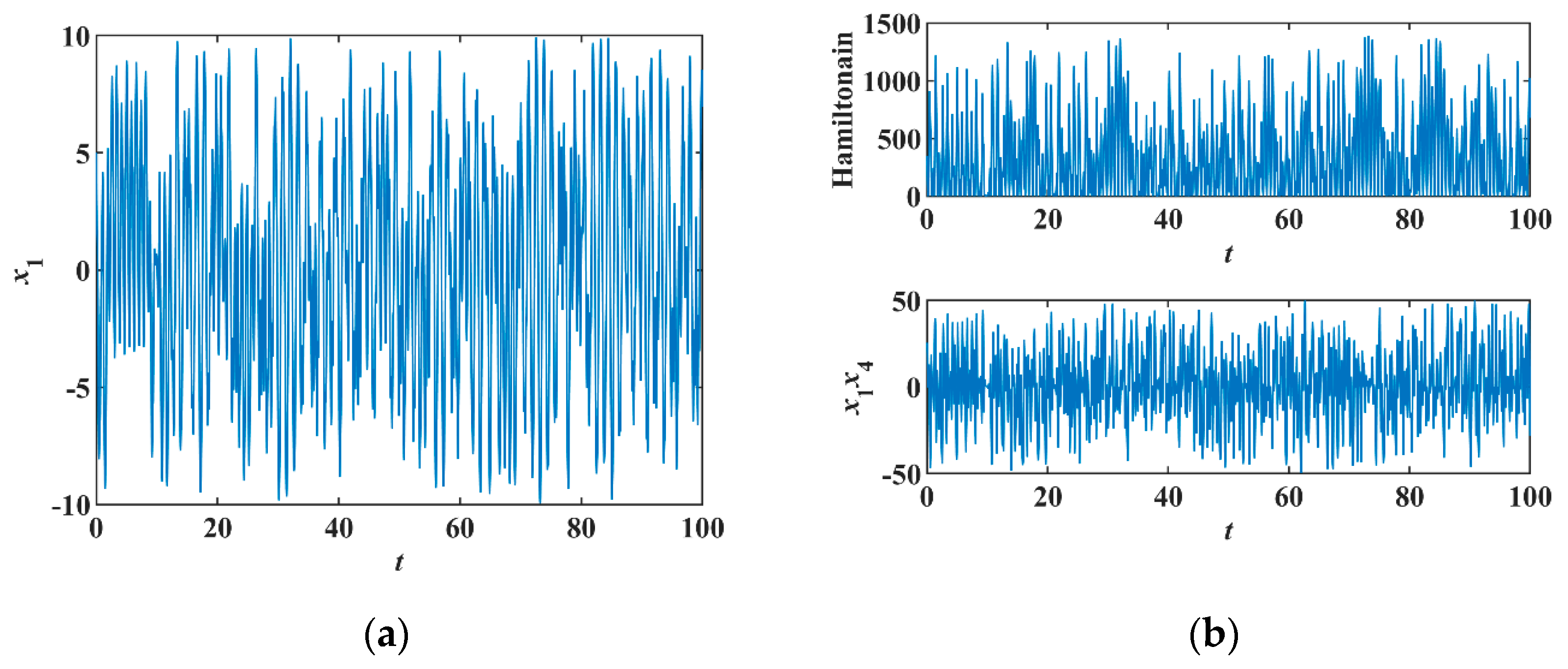
Thus, the system is non-conservative in Hamiltonian energy but conservative in phase volume. Setting initial conditions
, constant
and sampling time
s, this system produces chaotic orbits [
Figure 5a]; therefore, the Hamiltonian of Equation (12) is non-conservative because the positive and negative changes of
[
Figure 5b].
When the three-terminal memristor is coupled with the 4D Euler equation, can chaos be generated using a similar way? The memristor model is regarded as a device inserted in the 4D rigid body to replace
and
. To get the input of the memristor, we added another variable
as the input of the memristor. Thus, the memristor is
, and the new system is described as
Here
is the three-terminal memristor weight parameter. Therefore, the memristor is added as a feedback term to Equation (12). The divergence of Equation (17) is
which means the phase volume of the system (17) is still conservative.
Now, we test whether the Hamiltonian energy is still conservative. The generalized Hamiltonian form was used [
33]. We consider the input of the fifth term as a non-conservative force, and get
where
with new Hamiltonian
and
is no longer skew-symmetric but is decomposed into the sum of a skew-symmetric matrix
and a symmetric matrix
. The total force exerted on the system is non-conservative. Differentiating the Hamilton function, we get
which indicates Hamiltonian energy function is no longer conservative. We divide
of Equation (21) into
with
It can be proved that
, but
. Therefore,
represents the conservative energy of the system, and
is the non-conservative part. According to [
17], there are two categories of conservative systems: the Hamiltonian conservative chaotic system, in which both the volume and Hamiltonian of the system are constant, and the non-Hamiltonian conservative chaotic system, in which only the phase volume is conservative. Thus, the proposed three-terminal-memristor-based system (i.e., Equation (17)) is a typical non-Hamiltonian conservative chaotic system.
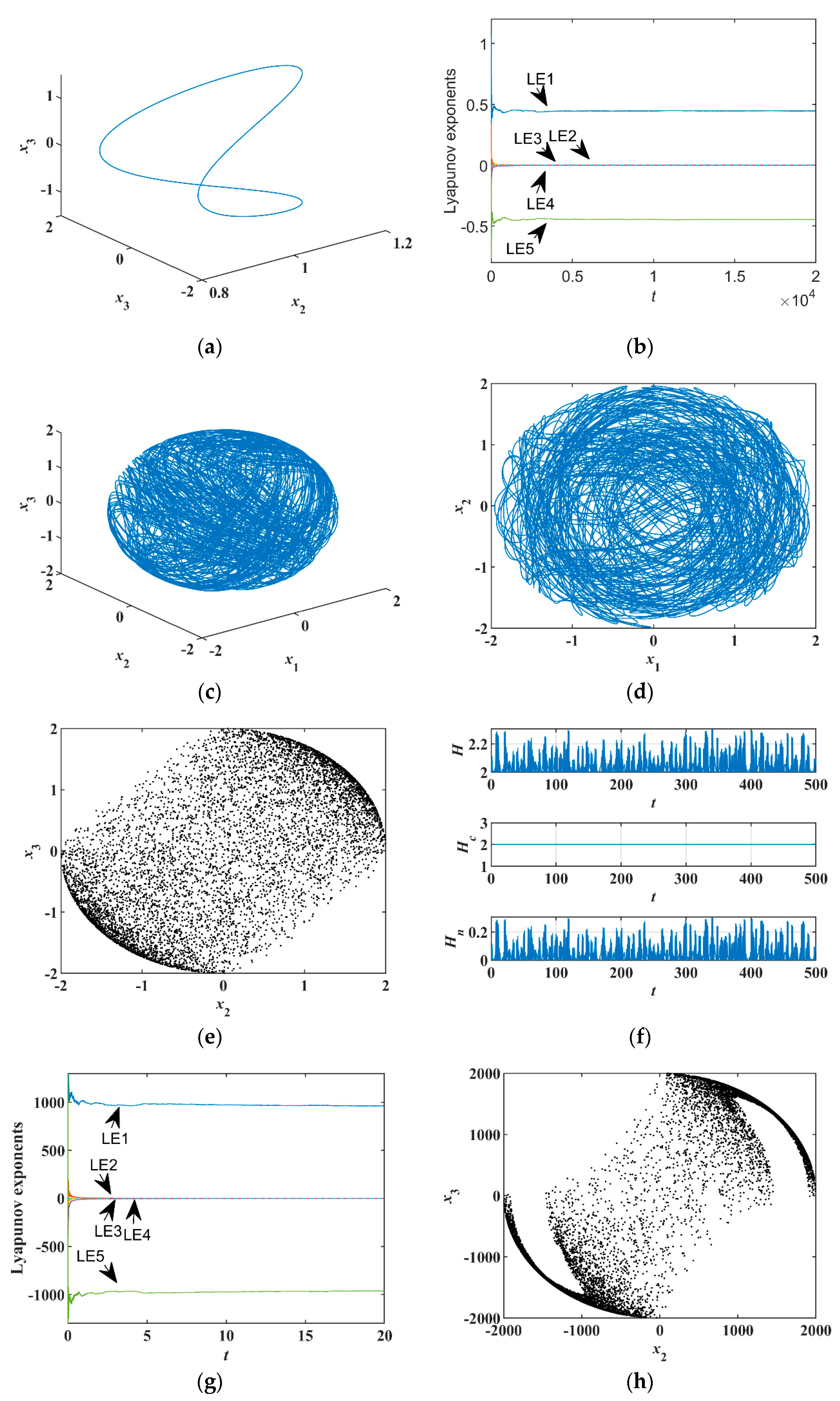
4. Equilibria and Their Stability of Three-Terminal Memristor Conservative System
The equilibria point plays an essential role in analyzing the system’s properties and we examined whether it meets the requirements of the conservative chaotic system. For a conservative system, only saddles and centers exist. There are no stable or unstable nodes and foci to exist in a conservative system. Equation (17) can be rewritten as
Setting the left of Equation (24) equal to 0, we can get three cases:
Case 1: , we can get . This case has three sub-cases as follows:
Case 1.1:
Case 1.2:
Case 1.3:
Case 2:
Case 3:
In Case 2, we derive
, but parameters
and the weight parameter
,
holds. Since
, we have
which contradicts the premise. Therefore, Case 2 does not hold. Case 3 has the same problem as Case 2. Therefore, from Case 1, the system has line equilibria
, plane equilibria
, and
. The Jacobi matrix of the system is
By substituting
into the characteristic equation, we find the eigenvalues of
as
Hence, line equilibria are centers.
For the plane equilibrium
, we find the eigenvalues as
where
where
is the imaginary unit. If
holds,
must be centers from Equation (24). If
, we can find out if
,
is a positive real number and the real parts of
must be negative. If
,
is a negative real number and the real parts of
must be positive. Therefore, if
,
must be saddles. Likewise, plane equilibrium
has the same properties as
. In sum, both
and
are either natural elliptic (centers) or saddles. Thus, from the perspective of these equilibria, the system fully meets the characteristics that the conservative system in phase space only has either saddle or center [
17,
18,
19].
6. Circuit Implementation
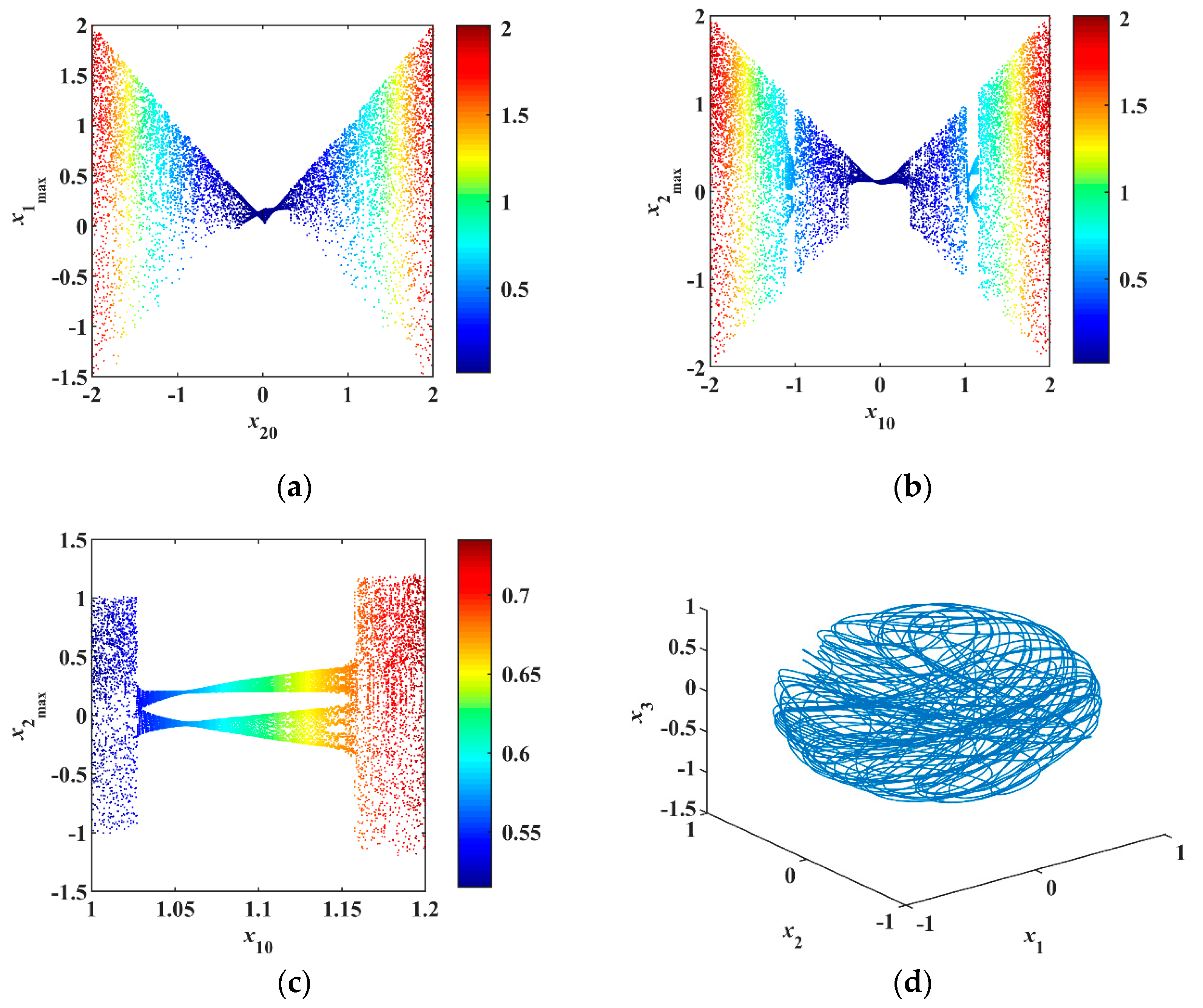
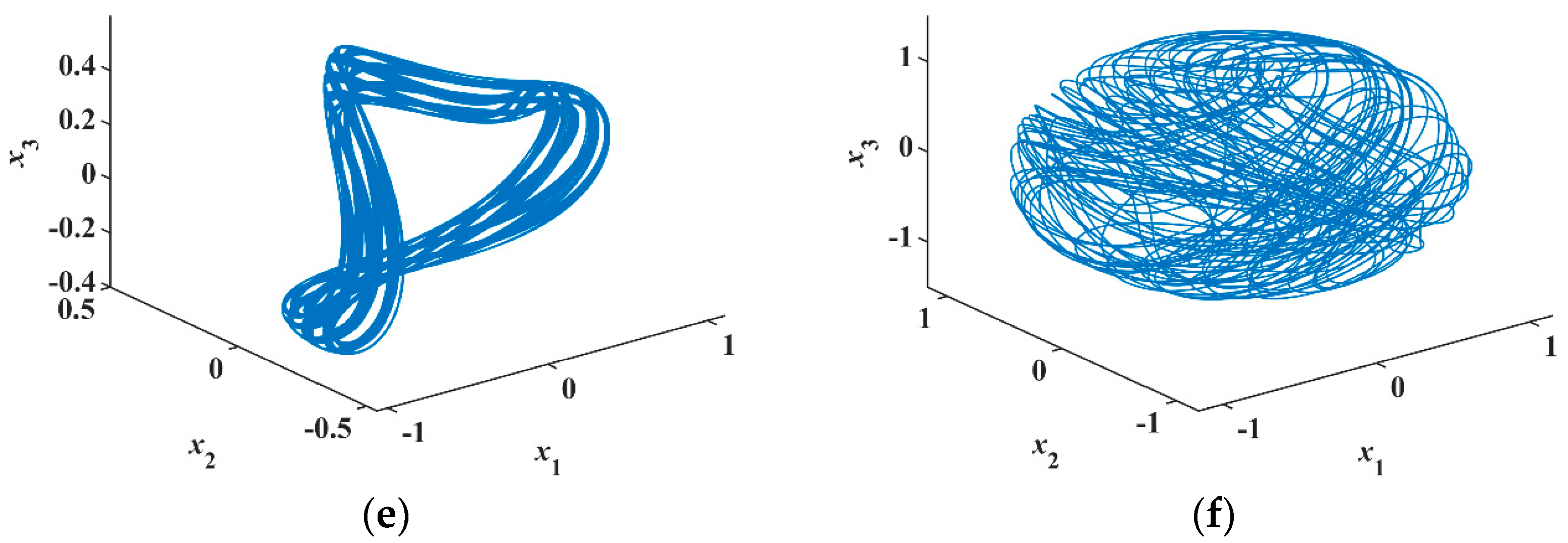
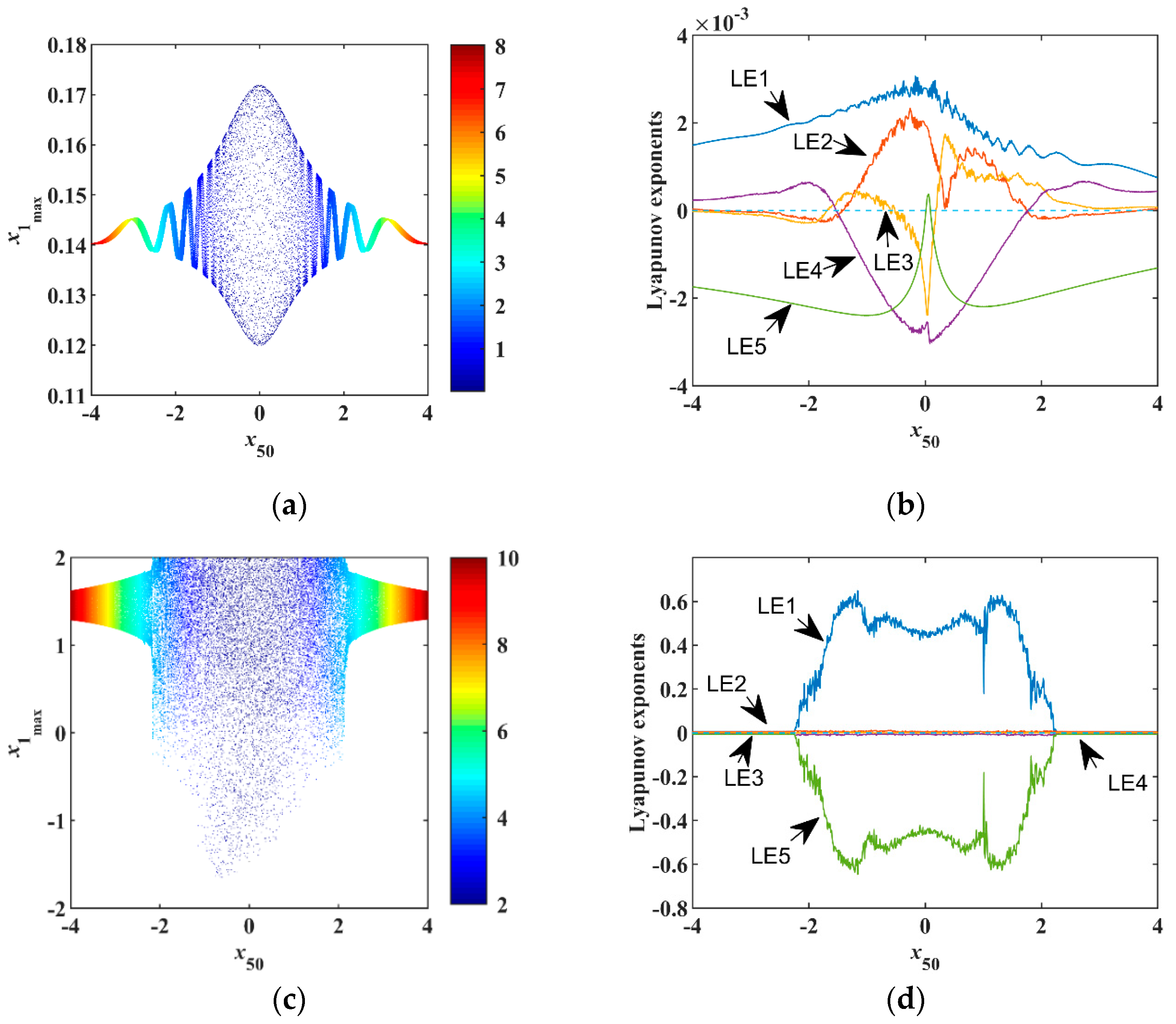
There are three methods for the simulation of nonlinear systems: chaotic system simulation circuit, FPGA (Field Programmable Gate Array), and computer numerical simulation. For the most dissipative systems, the required accuracy is not high, so all three simulation methods can be implemented. However, for conservative systems, the required accuracy is very high, especially FPGA and numerical simulation. Even if the accuracy is high, there still are problems such as algorithms, sampling, discretization, and the number of bits of computer operations causing errors. The conservative system divergence is zero, so a little bit of error will make the divergence either larger than zero leading to instability, or less than zero leading to shrinking. Both situations cause the conservative chaotic phase diagram to disappear. The hardware implementation is challenging. Therefore, for conservative systems, analog circuit simulation is indispensable because it is a real analog simulation.
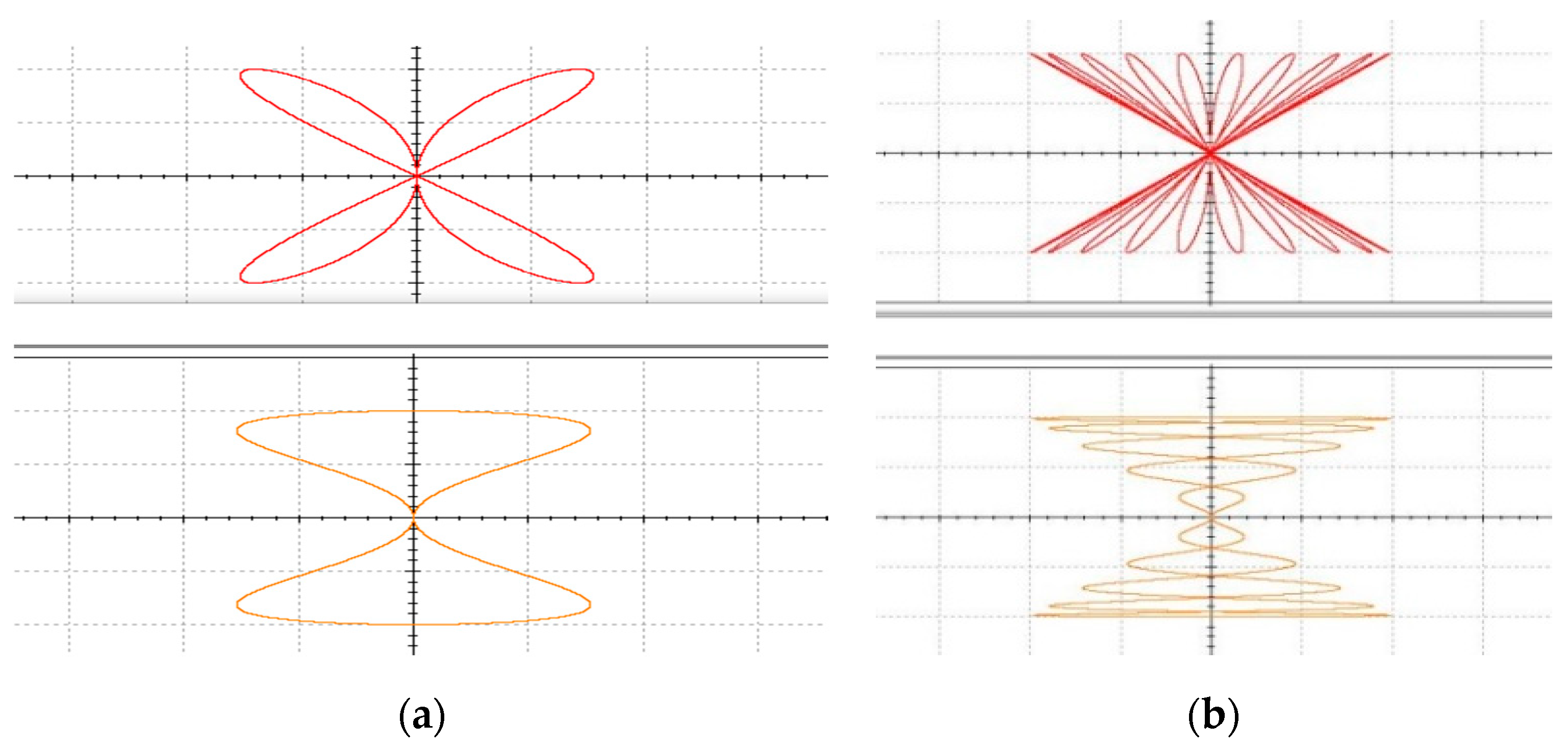
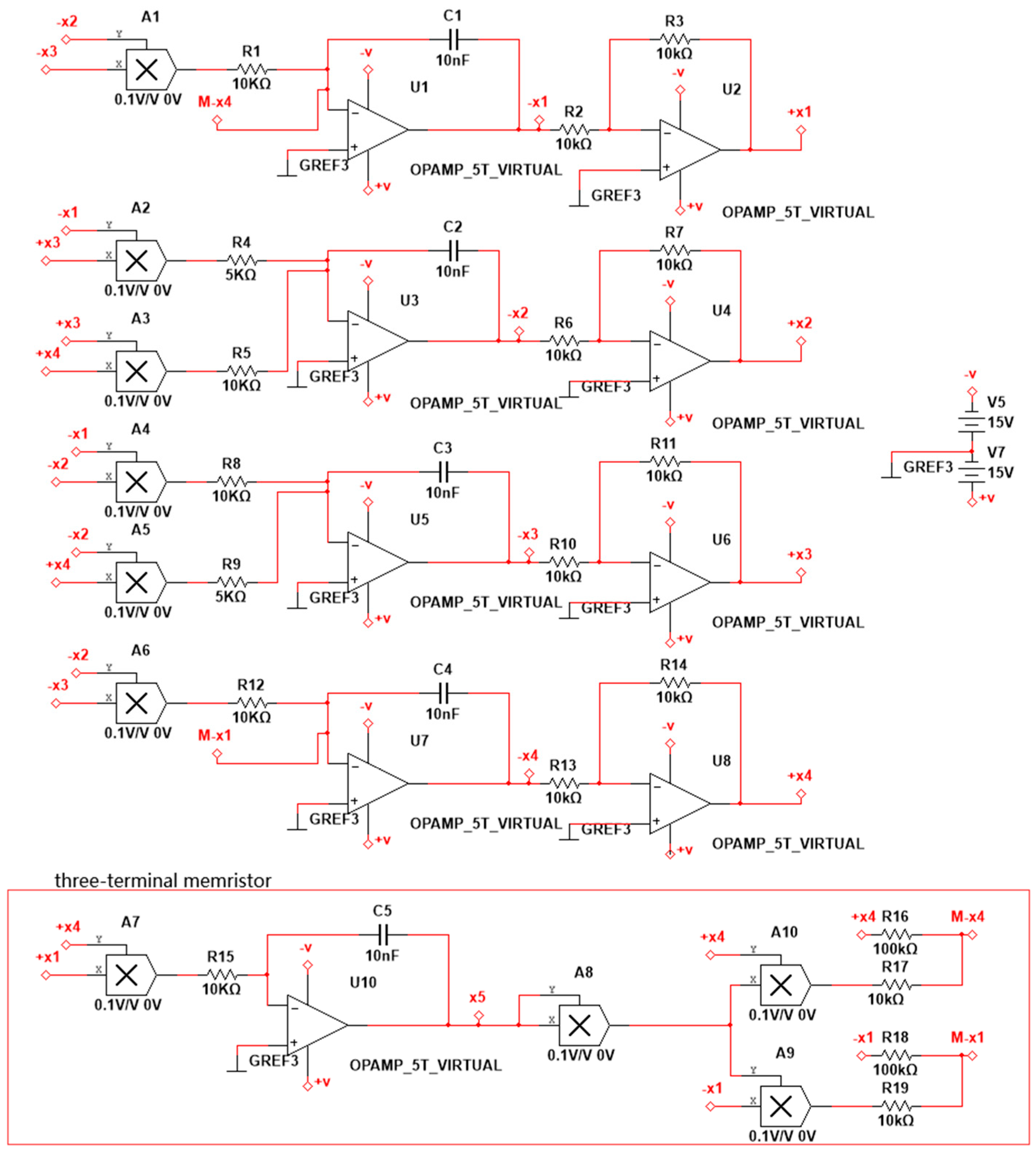
As shown in
Figure 9, the system is implemented by an analog electronic circuit without scale transformation. A total of 10 analog multipliers accomplish seven quadratic terms and two cubic terms in the system. Besides, there are five integrators and four inverters, which are composed of some capacitors and resistors. The three-terminal memristor is constructed at the bottom of
Figure 9.
Selecting the initial values
and parameters
, the phase portraits of numerical simulation are shown in
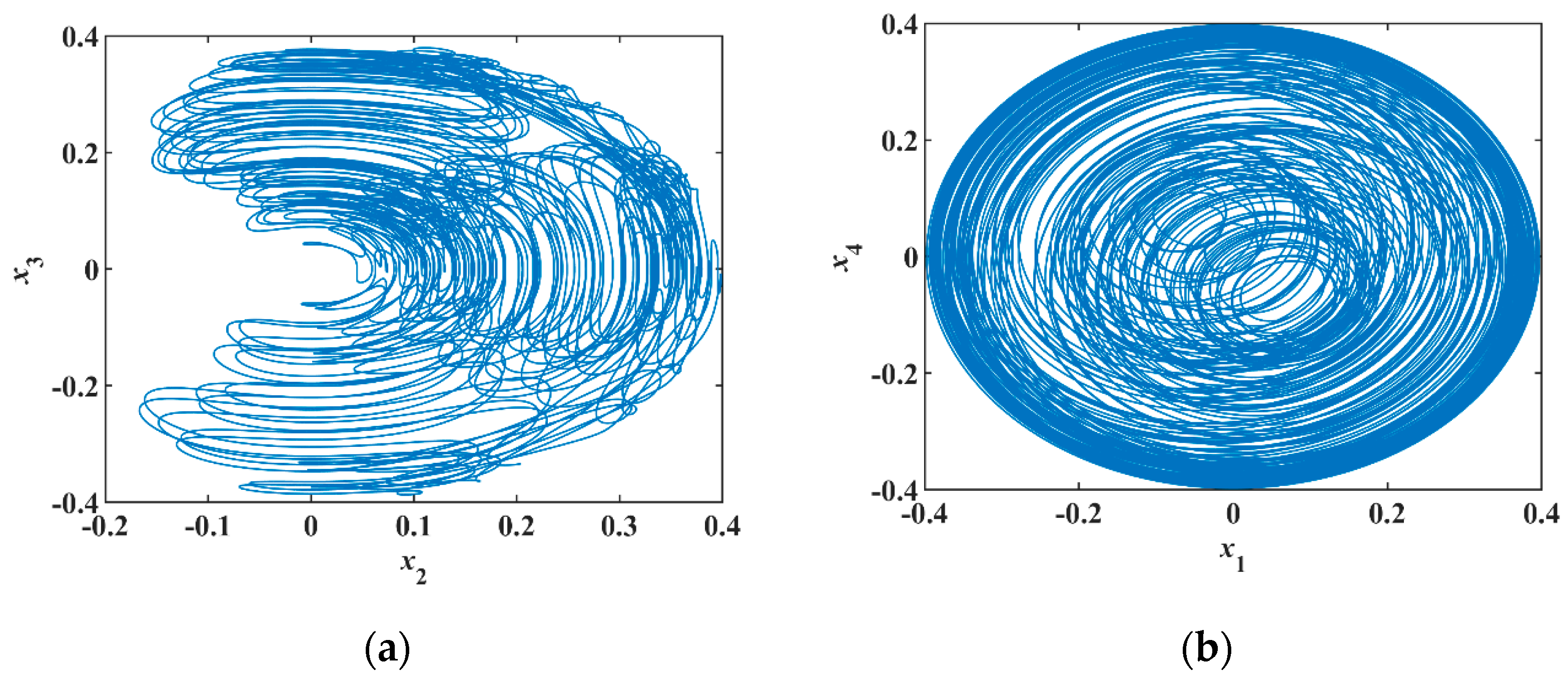
Figure 10a,b. In the analog circuit, the chips have a slight voltage deviation that corresponds to a small initial value, so there is no need to add the initial voltage between the capacitor’s two pins.
Figure 11a,b showing different phase diagrams are consistent with the results of a numerical simulation showing in
Figure 10a,b. It is verified that the proposed system produces conservative chaos.