Cryptographic Algorithm Using Newton-Raphson Method and General Bischi-Naimzadah Duopoly System
Abstract
1. Introduction
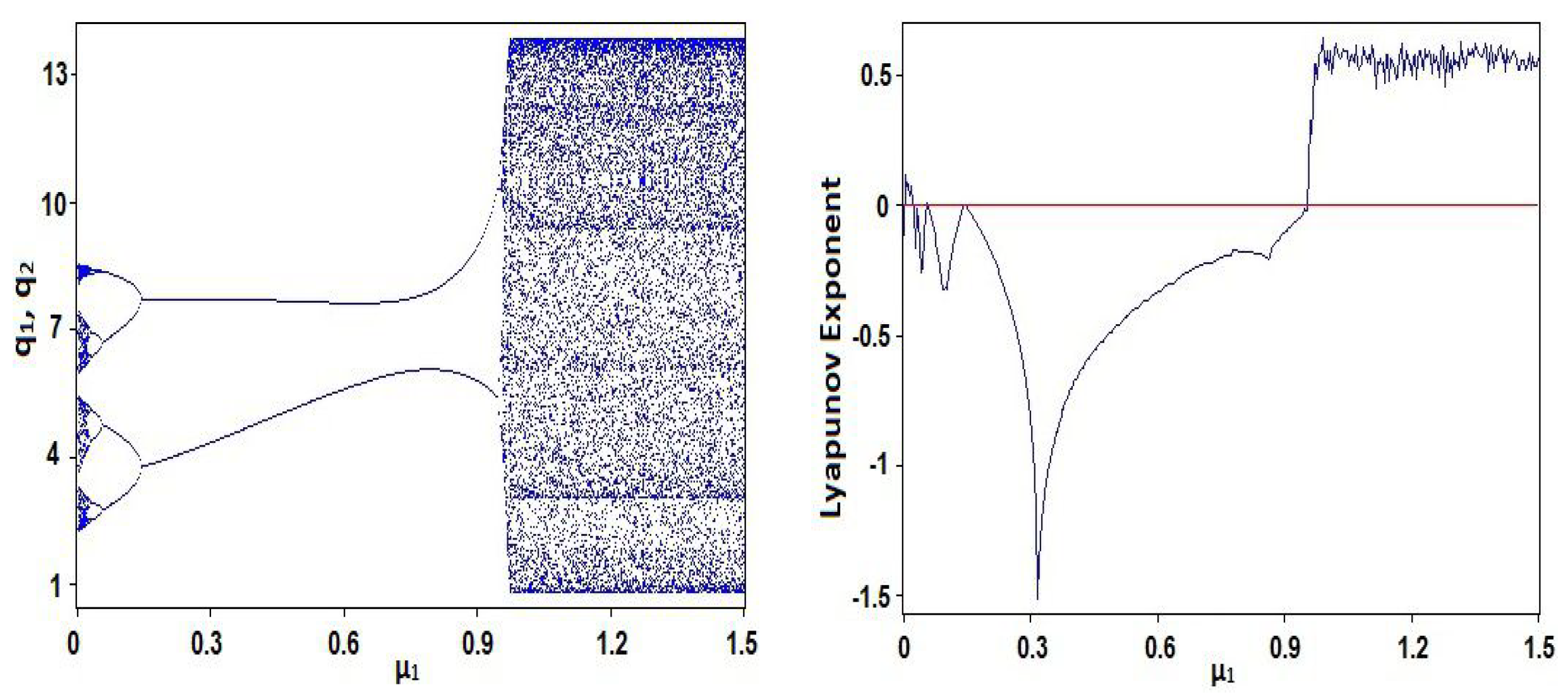
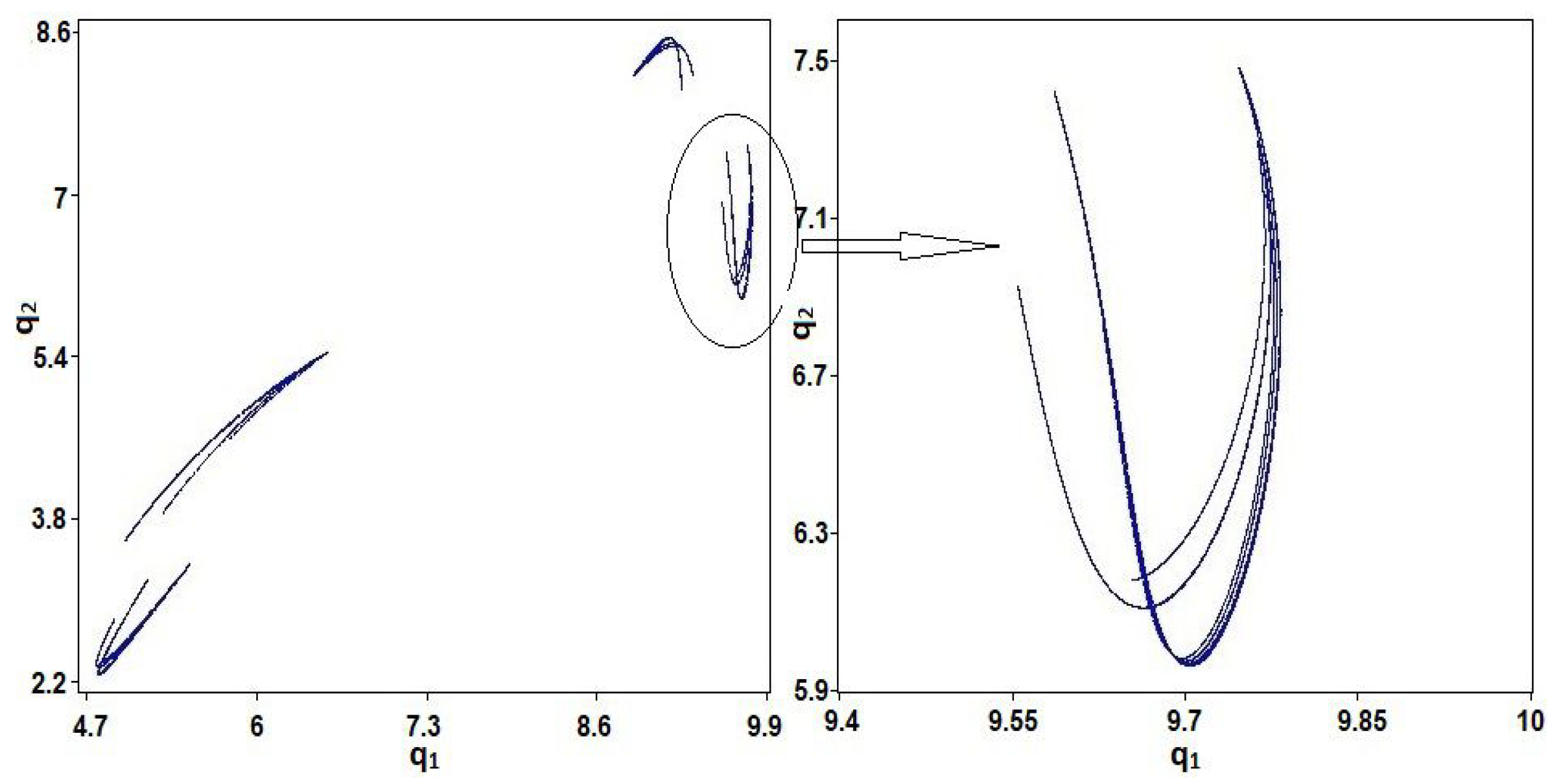
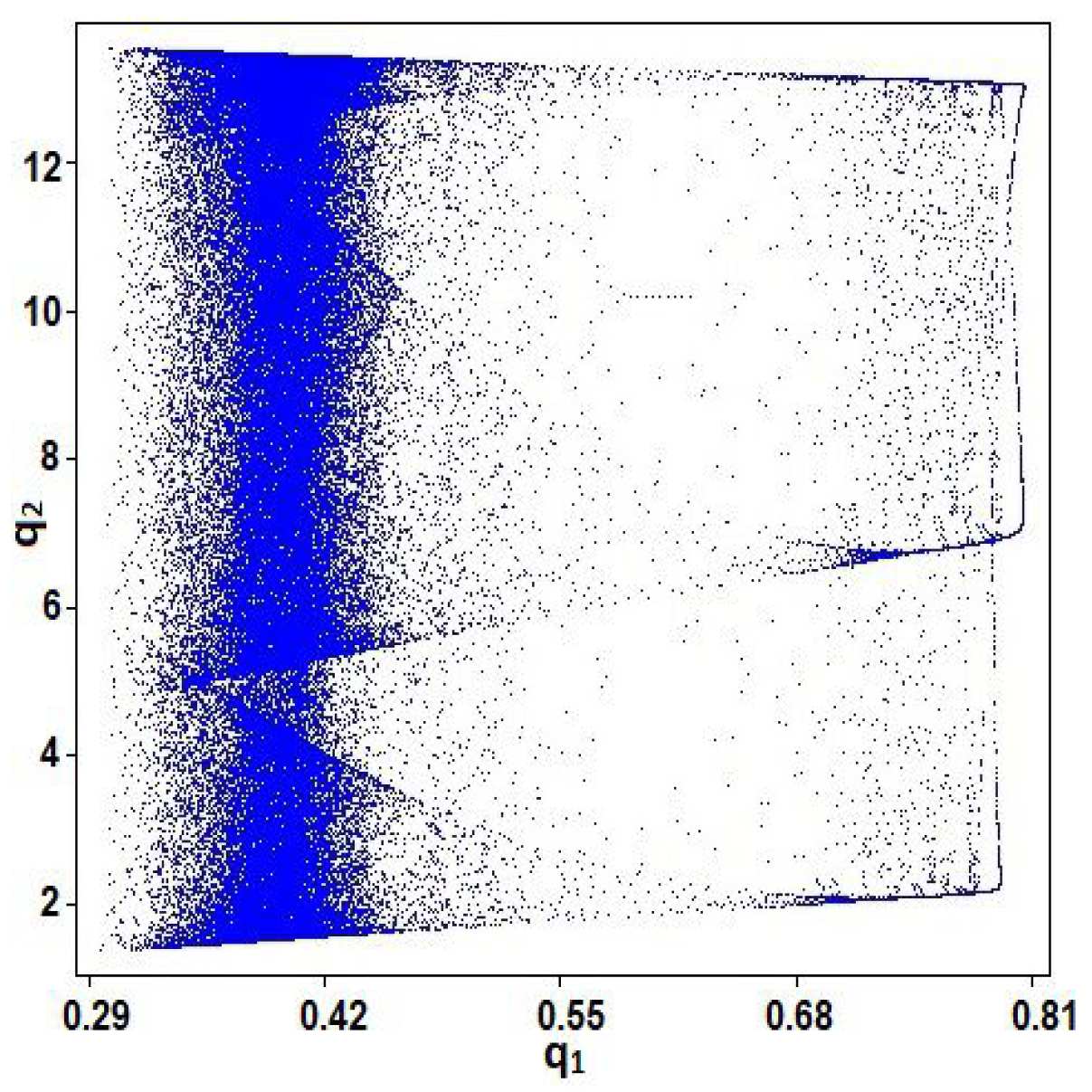
2. General Bischi-Naimzadah Duopoly System (GBNDS)
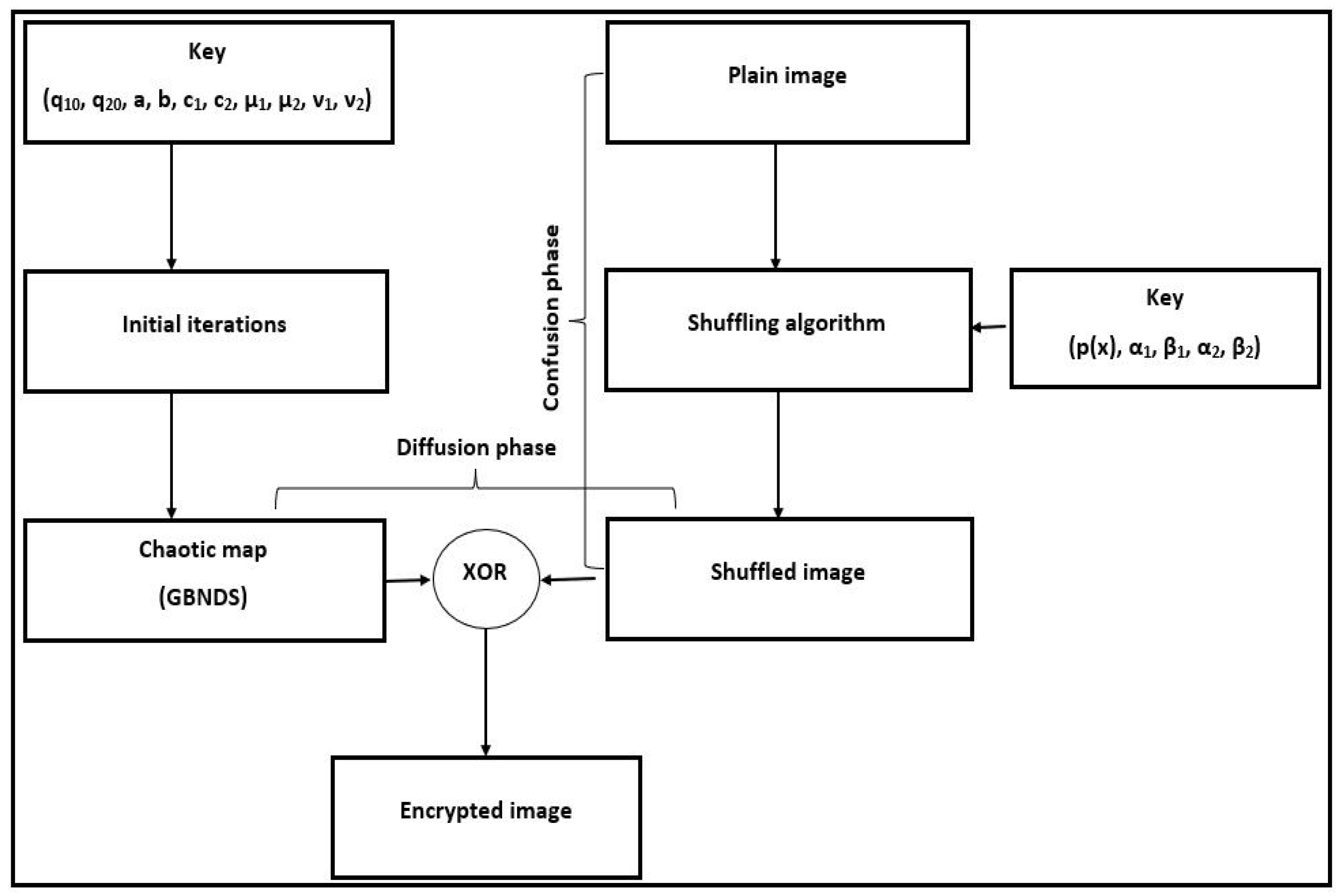
3. The Proposed Algorithm
3.1. The Key Generation
3.2. Rows/Columns Shuffling (Confusion Phase)
| Algorithm 1 Random-Permutation algorithm |
| Input: Size of random numbers, n, the polynomial , , and . Output: S, the random permutation of the integers . Step 1: Set , , Step 2: For to n, compute End For Step 3: S |
3.3. Diffusion Phase
| Algorithm 2 Row/Columns shuffling algorithm |
| Input: The plain image, O, the polynomial , , and . Output: H, the shuffled image. Step 1: Set Step 2: Use Algorithm 1, with polynomial , and interval , to generate a random permutation of size M for shuffling the rows, say . Step 3: Use Algorithm 1, with polynomial , and interval , to generate a random permutation of size N for shuffling the columns, say . Step 4: For to M, compute For to N, compute End For j End For i Step 5: H, the shuffled image. |
| Algorithm 3 Diffusion algorithm |
| Input: The shuffled image, H, , and . Output: D, the diffusion vector. Step 1: Reshape H, . Step 2: Covert H to binary, . Step 3: Set . Step 4: Perform initial iterations, For to 999 End For Step 5: Set . Step 6: For to End For Step 7: Preprocess the values of as follows: . Step 8: Covert Q to binary, . Step 9: Perform between and , say . |
3.4. The Encryption/Decryption Algorithm
| Algorithm 4 Image encryption algorithm |
| Input: The plain image, O, the polynomial , , , , and . Output: E, the encrypted image. Step 1: Read the plain image, O. Step 2: Generate the secret key by using the key mixing proportion factor. Step 3: Call Algorithm 2 to get the shuffled image H. Step 4: Call Algorithm 3 to get the diffusion vector D. Step 5: Covert D to decimal, say . Step 6: Change the dimension of to , say E. Step 7: E is the encrypted image. |
4. Experimental Results
4.1. Key Space Analysis
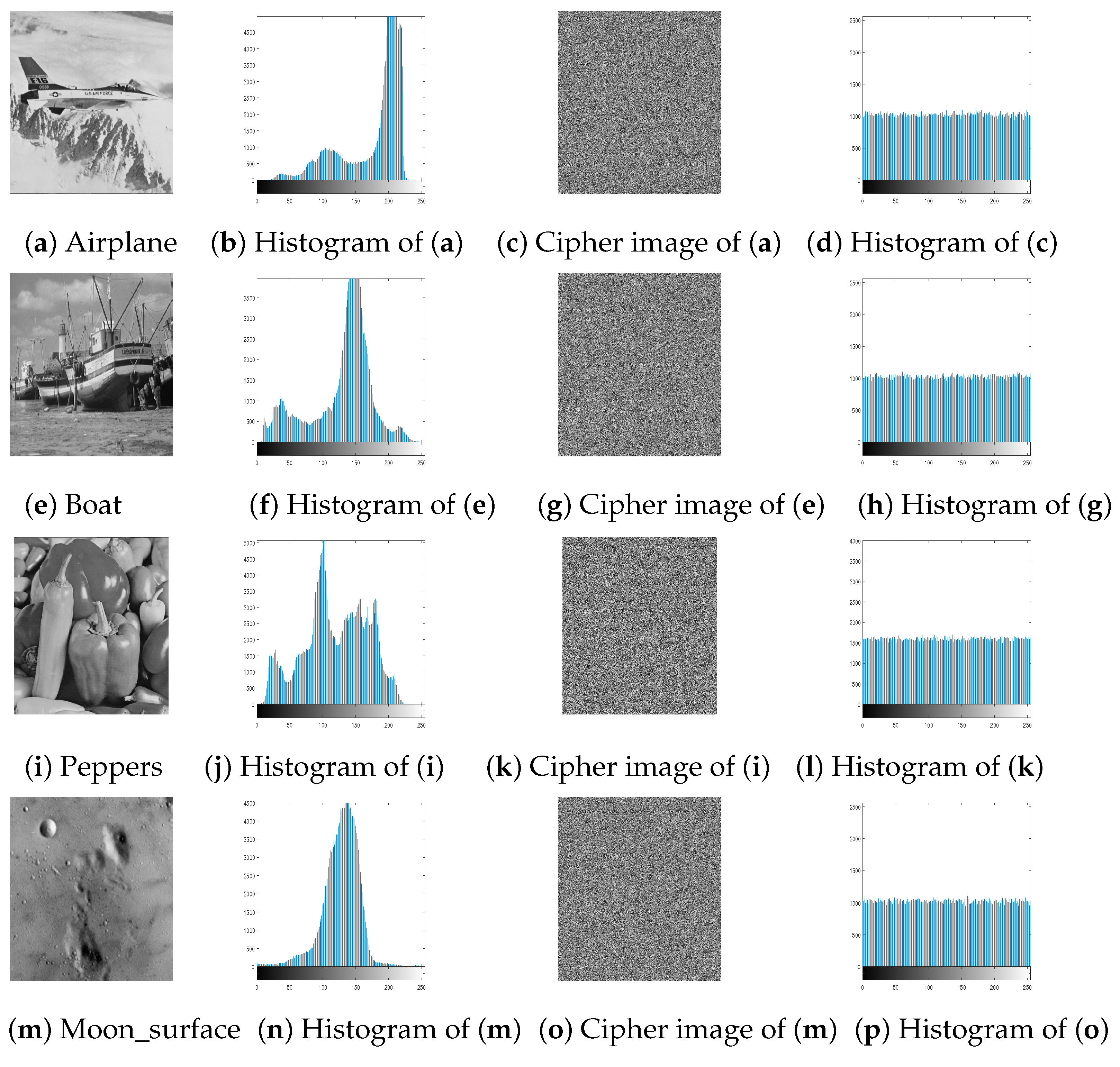
4.2. Histogram Analysis
Histogram Statistics
4.3. Entropy Analysis
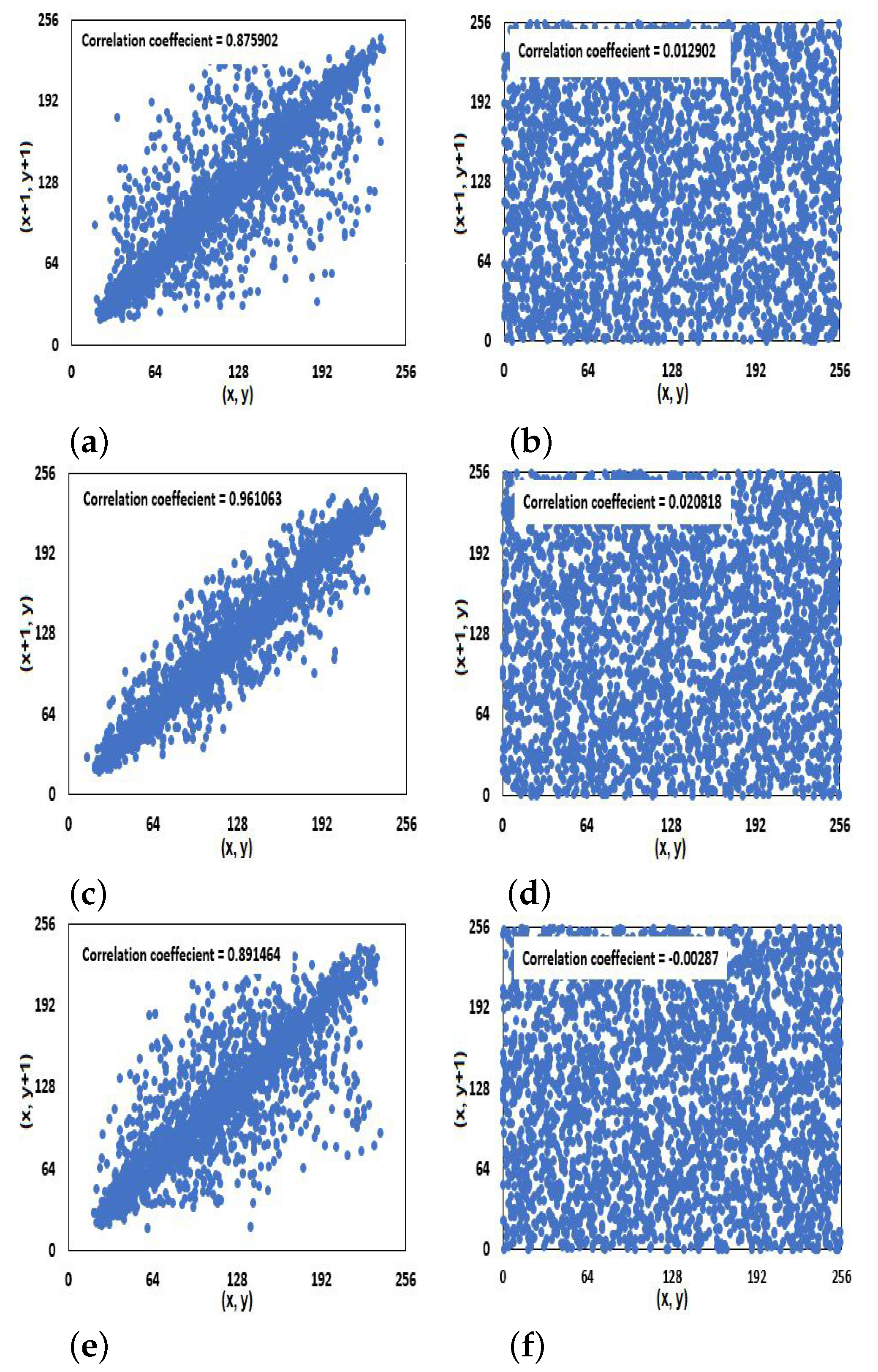
4.4. Correlation Coefficients Analysis
4.5. Differential Attack Analysis
4.6. Key Sensitivity Analysis
4.7. Robustness Analysis
4.8. Chosen Plaintext Attack Analysis
- P:
- plain image,
- E:
- encrypted image of P,
- D:
- designed image, where ,
- :
- encrypted image of D,
- :
- decrypted image of E.
4.9. Computational Analysis
4.10. NIST Statistical Tests
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arab, A.; Rostami, M.; Ghavami, B. An image encryption method based on chaos system and AES algorithm. J. Supercomput. 2019, 75, 6663–6682. [Google Scholar] [CrossRef]
- Yin, Q.; Wang, C. A new chaotic image encryption scheme using breadth-first search and dynamic diffusion. Int. J. Bifurc. Chaos 2018, 28, 1850047. [Google Scholar] [CrossRef]
- Askar, S.; Karawia, A.; Alammar, F. Cryptographic algorithm based on pixel shuffling and dynamical chaotic economic map. IET Image Process 2018, 12, 158–167. [Google Scholar] [CrossRef]
- Karawia, A. Encryption Algorithm of Multiple-Image Using Mixed Image Elements and Two Dimensional Chaotic Economic Map. Entropy 2018, 20, 801. [Google Scholar] [CrossRef]
- Askar, S.; Karawia, A.; Al-Khedhairi, A.; Alammar, F. An Algorithm of Image Encryption Using Logistic and Two-Dimensional Chaotic Economic Maps. Entropy 2019, 1, 44. [Google Scholar] [CrossRef]
- Karawia, A. Image encryption based on Fisher-Yates shuffling and three dimensional chaotic economic map. IET Image Process 2019, 13, 2086–2097. [Google Scholar] [CrossRef]
- Wu, X.; Wang, K.; Wang, X.; Kan, H. Lossless chaotic color image cryptosystem based on DNA encryption and entropy. Nonlinear Dynam. 2017, 90, 855–875. [Google Scholar] [CrossRef]
- Wu, X.; Wang, D.; Kurths, J.; Kan, H. A novel lossless color image encryption scheme using 2d dwt and 6d hyperchaotic system. Inf. Sci. 2016, 349, 137–153. [Google Scholar] [CrossRef]
- Ivanov, G.; Nikolov, N.; Nikova, S. Cryptographically strong S-boxes generated by modified immune algorithm. In Proceedings of the International Conference on Cryptography and Information Security in the Balkans, Koper, Slovenia, 3–4 September 2015; pp. 31–42. [Google Scholar]
- Azam, N.; Hayat, U.; Ikram, U. Efficient construction of a substitution box based on a Mordell elliptic curve over a finite field. Front. Inform. Technol. El 2019, 20, 1378–1389. [Google Scholar] [CrossRef]
- Jia, N.; Liu, S.; Ding, Q.; Wu, S.; Pan, X. A New Method of Encryption Algorithm Based on Chaos and ECC. J. Inf. Hiding Multimed. Signal Process. 2016, 7, 637–643. [Google Scholar]
- Hayat, U.; Azam, N. A novel image encryption scheme based on an elliptic curve. Signal Process. 2019, 155, 391–402. [Google Scholar] [CrossRef]
- Tonga, X.; Zhanga, M.; Wang, Z.; Liu, Y.; Ma, J. An image encryption scheme based on a new hyperchaotic finance system. Optik 2015, 126, 2445–2452. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, X.; Zhao, X.; Yu, H.; Zhang, L. Quadratic function chaotic system and its application on digital image encryption. IEEE Access 2020, 8, 55540–55549. [Google Scholar] [CrossRef]
- Pareschi, F.; Setti, G.; Rovatti, R. Implementation and testing of high-speed cmos true random number generators based on chaotic systems. IEEE Trans. Circuits-I 2010, 57, 3124–3137. [Google Scholar] [CrossRef]
- Seyedzadeh, S.M.; Norouzi, B.; Mosavi, M.R.; Mirzakuchaki, S. A novel color image encryption algorithm based on spatial permutation and quantum chaotic map. Nonlinear Dynam. 2015, 81, 511–529. [Google Scholar] [CrossRef]
- Wu, Y.; Hua, Z.; Zhou, Y. N-dimensional discrete cat map generation using laplace expansions. IEEE Trans. Cybern. 2016, 46, 2622–2633. [Google Scholar] [CrossRef]
- Lian, S.; Sun, J.; Wang, Z. Security analysis of a chaos-based image encryption algorithm. Phys. A 2005, 351, 645–661. [Google Scholar] [CrossRef]
- Skrobek, A. Cryptanalysis of chaotic stream cipher. Phys. Lett. A 2007, 363, 84–90. [Google Scholar] [CrossRef]
- Yang, T.; Yang, L.; Yang, C. Cryptanalyzing chaotic secure communications using return maps. Phys. Lett. A 1998, 245, 495–510. [Google Scholar] [CrossRef]
- Shakiba, A. A randomized CPA-secure asymmetric-key chaotic color image encryption scheme based on the Chebyshev mappings and one-time pad. J. King Saud Univ. Comput. Inf. Sci. 2019. [Google Scholar] [CrossRef]
- Xiao, S.; Yu, Z.; Deng, Y. Design and analysis of a novel chaos-based image encryption algorithm via switch control mechanism. Secur. Commun. Netw. 2020, 2020. [Google Scholar] [CrossRef]
- Cao, C.; Sun, K.; Liu, W. A novel bit-level image encryption algorithm based on 2d-LICM hyperchaotic map. Signal Process. 2018, 143, 122–133. [Google Scholar] [CrossRef]
- Shakiba, A. A novel randomized one-dimensional chaotic chebyshev mapping for chosen plaintext attack secure image encryption with a novel chaotic breadth first traversal. Multimed. Tools Appl. 2019, 78, 34773–34799. [Google Scholar] [CrossRef]
- Pak, C.; Huang, L. A new color image encryption using combination of the 1d chaotic map. Signal Process. 2017, 138, 129–137. [Google Scholar] [CrossRef]
- Rajendran, R.; Manivannan, D. A secure image cryptosystem using 2D arnold cat map and logistic map. Int. J. Pharm. Technol. 2016, 8, 25173–25182. [Google Scholar]
- Gu, G.; Ling, J. A fast image encryption method by using chaotic 3D cat maps. Optik 2014, 125, 4700–4705. [Google Scholar] [CrossRef]
- Mohamed, N.; El-Azeim, M.; Zaghloul, A. Improving Image Encryption Using 3D Cat Map and Turing Machine. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 208–215. [Google Scholar]
- Zhao, Y.; Gao, C.; Liu, J.; Dong, S. A Self-perturbed Pseudo-random Sequence Generator Based on Hyperchaos. Chaos Soliton Fract. X 2019, 4, 100023. [Google Scholar] [CrossRef]
- Li, C.; Chen, M.; Lo, K. Breaking an image encryption algorithm based on chaos. Int. J. Bifurcat. Chaos 2011, 21, 3518–3524. [Google Scholar] [CrossRef]
- Wang, X.; Teng, L.; Qin, X. A novel colour image encryption algorithm based on chaos. Signal Process. 2012, 92, 1101–1108. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Li, L.; Zhu, X. A novel plaintext-related image encryption scheme using hyper-chaotic system. Nonlinear Dynam. 2018, 94, 1319–1333. [Google Scholar] [CrossRef]
- Lindell, Y.; Katz, J. Introduction to Modern Cryptography; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Li, C.; Zhang, L.; Ou, R.; Wong, K.; Shu, S. Breaking a novel colour image encryption algorithm based on chaos. Nonlinear Dynam. 2012, 70, 2383–2388. [Google Scholar] [CrossRef]
- Ding, L.; Ding, Q. A Novel Image Encryption Scheme Based on 2D Fractional Chaotic Map, DWT and 4D Hyper-chaos. Electronics 2020, 9, 1280. [Google Scholar] [CrossRef]
- Enzeng, D.; Zengqiang, C.; Zhuzhi, Y.; Zaiping, C. A chaotic images encryption algorithm with the key mixing proportion factor. In Proceedings of the 2008 International Conference on Information Management, Innovation Management and Industrial Engineering, Taipei, Taiwan, 19–21 December 2008; pp. 169–174. [Google Scholar]
- Hosny, K. Multimedia Security Using Chaotic Maps: Principles and Methodologies. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Askar, S.; Al-Khedhairi, A. Local and Global Dynamics of a Constraint Profit Maximization for Bischi-Naimzada Competition Duopoly Game. Mathematics 2020, 8, 1458. [Google Scholar] [CrossRef]
- Zhang, L.; Li, C.; Wong, K.; Shu, S.; Chen, G. Cryptanalyzing a chaos-based image encryption algorithm using alternate structure. J. Syst. Softw. 2012, 85, 2077–2085. [Google Scholar] [CrossRef]
- Shakiba, A. A novel randomized bit-level two-dimensional hyperchaotic image encryption algorithm. Multimed. Tools Appl. 2020. [Google Scholar] [CrossRef]
- Escobar, M.; Castillon, M.; Gutierrez, R.; Hernandez, C. Suggested Integral Analysis for Chaos-Based Image Cryptosystems. Entropy 2019, 21, 815. [Google Scholar] [CrossRef]
- Ahmad, M.; Shamsi, U.; Khan, I. An enhanced image encryption algorithm using fractional chaotic systems. Procedia Comput. Sci. 2015, 57, 852–859. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. NIST Special Publication 800-822 2001. Available online: http://www.nist.gov/manuscript-publication-search.cfm?pub_id=151222 (accessed on 15 May 2001).


| Statistical Test | PRNG | Result |
|---|---|---|
| Frequency monobit test | 100/100 | PASS |
| Block frequency test | 99/100 | PASS |
| Rank test | 99/100 | PASS |
| Runs test | 97/100 | PASS |
| Longest runs test | 99/100 | PASS |
| Cumulative sums test | 100/100 | PASS |
| Discrete Fourier transform | 100/100 | PASS |
| Random excursion test | 56/58 | PASS |
| Random excursion variant test | 57/58 | PASS |
| Universal test | 96/100 | PASS |
| Approximate entropy | 97/100 | PASS |
| Linear complexity test | 99/100 | PASS |
| Serial | 99/100 | PASS |
| Non Overlapping templates test | 97/100 | PASS |
| Overlapping templates test | 100/100 | PASS |
| Algorithm | IEGBNDS Algorithm | [5] | [23] | [40] |
|---|---|---|---|---|
| Key space | >10 |
| Image | -Value |
|---|---|
| Lena | 286.52 |
| Barbara | 256.74 |
| Cameraman | 252.88 |
| Mandrill | 275.24 |
| Airplane | 279.64 |
| Boat | 260.23 |
| Peppers | 288.74 |
| Moon_surface | 249.12 |
| Image | Plain Image | Cipher Image | ||||
|---|---|---|---|---|---|---|
| IEGBNDS | [41] | |||||
| V | S | V | S | V | S | |
| lena ( | 38451 | 196.1 | 396 | 19.9 | 414 | 20.3 |
| lena ( | 633397 | 795.9 | 3171 | 56.3 | 3340 | 57.8 |
| Image | Information Entropy | |
|---|---|---|
| Plain Image | Encrypted Image | |
| Lena | 7.4475 | 7.9992 |
| Barbara | 7.6338 | 7.9993 |
| Cameraman | 7.0518 | 7.9993 |
| Mandrill | 7.2933 | 7.9992 |
| Airplane | 6.6823 | 7.9992 |
| Boat | 7.2151 | 7.9993 |
| Peppers | 7.4849 | 7.9992 |
| Moon_surface | 6.6974 | 7.9993 |
| Average | 7.1883 | 7.99925 |
| [5] (Average) | – | 7.99867 |
| [23] (Average) | – | 7.90252 |
| [40] (Average) | 7.266297 | 7.999224 |
| Image | Correlation Coefficient | ||
|---|---|---|---|
| Horizontal | Vertical | Diagonal | |
| Lena | 0.0011 | −0.0026 | −0.0015 |
| Barbara | −0.0006 | −0.0015 | −0.0010 |
| Cameraman | −0.0035 | −0.0029 | −0.0015 |
| Mandrill | −0.0002 | −0.0005 | −0.0026 |
| Airplane | 0.0029 | −0.0020 | −0.0049 |
| Boat | −0.0034 | −0.0019 | 0.0010 |
| Peppers | −0.0035 | 0.0032 | 0.0017 |
| Moon_surface | −0.0013 | 0.0000 | 0.0011 |
| Average | 0.002063 | 0.001825 | 0.001913 |
| [5] (Average) | 0.007067 | 0.007867 | 0.014567 |
| [23] (Average) | 0.001544 | 0.001772 | 0.002678 |
| [40] (Average) | 0.003134 | 0.006602 | 0.004525 |
| Image | NPCR (%) | UACI% |
|---|---|---|
| Ideal value [23] | 99.6094 | 33.4635 |
| Lena | 99.6326 | 33.4584 |
| Barbara | 99.6082 | 33.5339 |
| Cameraman | 99.6044 | 33.5797 |
| Mandrill | 99.6204 | 33.4392 |
| Airplane | 99.5907 | 33.4608 |
| Boat | 99.6086 | 33.4599 |
| Peppers | 99.6033 | 33.4868 |
| Moon_surface | 99.5998 | 33.4590 |
| Average | 99.6085 | 33.48471 |
| [5] (Average) | 99.6067 | 33.4267 |
| [23] (Average) | 99.6083 | 33.4521 |
| [40] (Average) | 99.6060 | 33.4646 |
| Cipher | Decrypted with | Decrypted with | Decrypted with |
| image | true key | wrong key | wrong key |
 |  |  |  |
| Decrypted with | Decrypted with | Decrypted with | Decrypted with |
| wrong key | wrong key | wrong key | wrong key |
 |  |  |  |
| Encrypted with | Decryption of | Encrypted with | Decryption of |
| salt&pepper(0.01) | previous image | salt&pepper(0.05) | previous image |
 |  |  |  |
| Encrypted with | Decryption of | Encrypted with | Decryption of |
| salt&pepper(0.1) | previous image | corp of | previous image |
 |  |  |  |
| Algorithm | Image Size | Running Time (ms) |
|---|---|---|
| IEGBNDS | ||
| [40] | ||
| [23] |
| Statistical Test | IEGBNDS Algorithm | Result |
|---|---|---|
| Frequency monobit test | 100/100 | PASS |
| Block frequency test | 99/100 | PASS |
| Rank test | 99/100 | PASS |
| Runs test | 99/100 | PASS |
| Longest runs test | 100/100 | PASS |
| Cumulative sums test | 99/100 | PASS |
| Discrete Fourier transform | 98/100 | PASS |
| Random excursion test | 56/58 | PASS |
| Random excursion variant test | 57/58 | PASS |
| Universal test | 99/100 | PASS |
| Approximate entropy | 98/100 | PASS |
| Linear complexity test | 100/100 | PASS |
| Serial | 100/100 | PASS |
| Non Overlapping templates test | 99/100 | PASS |
| Overlapping templates test | 100/100 | PASS |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karawia, A. Cryptographic Algorithm Using Newton-Raphson Method and General Bischi-Naimzadah Duopoly System. Entropy 2021, 23, 57. https://doi.org/10.3390/e23010057
Karawia A. Cryptographic Algorithm Using Newton-Raphson Method and General Bischi-Naimzadah Duopoly System. Entropy. 2021; 23(1):57. https://doi.org/10.3390/e23010057
Chicago/Turabian StyleKarawia, Abdelrahman. 2021. "Cryptographic Algorithm Using Newton-Raphson Method and General Bischi-Naimzadah Duopoly System" Entropy 23, no. 1: 57. https://doi.org/10.3390/e23010057
APA StyleKarawia, A. (2021). Cryptographic Algorithm Using Newton-Raphson Method and General Bischi-Naimzadah Duopoly System. Entropy, 23(1), 57. https://doi.org/10.3390/e23010057





