On Default Priors for Robust Bayesian Estimation with Divergences
Abstract
1. Introduction
2. Robust Bayesian Estimation Using Divergences
2.1. Framework of Robustness
2.2. General Bayesian Updating
2.3. Assumptions and Previous Works
- (A1)
- The support of the density function does not depend on unknown parameter , and is fifth-order differentiable with respect to in neighborhood U of .
- (A2)
- The interchange of the order of integration with respect to x and differentiation as is justified. The expectations:are all finite, and exists such that:and for all , where and , while is the expectation of X with respect to a probability density function g.
- (A3)
- For any , with probability one:for some and for all sufficiently large n.
3. Main Results
3.1. Moment Matching Priors
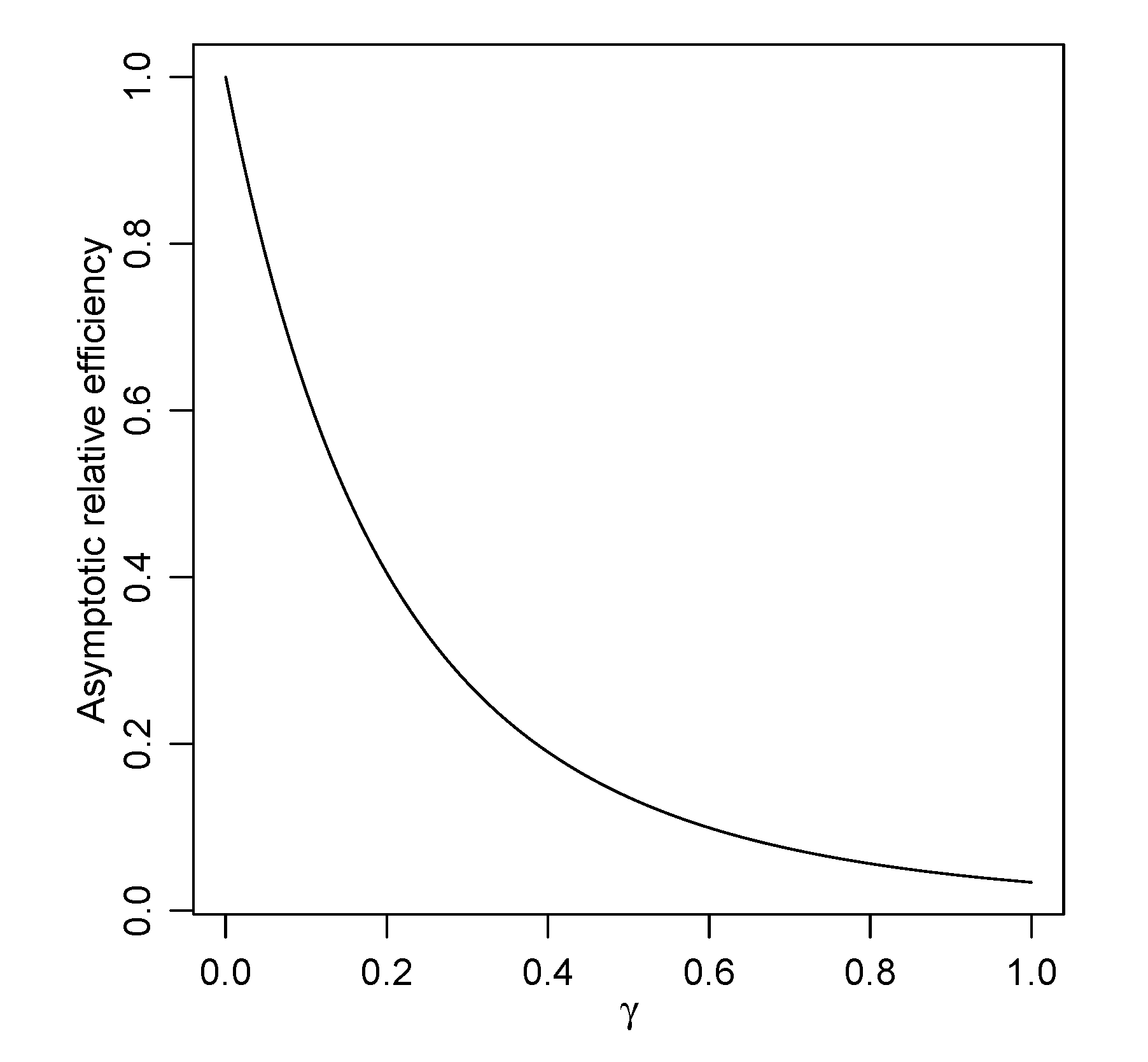
3.2. Robustness of Objective Priors
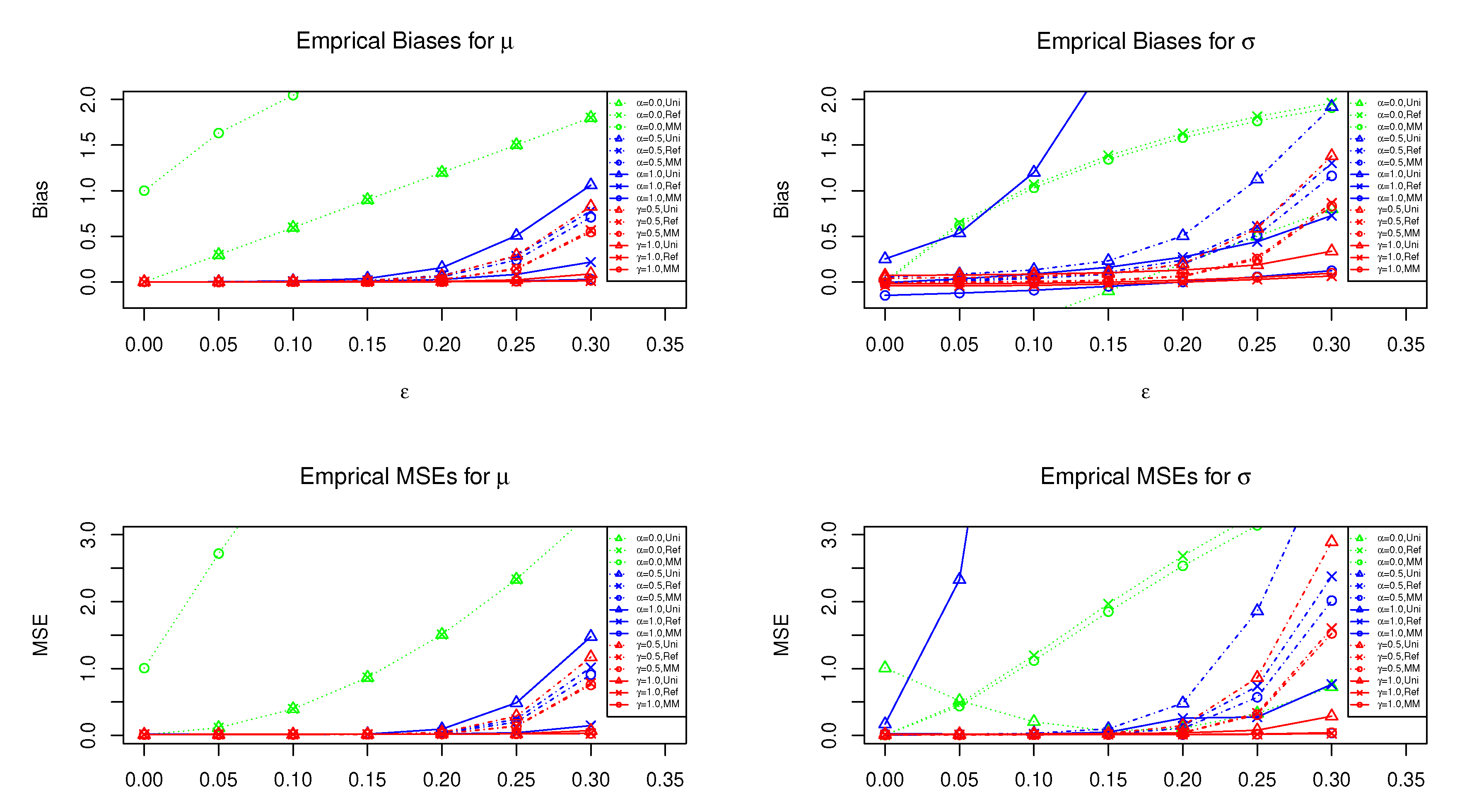
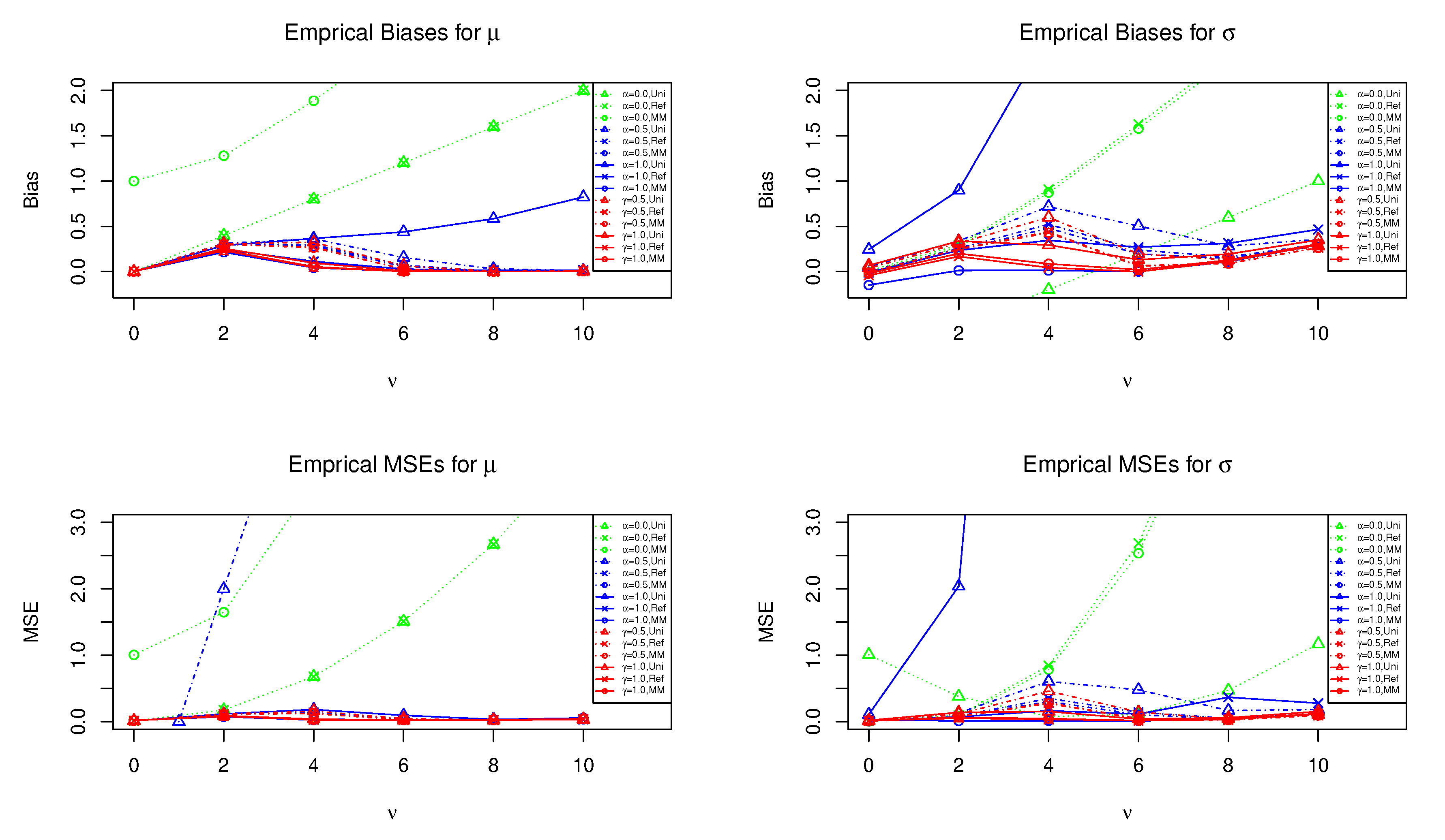
4. Simulation Studies
4.1. Setting and Results
4.2. Selection of Tuning Parameters
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Some Derivative Functions
References
- Huber, J.; Ronchetti, E.M. Robust Statistics, 2nd ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Basu, A.; Shioya, H.; Park, C. Statistical Inference: The Minimum Distance Approach; Chapman & Hall: Boca Raton, FL, USA, 2011. [Google Scholar]
- Basu, A.; Harris, I.R.; Hjort, N.L.; Jones, M. Robust and efficient estimation by minimising a density power divergence. Biometrika 1998, 85, 549–559. [Google Scholar] [CrossRef]
- Jones, M.; Hjort, N.L.; Harris, I.R.; Basu, A. A comparison of related density-based minimum divergence estimators. Biometrika 2001, 88, 865–873. [Google Scholar] [CrossRef]
- Fujisawa, H.; Eguchi, S. Robust parameter estimation with a small bias against heavy contamination. J. Multivar. Anal. 2008, 99, 2053–2081. [Google Scholar] [CrossRef]
- Hirose, K.; Fujisawa, H.; Sese, J. Robust sparse Gaussian graphical modeling. J. Multivar. Anal. 2016, 161, 172–190. [Google Scholar] [CrossRef]
- Kawashima, T.; Fujisawa, H. Robust and sparse regression via γ-divergence. Entropy 2017, 19, 608. [Google Scholar] [CrossRef]
- Hirose, K.; Masuda, H. Robust relative error estimation. Entropy 2018, 20, 632. [Google Scholar] [CrossRef] [PubMed]
- Bissiri, P.G.; Holmes, C.C.; Walker, S.G. A general framework for updating belief distributions. J. R. Stat. Soc. Ser. B Stat. Methodol. 2016, 78, 1103–1130. [Google Scholar] [CrossRef] [PubMed]
- Hooker, G.; Vidyashankar, A.N. Bayesian model robustness via disparities. Test 2014, 23, 556–584. [Google Scholar] [CrossRef]
- Ghosh, A.; Basu, A. Robust Bayes estimation using the density power divergence. Ann. Inst. Stat. Math. 2016, 68, 413–437. [Google Scholar] [CrossRef]
- Nakagawa, T.; Hashimoto, S. Robust Bayesian inference via γ-divergence. Commun. Stat. Theory Methods 2020, 49, 343–360. [Google Scholar] [CrossRef]
- Jewson, J.; Smith, J.Q.; Holmes, C. Principles of Bayesian inference using general divergence criteria. Entropy 2018, 20, 442. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, S.; Sugasawa, S. Robust Bayesian regression with synthetic posterior distributions. Entropy 2020, 22, 661. [Google Scholar] [CrossRef] [PubMed]
- Bernardo, J.M. Reference posterior distributions for Bayesian inference. J. R. Stat. Soc. Ser. B Methodol. 1979, 41, 113–128. [Google Scholar] [CrossRef]
- Ghosh, M.; Liu, R. Moment matching priors. Sankhya A 2011, 73, 185–201. [Google Scholar] [CrossRef]
- Giummolè, F.; Mameli, V.; Ruli, E.; Ventura, L. Objective Bayesian inference with proper scoring rules. Test 2019, 28, 728–755. [Google Scholar] [CrossRef]
- Kanamori, T.; Fujisawa, H. Affine invariant divergences associated with proper composite scoring rules and their applications. Bernoulli 2014, 20, 2278–2304. [Google Scholar] [CrossRef]
- Ghosh, M.; Mergel, V.; Liu, R. A general divergence criterion for prior selection. Ann. Inst. Stat. Math. 2011, 63, 43–58. [Google Scholar] [CrossRef]
- Liu, R.; Chakrabarti, A.; Samanta, T.; Ghosh, J.K.; Ghosh, M. On divergence measures leading to Jeffreys and other reference priors. Bayesian Anal. 2014, 9, 331–370. [Google Scholar] [CrossRef]
- Hashimoto, S. Reference priors via α-divergence for a certain non-regular model in the presence of a nuisance parameter. J. Stat. Plan. Inference 2021, 213, 162–178. [Google Scholar] [CrossRef]
- Hashimoto, S. Moment matching priors for non-regular models. J. Stat. Plan. Inference 2019, 203, 169–177. [Google Scholar] [CrossRef]
- Robert, C.P.; Casella, G. Monte Carlo Statistical Methods; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Serfling, R. Approximation Theorems of Mathematical Statistics; Wiley: Hoboken, NJ, USA, 1980. [Google Scholar]
- Warwick, J.; Jones, M. Choosing a robustness tuning parameter. J. Stat. Comput. Simul. 2005, 75, 581–588. [Google Scholar] [CrossRef]
- Sugasawa, S. Robust empirical Bayes small area estimation with density power divergence. Biometrika 2020, 107, 467–480. [Google Scholar] [CrossRef]
- Basak, S.; Basu, A.; Jones, M. On the ‘optimal’ density power divergence tuning parameter. J. Appl. Stat. 2020, 1–21. [Google Scholar] [CrossRef]
- Kanamori, T.; Fujisawa, H. Robust estimation under heavy contamination using unnormalized models. Biometrika 2015, 102, 559–572. [Google Scholar] [CrossRef]
| Bayes | -Posterior | -Posterior | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Uniform prior | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| Reference prior | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| Moment matching prior | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| Bayes | -Posterior | -Posterior | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Uniform prior | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| Reference prior | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| Moment matching prior | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| Bayes | -Posterior | -Posterior | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Uniform prior | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| Reference prior | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| Moment matching prior | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| Bayes | -Posterior | -Posterior | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Uniform prior | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| Reference prior | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| Moment matching prior | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| 20 | ||||||||||
| 50 | ||||||||||
| 100 | ||||||||||
| ARE | 0.951489 | 0.6222189 | 0.2731871 | 0.1359501 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakagawa, T.; Hashimoto, S. On Default Priors for Robust Bayesian Estimation with Divergences. Entropy 2021, 23, 29. https://doi.org/10.3390/e23010029
Nakagawa T, Hashimoto S. On Default Priors for Robust Bayesian Estimation with Divergences. Entropy. 2021; 23(1):29. https://doi.org/10.3390/e23010029
Chicago/Turabian StyleNakagawa, Tomoyuki, and Shintaro Hashimoto. 2021. "On Default Priors for Robust Bayesian Estimation with Divergences" Entropy 23, no. 1: 29. https://doi.org/10.3390/e23010029
APA StyleNakagawa, T., & Hashimoto, S. (2021). On Default Priors for Robust Bayesian Estimation with Divergences. Entropy, 23(1), 29. https://doi.org/10.3390/e23010029





