Variationally Inferred Sampling through a Refined Bound
Abstract
1. Introduction
2. Background
2.1. Inference as Optimization
2.2. Inference as Sampling
3. A Variationally Inferred Sampling Framework
- Sample an initial set of particles, .
- Refine the particles through the sampler, .
- Compute the ELBO objective from Equation (4).
- Perform automatic differentiation on the objective wrt parameters to update them.
- Sample an initial set of particles, .
- Use the MCMC sampler as .
3.1. The Sampler
3.2. Approximating the Entropy Term
3.2.1. Particle Approximation (VIS-P)
3.2.2. MC Approximation (VIS-MC)
3.2.3. Gaussian Approximation (VIS-G)
3.2.4. Fokker–Planck Approximation (VIS-FP)
3.3. Back-Propagating through the Sampler
4. Analysis of Vis
4.1. Consistency
4.2. Refinement of ELBO
4.3. Taylor Expansion
4.4. Two Automatic Differentiation Modes for Refined ELBO Optimization
Complexity
5. Experiments
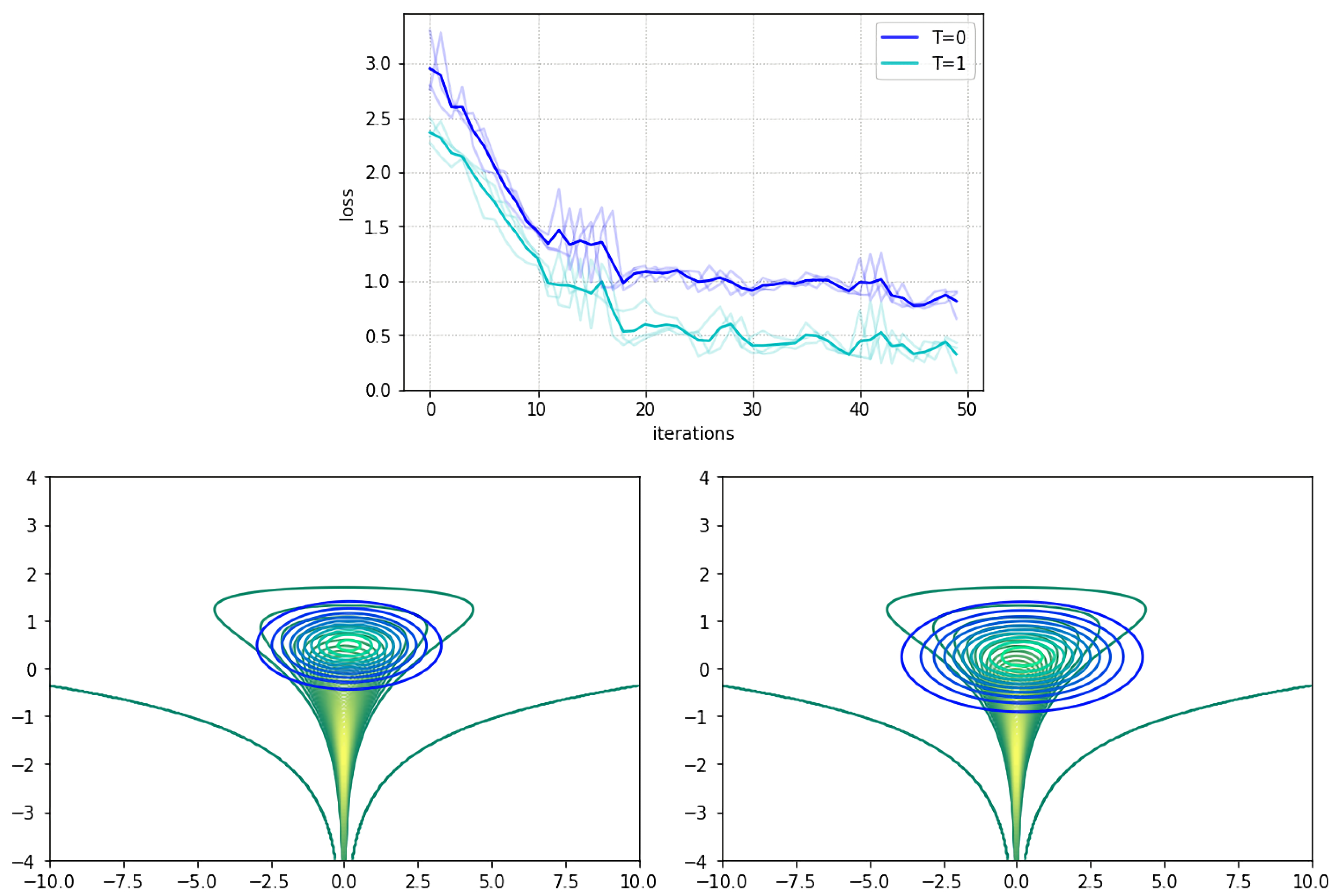
5.1. Funnel Density
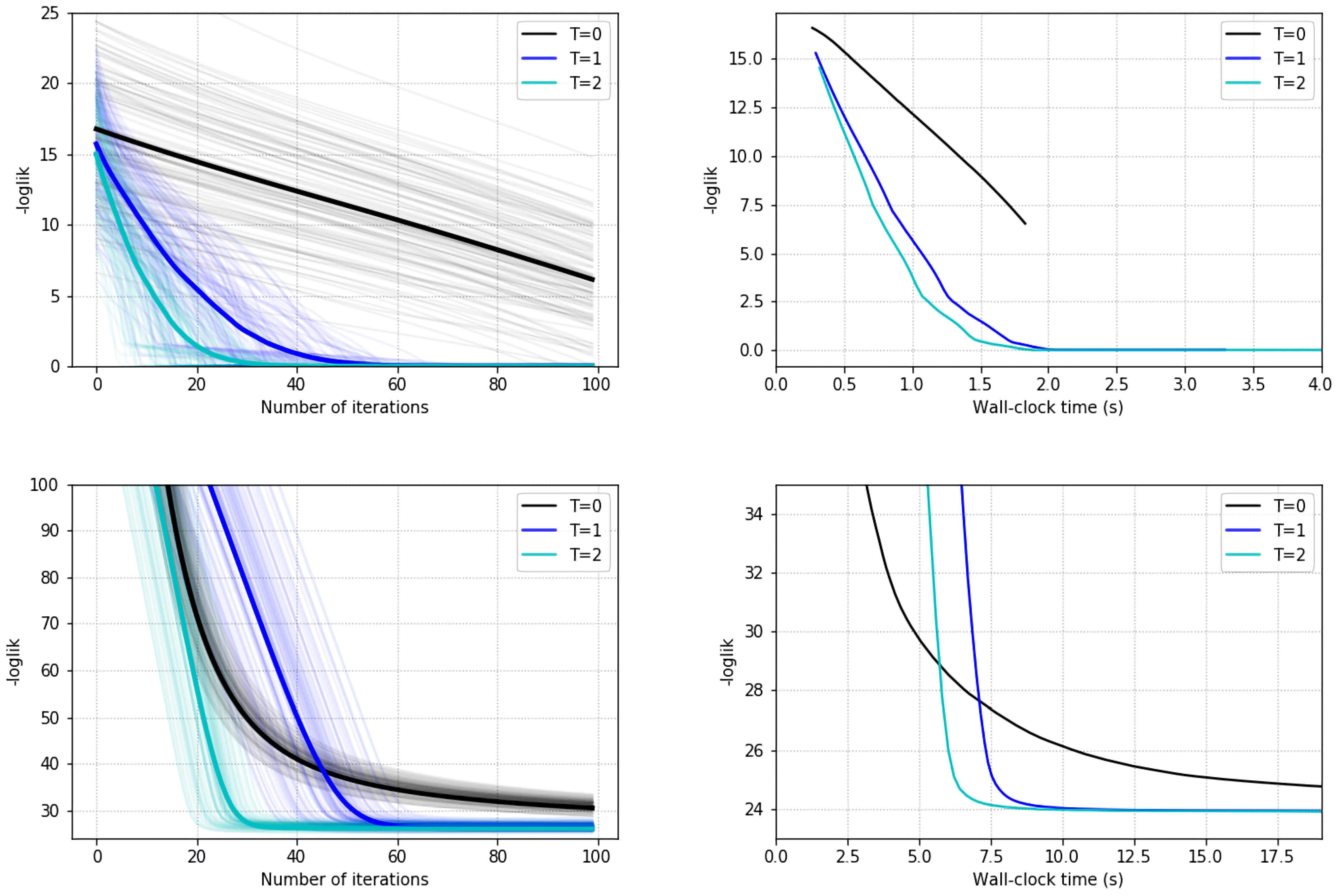
5.2. State-Space Markov Models
5.2.1. Prediction with an HMM
5.2.2. Prediction with a DLM
5.3. Variational Autoencoder
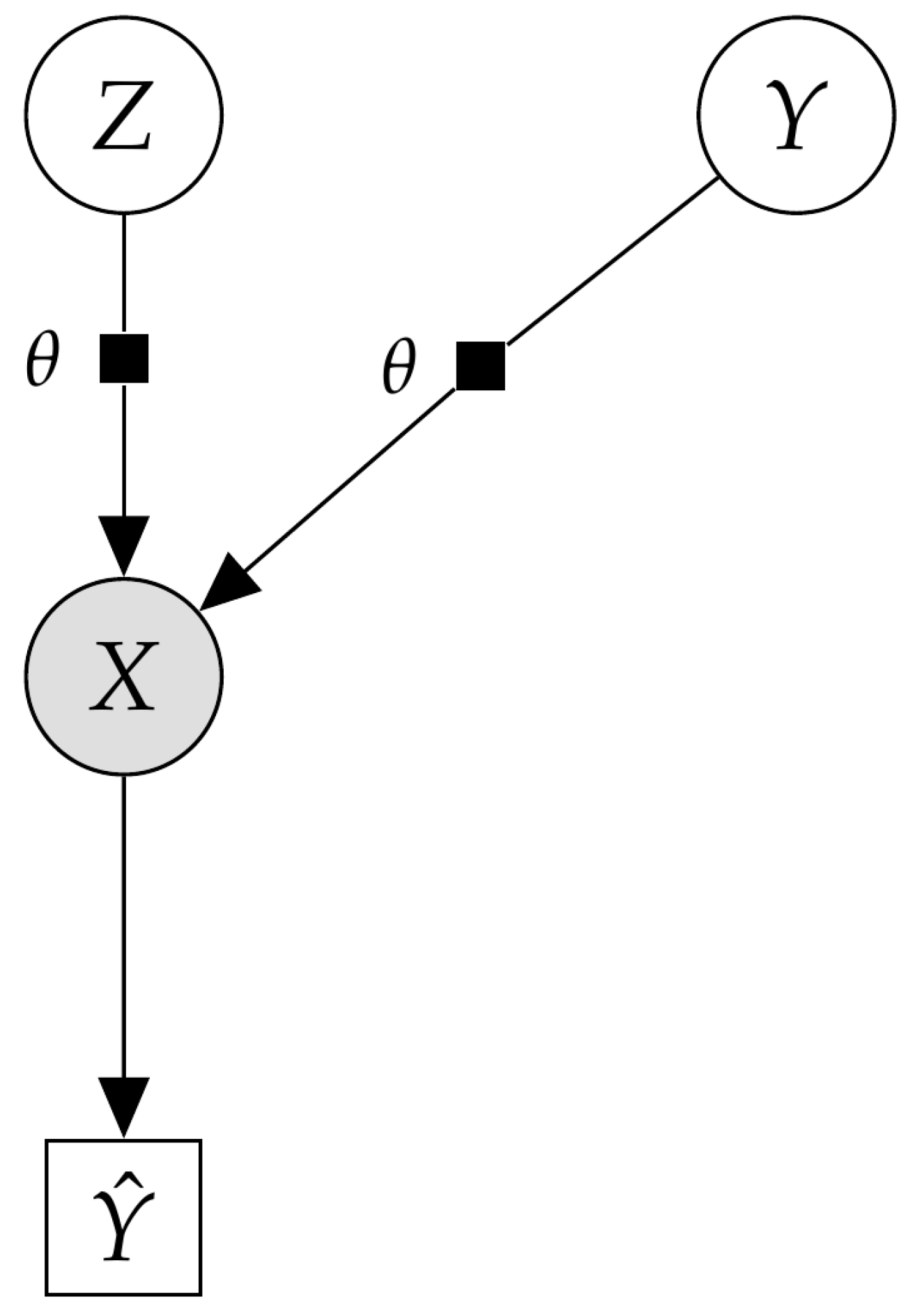
5.4. Variational Autoencoder as a Deep Bayes Classifier
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Fokker-Planck Approximation (Vis-Fp)
Appendix B. Experiment Details
Appendix B.1. State-Space Models
Appendix B.1.1. Initial Experiments
Appendix B.1.2. Prediction Task in a DLM
Appendix B.2. Vae
Appendix B.2.1. Model Details
Appendix B.2.2. Hyperparameter Settings
Appendix B.3. cVAE
Appendix B.3.1. Model Details


Appendix B.3.2. Hyperparameter Settings
References
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Insua, D.; Ruggeri, F.; Wiper, M. Bayesian Analysis of Stochastic Process Models; John Wiley & Sons: New York, NY, USA, 2012; Volume 978. [Google Scholar]
- Alquier, P. Approximate Bayesian Inference. Entropy 2020, 22, 1272. [Google Scholar] [CrossRef] [PubMed]
- Kucukelbir, A.; Tran, D.; Ranganath, R.; Gelman, A.; Blei, D.M. Automatic differentiation variational inference. J. Mach. Learn. Res. 2017, 18, 430–474. [Google Scholar]
- Riquelme, C.; Johnson, M.; Hoffman, M. Failure modes of variational inference for decision making. In Proceedings of the Prediction and Generative Modeling in RL Workshop (AAMAS, ICML, IJCAI), Stockholm, Sweden, 15 July 2018. [Google Scholar]
- Andrieu, C.; Doucet, A.; Holenstein, R. Particle Markov chain Monte Carlo methods. J. R. Stat. Soc. Ser. B Stat. Methodol. 2010, 72, 269–342. [Google Scholar] [CrossRef]
- Neal, R.M. MCMC using Hamiltonian dynamics. In Handbook of Markov Chain Monte Carlo; CRC Press: Boca Raton, FL, USA, 2011; Volume 2, p. 2. [Google Scholar]
- Van Ravenzwaaij, D.; Cassey, P.; Brown, S.D. A simple introduction to Markov Chain Monte–Carlo sampling. Psychon. Bull. Rev. 2018, 25, 143–154. [Google Scholar] [CrossRef] [PubMed]
- Nalisnick, E.; Hertel, L.; Smyth, P. Approximate inference for deep latent gaussian mixtures. In Proceedings of the NIPS Workshop on Bayesian Deep Learning, Barcelona, Spain, 10 December 2016. [Google Scholar]
- Salimans, T.; Kingma, D.; Welling, M. Markov chain Monte Carlo and variational inference: Bridging the gap. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1218–1226. [Google Scholar]
- Tran, D.; Ranganath, R.; Blei, D.M. The variational Gaussian process. In Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Wood, F.; Meent, J.W.; Mansinghka, V. A new approach to probabilistic programming inference. In Proceedings of the Artificial Intelligence and Statistics, Reykjavik, Iceland, 22–25 April 2014; pp. 1024–1032. [Google Scholar]
- Ge, H.; Xu, K.; Ghahramani, Z. Turing: A language for flexible probabilistic inference. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Lanzarote, Spain, 9–11 April 2018; pp. 1682–1690. [Google Scholar]
- Papaspiliopoulos, O.; Roberts, G.O.; Sköld, M. A general framework for the parametrization of hierarchical models. Stat. Sci. 2007, 22, 59–73. [Google Scholar] [CrossRef]
- Hoffman, M.; Sountsov, P.; Dillon, J.V.; Langmore, I.; Tran, D.; Vasudevan, S. Neutra-lizing bad geometry in hamiltonian Monte Carlo using neural transport. arXiv 2019, arXiv:1903.03704. [Google Scholar]
- Li, S.H.; Wang, L. Neural Network Renormalization Group. Phys. Rev. Lett. 2018, 121, 260601. [Google Scholar] [CrossRef]
- Parno, M.; Marzouk, Y. Transport map accelerated markov chain monte carlo. arXiv 2014, arXiv:1412.5492. [Google Scholar] [CrossRef]
- Rezende, D.; Mohamed, S. Variational Inference with Normalizing Flows. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1530–1538. [Google Scholar]
- Chen, C.; Li, C.; Chen, L.; Wang, W.; Pu, Y.; Carin, L. Continuous-Time Flows for Efficient Inference and Density Estimation. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 25–31 July 2018. [Google Scholar]
- Liu, G.; Liu, Y.; Guo, M.; Li, P.; Li, M. Variational inference with Gaussian mixture model and householder flow. Neural Netw. 2019, 109, 43–55. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, USA, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Mandt, S.; Hoffman, M.D.; Blei, D.M. Stochastic Gradient Descent as Approximate Bayesian Inference. J. Mach. Learn. Res. 2017, 18, 4873–4907. [Google Scholar]
- Huszár, F. Variational inference using implicit distributions. arXiv 2017, arXiv:1702.08235. [Google Scholar]
- Titsias, M.K.; Ruiz, F. Unbiased Implicit Variational Inference. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, Naha, Japan, 16–18 April 2019; pp. 167–176. [Google Scholar]
- Yin, M.; Zhou, M. Semi-Implicit Variational Inference. arXiv 2018, arXiv:1805.11183. [Google Scholar]
- Hoffman, M.D. Learning deep latent Gaussian models with Markov chain Monte Carlo. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 22–31 July 2017; pp. 1510–1519. [Google Scholar]
- Feng, Y.; Wang, D.; Liu, Q. Learning to draw samples with amortized stein variational gradient descent. arXiv 2017, arXiv:1707.06626. [Google Scholar]
- Cremer, C.; Li, X.; Duvenaud, D. Inference suboptimality in variational autoencoders. arXiv 2018, arXiv:1801.03558. [Google Scholar]
- Ruiz, F.; Titsias, M. A Contrastive Divergence for Combining Variational Inference and MCMC. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 5537–5545. [Google Scholar]
- Dai, B.; Dai, H.; He, N.; Liu, W.; Liu, Z.; Chen, J.; Xiao, L.; Song, L. Coupled variational bayes via optimization embedding. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, USA, 3–8 December 2018; pp. 9690–9700. [Google Scholar]
- Fang, L.; Li, C.; Gao, J.; Dong, W.; Chen, C. Implicit Deep Latent Variable Models for Text Generation. arXiv 2019, arXiv:1908.11527. [Google Scholar]
- Welling, M.; Teh, Y.W. Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Montreal, QC, USA, 11–13 June 2014; pp. 681–688. [Google Scholar]
- Li, C.; Chen, C.; Carlson, D.; Carin, L. Preconditioned stochastic gradient Langevin dynamics for deep neural networks. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Li, C.; Chen, C.; Fan, K.; Carin, L. High-order stochastic gradient thermostats for Bayesian learning of deep models. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Abbati, G.; Tosi, A.; Osborne, M.; Flaxman, S. Adageo: Adaptive geometric learning for optimization and sampling. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Canary Islands, Spain, 9–11 April 2018; pp. 226–234. [Google Scholar]
- Gallego, V.; Insua, D.R. Stochastic Gradient MCMC with Repulsive Forces. arXiv 2018, arXiv:1812.00071. [Google Scholar]
- Ma, Y.A.; Chen, T.; Fox, E. A complete recipe for stochastic gradient MCMC. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 2917–2925. [Google Scholar]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2017, 18, 5595–5637. [Google Scholar]
- Pavliotis, G. Stochastic Processes and Applications: Diffusion Processes, the Fokker-Planck and Langevin Equations. In Texts in Applied Mathematics; Springer: New York, NY, USA, 2014. [Google Scholar]
- Liu, Q.; Wang, D. Stein variational gradient descent: A general purpose Bayesian inference algorithm. In Proceedings of the Advances In Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2378–2386. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Graves, T.L. Automatic step size selection in random walk Metropolis algorithms. arXiv 2011, arXiv:1103.5986. [Google Scholar]
- Brooks, S.; Gelman, A.; Jones, G.; Meng, X.L. Handbook of Markov Chain Monte Carlo; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Murray, I.; Salakhutdinov, R. Notes on the KL-Divergence between a Markov Chain and Its Equilibrium Distribution; 2008. Available online: http://www.cs.toronto.edu/~rsalakhu/papers/mckl.pdf (accessed on 12 June 2020).
- Franceschi, L.; Donini, M.; Frasconi, P.; Pontil, M. Forward and reverse gradient-based hyperparameter optimization. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 22–31 July 2017; pp. 1165–1173. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Granada, Spain, 2019; pp. 8024–8035. [Google Scholar]
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Zarchan, P.; Musoff, H. Fundamentals of Kalman filtering: A Practical Approach; American Institute of Aeronautics and Astronautics, Inc.: Washington, DC, USA, 2013. [Google Scholar]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Keeling, C.D. Atmospheric Carbon Dioxide Record from Mauna Loa; Scripps Institution of Oceanography, The University of California: La Jolla, CA, USA, 2005. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- LeCun, Y.; Cortes, C. MNIST handwritten Digit Database. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 12 May 2020).
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Shi, J.; Sun, S.; Zhu, J. A Spectral Approach to Gradient Estimation for Implicit Distributions. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 25–31 July 2018; pp. 4651–4660. [Google Scholar]
- Duvenaud, D.; Maclaurin, D.; Adams, R. Early stopping as nonparametric variational inference. In Proceedings of the Artificial Intelligence and Statistics, Cadiz, Spain, 9–11 May 2016; pp. 1070–1077. [Google Scholar]
- Lunn, D.J.; Thomas, A.; Best, N.; Spiegelhalter, D. WinBUGS-a Bayesian modelling framework: Concepts, structure, and extensibility. Stat. Comput. 2000, 10, 325–337. [Google Scholar] [CrossRef]
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.; Guo, J.; Li, P.; Riddell, A. Stan: A probabilistic programming language. J. Stat. Softw. 2017, 76. [Google Scholar] [CrossRef]
- Tran, D.; Hoffman, M.W.; Moore, D.; Suter, C.; Vasudevan, S.; Radul, A. Simple, distributed, and accelerated probabilistic programming. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 7609–7620. [Google Scholar]
- Bingham, E.; Chen, J.P.; Jankowiak, M.; Obermeyer, F.; Pradhan, N.; Karaletsos, T.; Singh, R.; Szerlip, P.; Horsfall, P.; Goodman, N.D. Pyro: Deep Universal Probabilistic Programming. arXiv 2018, arXiv:1810.09538. [Google Scholar]
- West, M.; Harrison, J. Bayesian Forecasting and Dynamic Models; Springer: New York, NY, USA, 2006. [Google Scholar]
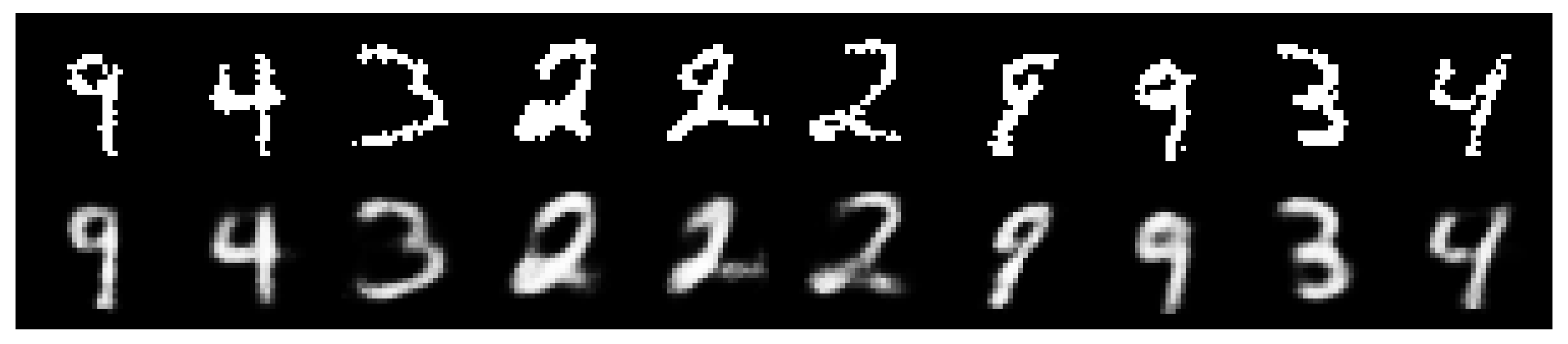

| accuracy | ||
| predictive entropy | ||
| logarithmic score |
| MAE | ||
| predictive entropy | ||
| interval score () |
| Method | MNIST | fMNIST |
|---|---|---|
| Results from [24] | ||
| UIVI | ||
| SIVI | ||
| VAE | ||
| Results from [29] | ||
| VCD | ||
| HMC-DLGM | ||
| This paper | ||
| VIS-5-10 | ||
| VIS-0-10 | ||
| VAE (VIS-0-0) | ||
| Acc. (Test) | ||
|---|---|---|
| 0 | 0 | % |
| 0 | 10 | % |
| 5 | 10 | % |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallego, V.; Ríos Insua, D. Variationally Inferred Sampling through a Refined Bound. Entropy 2021, 23, 123. https://doi.org/10.3390/e23010123
Gallego V, Ríos Insua D. Variationally Inferred Sampling through a Refined Bound. Entropy. 2021; 23(1):123. https://doi.org/10.3390/e23010123
Chicago/Turabian StyleGallego, Víctor, and David Ríos Insua. 2021. "Variationally Inferred Sampling through a Refined Bound" Entropy 23, no. 1: 123. https://doi.org/10.3390/e23010123
APA StyleGallego, V., & Ríos Insua, D. (2021). Variationally Inferred Sampling through a Refined Bound. Entropy, 23(1), 123. https://doi.org/10.3390/e23010123





