A Novel Measure Inspired by Lyapunov Exponents for the Characterization of Dynamics in State-Transition Networks
Abstract
1. Introduction
2. Results
2.1. State-Transition Networks
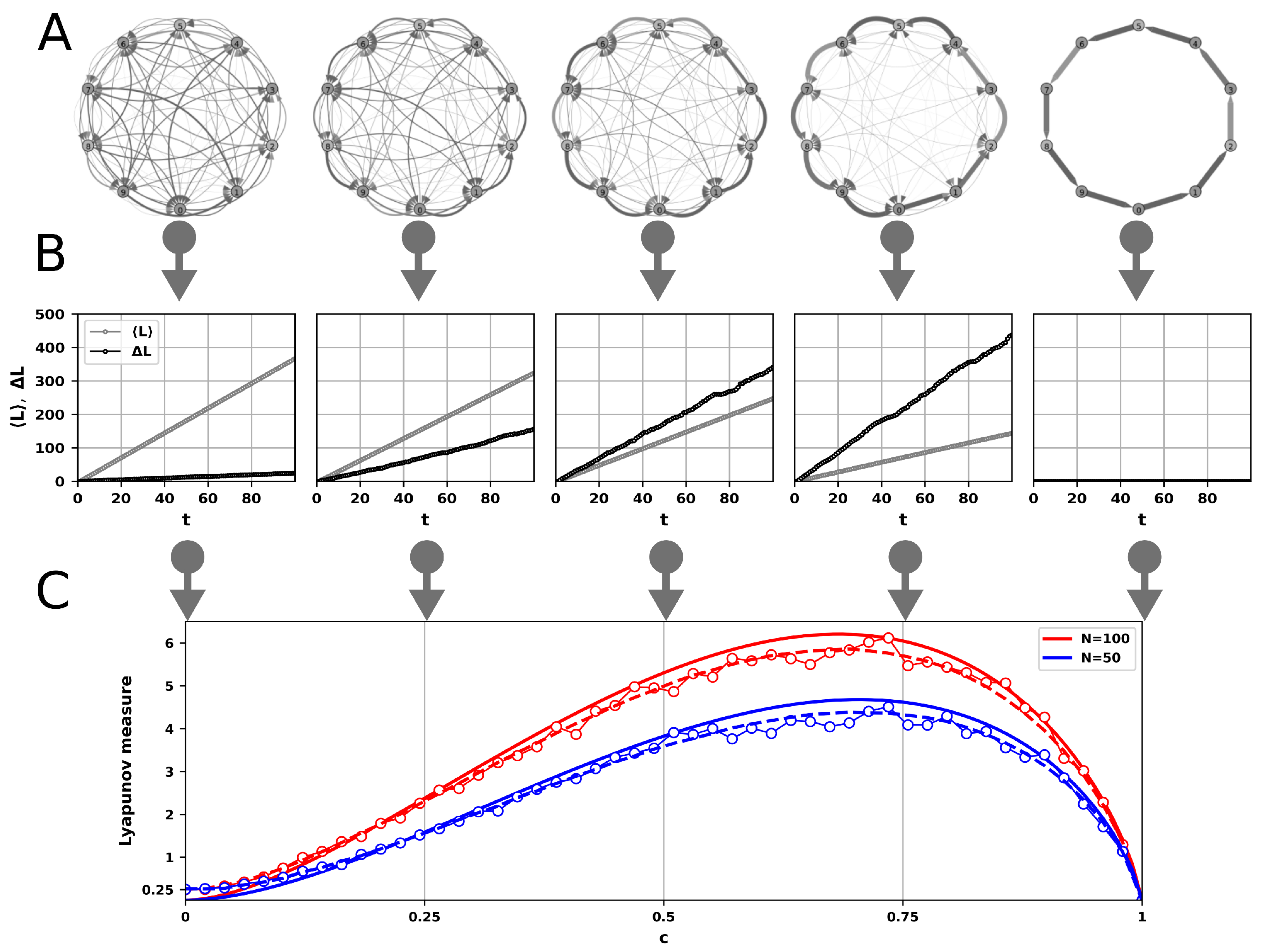
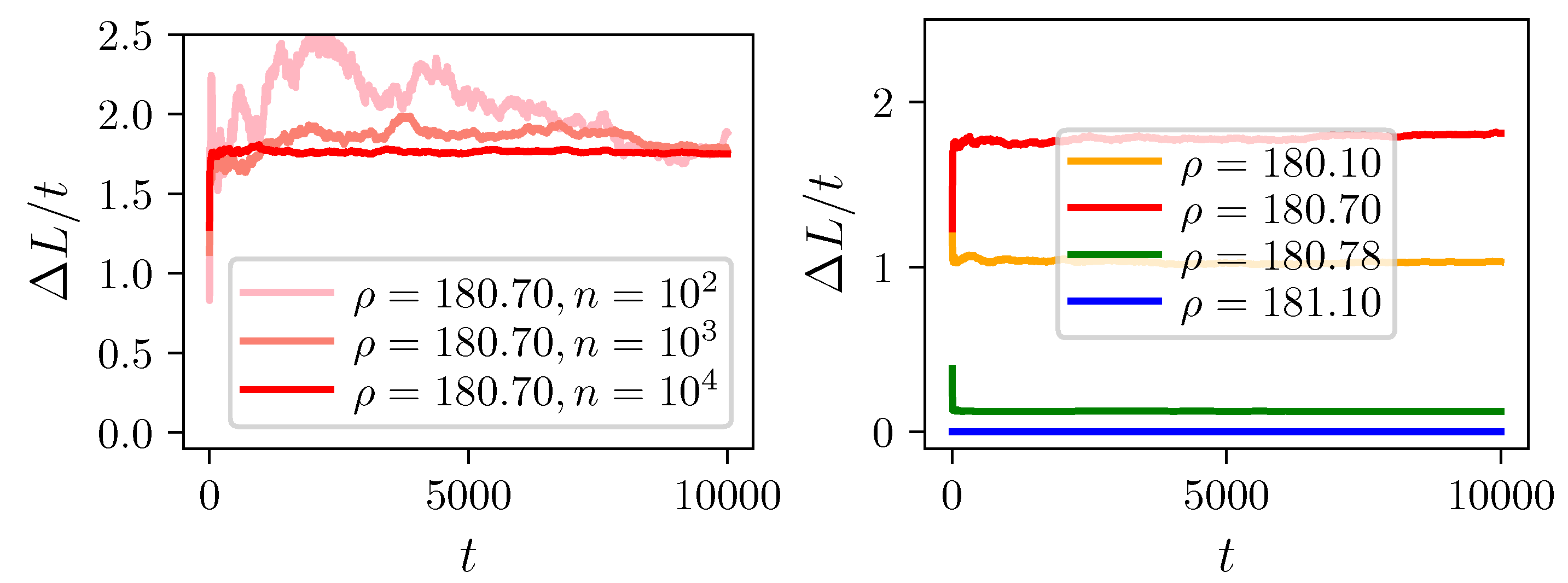
2.2. Lyapunov Measure
2.2.1. Properties of the Lyapunov Measure
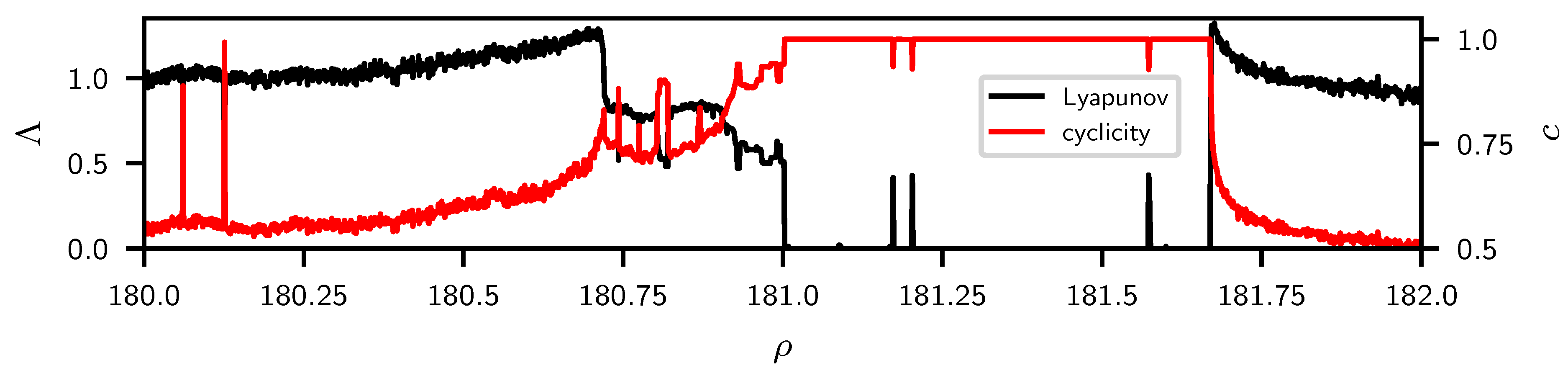
2.2.2. Analytical Study of the Lyapunov Measure
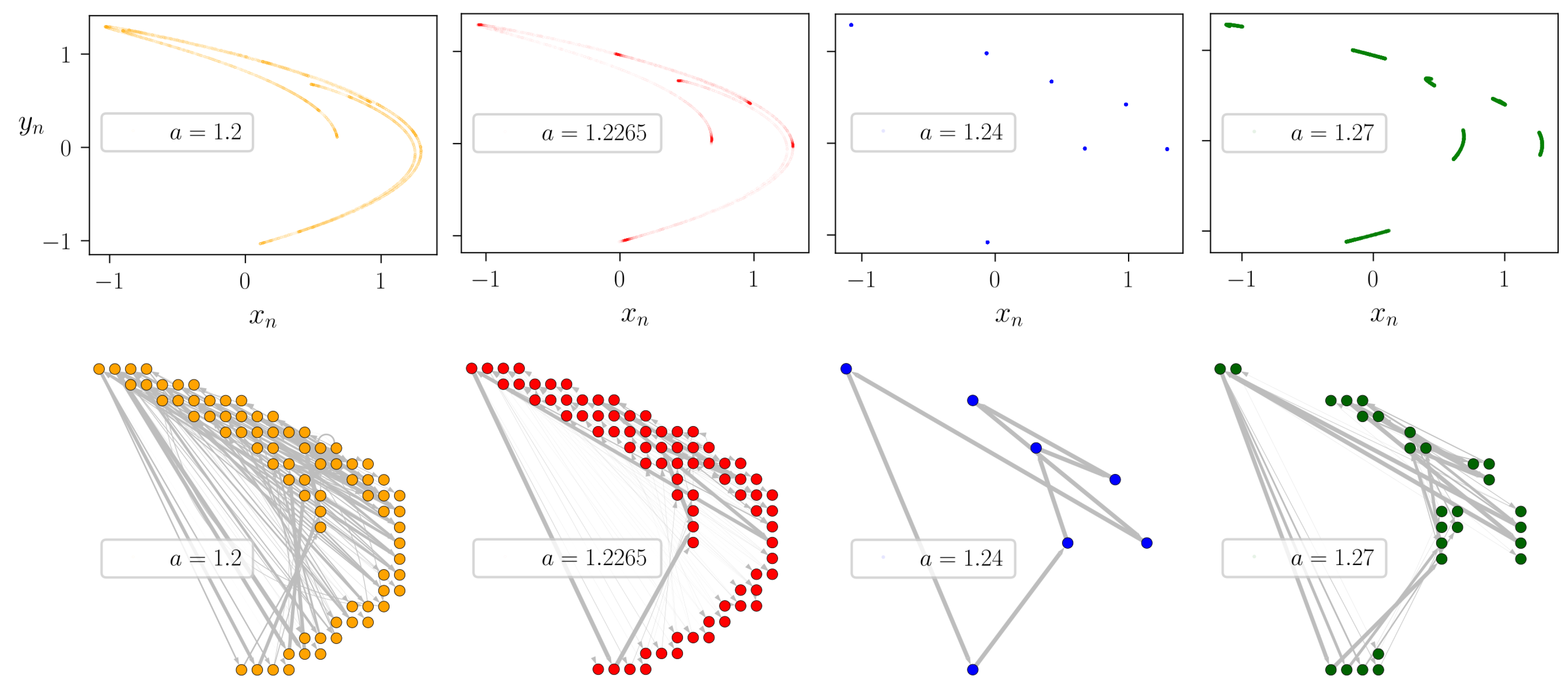
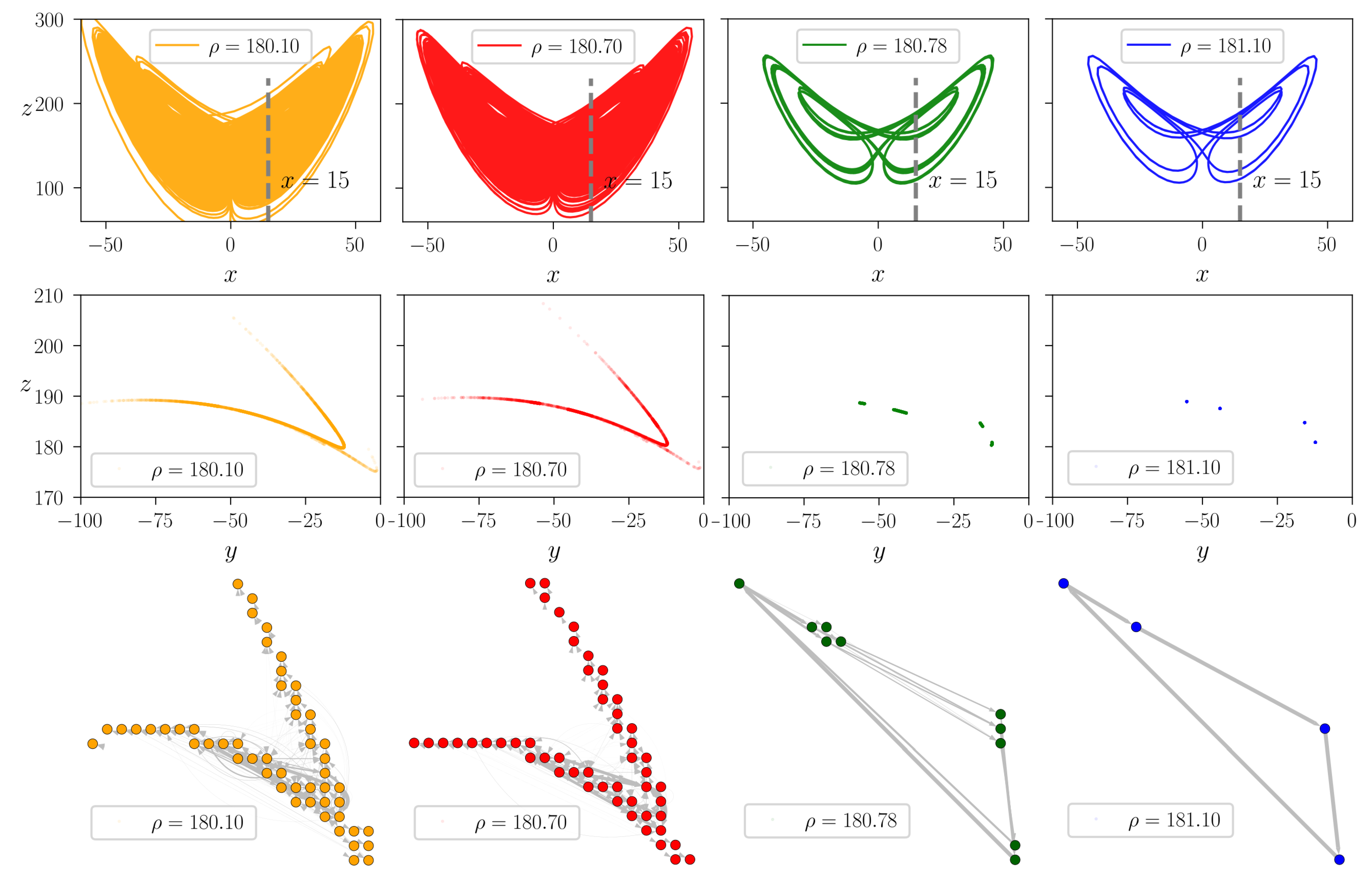
2.3. Time Series Analysis with STNs
Construction of STNs
2.4. Network Measures
3. Materials and Methods
3.1. Discrete- and Continuous-Time Dynamical Systems
3.2. Phase-Space Discretization and Poincare Sections
3.3. Ensemble Averages and Asymptotic Behavior
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Offset at c = 0 in the Lyapunov Measure According to the Random Network Model
Appendix B. Location and Size of the Maximum in the Lyapunov Measure According to the Random Network Model
Appendix C. Distribution of Uniform Random Numbers Normalized over Large Sets
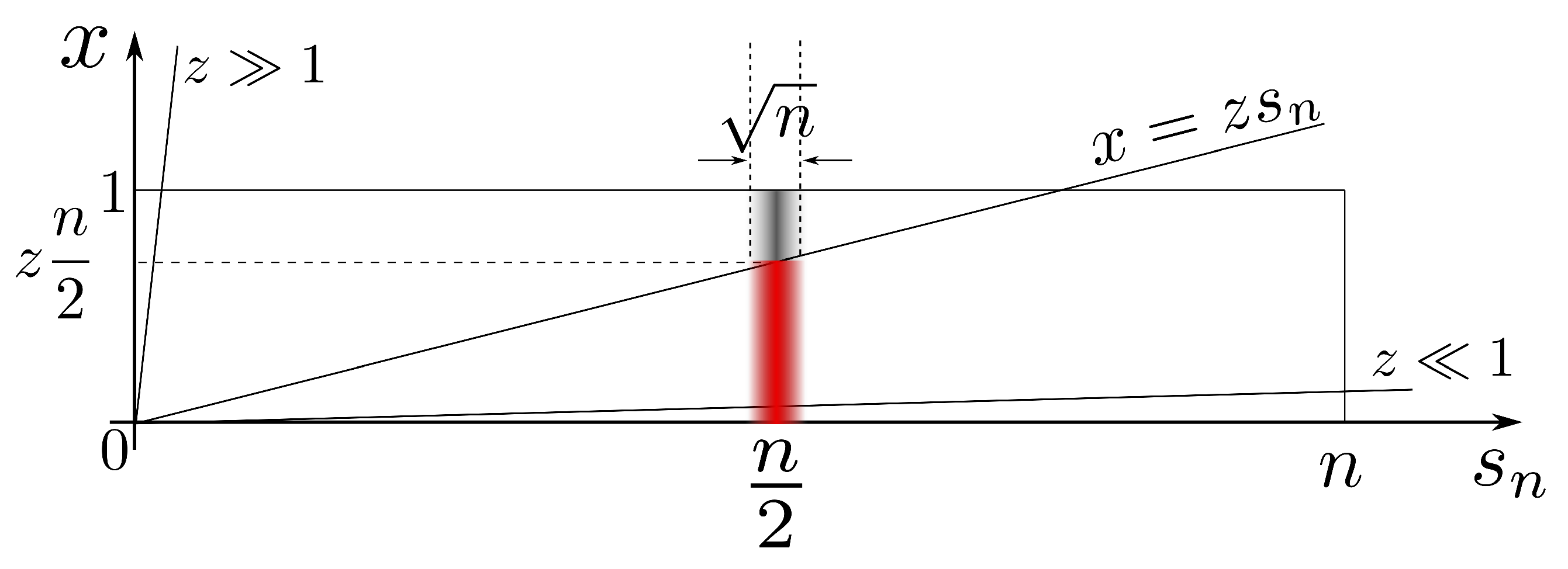
Appendix D. Insight into the Emergence of Precursor Peaks
References
- Newman, M. Networks, 2nd ed.; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Zou, Y.; Donner, R.V.; Marwan, N.; Donges, J.F.; Kurths, J. Complex network approaches to nonlinear time series analysis. Phys. Rep. 2019, 787, 1–97. [Google Scholar] [CrossRef]
- Donner, R.V.; Small, M.; Donges, J.F.; Marwan, N.; Zou, Y.; Xiang, R.; Kurths, J. Recurrence-Based Time Series Analysis by Means of Complex Network Methods. Int. J. Bifurc. Chaos 2011, 21, 1019–1046. [Google Scholar] [CrossRef]
- Marwan, N.; Donges, J.F.; Zou, Y.; Donner, R.V.; Kurths, J. Complex network approach for recurrence analysis of time series. Phys. Lett. A 2009, 373, 4246–4254. [Google Scholar] [CrossRef]
- Jacob, R.; Harikrishnan, K.; Misra, R.; Ambika, G. Characterization of chaotic attractors under noise: A recurrence network perspective. Commun. Nonlinear Sci. Numer. Simul. 2016, 41, 32–47. [Google Scholar] [CrossRef]
- Jacob, R.; Harikrishnan, K.P.; Misra, R.; Ambika, G. Uniform framework for the recurrence-network analysis of chaotic time series. Phys. Rev. E 2016, 93. [Google Scholar] [CrossRef] [PubMed]
- Ávila, G.M.R.; Gapelyuk, A.; Marwan, N.; Walther, T.; Stepan, H.; Kurths, J.; Wessel, N. Classification of cardiovascular time series based on different coupling structures using recurrence networks analysis. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20110623. [Google Scholar] [CrossRef] [PubMed]
- Mosdorf, R.; Górski, G. Detection of two-phase flow patterns using the recurrence network analysis of pressure drop fluctuations. Int. Commun. Heat Mass Transf. 2015, 64, 14–20. [Google Scholar] [CrossRef]
- Feldhoff, J.H.; Donner, R.V.; Donges, J.F.; Marwan, N.; Kurths, J. Geometric signature of complex synchronisation scenarios. EPL Europhys. Lett. 2013, 102, 30007. [Google Scholar] [CrossRef]
- de Berg, M.; van Kreveld, M.; Overmars, M.; Schwarzkopf, O.C. Computational Geometry; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Donner, R.V.; Donges, J.F. Visibility graph analysis of geophysical time series: Potentials and possible pitfalls. Acta Geophys. 2012, 60, 589–623. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M.; Ramirez-Rojas, A.; Flores-Marquez, L. Investigating the time dynamics of seismicity by using the visibility graph approach: Application to seismicity of Mexican subduction zone. Phys. A Stat. Mech. Appl. 2013, 392, 6571–6577. [Google Scholar] [CrossRef]
- Gao, Z.K.; Cai, Q.; Yang, Y.X.; Dang, W.D.; Zhang, S.S. Multiscale limited penetrable horizontal visibility graph for analyzing nonlinear time series. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Ahmadlou, M.; Adeli, H.; Adeli, A. Improved visibility graph fractality with application for the diagnosis of Autism Spectrum Disorder. Phys. A Stat. Mech. Appl. 2012, 391, 4720–4726. [Google Scholar] [CrossRef]
- Donner, R.; Hinrichs, U.; Scholz-Reiter, B. Symbolic recurrence plots: A new quantitative framework for performance analysis of manufacturing networks. Eur. Phys. J. Spec. Top. 2008, 164, 85–104. [Google Scholar] [CrossRef]
- Small, M. Complex networks from time series: Capturing dynamics. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS2013), Beijing, China, 19–23 May 2013. [Google Scholar] [CrossRef]
- Deritei, D.; Aird, W.C.; Ercsey-Ravasz, M.; Regan, E.R. Principles of dynamical modularity in biological regulatory networks. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- McCullough, M.; Small, M.; Stemler, T.; Iu, H.H.C. Time lagged ordinal partition networks for capturing dynamics of continuous dynamical systems. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 053101. [Google Scholar] [CrossRef] [PubMed]
- Kulp, C.W.; Chobot, J.M.; Freitas, H.R.; Sprechini, G.D. Using ordinal partition transition networks to analyze ECG data. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 073114. [Google Scholar] [CrossRef] [PubMed]
- Antoniades, I.P.; Stavrinides, S.G.; Hanias, M.P.; Magafas, L. Complex Network Time Series Analysis of a Macroeconomic Model. In Chaos and Complex Systems; Springer International Publishing: Berlin, Germany, 2020; pp. 135–147. [Google Scholar] [CrossRef]
- Ruan, Y.; Donner, R.V.; Guan, S.; Zou, Y. Ordinal partition transition network based complexity measures for inferring coupling direction and delay from time series. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 043111. [Google Scholar] [CrossRef]
- Gagniuc, P.A. Markov Chains: From Theory to Implementation and Experimentation; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Asmussen, S.R. Markov Chains. Appl. Probab. Queues. Stoch. Model. Appl. Probab. 2003, 51, 3–8. [Google Scholar] [CrossRef]
- Sinai, Y.G. On the Notion of Entropy of a Dynamical System. Dokl. Akad. Nauk SSSR 1959, 124, 768–771. [Google Scholar]
- Pikovsky, A.; Politi, A. Lyapunov Exponents, a Tool to Explore Complex Dynamics; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Hénon, M. A two-dimensional mapping with a strange attractor. Commun. Math. Phys. 1976, 50, 69–77. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Ercsey-Ravasz, M.; Markov, N.T.; Lamy, C.; Essen, D.C.V.; Knoblauch, K.; Toroczkai, Z.; Kennedy, H. A Predictive Network Model of Cerebral Cortical Connectivity Based on a Distance Rule. Neuron 2013, 80, 184–197. [Google Scholar] [CrossRef] [PubMed]
- Gantmakher, F.; Hirsch, K.; Society, A.M.; Collection, K.M.R. The Theory of Matrices; Number v. 1 in AMS Chelsea Publishing Series; Chelsea Publishing Company: New York, NY, USA, 1959. [Google Scholar]
- Wernecke, H.; Sándor, B.; Gros, C. How to test for partially predictable chaos. Sci. Rep. 2017, 7, 1087. [Google Scholar] [CrossRef] [PubMed]
- Tél, T.; Gruiz, M. Chaotic Dynamics: An Introduction Based on Classical Mechanics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sándor, B.; Schneider, B.; Lázár, Z.I.; Ercsey-Ravasz, M. A Novel Measure Inspired by Lyapunov Exponents for the Characterization of Dynamics in State-Transition Networks. Entropy 2021, 23, 103. https://doi.org/10.3390/e23010103
Sándor B, Schneider B, Lázár ZI, Ercsey-Ravasz M. A Novel Measure Inspired by Lyapunov Exponents for the Characterization of Dynamics in State-Transition Networks. Entropy. 2021; 23(1):103. https://doi.org/10.3390/e23010103
Chicago/Turabian StyleSándor, Bulcsú, Bence Schneider, Zsolt I. Lázár, and Mária Ercsey-Ravasz. 2021. "A Novel Measure Inspired by Lyapunov Exponents for the Characterization of Dynamics in State-Transition Networks" Entropy 23, no. 1: 103. https://doi.org/10.3390/e23010103
APA StyleSándor, B., Schneider, B., Lázár, Z. I., & Ercsey-Ravasz, M. (2021). A Novel Measure Inspired by Lyapunov Exponents for the Characterization of Dynamics in State-Transition Networks. Entropy, 23(1), 103. https://doi.org/10.3390/e23010103







