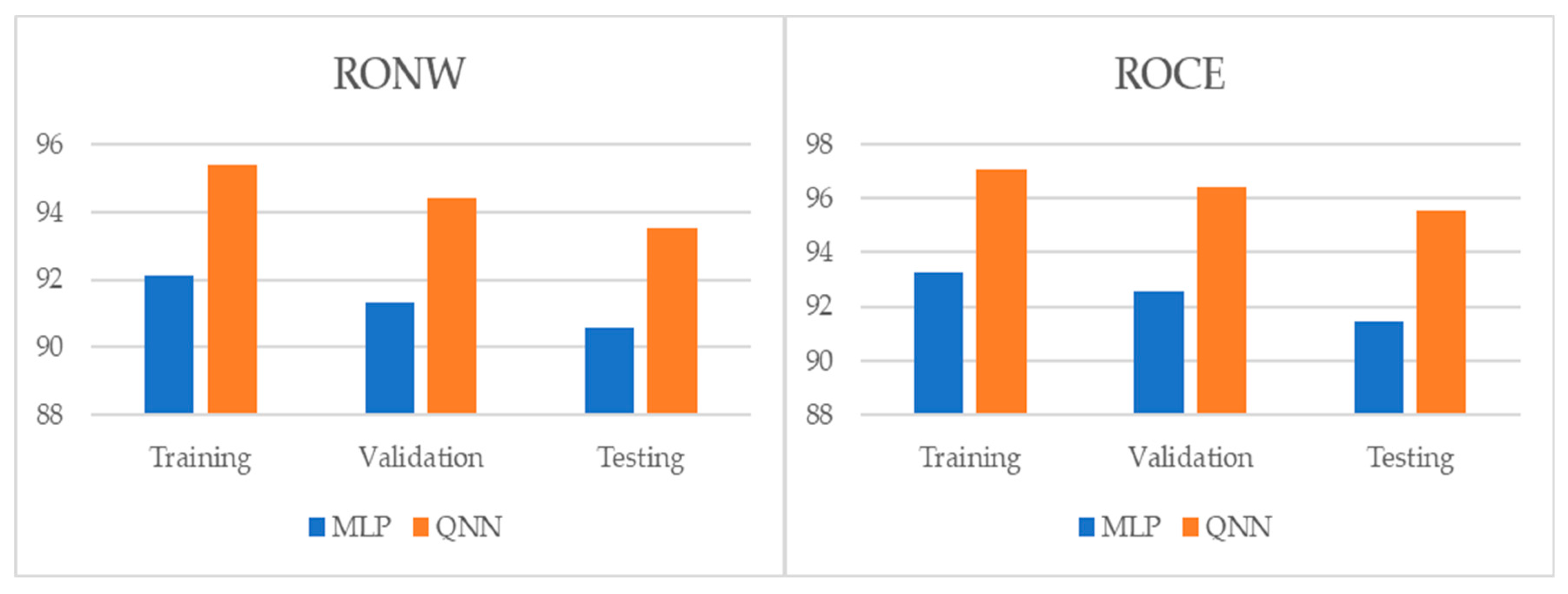
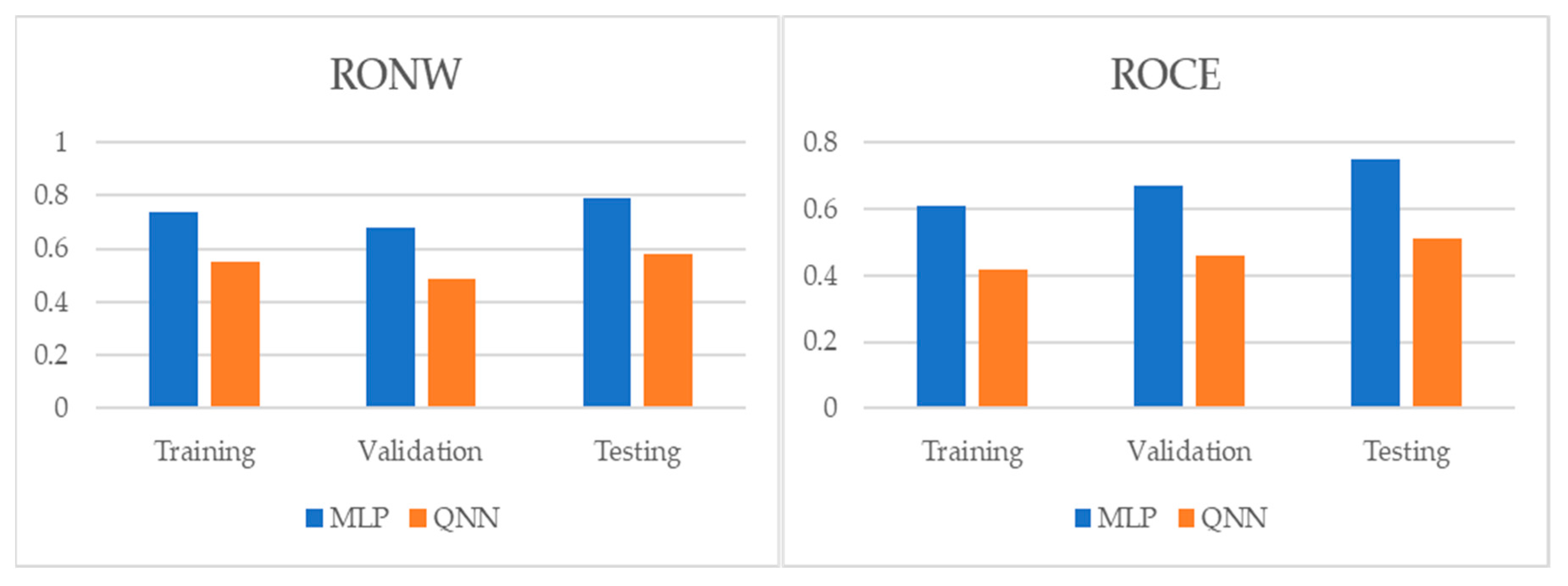
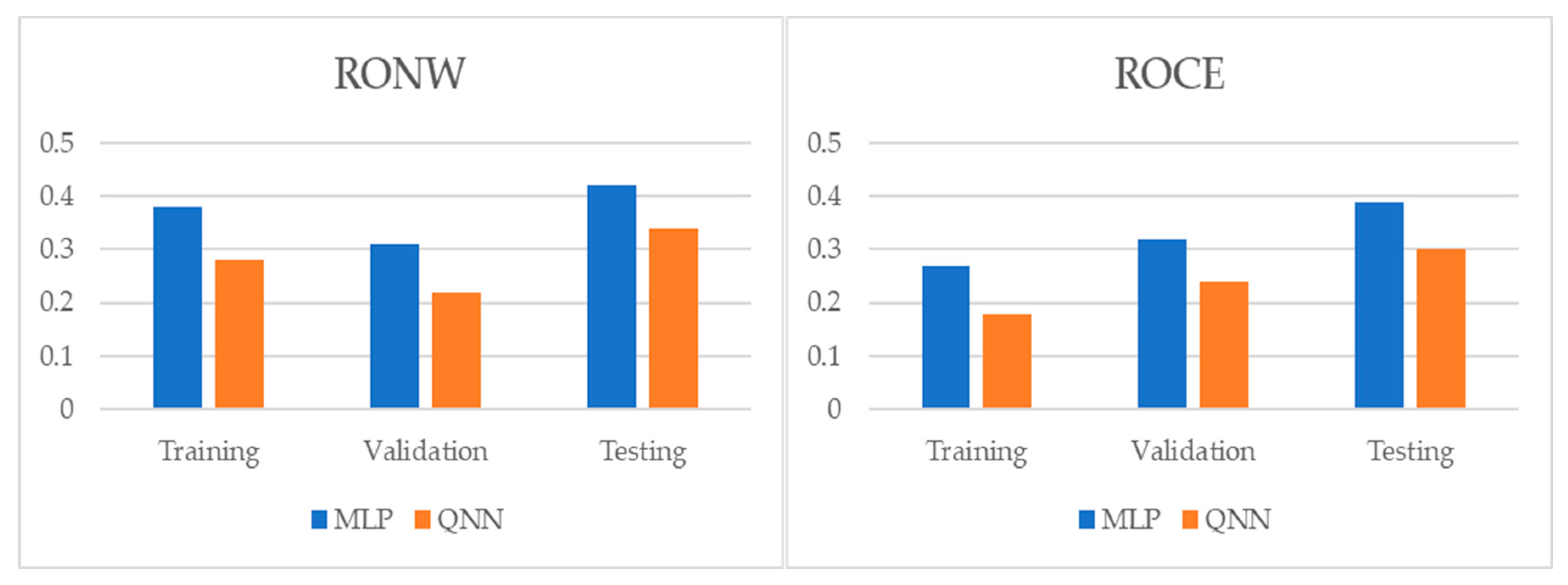
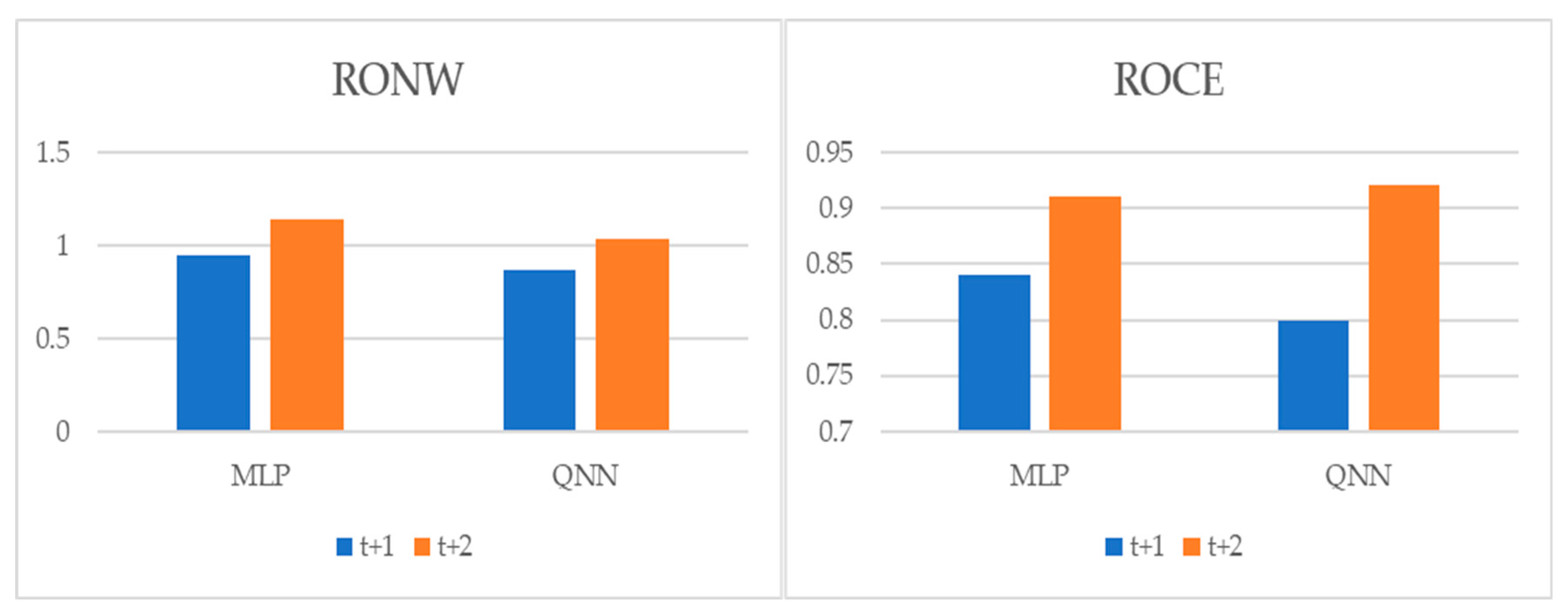
3.1. Multilayer Perceptron (MLP)
When we talk about neuronal systems, it is important to define the concept of an artificial neuron, a basic element of this type of system, whose description is inherited from the neurobiological principles that describe the behavior of neurons in the cerebral cortex. The artificial neuron consists of input and output elements that are processed in the central unit, as well as the processing elements that will allow the neuron to generalize and learn concepts. From this basic structure, the neuron can map the inputs to obtain at the output, the desired response that could belong to a certain function, and that, due to the activation function that generates it, can fall into two categories. This response depends firstly on the inputs of the neuron and secondly on the operations carried out within the neuron [
16,
17].
The design of the multilayer perceptron implies the determination of the activation function to be used, the number of neurons, and the number of layers of the network. As mentioned above, the choice of the activation function is usually made based on the desired path, and the fact of choosing one or the other generally does not influence the ability of the network to solve the problem. Regarding the number of neurons and layers, some of these parameters are given by the problem and others must be chosen by the designer. Thus, for example, both the number of neurons in the input layer and the number of neurons in the output layer are given by the variables that define the problem. In some practical applications, there is no question about the number of inputs and outputs. However, there are problems where the number of input variables relevant to the problem is not exactly known. In these cases, many variables are available, some of which may not provide relevant information to the network, and their use may complicate learning since it will involve large architectures with high connectivity. In these situations, it is convenient to carry out a prior analysis of the most relevant input variables to the problem and discard those that do not provide information to the network. This analysis can become a complicated task and require advanced techniques, such as techniques based on correlation analysis, principal component analysis, relative importance analysis, and sensitivity analysis, or techniques based on genetic algorithms, among others. The number of hidden layers and the number of neurons in these layers must be chosen by the designer. No method or rule determines the optimal number of hidden neurons to solve a given problem. In most practical applications, these parameters are determined by trial and error. Starting from an architecture that has already been trained, changes are made by increasing or decreasing the number of hidden neurons and the number of layers until an adequate architecture is achieved for the problem to be solved, which may not be optimal, but which provides a solution.
Let it be a multilayer perceptron with C layers—C 2 hidden layers—and nc neurons in layer c, for c = 1,2, …, C. Let Wc = () be the weight matrix where represents the weight from the connection of neuron i of layer c to c = 2, …, C. We will denote as to the activation of neuron i of layer c. These activations are calculated as follows:
First, the activation of input layer neurons (
). The neurons of the input layer are responsible for transmitting the signals received from the outside to the network. So:
where
X = (
x1;
x2;::::;
xn1) represents the vector or pattern of input to the network.
Second, activation of the neurons of the hidden layer
c (
): The hidden neurons of the network process the information received by applying the activation function f to the sum of the products of the activations received by their corresponding weights, that is:
where
Y = (
y1,
y2, …,
ynC). The function
f is the so-called activation function. For this multilayer perceptron, we used the sigmoidal function. These functions have as an image a continuous interval of values within the intervals [0; 1]:
The neural networks used in this project used the supervised learning paradigm and the error correction algorithm, sometimes known as the delta rule. When we speak of supervised learning, we refer to the type of training in which the system is provided with information on the inputs as well as the expected outputs or destinations corresponding to said inputs so that the system has the destinations as a point reference to evaluate its performance based on the difference of these values and modify the free parameters based on this difference.
The equation of the minimization of error is composed of learning patters {(
x1,
y1), (
x2,
y2)
… (
xp,
yp)} and an error function
ε (
W,
X,
Y), where the training process tries to seek the weights that minimize the learning error
E (
W), as is shown in (4).
Regarding the number of neurons and layers, some of these parameters are given by the problem and others must be chosen by the designer. Thus, for example, both the number of neurons in the input layer and the number of neurons in the output layer are given by the variables that define the problem. In some practical applications, there is no room for doubt about the number of inputs and outputs. However, there are problems where the number of input variables relevant to the problem is not exactly known. In these cases, a large number of variables are available, some of which may not provide relevant information to the network, and their use could complicate learning since it would imply large-scale architectures with high connectivity. In these situations, it is convenient to carry out a preliminary analysis of the input variables most relevant to the problem and discard those that do not provide information to the network. This analysis can become a complicated task and requires advanced techniques, where the main technique is the sensitivity analysis [
17]. Furthermore, and for MLP to be able to report on the importance of each variable in the results of the constructed model, it is possible to perform a sensitivity analysis [
18]. This sensibility analysis starts from the total data to divide this database into groups, and each group works on the network as many times as there are model variables. As soon as the value of one of the variables changes, a value of zero is placed. This can be done because the network works by evaluating your responses against already known ranking values, after defining the expression (5).
where
is the value of the network output when the variable
Xi is zero,
is the known classification value,
Xi is the significant variable, and
Sxi is the sensitivity result of each variable.
3.2. Quantum Neural Networks (QNN)
The QNN is built from quantum computation techniques. Qubit is defined as the smallest unit of information in quantum computation, which is a probabilistic representation. A qubit may either be in the “1” or “0” or any superposition of the two [
19]. The state of the qubit can be defined as follows:
where α and are the numbers that point out the amplitude of the corresponding states such that
. A qubit is defined as the smallest unit of information in quantum computation. It is determined as a pair of numbers
. An angle
θ is a specification that represents geometrical aspects and is defined such that:
cos(
θ) =|
α| and
sin(
θ) =|
β|. Quantum gates may be applied for adjusting the probabilities because of weight upgrading [
19]. An example of a rotation gate can be:
A state of the qubit can be upgraded by applying the quantum gate explained previously. The application of the rotation gate on a qubit is defined as follows:
The hybrid quantum-inspired neural network is begun with a quantum hidden neuron from the state
, preparing the superposition as:
where
p represents the random probability of initializing the system in the state ∣0〉. The desired state can be reached by using rotation gate
R:
The classical neurons are initiated by random number generation. The output from the quantum neuron is determined as follows:
where
f is a problem-dependent sigmoid or Gaussian function. The output from the network is represented as:
The desired output is the
ok corresponding squared error, which is:
The learning follows the rules of the feedforward backpropagation algorithm. The upgrading of the output layer weight is defined as follows:
The weights are upgraded by a quantum gate as appears in Equation (6), so in this case, the equation would be:
where
obtaining this result using the chain rule. The variable
is a step of
such that:
to develop the last step of
should be
;
is the learning rate [
19]. This ratio usually takes the value 0.1.