A Novel Hybrid Approach for Partial Discharge Signal Detection Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Approximate Entropy
Abstract
1. Introduction
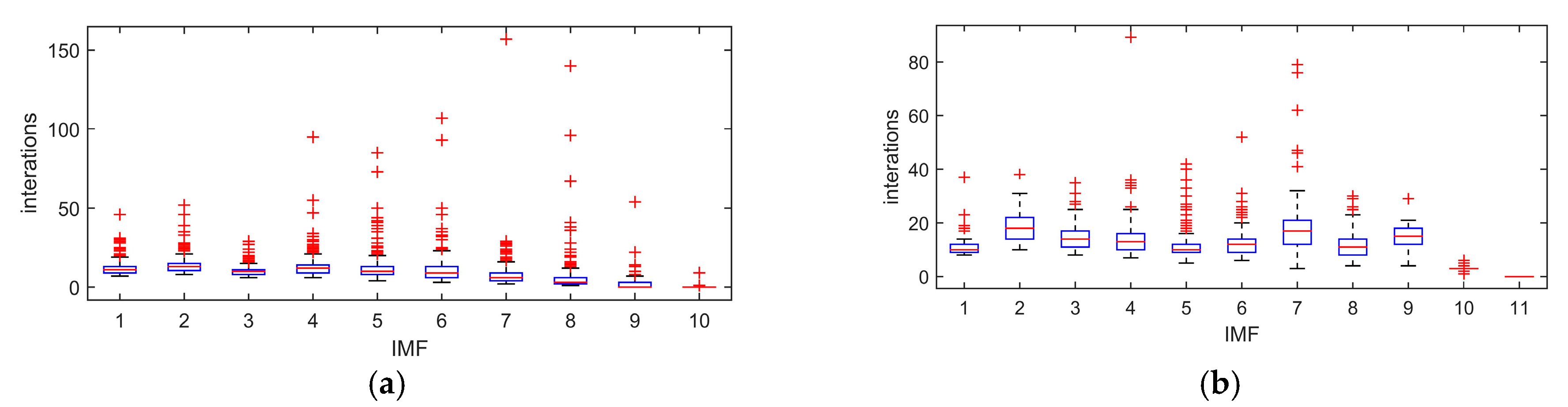
2. Review of CEEMDAN
3. Review of Approximate Entropy
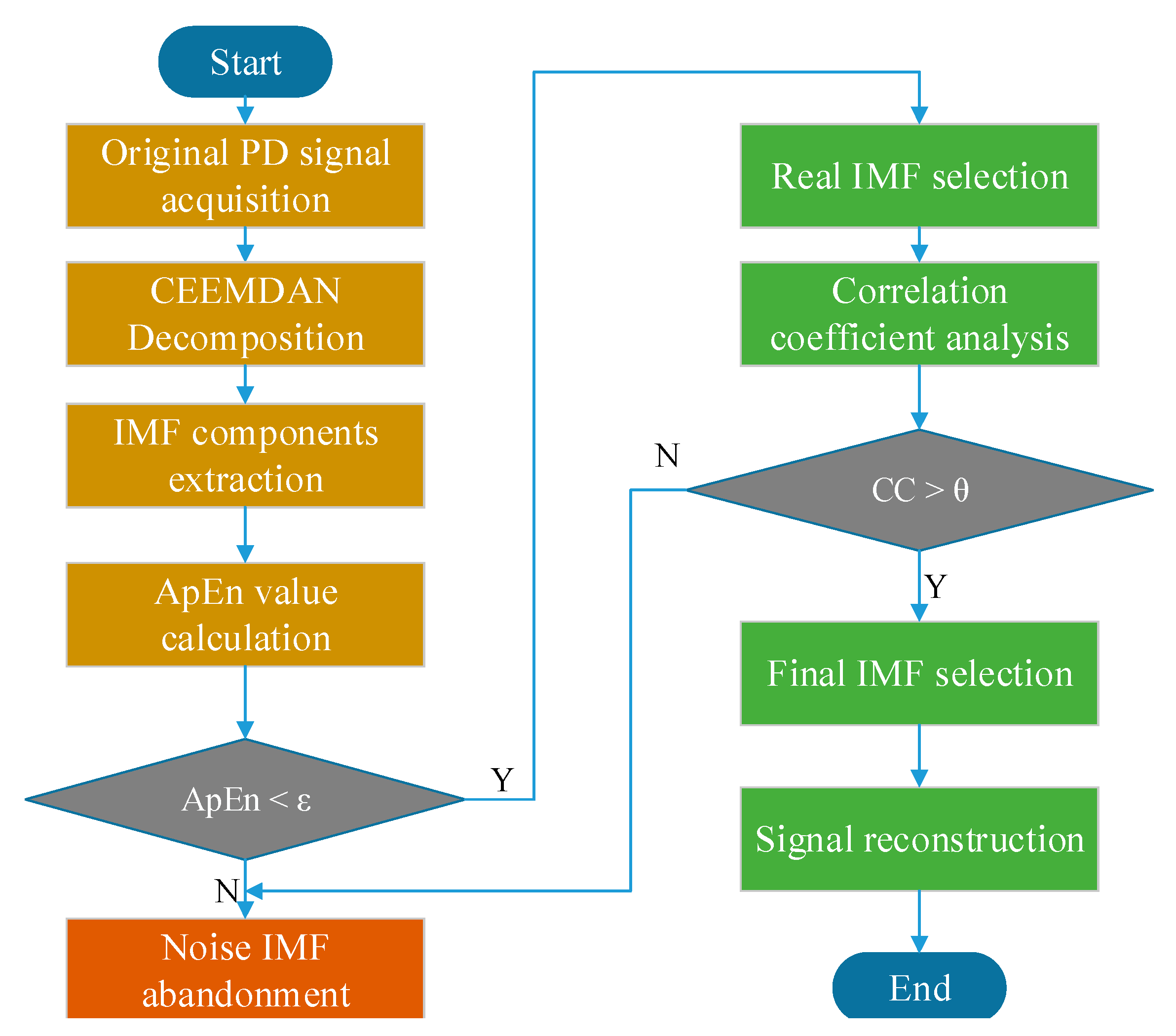
4. PD Signal De-Noising Based on CEEMDAN and ApEn
4.1. Algorithm Principle
4.2. Algorithm Procedure
- Extract the original PD signals. Because of the complexity of power transformers’ field environments, PD signals are always interfered with by various noises.
- Decompose the original PD signal into different IMFs with CEEMDAN. These IMFs may consist of real PD information and complex noise interference.
- Calculate ApEn values of IMFs extracted from CEEMDAN decomposition. ApEn represents the complexity of signals in different scales and frequencies. Owing to the non-stationary of original PD signals, the ApEn values may be different from each other.
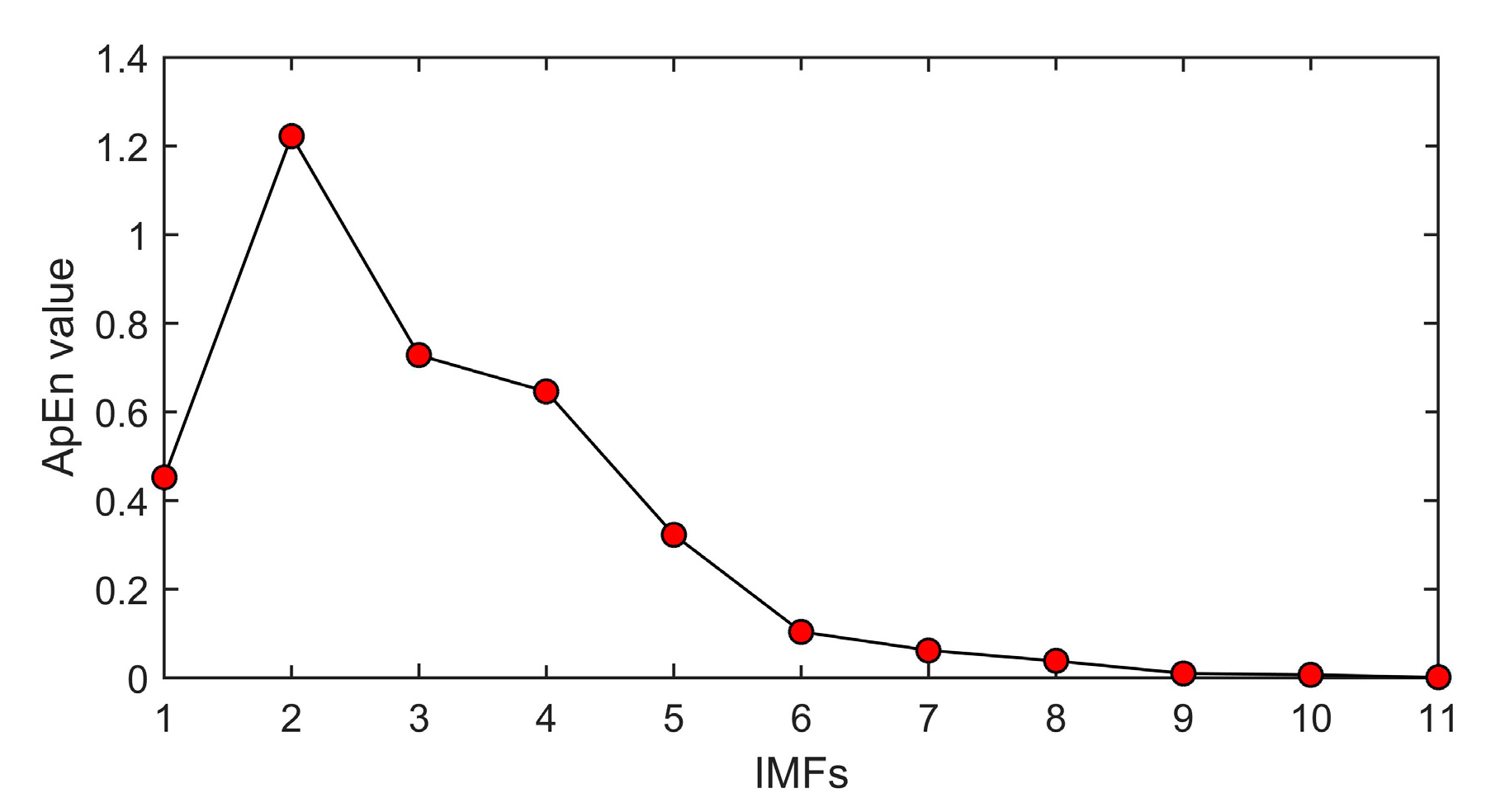
- Remove those IMFs that represent noise components. According to ApEn theory, noise and PD signals can be distinguished by different ApEn values. If the ApEn value is above a certain threshold, then the IMF is regarded as noise and abandoned. Otherwise, the IMF contains PD information and will be kept.
- Calculate the correlation coefficient between the original PD signal and each selected IMF. As known, the CC value of the IMF that contains little PD information will be small. Therefore, real IMFs similar to the original signal will be selected as final parts through a certain threshold.
- Reconstruct clean PD signal with final IMFs. These IMFs contain dominant PD features and show a strong correlation with original signals. This reconstruction method can efficiently recover the clean PD pulses from noisy signals.
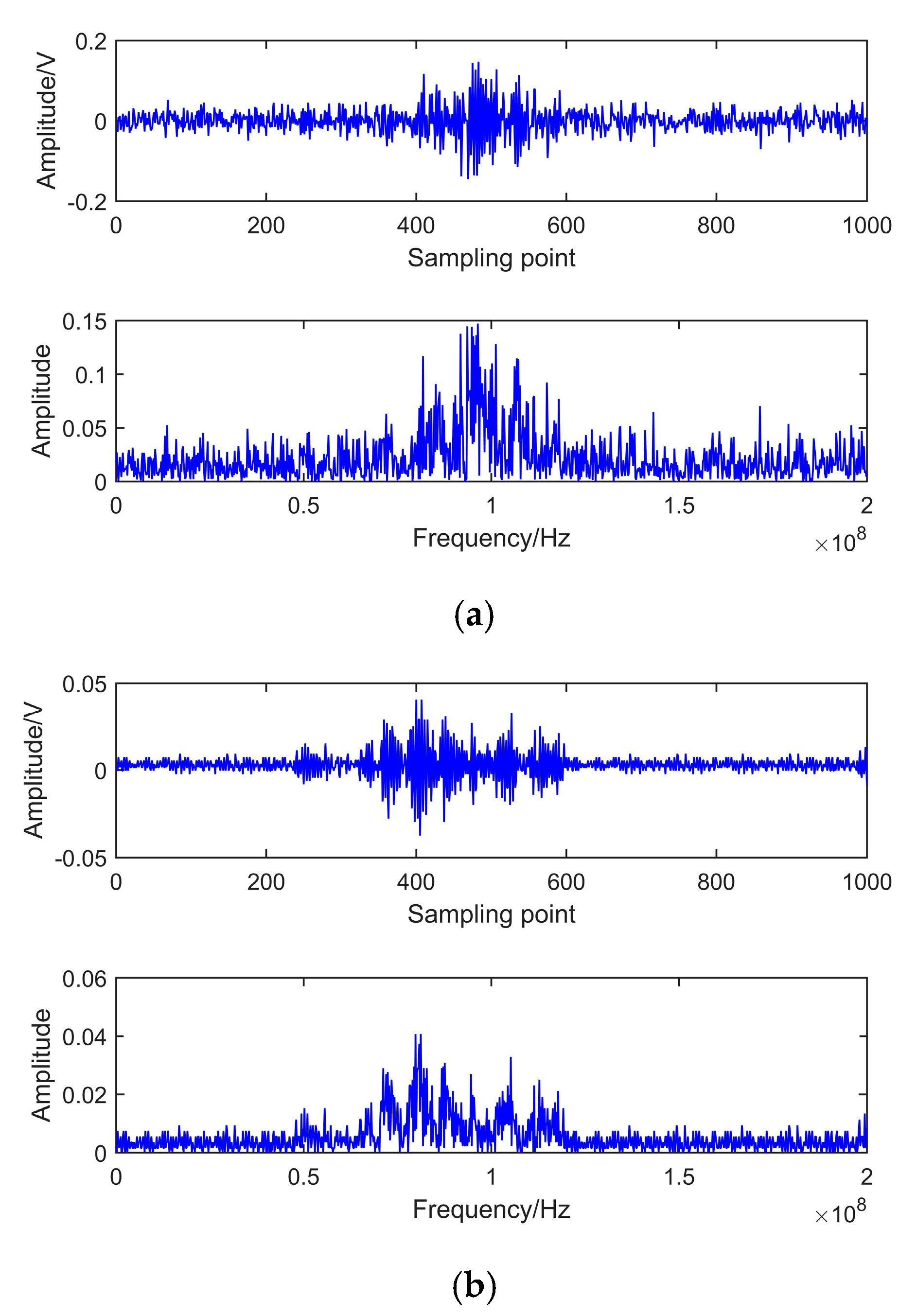
5. Simulation Analysis
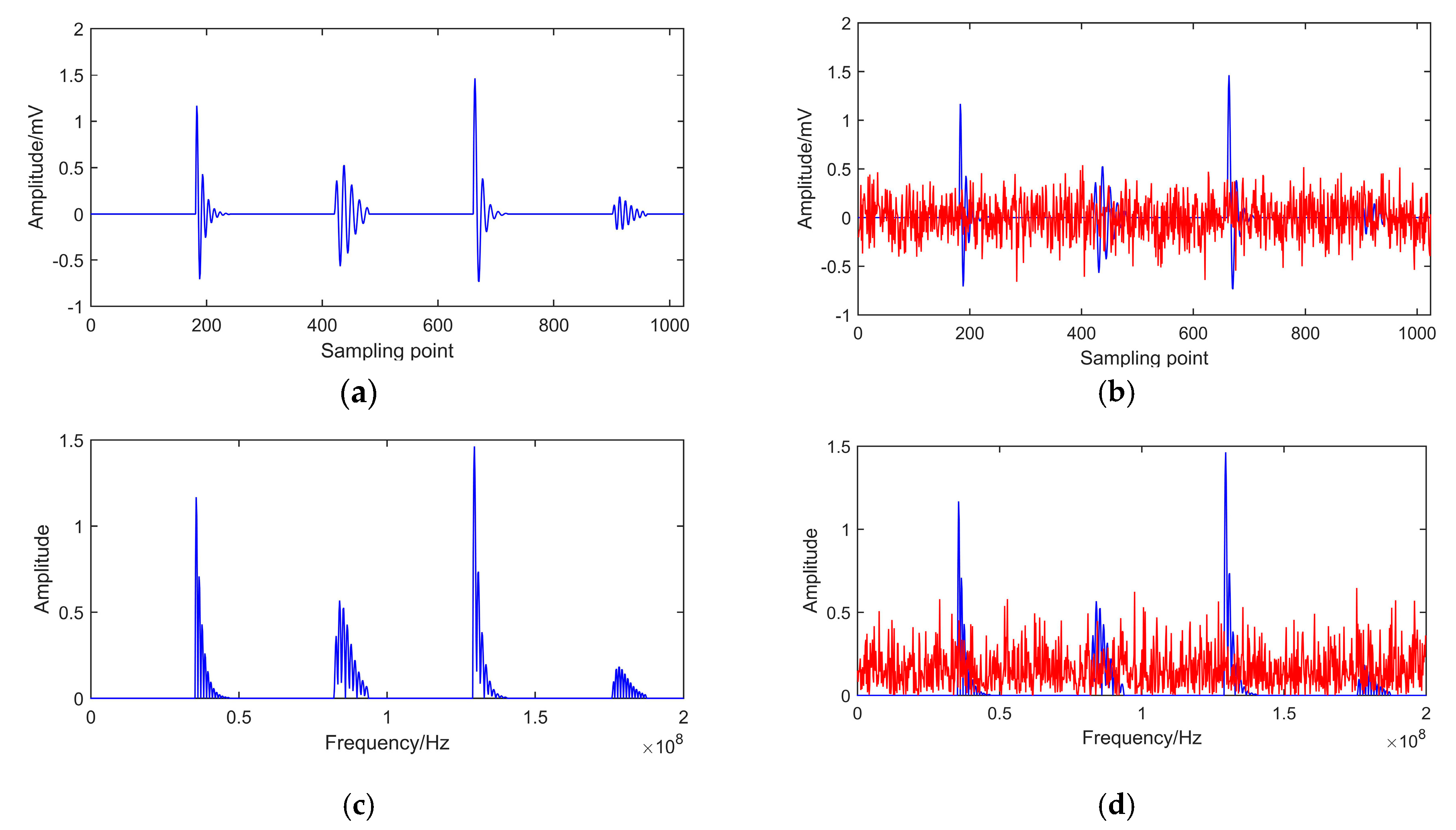
5.1. Simulated Signal
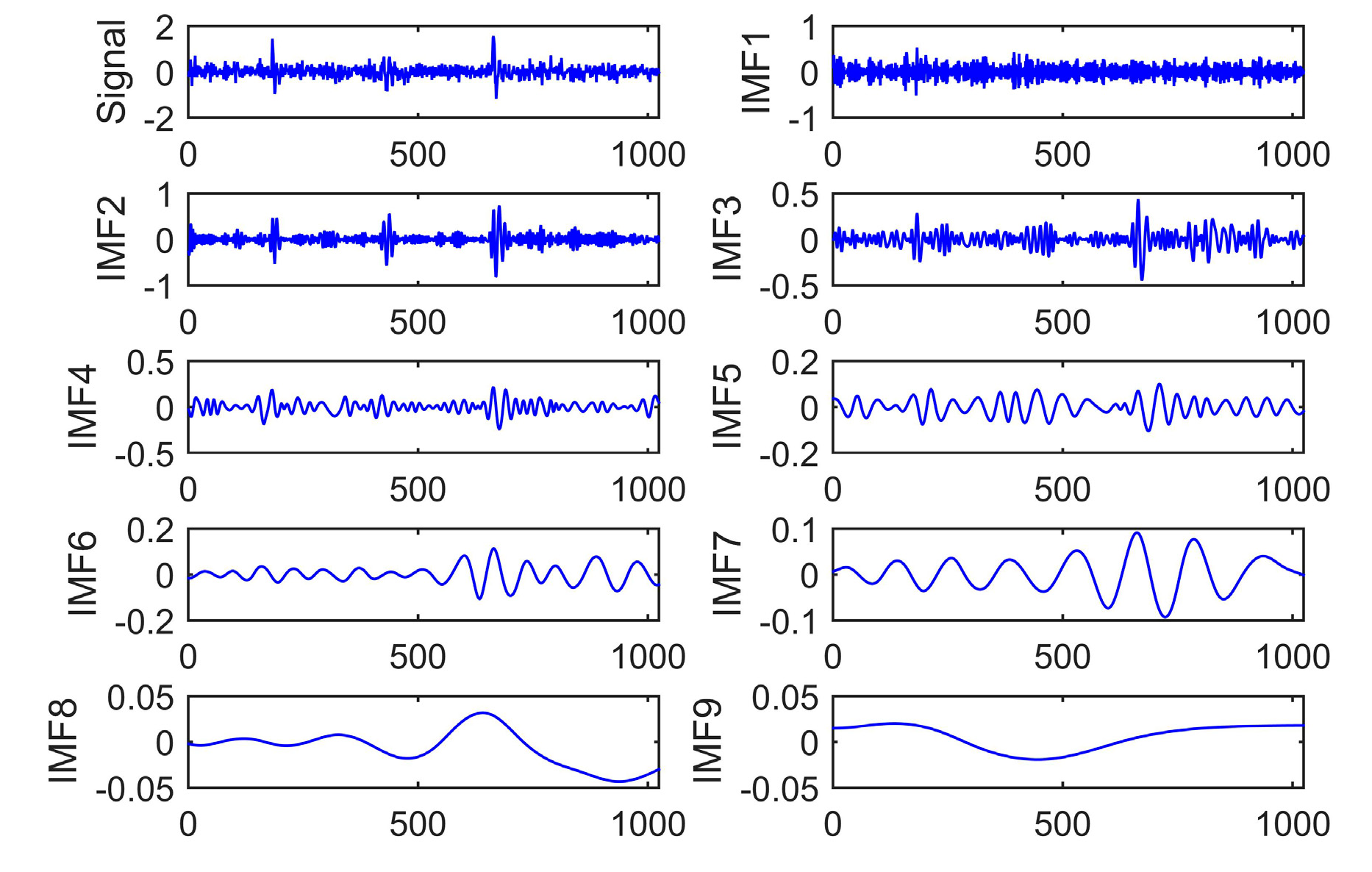
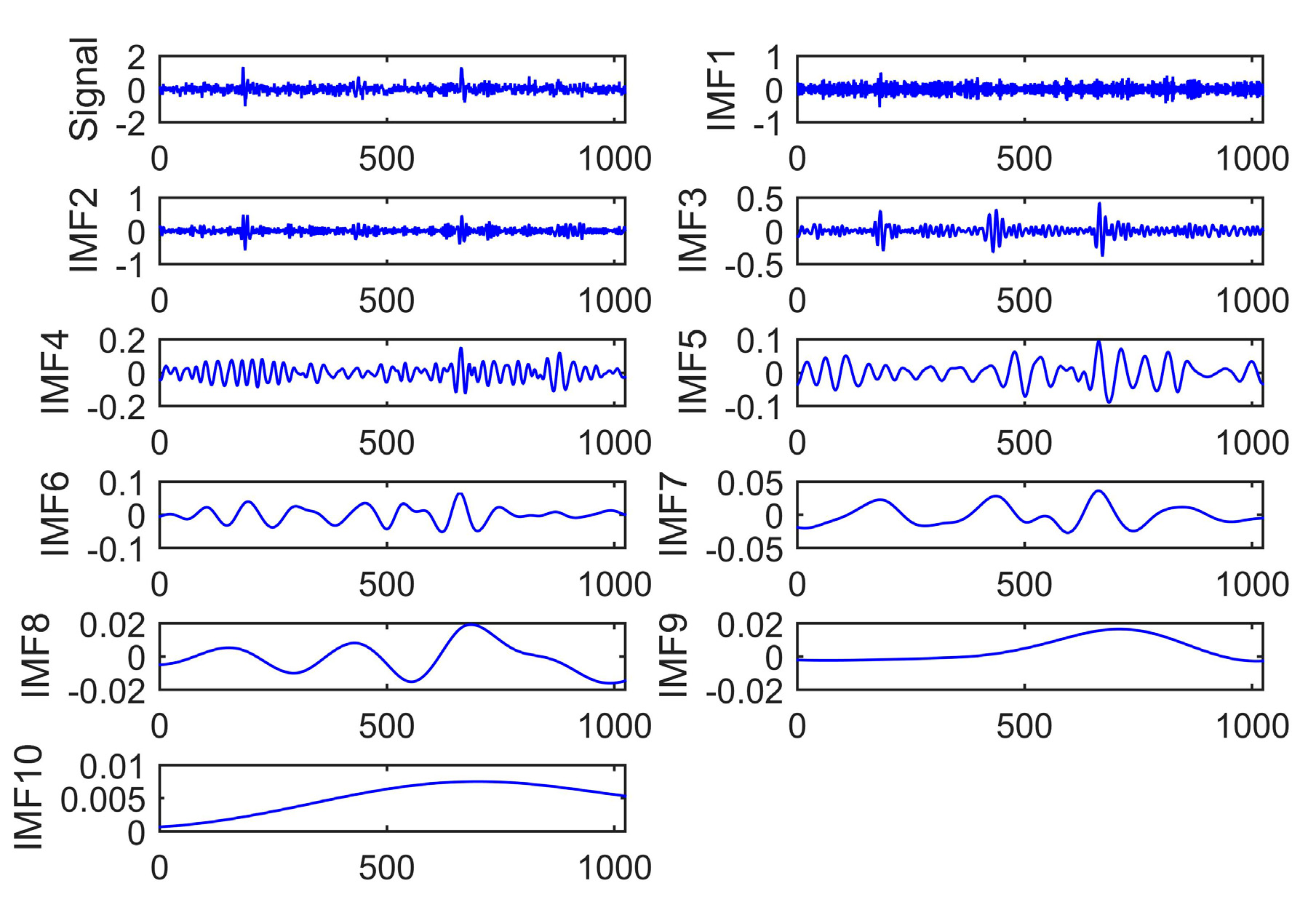
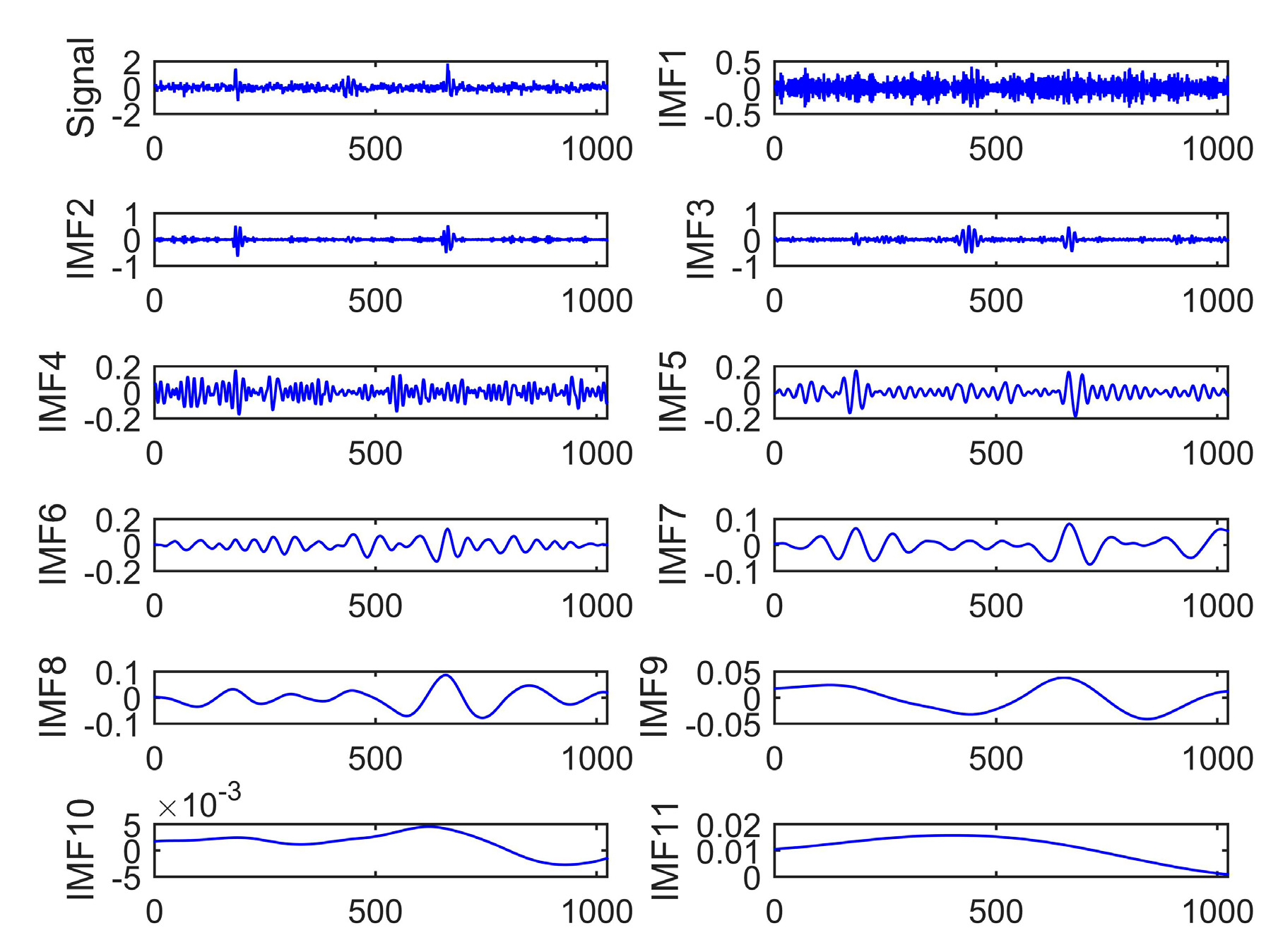
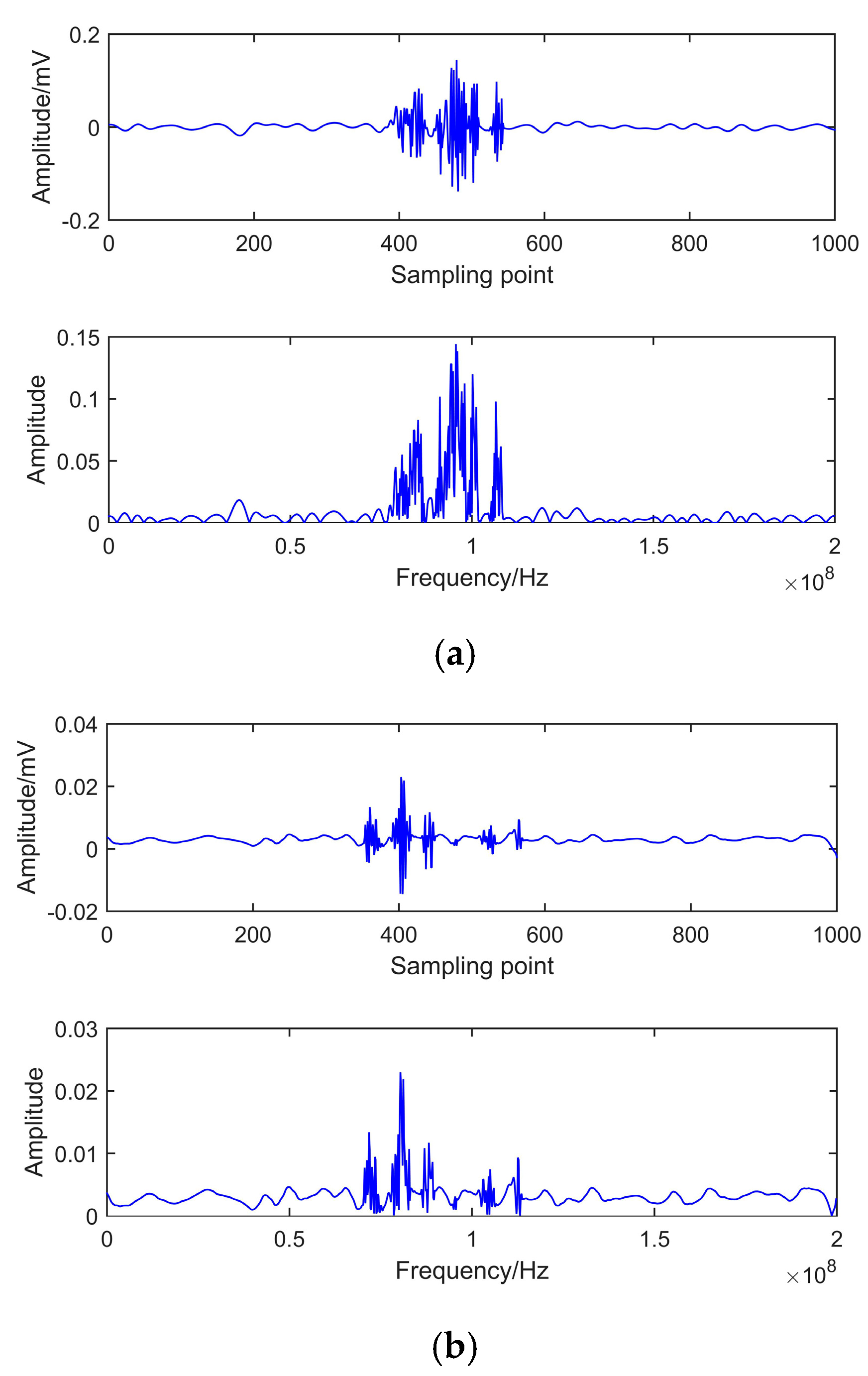
5.2. Signal Decomposition
5.3. Approximate Entropy Calculation
5.4. Correlation Coefficient Analysis
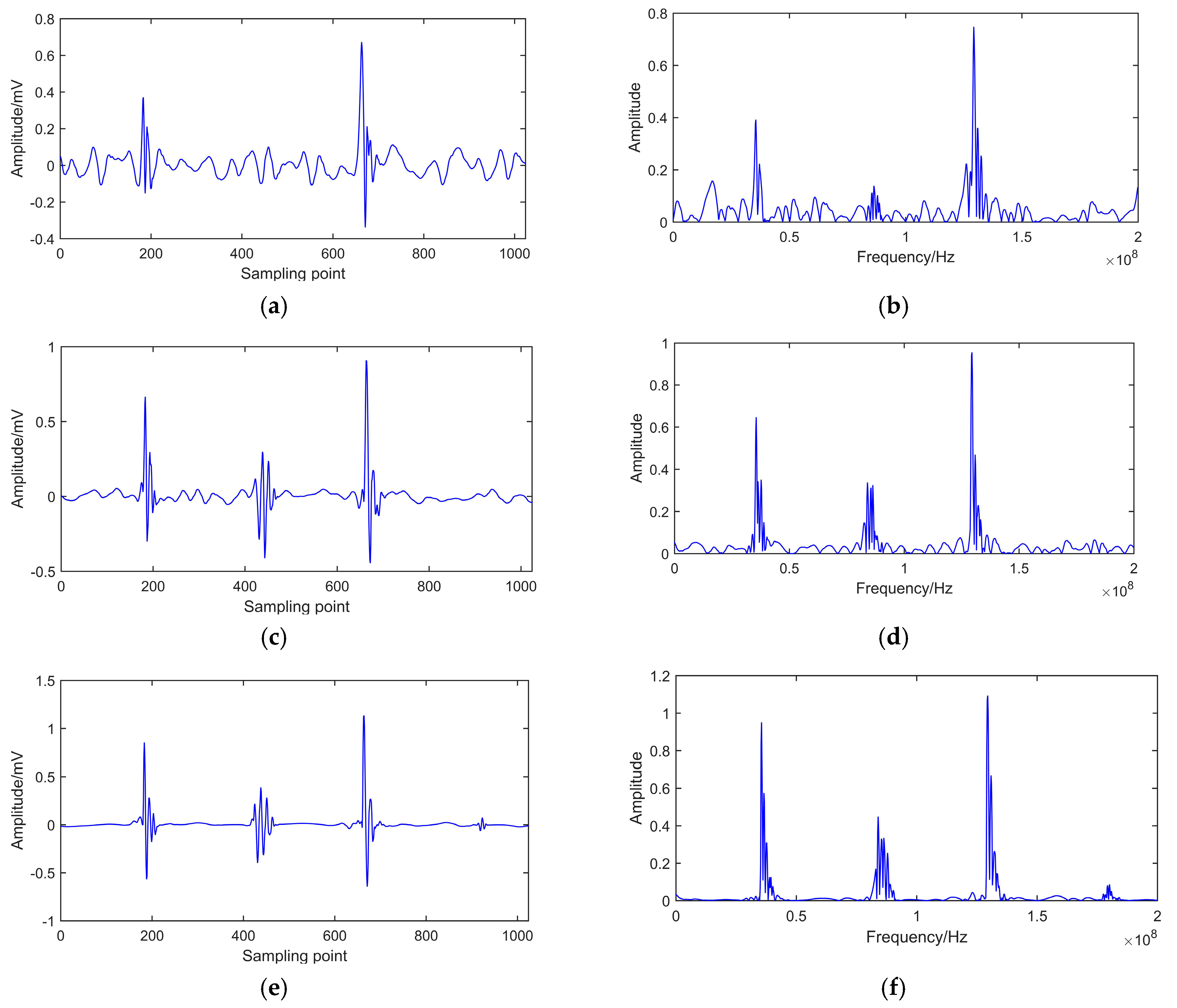
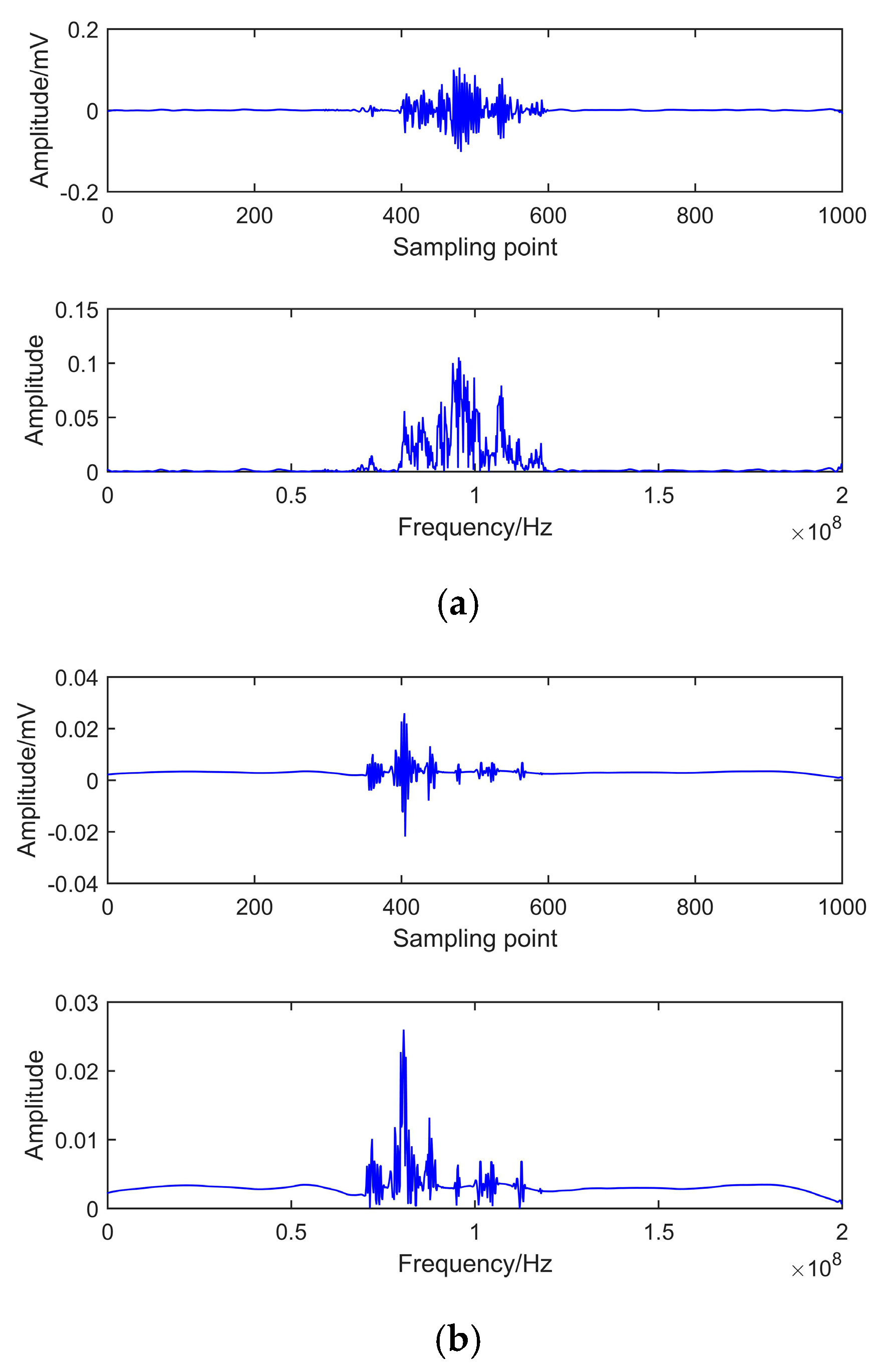
5.5. De-Noising Results Analysis
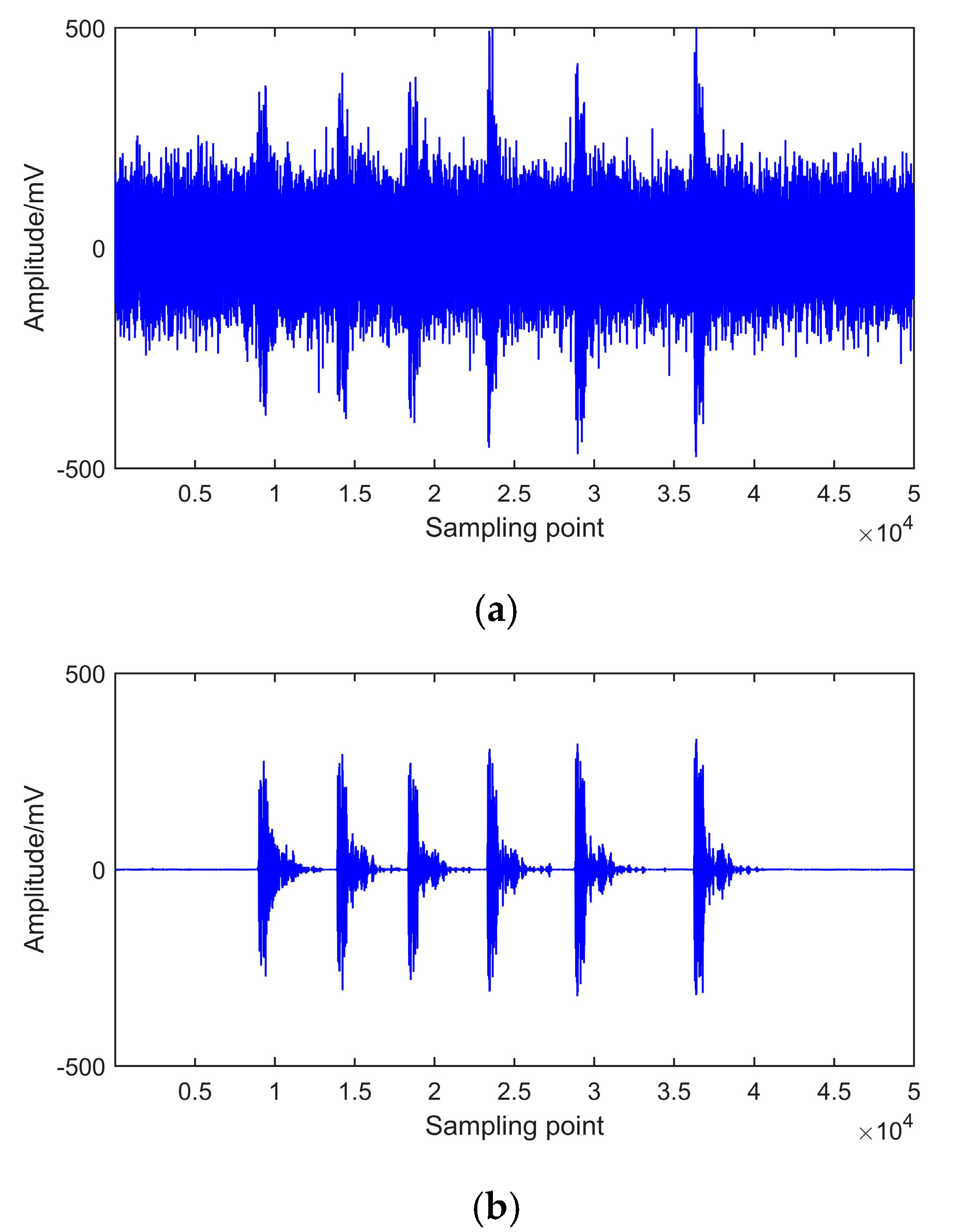
6. Experimental and On-Site PD Signal Analysis
6.1. Experimental PD Signal
6.2. On-Site PD Signal
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alexander, P.; Uwe, S. Partial discharge measurement at DC voltage—Evaluation and characterization by NoDi* pattern. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 883–891. [Google Scholar]
- Wang, J.Y.; Liang, H.J.; Kang, A.M. Researches of Power Transformer Partial Discharge Location Using Ultrasonic Method in China. J. Northeast Dianli Univ. 2019, 39, 10–14. [Google Scholar]
- Darwish, A.; Refaat, S.S.; Toliyat, H.A.; Abu-Rub, H. On the Electromagnetic Wave Behavior Due to Partial Discharge in Gas Insulated Switchgears: State-of-Art Review. IEEE Access 2019, 7, 75822–75836. [Google Scholar] [CrossRef]
- Torii, H.; Hayase, Y.; Yamashiro, K.; Matsumoto, S. Noise discrimination method for partial discharge current focused on damped oscillation waveform. IEEE Trans. Fundam. Mater. 2018, 138, 64–70. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Lu, W.; Lu, X.; Han, J.; Zhao, Z.; Du, X. Online Estimation of ESR for DC-Link Capacitor of Boost PFC Converter Using Wavelet Transform Based Time–Frequency Analysis Method. IEEE Trans. Power Electron. 2020, 35, 7755–7764. [Google Scholar] [CrossRef]
- Liaw, J.-J.; Lu, C.-P.; Huang, Y.-F.; Liao, Y.-H.; Huang, S.-C. Improving Census Transform by High-Pass with Haar Wavelet Transform and Edge Detection. Sensors 2020, 20, 2537. [Google Scholar] [CrossRef]
- Dangdang, D.A.I.; Xianpei, W.A.N.G.; Jiachuan, L.O.N.G. De-noising Method of Ultra-high Frequency Partial Discharge Signal Based on Improved Protrugram and Wavelet Transform. High Volt. Eng. 2018, 44, 3577–3586. [Google Scholar]
- Ghorat, M.; Gharehpetian, G.B.; Latifi, H.; Hejazi, M.A. A New Partial Discharge Signal Denoising Algorithm Based on Adaptive Dual-Tree Complex Wavelet Transform. IEEE Trans. Instrum. Meas. 2018, 67, 2262–2272. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, J.; Shi, W.; Guo, J. Extraction of Partial Discharge Pulses from the Complex Noisy Signals of Power Cables Based on CEEMDAN and Wavelet Packet. Energies 2019, 12, 3242. [Google Scholar] [CrossRef]
- Boudraa, A.O.; Cexus, J.C. EMD-Based Signal Filtering. IEEE Trans. Instrum. Meas. 2007, 56, 2196–2202. [Google Scholar] [CrossRef]
- Ziani, R.; Hammami, A.; Chaari, F.; Felkaoui, A.; Haddar, M. Gear fault diagnosis under non-stationary operating mode based on EMD, TKEO, and Shock Detector. Comptes Rendus Mécanique 2019, 347, 663–675. [Google Scholar] [CrossRef]
- Das, K.; Nath, D.; Pradhan, S. FPGA and ASIC Realization of EMD Algorithm for Real-Time Signal Processing. IET Circuits Devices Syst. 2019. [Google Scholar] [CrossRef]
- Chen, X.J.; Yang, Y. Analysis of the partial discharge of ultrasonic signals in large motor based on Hilbert-Huang transform. Appl. Acoust. 2018, 131, 165–173. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Guo, L.; Zhang, S. Partial Discharge Detection for GIS Based on Normalized Autocorrelation Function and Similar Wavelet Soft Threshold. High Volt. Apparatus 2018, 54, 17–24. [Google Scholar]
- Wang, M.-H.; Lu, S.-D.; Lin, K.-D.; Pan, C.-Y. Application of Extension Neural Network Algorithm and Empirical Mode Decomposition Method to Partial Discharge Diagnosis of Power Capacitors. Sens. Mater. 2019, 31, 3959–3972. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, M.; Yu, Q.; Zhang, H. Comparing the applications of EMD and EEMD on time–frequency analysis of seismic signal. J. Appl. Geophys. 2012, 83, 29–34. [Google Scholar] [CrossRef]
- Tan, Q.-F.; Lei, X.; Wang, X.; Wang, H.; Wen, X.; Ji, Y.; Kang, A.-Q. An adaptive middle and long-term runoff forecast model using EEMD-ANN hybrid approach. J. Hydrol. 2018, 567, 767–780. [Google Scholar] [CrossRef]
- Yu, Y.H.; Zhang, H.; Singh, V. Forward Prediction of Runoff Data in Data-Scarce Basins with an Improved Ensemble Empirical Mode Decomposition (EEMD) Model. Water 2018, 10, 388. [Google Scholar] [CrossRef]
- Jin, T.; Li, Q.; Mohamed, M.A. A Novel Adaptive EEMD Method for Switchgear Partial Discharge Signal Denoising. IEEE Access 2019, 7, 58139–58147. [Google Scholar] [CrossRef]
- Chan, J.C.; Ma, H.; Saha, T.K.; Ekanayake, C. Self-adaptive partial discharge signal de-noising based on ensemble empirical mode decomposition and automatic morphological thresholding. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 294–303. [Google Scholar] [CrossRef]
- Torres, M.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Zhang, W.; Qu, Z.; Zhang, K.; Mao, W.; Ma, Y.; Fan, X. A combined model based on CEEMDAN and modified flower pollination algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 136, 439–451. [Google Scholar] [CrossRef]
- Kuai, M.; Cheng, G.; Pang, Y.; Li, Y. Research of Planetary Gear Fault Diagnosis Based on Permutation Entropy of CEEMDAN and ANFIS. Sensors 2018, 18, 782. [Google Scholar] [CrossRef] [PubMed]
- Mumtaz, A.; Prasad, R. Significant wave height forecasting via an extreme learning machine model integrated with improved complete ensemble empirical mode decomposition. Renew. Sustain. Energy Rev. 2019, 104, 281–295. [Google Scholar]
- Pincus, S. Approximate entropy (ApEn) as a complexity measure. Chaos 1995, 5, 110–117. [Google Scholar] [CrossRef]
- Xiao, M.-X.; Wei, H.-C.; Xu, Y.-J.; Wu, H.-T.; Sun, C.-K. Combination of R-R Interval and Crest Time in Assessing Complexity Using Multiscale Cross-Approximate Entropy in Normal and Diabetic Subjects. Entropy 2018, 20, 497. [Google Scholar] [CrossRef]
- Singh, V.; Gupta, A.; Sohal, J.S.; Singh, A. A unified non-linear approach based on recurrence quantification analysis and approximate entropy: Application to the classification of heart rate variability of age-stratified subjects. Med. Biol. Eng. 2018, 57, 741–755. [Google Scholar] [CrossRef]
- Ryan, G.; Mosca, A.; Chang, J.-S.; Wu, E. At a Glance: Pixel Approximate Entropy as a Measure of Line Chart Complexity. IEEE Trans. Vis. Comput. Graph. 2018, 25, 872–881. [Google Scholar] [CrossRef]
- Chen, W.; Jiang, F.; Chen, X.; Feng, Y.; Miao, J.; Chen, S.; Jiao, C.; Chen, H. Photoplethysmography-derived approximate entropy and sample entropy as measures of analgesia depth during propofol-remifentanil anesthesia. Int. J. Clin. Monit. Comput. 2020, 10, 1007. [Google Scholar] [CrossRef]
- Nur, B.A.; No-Weon, K.; Jae-Yong, K. Field Uniformity and Correlation Coefficient Analysis of KRISS Reverberation Chamber. Ieice Trans. Commun. 2018, 101, 2289–2296. [Google Scholar]
- Li, S.; Qin, N.; Huang, D.; Huang, D.; Ke, L. Damage Localization of Stacker’s Track Based on EEMD-EMD and DBSCAN Cluster Algorithms. IEEE Trans. Instrum. Meas. 2020, 69, 1981–1992. [Google Scholar] [CrossRef]
- Bouhalais, M.L.; Djebala, A.; Ouelaa, N.; Babouri, M.K. CEEMDAN and OWMRA as a hybrid method for rolling bearing fault diagnosis under variable speed. Int. J. Adv. Manuf. Technol. 2017, 94, 2475–2489. [Google Scholar] [CrossRef]
- Kumar, S.; Danas, K.; Kochmann, D.M. Enhanced local maximum-entropy approximation for stable meshfree simulations. Comput. Methods Appl. Mech. Eng. 2019, 344, 858–886. [Google Scholar] [CrossRef]
- Xie, M.; Zhou, K.; Huang, Y.L.; He, M.; Wang, X.J. A White Noise Suppression Method for Partial Discharge Based on Short Time Singular Value Decomposition. Proc. CSEE 2019, 3, 915–922. [Google Scholar]
- Fu, L.; He, Z.Y.; Mai, R.K.; Qian, Q.Q. Application of Approximate Entropy to Fault Signal Analysis in Electric Power System. Proc. CSEE 2018, 28, 68–73. [Google Scholar]
- Jiang, F.; Zhu, Z.; Li, W.; Ren, Y.; Zhou, G.; Chang, Y. A Fusion Feature Extraction Method Using EEMD and Correlation Coefficient Analysis for Bearing Fault Diagnosis. Appl. Sci. 2018, 8, 1621. [Google Scholar] [CrossRef]
- Shang, H.K.; Lo, K.; Li, F. Partial Discharge Feature Extraction Based on Ensemble Empirical Mode Decomposition and Sample Entropy. Entropy 2017, 19, 439. [Google Scholar] [CrossRef]



| Amplitude/mV | Attenuation Coefficient/us | Oscillation Frequency/MHz | |
|---|---|---|---|
| Pulse 1 | 1.5 | 0.05 | 20 |
| Pulse 2 | 3 | 0.1 | 15 |
| Pulse 3 | 2 | 0.05 | 15 |
| Pulse 4 | 1 | 0.1 | 20 |
| IMF1 | IMF5 | IMF6 | IMF7 | IMF8 | IMF9 | IMF10 | IMF11 |
|---|---|---|---|---|---|---|---|
| 0.552 | 0.823 | 0.906 | 0.932 | 0.773 | 0.521 | 0.328 | 0.195 |
| SNR/dB | MSE/dB | NCC | |
|---|---|---|---|
| Original Signal | −5.3024 | 0.9356 | 1 |
| EMD | 15.8726 | 0.4067 | 0.772 |
| EEMD | 21.6218 | 0.1068 | 0.985 |
| CEEMDAN-ApEn | 28.2298 | 0.0326 | 0.993 |
| NRR/dB | |
|---|---|
| EEMD | 16.5825 |
| CEEMDAN-ApEn | 28.3012 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, H.; Li, Y.; Xu, J.; Qi, B.; Yin, J. A Novel Hybrid Approach for Partial Discharge Signal Detection Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Approximate Entropy. Entropy 2020, 22, 1039. https://doi.org/10.3390/e22091039
Shang H, Li Y, Xu J, Qi B, Yin J. A Novel Hybrid Approach for Partial Discharge Signal Detection Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Approximate Entropy. Entropy. 2020; 22(9):1039. https://doi.org/10.3390/e22091039
Chicago/Turabian StyleShang, Haikun, Yucai Li, Junyan Xu, Bing Qi, and Jinliang Yin. 2020. "A Novel Hybrid Approach for Partial Discharge Signal Detection Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Approximate Entropy" Entropy 22, no. 9: 1039. https://doi.org/10.3390/e22091039
APA StyleShang, H., Li, Y., Xu, J., Qi, B., & Yin, J. (2020). A Novel Hybrid Approach for Partial Discharge Signal Detection Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Approximate Entropy. Entropy, 22(9), 1039. https://doi.org/10.3390/e22091039




