Market of Stocks during Crisis Looks Like a Flock of Birds
Abstract
1. Introduction
2. The Validation of the Framework
Prototype Implementation
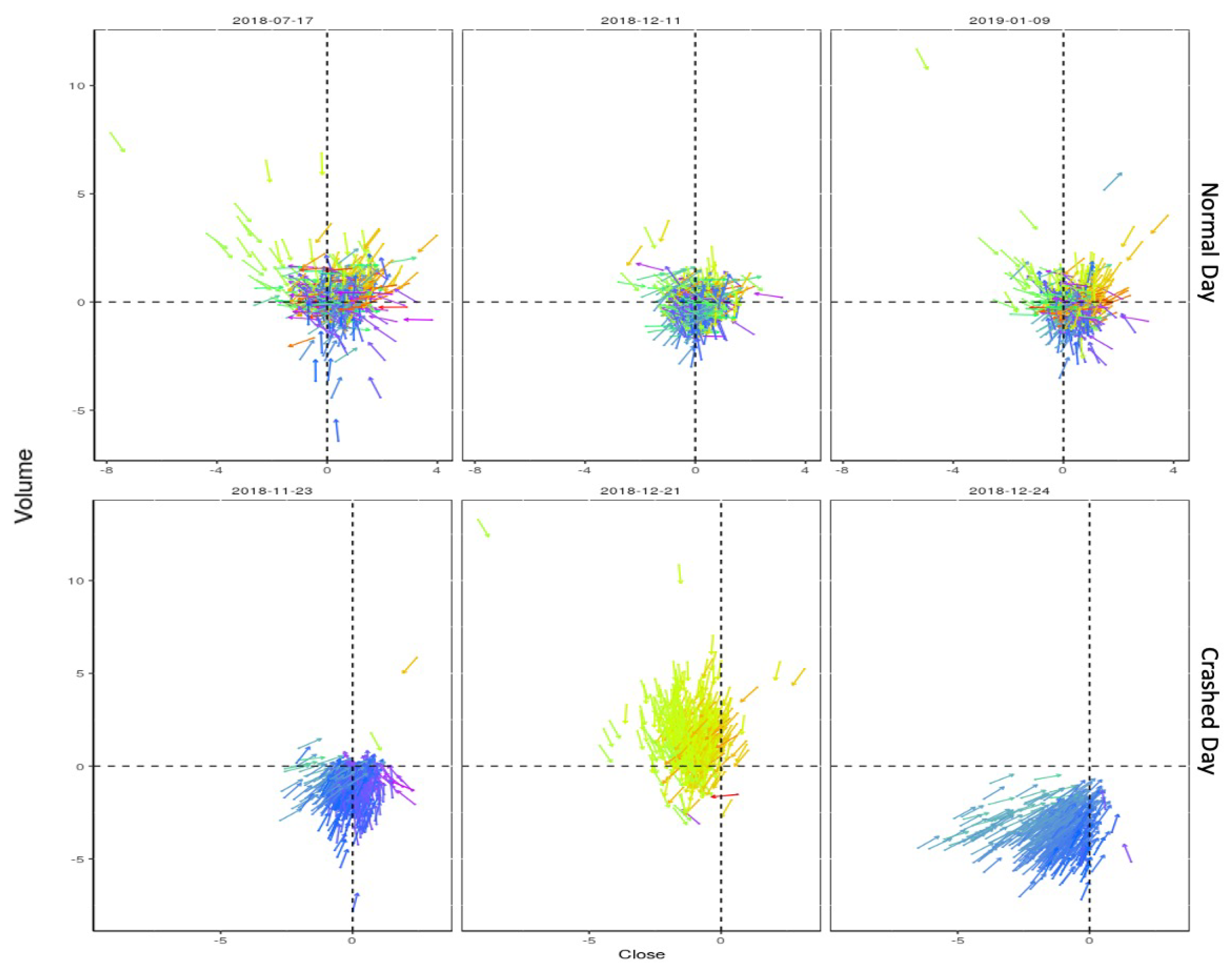
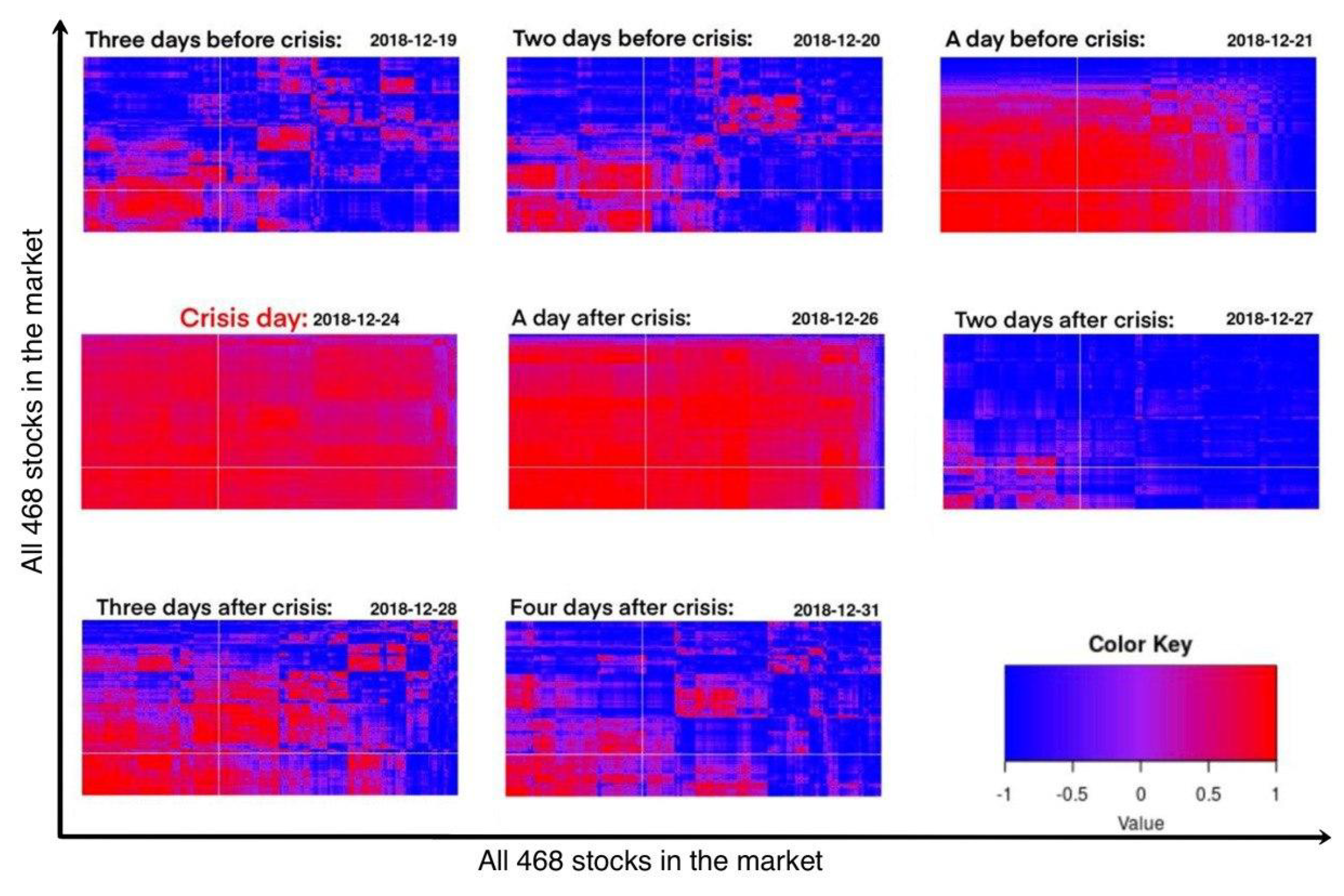
3. Results and Discussion
- Drawing an imaginary circle and lay the start point of the velocity vectors of each share on the center of the circle.
- Dividing the circle into 12 equal slices and assigning a number to each of them, so each velocity vector is located in one slice.
- Mapping each share to one slice number. For example, the velocity vector of i-th share in the division l is shown as , where t denotes time. l can only accept integer values and it returns the number of the slice that velocity vector is located, and is the degree of each slice which in this research assumed 30 degrees.l equals to the integer part of the right hand side of Equation (9).
- Coupling the joint shares. For example, if share i is in slice l and share j is in slice m, the return of the joint l-m or m-l will be considered. l-m and m-l are considered as one possible combination of joint shares. Therefore, the joint probability of both i and j to be placed in l and m divisions equals 1.
- Counting the possible combinations of joint shares . For example, 0-0, 0-1, 0-2, ..., 10-11, 11-11. It can be a maximum of 78 combinations of joint shares.
- The velocity vector of i-th share at time t is shown by .
- The alignment of the velocity vectors of two separate shares can be calculated by Formula (12). The basis of this calculation is the cosine of the angle between the two velocity vectors.
- The stocks normally are correlated to each other. Thus, the change in one stock can affect the other stocks. This effect does not happen at once. Thus, we considered a delay for the calculations.Equation (13) selects the maximum alignment factor between velocity vectors of two shares for two consecutive days. which is the added lag for alignment matrix calculations has been assumed 1 day.
- The alignment matrix has been constructed using calculated in Equation (13). The alignment matrix has been generated using dendrogram to present the stocks which are grouped together.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lao, P.; Singh, H. Herding behaviour in the Chinese and Indian stock markets. J. Asian Econ. 2011, 22, 495–506. [Google Scholar] [CrossRef]
- Giardina, I. Collective behavior in animal groups: Theoretical models and empirical studies. HFSP J. 2008, 2, 205–219. [Google Scholar] [CrossRef] [PubMed]
- Lukeman, R.; Li, Y.X.; Edelstein-Keshet, L. Inferring individual rules from collective behavior. Proc. Natl. Acad. Sci. USA 2010, 107, 12576–12580. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Hsiao, C.; Li, Q.; Wang, Z. The Emerging Market Crisis and Stock Market Linkages: Further Evidence. J. Appl. Econom. 2006, 21, 727–744. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, J.; Bessler, D.A. Financial crisis and African stock market integration. Appl. Econ. Lett. 2003, 10, 527–533. [Google Scholar] [CrossRef]
- Xu, R.; Chang, J.; Li, C.; Wang, W. Research on the influence of equity pledge on stock price crash risk: Based on financial shock of 2015 stock market crisis. Econ. Political Stud. 2019, 7, 480–505. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, X.; Gong, X.; Yang, X.; Huang, C. Systemic Importance of China’s Financial Institutions: A Jump Volatility Spillover Network Review. Entropy 2020, 22, 588. [Google Scholar] [CrossRef]
- Memon, B.; Yao, H. Structural Change and Dynamics of Pakistan Stock Market During Crisis: A Complex Network Perspective. Entropy 2019, 21, 248. [Google Scholar] [CrossRef]
- Iren, P. Behavior of Foreign Investors in the Malaysian Stock Market in Times of Crisis: A Nonlinear Approach. J. Asian Econ. 2018, 60, 85–100. [Google Scholar] [CrossRef]
- Namaki, A.; Shirazi, A.H.; Raei, R.; Jafari, G.R. Network analysis of a financial market based on genuine correlation and threshold method. Phys. A Stat. Mech. Its Appl. 2011, 390, 3835–3841. [Google Scholar] [CrossRef]
- Mandes, A. Algorithmic and High-Frequency Trading Strategies: A Literature Review; MAGKS Joint Discussion Paper Series in Economics, No. 25-2016; Philipps-Universität Marburg, Faculty of Business Administration and Economics, Department of Economics: Marburg, Germany, 2016. [Google Scholar]
- Gerig, A. High-Frequency Trading Synchronizes Prices in Financial Markets. SSRN Electron. J. 2015. [Google Scholar] [CrossRef][Green Version]
- Crawford, B.; Soto, R.; Martín, M.; de la Fuente-Mella, H.; Castro, C.; Paredes, F. Automatic High-Frequency Trading: An Application to Emerging Chilean Stock Market. Sci. Program. 2018, 1–12. [Google Scholar] [CrossRef]
- Malekian, E.; Fakhari, H.; Qasemi, J.; Farzad, S. A Comparative Study of Prediction Stock Crash Risk by using Meta-Heuristic & Regression. Int. J. Financ. Manag. Account. 2018, 3, 63–77. [Google Scholar]
- Peron, T.; Rodrigues, F. Collective behavior in financial markets. EPL Europhys. Lett. 2011, 96, 48004. [Google Scholar] [CrossRef]
- Toner, J.; Tu, Y. Flocks, herds, and schools: A quantitative theory of flocking. Phys. Rev. E 1998, 58, 4828–4858. [Google Scholar] [CrossRef]
- Jung, N.; Kim, P. Marginalized ordering and adaptive reaction time in bird flocks. arXiv 2019, arXiv:1902.09288. [Google Scholar]
- Saeedian, M.; Jamali, T.; Kamali, M.Z.; Bayani, H.; Yasseri, T.; Jafari, G.R. Emergence of world-stock-market network. Phys. A Stat. Mech. Its Appl. 2019, 526, 120792. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel Type of Phase Transition in a System of Self-Driven Particles. Phys. Rev. Lett. 1995, 75, 1226–1229. [Google Scholar] [CrossRef]
- Czirók, A.; Barabási, A.L.; Vicsek, T. Collective Motion of Self-Propelled Particles: Kinetic Phase Transition in One Dimension. Phys. Rev. Lett. 1999, 82, 209–212. [Google Scholar] [CrossRef]
- Levine, H.; Rappel, W.J.; Cohen, I. Self-organization in systems of self-propelled particles. Phys. Rev. E 2000, 63, 017101. [Google Scholar] [CrossRef]
- Buhl, J.; Sumpter, D.J.T.; Couzin, I.D.; Hale, J.J.; Despl, E.; Miller, E.R.; Simpson, S.J. From Disorder to Order in Marching Locusts. Science 2006, 312, 1402–1406. [Google Scholar] [CrossRef] [PubMed]
- Peruani, F.; Deutsch, A.; Bär, M. Nonequilibrium clustering of self-propelled rods. Phys. Rev. E 2006, 74, 030904. [Google Scholar] [CrossRef]
- Chaté, H.; Ginelli, F.; Montagne, R. Simple Model for Active Nematics: Quasi-Long-Range Order and Giant Fluctuations. Phys. Rev. Lett. 2006, 96, 180602. [Google Scholar] [CrossRef] [PubMed]
- Cucker, F.; Smale, S. Emergent Behavior in Flocks. IEEE Trans. Autom. Control 2007, 52, 852–862. [Google Scholar] [CrossRef]
- Galam, S. Modelling rumors: The no plane Pentagon French hoax case. Phys. A Stat. Mech. Its Appl. 2003, 320, 571–580. [Google Scholar] [CrossRef]
- Chepizhko, A.A.; Kulinskii, V.L. On the relation between Vicsek and Kuramoto models of spontaneous synchronization. Phys. A Stat. Mech. Its Appl. 2010, 389, 5347–5352. [Google Scholar] [CrossRef]
- Ginelli, F. The Physics of the Vicsek model. Eur. Phys. J. Spec. Top. 2016, 225, 2099–2117. [Google Scholar] [CrossRef]
- Amaral, L.A.N.; Cizeau, P.; Gopikrishnan, P.; Liu, Y.; Meyer, M.; Peng, C.-K.; Stanley, H.E. Econophysics: Can statistical physics contribute to the science of economics? Comput. Phys. Commun. 1999, 121, 145–152. [Google Scholar] [CrossRef]
- Aldana, M.; Dossetti, V.; Huepe, C.; Kenkre, V.M.; Larralde, H. Phase Transitions in Systems of Self-Propelled Agents and Related Network Models. Phys. Rev. Lett. 2007, 98, 095702. [Google Scholar] [CrossRef]
- Baglietto, G.; Albano, E.V. Nature of the order-disorder transition in the Vicsek model for the collective motion of self-propelled particles. Phys. Rev. E 2009, 80, 050103. [Google Scholar] [CrossRef]
- Available online: https://www.washingtonpost.com/graphics/2018/business/stock-market-crash-comparison/ (accessed on 1 September 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afsharizand, B.; Chaghoei, P.H.; Kordbacheh, A.A.; Trufanov, A.; Jafari, G. Market of Stocks during Crisis Looks Like a Flock of Birds. Entropy 2020, 22, 1038. https://doi.org/10.3390/e22091038
Afsharizand B, Chaghoei PH, Kordbacheh AA, Trufanov A, Jafari G. Market of Stocks during Crisis Looks Like a Flock of Birds. Entropy. 2020; 22(9):1038. https://doi.org/10.3390/e22091038
Chicago/Turabian StyleAfsharizand, Bahar, Pooya H. Chaghoei, Amirhossein A. Kordbacheh, Andrey Trufanov, and Golamreza Jafari. 2020. "Market of Stocks during Crisis Looks Like a Flock of Birds" Entropy 22, no. 9: 1038. https://doi.org/10.3390/e22091038
APA StyleAfsharizand, B., Chaghoei, P. H., Kordbacheh, A. A., Trufanov, A., & Jafari, G. (2020). Market of Stocks during Crisis Looks Like a Flock of Birds. Entropy, 22(9), 1038. https://doi.org/10.3390/e22091038





