Data-Dependent Conditional Priors for Unsupervised Learning of Multimodal Data †
Abstract
1. Introduction
2. From Variational Inference (VI) Objective to VAE Objective
2.1. Variational Inference
2.2. Variational Autoencoders
2.3. Posterior Collapse and Mismatch between the True and the Approximate Posterior
2.4. Optimal Prior
3. Related Work
4. VAE with Data-Dependent Conditional Priors
4.1. Two-Level Generative Process
Data-Dependent Conditional Priors
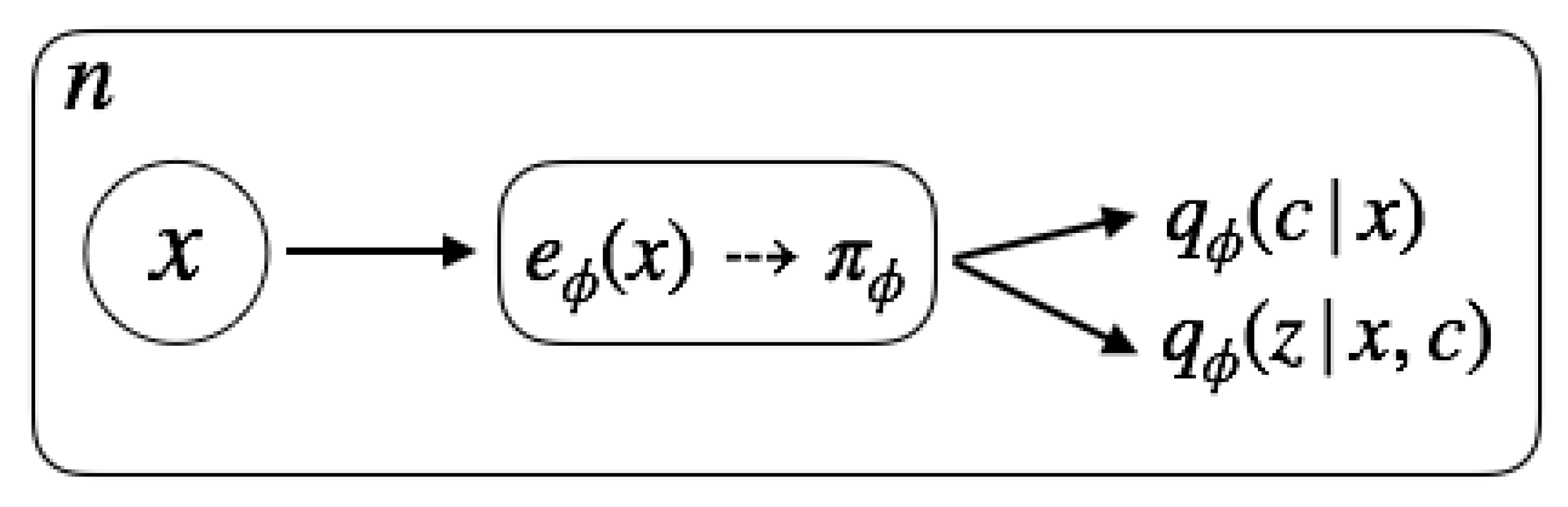
4.2. Inference Model
4.3. Optimization Objective
4.3.1. Analysis of the Objective
5. VAE with Continuous and Discrete Components
5.1. Comparing the Alternative Models
5.2. Assuming Uniform Approximate Categorical Posterior
6. Empirical Evaluation
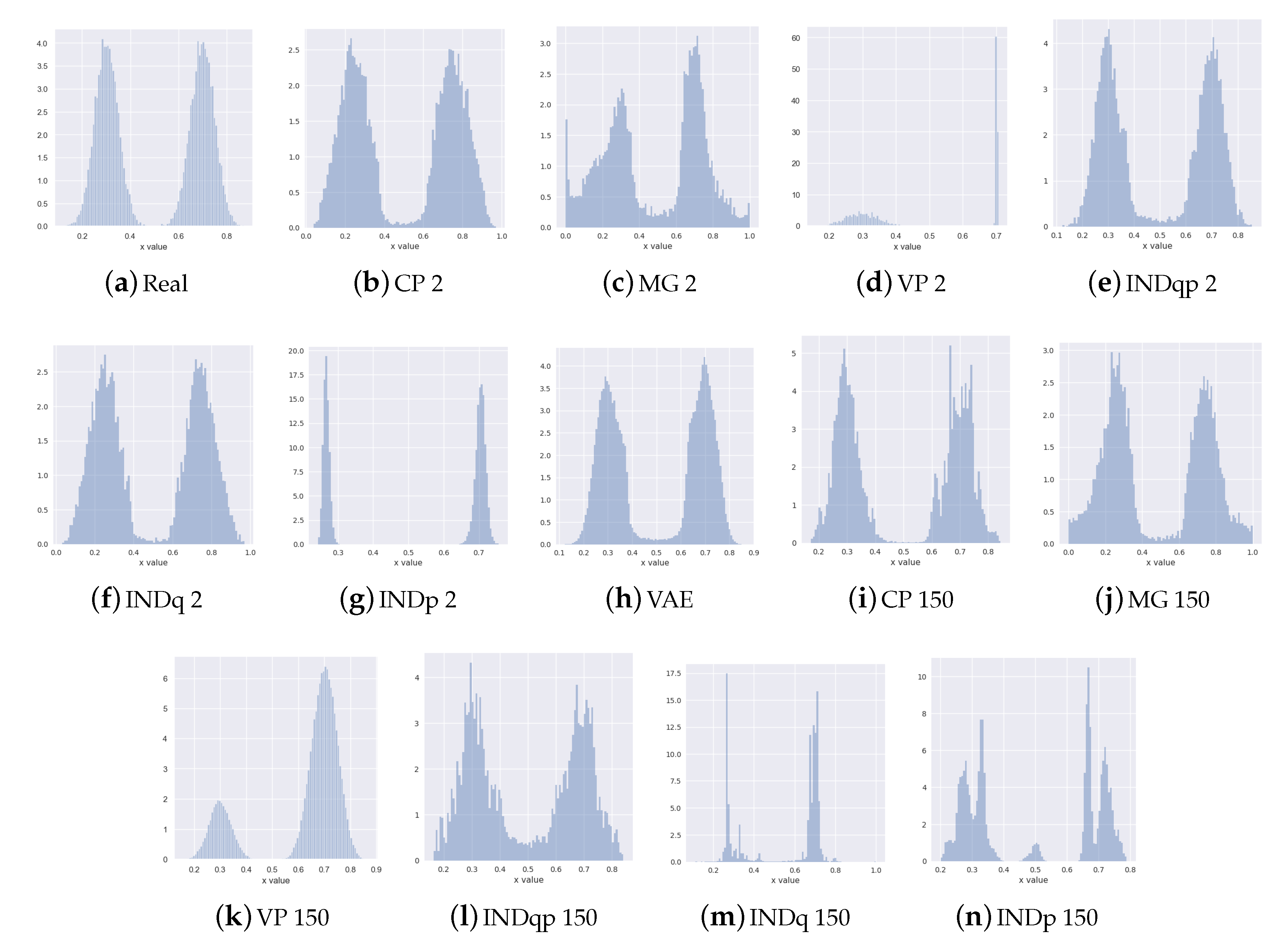
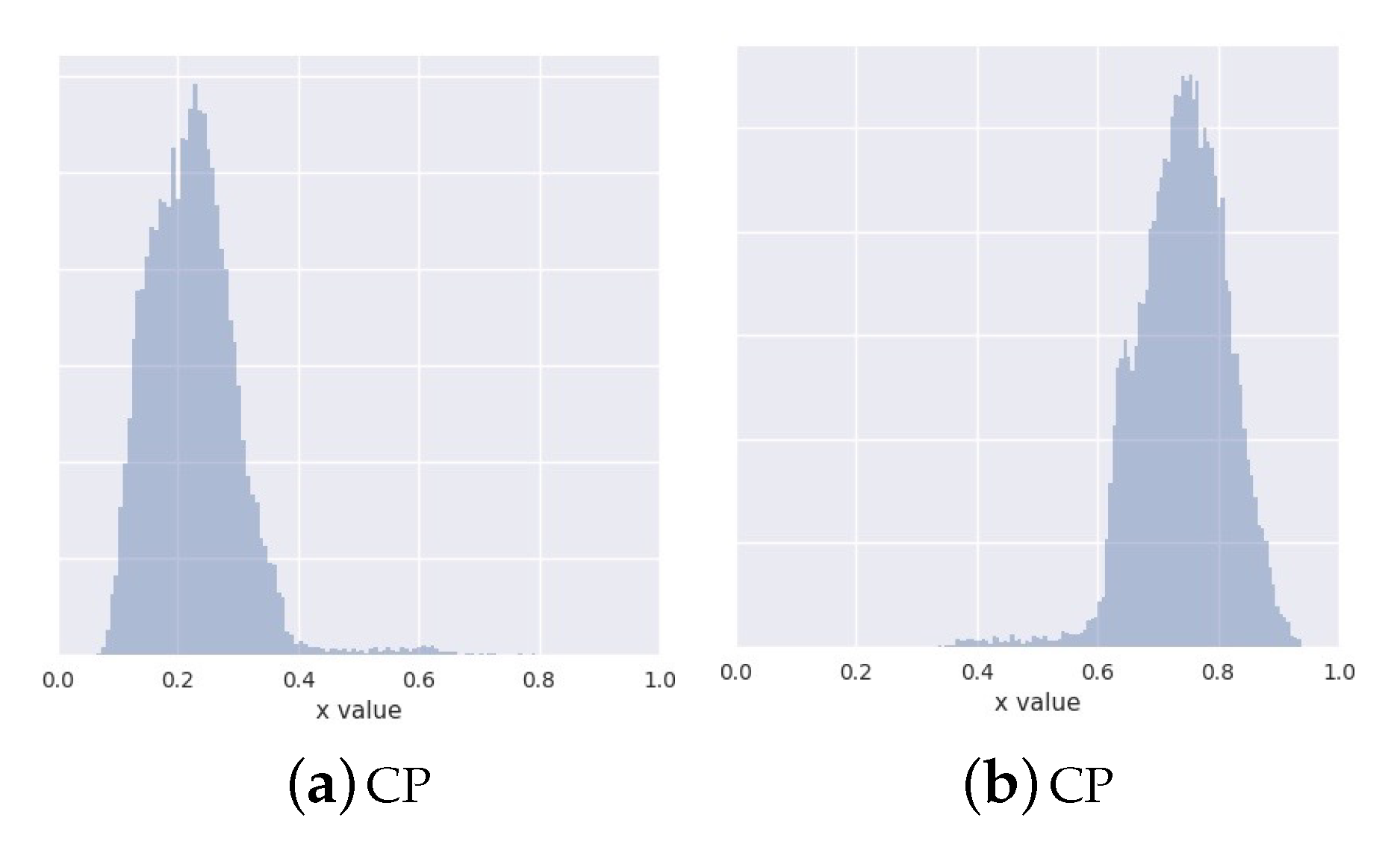
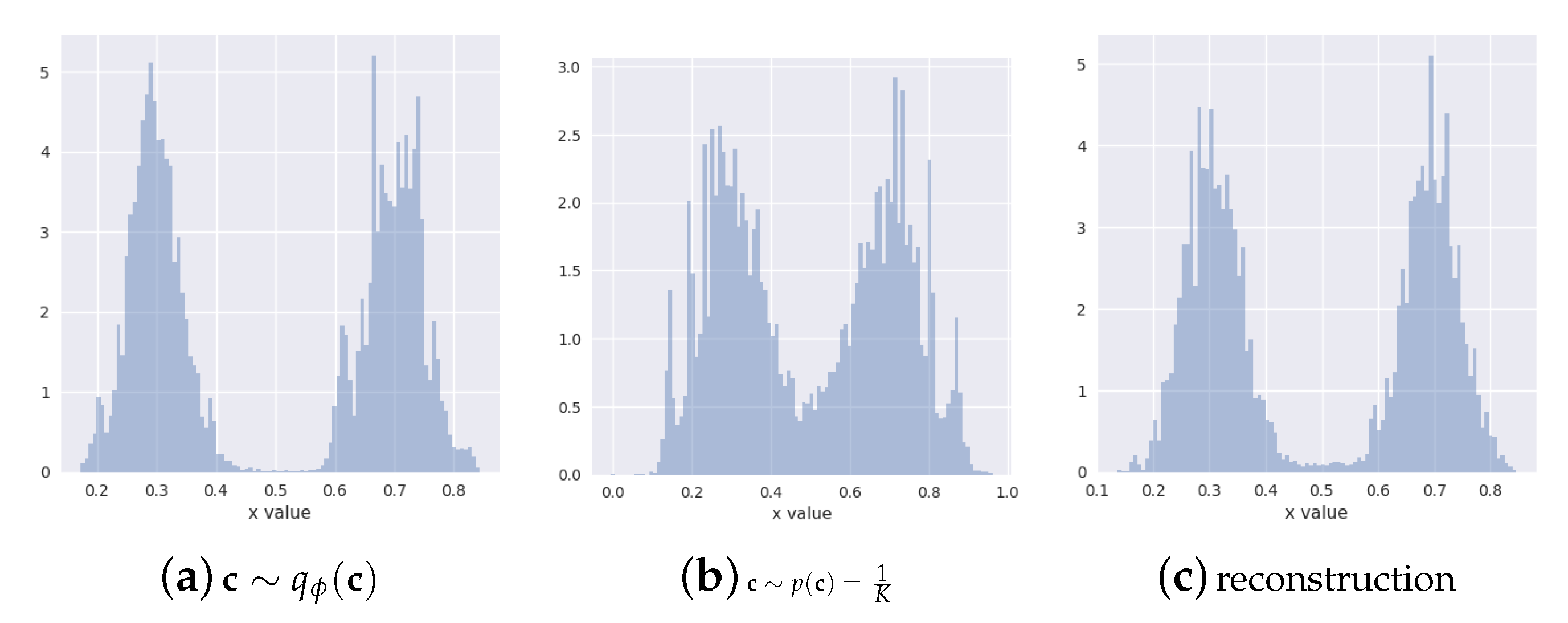
6.1. Synthetic Data Experiments
- known number of components: discrete latent variable with two categories (corresponding to the ground-truth two mixture components)
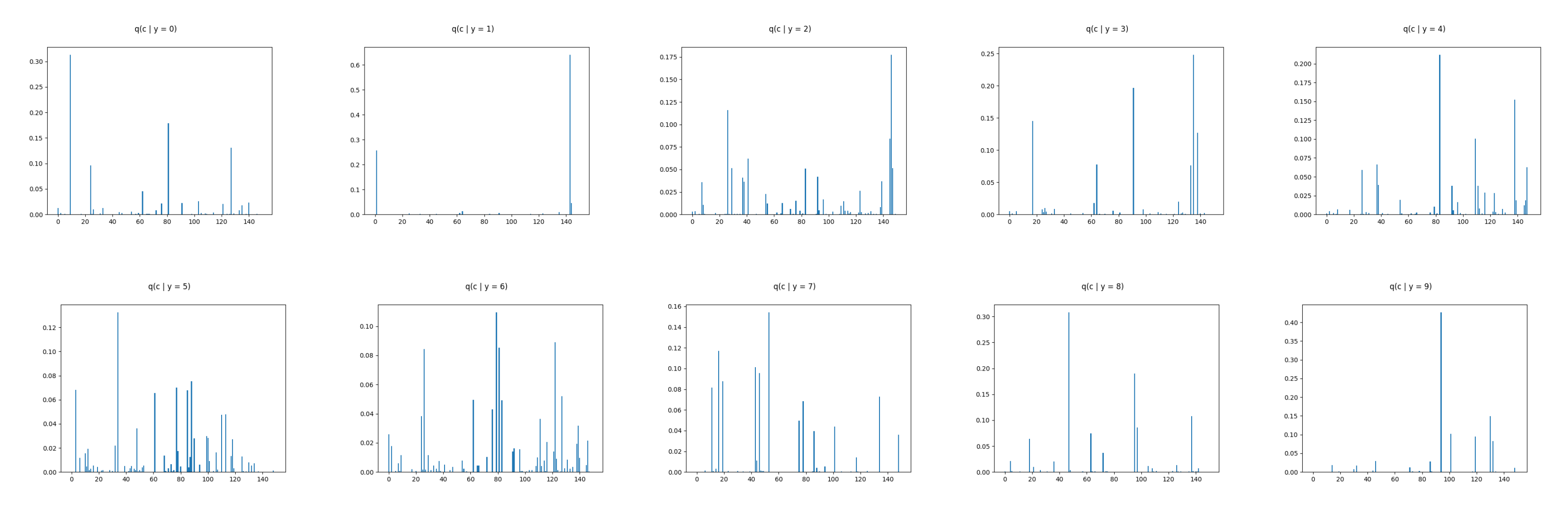
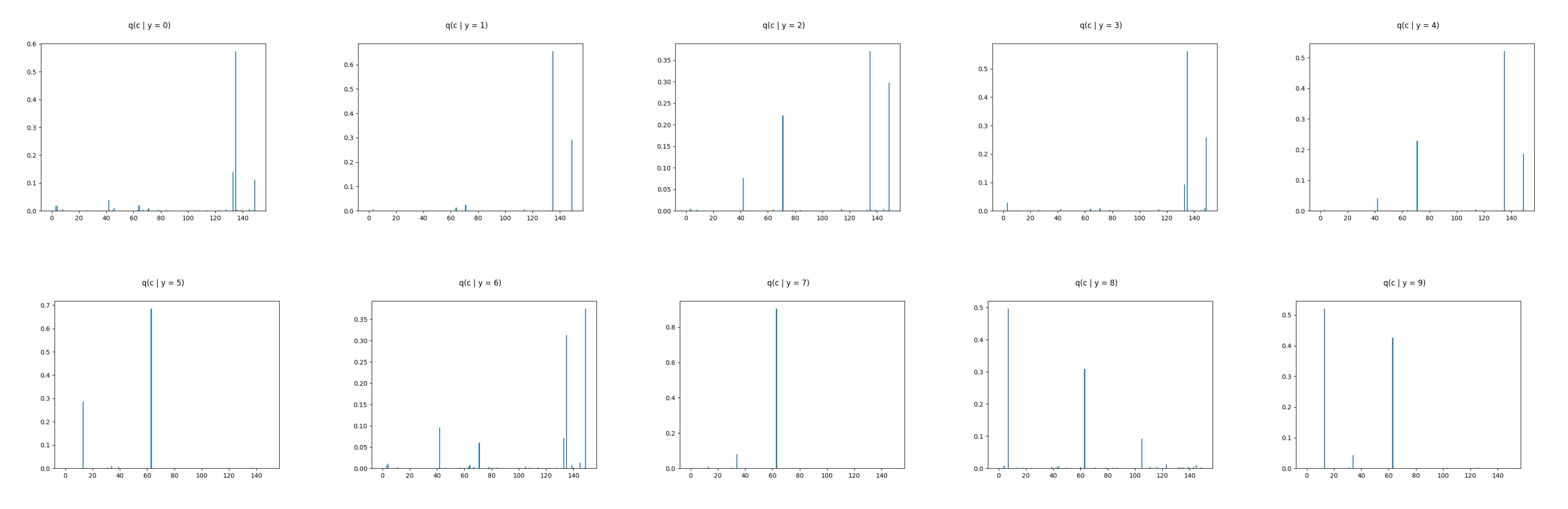
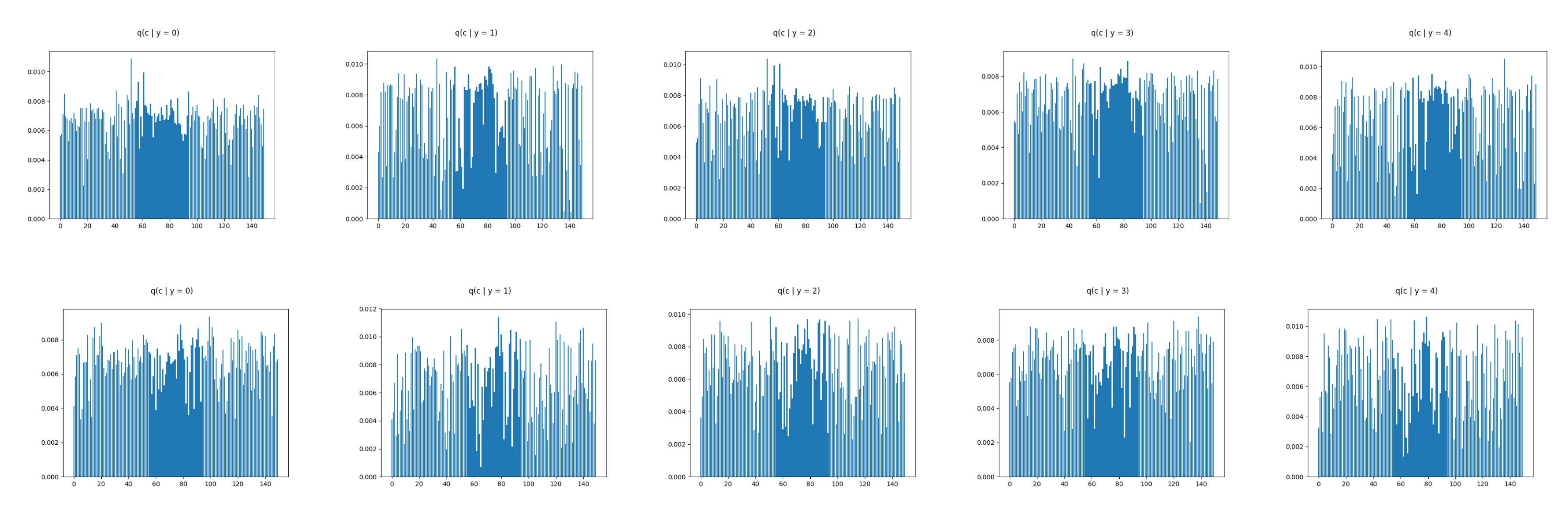
- unknown number of components: discrete latent variable with 150 categories
6.2. Real Data Experiments
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proofs
Appendix A.1. Proofs of Section 4
Appendix A.2. Proofs of Section 5
Appendix A.3. Proofs of Section 5.2
Appendix A.4. Maximizing the Negative RE is Equivalent to Maximizing a Lower Bound on MI between the Latent Variables (z,c) and x
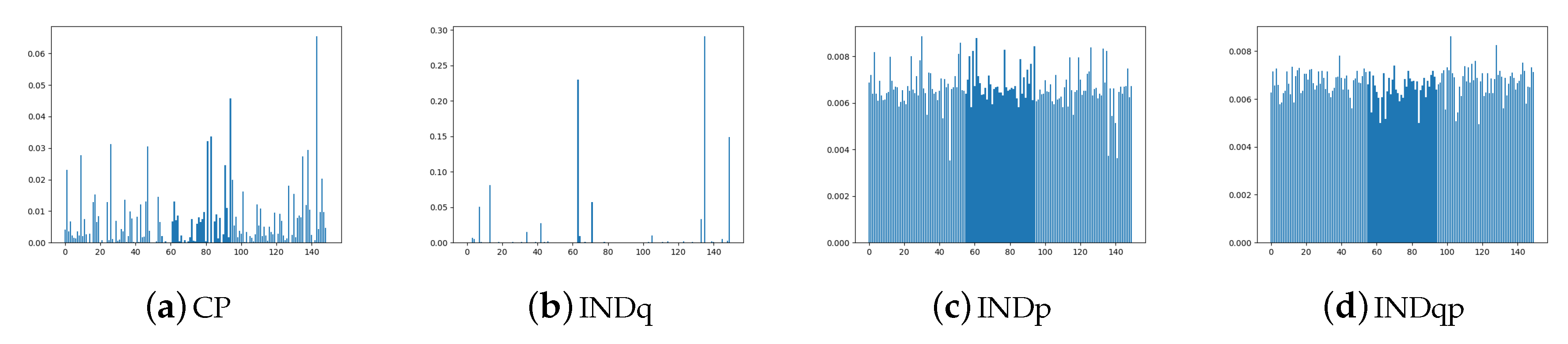
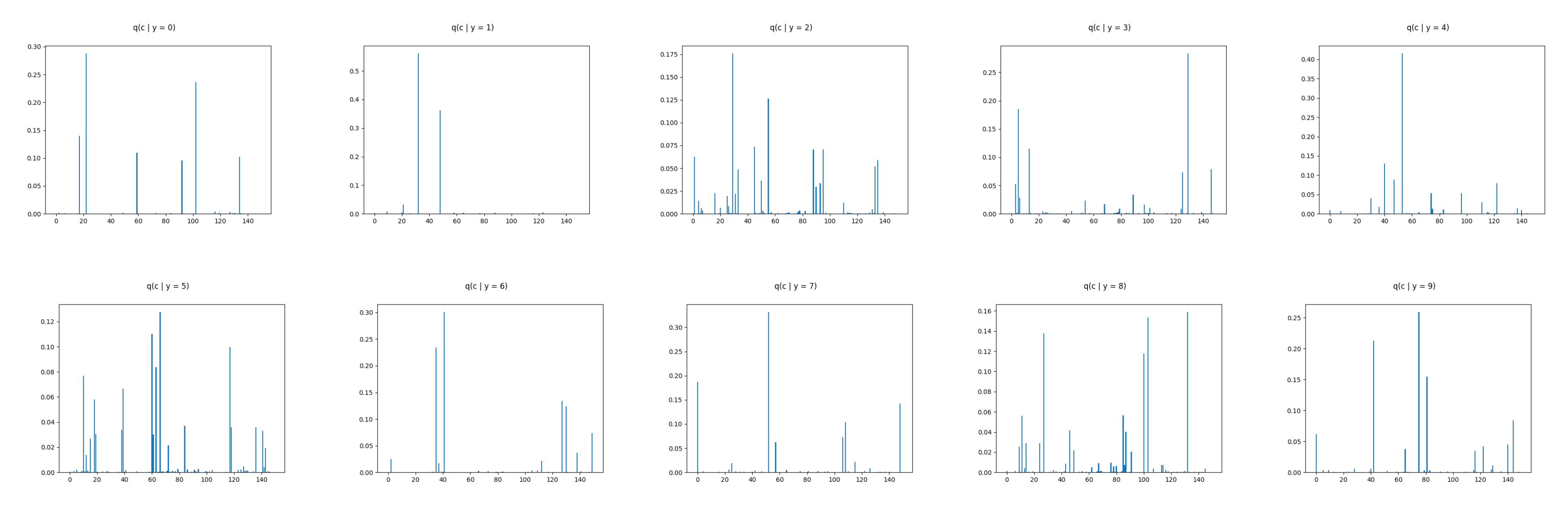
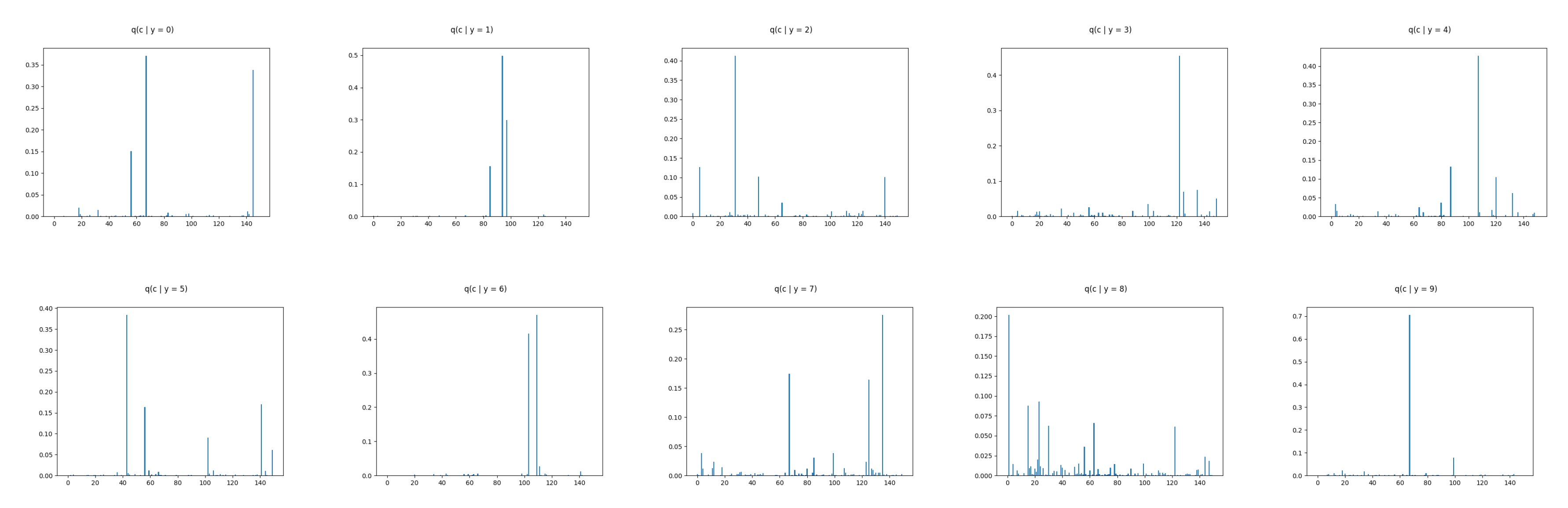
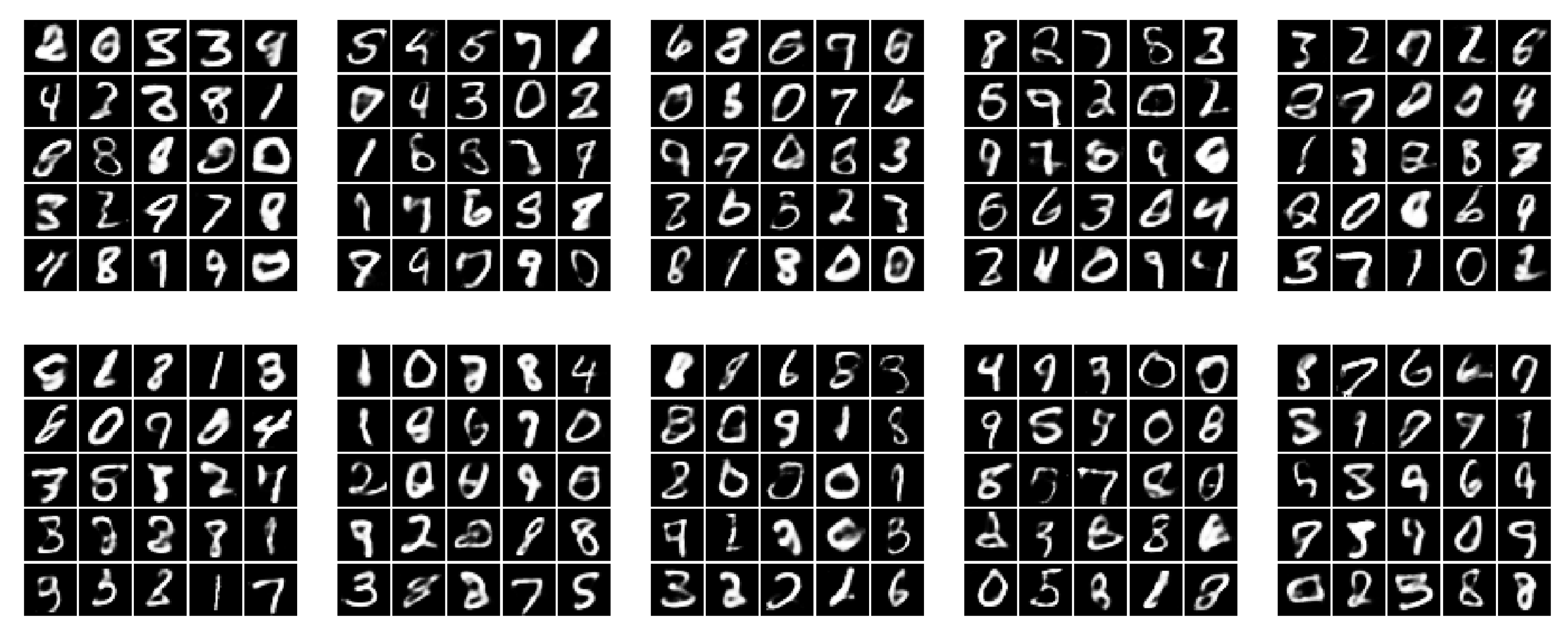
Appendix B. MNIST
| CPVAE | INDq | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| label 0 | 22 | 102 | 17 | 59 | 134 | 67 | 145 | 56 | 18 | 32 |
| label 1 | 32 | 48 | 21 | 9 | 20 | 94 | 97 | 85 | 124 | 67 |
| label 2 | 29 | 55 | 45 | 95 | 88 | 31 | 5 | 48 | 140 | 65 |
| label 3 | 129 | 5 | 13 | 146 | 125 | 122 | 135 | 125 | 149 | 99 |
| label 4 | 53 | 40 | 47 | 122 | 74 | 107 | 87 | 120 | 132 | 80 |
| label 5 | 66 | 60 | 117 | 63 | 10 | 43 | 141 | 56 | 102 | 149 |
| label 6 | 41 | 35 | 127 | 130 | 149 | 109 | 103 | 111 | 141 | 98 |
| label 7 | 52 | 0 | 148 | 108 | 106 | 135 | 67 | 125 | 2 | 99 |
| label 8 | 132 | 103 | 27 | 100 | 85 | 1 | 23 | 15 | 63 | 40 |
| label 9 | 75 | 42 | 81 | 144 | 0 | 67 | 99 | 18 | 34 | 79 |


Appendix C. Omniglot




References
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. In Proceedings of the 2nd International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Rezende, D.J.; Mohamed, S.; Wierstra, D. Stochastic backpropagation and approximate inference in deep generative models. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1278–1286. [Google Scholar]
- Rezende, D.J.; Mohamed, S. Variational inference with normalizing flows. In Proceedings of the 32 International Conference on Machine Learning, Lille, France, 6–11 July 2015; p. 9. [Google Scholar]
- Burda, Y.; Grosse, R.B.; Salakhutdinov, R. Importance weighted autoencoders. In Proceedings of the 4th International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Kingma, D.P.; Salimans, T.; Jozefowicz, R.; Chen, X.; Sutskever, I.; Welling, M. Improved variational inference with inverse autoregressive flow. In Proceedings of the Advances in Neural Information Processing Systems 2016, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Chen, X.; Kingma, D.P.; Salimans, T.; Duan, Y.; Dhariwal, P.; Schulman, J.; Sutskever, I.; Abbeel, P. Variational lossy autoencoders. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017; p. 17. [Google Scholar]
- Jiang, Z.; Zheng, Y.; Tan, H.; Tang, B.; Zhou, H. Variational deep embedding: An unsupervised and generative approach to clustering. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017. [Google Scholar]
- Nalisnick, E.; Smyth, P. Stick-breaking variational autoencoders. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Zhao, S.; Song, J.; Ermon, S. InfoVAE: Information maximizing variational autoencoders. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence (AAAI) 2017, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Alemi, A.A.; Poole, B.; Fischer, I.; Dillon, J.V.; Saurous, R.A.; Murphy, K. Fixing a broken ELBO. In Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Davidson, T.R.; Falorsi, L.; De Cao, N.; Kipf, T.; Tomczak, J.M. Hyperspherical variational auto-encoders. arXiv 2018, arXiv:1804.00891. [Google Scholar]
- Dai, B.; Wipf, D. Diagnosing and enhancing VAE models. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Ramapuram, J.; Gregorova, M.; Kalousis, A. Lifelong generative modeling. arXiv 2019, arXiv:1705.09847. [Google Scholar] [CrossRef]
- Lavda, F.; Ramapuram, J.; Gregorova, M.; Kalousis, A. Continual classification learning using generative models. Continual learning workshop, Advances in Neural Information Processing Systems2018, Montreal, QC, Canada, 3–8 December 2018. arXiv 2018, arXiv:1810.10612. [Google Scholar]
- Locatello, F.; Bauer, S.; Lucic, M.; Rätsch, G.; Gelly, S.; Schölkopf, B.; Bachem, O. Challenging common assumptions in the unsupervised learning of disentangled representations. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019. [Google Scholar]
- Bowman, S.R.; Vilnis, L.; Vinyals, O.; Dai, A.; Jozefowicz, R.; Bengio, S. Generating Sentences from a Continuous Space. In Proceedings of the 20th SIGNLL Conference on Computational Natural Language Learning; Association for Computational Linguistics: Berlin, Germany, 2016; pp. 10–21. [Google Scholar] [CrossRef]
- Tomczak, J.M.; Welling, M. VAE with a VampPrior. In Proceedings of the 21st International Conference on Artificial Intelligence and Statistics (AISTATS), Playa Blanca, Lanzarote, Spain, 9–11 April 2018. [Google Scholar]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. Beta-VAE: Learning basic visual concepts with a constrained variational framework. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Hoffman, M.D.; Johnson, M.J. ELBO surgery: Yet another way to carve up the variational evidence lower bound. In Proceedings of the NIPS Symposium on Advances in Approximate Bayesian Inference, Montreal, QC, Canada, 2 December 2018; p. 4. [Google Scholar]
- Kim, H.; Mnih, A. Disentangling by factorising. arXiv 2018, arXiv:1802.05983. [Google Scholar]
- Dupont, E. Learning disentangled joint continuous and discrete representations. In Proceedings of the Advances in Neural Information Processing Systems 2018, Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Gulrajani, I.; Kumar, K.; Ahmed, F.; Taiga, A.A.; Visin, F.; Vazquez, D.; Courville, A. PixelVAE: A latent variable model for natural images. In Proceedings of the International Conference on Learning Representations (ICLR) 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Chung, J.; Kastner, K.; Dinh, L.; Goel, K.; Courville, A.C.; Bengio, Y. A recurrent latent variable model for sequential data. In Advances in Neural Information Processing Systems 28; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2015; pp. 2980–2988. [Google Scholar]
- Xu, J.; Durrett, G. Spherical latent spaces for stable variational autoencoders. In Proceedings of the Conference on Empirical Methods in Natural Language Processing 2018, Brussels, Belgium, 31 October–4 November 2018. [Google Scholar]
- Takahashi, H.; Iwata, T.; Yamanaka, Y.; Yamada, M.; Yagi, S. Variational autoencoder with implicit optimal priors. In Proceedings of the AAAI Conference on Artificial Intelligence 2019, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 5066–5073. [Google Scholar]
- Dilokthanakul, N.; Mediano, P.A.M.; Garnelo, M.; Lee, M.C.H.; Salimbeni, H.; Arulkumaran, K.; Shanahan, M. Deep unsupervised clustering with gaussian mixture variational autoencoders. arXiv 2017, arXiv:1611.02648. [Google Scholar]
- Goyal, P.; Hu, Z.; Liang, X.; Wang, C.; Xing, E. Nonparametric variational auto-encoders for hierarchical representation learning. In Proceedings of the IEEE International Conference on Computer Vision 2017, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Li, X.; Chen, Z.; Poon, L.K.M.; Zhang, N.L. Learning Latent Superstructures in Variational Autoencoders for Deep Multidimensional Clustering. In Proceedings of the International Conference on Learning Representations 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Mohamed, S.; Rosca, M.; Figurnov, M.; Mnih, A. Monte carlo gradient estimation in machine learning. arXiv 2019, arXiv:1906.10652. [Google Scholar]
- Jang, E.; Gu, S.; Poole, B. Categorical reparameterization with gumbel-softmax. In Proceedings of the International Conference on Learning Representations (ICLR) 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Makhzani, A.; Shlens, J.; Jaitly, N.; Goodfellow, I.; Frey, B. Adversarial autoencoders. arXiv 2016, arXiv:1511.05644. [Google Scholar]
- Kingma, D.P.; Mohamed, S.; Jimenez Rezende, D.; Welling, M. Semi-supervised learning with deep generative models. In Advances in Neural Information Processing Systems 27; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014; pp. 3581–3589. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Lake, B.M.; Salakhutdinov, R.; Tenenbaum, J.B. Human-level concept learning through probabilistic program induction. Science 2015, 350, 1332–1338. [Google Scholar] [CrossRef] [PubMed]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Dauphin, Y.N.; Fan, A.; Auli, M.; Grangier, D. Language modeling with gated convolutional networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Salakhutdinov, R.; Murray, I. On the quantitative analysis of deep belief networks. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 872–879. [Google Scholar]
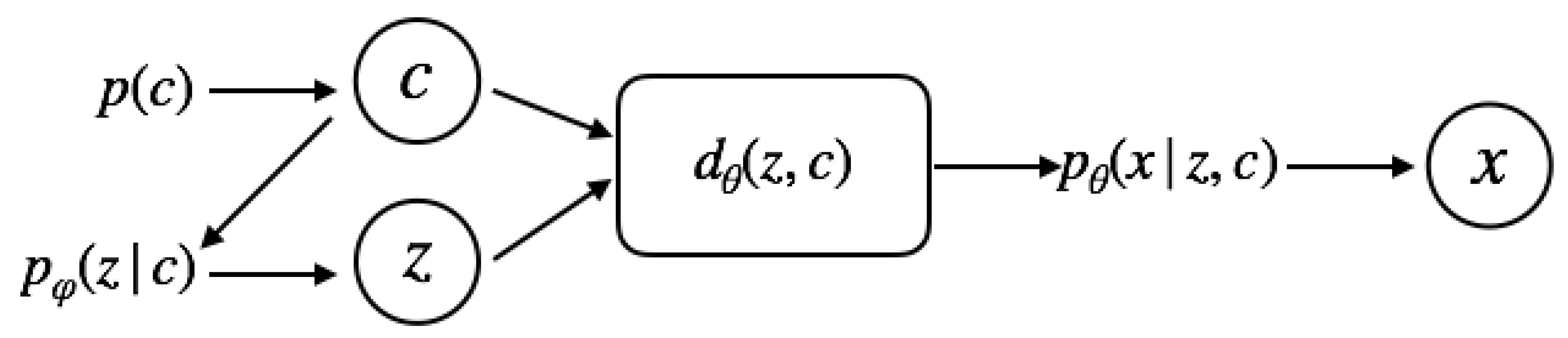



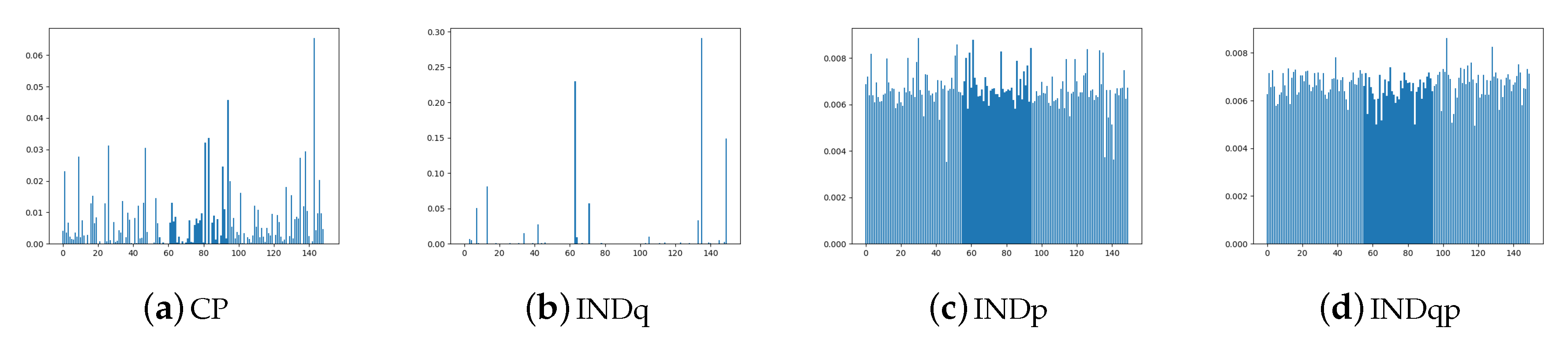




| Model | Refs. | ||||
|---|---|---|---|---|---|
| CP-VAE | |||||
| INDq | [7] | ||||
| INDp | [26,34] | ||||
| INDqp | [13,21] |
| CPVAE | INDq | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| label 0 | 9 | 80 | 127 | 24 | 62 | 135 | 133 | 149 | 42 | 64 |
| label 1 | 143 | 1 | 144 | 64 | 135 | 135 | 149 | 71 | 64 | 3 |
| label 2 | 146 | 25 | 145 | 41 | 29 | 135 | 149 | 71 | 42 | 3 |
| label 3 | 135 | 91 | 17 | 138 | 64 | 135 | 149 | 133 | 3 | 148 |
| label 4 | 83 | 138 | 109 | 37 | 147 | 135 | 71 | 149 | 42 | 114 |
| label 5 | 34 | 88 | 77 | 3 | 85 | 63 | 13 | 34 | 39 | 31 |
| label 6 | 79 | 122 | 81 | 26 | 127 | 149 | 135 | 42 | 133 | 71 |
| label 7 | 53 | 16 | 43 | 46 | 19 | 63 | 34 | 13 | 31 | 126 |
| label 8 | 47 | 95 | 137 | 97 | 63 | 7 | 63 | 105 | 123 | 145 |
| label 9 | 94 | 130 | 101 | 119 | 132 | 13 | 63 | 34 | 31 | 145 |
| MNIST | FashionMNIST | |||||||
|---|---|---|---|---|---|---|---|---|
| CP | 87.15 | 88.53 | 89.91 | 232.52 | 233.79 | 234.89 | 117.51 | 120.64 |
| INDq | 89.67 | 92.15 | 93.38 | 232.71 | 234.41 | 234.93 | 125.28 | 124.48 |
| INDp | 88.20 | 88.77 | 88.53 | 229.83 | 230.41 | 231.34 | 120.92 | 121.83 |
| INDqp | 87.93 | 88.21 | 88.98 | 228.65 | 230.98 | 231.18 | 119.99 | 120.82 |
| VAE | 88.75 | — | — | 231.49 | — | — | 115.06 | — |
| MG | 89.43 | 88.96 | 88.85 | 267.07 | 272.60 | 274.55 | 116.31 | 116.12 |
| VP | 87.94 | 86.55 | 86.07 | 230.87 | 229.82 | 270.83 | 114.01 | 113.74 |
| HVAE | 86.7 | — | — | 230.10 | — | — | 110.81 | — |
| HVP | 85.90 | 85.09 | 85.01 | 229.67 | 229.36 | 229.62 | 110.50 | 110.16 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lavda, F.; Gregorová, M.; Kalousis, A. Data-Dependent Conditional Priors for Unsupervised Learning of Multimodal Data. Entropy 2020, 22, 888. https://doi.org/10.3390/e22080888
Lavda F, Gregorová M, Kalousis A. Data-Dependent Conditional Priors for Unsupervised Learning of Multimodal Data. Entropy. 2020; 22(8):888. https://doi.org/10.3390/e22080888
Chicago/Turabian StyleLavda, Frantzeska, Magda Gregorová, and Alexandros Kalousis. 2020. "Data-Dependent Conditional Priors for Unsupervised Learning of Multimodal Data" Entropy 22, no. 8: 888. https://doi.org/10.3390/e22080888
APA StyleLavda, F., Gregorová, M., & Kalousis, A. (2020). Data-Dependent Conditional Priors for Unsupervised Learning of Multimodal Data. Entropy, 22(8), 888. https://doi.org/10.3390/e22080888




