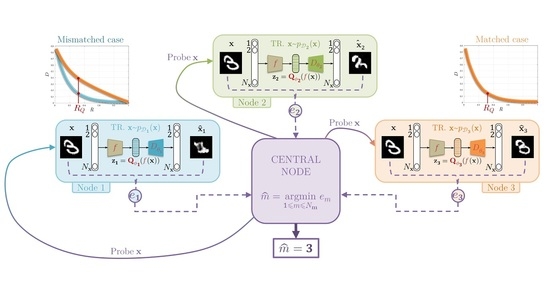
Information Bottleneck Classification in Extremely Distributed Systems
Abstract
1. Introduction
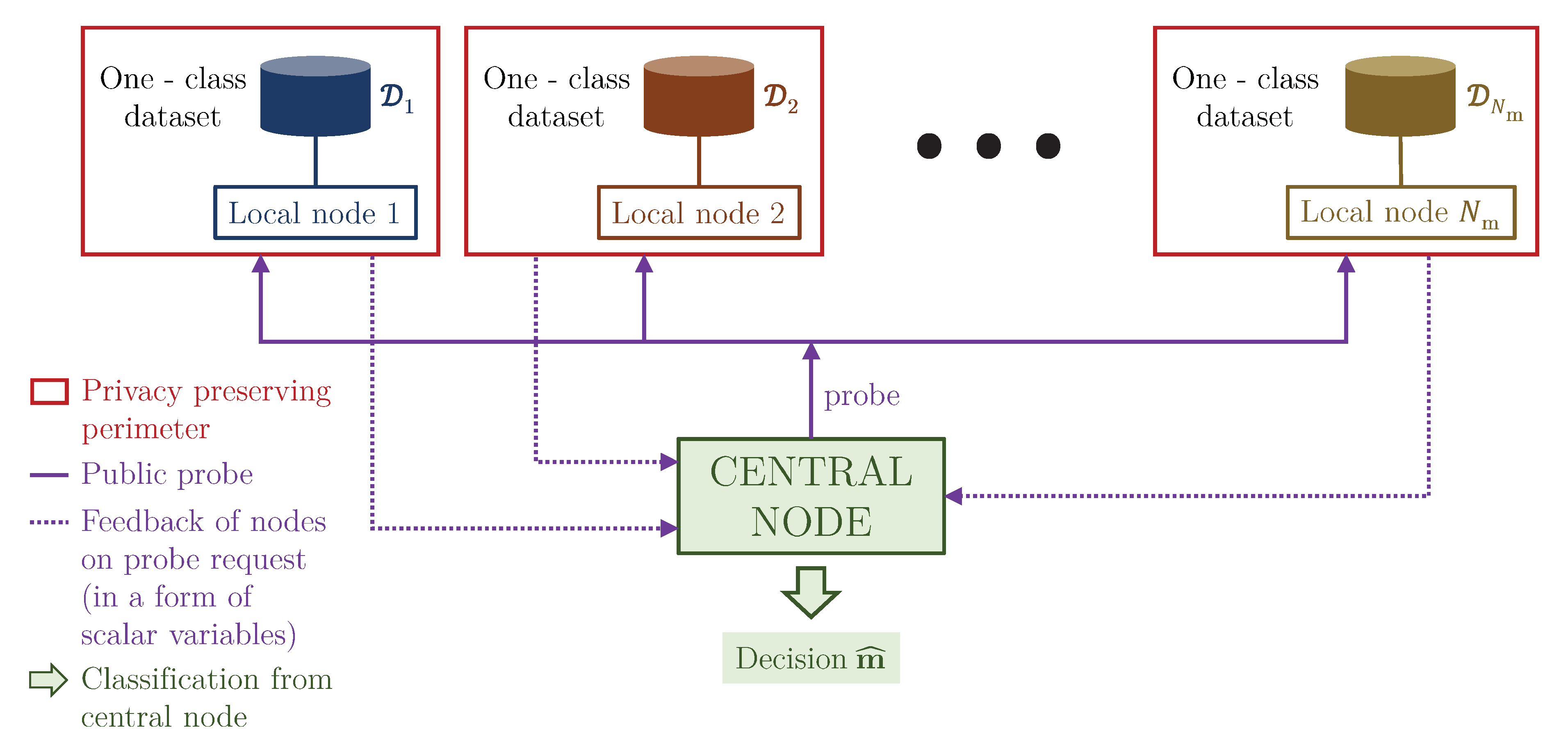
2. Problem Formulation: The One Node–One Class Setup
3. Related Work
- We propose a fully distributed learning framework without any gradient communication to the centralized node as it is done in the distributed systems based on FL. As pointed out in [11,26] this resolves many common issues of FL related to the communication burden at the training stage and the need for gradient obfuscation for privacy reasons.
- We consider a new problem formulation of decentralized learning, where each node has an access only to the samples of some class. No communication between the nodes is assumed. We call this extreme case of Non-IID Federated Learning as ON-OC setup.
- We propose a theoretical model behind the proposed decentralized system based on the information bottleneck principle and justify the role of lossy feature compression as an important part of the information bottleneck implementation for the considered ON-OC classification.
- In contrast to the centralized classification systems and distributed Federated Learning, which both mimic the learning of decision boundaries between classes based on the simultaneously available training samples from all classes, we propose a novel approach, which tries to learn the data manifolds of each individual class at the local nodes and make the decision based on the proximity of a probe to each data manifold at the centralized node.
- The manifold learning is also accomplished in a new way using a system similar to an auto-encoder architecture [27] but keeping the encoder fixed for all classes. Thus, the only learnable parts of each node are compressor and decoder. This leads to the reduced training complexity and flexibility in the design of compression strategies. Additionally, by choosing the encoder based on the geometrically invariant network a.k.a. ScatNet [28], one can hope that the amount of training data needed to cope with the geometrical variability in training data might be reduced as suggested by the authors of [28].
- Finally, the proposed approach also differs to our previous framework [29] in the following way:
- The framework in [29] was not based on the IB principle, while the current work explicitly extends the IB framework.
- The previous work [29] did not use the compression in the latent space while the current work uses an explicit compression in a form of a vector quantization. The use of quantization is an important element of the IB framework in the considered ON-OC setup. In this work that the results of classification with the properly selected compression are considerably improved with respect to the unquantized latent space case considered in our prior work [29].
- The [29] was based on the concept of Variational Auto-Encoder (VAE), which includes the training of the encoder and decoder parts. This requires sufficient amount of data to obtain the invariance of the encoder to the different types of geometrical deviations. At the same time, the current work is based on the use of geometrically invariant transform, in particular ScatNet, which is designed to be invariant to the geometrical deviations. This allows, first of all, to avoid the training of encoder and, secondly, to train the system without big amount of labeled data or necessity to observe the data from all classes.
- In the case of VAE-based system the latent space is difficult to interpret in terms of the selection of dimensions for the quantization. In the case of use of ScanNet as an encoder part the latent space is well interpretable, and its different sub-bands correspond to different frequencies. In this respect, it becomes evident which sub-bands should be preserved and which ones could be suppressed (depending on the solved problem).
- Finally, this new setup shows higher classification accuracy for the ON-OC setup.
4. Theoretical Model
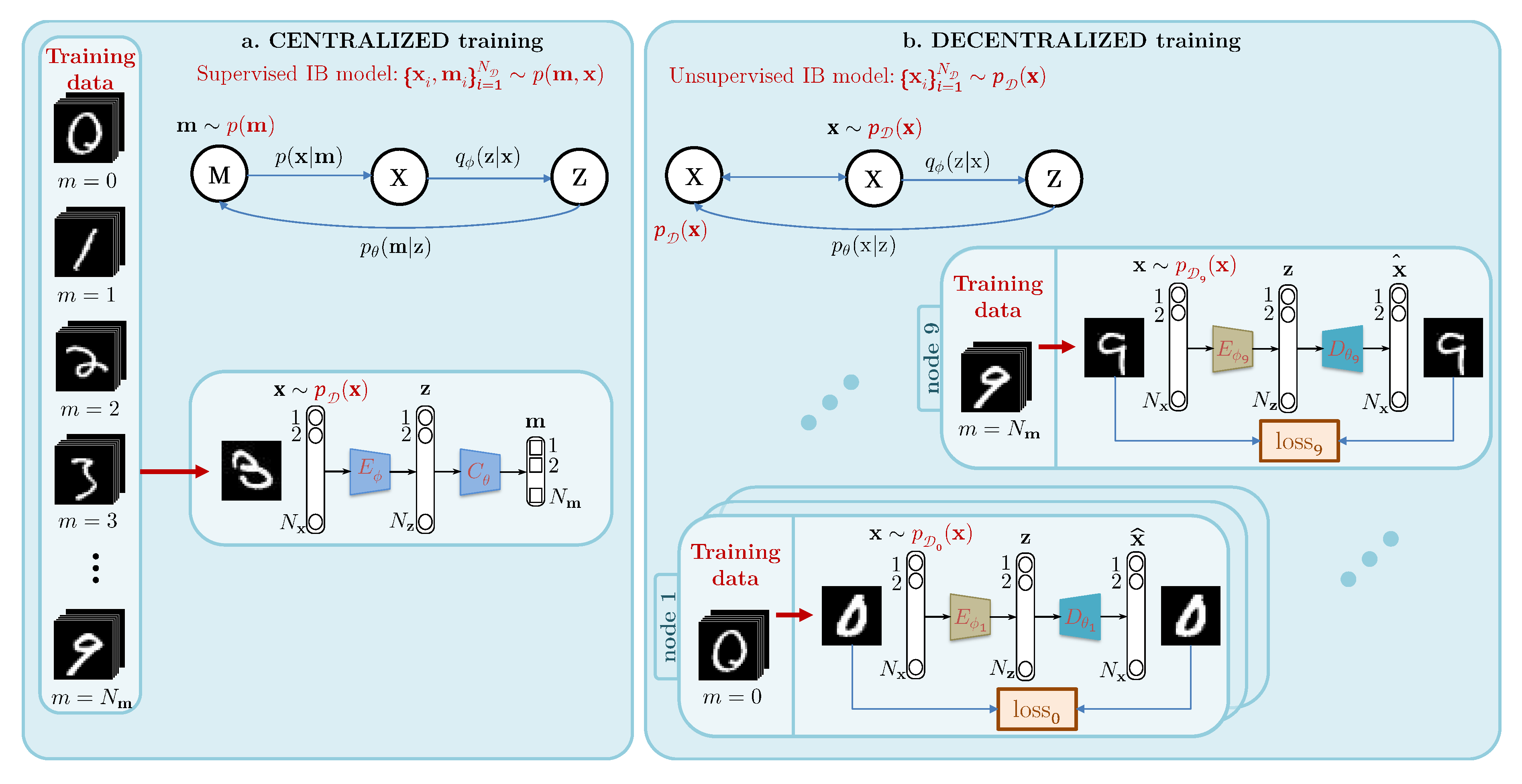
4.1. Information Bottleneck Concept of Centralized Systems
- A minimization of such that should contain as little information as possible about for compression purposes; therefore one has to compress at the encoding . In general, this compressing encoding is learned by optimizing . We simplified the learning process by using a deterministic compression map , where is a feature extractor and is a vector quantizer. Accordingly, the rate is determined by the number of centroids K in the considered vector quantizer, with equality, if and only if all centroids are equiprobable.
- A maximization of under the deterministic encoding reduces to zero and thus: in Equation (3).
- A minimization of , which represents the cross-entropy between the distribution of the true labels and the estimated ones :
4.2. Information Bottleneck Concept of Decentralized Systems
5. Implementation Details
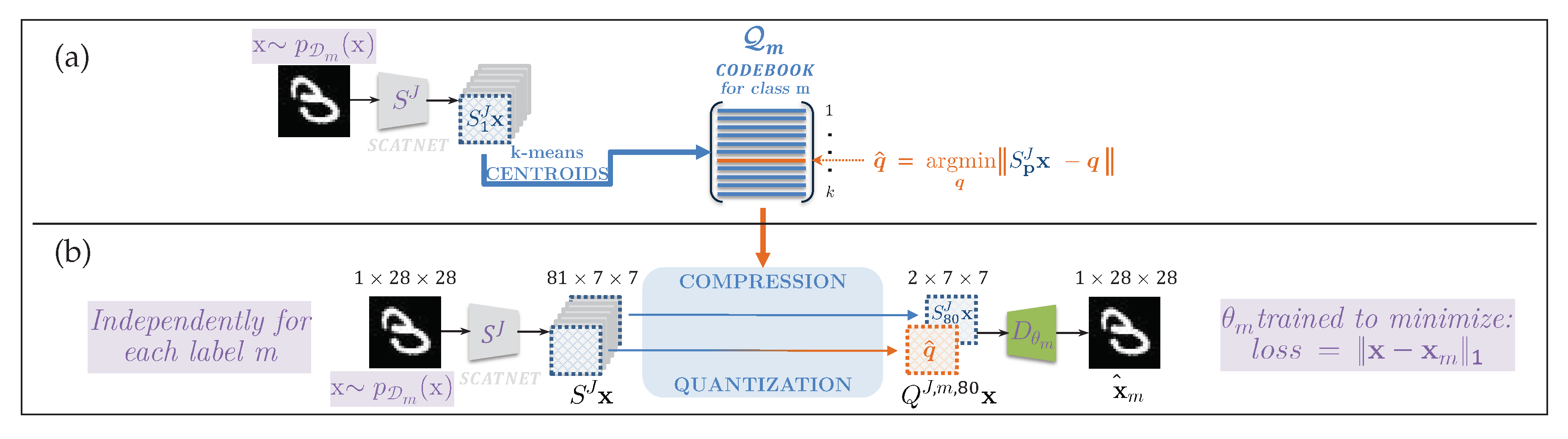
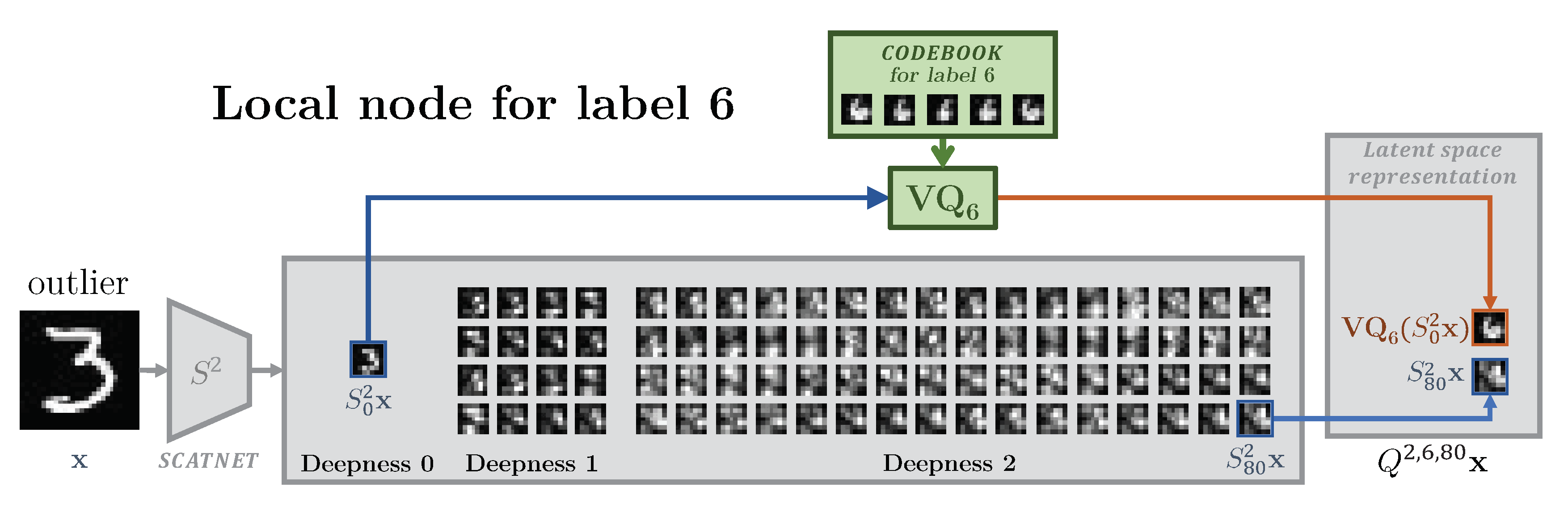
5.1. Training of Local Encoders
5.1.1. Structure of the Scattering Transform
5.1.2. Training of Local Quantizers
5.2. Training of Local Decoders
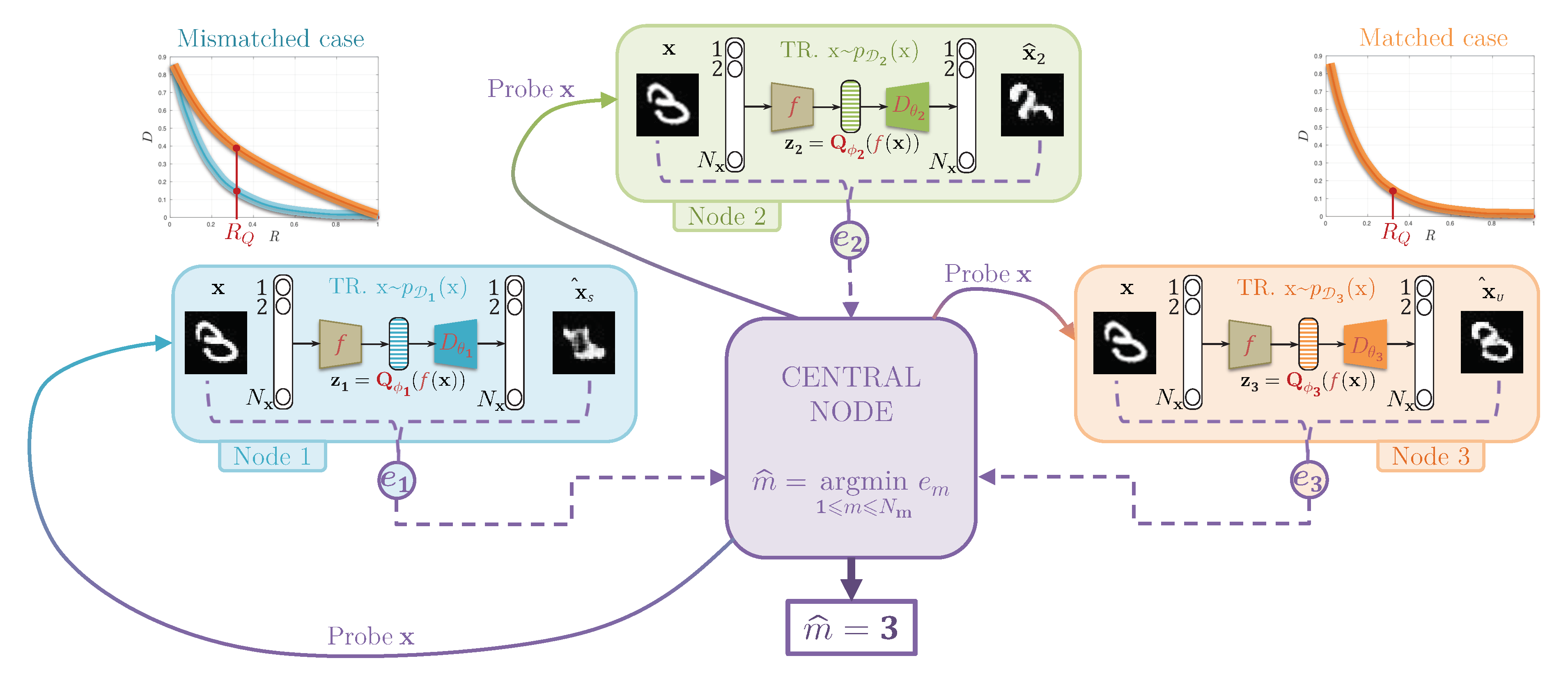
5.3. Central Classification Procedure
- the Manhattan distance ,
- the perceptual distance defined in [37],
- the pseudo-distance , which counts the number of pixels with an absolute error larger than a threshold t:
6. Experiments
6.1. Results
6.1.1. MNIST
6.1.2. FashionMNIST
7. Discussion
7.1. Investigation of the Bottleneck Role
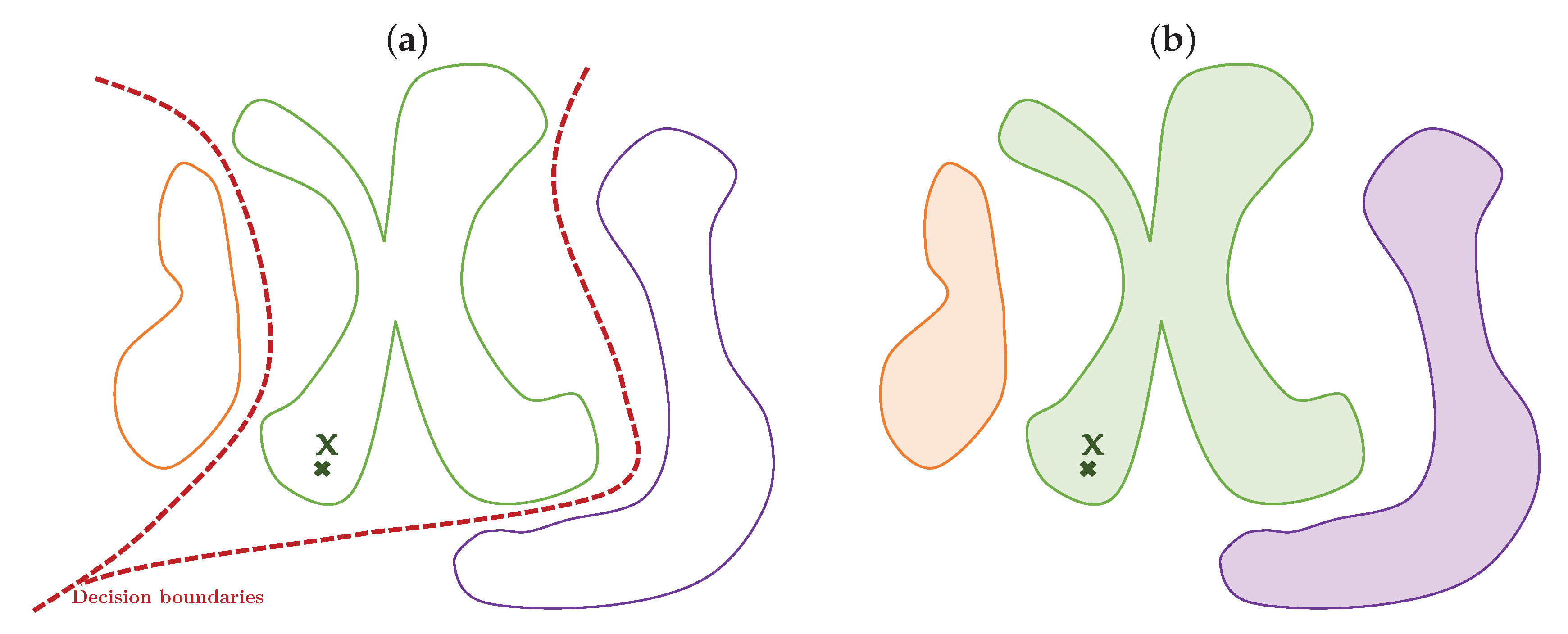
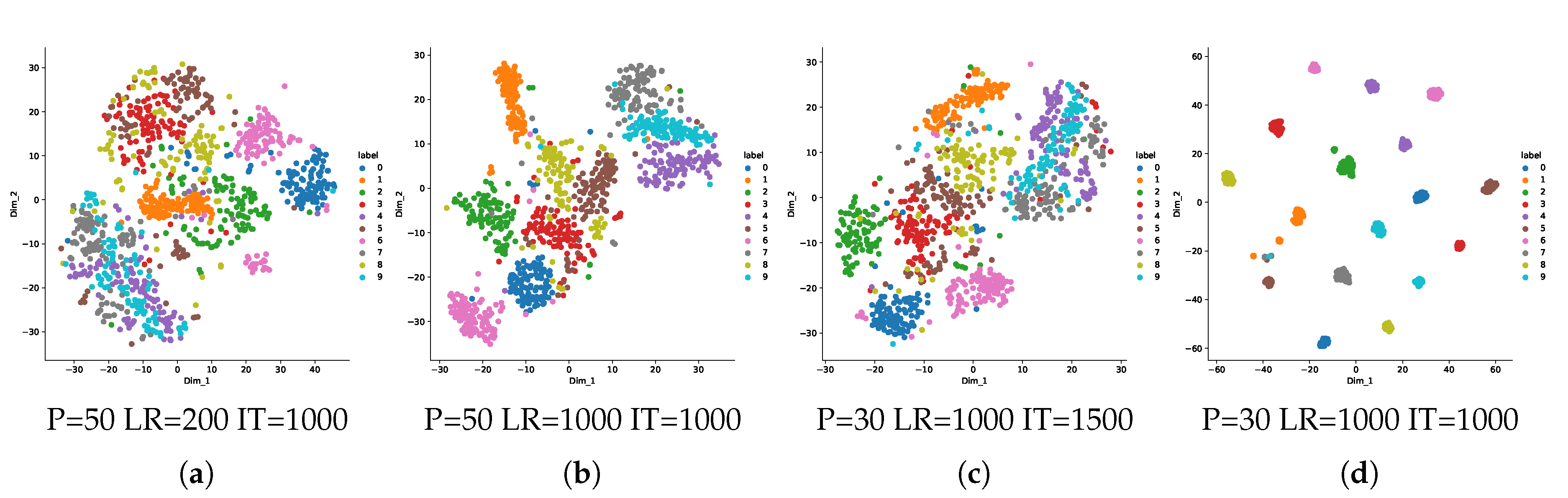
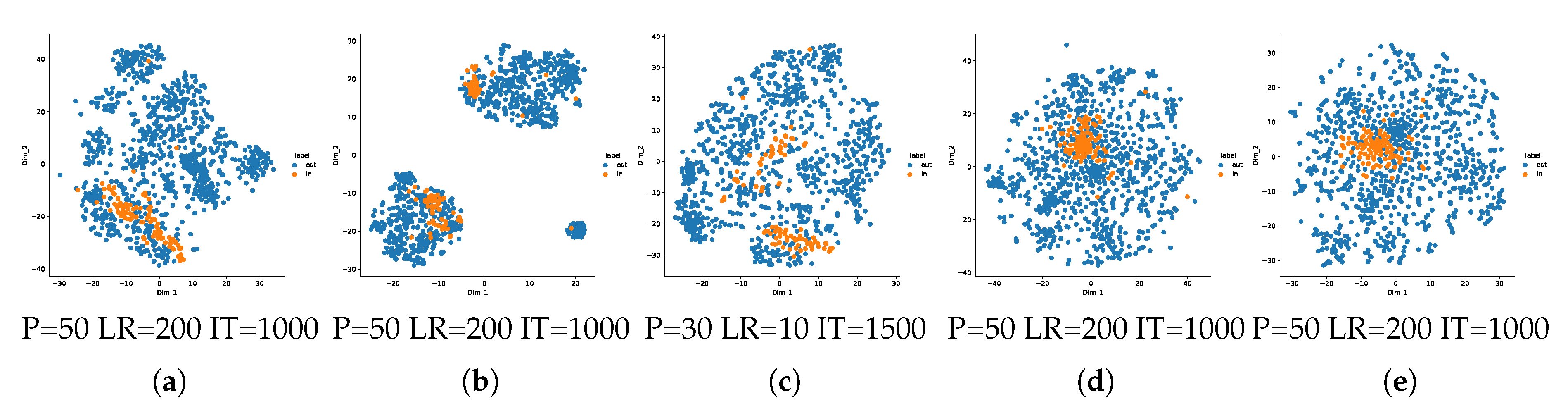
7.2. One-Class Manifold Learning for Separability
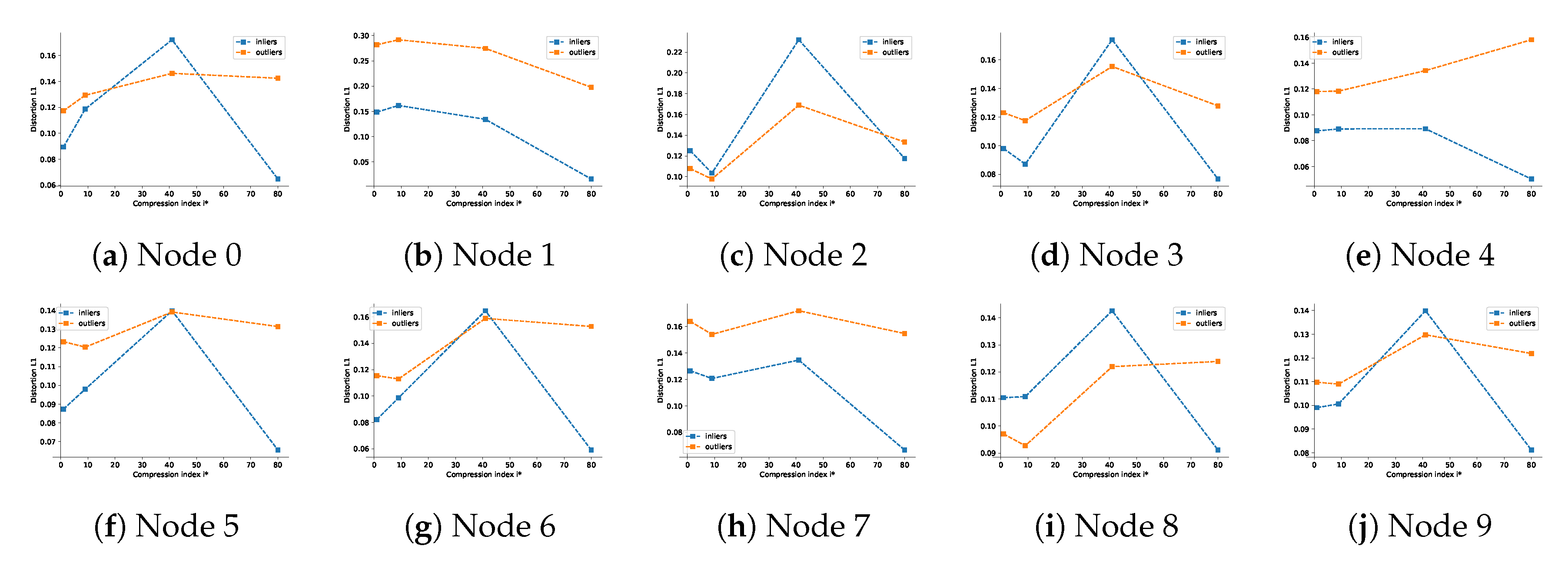
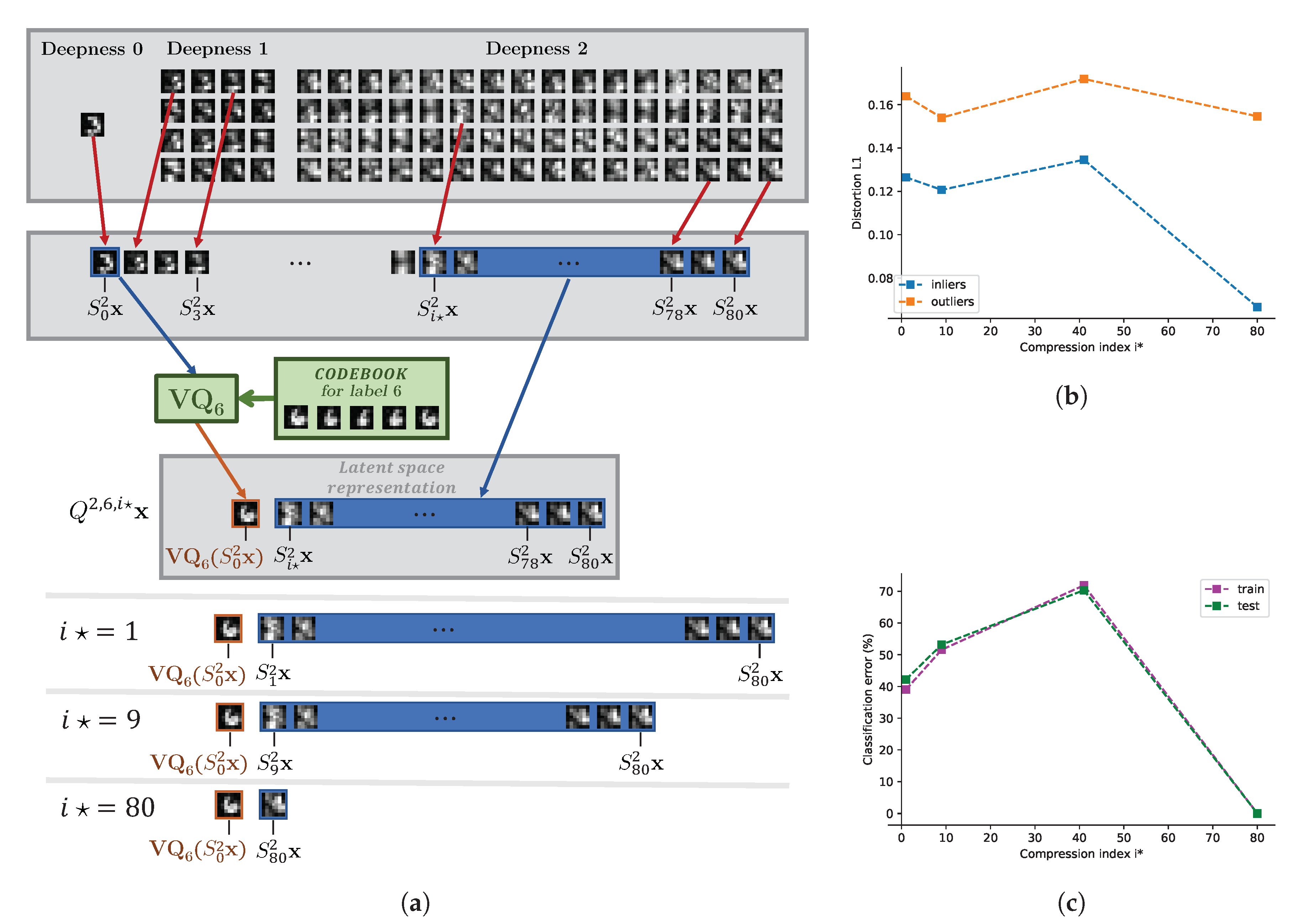
7.3. Influence of Feature Selection and Link to the Rate of Compression
7.3.1. Influence of the Parameter
7.3.2. Influence of the Parameter K
- achieves smallest classification error in the central node,
- near there is a smooth behavior and remains optimal in terms of classification.
- leads to the overfitting as the table shows a drop of performance between the train and the test datasets,
- for , the table shows a drop in performance due to non-separability of rates of distortions between nodes.
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
Appendix A. Bottleneck Interpretation


Appendix B. Nodes Analysis
Appendix B.1. One-Class Manifold Learning
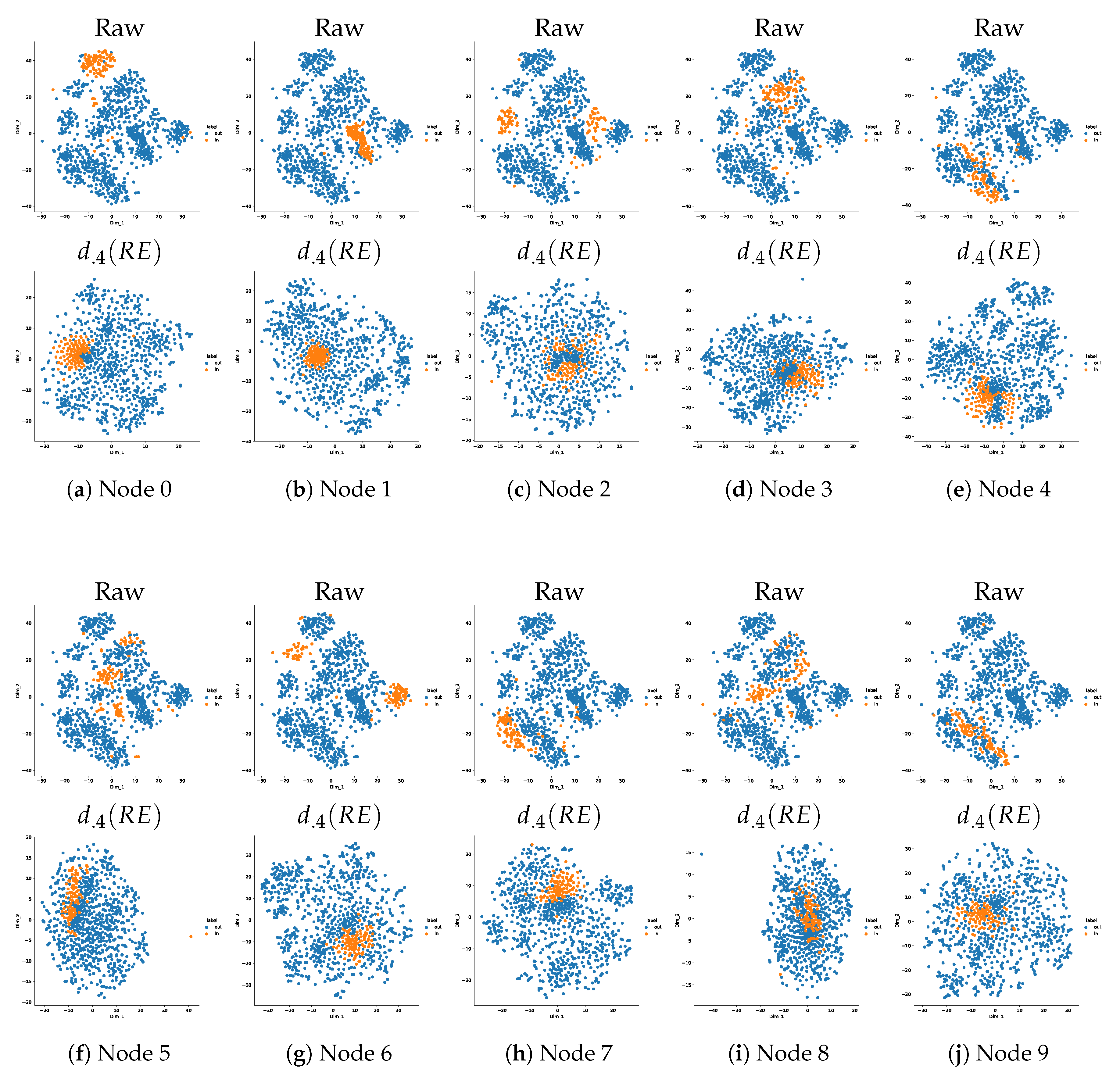

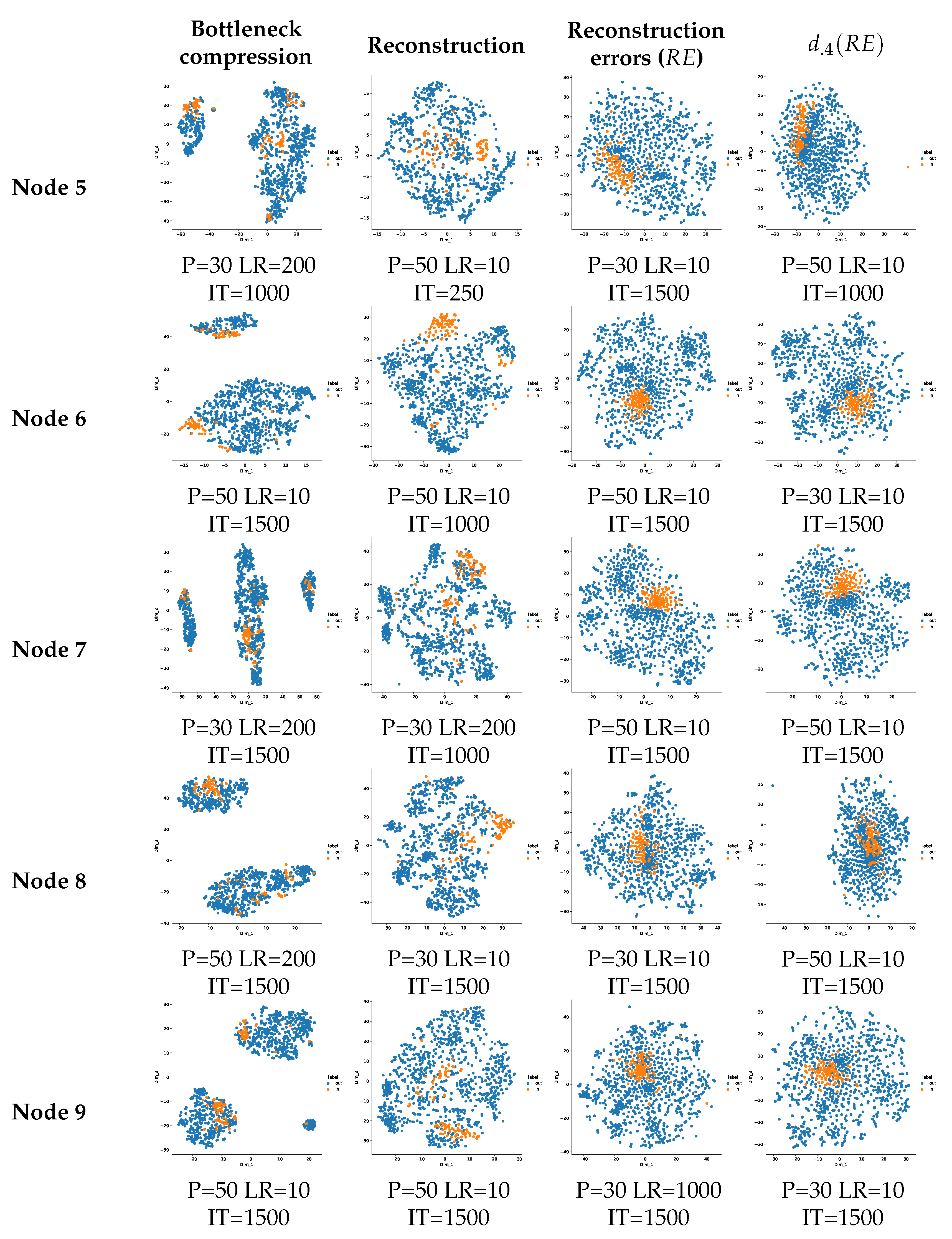
Appendix B.2. Influence of the Rate
References
- Delalleau, O.; Bengio, Y. Parallel Stochastic Gradient Descent; CIAR Summer School: Toronto, ON, Canada, 2007. [Google Scholar]
- Tian, L.; Jayaraman, B.; Gu, Q.; Evans, D. Aggregating Private Sparse Learning Models Using Multi-Party Computation. In Proceedings of the Private MultiParty Machine Learning (NIPS 2016 Workshop), Barcelona, Spain, 8 December 2016. [Google Scholar]
- McMahan, H.B.; Moore, E.; Ramage, D.; y Arcas, B.A. Federated Learning of Deep Networks using Model Averaging. arXiv 2016, arXiv:1602.05629. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, AISTATS 2017, Fort Lauderdale, FL, USA, 20–22 April 2017. [Google Scholar]
- Oyallon, E.; Belilovsky, E.; Zagoruyko, S. Scaling the Scattering Transform: Deep Hybrid Networks. arXiv 2017, arXiv:1703.08961. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep Learning and the Information Bottleneck Principle. In Proceedings of the 2015 IEEE Information Theory Workshop (ITW), Jerusalem, Israel, 26 April–1 May 2015. [Google Scholar]
- Voloshynovskiy, S.; Kondah, M.; Rezaeifar, S.; Taran, O.; Holotyak, T.; Rezende, D.J. Information bottleneck through variational glasses. In Proceedings of the Bayesian Deep Learning (NeurIPS 2019 Workshop), Vancouver, BC, Canada, 13 December 2019. [Google Scholar]
- Gibiansky, A. Bringing HPC Techniques to Deep Learning. Available online: https://andrew.gibiansky.com/blog/machine-learning/baidu-allreduce/ (accessed on 28 October 2020).
- You, S.; Xu, C.; Xu, C.; Tao, D. Learning from multiple teacher networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1285–1294. [Google Scholar]
- Lin, T.; Kong, L.; Stich, S.U.; Jaggi, M. Ensemble Distillation for Robust Model Fusion in Federated Learning. arXiv 2020, arXiv:2006.07242. [Google Scholar]
- Asad, M.; Moustafa, A.; Ito, T.; Aslam, M. Evaluating the Communication Efficiency in Federated Learning Algorithms. arXiv 2020, arXiv:2004.02738. [Google Scholar]
- Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated Learning with Non-IID Data. arXiv 2018, arXiv:1806.00582. [Google Scholar]
- Hsieh, K.; Phanishayee, A.; Mutlu, O.; Gibbons, P.B. The Non-IID Data Quagmire of Decentralized Machine Learning. arXiv 2019, arXiv:1910.00189. [Google Scholar]
- Fung, C.; Yoon, C.J.M.; Beschastnikh, I. Mitigating Sybils in Federated Learning Poisoning. arXiv 2018, arXiv:1808.04866. [Google Scholar]
- Deng, L. The MNIST Database of Handwritten Digit Images for Machine Learning Research. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- Kingma, D.P.; Rezende, D.J.; Mohamed, S.; Welling, M. Semi-Supervised Learning with Deep Generative Models. arXiv 2014, arXiv:1406.5298. [Google Scholar]
- Gordon, J.; Hernández-Lobato, J.M. Bayesian Semisupervised Learning with Deep Generative Models. arXiv 2017, arXiv:1706.09751. [Google Scholar]
- Tax, D.M.; Duin, R.P. Support vector data description. Mach. Learn. 2004, 54, 45–66. [Google Scholar] [CrossRef]
- Sabokrou, M.; Khalooei, M.; Fathy, M.; Adeli, E. Adversarially Learned One-Class Classifier for Novelty Detection. arXiv 2018, arXiv:1802.09088. [Google Scholar]
- Pidhorskyi, S.; Almohsen, R.; Adjeroh, D.A.; Doretto, G. Generative Probabilistic Novelty Detection with Adversarial Autoencoders. arXiv 2018, arXiv:1807.02588. [Google Scholar]
- Perera, P.; Nallapati, R.; Xiang, B. OCGAN: One-class Novelty Detection Using GANs with Constrained Latent Representations. arXiv 2019, arXiv:1903.08550. [Google Scholar]
- Dewdney, P.; Turner, W.; Braun, R.; Santander-Vela, J.; Waterson, M.; Tan, G.H. SKA1 System Baselinev2 Description; SKA Organisation: Macclesfield, UK, 2015. [Google Scholar]
- Alemi, A.A.; Fischer, I.; Dillon, J.V.; Murphy, K. Deep variational information bottleneck. arXiv 2016, arXiv:1612.00410. [Google Scholar]
- Estella-Aguerri, I.; Zaidi, A. Distributed variational representation learning. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 1. [Google Scholar] [CrossRef]
- Razeghi, B.; Stanko, T.; Škoric´, B.; Voloshynovskiy, S. Single-Component Privacy Guarantees in Helper Data Systems and Sparse Coding with Ambiguation. In Proceedings of the IEEE International Workshop on Information Forensics and Security (WIFS), Delft, The Netherlands, 9–12 December 2019. [Google Scholar]
- Chen, Y.; Sun, X.; Jin, Y. Communication-Efficient Federated Deep Learning with Asynchronous Model Update and Temporally Weighted Aggregation. arXiv 2019, arXiv:1903.07424. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Bruna, J.; Mallat, S. Invariant scattering convolution networks. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1872–1886. [Google Scholar] [CrossRef]
- Rezaeifar, S.; Taran, O.; Voloshynovskiy, S. Classification by Re-generation: Towards Classification Based on Variational Inference. arXiv 2018, arXiv:1809.03259. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing); Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Zhang, Y.; Ozay, M.; Sun, Z.; Okatani, T. Information Potential Auto-Encoders. arXiv 2017, arXiv:1706.04635. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Mallat, S. Group invariant scattering. Commun. Pure Appl. Math. 2012, 65, 1331–1398. [Google Scholar] [CrossRef]
- Bernstein, S.; Bouchot, J.L.; Reinhardt, M.; Heise, B. Generalized analytic signals in image processing: Comparison, theory and applications. In Quaternion and Clifford Fourier Transforms and Wavelets; Birkhäuser: Basel, Switzerland, 2013; pp. 221–246. [Google Scholar]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Is L2 a Good Loss Function for Neural Networks for Image Processing. arXiv 2015, arXiv:1511.08861. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. arXiv 2016, arXiv:1609.04802. [Google Scholar]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Byerly, A.; Kalganova, T.; Dear, I. A Branching and Merging Convolutional Network with Homogeneous Filter Capsules. arXiv 2020, arXiv:2001.09136. [Google Scholar]
- Hirata, D.; Takahashi, N. Ensemble learning in CNN augmented with fully connected subnetworks. arXiv 2020, arXiv:2003.08562. [Google Scholar]
- Kowsari, K.; Heidarysafa, M.; Brown, D.E.; Meimandi, K.J.; Barnes, L.E. RMDL: Random Multimodel Deep Learning for Classification. arXiv 2018, arXiv:1805.01890. [Google Scholar]
- Harris, E.; Marcu, A.; Painter, M.; Niranjan, M.; Prügel-Bennett, A.; Hare, J. FMix: Enhancing Mixed Sample Data Augmentation. arXiv 2020, arXiv:2002.12047. [Google Scholar]
- Bhatnagar, S.; Ghosal, D.; Kolekar, M.H. Classification of fashion article images using convolutional neural networks. In Proceedings of the 2017 Fourth International Conference on Image Information Processing (ICIIP), Shimla, India, 21–23 December 2017. [Google Scholar]
- Hao, W.; Mehta, N.; Liang, K.J.; Cheng, P.; El-Khamy, M.; Carin, L. WAFFLe: Weight Anonymized Factorization for Federated Learning. arXiv 2020, arXiv:2008.05687. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Hahnloser, R.H.R.; Sarpeshkar, R.; Mahowald, M.A.; Douglas, R.J.; Seung, H.S. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature 2000, 405, 947–951. [Google Scholar] [CrossRef] [PubMed]
- HasanPour, S.H.; Rouhani, M.; Fayyaz, M.; Sabokrou, M. Lets keep it simple, Using simple architectures to outperform deeper and more complex architectures. arXiv 2016, arXiv:1608.06037. [Google Scholar]
- Belghazi, M.I.; Baratin, A.; Rajeswar, S.; Ozair, S.; Bengio, Y.; Courville, A.; Hjelm, R.D. MINE: Mutual Information Neural Estimation. arXiv 2018, arXiv:1801.04062. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Quattoni, A.; Torralba, A. Recognizing indoor scenes. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 413–420. [Google Scholar]
- Huang, G.B.; Ramesh, M.; Berg, T.; Learned-Miller, E. Labeled Faces in the Wild: A Database for Studying Face Recognition in Unconstrained Environments Technical Report 07-49; University of Massachusetts: Amherst, MA, USA, 2007. [Google Scholar]


| Scattering Features for One Given | Number of | Tensors | ||||
|---|---|---|---|---|---|---|
| Path by Growing Deepness | Channels | Sizes | ||||
| 1 | 1 | 1 | 81 | 729 | ||
| 16 | 24 | |||||
| 64 | 192 | |||||
| 0 | 512 |
| Stage | Number of Channels | Filter Size | Stride | Size Scale | Activation |
|---|---|---|---|---|---|
| input | |||||
| Batch Normalization | |||||
| Convolution | |||||
| Deconvolution | |||||
| Batch Normalization | |||||
| Deconvolution | |||||
| Batch Normalization | |||||
| ⋮ | |||||
| Deconvolution, output: | c | 1 | |||
| Centralized Methods | FedAvg | |||||||
|---|---|---|---|---|---|---|---|---|
| Method | BMCNN + HC | EnsNet | RMDL | IID | Non-IID | |||
| Testing Data Error | ||||||||
| Proposed fully decentralized ON–OC–IBC | ||||||||
| Method | ||||||||
| Training data error | ||||||||
| Testing data error | ||||||||
| Centralized Methods | FedAvg | WAFFLe | ||||||
|---|---|---|---|---|---|---|---|---|
| Method | RN18+FMix | CNN | CNN++ | LSTM | Uni | Multi | Uni | Multi |
| Testing data error | ||||||||
| Proposed fully decentralized ON–OC–IBC | ||||||||
| Method | ||||||||
| Testing data error | 12 | |||||||
| K | 1 | 4 | 5 | 6 | 15 | 20 | 50 | 100 | ∞ |
|---|---|---|---|---|---|---|---|---|---|
| on train (%) | 0 | ||||||||
| on test (%) | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullmann, D.; Rezaeifar, S.; Taran, O.; Holotyak, T.; Panos, B.; Voloshynovskiy, S. Information Bottleneck Classification in Extremely Distributed Systems. Entropy 2020, 22, 1237. https://doi.org/10.3390/e22111237
Ullmann D, Rezaeifar S, Taran O, Holotyak T, Panos B, Voloshynovskiy S. Information Bottleneck Classification in Extremely Distributed Systems. Entropy. 2020; 22(11):1237. https://doi.org/10.3390/e22111237
Chicago/Turabian StyleUllmann, Denis, Shideh Rezaeifar, Olga Taran, Taras Holotyak, Brandon Panos, and Slava Voloshynovskiy. 2020. "Information Bottleneck Classification in Extremely Distributed Systems" Entropy 22, no. 11: 1237. https://doi.org/10.3390/e22111237
APA StyleUllmann, D., Rezaeifar, S., Taran, O., Holotyak, T., Panos, B., & Voloshynovskiy, S. (2020). Information Bottleneck Classification in Extremely Distributed Systems. Entropy, 22(11), 1237. https://doi.org/10.3390/e22111237