1. Introduction
The prediction process of stock values is always a challenging problem [
1] because of its long-term unpredictable nature. The dated market hypothesis believes that it is impossible to predict stock values and that stocks behave randomly, but recent technical analyses show that most stocks values are reflected in previous records; therefore the movement trends are vital to predict values effectively [
2]. Moreover, stock market groups and movements are affected by several economic factors such as political events, general economic conditions, commodity price index, investors’ expectations, movements of other stock markets, the psychology of investors, etc. [
3]. The value of stock groups is computed with high market capitalization. There are different technical parameters to obtain statistical data from the value of stock prices [
4]. Generally, stock indices are gained from prices of stocks with high market investment and they often give an estimation of the economic status in each country. For example, findings prove that economic growth in countries is positively impacted by the stock market capitalization [
5]. The nature of the stock values movement is ambiguous and makes investments risky for investors. In addition, it is usually difficult to detect the market status for governments. Indeed, the stock values are generally dynamic, non-parametric, and non-linear; therefore, they often cause the weak performance of the statistical models and disability to predict the accurate values and movements [
6,
7].
Popular theories suggest that stock markets are essentially a random walk, especially when it comes to the Iranian stock market, which comes with some rules of the close price of the previous day. Most conventional time series prediction methods are based on stationary trends; hence the prediction of stock prices deal with inherent difficulty. In addition, predicting stock prices is a challenging problem in itself because of the number of variables that are involved. In short term, the market behaves similar to a voting machine, but in the longer term, it acts similar to a weighing machine and hence there is scope for predicting the market movements for a longer timeframe [
8]. Machine learning (ML) is the most powerful tool which includes different algorithms to effectively develop their performance on a certain case study. It is a common belief that ML has a significant ability to identify valid information and detecting patterns from the dataset [
9]. In contrast with the traditional methods in the ML area, the ensemble models are a machine learning-based way in which some common algorithms are used to work out a particular problem, and have been confirmed to outperform each of the methods when predicting time series [
10,
11,
12]. For prediction problems in the machine learning area, boosting and bagging are effective and popular algorithms among ensemble ways. There is recent progress of tree-based models with introducing gradient boosting and XGBoost algorithms, which have been significantly employed by top data scientists in competitions. Indeed, a modern trend in ML, which is named deep learning (DL), can deem a deep nonlinear topology in its specific structure, and has an excellent ability from the financial time series to extract relevant information [
13]. Contrary to a simple artificial neural network, recurrent neural networks (RNNs) have achieved considerable success in the financial area on account of their great performance [
14,
15]. It is clear that the prediction process of the stock market is not only related to the current information, but the earlier data have a vital role, so the training will be insufficient if only the data are used at the latest time. RNN can employ the network to sustain the memory of recent events and build connections between each unit of a network, so, it is completely proper for the economic predictions [
16,
17]. Long short-term memory (LSTM) is an improved subset of the RNN method that used in the deep learning area. LSTM has three different gates to remove the problems in RNN cells and can also process single data points or whole sequences of data.
In academic fields, many studies have been conducted on market prediction ways. Long et al. [
18] examined a deep neural network model with public market data and the transaction records to evaluate stock price movement. The experimental results showed that bidirectional LSTM could predict the stock price for financial decisions, and the method acquired the best performance compared to other prediction models. Pang et al. [
19] tried to improve an innovative neural network method to get better stock market predictions. They proposed LSTM with an embedded layer and LSTM with an automatic encoder to evaluate the stock market movement. The results showed that the deep LSTM with embedded layer outperformed and the model’s accuracies for the Shanghai composite index are 57.2% and 56.9%, respectively. Kelotra and Pandey [
20] used the deep convolutional LSTM model as a predictor to effectively examine stock market movements. The model was trained with a Rider-based monarch butterfly optimization algorithm and they achieved a minimal MSE and RMSE of 7.2487 and 2.6923. Bouktif et al. [
21] investigated the predictability of the stock market trend direction with an improved way of sentiments analysis. As the final result, the proposed method outperformed adequately and predicted stock trends with higher accuracy of 60% in comparison with other sentiment-based stock market prediction methods involving deep learning. Zhong and Enke [
22] proposed a big comprehensive data of the SPDR S&P 500 ETF to evaluate return direction with 60 economic and financial features. Deep neural networks and artificial neural networks (ANN) were employed via principal component analysis (PCA) to predict the daily future of stock market index returns. The results showed that deep neural networks were superior as classifiers based on PCA-represented data compared to others. Das et al. [
23] implemented the feature optimization through considering the social and biochemical aspects of the firefly method. In their approach, they involved the objective value selection in the evolutionary context. The results indicated that firefly, with an evolutionary framework applied to the Online Sequential Extreme Learning Machine (OSELM) prediction method, was the best model among other experimented ones. Hoseinzade and Haratizadeh [
24] proposed a Convolutional Neural Networks (CNNs) framework, which can be applied to various data collections (involving different markets) to explore features for predicting the future movement of the markets. From the results, remarkable improvement in prediction’s performance in comparison with other recent baseline methods was achieved. Krishna Kumar and Haider [
25] compared the performance of single classifiers with a multi-level classifier, which was a hybrid of machine learning techniques (such as decision tree, support vector machine, and logistic regression classifier). The experimental results revealed that the multi-level classifiers outperformed the other works and led to a more accurate model with the best predictive ability, roughly 10 to 12% growth inaccuracy. Chung and Shin [
26] applied one of the deep learning methods (CNNs) for predicting the stock market movement. In addition, the Genetic algorithm (GA) was employed to optimize the parameters of the CNN method systematically, and results showed that the GA-CNN outperformed the comparative models as the hybrid method of GA and CNN. Sim et al. [
27] proposed CNN to predict stock prices as a new learning method. The study aimed to solve two problems, using CNNs and optimizing them for stock market data. Wen et al. [
28] applied the CNN algorithm on noisy temporal series by frequent patterns as a new method. The results proved that the method was adequately effective and outperformed traditional signal process methods with a 4 to 7% accuracy improvement.
Rekha et al. [
29] employed CNN and RNN to make a comparison between two algorithms’ results and actual results via stock market data. Lee et al. [
30] used CNNs to predict the global stock market and then trained and tested their model with data from other countries. The results demonstrated that the model could be trained on the relatively large data and tested on the small markets where there was not enough amount of data. Liu et al. [
31] investigated a numerical-based attention method with dual sources stock market data to find the complementarity between numerical data and news in the prediction of stock prices. As a result, the method filtered noises effectively and outperformed prior models in dual sources stock prediction. Baek and Kim [
32] proposed an approach for stock market index forecasting, which included a prediction LSTM module and an overfitting prevention LSTM module. The results confirmed that the proposed model had an excellent forecasting accuracy compared to a model without an overfitting prevention LSTM module. Chung and Shin [
33] employed a hybrid approach of LSTM and GA to improve a novel stock market prediction model. The final results showed that the hybrid model of the LSTM network and GA was superior in comparison with the benchmark model. Chen et al. [
34] used three neural networks, the radial basis function neural network, the extreme learning machine, and three traditional artificial neural networks, to evaluate their performance on high-frequency data of the stock market. Their results indicated that deep learning methods got transaction data from the nonlinear features and could predict the future of the market powerfully. Zhou et al. [
35] applied LSTM and CNN on high-frequency data from the stock market with the approach of rolling partition training and testing set to evaluate the update cycle effect on the performance of models. Based on extensive experimental results, Models could effectively reduce errors and increase prediction accuracy. Chong et al. [
36] tried to examine the performance of deep learning algorithms for stock market prediction with three unsupervised feature extraction ways, PCA, restricted Boltzmann machine and auto encoder. Final results with significant improvement suggested that additional information could be extracted by deep neural networks from the autoregressive model.
Long et al. [
37] suggested an innovative end-to-end model named multi-filters neural network (MFNN) specifically for price prediction task and feature extraction on financial time series data. Their results indicated that the network outperformed common machine learning methods, statistical models, and convolutional, recurrent, and LSTM networks in terms of accuracy, stability and profitability. Moews et al. [
38] proposed employing deep neural networks that use step-wise linear regressions in the preparatory feature engineering with exponential smoothing for this task, with regression slopes as movement strength indicators for a specified time interval. The final results showed the feasibility of the suggested method, with advanced accuracies and accounting for the statistical importance of the results for additional validation, as well as prominent implications for modern economics. Garcia et al. [
39] examined the effect of financial indicators on the German DAX-30 stock index by employing a hybrid fuzzy neural network to forecast the one-day ahead direction of the index with various methods. Their experimental works demonstrated that the fall in the dimension through the factorial analysis produces less risky and profitable strategies. Cervelló-Royo and Guijarro [
40] compared the performance of four machine learning models to validate the predicting capability of technical indicators in the technological NASDAQ index. The results showed that the random forest outperformed the other models deemed in their study, being able to predict the 10-days ahead market movement, with a normal accuracy of 80%. Konstantinos et al. [
41] suggested an ensemble prediction combination method as an alternative approach to forecast time series. The ensemble learning technique combined various learning models. Their results indicated the effectiveness proposed ensemble learning way, and the comparative analysis showed adequate evidence that the method could be used successfully to conduct prediction based on multivariate time series problems.
Overall, all researchers believe that stock price prediction and modeling have been challenging problems for study and speculators due to noisy and non-stationary characteristics of data. There is a minor difference between papers for choosing the most effective indicators for modeling and predicting the future of stock markets. Feature selection can be an important part of studies to achieve better accuracy; however, all studies indicate that uncertainty is an inherent part of these forecasting tasks because of fundamental variables. Employing new machine learning and deep learning methods such as recent ensemble learning models, CNNs and RNNs with high prediction ability is a significant advantage of recent studies that show the forecasting potential of these methods in comparison with traditional and common approaches such as statistical analyses.
Iran’s stock market has been highly popular recently because of the arising growth of Tehran Stock Exchange Dividend and Price Index-TEDPIX in the last decades, and one of the reasons is that most of the state-owned firms are being privatized under the general policies of article 44 in the Iranian constitution, and people are allowed to buy the shares of newly privatized firms under the specific circumstances. This market has some specific attributes in comparison with other country’s stock markets, one of them being dealing a price limitation of ±5% of the opening price of the day for every index. This issue hinders the abnormal market fluctuation and scatters market shocks, political issues, etc. over a specific time and could make the market smoother and more predictable. Trading takes place through licensed registered private brokers of exchange organization and the opening price of the next day is through the defined base-volume of the companies and transaction volume as well. However, the deficiency of valuable papers on this market to predict future values with machine learning models is clear.
This study concentrates on the process of future value prediction for stock market groups, which are crucial for investors. Despite significant development in Iran’s stock market in recent years, there has been not enough research on the stock price predictions and movements using novel machine learning methods. This paper aims to compare the performance of some regressors which applied on fluctuating data to evaluate predictor models, and the predictions are evaluated for 1, 2, 5, 10, 15, 20, and 30 days in advance. In addition, with tuning parameters, we try to reduce errors and increase the accuracy of models.
Ensemble learning models are broadly employed nowadays for its predictive performance progress. These methods combine multiple forecasts from one or multiple methods to improve the accuracy of simple prediction and to prevent possible overfitting problems. In addition, ANNs are universal approximators and flexible computing frameworks which can be used to an extensive range of time series predicting problems with a great degree of accuracy. Therefore, by considering the literature review, this research work examines the predictability of a set of cutting-edge machine learning methods, which involves tree-based models and deep learning methods. Employing the whole of tree-based methods, RNN, and LSTM techniques for regression problems and comparing their performance in Tehran stock exchange is a recent research activity presented in this study. This paper includes three different sections. At first, through the methodology section, the evolution of tree-based models with the introduction of each one is presented. Besides, the basic structure of neural networks and recurrent ones are described briefly. In the research data section, 10 technical indicators are shown in detail with selected methods parameters. At the final step, after introducing three regression metrics, machine learning results are reported for each group, and the model’s behavior is compared.
3. Research Data
This study aims to make a short run prediction for the emerging Iranian stock market and employ data from November 2009 to November 2019 (10 years) of four stock market groups, Diversified Financials, Petroleum, Non-metallic minerals, and Basic metals, which are completely generous. From the opening, close, low high, and prices of the groups, 10 technical indicators are calculated. The data for this study is supplied from the online repository of the Tehran Securities Exchange Technology Management Co (TSETMC) [
46]. Before using information for the training process, it is vital to take a preprocessing step. We employ data cleaning, which is the process of detecting and correcting inaccurate records from a dataset and refers to identifying inaccurate or irrelevant parts of the data and then replacing, modifying, or deleting the dirty data. The interquartile range (IQR score) is a measure of statistical dispersion and is robust against outliers, and this method is used to detect outliers and modify the dataset. Indeed, as an important point, to prevent the effect of the larger value of an indicator on the smaller ones, the values of 10 technical indicators for all groups are normalized independently. Data normalization refers to rescaling actual numeric features into a 0 to 1 range and is employed in machine learning to create a training model less sensitive to the scale of variables.
Table 1 indicates all the technical indicators, which are employed as input values based on domain experts and previous studies [
47,
48,
49]; the input values for calculating indicators in the table are opening, high, low and closing prices in each trading day; “t” means current time, and “t + 1” and “t − 1” mean one day ahead and one day before, respectively.
Table 2 shows the summary statistics of indicators for the groups.
SMA is calculated by the average of prices in a selected range, and this indicator can help to determine if a price will continue its trend. WMA gives us a weighted average of the last n values, where the weighting falls with each prior price. MOM calculates the speed of the rise or falls in stock prices and it is a very useful indicator of weakness or strength in evaluating prices. STCK is a momentum indicator over a particular period of time to compare a certain closing price of a stock to its price range. The oscillator sensitivity to market trends can be reduced by modifying that time period or by a moving average of results. STCD measures the relative position of the closing prices in comparison with the amplitude of price oscillations in a certain period. This indicator is based on the assumption that as prices increase, the closing price tends towards the values which belong to the upper part of the area of price movements in the preceding period and when prices decrease, the opposite is correct. LWR is a type of momentum indicator which evaluates oversold and overbought levels. Sometimes LWR is used to find exit and entry times in the stock market. MACD is another type of momentum indicator which indicates the relationship between two moving averages of a share’s price. Traders can usually use it to buy the stock when the MACD crosses above its signal line and sell the shares when the MACD crosses below the signal line. ADO is usually used to find out the flow of money into or out of stock. ADO line is normally employed by traders seeking to determine buying or selling time of stock or verify the strength of a trend. RSI is a momentum indicator that evaluates the magnitude of recent value changes to assess oversold or overbought conditions for stock prices. RSI is showed as an oscillator (a line graph which moves between two extremes) and moves between 0 to 100. CCI is employed as a momentum-based oscillator to determine when a stock price is reaching a condition of being oversold or overbought. CCI also measures the difference between the historical average price and the current price. The indicator determines the time of entry or exit for traders by providing trade signals.
Dataset used for all models—except RNN and LSTM models—are identical. There are 10 features (10 technical indicators) and one target (stock index of the group) for each sample of the dataset. As mentioned, all 10 features are normalized independently before being used to fit models and improve the performance of algorithms. Since the goal is developing models to predict stock group values, datasets are rearranged to incorporate the 10 features of each day to the target value of n-days ahead. In this study, models are evaluated by training them to predict the target value for 1, 2, 5, 10, 15, 20, and 30 days ahead. There are several parameters related to each model, but we tried to choose the most effective ones concerning our experimental works and prior studies. For tree-based models, several trees (ntrees) were the design parameter while other common parameters are set identical between all models. Parameters and their values for each model are listed in
Table 3.
The number of trees to perform tree-based models is fairly robust to over-fitting, so a large number typically results in better prediction. The maximum depth of the individual regression estimators limits the number of nodes in the tree. The best value depends on the interaction of the input variables. In machine learning, the learning rate is an important parameter in an optimization method that finds out the step size at each iteration while moving toward a minimum of a loss function. For RNN and LSTM networks, because of their time-series behavior, datasets are arranged to include the features of more than just one day. While for the ANN model, all parameters but epochs are constant; for RNN and LSTM models, the variable parameters are several days included in the training dataset and respective epochs. By increasing the number of days in the training set, the number of epochs is increased to train the models with an adequate number of epochs.
Table 4 presents all valid values for the parameters of each model. For example, if five days are included in the training set for ANN, RNN, or LSTM models, the number of epochs is set to 300 to thoroughly train the models.
The activation function of a node in ANNs describes the output of that node given an input or set of inputs. Optimizers are methods employed to change the attributes of ANNs, such as learning rate and weights to reduce the losses. An epoch is a term used in ANNs and shows the number of passes of the entire training dataset the ANN model has completed.
5. Results
Six tree-based models namely Decision Tree, Bagging, Random Forest, Adaboost, Gradient Boosting, and XGBoost, and also three neural networks-based algorithms (ANN, RNN, and LSTM) are employed in the prediction of the four stock market groups. For the purpose, prediction experiments for 1, 2, 5, 10, 15, 20, and 30 days in advance of time are conducted. Results for Diversified Financials are depicted in
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10 and
Table 11 for instance. For better understanding and reduction of the number of result tables, the average performance of algorithms for each group is demonstrated in
Table 12,
Table 13,
Table 14 and
Table 15, and also
Table 16 shows the average runtime per sample for all models. It is prominent to note that a comprehensive number of experiments are performed for each of the groups and prediction models with various model parameters. The following tables show the best parameters where a minimum prediction error is obtained. Indeed, it is clear from the results that error values generally rise when prediction models are created for a greater number of days ahead. For example, MAPE values of XGBoost are 0.88, 1.14, 1.45, 1.77, 2.03, 2.30, and 2.48 respectively. However, it is possible to observe a less strict ascending trend in some cases (which was seen in previous studies similarly) due to deficiency in the prediction ability of some models in some special cases based on the main dataset.
In this work, we use all of 10 technical indicators as 10 input features and the number of data is 2600. To prevent overfitting, we randomly split our main dataset into two parts, train data and test data, at the first step and then fit our models on the train data. Seventy percent of the main dataset (1820 data) is assigned to train data. Next, the models are used to predict future values and calculate metrics with test data (780 data). In addition, we employ regularization and validation data (20% of train data) to increase our accuracy and tune our hyperparameters during training (the training process for tree-based models and ANNs is different here).
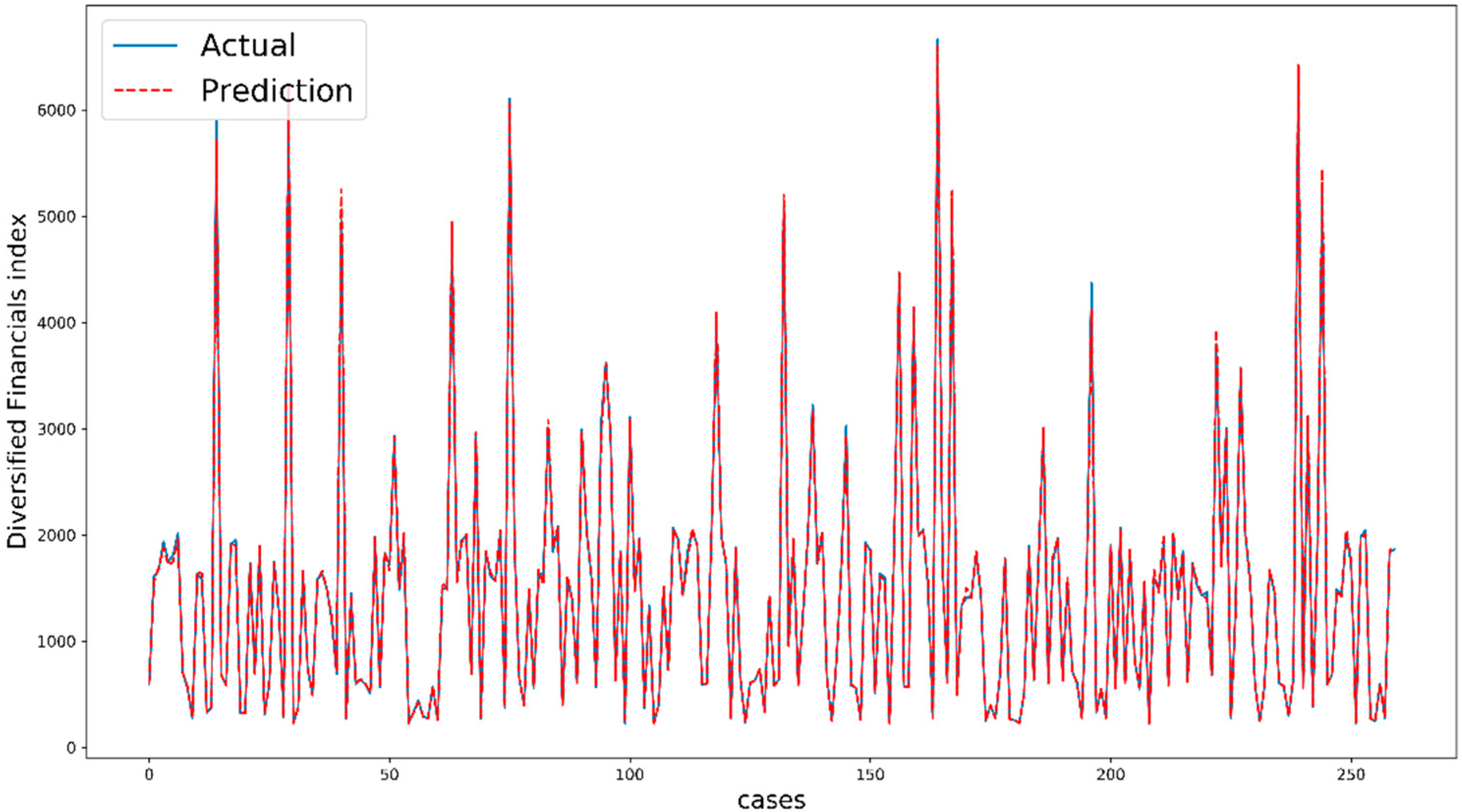
Figure 7 shows the performance of XGBoost for five days ahead of Diversified Financials as an example. The comparison between actual values and predicted values indicate the quality of modeling and the prediction task. It is important to note that the cases are not exactly consecutive trading days because we split our dataset randomly by shuffling.
By deeming the literature, our result in this study is one of the most accurate predictions and it can be interpreted by the dataset and the performance of models. It is true that the process of training is totally important, but we believe that the role of the dataset is greater here. The dataset is relatively specific because of some rules in Tehran stock exchange. For example, the value change of each stock is limited to +5% and −5%, or the closing price of a stock is close to the opening price on the next trading day. These rules are learned by machine learning algorithms and then the models are able to significantly predict our dataset from Tehran stock exchange.
Regarding the results of Diversified Financials as an example, Adaboost regressor and LSTM can predict the future prices well with normally 1.59% and 0.60% error; these values become more important when we know that the maximum range of changes is 10% (from −5% to +5%). So, with the specific dataset and powerful models, we still have noticeable errors, which indicate the effect of fundamental parameters. Fundamental analysis is a method of measuring a security’s intrinsic value by examining related economic and financial factors. This method of stock analysis is considered to be in contrast to technical analysis, which forecasts the direction of prices. Noticeably, most non-scientific factors such as policies, increase in tax etc. affect the groups in stock markets; for example, the pharmaceutical industries experience growth with Covid-19 at the present time.
Based on extensive experimental works and reported values the following results are obtained:
Among tree-based models
Decision Tree always has the lowest rank for predictions because it is not an ensemble method (average of MAPE: 2.07, 2.70, 2.18, 1.41)
For Diversified Financials and Petroleum, the best average performance belongs to Adaboost regressor (average of MAPE: 1.59 and 2.22)
For Non-metallic minerals and Basic metals, there is a stiff competition between Adaboost regressor, Gradient Boosting regressor and XGBoost regressor
Decision Tree has the lowest runtime and then Adaboost regressor is the fastest predictor (0.009 ms and 1.308 ms)
The runtime of XGBoost is considerably more than other performers (up to 65%)
Adaboost regressor is the best by considering accuracy, the strength of fitting and runtime all together
Through neural networks
ANN generally occupies the bottom for forecasting (average of MAPE: 3.86, 5.52, 4.67, 3.17)
LSTM model outperforms RNN significantly with lower error values (for example in Diversified Financials, MAPE: 0.60 versus 1.85)
The average runtime of LSTM is noticeably larger than RNN (802.902 ms versus 20.630 ms, roughly four times more)
On the whole
According to MAPE and RRMSE, the models are able to predict future values for Metals and Diversified Financials better than two other groups
Deep learning methods (RNN and LSTM) indicate a powerful ability to predict stock market prices because of using a large number of epochs and values related to some days before.
Based on RRMSE and MSE, the deep learning methods have a high ability to make the best fitting curve with the minimum distribution of residuals around it.
The average runtime of deep learning models is high compared to others
LSTM is powerfully the best model for prediction all stock market groups with the lowest error and the best ability to fit, but the problem is the great runtime
In spite of noticeable efforts to find valuable studies on the same stock market, there is not any important paper to report, and this deficiency is one of the novelties of this research. We believe that this paper can be a baseline to compare for future studies.