An Efficient Method Based on Framelets for Solving Fractional Volterra Integral Equations
Abstract
1. Introduction
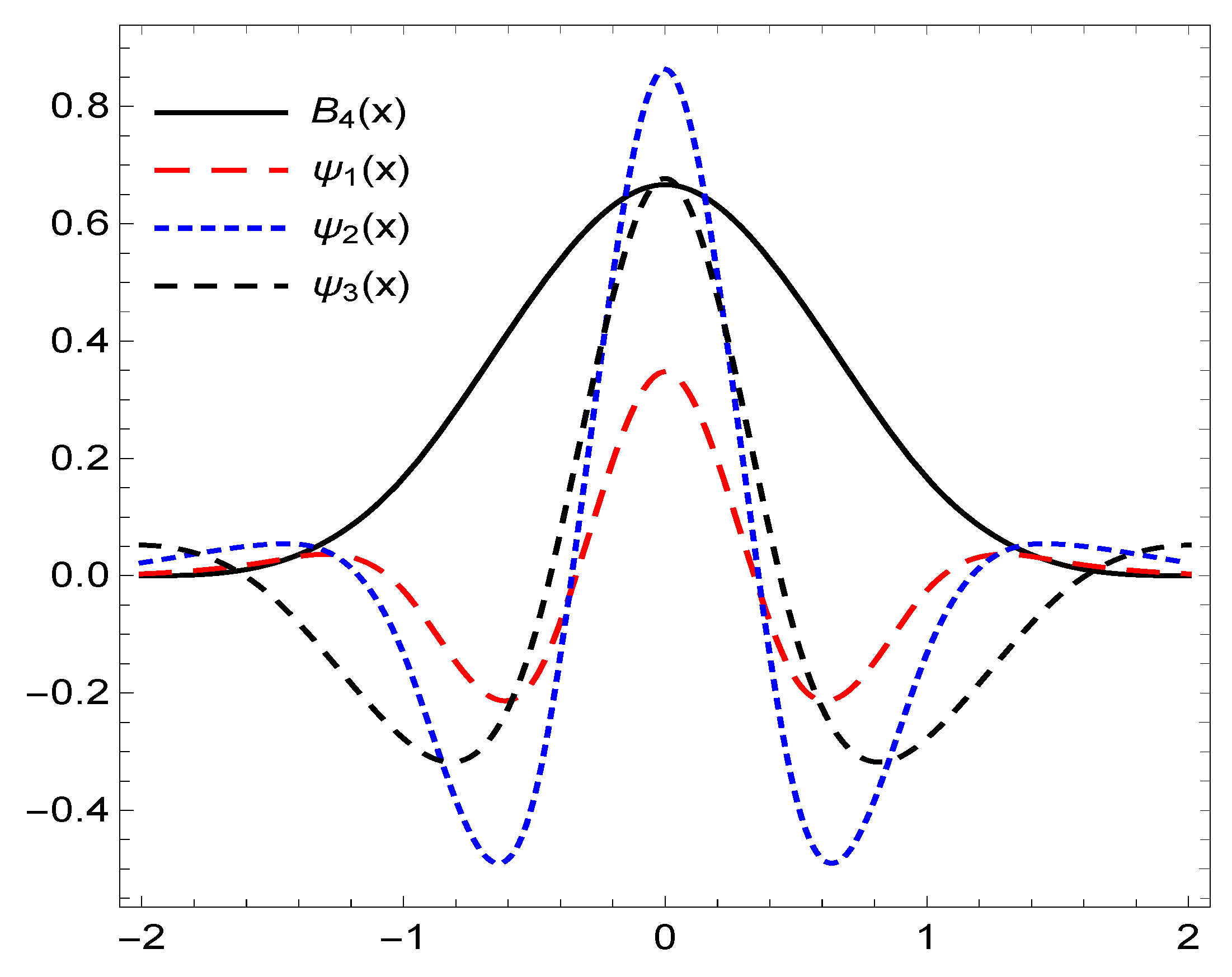
2. Matrix Formulation Using Framelets
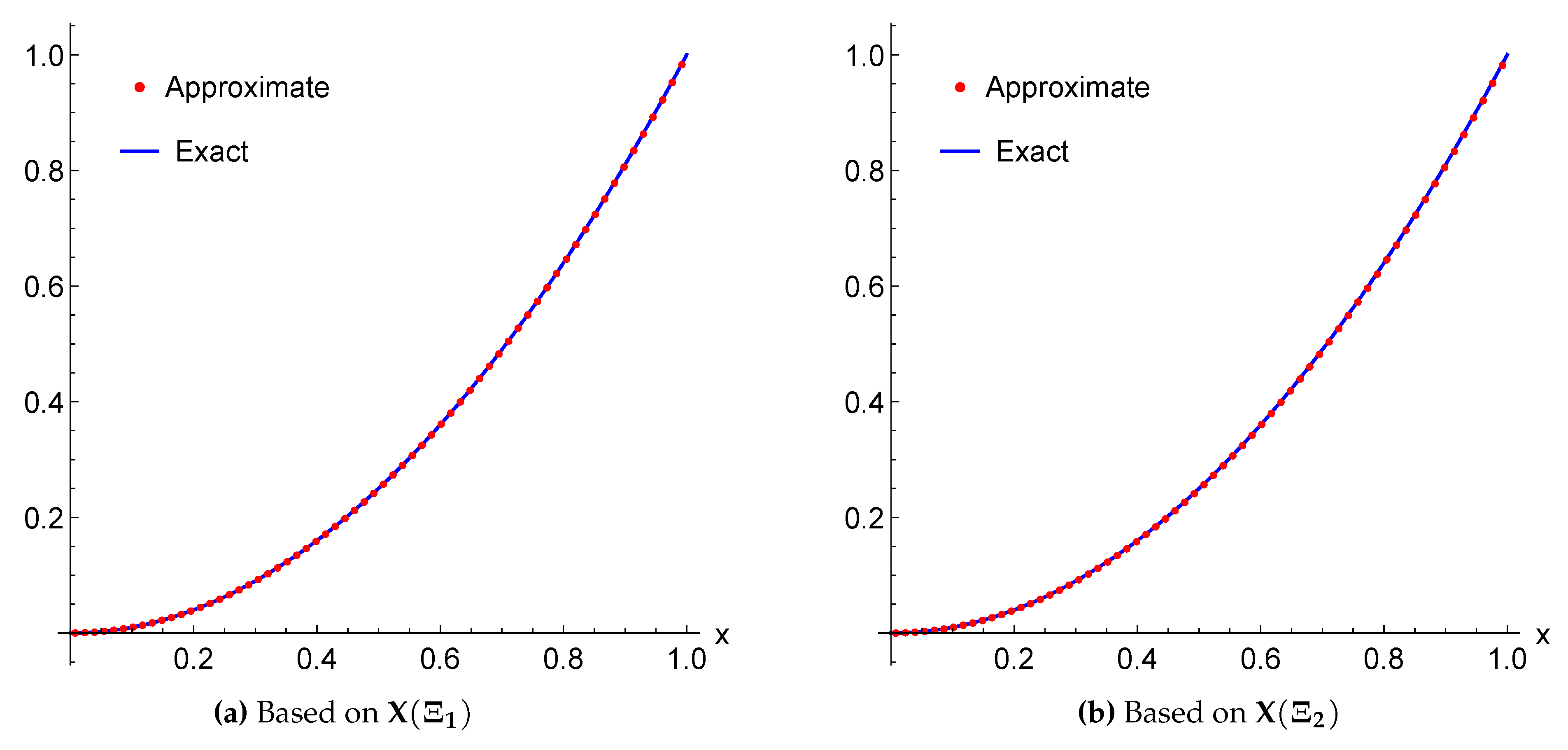
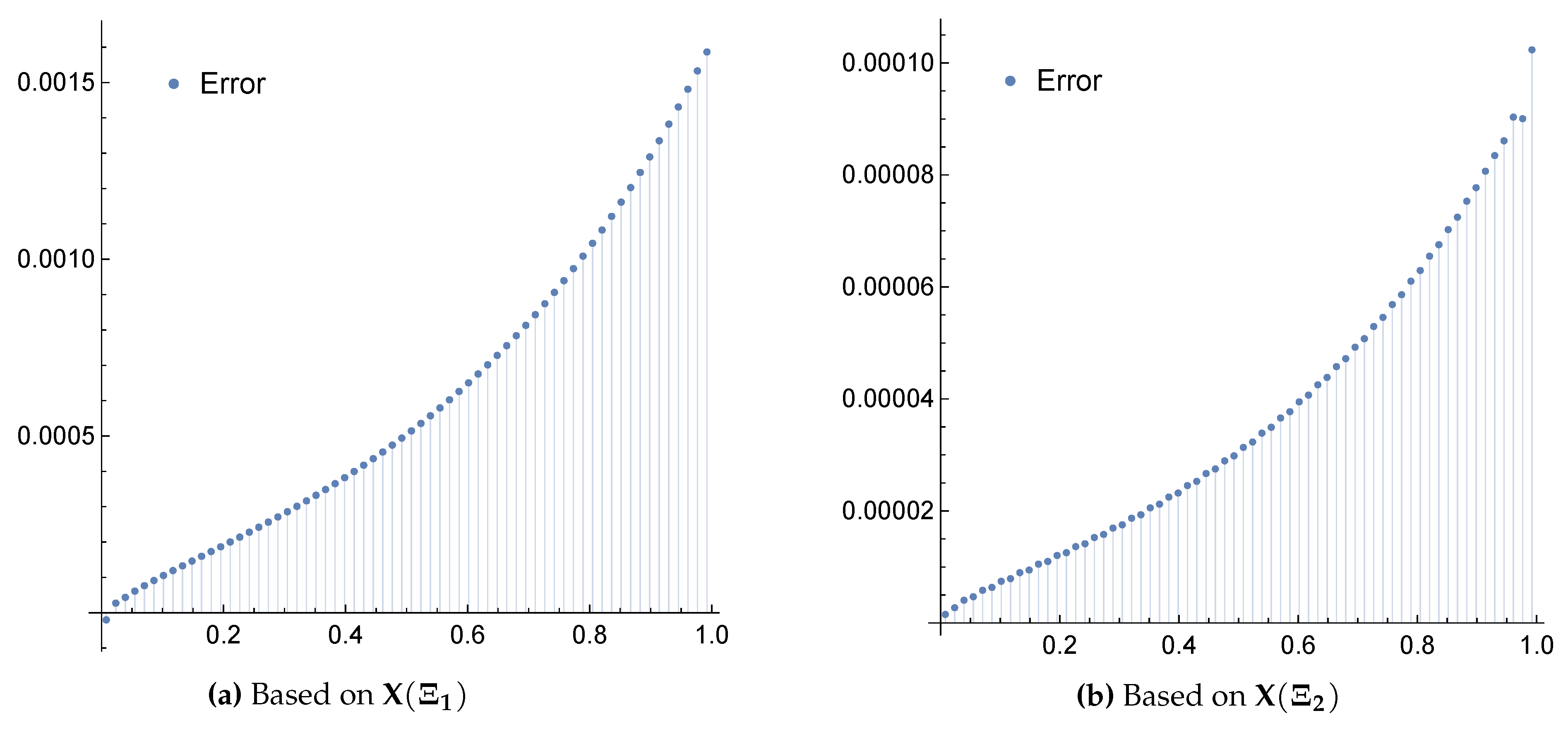
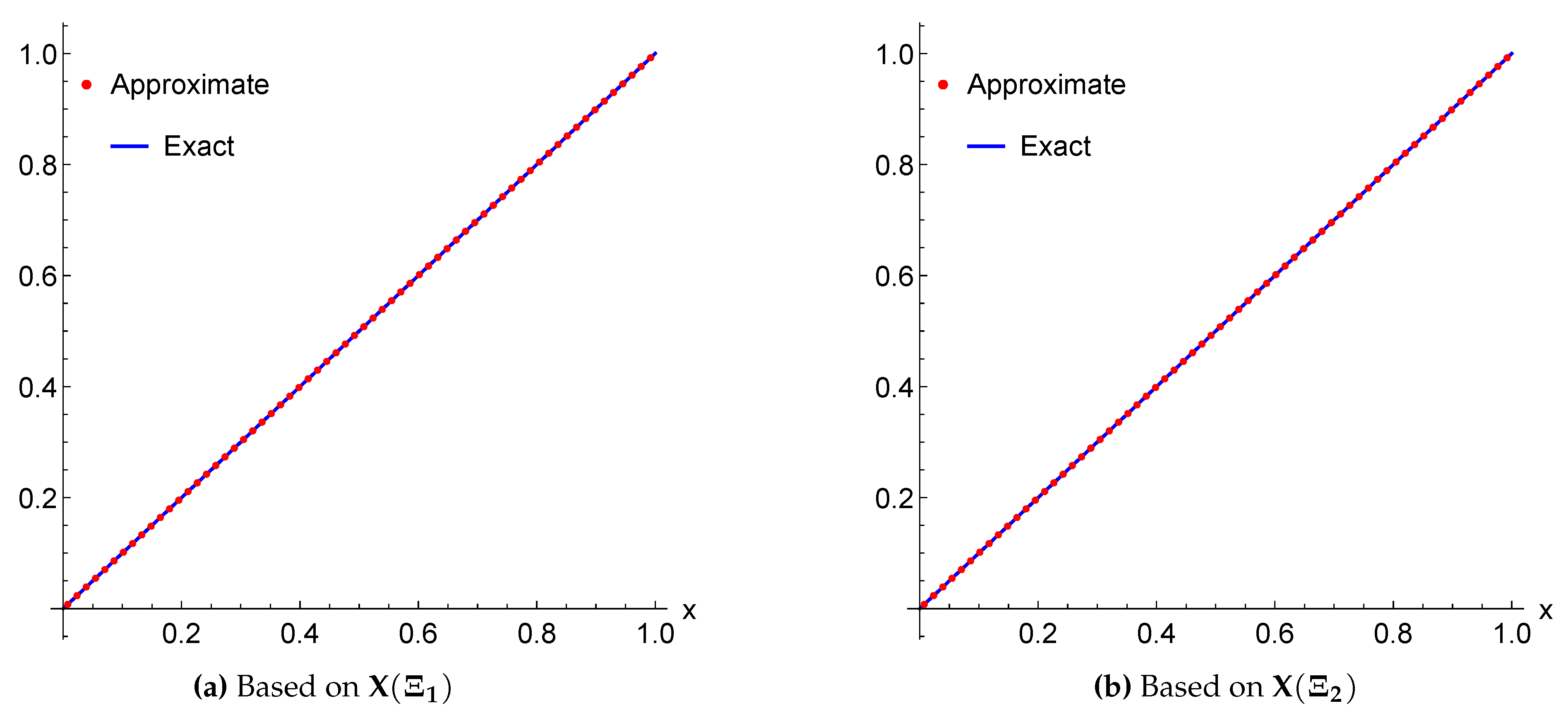
3. Numerical Performance
4. Conclusions
- 1.
- Number of terms of the partial sum of the framelet truncated expansion being used;
- 2.
- The vanishing moments order of the framelet system being used, where increasing these terms will result an increase in the accuracy as well as the efficiency of the algorithm.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abdon, A.; Dumitru, B. New fractional derivatives with non-local and nonsingular kernel, theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar]
- Caputo, M.; Michele, M. Linear model of dissipation whose Q is almost frequency independent. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Mohammad, M.; Cattani, C. Applications of bi-framelet systems for solving fractional order differential equations. Fractals 2020. [Google Scholar] [CrossRef]
- Mohammad, M.; Cattani, C. A collocation method via the quasi-affine biorthogonal systems for solving weakly singular type of Volterra-Fredholm integral equations. Alex. Eng. J. 2020, in press. [Google Scholar] [CrossRef]
- Mohammad, M.; Trounev, A.; Cattani, C. The dynamics of COVID-19 in the UAE based on fractional derivative modeling using Riesz wavelets simulation. Preprint 2020. [Google Scholar] [CrossRef]
- Ghanbari, B.; Atangana, A. A new application of fractional Atangana–Baleanu derivatives: Designing ABC-fractional masks in image processing. Phys. A: Stat. Mech. Its Appl. 2020, 542, 123516. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex. Eng. J. 2020, in press. [Google Scholar] [CrossRef]
- Atangana, A.; Bonyah, E.; Elsadany, A. A fractional order optimal 4D chaotic financial model with Mittag-Leffler law. Chin. J. Phys. 2020, 65, 38–53. [Google Scholar] [CrossRef]
- Atangana, A.; Aguilar, J.; Kolade, M.; Hristov, J. Fractional differential and integral operators with non-singular and non-local kernel with application to nonlinear dynamical systems. Chaos Solitons Fractals 2020, 132, 109493. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, I. Chaos in a simple nonlinear system with Atangana–Baleanu derivatives with fractional order. Chaos Solitons Fractals 2016, 89, 447–454. [Google Scholar] [CrossRef]
- Atangana, A. On the new fractional derivative and application to nonlinear Fisher’s reaction–diffusion equation. Appl. Math. Comput. 2016, 273, 948–956. [Google Scholar] [CrossRef]
- Atangana, A.; Aguilar, J. Decolonisation of fractional calculus rules: Breaking commutativity and associativity to capture more natural phenomena. Eur. Phys. J. Plus 2018, 133, 166. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Baskonusc, H.; Prakash, D.; Kumar, P. A new study of unreported cases of 2019-nCOV epidemic outbreaks. Chaos Solitons Fractals 2020. [Google Scholar] [CrossRef]
- Asif, Y.; Sema, G. Numerical Solutions with Linearization Techniques of the Fractional Harry Dym Equation. Appl. Math. Nonlinear Sci. 2019, 4, 35–42. [Google Scholar]
- Kumar, D.; Singh, J.; Baleanu, D. A new analysis of the Fornberg-Whitham equation pertaining to a fractional derivative with Mittag-Leffler-type kernel. Eur. Phys. J. Plus 2018, 133, 1–10. [Google Scholar] [CrossRef]
- Aidara, S.; Sagna, Y. BSDEs driven by two mutually independent fractional Brownian motions with stochastic Lipschitz coefficients. Appl. Math. Nonlinear Sci. 2019, 4, 139–150. [Google Scholar] [CrossRef]
- Bhatter, S.; Mathur, A.; Kumar, D.; Singh, J. A new analysis of fractional Drinfeld–Sokolov–Wilson model with exponential memory. Phys. A Stat. Mech. Its Appl. 2020, 537, 122578. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Baskonusc, H.; Mehmet, H. Novel Dynamic Structures of 2019-nCoV with Nonlocal Operator via Powerful Computational Technique. Biology 2020, 9, 107. [Google Scholar] [CrossRef]
- Jianzhang, W.; Jiabin, Y.; Gao, W. Analysis of fractional factor system for data transmission in SDN. Appl. Math. Nonlinear Sci. 2019, 4, 283–288. [Google Scholar]
- Al-Ghafri, K.; Rezazadeh, H. Solitons and other solutions of (3 + 1)-dimensional space–time fractional modified KdV–Zakharov–Kuznetsov equation. Appl. Math. Nonlinear Sci. 2019, 4, 289–304. [Google Scholar] [CrossRef]
- Gao, W.; Veeresh, P.; Gowada, D.; Mehmet, H.; Yel, B. A New Numerical Results for the Time-Fractional Phi-Four Equation Using a Novel Analytical Approach. Symmetry 2020, 12, 478. [Google Scholar] [CrossRef]
- Mundewadi, R.; Kumbinarasaiah, S. Numerical Solution of Abel’ s Integral Equations using Hermite Wavelet. Appl. Math. Nonlinear Sci. 2019, 4, 395–406. [Google Scholar] [CrossRef]
- Gao, W. New approach for the model describing the deathly disease in pregnant women using Mittag-Leffler function. Chaos Solitons Fractals 2020, 134, 109696. [Google Scholar] [CrossRef]
- Ziane, D.; Cherif, M.H.; Cattani, C.; Belghaba, K. Yang-laplace decomposition method for nonlinear system of local fractional partial differential equations. Appl. Math. Nonlinear Sci. 2019, 4, 489–502. [Google Scholar] [CrossRef]
- Gao, W.; Yel, G.; Mehmet, H.; Cattani, C. Complex solitons in the conformable (2+1)-dimensional Ablowitz-Kaup-Newell-Segur equation. AIMS Math. 2020, 5, 507–521. [Google Scholar] [CrossRef]
- Kurt, A.; Şenol, M.; Tasbozan, O.; Chand, M. Two reliable methods for the solution of fractional coupled Burgers’ equation arising as a model of polydispersive sedimentation. Appl. Math. Nonlinear Sci. 2019, 4, 523–534. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Bulut, H.; Atas, S.S. Optical solitons to the fractional Schrödinger-Hirota equation. Appl. Math. Nonlinear Sci. 2019, 4, 535–542. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Hammouch, Z.; Atangana, A. A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 2018, 316, 504–515. [Google Scholar] [CrossRef]
- Danane, J.; Allali, K.; Hammouch, Z. Mathematical analysis of a fractional differential model of HBV infection with antibody immune response. Chaos Solitons Fractals 2020, 136, 109787. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. A new numerical algorithm for fractional Fitzhugh–Nagumo equation arising in transmission of nerve impulses. Nonlinear Dyn. 2018, 91, 307–317. [Google Scholar] [CrossRef]
- Panda, S.K.; Abdeljawad, T.; Ravichandran, C. A complex valued approach to the solutions of Riemann-Liouville integral, Atangana-Baleanu integral operator and non-linear Telegraph equation via fixed point method. Chaos Solitons Fractals 2020, 130, 109439. [Google Scholar] [CrossRef]
- Rahmoune, A.; Ouchenane, D.; Boulaaras, S.; Agarwal, P. Growth of solutions for a coupled nonlinear Klein–Gordon system with strong damping, source, and distributed delay terms. Adv. Differ. Equ. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Agarwal, P.; Hyder, A.-A.; Zakarya, M. Well-posedness of stochastic modified Kawahara equation. Adv. Differ. Equ. 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Hassan, S.; De la Sen, M.; Agarwal, P.; Ali, Q.; Hussain, A. A New Faster Iterative Scheme for Numerical Fixed Points Estimation of Suzuki’s Generalized Nonexpansive Mappings. Math. Probl. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Agarwal, P.; El-Sayedef, A.; Tariboon, J. Vieta–Fibonacci operational matrices for spectral solutions of variable-order fractional integro-differential equations. J. Comput. Appl. Math. 2020, 2020, 113063. [Google Scholar]
- Agarwal, P.; Attary, M.; Maghasedi, M.; Kumam, P. Solving Higher-Order Boundary and Initial Value Problems via Chebyshev–Spectral Method: Application in Elastic Foundation. Symmetry 2020, 12, 987. [Google Scholar] [CrossRef]
- Alderremy, A.; Saad, K.M.; Agarwal, P.; Aly, S.; Jain, S. Certain new models of the multi space-fractional Gardner equation. Phys. A Stat. Mech. Its Appl. 2020, 545, 123806. [Google Scholar] [CrossRef]
- Han, B. Framelets and wavelets: Algorithms, analysis, and applications, Applied and Numerical Harmonic Analysis; Springer: Birkhauser, Basel, 2017. [Google Scholar]
- Han, B.; Michelle, M. Construction of wavelets and framelets on a bounded interval. Anal. Appl. 2018, 16, 807–849. [Google Scholar] [CrossRef]
- Han, B.; Lu, R. Compactly Supported Quasi-tight Multiframelets with High Balancing Orders and Compact Framelet Transforms. arXiv 2020, arXiv:2001.06032. [Google Scholar]
- Ashpazzadeh, E.; Han, B.; Lakestani, M.; Razzaghi, M. Derivative-orthogonal wavelets for discretizing constrained optimal control problems. Int. J. Syst. Sci. 2020, 51, 1–25. [Google Scholar] [CrossRef]
- Mohammad, M.; Lin, E.-B. Gibbs phenomenon in tight framelet expansions. Commun. Nonlinear Sci. Numer. Simul. 2018, 55, 84–92. [Google Scholar] [CrossRef]
- Mohammad, M.; Lin, E. Gibbs effects using daubechies and coiflet tight framelet systems. Contemp. Math 2018, 1, 271–282. [Google Scholar]
- Mohammad, M. Special B-spline Tight Framelet and It’s Applications. J. Adv. Math. Comput. Sci. 2018, 29, 1–18. [Google Scholar] [CrossRef]
- Mohammad, M. On the Gibbs Effect Based on the Quasi-Affine Dual Tight Framelets System Generated Using the Mixed Oblique Extension Principle. Mathematics 2019, 7, 952. [Google Scholar] [CrossRef]
- Mohammad, M. Biorthogonal-Wavelet-Based Method for Numerical Solution of Volterra Integral Equations. Entropy 2019, 21, 1098. [Google Scholar] [CrossRef]
- Mohammad, M. A Numerical Solution of Fredholm Integral Equations of the Second Kind Based on Tight Framelets Generated by the Oblique Extension Principle. Symmetry 2019, 11, 854. [Google Scholar] [CrossRef]
- Mohammad, M. Bi-orthogonal wavelets for investigating Gibbs effects via oblique extension principle. J. Phys.: Conf. Ser. 2020, 1489, 012009. [Google Scholar]
- Mohammad, M.; Trounev, A. Implicit Riesz wavelets based-method for solving singular fractional integro-differential equations with applications to hematopoietic stem cell modeling. Chaos Solitons Fractals 2020, 138, 109991. [Google Scholar] [CrossRef]
- Lin, E.; Al-Jarrah, Y. Wavelet Based Methods for Numerical Solutions of Two Dimensional Integral Equations. Math. Aeterna 2014, 4, 839–853. [Google Scholar]
- Al-Jarrah, Y.; Lin, E. Wavelet Interpolation Method for Solving Singular. Integral Equations Appl. Math. 2013, 4, 1–4. [Google Scholar]
- Al-Jarrah, Y.; Lin, E. Numerical Solutions of Fredholm-Volterra Integral, Equations by Using Scaling Function Interpolation Method. Applied Mathematics 2013, 4, 204–209. [Google Scholar] [CrossRef]
- Lin, E.B.; Liu, N. Generalized Legendre expansion methods and functional differential equations. Int. J. Numer. Methods Appl. 2011, 6, 115–121. [Google Scholar]
- Lin, E.B.; Liu, N. Legendre Wavelet Method for Numerical Solutions of Partial Differential Equations. Numer. Methods Partial. Differ. Equ. 2010, 26, 81–94. [Google Scholar]


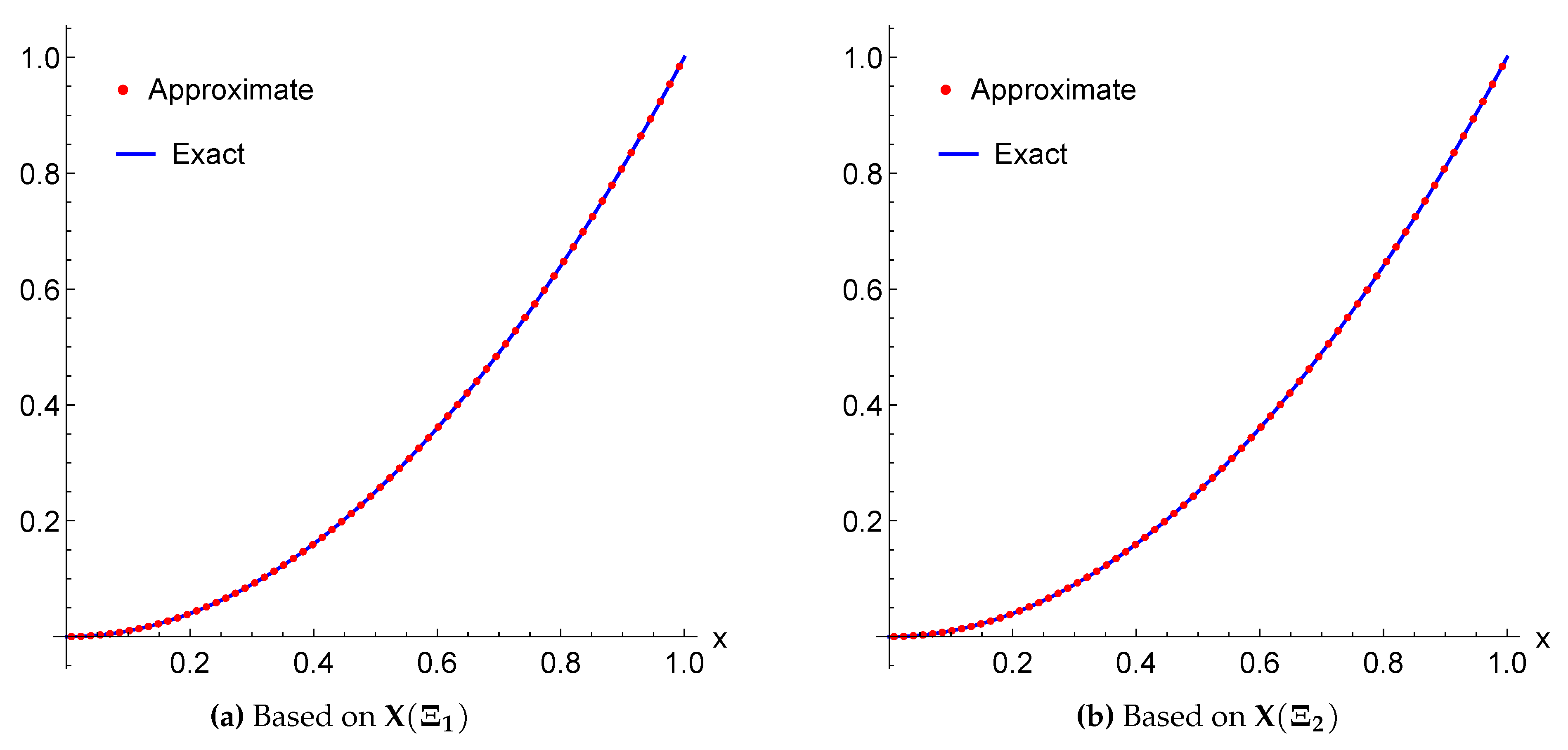

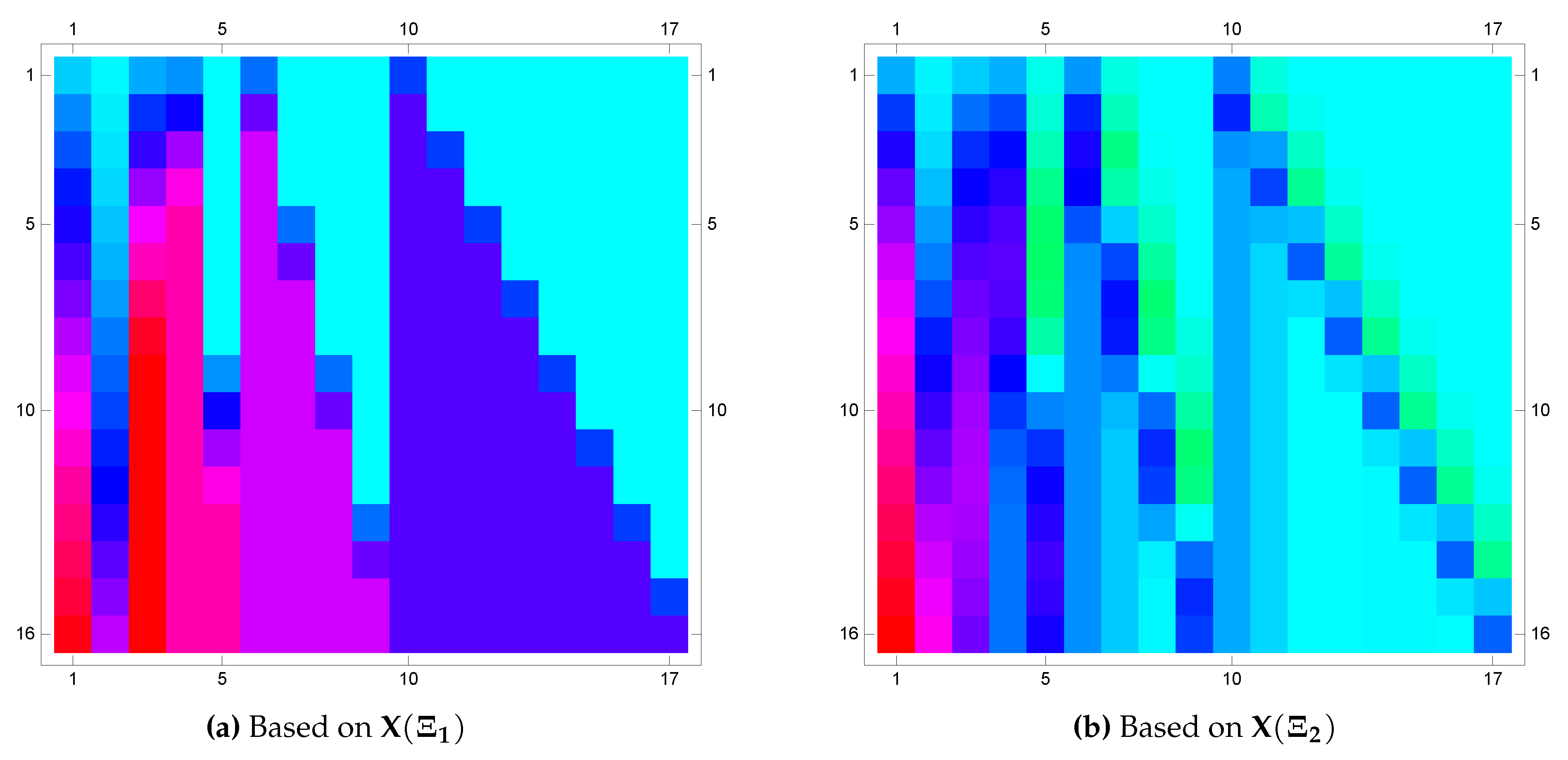
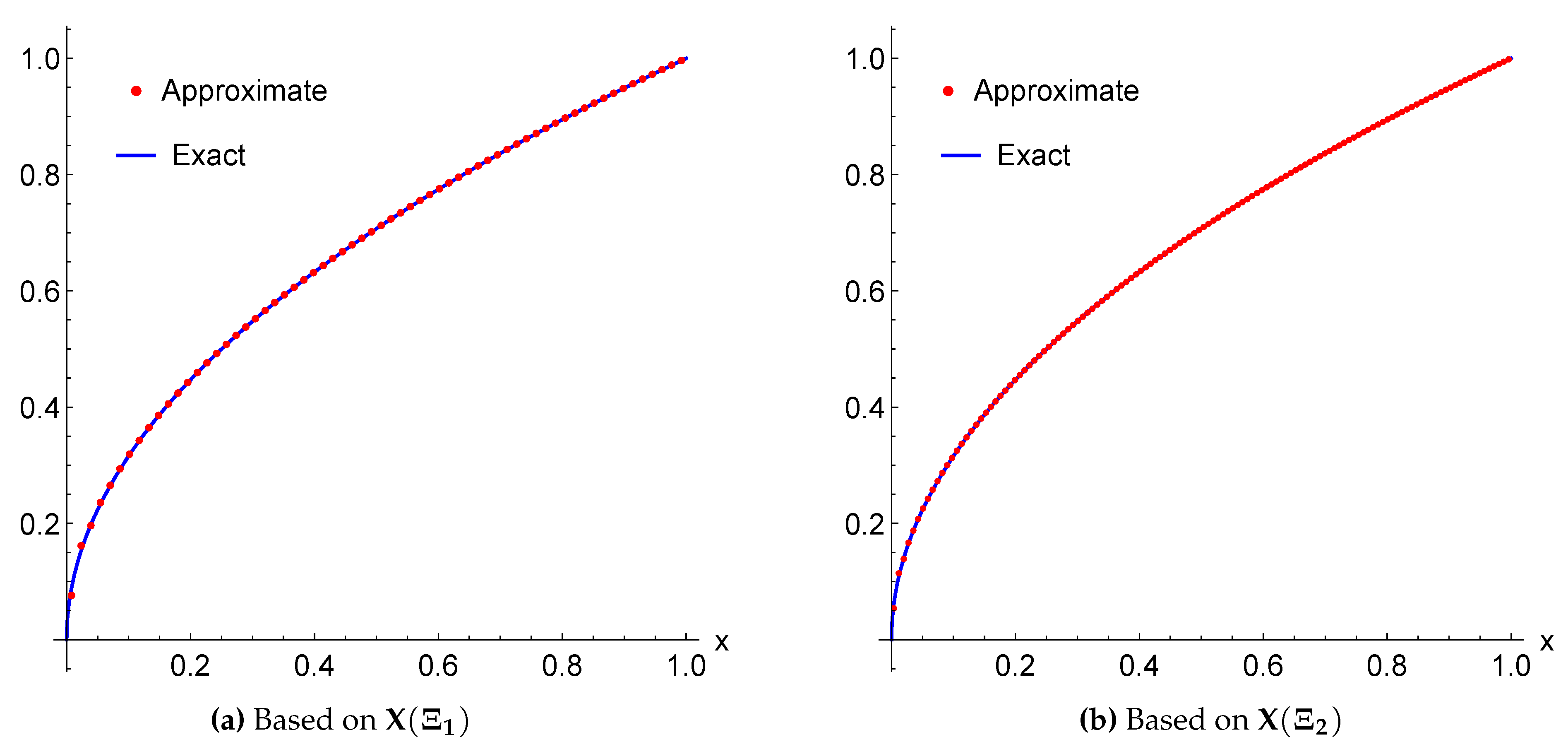
| x | Exact | via | via |
|---|---|---|---|
| 0.1 | 0.01 | 7.26467 × | 1.85352 × |
| 0.2 | 0.04 | 9.10220 × | 6.91144 × |
| 0.3 | 0.09 | 1.82277 × | 1.51510 × |
| 0.4 | 0.16 | 3.51120 × | 2.67941 × |
| 0.5 | 0.25 | 4.47280 × | 4.28731 × |
| 0.6 | 0.36 | 8.36896 × | 7.18203 × |
| 0.7 | 0.49 | 1.17160 × | 1.06917 × |
| 0.8 | 0.64 | 1.64979 × | 1.51795 × |
| 0.9 | 0.81 | 2.29604 × | 2.08445 × |
| 1.0 | 1.00 | 2.99714 × | 2.72612 × |
| x | Exact | via | via |
|---|---|---|---|
| 0.1 | 0.01 | 3.64554 × | 1.73553 × |
| 0.2 | 0.04 | 5.91254 × | 2.96533 × |
| 0.3 | 0.09 | 4.66455 × | 1.09373 × |
| 0.4 | 0.16 | 2.51037 × | 2.35522 × |
| 0.5 | 0.25 | 2.46092 × | 4.22966 × |
| 0.6 | 0.36 | 4.63545 × | 7.11944 × |
| 0.7 | 0.49 | 1.30932 × | 1.55358 × |
| 0.8 | 0.64 | 2.35355 × | 1.24774 × |
| 0.9 | 0.81 | 1.38865 × | 1.04342 × |
| 1.0 | 1.00 | 3.53446 × | 3.39882 × |
| x | Exact | via | via |
|---|---|---|---|
| 0.1 | 0.01 | 7.88293 × | 2.92921 × |
| 0.2 | 0.04 | 7.67236 × | 1.36504 × |
| 0.3 | 0.09 | 2.36706 × | 1.05287 × |
| 0.4 | 0.16 | 1.09108 × | 2.91769 × |
| 0.5 | 0.25 | 1.27581 × | 4.42031 × |
| 0.6 | 0.36 | 1.69445 × | 5.90872 × |
| 0.7 | 0.49 | 2.44359 × | 1.06485 × |
| 0.8 | 0.64 | 3.32952 × | 1.27942 × |
| 0.9 | 0.81 | 4.33451 × | 2.18122 × |
| 1.0 | 1.00 | 5.43243 × | 2.98557 × |
| x | Exact | via | via |
|---|---|---|---|
| 0.1 | 0.01 | 1.31612 × | 1.91626 × |
| 0.2 | 0.04 | 51.7061 × | 1.45913 × |
| 0.3 | 0.09 | 6.39942 × | 1.06851 × |
| 0.4 | 0.16 | 0.41406 × | 3.21467 × |
| 0.5 | 0.25 | 0.49218 × | 6.80432 × |
| 0.6 | 0.36 | 0.60156 × | 1.20816 × |
| 0.7 | 0.49 | 0.69531 × | 3.03948 × |
| 0.8 | 0.64 | 8.53345 × | 4.26697 × |
| 0.9 | 0.81 | 1.10689 × | 5.81013 × |
| 1.0 | 1.00 | 1.38297 × | 7.36015 × |
| x | Exact | via | via |
|---|---|---|---|
| 0.1 | 0.01 | 1.62034 × | 8.34395 × |
| 0.2 | 0.04 | 1.03814 × | 5.23015 × |
| 0.3 | 0.09 | 3.56716 × | 1.85430 × |
| 0.4 | 0.16 | 7.48135 × | 3.84891 × |
| 0.5 | 0.25 | 1.45995 × | 6.85008 × |
| 0.6 | 0.36 | 2.32864 × | 1.10671 × |
| 0.7 | 0.49 | 3.47190 × | 1.73964 × |
| 0.8 | 0.64 | 5.19781 × | 2.46654 × |
| 0.9 | 0.81 | 7.05227 × | 3.56779 × |
| 1.0 | 1.00 | 9.28981 × | 4.45749 × |
| x | Exact | via | via |
|---|---|---|---|
| 0.1 | 0.01 | 1.65534 × | 3.23863 × |
| 0.2 | 0.04 | 2.34587 × | 5.74663 × |
| 0.3 | 0.09 | 2.63882 × | 0.64773 × |
| 0.4 | 0.16 | 8.38292 × | 1.33748 × |
| 0.5 | 0.25 | 6.37474 × | 2.92292 × |
| 0.6 | 0.36 | 7.38381 × | 7.35377 × |
| 0.7 | 0.49 | 1.22234 × | 4.43444 × |
| 0.8 | 0.64 | 4.10292 × | 1.92556 × |
| 0.9 | 0.81 | 5.37333 × | 2.01111 × |
| 1.0 | 1.00 | 2.32444 × | 2.22298 × |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammad, M.; Trounev, A.; Cattani, C. An Efficient Method Based on Framelets for Solving Fractional Volterra Integral Equations. Entropy 2020, 22, 824. https://doi.org/10.3390/e22080824
Mohammad M, Trounev A, Cattani C. An Efficient Method Based on Framelets for Solving Fractional Volterra Integral Equations. Entropy. 2020; 22(8):824. https://doi.org/10.3390/e22080824
Chicago/Turabian StyleMohammad, Mutaz, Alexander Trounev, and Carlo Cattani. 2020. "An Efficient Method Based on Framelets for Solving Fractional Volterra Integral Equations" Entropy 22, no. 8: 824. https://doi.org/10.3390/e22080824
APA StyleMohammad, M., Trounev, A., & Cattani, C. (2020). An Efficient Method Based on Framelets for Solving Fractional Volterra Integral Equations. Entropy, 22(8), 824. https://doi.org/10.3390/e22080824






