A Novel Image-Encryption Scheme Based on a Non-Linear Cross-Coupled Hyperchaotic System with the Dynamic Correlation of Plaintext Pixels
Abstract
1. Introduction
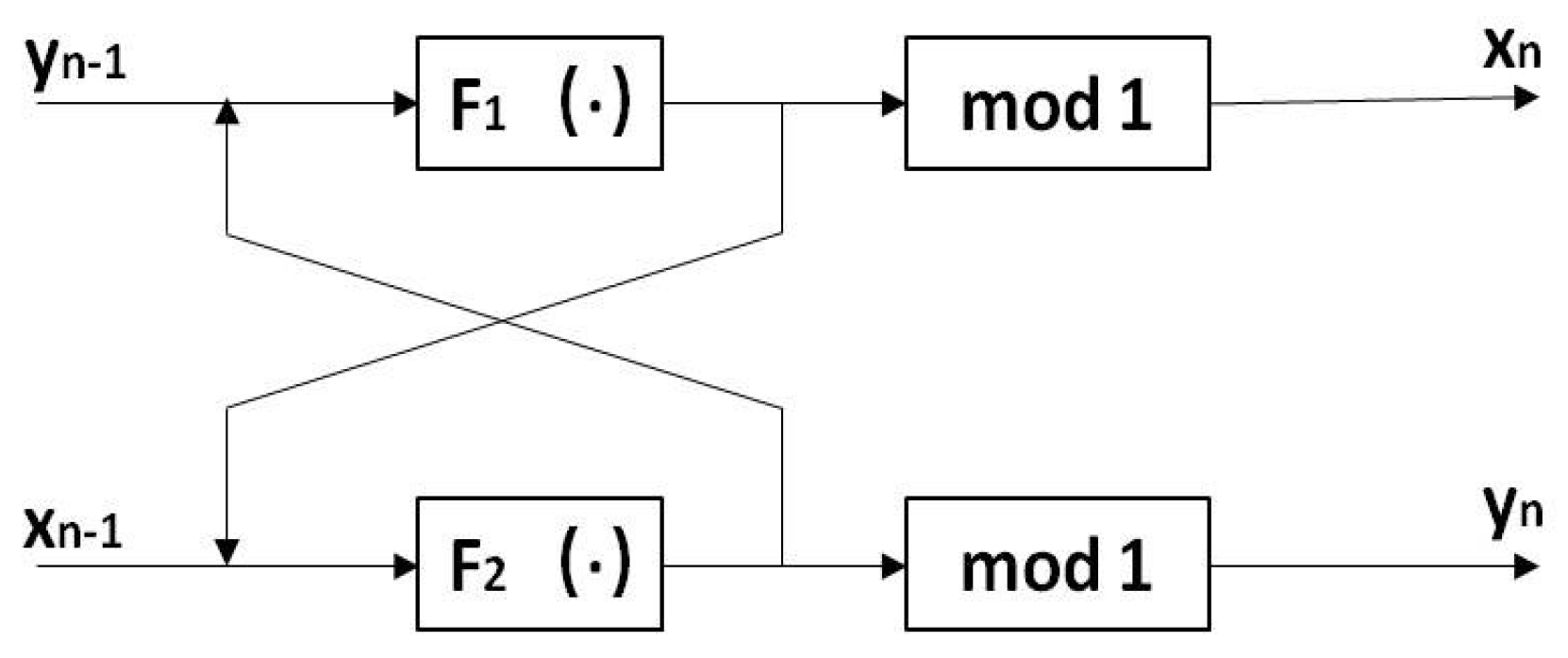
2. Non-Linear Cross-Coupled Chaotic Map
2.1. Performance Evaluation of LF-NCHM Model
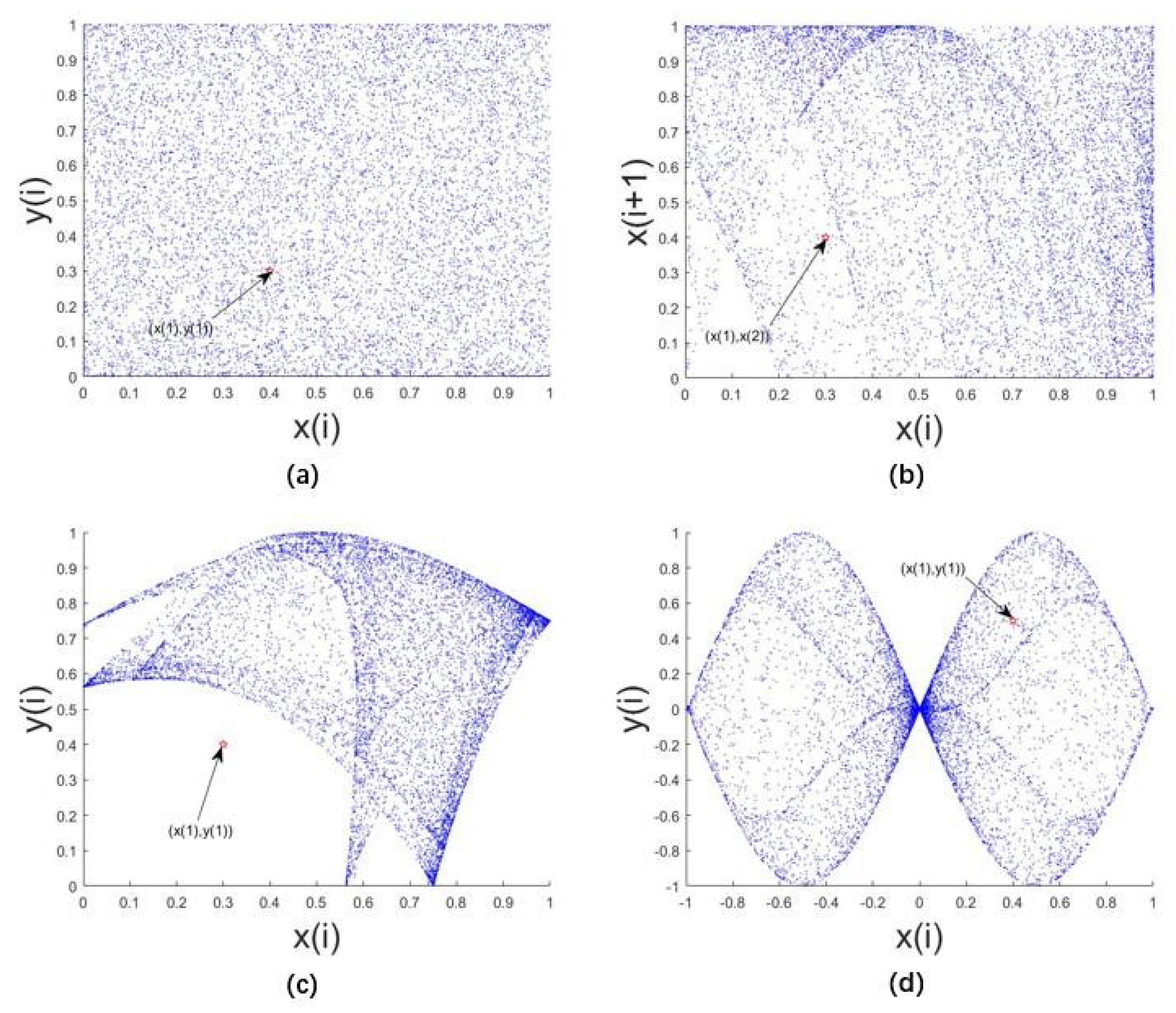
2.1.1. Trajectory
2.1.2. Bifurcation Diagram
2.1.3. Lyapunov Exponent
2.1.4. Permutation Entropy
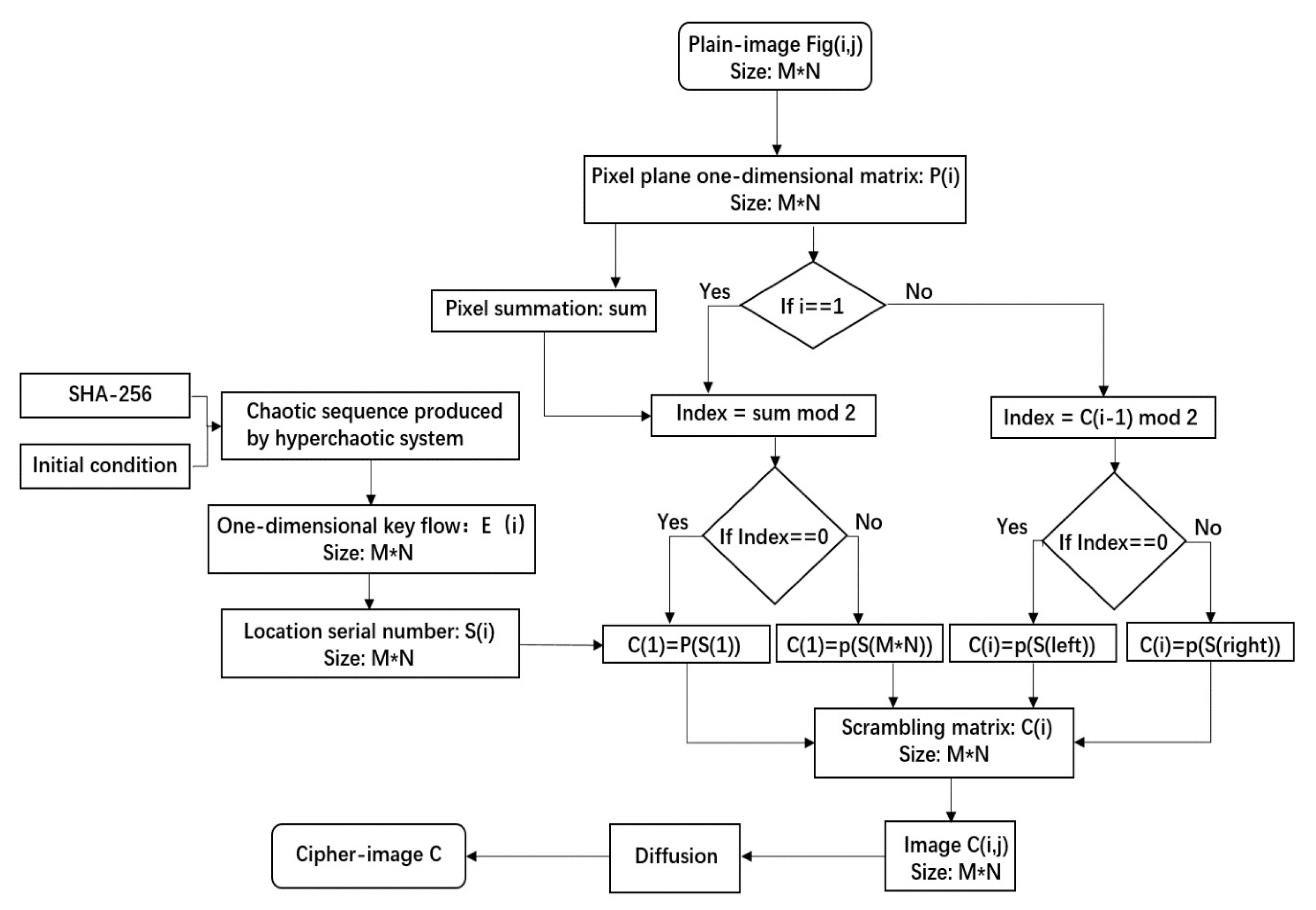
3. The Image-Encryption Algorithm Related to Plaintext Pixels in the Scrambling Process
3.1. The Generation of Keys and Hyperchaotic Sequences
- Use the image file to generate hash values, Obtain the K = k, k, ……, k. They are composed of 8 bits of data.
- Calculate the intermediate variables h, h, h, h through k, k, ……, k. The calculation rules are shown in Formula (3).
- Calculate the initial values , , x and y according to h, h, h and h. The calculation rules are shown in Formula (4).where μ, λ, x and y are the initial values given. In the algorithm of this chapter, = 3.0, = 4.5, x = 0.4 and y = 0.3.
- Bring the initial conditions generated by the hash algorithm into LF-NCHM to produce a sequence of the required length.
3.2. A Scrambling Method Based on Pixel Values
- Convert the plaintext image Fig with the size of M*N into the one-dimensional vector P(i), and the size of the one-dimensional vector is M*N.
- According to the dynamic secret key K related to the plaintext and hyperchaotic system LF-NCHM mentioned above, generate a one-dimensional key stream E(i) with the size of M*N.
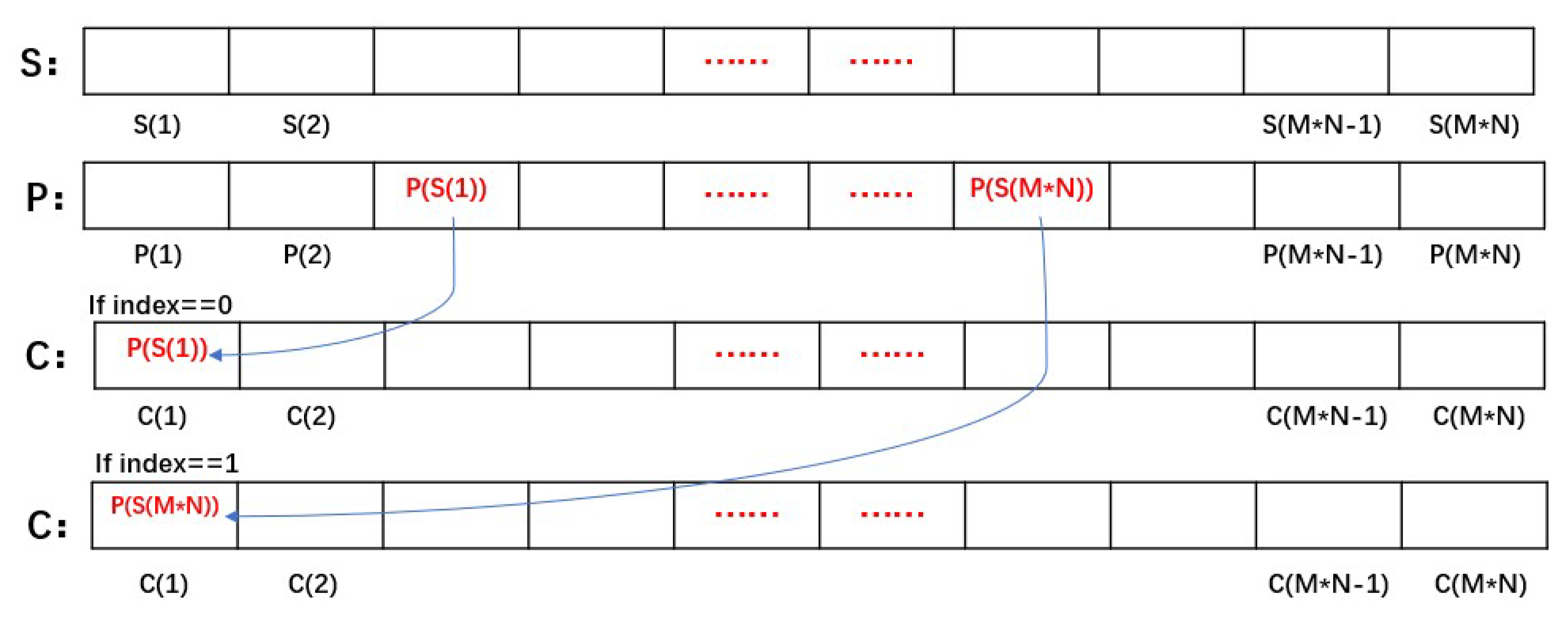
- Sort E(i), and a one-dimensional vector of position sequence number with the size of M*N is obtained. The vector of the position sequence number is named S(i). An example of this rule is shown in Figure 8.
- Calculate the sum of the pixel values and index for the plaintext image. index = sum mod 2.
- Use the MATLAB library function zeros to produce a one-dimensional vector C(i) of size M*N, which is used to save the pixel scrambling results.
- Judge the index. If the index is equal to zero, select the location information from the left side of , . If the index is equal to one, choose to take the location information from the right side of , (M*N)). Figure 9 shows this operation.
- Calculate index. mod 2, i ≥ 2. If the index is equal to zero, select the location information from the left side of . , and left represents the latest sequence number of location sequence from the left. If index is equal to one, select the location information from the right side of . , right represents the latest sequence number of the position sequence starting from the right side. Repeat the operation until the assignment of C(M*N) is completed.
- Restore the one-dimensional vector to the two-dimensional matrix with the size of M*N, and the scrambling process is completed.
3.3. Diffusion Process
- According to the generation rules of the key and hyperchaotic sequences, generate sequences with the size of M*N. The sequences are transformed into two-dimensional matrixes of size M*N.
- Diffuse the scrambled image . First, from the lower right corner of the image, from right to left, from bottom to top. The current pixel is associated with the adjacent pixels on the right and bottom, and the intermediate image P1 is obtained. The specific operations are as follows:where ⊕ indicates that binary values corresponding to two numbers are exclusive or by bits, and indicates the largest integer not greater than x. P1 is the first round of diffusion of encrypted images.Here we use four pixels as an example to give the calculation method. Figure 10 shows the operation process.
- Carry out the second round of diffusion on P1. Starting from the upper left corner of the image, from left to right, and from top to bottom, the current pixel is associated with the adjacent pixels on the left and upper sides to obtain the encrypted image P2. The specific operations are as follows:This process is the reverse of Step 2.
3.4. Decryption Process
- Using key K, the hyperchaotic sequences for inverse diffusion and the hyperchaotic sequence for the inverse scrambling are obtained.
- Through , the first round of reverse diffusion is carried out, and the result is P3. The method is as follows.This process starts from i = M and j = N, ⊕ indicates that the binary values corresponding to the two numbers are bitwise exclusive or, is the largest integer not greater than x, and P3 is the transformed image.
- Carry out the second round of reverse diffusion through , and obtain P4. The method is similar to Step 2 and will not be repeated.
- According to the scrambling method, P4 is transformed into a one-dimensional matrix C and the pixel sum of P4 is calculated.
- Sort to obtain the position serial number .
- Calculate the index’. . If index’ equals zero, . Otherwise, P(S’(M*N))= C’(1).
- Calculate the index’. . If index’ equals zero, P(S’(left))=C’(i), left = left +1. Otherwise, . Until i is equal to M*N.
- Restore vector P(i) to a decrypted image P of size M*N.
4. Simulation Results and Attack Test
4.1. Simulation Results
4.2. Statistical Analysis
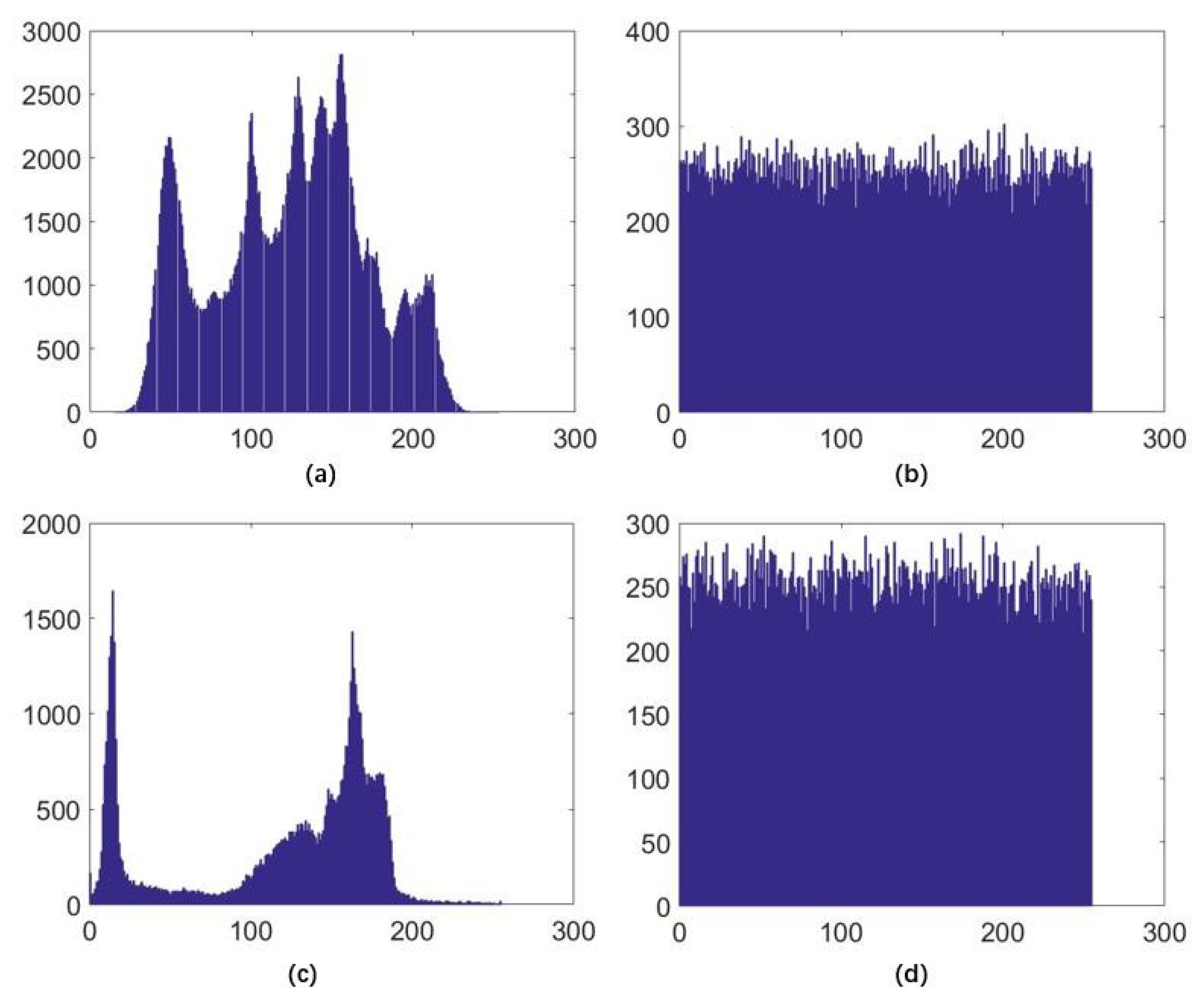
4.2.1. Histogram Analysis
4.2.2. Correlation Analysis
4.3. Key Space Analysis
4.4. Sensitivity Analysis
4.4.1. Key Sensitivity
4.4.2. Differential Attack
4.5. Information Entropy Analysis
4.6. Chosen-Plaintext Analysis and Known-Plaintext Analysis
4.7. Encryption Efficiency
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Matthews, R. On the derivation of a “Chaotic encryption algorithm”. Cryptologia 1989, 13, 29–42. [Google Scholar] [CrossRef]
- Fridrich, J. Symmetric ciphers based on two-dimensional chaotic maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Mirzaei, O.; Yaghoobi, M.; Irani, H. A new image encryption method: Parallel sub-image encryption with hyper chaos. Nonlinear Dyn. 2012, 67, 557–566. [Google Scholar] [CrossRef]
- Wong, K.W.; Kwok, B.S.H.; Law, W.S. A fast image encryption scheme based on chaotic standard map. Phys. Lett. A 2008, 372, 2645–2652. [Google Scholar] [CrossRef]
- Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Opt. Lasers Eng. 2012, 78, 17–25. [Google Scholar] [CrossRef]
- Cao, C.; Sun, K.; Liu, W. A novel bit-level image encryption algorithm based on 2D-LICM hyperchaotic map. Signal Process. 2018, 143, 122–133. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X. Color image encryption using spatial bit-level permutation and high-dimension chaotic system. Opt. Commun. 2011, 284, 3895–3903. [Google Scholar] [CrossRef]
- Teng, L.; Wang, X. A bit-level image encryption algorithm based on spatiotemporal chaotic system and self-adaptive. Opt. Commun. 2012, 285, 4048–4054. [Google Scholar] [CrossRef]
- Patidar, V.; Pareek, N.K.; Purohit, G.; Sud, K.K. Modified substitution–diffusion image cipher using chaotic standard and logistic maps. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2755–2765. [Google Scholar] [CrossRef]
- Wong, K.-W.; Kwok, B.S.-H.; Yuen, C.-H. An efficient diffusion approach for chaos-based image encryption. Chaos Solitons Fractals 2009, 41, 2652–2663. [Google Scholar] [CrossRef]
- Fu, C.; Chen, J.; Zou, H.; Meng, W.; Zhan, Y.; Yu, Y. A chaos-based digital image encryption scheme with an improved diffusion strategy. Opt. Express 2012, 20, 2363–2378. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wong, K.W.; Liao, X.; Xiang, T.; Chen, G. A chaos-based image encryption algorithm with variable control parameters. Chaos Solitons Fractals 2009, 41, 1773–1783. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Z.; Fu, C.; Yu, H. An improved permutation-diffusion type image cipher with a chaotic orbit perturbing mechanism. Opt. Express 2013, 21, 27873–27890. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xiao, D.; Shu, Y.; Li, J. A novel image encryption scheme based on a linear hyperbolic chaotic system of partial differential equations. Signal Process. Image Commun. 2013, 28, 292–300. [Google Scholar] [CrossRef]
- Wang, X.Y.; Yang, L.; Liu, R.; Kadir, A. A chaotic image encryption algorithm based on perceptron model. Nonlinear Dyn. 2010, 62, 615–621. [Google Scholar] [CrossRef]
- Tong, X.J.; Zhang, M.; Wang, Z.; Ma, J. A joint color image encryption and compression scheme based on hyper-chaotic system. Nonlinear Dyn. 2016, 84, 2333–2356. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, C.; Chen, H. A novel color image encryption algorithm based on hyperchaotic system and permutation-diffusion architecture. Int. J. Bifurc. Chaos 2019, 29, 1950115. [Google Scholar] [CrossRef]
- Wang, X.; Teng, L.; Qin, X. A novel colour image encryption algorithm based on chaos. Signal Process. 2012, 92, 1101–1108. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Pun, C.M.; Chen, C.L.P. 2D Sine Logistic modulation map for image encryption. Inf. Sci. Int. J. 2015, 297, 80–94. [Google Scholar] [CrossRef]
- Belazi, A.; El-Latif, A.A.A.; Belghith, S. A novel image encryption scheme based on substitution-permutation network and chaos. Signal Process. 2016, 128, 155–170. [Google Scholar] [CrossRef]
- Arroyo, D.; Rhouma, R.; Alvarez, G.; Li, S.; Fernandez, V. On the security of a new image encryption scheme based on chaotic map lattices. Chaos Interdiscip. Nonlinear Sci. 2008, 18, 033112. [Google Scholar] [CrossRef] [PubMed]
- Arroyo, D.; Diaz, J.; Rodriguez, F.B. Cryptanalysis of a one round chaos-based Substitution Permutation Network. Signal Process. 2013, 93, 1358–1364. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, L.; Chen, C.L.P. Image encryption using a new parametric switching chaotic system. Signal Process. 2013, 93, 3039–3052. [Google Scholar] [CrossRef]
- Xian, Y.; Wang, X.; Yan, X.; Li, Q.; Wang, X. Image Encryption Based on Chaotic Sub-Block Scrambling and Chaotic Digit Selection Diffusion. Opt. Lasers Eng. 2020, 134, 106202. [Google Scholar] [CrossRef]
- Solak, E.; Çokal, C.; Yildiz, O.T.; Türker, B. Cryptanalysis of Fridrich’s chaotic image encryption. Int. J. Bifurc. Chaos 2010, 20, 1405–1413. [Google Scholar] [CrossRef]
- Rhouma, R.; Solak, E.; Belghith, S. Cryptanalysis of a new substitution–diffusion based image cipher. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1887–1892. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Lo, K.T. Breaking a modified substitution–diffusion image cipher based on chaotic standard and logistic maps. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 837–843. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Xie, T.; Chen, M.Z.Q. Breaking a novel image encryption scheme based on improved hyperchaotic sequences. Nonlinear Dyn. 2013, 73, 2083–2089. [Google Scholar] [CrossRef]
- Cokal, C.; Solak, E. Cryptanalysis of a chaos-based image encryption algorithm. Phys. Lett. A 2009, 373, 1357–1360. [Google Scholar] [CrossRef]
- Jeng, F.G.; Huang, W.L.; Chen, T.H. Cryptanalysis and improvement of two hyper-chaos-based image encryption schemes. Signal Process. Image Commun. 2015, 34, 45–51. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Z.; Chen, R. Cryptanalysis and improvement in a plaintext-related image encryption scheme based on hyper chaos. IEEE Access 2019, 7, 126450–126463. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Z.; Fu, C.; Yu, H.; Zhang, L. A fast chaos-based image encryption scheme with a dynamic state variables selection mechanism. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 846–860. [Google Scholar] [CrossRef]
- Paral, P.; Dasgupta, T.; Bhattacharya, S. Colour image encryption based on cross-coupled chaotic map and fractional order chaotic systems. In Proceedings of the 2014 International Conference on Communication and Signal Processing, Bangkok, Thailand, 10–12 October 2014; pp. 1947–1952. [Google Scholar]
- Li, S.; Yin, B.; Ding, W.; Zhang, T.; Ma, Y. A nonlinearly modulated logistic map with delay for image encryption. Electronics 2018, 7, 326. [Google Scholar] [CrossRef]
- Liu, W.; Sun, K.; Zhu, C. A fast image encryption algorithm based on chaotic map. Opt. Lasers Eng. 2016, 84, 26–36. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Gu, S.; Zhang, Y. Novel image encryption algorithm based on cycle shift and chaotic system. Opt. Lasers Eng. 2015, 68, 126–134. [Google Scholar] [CrossRef]
- Ye, G.; Huang, X. A feedback chaotic image encryption scheme based on both bit-level and pixel-level. J. Vib. Control 2016, 22, 1171–1180. [Google Scholar] [CrossRef]
- Cai, S.; Huang, L.; Chen, X.; Xiong, X. A Symmetric Plaintext-Related Color Image Encryption System Based on Bit Permutation. Entropy 2018, 20, 282. [Google Scholar] [CrossRef]
- Huang, X.; Ye, G. An efficient self-adaptive model for chaotic image encryption algorithm. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 4094–4104. [Google Scholar] [CrossRef]






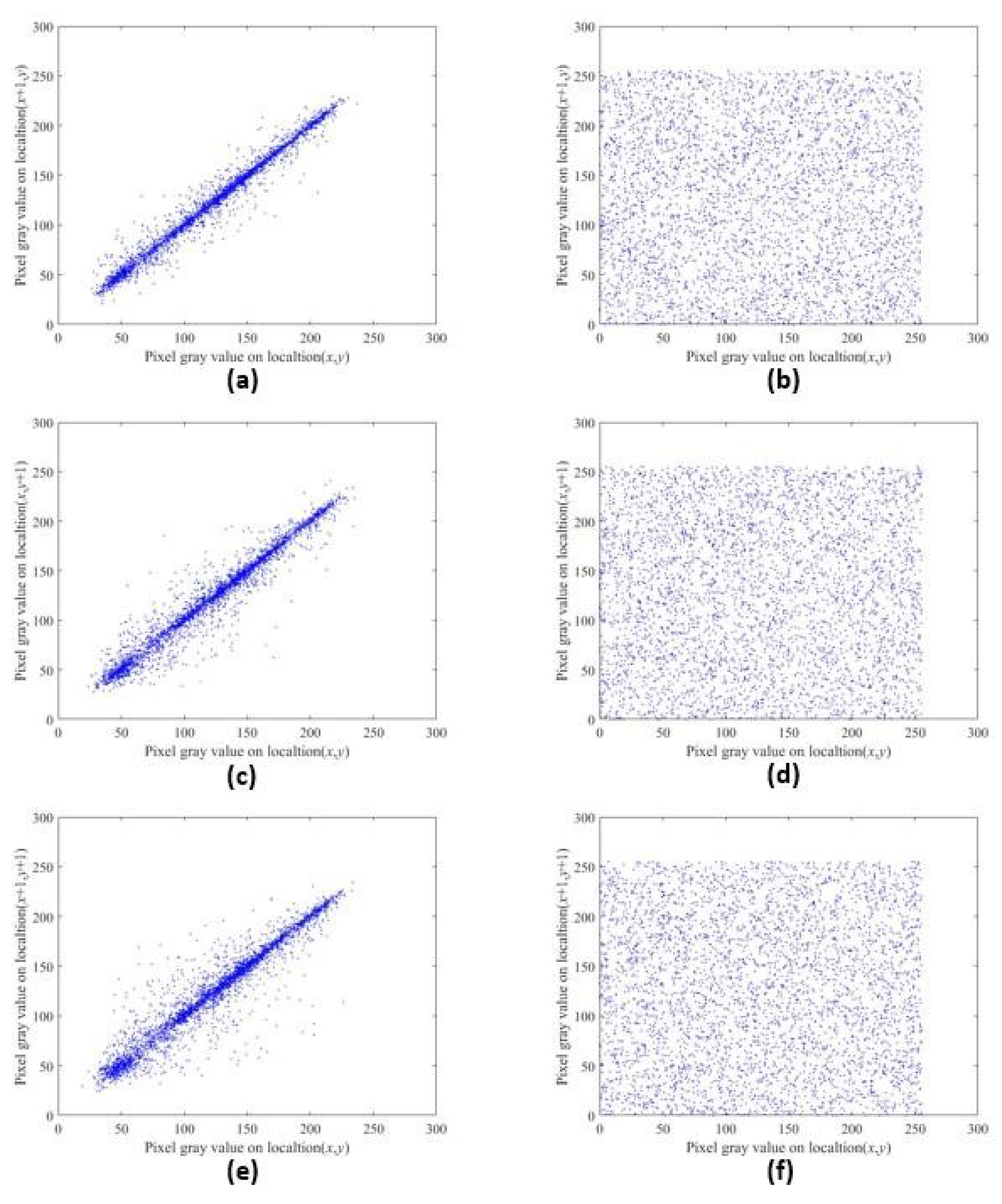

| Horizontal | Vertical | Diagonal | |
|---|---|---|---|
| Lena | 0.9874 | 0.9973 | 0.9662 |
| Encrypted Lena | 0.0009 | −0.0006 | 0.0007 |
| Cameraman | 0.9606 | 0.9355 | 0.9001 |
| Encrypted Cameraman | 0.0181 | 0.0004 | −0.0024 |
| Horizontal | Vertical | Diagonal | |
|---|---|---|---|
| Lena | 0.9874 | 0.9973 | 0.9662 |
| Encrypted Lena | 0.0009 | −0.0006 | 0.0007 |
| [34] | 0.0008 | 0.0015 | 0.0032 |
| [19] | 0.0024 | −0.0086 | 0.0402 |
| [35] | 0.0030 | −0.0024 | −0.0013 |
| Index | Lena | Cameraman | 4.1.01 | Theoretical Value |
|---|---|---|---|---|
| NPCR | 99.6078 | 99.5575 | 99.6307 | 99.6094 |
| UACI | 33.4404 | 33.4058 | 33.4920 | 33.4635 |
| BACI | 26.7386 | 26.8189 | 26.6824 | 26.7712 |
| NPCR | UACI | |
|---|---|---|
| Ours | 99.6078 | 33.4404 |
| [34] | 99.6262 | 33.4384 |
| [37] | 99.8214 | 33.4636 |
| [38] | 99.5727 | 33.4838 |
| Information Entropy | |
|---|---|
| Lena | 7.4486 |
| Encrypted Lena | 7.9970 |
| Cameraman | 7.1048 |
| Encrypted Cameraman | 7.9974 |
| 4.1.01 | 6.8981 |
| Encrypted 4.1.01 | 7.9973 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, W.; Li, S.; He, J.; Ma, Y. A Novel Image-Encryption Scheme Based on a Non-Linear Cross-Coupled Hyperchaotic System with the Dynamic Correlation of Plaintext Pixels. Entropy 2020, 22, 779. https://doi.org/10.3390/e22070779
Hou W, Li S, He J, Ma Y. A Novel Image-Encryption Scheme Based on a Non-Linear Cross-Coupled Hyperchaotic System with the Dynamic Correlation of Plaintext Pixels. Entropy. 2020; 22(7):779. https://doi.org/10.3390/e22070779
Chicago/Turabian StyleHou, Wenjin, Shouliang Li, Jiapeng He, and Yide Ma. 2020. "A Novel Image-Encryption Scheme Based on a Non-Linear Cross-Coupled Hyperchaotic System with the Dynamic Correlation of Plaintext Pixels" Entropy 22, no. 7: 779. https://doi.org/10.3390/e22070779
APA StyleHou, W., Li, S., He, J., & Ma, Y. (2020). A Novel Image-Encryption Scheme Based on a Non-Linear Cross-Coupled Hyperchaotic System with the Dynamic Correlation of Plaintext Pixels. Entropy, 22(7), 779. https://doi.org/10.3390/e22070779







