A New Belief Entropy in Dempster–Shafer Theory Based on Basic Probability Assignment and the Frame of Discernment
Abstract
:1. Introduction
2. Preliminaries
2.1. D-S Theory
2.1.1. Basic Belief Assignment
2.1.2. Belief Function
2.1.3. Plausibility Function
2.1.4. Dempster’s Combination Rule
2.2. Origin of Information Entropy
2.2.1. Hartley Measure
2.2.2. Shannon Entropy
3. Properties of the Uncertainty Measure in D-S Theory
3.1. Non-Negativity
3.2. Maximum Entropy
3.3. Monotonicity
3.4. Probability Consistency
3.5. Additivity
3.6. Sub-Additivity
3.7. Range
4. The Development of Entropy Based on D-S Theory
5. A New Belief Entropy Based on Evidence Theory
6. Numerical Example and Simulation
6.1. Numerical Example
6.1.1. Example 1
6.1.2. Example 2
6.1.3. Example 3
6.1.4. Example 4
6.1.5. Example 5
6.1.6. Example 6
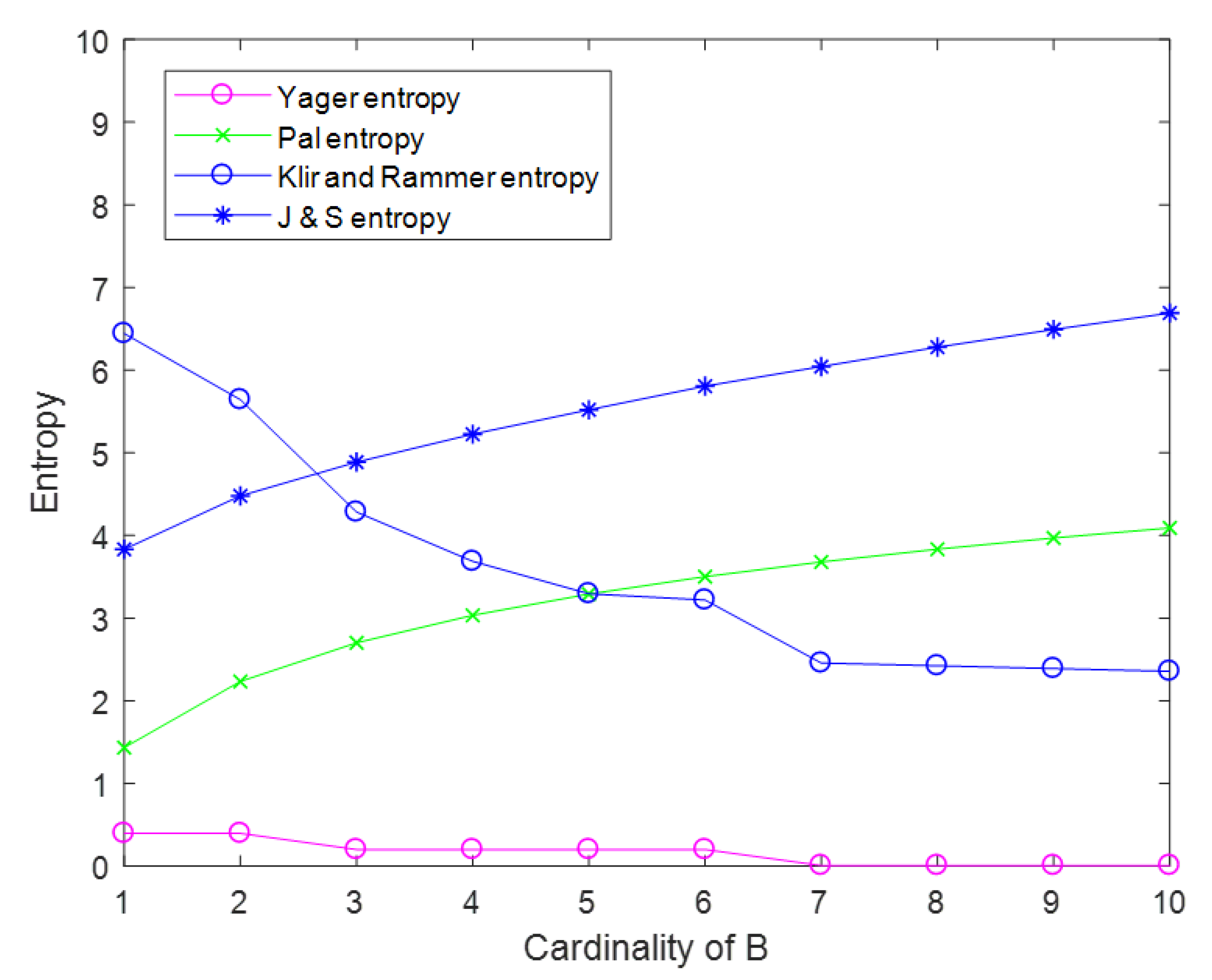
6.1.7. Example Summary
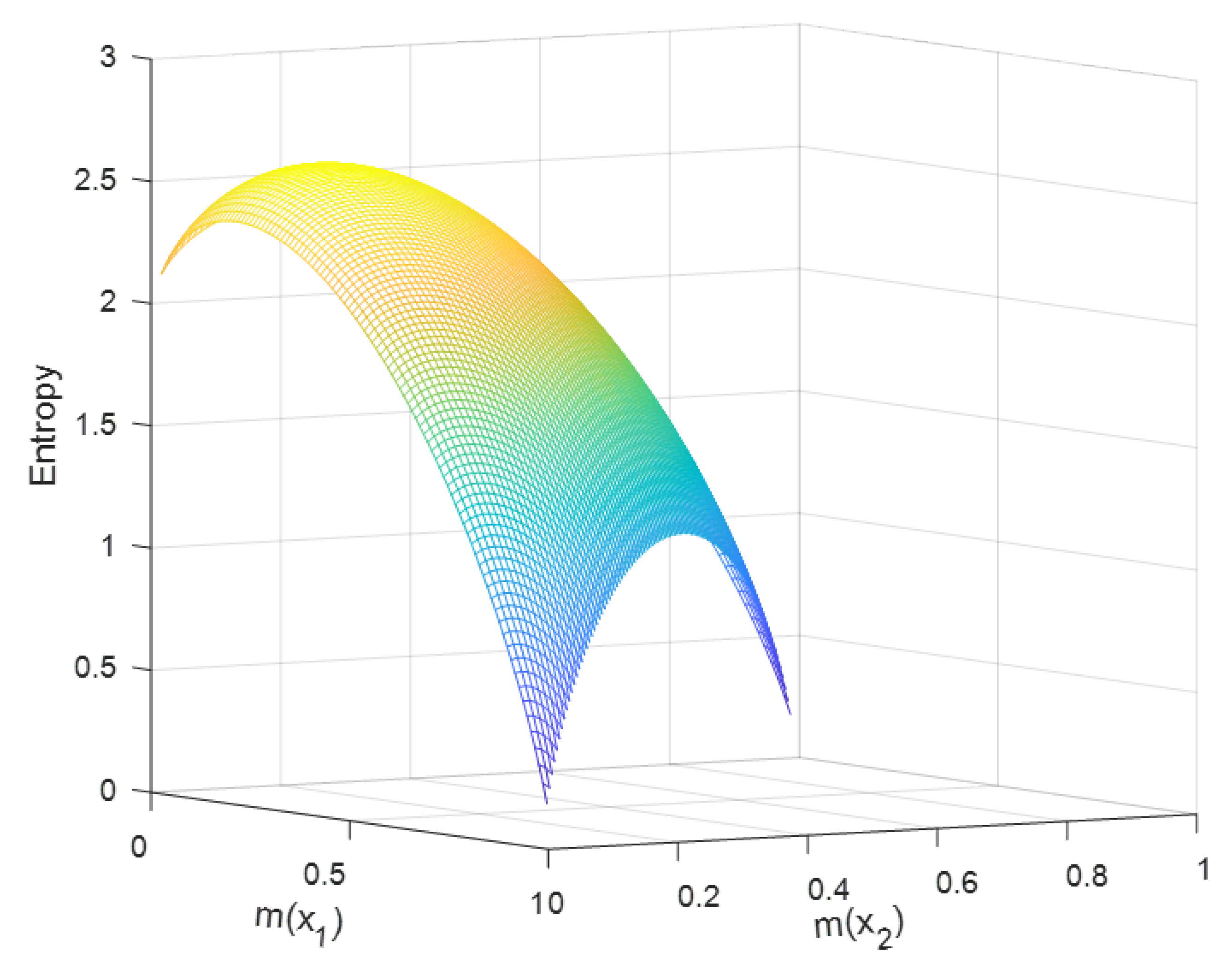
6.2. Simulation
7. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 2. [Google Scholar]
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. In Classic Works of the Dempster–Shafer Theory of Belief Functions; Springer: Berlin, Germany, 2008; pp. 57–72. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; Volume 42. [Google Scholar]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Deng, Y. Generalized evidence theory. Appl. Intell. 2015, 43, 530–543. [Google Scholar] [CrossRef] [Green Version]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers, and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Quan, W.; Huang, W. A new approach to construct similarity measure for intuitionistic fuzzy sets. Soft Comput. 2019, 23, 1985–1998. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L.; Li, Z.; Ding, L. Improved fuzzy Bayesian network-based risk analysis with interval-valued fuzzy sets and DS evidence theory. In IEEE Transactions on Fuzzy Systems; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Düğenci, M. A new distance measure for interval valued intuitionistic fuzzy sets and its application to group decision making problems with incomplete weights information. Appl. Soft Comput. 2016, 41, 120–134. [Google Scholar] [CrossRef]
- Liu, Q.; Tian, Y.; Kang, B. Derive knowledge of Z-number from the perspective of Dempster–Shafer evidence theory. Eng. Appl. Artif. Intell. 2019, 85, 754–764. [Google Scholar] [CrossRef]
- Jiang, W.; Cao, Y.; Deng, X. A novel Z-network model based on Bayesian network and Z-number. In IEEE Transactions on Fuzzy Systems; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Deng, Y. D numbers: theory and applications. J. Inf. Comput. Sci. 2012, 9, 2421–2428. [Google Scholar]
- Liu, B.; Deng, Y. Risk Evaluation in Failure Mode and Effects Analysis Based on D Numbers Theory. Int. J. Comput. Commun. Control 2019, 14, 672–691. [Google Scholar]
- Deng, X.; Jiang, W. Evaluating green supply chain management practices under fuzzy environment: a novel method based on D number theory. Int. J. Fuzzy Syst. 2019, 21, 1389–1402. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, Y. Performer Selection in Human Reliability Analysis: D numbers Approach. Int. J. Comput. Commun. Control 2019, 14, 437–452. [Google Scholar] [CrossRef] [Green Version]
- George, T.; Pal, N.R. Quantification of conflict in Dempster–Shafer framework: a new approach. Int. J. Gen. Syst. 1996, 24, 407–423. [Google Scholar] [CrossRef]
- Sabahi, F.; Akbarzadeh-T, M.R. A qualified description of extended fuzzy logic. Inf. Sci. 2013, 244, 60–74. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Y.; Zhou, D. An improved genetic algorithm with initial population strategy for symmetric TSP. Math. Probl. Eng. 2015, 2015, 212794. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Han, D. A new distance-based total uncertainty measure in the theory of belief functions. Knowl.-Based Syst. 2016, 94, 114–123. [Google Scholar] [CrossRef]
- Sabahi, F.; Akbarzadeh-T, M.R. Introducing validity in fuzzy probability for judicial decision-making. Int. J. Approx. Reason. 2014, 55, 1383–1403. [Google Scholar] [CrossRef]
- Deng, Y. Fuzzy analytical hierarchy process based on canonical representation on fuzzy numbers. J. Comput. Anal. Appl. 2017, 22, 201–228. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Hartley, R.V. Transmission of information 1. Bell Syst. Tech. J. 1928, 7, 535–563. [Google Scholar] [CrossRef]
- Hohle, U. Entropy with respect to plausibility measures. In Proceedings of the 12th IEEE International Symposium on Multiple-Valued Logic, Paris, France, 25–26 May 1982. [Google Scholar]
- Nguyen, H.T. On entropy of random sets and possibility distributions. Anal. Fuzzy Inf. 1987, 1, 145–156. [Google Scholar]
- Dubois, D.; Prade, H. Properties of measures of information in evidence and possibility theories. Fuzzy Sets Syst. 1987, 24, 161–182. [Google Scholar] [CrossRef]
- Klir, G.J.; Ramer, A. Uncertainty in the Dempster–Shafer theory: a critical re-examination. Int. J. Gen. Syst. 1990, 18, 155–166. [Google Scholar] [CrossRef]
- Jiroušek, R.; Shenoy, P.P. A new definition of entropy of belief functions in the Dempster–Shafer theory. Int. J. Approx. Reason. 2018, 92, 49–65. [Google Scholar] [CrossRef] [Green Version]
- Pal, N.R.; Bezdek, J.C.; Hemasinha, R. Uncertainty measures for evidential reasoning I: A review. Int. J. Approx. Reason. 1992, 7, 165–183. [Google Scholar] [CrossRef] [Green Version]
- Pal, N.R.; Bezdek, J.C.; Hemasinha, R. Uncertainty measures for evidential reasoning II: A new measure of total uncertainty. Int. J. Approx. Reason. 1993, 8, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y. Deng entropy. Chaos Solitons Fractals 2016, 91, 549–553. [Google Scholar] [CrossRef]
- Pan, L.; Deng, Y. A new belief entropy to measure uncertainty of basic probability assignments based on belief function and plausibility function. Entropy 2018, 20, 842. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Gao, J.; Wei, D. A New Belief Entropy Based on Deng Entropy. Entropy 2019, 21, 987. [Google Scholar] [CrossRef] [Green Version]
- Frikha, A.; Moalla, H. Analytic hierarchy process for multi-sensor data fusion based on belief function theory. Eur. J. Oper. Res. 2015, 241, 133–147. [Google Scholar] [CrossRef]
- Khodabandeh, M.; Shahri, A.M. Uncertainty evaluation for a Dezert–Smarandache theory-based localization problem. Int. J. Gen. Syst. 2014, 43, 610–632. [Google Scholar] [CrossRef]
- Zhou, D.; Tang, Y.; Jiang, W. A modified belief entropy in Dempster–Shafer framework. PLoS ONE 2017, 12, e0176832. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Zhou, D.; He, Z.; Xu, S. An improved belief entropy–based uncertainty management approach for sensor data fusion. Int. J. Distrib. Sens. Networks 2017, 13, 1550147717718497. [Google Scholar] [CrossRef]
- Denoeux, T. A k-nearest neighbor classification rule based on Dempster–Shafer theory. In Classic Works of the Dempster–Shafer Theory of Belief Functions; Springer: Berlin, Germany, 2008; pp. 737–760. [Google Scholar]
- Liu, Z.G.; Pan, Q.; Dezert, J. A new belief-based K-nearest neighbor classification method. Pattern Recognit. 2013, 46, 834–844. [Google Scholar] [CrossRef]
- Ma, J.; Liu, W.; Miller, P.; Zhou, H. An evidential fusion approach for gender profiling. Inf. Sci. 2016, 333, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.G.; Pan, Q.; Dezert, J.; Mercier, G. Credal classification rule for uncertain data based on belief functions. Pattern Recognit. 2014, 47, 2532–2541. [Google Scholar] [CrossRef]
- Han, D.; Liu, W.; Dezert, J.; Yang, Y. A novel approach to pre-extracting support vectors based on the theory of belief functions. Knowl.-Based Syst. 2016, 110, 210–223. [Google Scholar] [CrossRef]
- Liu, Z.G.; Pan, Q.; Dezert, J.; Martin, A. Adaptive imputation of missing values for incomplete pattern classification. Pattern Recognit. 2016, 52, 85–95. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Wei, B.; Xie, C.; Zhou, D. An evidential sensor fusion method in fault diagnosis. Adv. Mech. Eng. 2016, 8, 1687814016641820. [Google Scholar] [CrossRef] [Green Version]
- Yuan, K.; Xiao, F.; Fei, L.; Kang, B.; Deng, Y. Modeling sensor reliability in fault diagnosis based on evidence theory. Sensors 2016, 16, 113. [Google Scholar] [CrossRef] [Green Version]
- Yuan, K.; Xiao, F.; Fei, L.; Kang, B.; Deng, Y. Conflict management based on belief function entropy in sensor fusion. SpringerPlus 2016, 5, 638. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Xie, C.; Zhuang, M.; Shou, Y.; Tang, Y. Sensor data fusion with z-numbers and its application in fault diagnosis. Sensors 2016, 16, 1509. [Google Scholar] [CrossRef] [PubMed]
- Yager, R.R.; Liu, L. Classic Works of the Dempster–Shafer Theory of Belief Functions; Springer: Berlin, Germany, 2008; Volume 219. [Google Scholar]
- Liu, Z.G.; Pan, Q.; Dezert, J.; Mercier, G. Credal c-means clustering method based on belief functions. Knowl.-Based Syst. 2015, 74, 119–132. [Google Scholar] [CrossRef]
- Yager, R.R.; Alajlan, N. Decision making with ordinal payoffs under Dempster–Shafer type uncertainty. Int. J. Intell. Syst. 2013, 28, 1039–1053. [Google Scholar] [CrossRef]
- Merigó, J.M.; Casanovas, M. Induced aggregation operators in decision making with the Dempster–Shafer belief structure. Int. J. Intell. Syst. 2009, 24, 934–954. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.M.; Elhag, T.M. A comparison of neural network, evidential reasoning and multiple regression analysis in modelling bridge risks. Expert Syst. Appl. 2007, 32, 336–348. [Google Scholar] [CrossRef]
- Su, X.; Deng, Y.; Mahadevan, S.; Bao, Q. An improved method for risk evaluation in failure modes and effects analysis of aircraft engine rotor blades. Eng. Fail. Anal. 2012, 26, 164–174. [Google Scholar] [CrossRef]
- Fu, C.; Yang, J.B.; Yang, S.L. A group evidential reasoning approach based on expert reliability. Eur. J. Oper. Res. 2015, 246, 886–893. [Google Scholar] [CrossRef]
- Zhang, X.; Mahadevan, S.; Deng, X. Reliability analysis with linguistic data: An evidential network approach. Reliab. Eng. Syst. Saf. 2017, 162, 111–121. [Google Scholar] [CrossRef]
- Yager, R.R. Arithmetic and other operations on Dempster–Shafer structures. Int. J. Man-Mach. Stud. 1986, 25, 357–366. [Google Scholar] [CrossRef]
- Li, Y.; Deng, Y. Intuitionistic evidence sets. IEEE Access 2019, 7, 106417–106426. [Google Scholar] [CrossRef]
- Song, Y.; Deng, Y. Divergence measure of belief function and its application in data fusion. IEEE Access 2019, 7, 107465–107472. [Google Scholar] [CrossRef]
- Klir, G.J.; Wierman, M.J. Uncertainty-Based Information: Elements of Generalized Information Theory; Springer: Berlin, Germany, 2013; Volume 15. [Google Scholar]
- Klir, G.; Folger, T. Fuzzy Sets, Uncertainty, and Information; Prentice Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Yager, R.R. Entropy and specificity in a mathematical theory of evidence. Int. J. Gen. Syst. 1983, 9, 249–260. [Google Scholar] [CrossRef]
- Lamata, M.T.; Moral, S. Measures of entropy in the theory of evidence. Int. J. Gen. Syst. 1988, 14, 297–305. [Google Scholar] [CrossRef]
- Jousselme, A.L.; Liu, C.; Grenier, D.; Bossé, É. Measuring ambiguity in the evidence theory. In IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans; IEEE: Piscataway, NJ, USA, 2006; Volume 36, pp. 890–903. [Google Scholar]
- Smets, P. Constructing the Pignistic Probability Function in a Context of Uncertainty. UAI 1989, 89, 29–40. [Google Scholar]
- Abellán, J. Analyzing properties of Deng entropy in the theory of evidence. Chaos Solitons Fractals 2017, 95, 195–199. [Google Scholar] [CrossRef]



| Cases | Dubois Entropy | Deng Entropy | Pan–Deng Entropy | New Entropy |
|---|---|---|---|---|
| 0.4114 | 2.6623 | 16.1443 | 5.1363 | |
| 1.2114 | 3.9303 | 17.4916 | 13.1363 | |
| 1.6794 | 4.9082 | 19.8608 | 17.8160 | |
| 2.0114 | 5.7878 | 20.8229 | 21.1363 | |
| 2.2690 | 6.6256 | 21.8314 | 23.7118 | |
| 2.4794 | 7.4441 | 22.7521 | 25.8160 | |
| 2.6573 | 8.2532 | 24.1331 | 27.5952 | |
| 2.8114 | 9.0578 | 25.0685 | 29.1363 | |
| 2.9474 | 9.8600 | 26.0212 | 30.4957 | |
| 3.0690 | 10.6612 | 27.1947 | 31.7118 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Pan, Q. A New Belief Entropy in Dempster–Shafer Theory Based on Basic Probability Assignment and the Frame of Discernment. Entropy 2020, 22, 691. https://doi.org/10.3390/e22060691
Li J, Pan Q. A New Belief Entropy in Dempster–Shafer Theory Based on Basic Probability Assignment and the Frame of Discernment. Entropy. 2020; 22(6):691. https://doi.org/10.3390/e22060691
Chicago/Turabian StyleLi, Jiapeng, and Qian Pan. 2020. "A New Belief Entropy in Dempster–Shafer Theory Based on Basic Probability Assignment and the Frame of Discernment" Entropy 22, no. 6: 691. https://doi.org/10.3390/e22060691
APA StyleLi, J., & Pan, Q. (2020). A New Belief Entropy in Dempster–Shafer Theory Based on Basic Probability Assignment and the Frame of Discernment. Entropy, 22(6), 691. https://doi.org/10.3390/e22060691





