Time Evolution Features of Entropy Generation Rate in Turbulent Rayleigh-Bénard Convection with Mixed Insulating and Conducting Boundary Conditions
Abstract
1. Introduction
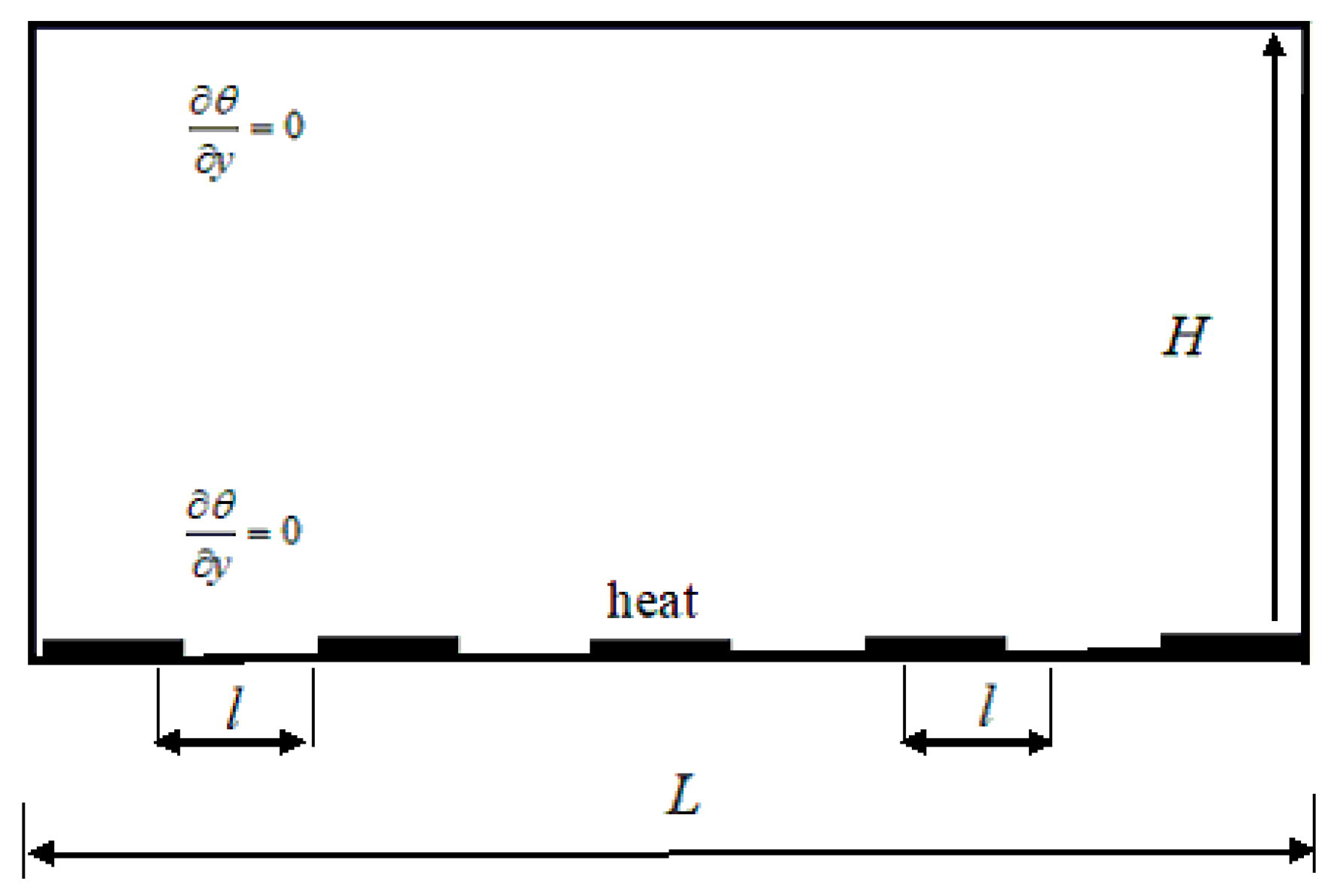
2. Convection Diffusion Equation and Numerical Method
2.1. Convection Diffusion Equation of Thermal Fluid
2.2. Numerical Method for Convection Diffusion Equation of Thermal Fluid
3. Results and Discussions
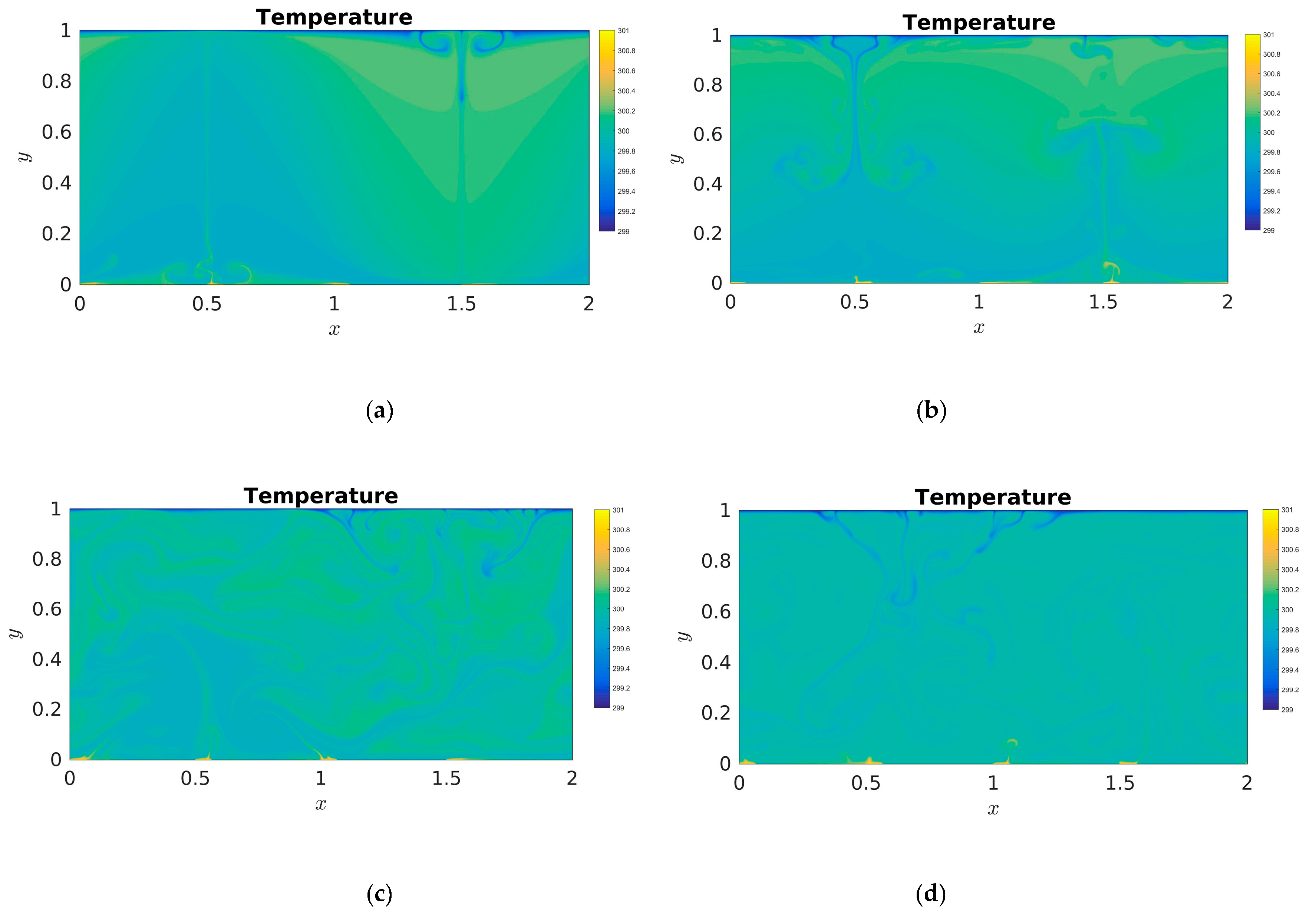
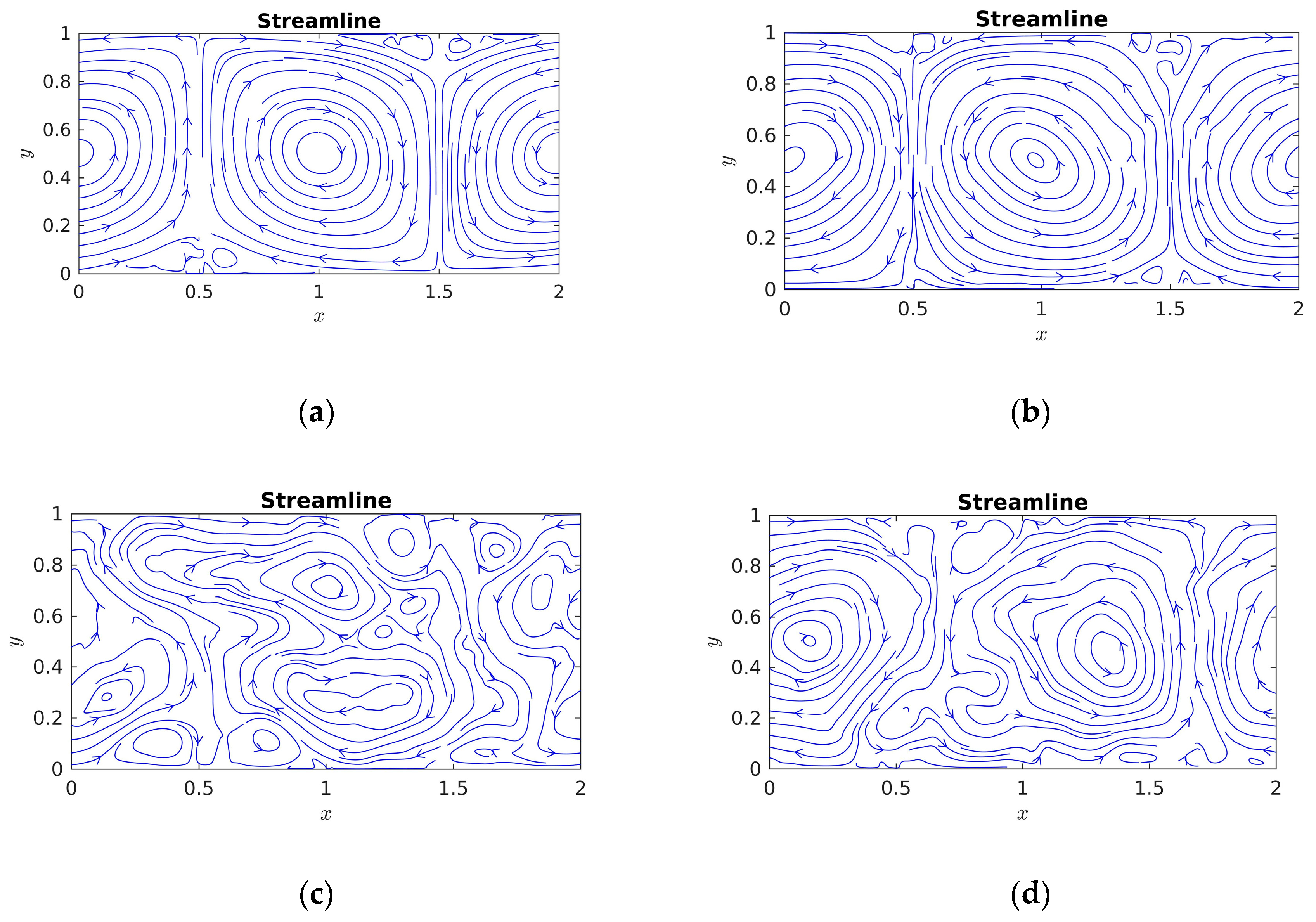
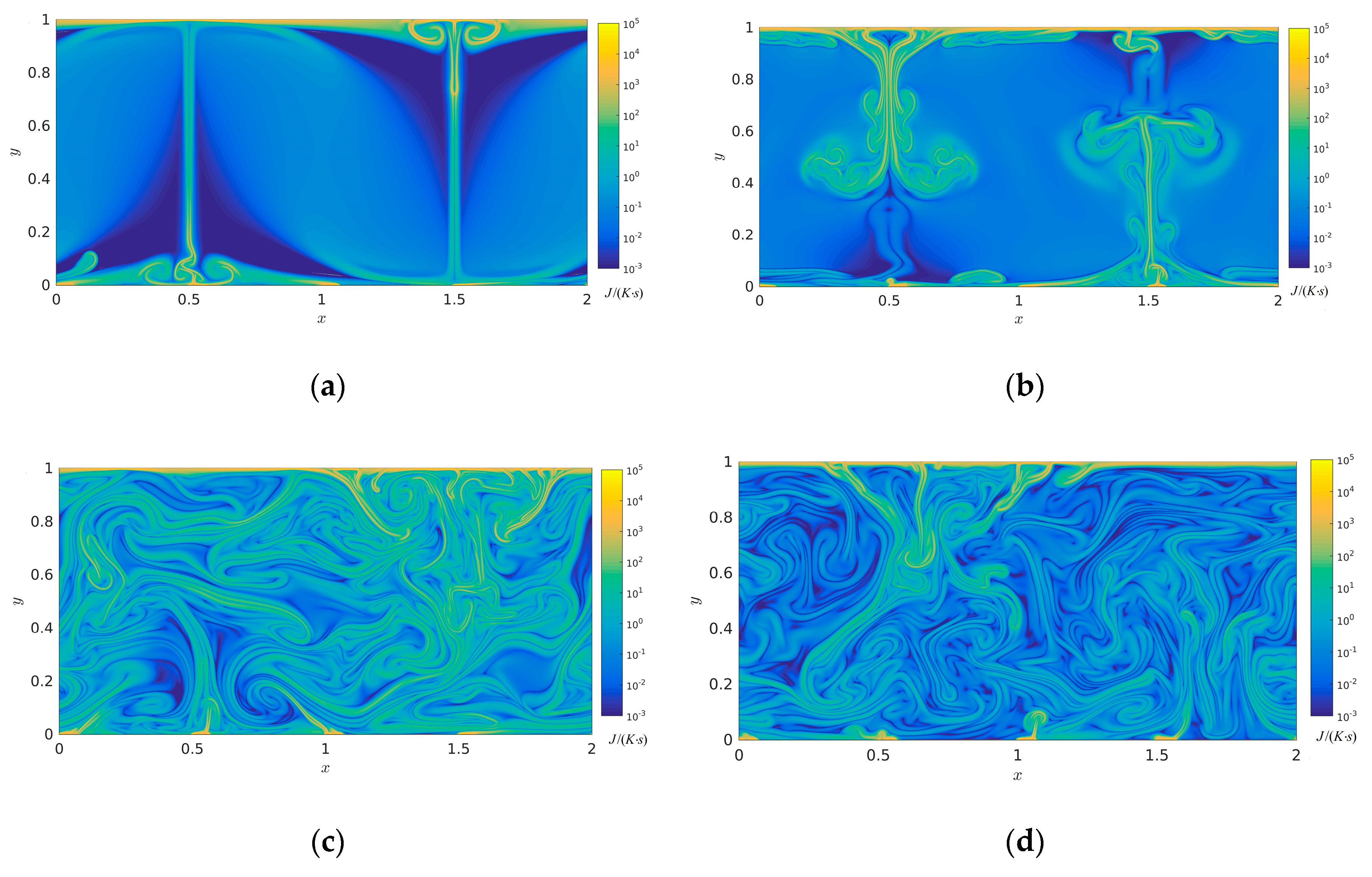
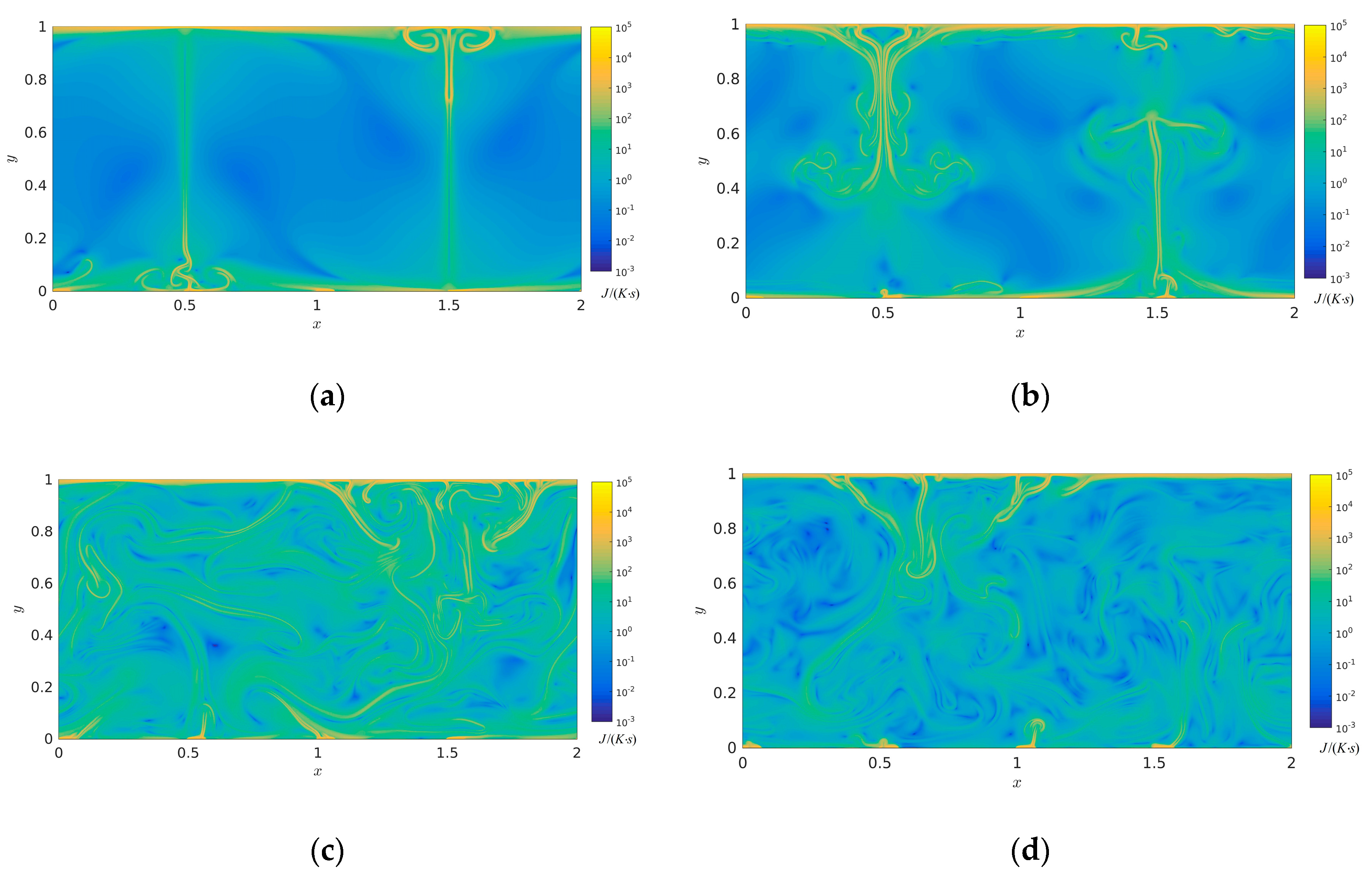
3.1. Analysis of Flow and Temperature Field
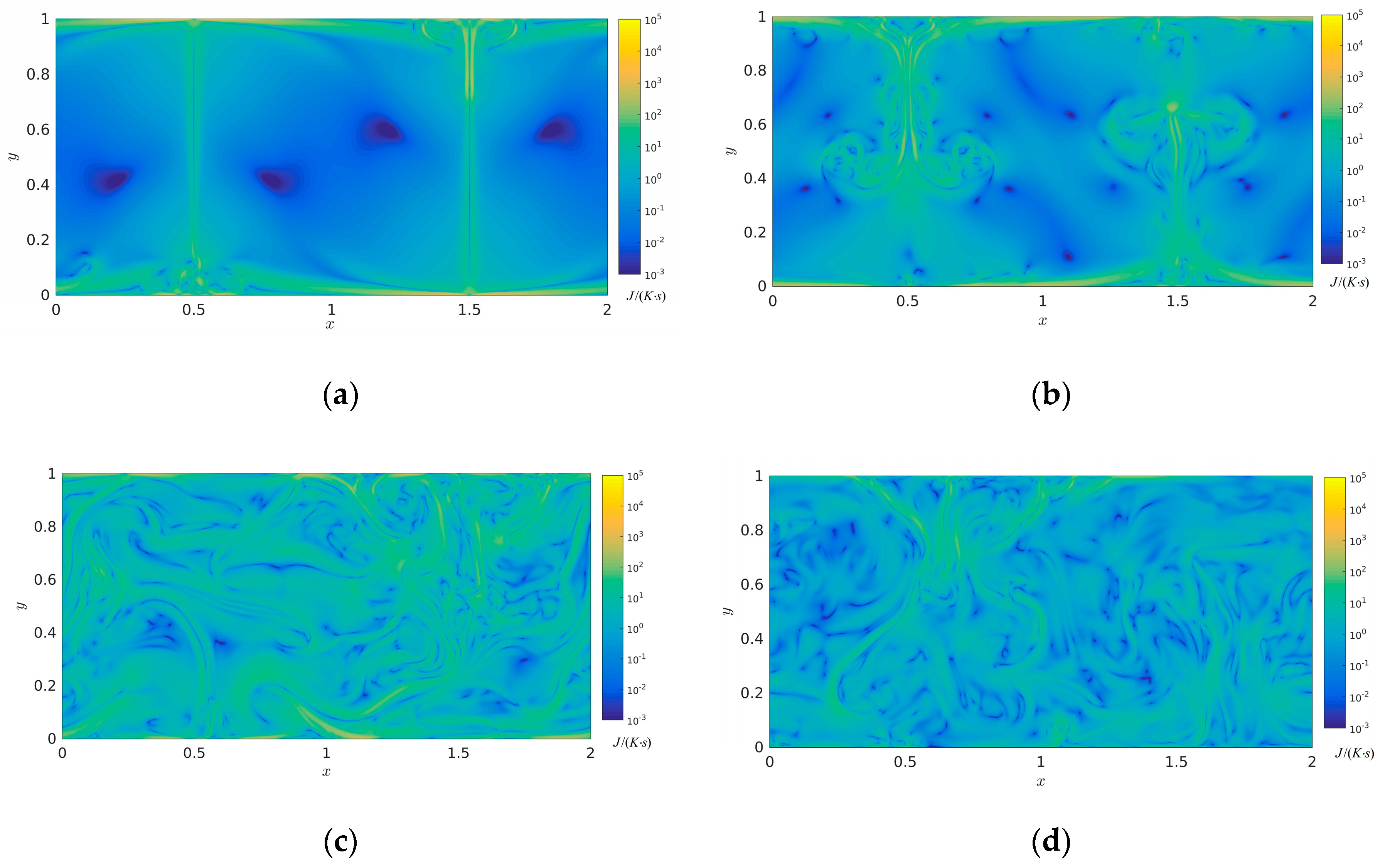
3.2. Analysis of Entropy Generation Rate
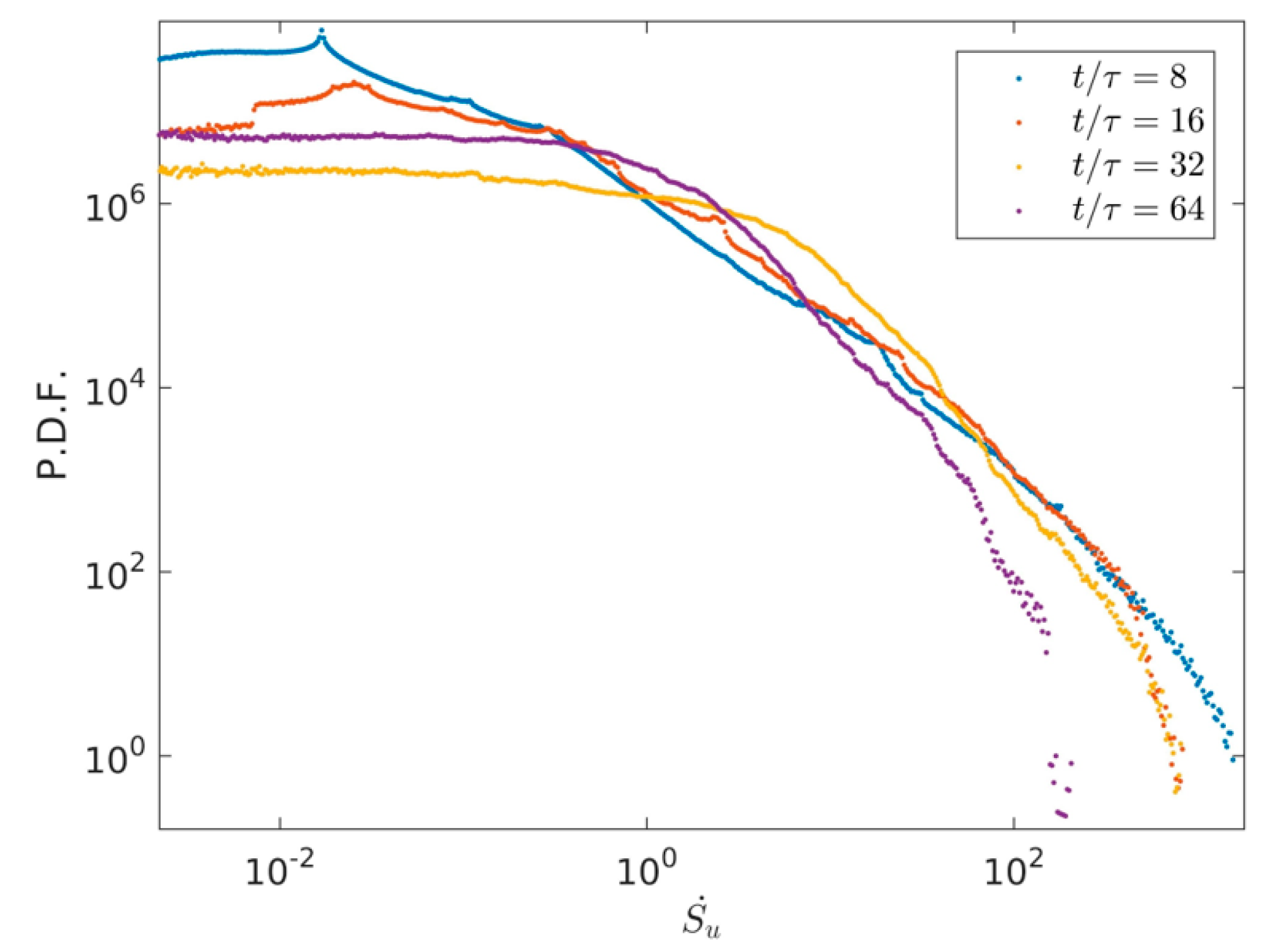
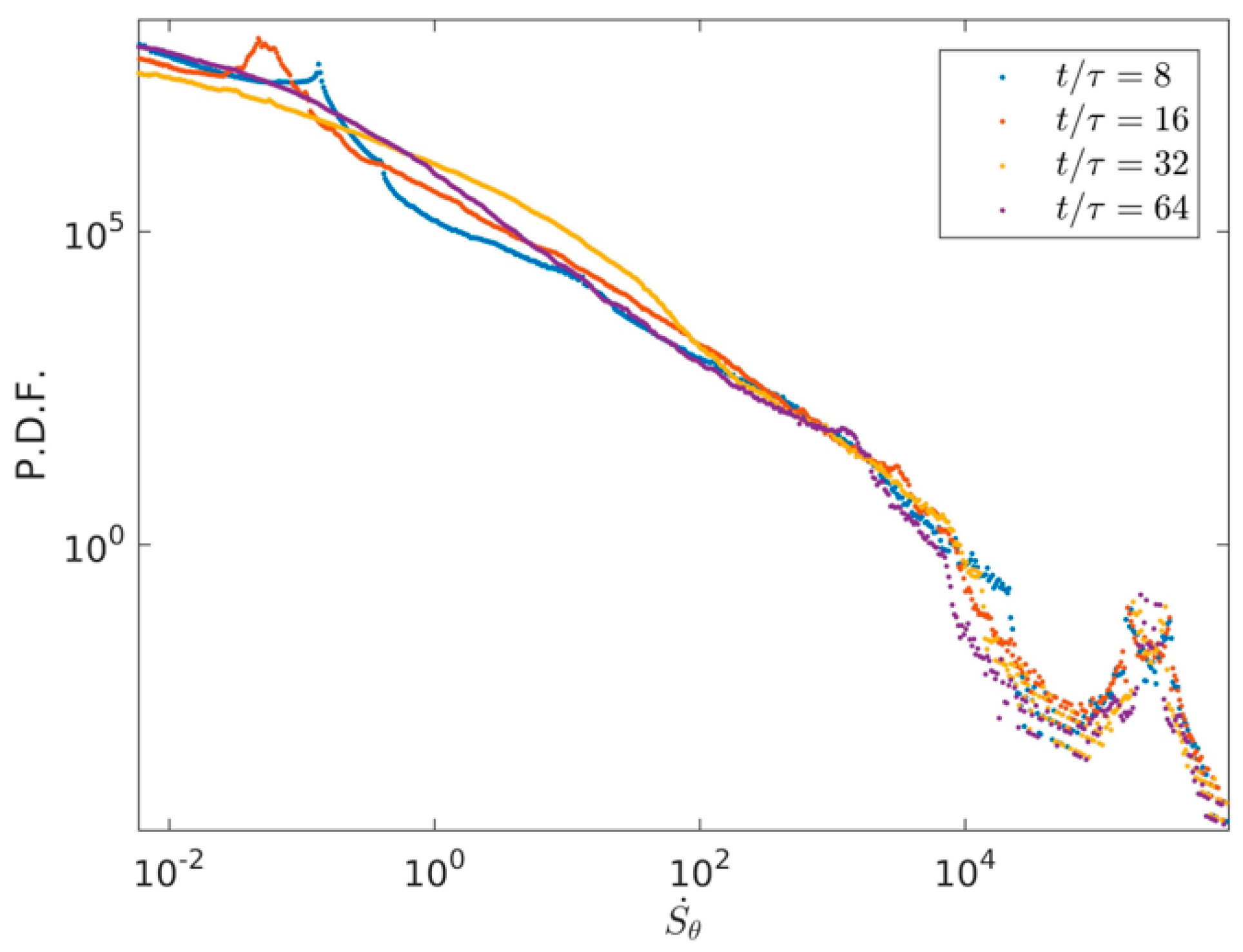
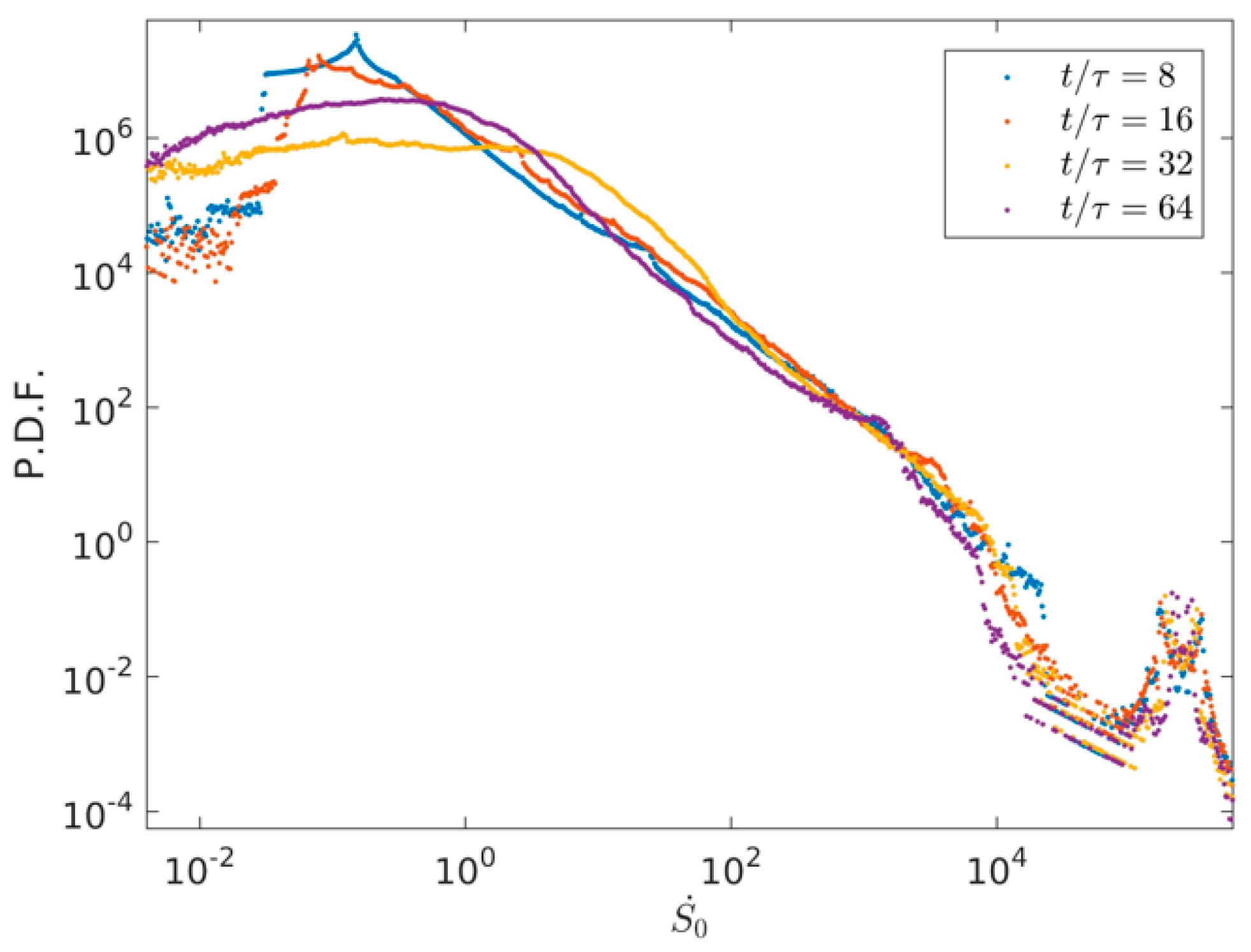
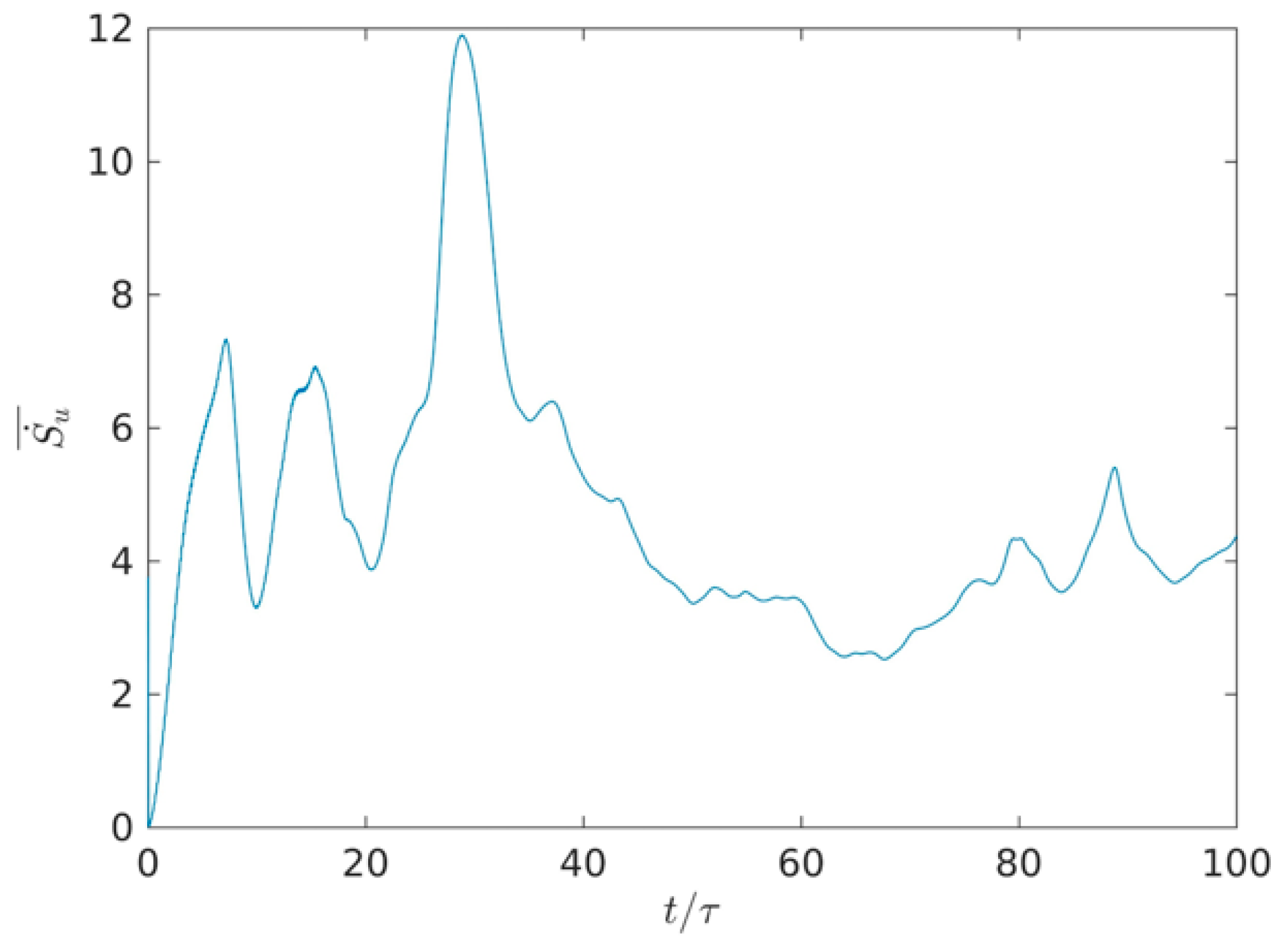
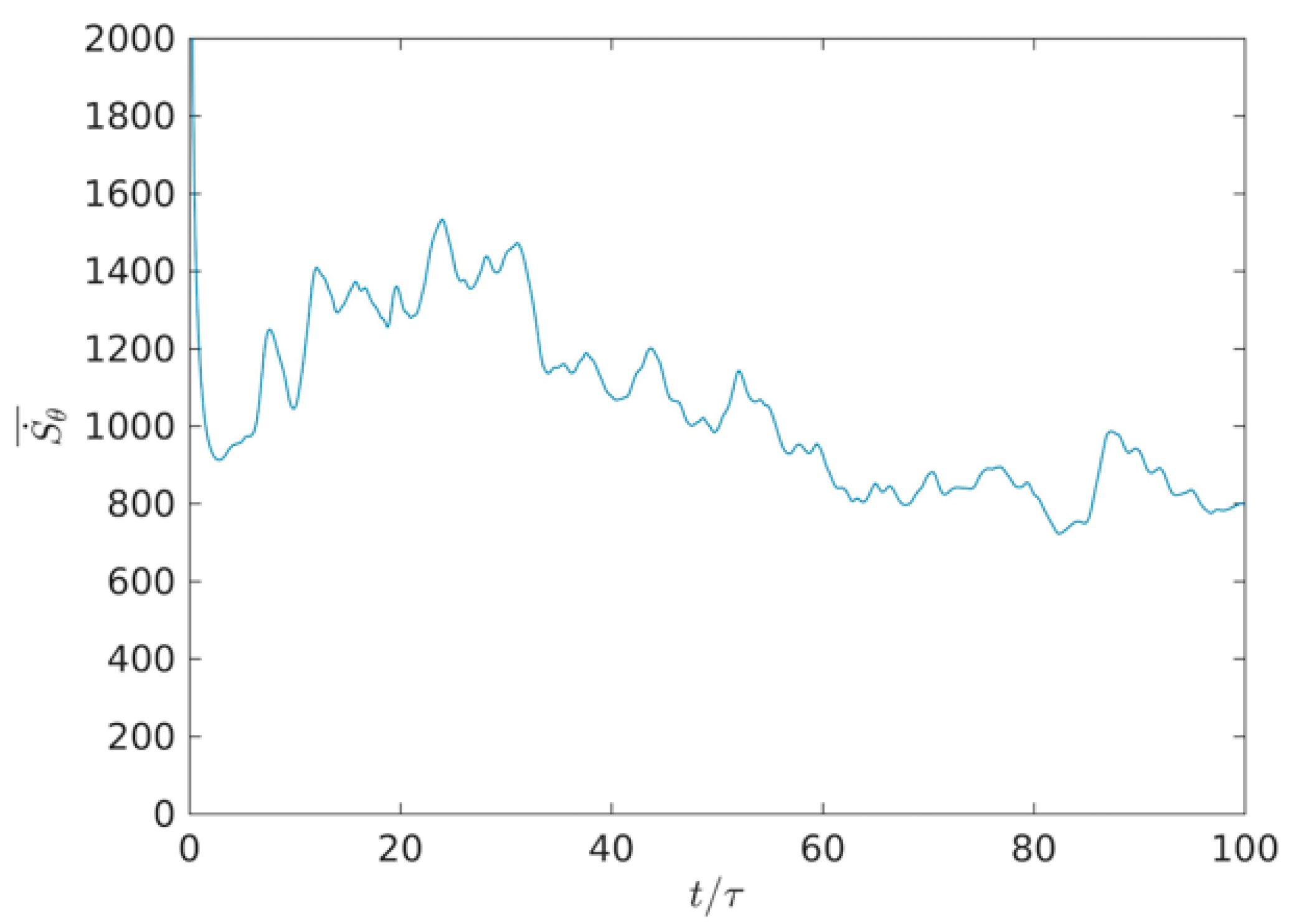
3.3. Quantitative Analysis of Entropy Generation Rate with Time Evolution
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lage, J.L.; Lim, J.S.; Bejan, A. Natural convection with radiation in a cavity with open top end. J. Heat Transf. 1992, 114, 479–486. [Google Scholar] [CrossRef]
- Xu, F.; Saha, S.C. Transition to an unsteady flow induced by a fin on the sidewall of a differentially heated air-filled square cavity and heat transfer. Int. J. Heat Mass Transf. 2014, 71, 236–244. [Google Scholar] [CrossRef]
- Nelson, J.E.B.; Balakrishnan, A.R.; Murthy, S.S. Experiments on stratified chilled-water tanks. Int. J. Refrig. 1999, 22, 216–234. [Google Scholar] [CrossRef]
- Ampofo, F.; Karayiannis, T.G. Experimental benchmark data for turbulent natural convection in an air filled square cavity. Int. J. Heat. Mass Transf. 2003, 19, 3551–3572. [Google Scholar] [CrossRef]
- Adeyinka, O.B.; Naterer, G.F. Experimental uncertainty of measured entropy production with pulsed laser PIV and planar laser induced fluorescence. Appl. Ther. Eng. 2005, 48, 1450–1461. [Google Scholar] [CrossRef]
- Lohse, D.; Xia, K.Q. Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 2010, 42, 335–364. [Google Scholar] [CrossRef]
- Xu, F.; Patterson, J.C.; Lei, C. On the double-layer structure of the thermal boundary layer in a differentially heated cavity. Int. J. Heat Mass Transf. 2008, 51, 3803–3815. [Google Scholar] [CrossRef]
- Ahlers, G.; Grossmann, S.; Lohse, D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection. Rev. Mod. Phys. 2009, 81, 503–537. [Google Scholar] [CrossRef]
- Sun, C.; Zhou, Q.; Xia, K.Q. Cascades of velocity and temperature fluctuations in buoyancy-driven thermal turbulence. Phys. Rev. Lett. 2006, 97, 144504–144509. [Google Scholar] [CrossRef] [PubMed]
- Bailon-Cuba, J.; Emran, M.S.; Schumacher, J. Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 2010, 655, 152–173. [Google Scholar] [CrossRef]
- Scheel, J.D.; Kim, E.; White, K.R. Thermal and viscous boundary layers in turbulent Rayleigh-Benard convection. J. Fluid Mech. 2012, 711, 281–305. [Google Scholar] [CrossRef]
- Zhou, Q.; Xia, K.Q. Physical and geometrical properties of thermal plumes in turbulent Rayleigh-Bénard convection. New J. Phys. 2012, 12, 075006–075018. [Google Scholar] [CrossRef]
- Shi, N.; Emran, M.S.; Schumacher, J. Boundary layer structure in turbulent Rayleigh-Benard convection. J. Fluid Mech. 2012, 706, 5–33. [Google Scholar] [CrossRef]
- Shishkina, O.; Stevens, R.A.J.M.; Grossmann, S.; Lohse, D. Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 2010, 12, 075022. [Google Scholar] [CrossRef]
- Shishkina, O.; Wagner, C. Analysis of sheet like thermal plumes in turbulent Rayleigh-Bénard convection. J. Fluid Mech. 2012, 599, 383–404. [Google Scholar] [CrossRef]
- Lami, P.A.K.; Praka, K.A. A numerical study on natural convection and entropy generation in a porous enclosure with heat sources. Int. J. Heat Mass Transf. 2014, 69, 390–407. [Google Scholar] [CrossRef]
- Zahmatkesh, I. On the importance of thermal boundary conditions in heat transfer and entropy generation for natural convection inside a porous enclosure. Int. J. Therm. Sci. 2008, 47, 339–346. [Google Scholar] [CrossRef]
- Andreozzi, A.; Auletta, A.; Manca, O. Entropy generation in natural convection in a symmetrically and uniformly heated vertical channel. Int. J. Heat Mass Transf. 2006, 49, 3221–3228. [Google Scholar] [CrossRef]
- Dagtekin, I.; Oztop, H.F.; Bahloul, A. Entropy generation for natural convection in Γ-shaped enclosures. Int. Commun. Heat Mass Transf. 2007, 34, 502–510. [Google Scholar] [CrossRef]
- Kaczorowski, M.; Wagner, C. Analysis of the thermal plumes in turbulent Rayleigh-Bénard convection based on well-resolved numerical simulations. J. Fluid Mech. 2011, 618, 89–112. [Google Scholar] [CrossRef]
- Usman, M.; Soomro, F.A.; Haq, R.U.; Wang, W.; Defterli, O. Thermal and velocity slip effects on Casson nanofluid flow over an inclined permeable stretching cylinder via collocation method. Int. J. Heat Mass Transf. 2018, 122, 1255–1263. [Google Scholar] [CrossRef]
- Wang, Z.D.; Qian, Y.H. Numerical study on entropy generation in thermal convection with differentially discrete heat boundary conditions. Entropy 2018, 20, 351. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Verda, V.; Sciubba, E. Entropy generation analysis as a design tool—A review. Renew. Sustain. Energy Rev. 2015, 43, 1167–1181. [Google Scholar] [CrossRef]
- Wei, Y.K.; Wang, Z.D.; Qian, Y.H. A numerical study on entropy generation in two-dimensional Rayleigh-Bénard convection at different Prandtl number. Entropy 2017, 19, 443. [Google Scholar] [CrossRef]
- Jin, Y. Second-law analysis: A powerful tool for analyzing Computational Fluid Dynamics results. Entropy 2017, 19, 679. [Google Scholar] [CrossRef]
- Pizzolato, A.; Sciacovelli, A.; Verda, V. Transient local entropy generation analysis for the design improvement of a thermocline thermal energy storage. Appl. Therm. Eng. 2016, 101, 622–629. [Google Scholar] [CrossRef]
- Rejane, D.C.; Mario, H.; Copetti, J.B. Entropy generation and natural convection in rectangular cavities. Appl. Therm. Eng. 2009, 29, 1417–1425. [Google Scholar]
- Mahian, O.; Kianifar, A.; Pop, I. A review on entropy generation in nanofluid flow. Int. J. Heat Mass Transf. 2013, 65, 514–532. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Rashidi, M.M. Entropy generation with nonlinear thermal radiation in MHD boundary layer flow over a permeable shrinking/stretching sheet: Numerical solution. J. Nanofluids 2016, 5, 543–554. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of Entropy Generation in the Flow of Peristaltic Nanofluids in Channels with Compliant Walls. Entropy 2016, 18, 90. [Google Scholar] [CrossRef]
- Lun, Y.X.; Lin, L.M.; He, H.J.; Zhu, Z.C.; Wei, Y.K. Effects of Vortex Structure on Performance Characteristics of a Multiblade Fan with Inclined tongue. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019, 233, 1007–1021. [Google Scholar] [CrossRef]
- Zheng, X.; Lin, Z.; Xu, B.Y. Thermal conductivity and sorption performance of nano-silver powder/FAPO-34 composite fin. Appl. Therm. Eng. 2019, 160, 114055–114063. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, Z.X.; Liu, Q.; Li, Y. Fluidization characteristics of particles in a groove induced by horizontal air flow. Powder Technol. 2020, 363, 442–447. [Google Scholar] [CrossRef]
- Yang, H.; Yu, P.Q.; Xu, J.; Zhu, Z.C. Experimental investigations on the performance and noise characteristics of a forward-curved fan with the stepped tongue. Meas. Control 2019, 52, 1480–1488. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, X.P.; Zhu, Z.C. Partitioning effect on natural convection in a circular enclosure with an asymmetrically placed inclined plate. Int. Commun. Heat Mass Transf. 2018, 90, 11–22. [Google Scholar] [CrossRef]
- Xu, H.; Cantwell, C.D.; Monteserin, C.; Eskilsson, A.P.; Engsig-Karup, A.P.; Sherwin, S.J. Spectral/hp element methods: Recent developments, applications, and perspectives. J. Hydrodyn. 2018, 30, 1–22. [Google Scholar] [CrossRef]
- Liu, H.H.; Valocch, A.J.; Zhang, Y.H.; Kang, Q.J. Lattice Boltzmann Phase Field Modeling Thermocapillary Flows in a Confined Microchannel. J. Comput. Phys. 2014, 256, 334–356. [Google Scholar] [CrossRef]
- Shan, X. Simulation of Rayleigh-Bénard convection using a lattice Boltzmann method. Phys. Rev. E 1997, 55, 2780–2788. [Google Scholar] [CrossRef]
- Liang, H.; Xu, J.; Chai, Z.H.; Shi, B.C. Lattice boltzmann modeling of wall-bounded ternary fluid flows. Appl. Math. Model. 2019, 73, 487–513. [Google Scholar] [CrossRef]
- Wei, Y.K.; Wang, Z.D.; Yang, J.F.; Dou, H.S.; Qian, Y.H. Simulation of natural convection heat transfer in an enclosure at different Rayleigh number using lattice Boltzmann method. Comput. Fluids 2016, 124, 30–38. [Google Scholar] [CrossRef]
- Wei, Y.K.; Wang, Z.D.; Dou, H.S.; Qian, Y.H. A novel two-dimensional coupled lattice Boltzmann model for incompressible flow in application of turbulence Rayleigh-Taylor instability. Comput. Fluids 2017, 156, 97–102. [Google Scholar] [CrossRef]
- Chen, S.Y.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Wang, Z.D.; Wei, Y.; Qian, Y.H. A bounce back-immersed boundary-lattice Boltzmann model for curved boundary. Appl. Math. Model. 2020, 81, 428–440. [Google Scholar] [CrossRef]
- Chen, Z.; Shu, C. Simplified lattice Boltzmann method for non-Newtonian power-law fluid flows. Int. J. Numer. Methods Fluids 2020, 92, 38–54. [Google Scholar] [CrossRef]
- Mohamed, K.; Ismai, T.; Mohamed, R.E. A new analytical solution of longitudinal fin with variable heat generation and thermal conductivity using DRA. Eur. Phys. J. Plus 2020, 135, 120–129. [Google Scholar]
- Nawel, B.; Mohamed, K.; Ismai, T.; Mohamed, R.E. On numerical and analytical solutions for mixed convection Falkner-Skan flow of nanofluids with variable thermal conductivity. Waves Random Complex Media 2019, 1–19. [Google Scholar] [CrossRef]
- Mohamed, R.E. Effects of NP Shapes on Non-Newtonian Bio-Nanofluid Flow in Suction/Blowing Process with Convective Condition: Sisko Model. J. Non-Equilib. Thermodyn. 2020, 45, 97–108. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Shen, P.; Wang, Z.; Liang, H.; Qian, Y. Time Evolution Features of Entropy Generation Rate in Turbulent Rayleigh-Bénard Convection with Mixed Insulating and Conducting Boundary Conditions. Entropy 2020, 22, 672. https://doi.org/10.3390/e22060672
Wei Y, Shen P, Wang Z, Liang H, Qian Y. Time Evolution Features of Entropy Generation Rate in Turbulent Rayleigh-Bénard Convection with Mixed Insulating and Conducting Boundary Conditions. Entropy. 2020; 22(6):672. https://doi.org/10.3390/e22060672
Chicago/Turabian StyleWei, Yikun, Pingping Shen, Zhengdao Wang, Hong Liang, and Yuehong Qian. 2020. "Time Evolution Features of Entropy Generation Rate in Turbulent Rayleigh-Bénard Convection with Mixed Insulating and Conducting Boundary Conditions" Entropy 22, no. 6: 672. https://doi.org/10.3390/e22060672
APA StyleWei, Y., Shen, P., Wang, Z., Liang, H., & Qian, Y. (2020). Time Evolution Features of Entropy Generation Rate in Turbulent Rayleigh-Bénard Convection with Mixed Insulating and Conducting Boundary Conditions. Entropy, 22(6), 672. https://doi.org/10.3390/e22060672




