Entropy Wake Law for Streamwise Velocity Profiles in Smooth Rectangular Open Channels
Abstract
1. Introduction
2. Experimental Set-Up
3. The Proposed Model
3.1. Shannon’s Entropy-Based Velocity Distribution
3.2. A New Entropy-Wake Law
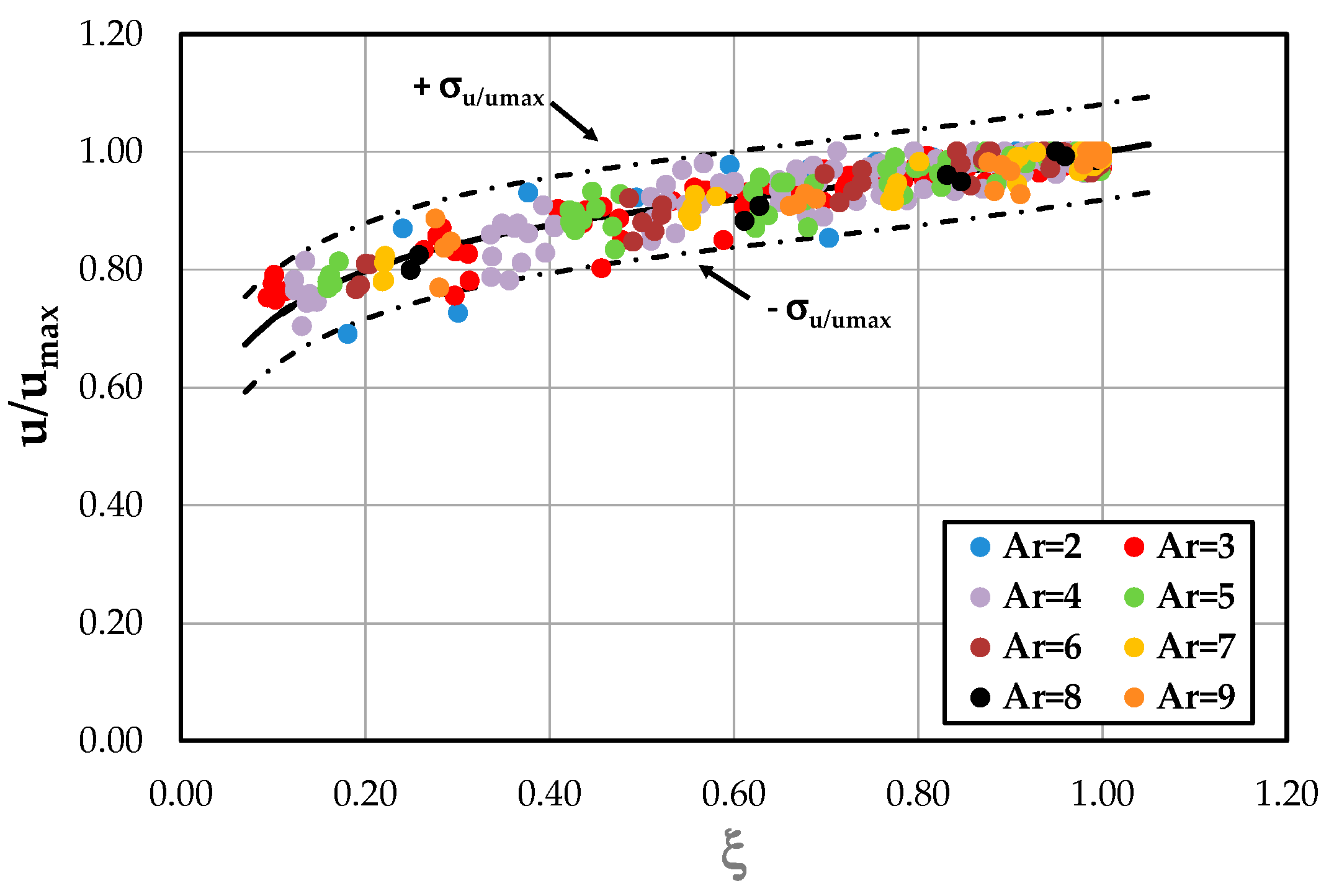
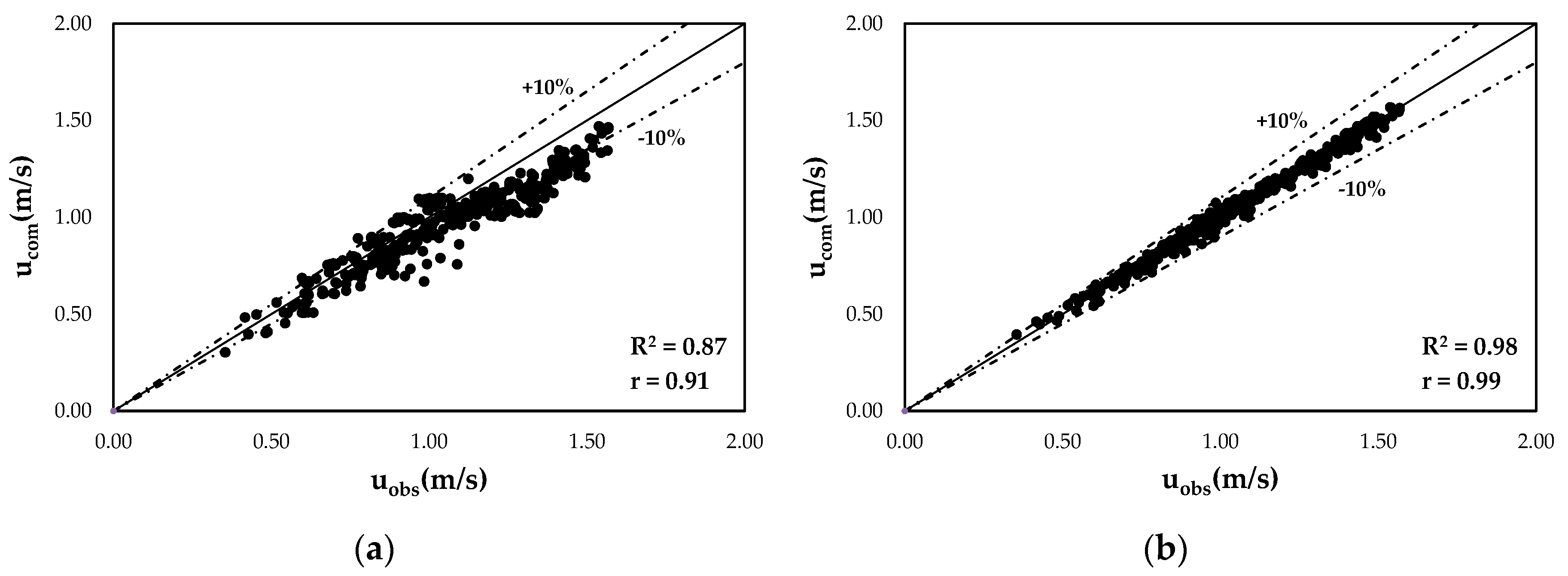
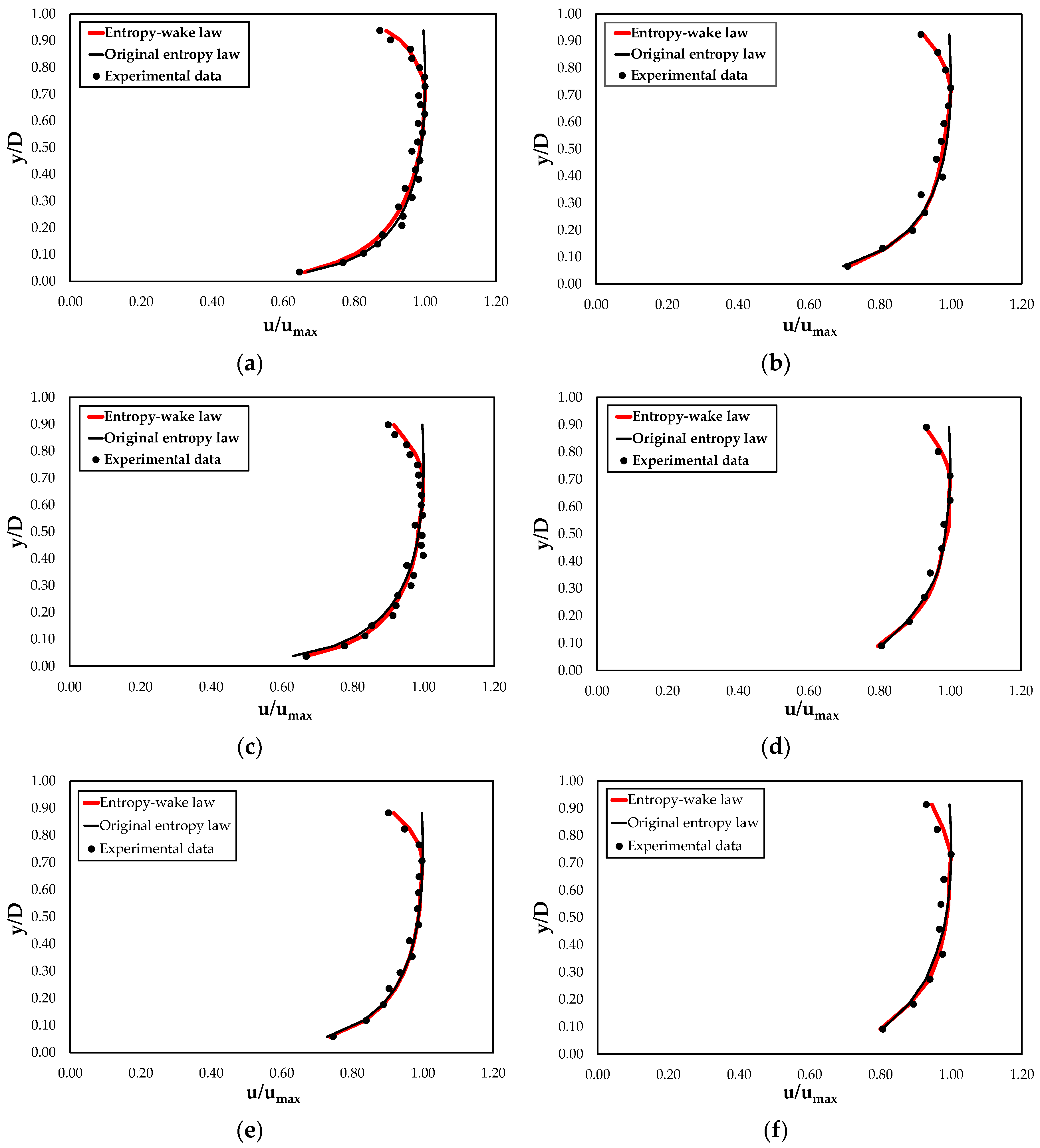
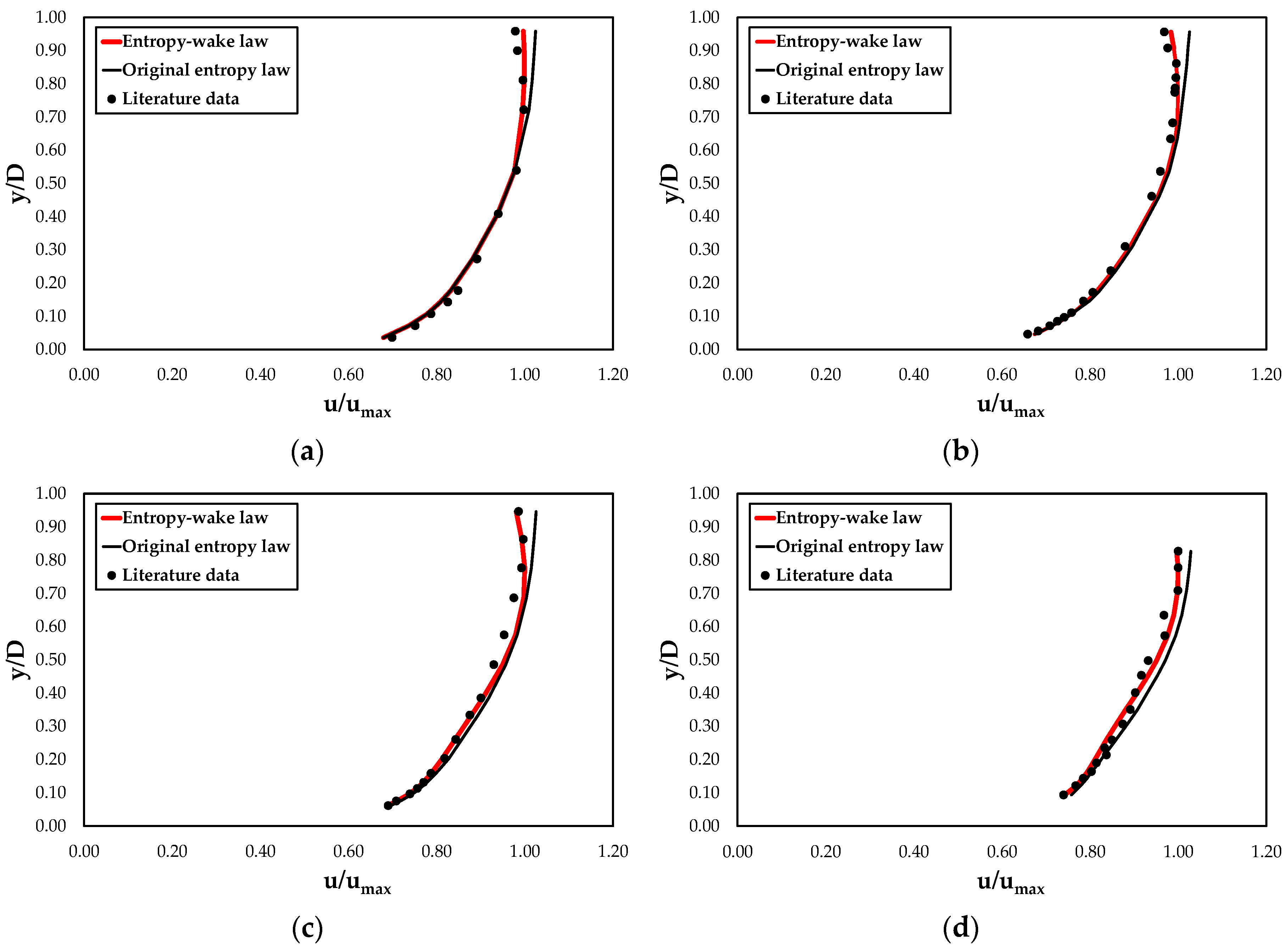
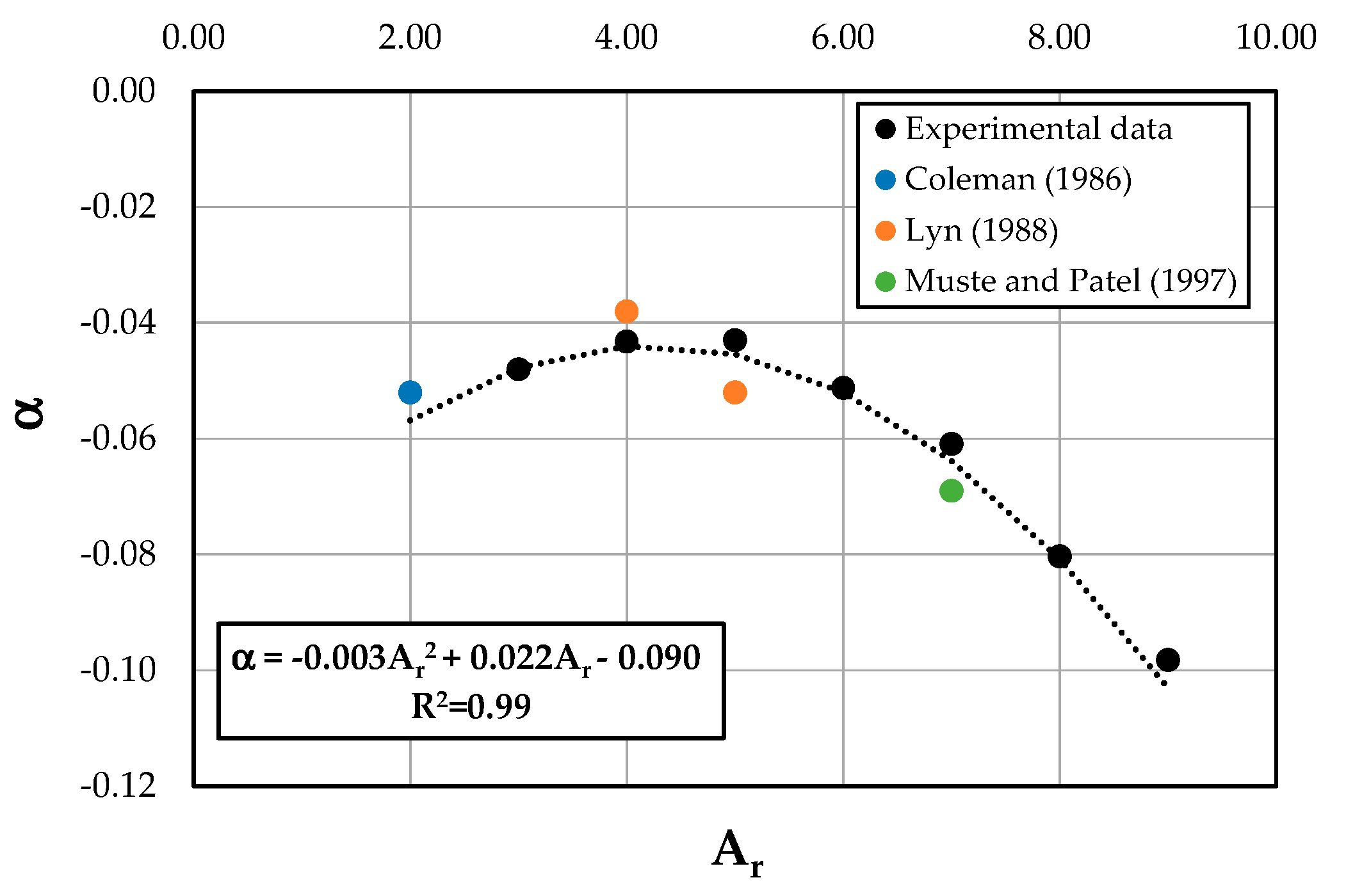
4. Discussion of Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Afzalimehr, H.; Anctil, F. Velocity distribution and shear velocity behaviour of decelerating flows over a gravel bed. Can. J. Civ. Eng. 1999, 26, 468–475. [Google Scholar] [CrossRef]
- Lee, J.S.; Julien, P.Y. Electromagnetic Wave Surface Velocimetry. J. Hydraul. Eng. 2006, 132, 146–153. [Google Scholar] [CrossRef]
- Binesh, N.; Bonakdari, H. Longitudinal Velocity Distribution in Compound Open Channels: Comparison of Different Mathematical Models. Int. Res. J. Appl. Basic Sci. 2014, 8, 1149–1157. [Google Scholar]
- Han, Y.; Yang, S.-Q.; Dharmasiri, N.; Sivakumar, M. Effects of sample size and concentration of seeding in LDA measurements on the velocity bias in open channel flow. Flow Meas. Instrum. 2014, 38, 92–97. [Google Scholar] [CrossRef]
- Stoesser, T.; McSherry, R.; Fraga, B. Secondary currents and turbulence over a non-uniformly roughened open-channel bed. Water 2015, 7, 4896–4913. [Google Scholar] [CrossRef]
- Schneider, J.M.; Rickenmann, D.; Turowski, J.M.; Kirchner, J.W. Self-adjustment of stream bed roughness and flow velocity in a steep mountain channel. Water Resour. Res. 2015, 51, 7838–7859. [Google Scholar] [CrossRef]
- Kästner, K.; Hoitink, A.J.F.; Torfs, P.J.J.F.; Vermeulen, B.; Ningsih, N.S.; Pramulya, M. Prerequisites for accurate monitoring of river discharge based on fixed location velocity measurements. Water Resour. Res. 2018, 54, 1058–1076. [Google Scholar] [CrossRef]
- Mirauda, D.; Ostoich, M. Assessment of Pressure Sources and Water Body Resilience: An Integrated Approach for Action Planning in a Polluted River Basin. Int. J. Environ. Res. Public Health 2018, 15, 390. [Google Scholar] [CrossRef]
- Henderson, F.M. Open-Channel Flow; Macmillan Publishing Co., Inc.: New York, NY, USA, 1966. [Google Scholar]
- Nezu, I.; Rodi, W. Open-channel flow measurements with a laser doppler anemometer. J. Hydraul. Eng. 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Cardoso, A.H.; Graf, W.H.; Gust, G. Uniform flow in a smooth open channel. J. Hydraul. Res. 1989, 27, 603–616. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H. Turbulence in Open-Channel Flows; Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Mahananda, M.; Hanmaiahgari, P.R.; Ojha, C.S.P.; Balachandar, R. A New Analytical Model for Dip Modified Velocity Distribution in Fully Developed Turbulent Open Channel Flow. Can. J. Civ. Eng. 2019, 46, 657–668. [Google Scholar] [CrossRef]
- Kumbhakar, M.; Ghoshal, K.; Singh, V.P. Two-dimensional distribution of streamwise velocity in open channel flow using maximum entropy principle: Incorporation of additional constraints based on conservation laws. Comput. Methods Appl. Mech. Eng. 2020, 361, 112738. [Google Scholar] [CrossRef]
- Coles, D. The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1956, 1, 191–226. [Google Scholar] [CrossRef]
- Coleman, N.L. Effects of Suspended Sediment on the Open-Channel Velocity Distribution. Water Resour. Res. 1986, 22, 1377–1384. [Google Scholar] [CrossRef]
- Kirkgoz, M.S. Turbulent velocity profiles for smooth and rough open channel flow. J. Hydraul. Eng. 1989, 115, 1543–1561. [Google Scholar] [CrossRef]
- Kironoto, B.A.; Graf, W.H. Turbulence characteristics in rough non-uniform open-channel flow. Proc. Inst. Civ. Eng. Water Marit. Energy 1995, 112, 336–348. [Google Scholar] [CrossRef]
- Sarma, K.V.N.; Prasad, B.V.R.; Sarma, A.K. Detailed study of binary law for open channels. J. Hydraul. Eng. 2000, 126, 210–214. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Yu, M.; Li, D. Velocity profile of sediment suspensions and comparison of log-law and wake-law. J. Hydraul. Res. 2001, 39, 211–217. [Google Scholar] [CrossRef]
- Guo, J.; Julien, P.Y. Modified log-wake law for turbulent flows in smooth pipes. J. Hydraul. Res. 2003, 41, 493–501. [Google Scholar] [CrossRef]
- Guo, J.; Julien, P.Y. Application of the modified log-wake law in open-channels. J. Appl. Fluid Mech. 2008, 1, 17–23. [Google Scholar]
- Guo, J.; Julien, P.Y.; Meroney, R.N. Modified Log-Wake Law in Zero-Pressure-Gradient Turbulent Boundary Layers. J. Hydraul. Res. 2005, 43, 421–430. [Google Scholar] [CrossRef]
- Guo, J. Modified log-wake-law for smooth rectangular open channel flow. J. Hydraul. Res. 2014, 52, 121–128. [Google Scholar] [CrossRef]
- Yang, S.Q.; Tan, S.K.; Lim, S.Y. Velocity distribution and dip-phenomenon in smooth uniform channel flows. J. Hydraul. Eng. 2004, 130, 1179–1186. [Google Scholar] [CrossRef]
- Absi, R. Analytical methods for velocity distribution and dip-phenomenon in narrow open-channel flows. In Environmental Hydraulics Theoretical, Experimental and Computational Solutions, Proceedings of the IWEH: International Workshop on Environmental Hydraulics Theoretical, Experimental and Computational Solutions, Valencia, Spain, 29–30 October 2009; Taylor & Francis: Oxford, UK, 2009; pp. 127–129. [Google Scholar]
- Absi, R. An ordinary differential equation for velocity distribution and dip-phenomenon in open channel flows. J. Hydraul. Res. 2011, 49, 82–89. [Google Scholar] [CrossRef]
- Kundu, S.; Ghoshal, K. An Analytical Model for Velocity Distribution and Dip-Phenomenon in Uniform Open Channel Flows. Int. J. Fluid Mech. Res. 2012, 39, 381–395. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Cheng, N.S. Secondary flows over artificial bed strips. Adv. Water Resour. 2005, 28, 441–450. [Google Scholar] [CrossRef]
- Bonakdari, H.; Larrarte, F.; Lassabatere, L.; Joannis, C. Turbulent velocity profile in fully-developed open channel flows. Environ. Fluid Mech. 2008, 8, 1–17. [Google Scholar] [CrossRef]
- Bonakdari, H. Modélisation des Écoulements en Collecteur d’Assainissement—Application à la Conception de Points de Mesures. Ph.D. Thesis, University of Caen, Basse Normandie, France, 2006. [Google Scholar]
- Larrarte, F. Velocity fields in sewers: An experimental study. Flow Meas. Instrum. 2006, 17, 282–290. [Google Scholar] [CrossRef]
- Lassabatere, L.; Pu, J.H.; Bonakdari, H.; Joannis, C.; Larrarte, F. Velocity distribution in Open Channel Flows: An analytical approach for the outer region. J. Hydraul. Eng. 2013, 139, 37–43. [Google Scholar] [CrossRef]
- Chen, C.L. Unified theory on power laws for flow resistance. J. Hydraul. Eng. 1991, 117, 371–389. [Google Scholar] [CrossRef]
- Landweber, L. Generalization of the logarithmic law of the boundary layer on a flat plate. Schiffstechnik 1957, 4, 110–113. [Google Scholar]
- Rouse, H. Advance Mechanics of Fluids; John Wiley and Sons Inc.: New York, NY, USA, 1959; pp. 346–350. [Google Scholar]
- Hinze, J.O. Turbulence: An Introduction to Its Mechanism and Theory, 2nd ed.; McGraw-Hill Book Company Inc.: New York, NY, USA, 1975. [Google Scholar]
- Karim, M.F.; Kennedy, J.F. Velocity and sediment concentration profiles in river flows. J. Hydraul. Eng. 1987, 113, 159–178. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory, 7th ed.; McGraw-Hill Book Company Inc.: New York, NY, USA, 1979. [Google Scholar]
- Cheng, N.S. Power law index for velocity profiles in open channel flows. Adv. Water Resour. 2007, 30, 1775–1784. [Google Scholar] [CrossRef]
- Afzal, N. Scaling of power law velocity profile in wall-bounded turbulent shear flows. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, NV, USA, 10–13 January 2005; pp. 10067–10078. [Google Scholar]
- Afzal, N.; Seena, A.; Bushra, A. Power law velocity profile in fully developed turbulent pipe and channel flows. J. Hydraul. Eng. 2007, 133, 1080–1086. [Google Scholar] [CrossRef]
- Castro-Orgaz, O. Hydraulics of developing chute flow. J. Hydraul. Res. 2009, 47, 185–194. [Google Scholar] [CrossRef]
- Shannon, C.E. The Mathematical Theory of Communications; Bell System Technical Journal: New York, NY, USA, 1948; Volume 27, pp. 379–423. [Google Scholar]
- Jaynes, E. Information theory and statistical mechanics: I. Phys. Rev. 1957, 106, 620–930. [Google Scholar] [CrossRef]
- Jaynes, E. Information theory and statistical mechanics: II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Jaynes, E. On the rationale of maximum entropy methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and probability concepts in hydraulics. J. Hydraul. Eng. 1987, 113, 583–600. [Google Scholar] [CrossRef]
- Chiu, C.L. Application of entropy concept in open-channel flow study. J. Hydraul. Eng. 1991, 117, 615–628. [Google Scholar] [CrossRef]
- Sterling, M.; Knight, D.W. An attempt at using the entropy approach to predict the transverse distribution of boundary shear stress in open channel flow. Stoch. Environ. Res. Risk Assess. 2002, 16, 127–142. [Google Scholar] [CrossRef]
- Sheikh, Z.; Bonakdari, H. Prediction of boundary shear stress in circular and trapezoidal channels with entropy concept. Urban Water J. 2015, 13, 629–636. [Google Scholar] [CrossRef]
- Kazemian-Kale-Kale, A.; Bonakdari, H.; Gholami, A.; Gharabaghi, B. The uncertainty of the Shannon entropy model for shear stress distribution in circular channels. Int. J. Sediment Res. 2020, 35, 57–68. [Google Scholar] [CrossRef]
- Chiu, C.; Jin, W.; Chen, Y. Mathematical models for distribution of sediment concentration. J. Hydraul. Eng. 2000, 126, 16–23. [Google Scholar] [CrossRef]
- Choo, T.H. An efficient method of the suspended sediment discharge measurement using entropy concept. Water Eng. Res. 2000, 1, 95–105. [Google Scholar]
- Kumbhakar, M.; Ghoshal, K.; Singh, V.P. Derivation of Rouse equation for sediment concentration using Shannon entropy. Phys. A Stat. Mech. Appl. 2017, 465, 494–499. [Google Scholar] [CrossRef]
- Kundu, S. Derivation of Hunt equation for suspension distribution using Shannon entropy theory. Phys. A Stat. Mech. Appl. 2017, 488, 96–111. [Google Scholar] [CrossRef]
- Mirauda, D.; De Vincenzo, A.; Pannone, M. Simplified entropic model for the evaluation of suspended load concentration. Water 2018, 10, 378. [Google Scholar] [CrossRef]
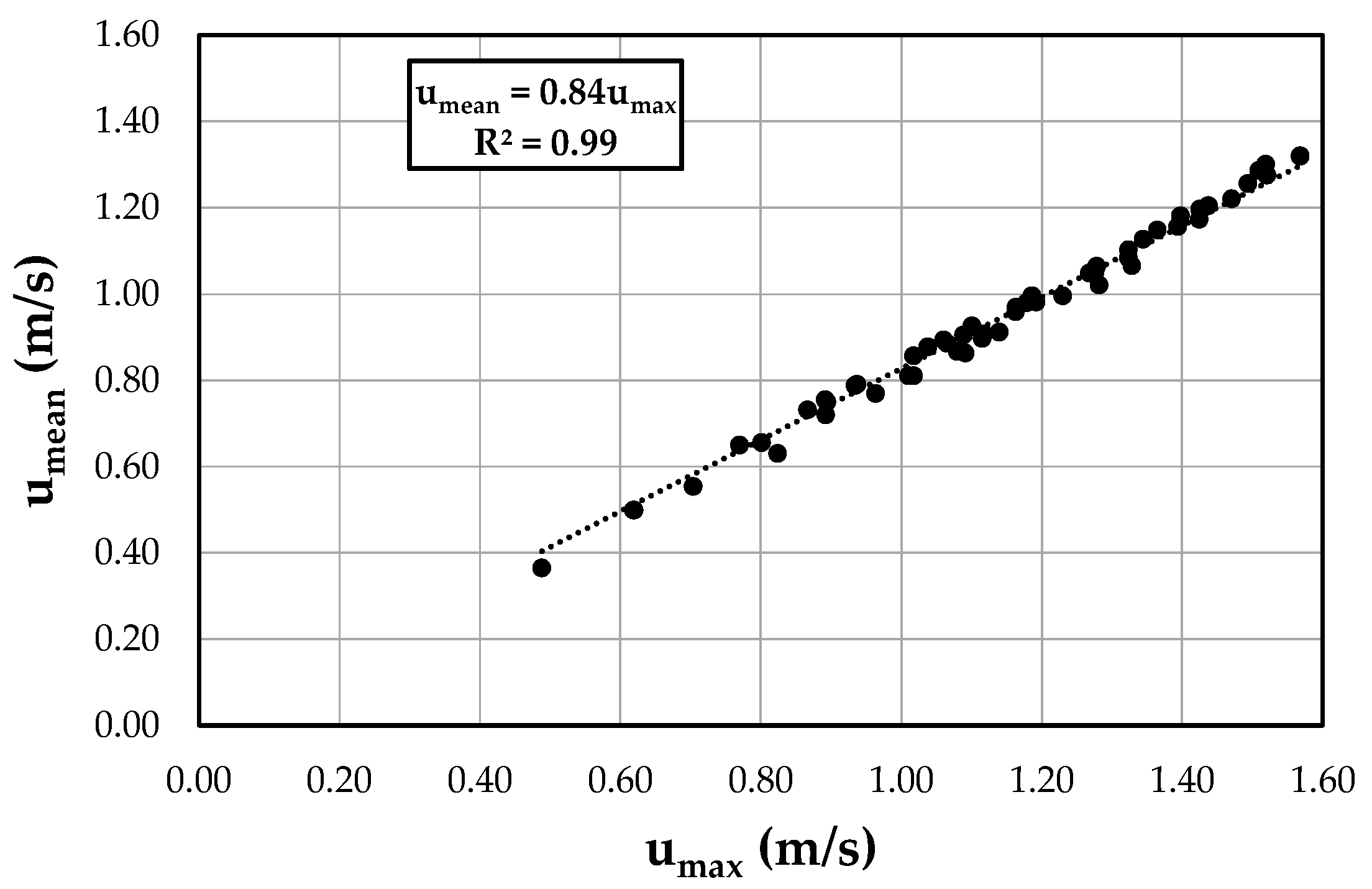
- Xia, R. Relation between mean and maximum velocities in a natural river. J. Hydraul. Eng. 1997, 123, 720–723. [Google Scholar] [CrossRef]
- Greco, M.; Mirauda, D.; Plantamura Volpe, A. Manning’s roughness through the entropy parameter for steady open channel flows in low submergence. Procedia Eng. 2014, 70, 773–780. [Google Scholar] [CrossRef]
- Greco, M.; Mirauda, D. Entropy parameter estimation in large-scale roughness open channel. J. Hydrol. Eng. 2015, 20, 04014047. [Google Scholar] [CrossRef]
- Mirauda, D.; Pannone, M.; de Vincenzo, A. An entropic model for the assessment of stream-wise velocity dip in wide open channels. Entropy 2018, 20, 69. [Google Scholar] [CrossRef]
- Moramarco, T.; Ammari, A.; Burnelli, A.; Mirauda, D.; Pascale, V. Entropy Theory Application for Flow Monitoring in Natural Channels. In Proceedings of the iEMSS 4th Biennial Meeting: International Congress on Environmental Modelling and Software (iEMSs 2008), Barcelona, Spain, 6–10 July 2008; pp. 430–437. [Google Scholar]
- Singh, V.P.; Luo, H. Entropy Theory for Distribution of One-Dimensional Velocity in Open Channels. J. Hydrol. Eng. 2011, 16, 725–735. [Google Scholar] [CrossRef]
- Kumbhakar, M.; Ghoshal, K. One-Dimensional velocity distribution in open channels using Renyi entropy. Stoch. Environ. Res. Risk Assess. 2017, 31, 949–959. [Google Scholar] [CrossRef]
- Luo, H.; Singh, V.; Schmidt, A. Comparative study of 1D entropy-based and conventional deterministic velocity distribution equations for open channel flows. J. Hydrol. 2018, 563, 679–693. [Google Scholar] [CrossRef]
- ISO. ISO 748, Measurement of Liquid Flow in Open Channel—Velocity-Area Methods. 1997. Available online: https://www.iso.org/standard/37573.html (accessed on 18 February 2020).
- Chiu, C.L. Velocity distribution in open channel flow. J. Hydraul. Eng. 1989, 115, 576–594. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and 2-D velocity distribution in open channels. J. Hydraul. Eng. 1988, 114, 738–756. [Google Scholar] [CrossRef]
- Chiu, C.L.; Said, C.A.A. Maximum and mean velocities and entropy in open-channel flow. J. Hydraul. Eng. 1995, 121, 26–35. [Google Scholar] [CrossRef]
- Nezu, I.; Rodi, W. Experimental study on secondary currents in open channel flows. In Proceedings of the 21th IAHR Congress, IAHR, Melbourne, Australia, 13–18 August 1985; Volume 2, pp. 115–119. [Google Scholar]
- Greco, M.; Mirauda, D. An Entropy Based Velocity Profile for Steady Flows with Large-Scale Roughness. In Engineering Geology for Society and Territory, River Basins, Reservoir Sedimentation and Water Resources; Lollino, G., Arattano, M., Rinaldi, M., Giustolisi, O., Marechal, J.C., Grant, G.E., Eds.; Springer International Publishing: Cham, Switzerland, 2015; Volume 3, pp. 641–645. ISBN 978-3-319-09054-2. [Google Scholar]
- Mirauda, D.; Russo, M.G. Information Entropy Theory Applied to the Dip-Phenomenon Analysis in Open Channel Flows. Entropy 2019, 21, 554. [Google Scholar] [CrossRef]
- Mirauda, D.; Russo, M.G. Modeling Bed Shear Stress Distribution in Rectangular Channels Using the Entropic Parameter. Entropy 2020, 22, 87. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Demissie, M. Hydrologic modelling of the Iroquois River watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2007, 41, 343–360. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–890. [Google Scholar] [CrossRef]
- Lyn, D. A similarity approach to turbulent sediment-laden flows in open-channels. J. Fluid Mech. 1988, 193, 1–26. [Google Scholar] [CrossRef]
- Muste, M.; Patel, V.C. Velocity profiles for particles and liquid in open-channel flow with suspended sediment. J. Hydraul. Eng. 1997, 123, 742–751. [Google Scholar] [CrossRef]

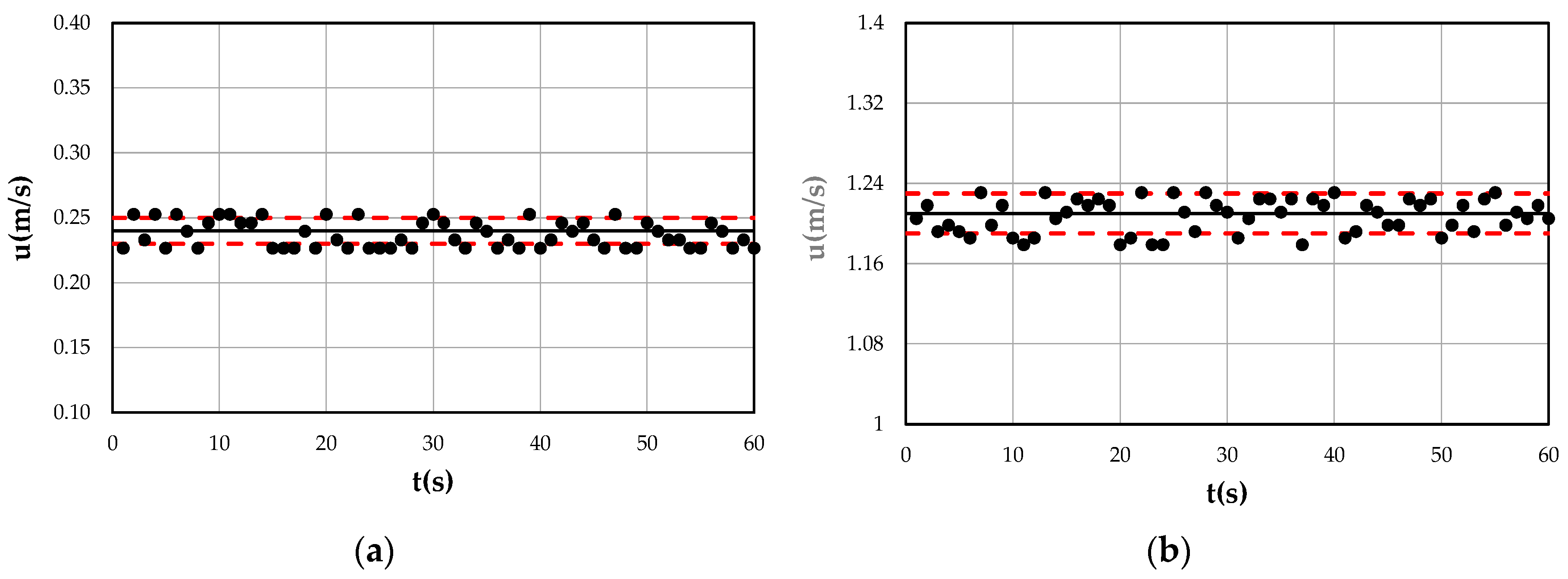
| t = 10 s | t = 20 s | t = 30 s | t = 40 s | t = 50 s | t = 60 s | ||
|---|---|---|---|---|---|---|---|
| Low velocity | μ (m/s) | 0.24 | 0.24 | 0.24 | 0.24 | 0.24 | 0.24 |
| σ2 (m2/s2) | 0.00014 | 0.00013 | 0.00013 | 0.00012 | 0.00011 | 0.00010 | |
| High velocity | μ (m/s) | 1.20 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 |
| σ2 (m2/s2) | 0.00024 | 0.00030 | 0.00034 | 0.00034 | 0.00031 | 0.00029 | |
| i (%) | Q (m3/s) | D (m) | Ar | umean (m/s) 1 | umax (m/s) 2 |
|---|---|---|---|---|---|
| 0 | 0.010–0.095 | 0.053–0.204 | 3.0–9.0 | 0.36–1.20 | 0.489–1.459 |
| 0.25 | 0.018–0.085 | 0.057–0.171 | 3.0–9.0 | 0.63–1.27 | 0.824–1.582 |
| 0.50 | 0.023–0.084 | 0.056–0.140 | 4.0–9.0 | 0.77–1.32 | 0.974–1.576 |
| 0.75 | 0.026–0.085 | 0.058–0.134 | 4.0–9.0 | 0.86–1.29 | 1.092–1.551 |
| 1.00 | 0.026–0.077 | 0.055–0.116 | 4.0–9.0 | 0.50–0.91 | 0.621–1.308 |
| Statistics | Performance Rating | |||
|---|---|---|---|---|
| Very Good | Good | Satisfactory | Unsatisfactory | |
| RSR | 0.00 ≤ RSR ≤ 0.50 | 0.50 < RSR ≤ 0.60 | 0.60 < RSR ≤ 0.70 | RSR > 0.70 |
| PBIAS | PBIAS < ±10 | ±10 ≤ PBIAS < ±15 | ±15 ≤ PBIAS < ±25 | PBIAS ≥ ±25 |
| NSE | 0.75 < NSE ≤ 1.00 | 0.65 < NSE ≤ 0.75 | 0.50 < NSE ≤ 0.65 | NSE ≤ 0.50 |
| Statistical Indices | Entropy Wake Law | Classical Entropy Law |
|---|---|---|
| RMSE | 0.04 | 0.14 |
| MAE | 2.52 | 13.07 |
| RSR | 0.15 | 0.66 |
| PBIAS | 0.61 | 10.41 |
| NSE | 0.98 | 0.56 |
| Data Set | Coleman (1986) | Lyn (1988) | Muste and Patel (1997) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RUN1 | RUN21 | RUN32 | C1 | C2 | C3 | C4 | CW01 | CW02 | CW03 | |
| i (%) | 0.200 | 0.2 | 0.2 | 0.206 | 0.270 | 0.296 | 0.401 | 0.0741 | 0.0768 | 0.0813 |
| Q (m3/s) | 0.064 | 0.064 | 0.064 | 0.011 | 0.013 | 0.011 | 0.013 | 0.0738 | 0.0735 | 0.0733 |
| D (m) | 0.172 | 0.169 | 0.173 | 0.0654 | 0.0653 | 0.0575 | 0.0569 | 0.130 | 0.128 | 0.127 |
| Ar | 2.07 | 2.11 | 2.06 | 4.08 | 4.09 | 4.64 | 4.69 | 7.00 | 7.11 | 7.16 |
| umax (m/s) | 1.06 | 1.05 | 1.03 | 0.753 | 0.875 | 0.857 | 1.019 | 0.700 | 0.708 | 0.715 |
| Statistical Indices | Entropy Wake Law | Classical Entropy Law | |
|---|---|---|---|
| Coleman (1986) | RMSE | 0.03 | 0.11 |
| MAE | 1.05 | 4.56 | |
| RSR | 0.18 | 0.72 | |
| PBIAS | 1.02 | 10.96 | |
| NSE | 0.96 | 0.54 | |
| Lyn (1988) | RMSE | 0.03 | 0.16 |
| MAE | 1.15 | 6.12 | |
| RSR | 0.21 | 0.77 | |
| b | 1.67 | 11.37 | |
| NSE | 0.95 | 0.48 | |
| Muste and Patel (1997) | RMSE | 0.09 | 0.22 |
| MAE | 1.45 | 7.01 | |
| RSR | 0.30 | 0.97 | |
| PBIAS | 1.94 | 12.12 | |
| NSE | 0.83 | 0.46 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirauda, D.; Russo, M.G. Entropy Wake Law for Streamwise Velocity Profiles in Smooth Rectangular Open Channels. Entropy 2020, 22, 654. https://doi.org/10.3390/e22060654
Mirauda D, Russo MG. Entropy Wake Law for Streamwise Velocity Profiles in Smooth Rectangular Open Channels. Entropy. 2020; 22(6):654. https://doi.org/10.3390/e22060654
Chicago/Turabian StyleMirauda, Domenica, and Maria Grazia Russo. 2020. "Entropy Wake Law for Streamwise Velocity Profiles in Smooth Rectangular Open Channels" Entropy 22, no. 6: 654. https://doi.org/10.3390/e22060654
APA StyleMirauda, D., & Russo, M. G. (2020). Entropy Wake Law for Streamwise Velocity Profiles in Smooth Rectangular Open Channels. Entropy, 22(6), 654. https://doi.org/10.3390/e22060654






