Information Theory in Computational Biology: Where We Stand Today
Abstract
1. Introduction
2. Basic Metrics in Information Theory
2.1. Self-Information and Entropy
2.2. Conditional Entropy
2.3. Relative Entropy
2.4. Mutual Information
2.5. Interaction Information
3. Applications of Information Theory in Computational Biology
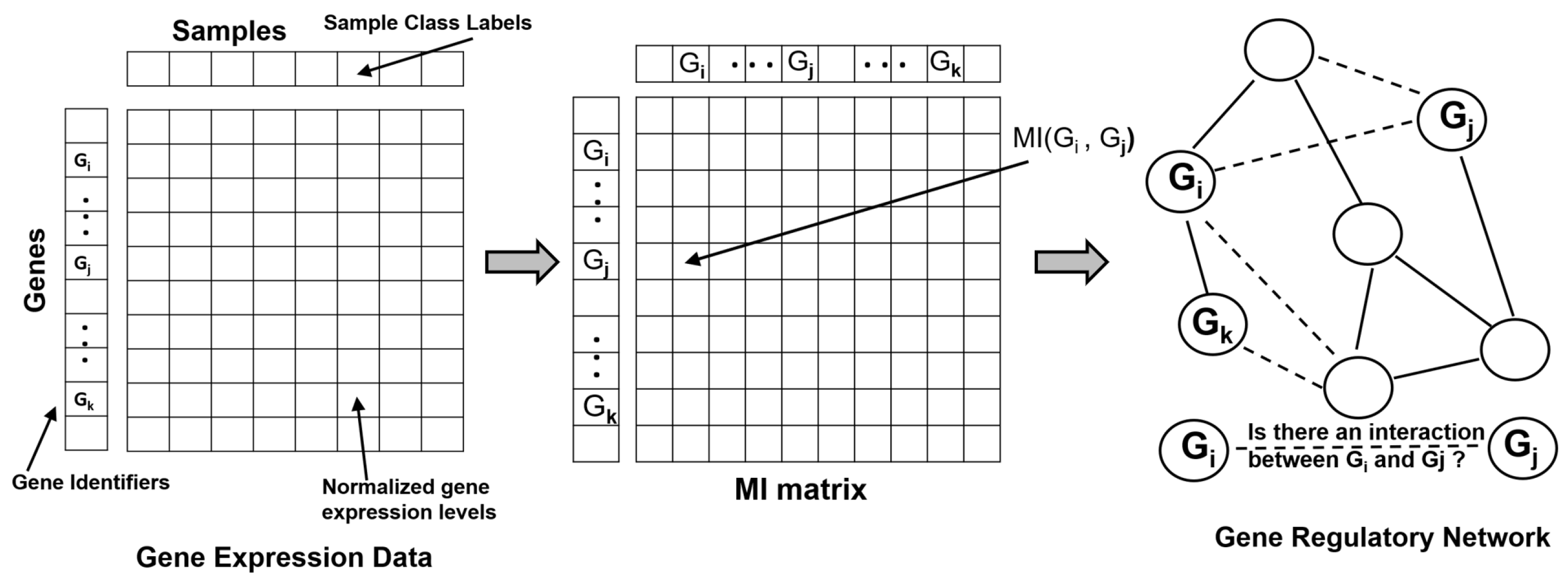
3.1. Gene Expression and Transcriptomics
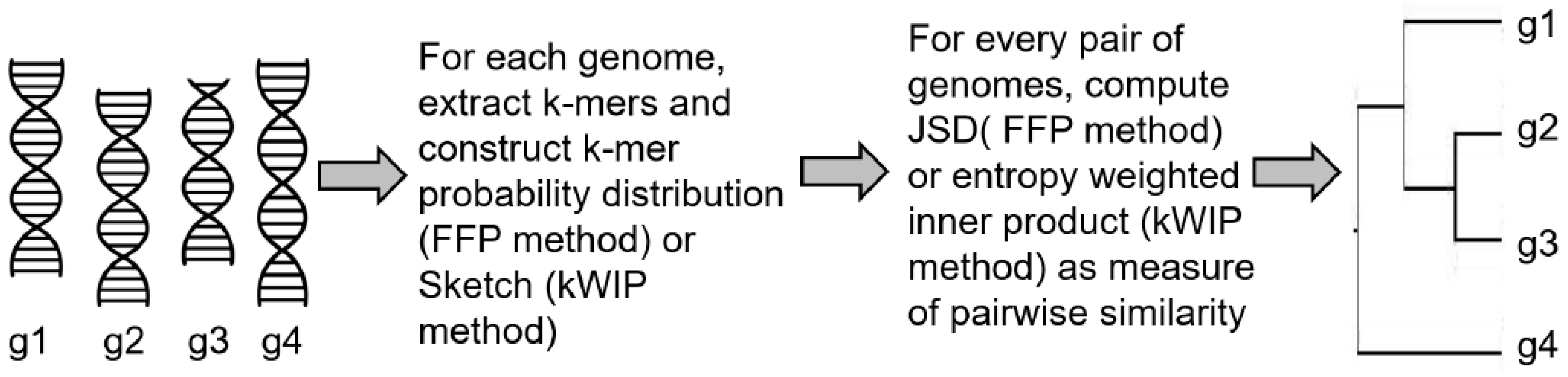
3.2. Alignment-Free Sequence Comparison
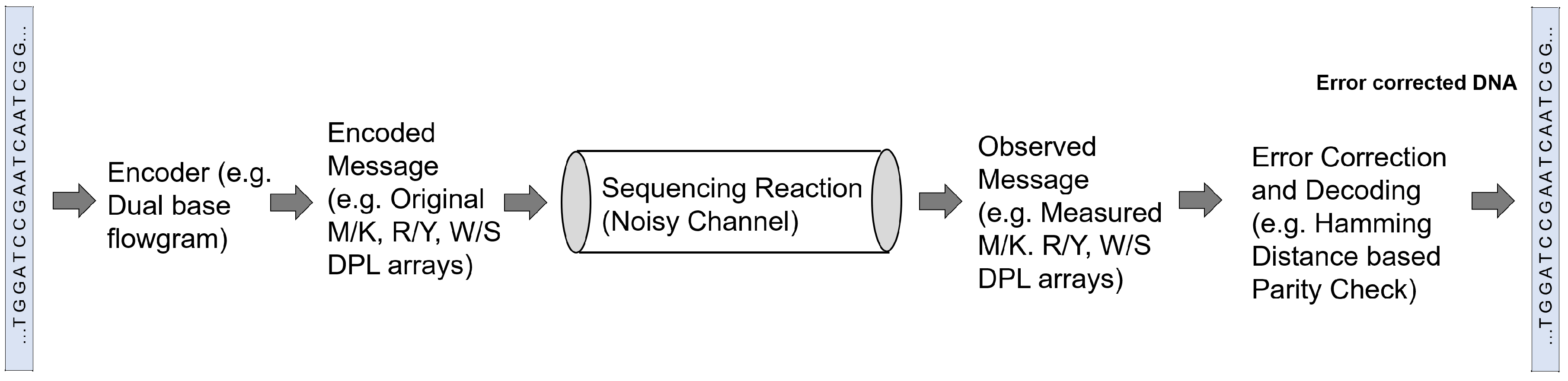
3.3. Sequencing and Error Correction
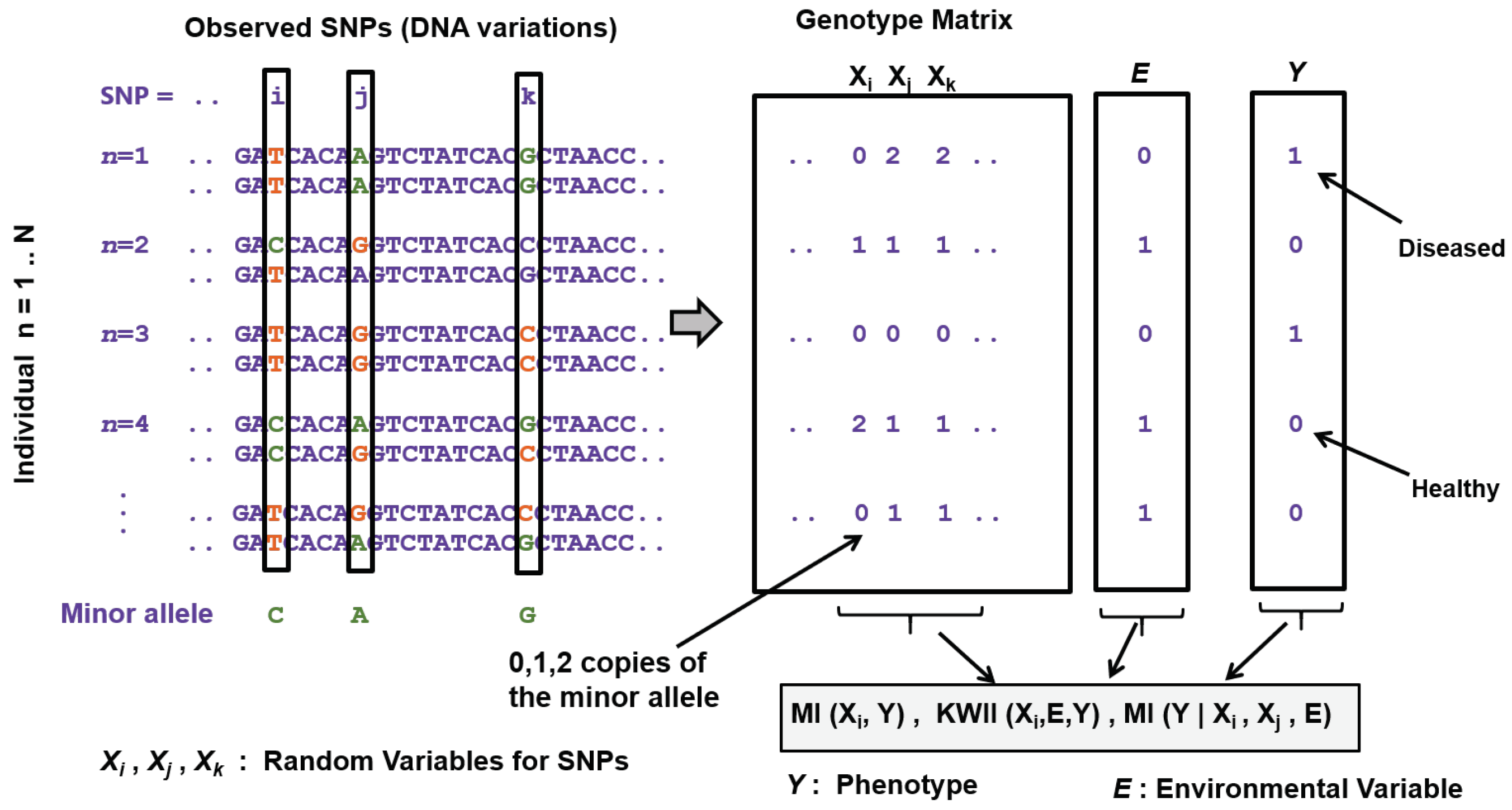
3.4. Genome-Wide Disease-Gene Association Mapping
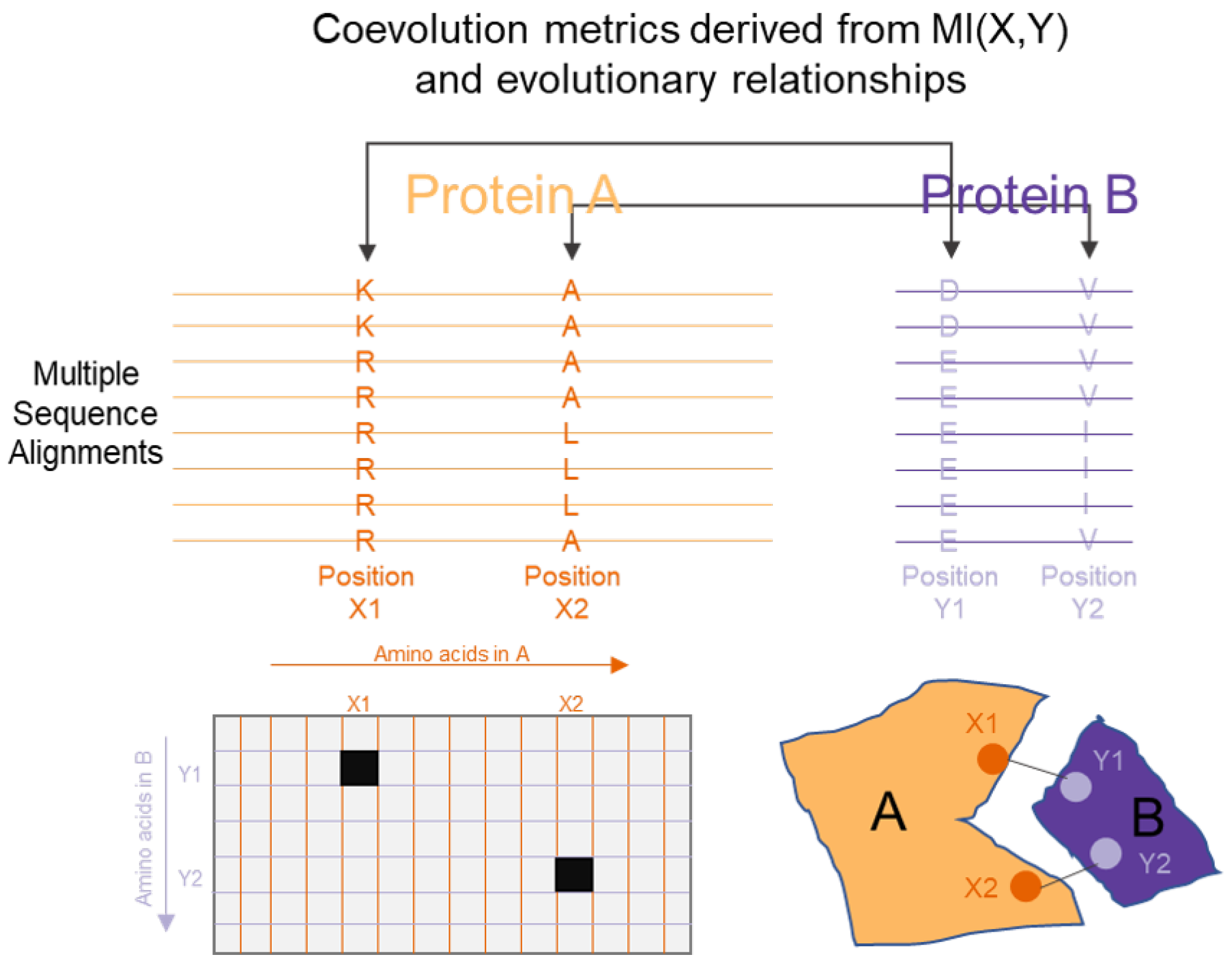
3.5. Protein Sequence, Structure and Interaction Analysis
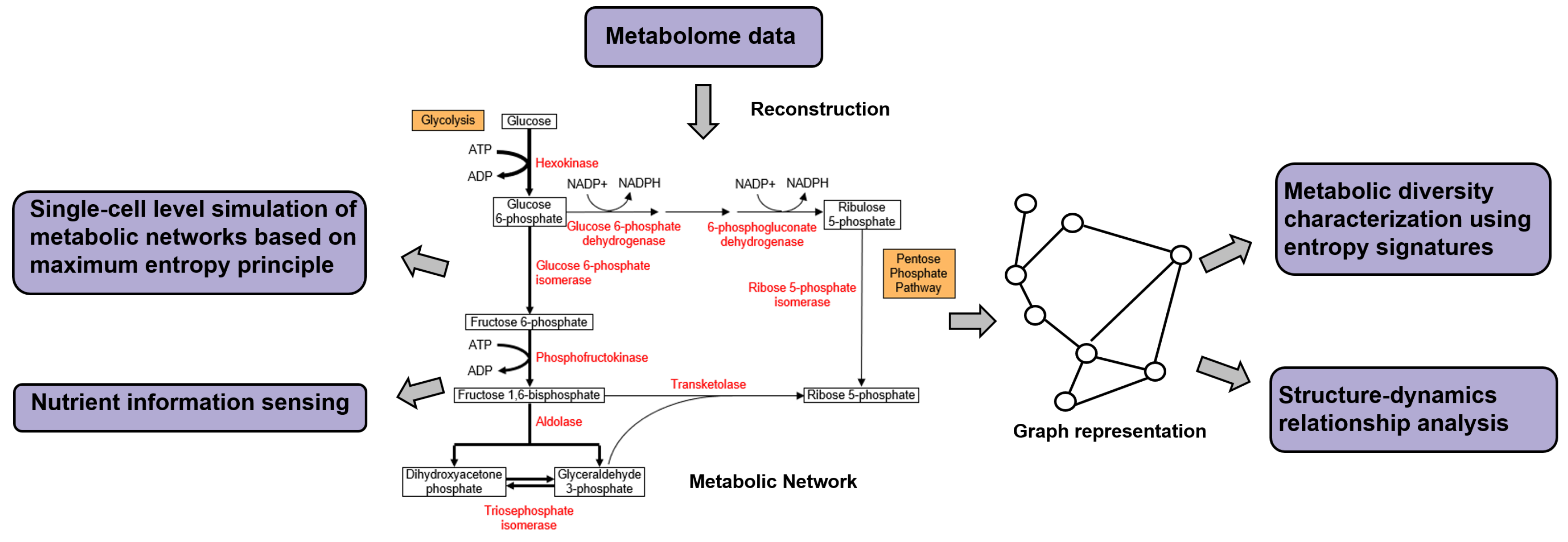
3.6. Metabolic Networks and Metabolomics
3.7. Connections to Optimization and Dimensionality Reduction in Biology
3.7.1. Optimization in Biology
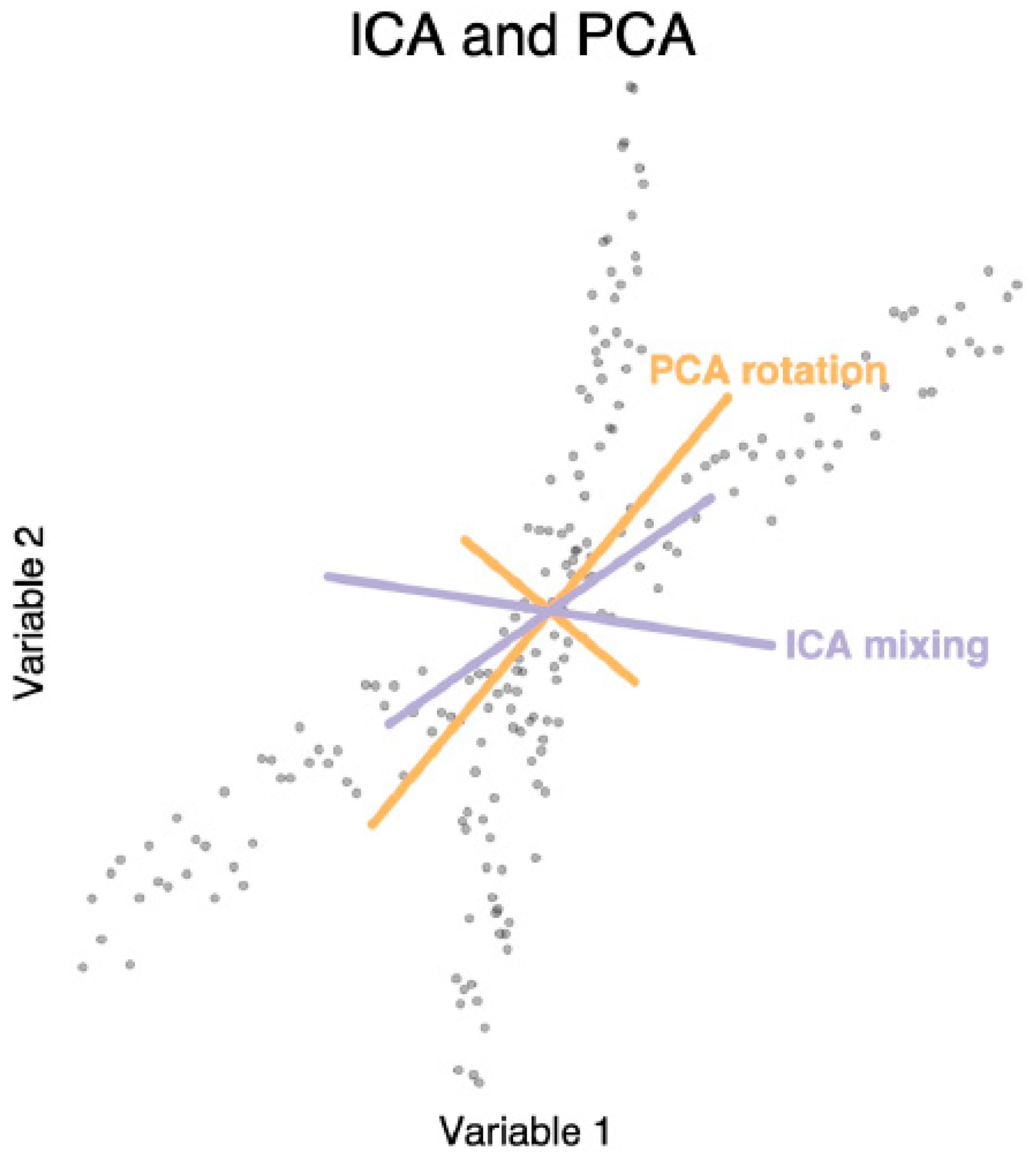
3.7.2. Dimensionality Reduction for Omics Analysis
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Tsimring, L.S. Noise in biology. Rep. Prog. Phys. 2014, 77, 026601. [Google Scholar] [CrossRef] [PubMed]
- Mousavian, Z.; Kavousi, K.; Masoudi-Nejad, A. Information Theory in Systems Biology. Part I: Gene Regulatory And Metabolic Networks; Seminars in Cell & Developmental Biology; Elsevier: Amsterdam, The Netherlands, 2016; Volume 51, pp. 3–13. [Google Scholar]
- Mousavian, Z.; Díaz, J.; Masoudi-Nejad, A. Information Theory in Systems Biology. Part II: Protein–Protein Interaction and Signaling Networks; Seminars in Cell & Developmental Biology; Elsevier: Amsterdam, The Netherlands, 2016; Volume 51, pp. 14–23. [Google Scholar]
- Vinga, S. Information theory applications for biological sequence analysis. Brief. Bioinform. 2014, 15, 376–389. [Google Scholar] [CrossRef] [PubMed]
- Waltermann, C.; Klipp, E. Information theory based approaches to cellular signaling. Biochim. Biophys. Acta 2011, 1810, 924–932. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Mar, J.C. Evaluating methods of inferring gene regulatory networks highlights their lack of performance for single cell gene expression data. BMC Bioinform. 2018, 19, 232. [Google Scholar] [CrossRef] [PubMed]
- Zielezinski, A.; Girgis, H.Z.; Bernard, G.; Leimeister, C.A.; Tang, K.; Dencker, T.; Lau, A.K.; Röhling, S.; Choi, J.J.; Waterman, M.S.; et al. Benchmarking of alignment-free sequence comparison methods. Genome Biol. 2019, 20, 144. [Google Scholar] [CrossRef]
- Little, D.Y.; Chen, L. Identification of Coevolving Residues and Coevolution Potentials Emphasizing Structure, Bond Formation and Catalytic Coordination in Protein Evolution. PLoS ONE 2009, 4, e4762. [Google Scholar] [CrossRef]
- Martínez de la Fuente, I. Quantitative analysis of cellular metabolic dissipative, self-organized structures. Int. J. Mol. Sci. 2010, 11, 3540–3599. [Google Scholar] [CrossRef]
- Schneider, T.D. A brief review of molecular information theory. Nano Commun. Netw. 2010, 1, 173–180. [Google Scholar] [CrossRef]
- Chen, H.D.; Chang, C.H.; Hsieh, L.C.; Lee, H.C. Divergence and Shannon information in genomes. Phys. Rev. Lett. 2005, 94, 178103. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.H.; Hsieh, L.C.; Chen, T.Y.; Chen, H.D.; Luo, L.; Lee, H.C. Shannon information in complete genomes. J. Bioinform. Comput. Biol. 2005, 3, 587–608. [Google Scholar] [CrossRef] [PubMed]
- Machado, J.T.; Costa, A.C.; Quelhas, M.D. Shannon, Rényie and Tsallis entropy analysis of DNA using phase plane. Nonlinear Anal. Real World Appl. 2011, 12, 3135–3144. [Google Scholar] [CrossRef]
- Athanasopoulou, L.; Athanasopoulos, S.; Karamanos, K.; Almirantis, Y. Scaling properties and fractality in the distribution of coding segments in eukaryotic genomes revealed through a block entropy approach. Phys. Rev. E 2010, 82, 051917. [Google Scholar] [CrossRef] [PubMed]
- Vinga, S. Biological sequence analysis by vector-valued functions: revisiting alignment-free methodologies for DNA and protein classification. Adv. Comput. Methods Biocomput. Bioimaging 2007, 71, 107. [Google Scholar]
- Vinga, S.; Almeida, J. Alignment-free sequence comparison—A review. Bioinformatics 2003, 19, 513–523. [Google Scholar] [CrossRef]
- Ladbury, J.E.; Arold, S.T. Noise in cellular signaling pathways: Causes and effects. Trends Biochem. Sci. 2012, 37, 173–178. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: London, UK, 1994. [Google Scholar]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Jakulin, A. Machine Learning Based on Attribute Interactions. Ph.D. Thesis, Univerza v Ljubljani, Ljubljana, Republika Slovenija, 2005. [Google Scholar]
- Chanda, P.; Zhang, A.; Brazeau, D.; Sucheston, L.; Freudenheim, J.L.; Ambrosone, C.; Ramanathan, M. Information-theoretic metrics for visualizing gene-environment interactions. Am. J. Hum. Genet. 2007, 81, 939–963. [Google Scholar] [CrossRef]
- Te Sun, H. Multiple mutual informations and multiple interactions in frequency data. Inf. Control 1980, 46, 26–45. [Google Scholar]
- Trapnell, C.; Cacchiarelli, D.; Grimsby, J.; Pokharel, P.; Li, S.; Morse, M.; Lennon, N.J.; Livak, K.J.; Mikkelsen, T.S.; Rinn, J.L. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 2014, 32, 381. [Google Scholar] [CrossRef]
- Chan, T.E.; Stumpf, M.P.; Babtie, A.C. Gene regulatory network inference from single-cell data using multivariate information measures. Cell Syst. 2017, 5, 251–267. [Google Scholar] [CrossRef] [PubMed]
- Moris, N.; Pina, C.; Arias, A.M. Transition states and cell fate decisions in epigenetic landscapes. Nat. Rev. Genet. 2016, 17, 693. [Google Scholar] [CrossRef] [PubMed]
- Zambelli, F.; Mastropasqua, F.; Picardi, E.; D’Erchia, A.M.; Pesole, G.; Pavesi, G. RNentropy: An entropy-based tool for the detection of significant variation of gene expression across multiple RNA-Seq experiments. Nucleic Acids Res. 2018, 46, e46. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Rahimzamani, A.; Wang, L.; Mao, Q.; Durham, T.; McFaline-Figueroa, J.L.; Saunders, L.; Trapnell, C.; Kannan, S. Towards inferring causal gene regulatory networks from single cell expression measurements. BioRxiv 2018. [Google Scholar] [CrossRef]
- Meyer, P.; Kontos, K.; Lafitte, F.; Bontempi, G. EURASIP J. Bioinf. Syst. Biol. 2007, 79879. [Google Scholar]
- Chaitankar, V.; Ghosh, P.; Perkins, E.J.; Gong, P.; Deng, Y.; Zhang, C. A novel gene network inference algorithm using predictive minimum description length approach. BMC Syst. Biol. 2010, 4, S7. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, X.M.; He, K.; Lu, L.; Cao, Y.; Liu, J.; Hao, J.K.; Liu, Z.P.; Chen, L. Inferring gene regulatory networks from gene expression data by path consistency algorithm based on conditional mutual information. Bioinformatics 2012, 28, 98–104. [Google Scholar] [CrossRef]
- Butte, A.J.; Kohane, I.S. Mutual information relevance networks: functional genomic clustering using pairwise entropy measurements. In Biocomputing 2000; World Scientific: Singapore, 1999; pp. 418–429. [Google Scholar]
- Butte, A.J.; Tamayo, P.; Slonim, D.; Golub, T.R.; Kohane, I.S. Discovering functional relationships between RNA expression and chemotherapeutic susceptibility using relevance networks. Proc. Natl. Acad. Sci. USA 2000, 97, 12182–12186. [Google Scholar] [CrossRef] [PubMed]
- Faith, J.J.; Hayete, B.; Thaden, J.T.; Mogno, I.; Wierzbowski, J.; Cottarel, G.; Kasif, S.; Collins, J.J.; Gardner, T.S. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 2007, 5, e8. [Google Scholar] [CrossRef] [PubMed]
- Margolin, A.A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Dalla Favera, R.; Califano, A. ARACNE: An Algorithm for the Reconstruction of Gene Regulatory Networks in a Mammalian Cellular Context; BMC Bioinformatics; Springer: Berlin, Germany, 2006; Volume 7, p. S7. [Google Scholar]
- Zoppoli, P.; Morganella, S.; Ceccarelli, M. TimeDelay-ARACNE: Reverse engineering of gene networks from time-course data by an information theoretic approach. BMC Bioinform. 2010, 11, 154. [Google Scholar] [CrossRef] [PubMed]
- Jang, I.S.; Margolin, A.; Califano, A. hARACNe: Improving the accuracy of regulatory model reverse engineering via higher-order data processing inequality tests. Interface Focus 2013, 3, 20130011. [Google Scholar] [CrossRef] [PubMed]
- Lachmann, A.; Giorgi, F.M.; Lopez, G.; Califano, A. ARACNe-AP: Gene network reverse engineering through adaptive partitioning inference of mutual information. Bioinformatics 2016, 32, 2233–2235. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. arXiv 2010, arXiv:1004.2515. [Google Scholar]
- Vân Anh Huynh-Thu, A.I.; Wehenkel, L.; Geurts, P. Inferring regulatory networks from expression data using tree-based methods. PLoS ONE 2010, 5, e12776. [Google Scholar]
- Matsumoto, H.; Kiryu, H.; Furusawa, C.; Ko, M.S.; Ko, S.B.; Gouda, N.; Hayashi, T.; Nikaido, I. SCODE: An efficient regulatory network inference algorithm from single-cell RNA-Seq during differentiation. Bioinformatics 2017, 33, 2314–2321. [Google Scholar] [CrossRef] [PubMed]
- Marbach, D.; Costello, J.C.; Küffner, R.; Vega, N.M.; Prill, R.J.; Camacho, D.M.; Allison, K.R.; Aderhold, A.; Bonneau, R.; Chen, Y.; et al. Wisdom of crowds for robust gene network inference. Nat. Methods 2012, 9, 796. [Google Scholar] [CrossRef] [PubMed]
- Zielezinski, A.; Vinga, S.; Almeida, J.; Karlowski, W.M. Alignment-free sequence comparison: Benefits, applications, and tools. Genome Biol. 2017, 18, 186. [Google Scholar] [CrossRef]
- Bonham-Carter, O.; Steele, J.; Bastola, D. Alignment-free genetic sequence comparisons: A review of recent approaches by word analysis. Brief. Bioinform. 2014, 15, 890–905. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Chen, L.; Chen, T.; Sun, F. Comparison of metatranscriptomic samples based on k-tuple frequencies. PLoS ONE 2014, 9, e84348. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, Y. A 2D graphical representation of protein sequence and its numerical characterization. Chem. Phys. Lett. 2009, 476, 281–286. [Google Scholar] [CrossRef]
- Randić, M.; Zupan, J.; Balaban, A.T. Unique graphical representation of protein sequences based on nucleotide triplet codons. Chem. Phys. Lett. 2004, 397, 247–252. [Google Scholar] [CrossRef]
- Jeffrey, H.J. Chaos game representation of gene structure. Nucleic Acids Res. 1990, 18, 2163–2170. [Google Scholar] [CrossRef] [PubMed]
- Almeida, J.S. Sequence analysis by iterated maps, a review. Brief. Bioinform. 2014, 15, 369–375. [Google Scholar] [CrossRef] [PubMed]
- Leimeister, C.A.; Boden, M.; Horwege, S.; Lindner, S.; Morgenstern, B. Fast alignment-free sequence comparison using spaced-word frequencies. Bioinformatics 2014, 30, 1991–1999. [Google Scholar] [CrossRef] [PubMed]
- Morgenstern, B.; Zhu, B.; Horwege, S.; Leimeister, C.A. Estimating evolutionary distances between genomic sequences from spaced-word matches. Algorithms Mol. Biol. 2015, 10, 5. [Google Scholar] [CrossRef] [PubMed]
- Sims, G.E.; Jun, S.R.; Wu, G.A.; Kim, S.H. Alignment-free genome comparison with feature frequency profiles (FFP) and optimal resolutions. Proc. Natl. Acad. Sci. USA 2009, 106, 2677–2682. [Google Scholar] [CrossRef]
- Murray, K.D.; Webers, C.; Ong, C.S.; Borevitz, J.; Warthmann, N. kWIP: The k-mer weighted inner product, a de novo estimator of genetic similarity. PLoS Comput. Biol. 2017, 13, e1005727. [Google Scholar] [CrossRef]
- Zhang, Q.; Pell, J.; Canino-Koning, R.; Howe, A.C.; Brown, C.T. These are not the k-mers you are looking for: efficient online k-mer counting using a probabilistic data structure. PLoS ONE 2014, 9, e101271. [Google Scholar] [CrossRef]
- Cormode, G.; Muthukrishnan, S. An improved data stream summary: The count-min sketch and its applications. J. Algorithms 2005, 55, 58–75. [Google Scholar] [CrossRef]
- Drouin, A.; Giguère, S.; Déraspe, M.; Marchand, M.; Tyers, M.; Loo, V.G.; Bourgault, A.M.; Laviolette, F.; Corbeil, J. Predictive computational phenotyping and biomarker discovery using reference-free genome comparisons. BMC Genom. 2016, 17, 1–15. [Google Scholar] [CrossRef]
- Glouzon, J.P.S.; Perreault, J.P.; Wang, S. The super-n-motifs model: A novel alignment-free approach for representing and comparing RNA secondary structures. Bioinformatics 2017, 33, 1169–1178. [Google Scholar] [CrossRef] [PubMed]
- Sarmashghi, S.; Bohmann, K.; Gilbert, M.T.P.; Bafna, V.; Mirarab, S. Skmer: assembly-free and alignment-free sample identification using genome skims. Genome Biol. 2019, 20, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Rhoads, A.; Au, K.F. PacBio sequencing and its applications. Genom. Proteom. Bioinform 2015, 13, 278–289. [Google Scholar] [CrossRef] [PubMed]
- Laver, T.; Harrison, J.; O’neill, P.; Moore, K.; Farbos, A.; Paszkiewicz, K.; Studholme, D.J. Assessing the performance of the oxford nanopore technologies minion. Biomol Detect. Quantif. 2015, 3, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Bansal, V.; Boucher, C. Sequencing Technologies and Analyses: Where Have We Been and Where Are We Going? iScience 2019, 18, 37. [Google Scholar] [CrossRef]
- Goodwin, S.; McPherson, J.D.; McCombie, W.R. Coming of age: Ten years of next-generation sequencing technologies. Nat. Rev. Genet. 2016, 17, 333. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zhou, W.; Qiao, S.; Kang, L.; Duan, H.; Xie, X.S.; Huang, Y. Highly accurate fluorogenic DNA sequencing with information theory–based error correction. Nat. Biotechnol. 2017, 35, 1170. [Google Scholar] [CrossRef]
- Motahari, A.S.; Bresler, G.; David, N. Information theory of DNA shotgun sequencing. IEEE Trans. Inf. Theory 2013, 59, 6273–6289. [Google Scholar] [CrossRef]
- Vinga, S.; Almeida, J.S. Rényi continuous entropy of DNA sequences. J. Theor. Biol. 2004, 231, 377–388. [Google Scholar] [CrossRef]
- Shomorony, I.; Courtade, T.; Tse, D. Do read errors matter for genome assembly? In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 919–923. [Google Scholar]
- Bresler, G.; Bresler, M.; Tse, D. Optimal Assembly for High Throughput Shotgun Sequencing; BMC Bioinformatics; Springer: Berlin, Germany, 2013; Volume 14, p. S18. [Google Scholar]
- Ganguly, S.; Mossel, E.; Rácz, M.Z. Sequence assembly from corrupted shotgun reads. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 265–269. [Google Scholar]
- Gabrys, R.; Milenkovic, O. Unique reconstruction of coded sequences from multiset substring spectra. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 2540–2544. [Google Scholar]
- Shomorony, I.; Heckel, R. DNA-Based Storage: Models and Fundamental Limits. arXiv 2020, arXiv:2001.06311. [Google Scholar]
- Marcovich, S.; Yaakobi, E. Reconstruction of Strings from their Substrings Spectrum. arXiv 2019, arXiv:1912.11108. [Google Scholar]
- Si, H.; Vikalo, H.; Vishwanath, S. Information-theoretic analysis of haplotype assembly. IEEE Trans. Inf. Theory 2017, 63, 3468–3479. [Google Scholar] [CrossRef]
- Sims, P.A.; Greenleaf, W.J.; Duan, H.; Xie, X.S. Fluorogenic DNA sequencing in PDMS microreactors. Nat. Methods 2011, 8, 575. [Google Scholar] [CrossRef]
- Mitchell, K.; Brito, J.J.; Mandric, I.; Wu, Q.; Knyazev, S.; Chang, S.; Martin, L.S.; Karlsberg, A.; Gerasimov, E.; Littman, R.; et al. Benchmarking of computational error-correction methods for next-generation sequencing data. Genome Biol. 2020, 21, 1–13. [Google Scholar] [CrossRef]
- Anavy, L.; Vaknin, I.; Atar, O.; Amit, R.; Yakhini, Z. Improved DNA based storage capacity and fidelity using composite DNA letters. bioRxiv 2018. [Google Scholar] [CrossRef]
- Choi, Y.; Ryu, T.; Lee, A.; Choi, H.; Lee, H.; Park, J.; Song, S.H.; Kim, S.; Kim, H.; Park, W.; et al. Addition of degenerate bases to DNA-based data storage for increased information capacity. bioRxiv 2018. [Google Scholar] [CrossRef]
- Reed, I.S.; Solomon, G. Polynomial codes over certain finite fields. J. Soc. Ind. Appl. Math. 1960, 8, 300–304. [Google Scholar] [CrossRef]
- Fu, S.; Wang, A.; Au, K.F. A comparative evaluation of hybrid error correction methods for error-prone long reads. Genome Biol. 2019, 20, 26. [Google Scholar] [CrossRef] [PubMed]
- Amarasinghe, S.L.; Su, S.; Dong, X.; Zappia, L.; Ritchie, M.E.; Gouil, Q. Opportunities and challenges in long-read sequencing data analysis. Genome Biol. 2020, 21, 1–16. [Google Scholar] [CrossRef]
- Mantere, T.; Kersten, S.; Hoischen, A. Long-read sequencing emerging in medical genetics. Front. Genet. 2019, 10, 426. [Google Scholar] [CrossRef]
- Nakano, K.; Shiroma, A.; Shimoji, M.; Tamotsu, H.; Ashimine, N.; Ohki, S.; Shinzato, M.; Minami, M.; Nakanishi, T.; Teruya, K.; et al. Advantages of genome sequencing by long-read sequencer using SMRT technology in medical area. Hum. Cell 2017, 30, 149–161. [Google Scholar] [CrossRef] [PubMed]
- Boldogkői, Z.; Moldován, N.; Balázs, Z.; Snyder, M.; Tombácz, D. Long-read sequencing—A powerful tool in viral transcriptome research. Trends Microbiol. 2019, 27, 578–592. [Google Scholar] [CrossRef]
- Heckel, R.; Shomorony, I.; Ramchandran, K.; David, N. Fundamental limits of DNA storage systems. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 3130–3134. [Google Scholar]
- Meiser, L.C.; Antkowiak, P.L.; Koch, J.; Chen, W.D.; Kohll, A.X.; Stark, W.J.; Heckel, R.; Grass, R.N. Reading and writing digital data in DNA. Nat. Protoc. 2020, 15, 86–101. [Google Scholar] [CrossRef] [PubMed]
- Lopez, R.; Chen, Y.J.; Ang, S.D.; Yekhanin, S.; Makarychev, K.; Racz, M.Z.; Seelig, G.; Strauss, K.; Ceze, L. DNA assembly for nanopore data storage readout. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Li, S.; Cui, Y. Genetic association studies: an information content perspective. Curr. Genom. 2012, 13, 566–573. [Google Scholar] [CrossRef]
- Kang, G.; Zuo, Y. Entropy-based joint analysis for two-stage genome-wide association studies. J. Hum. Genet. 2007, 52, 747–756. [Google Scholar] [CrossRef]
- Ruiz-Marín, M.; Matilla-García, M.; Cordoba, J.A.G.; Susillo-González, J.L.; Romo-Astorga, A.; González-Pérez, A.; Ruiz, A.; Gayán, J. An entropy test for single-locus genetic association analysis. BMC Genet. 2010, 11, 19. [Google Scholar] [CrossRef]
- Li, P.; Guo, M.; Wang, C.; Liu, X.; Zou, Q. An overview of SNP interactions in genome-wide association studies. Brief. Funct. Genom. 2015, 14, 143–155. [Google Scholar] [CrossRef]
- Tzeng, J.Y.; Devlin, B.; Wasserman, L.; Roeder, K. On the identification of disease mutations by the analysis of haplotype similarity and goodness of fit. Am. J. Hum. Genet. 2003, 72, 891–902. [Google Scholar] [CrossRef][Green Version]
- Zhao, J.; Boerwinkle, E.; Xiong, M. An entropy-based statistic for genomewide association studies. Am. J. Hum. Genet. 2005, 77, 27–40. [Google Scholar] [CrossRef]
- Zhao, J.; Jin, L.; Xiong, M. Nonlinear tests for genomewide association studies. Genetics 2006, 174, 1529–1538. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Kang, G.; Sun, K.; Qian, M.; Romero, R.; Fu, W. Gene-centric genomewide association study via entropy. Genetics 2008, 179, 637–650. [Google Scholar] [CrossRef] [PubMed]
- Cordell, H.J. Epistasis: what it means, what it doesn’t mean, and statistical methods to detect it in humans. Hum. Mol. Genet. 2002, 11, 2463–2468. [Google Scholar] [CrossRef] [PubMed]
- Fan, R.; Zhong, M.; Wang, S.; Zhang, Y.; Andrew, A.; Karagas, M.; Chen, H.; Amos, C.; Xiong, M.; Moore, J. Entropy-based information gain approaches to detect and to characterize gene-gene and gene-environment interactions/correlations of complex diseases. Genet. Epidemiol. 2011, 35, 706–721. [Google Scholar] [CrossRef]
- Yee, J.; Kwon, M.S.; Park, T.; Park, M. A modified entropy-based approach for identifying gene-gene interactions in case-control study. PLoS ONE 2013, 8, e69321. [Google Scholar] [CrossRef][Green Version]
- Dong, C.; Chu, X.; Wang, Y.; Wang, Y.; Jin, L.; Shi, T.; Huang, W.; Li, Y. Exploration of gene–gene interaction effects using entropy-based methods. Eur. J. Hum. Genet. 2008, 16, 229–235. [Google Scholar] [CrossRef]
- Ferrario, P.G.; König, I.R. Transferring entropy to the realm of GxG interactions. Brief. Bioinform. 2018, 19, 136–147. [Google Scholar] [CrossRef]
- Taylor, M.B.; Ehrenreich, I.M. Higher-order genetic interactions and their contribution to complex traits. Trends Genet. 2015, 31, 34–40. [Google Scholar] [CrossRef]
- Brunel, H.; Gallardo-Chacón, J.J.; Buil, A.; Vallverdú, M.; Soria, J.M.; Caminal, P.; Perera, A. MISS: A non-linear methodology based on mutual information for genetic association studies in both population and sib-pairs analysis. Bioinformatics 2010, 26, 1811–1818. [Google Scholar] [CrossRef]
- Varadan, V.; Miller III, D.M.; Anastassiou, D. Computational inference of the molecular logic for synaptic connectivity in C. elegans. Bioinformatics 2006, 22, e497–e506. [Google Scholar] [CrossRef]
- Anastassiou, D. Computational analysis of the synergy among multiple interacting genes. Mol. Syst. Biol. 2007, 3, 83. [Google Scholar] [CrossRef] [PubMed]
- Curk, T.; Rot, G.; Zupan, B. SNPsyn: detection and exploration of SNP–SNP interactions. Nucleic Acids Res. 2011, 39, W444–W449. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hu, T.; Sinnott-Armstrong, N.A.; Kiralis, J.W.; Andrew, A.S.; Karagas, M.R.; Moore, J.H. Characterizing genetic interactions in human disease association studies using statistical epistasis networks. BMC Bioinform. 2011, 12, 364. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Chen, Y.; Kiralis, J.W.; Collins, R.L.; Wejse, C.; Sirugo, G.; Williams, S.M.; Moore, J.H. An information-gain approach to detecting three-way epistatic interactions in genetic association studies. J. Am. Med. Inf. Assoc. 2013, 20, 630–636. [Google Scholar] [CrossRef]
- Hu, T.; Chen, Y.; Kiralis, J.W.; Moore, J.H. Vi SEN: Methodology and Software for Visualization of Statistical Epistasis Networks. Genet. Epidemiol. 2013, 37, 283–285. [Google Scholar] [CrossRef]
- Lee, W.; Sjölander, A.; Pawitan, Y. A critical look at entropy-based gene-gene interaction measures. Genet. Epidemiol. 2016, 40, 416–424. [Google Scholar] [CrossRef]
- Shang, J.; Zhang, J.; Sun, Y.; Zhang, Y. EpiMiner: a three-stage co-information based method for detecting and visualizing epistatic interactions. Digit. Signal Process. 2014, 24, 1–13. [Google Scholar] [CrossRef]
- Mielniczuk, J.; Rdzanowski, M. Use of information measures and their approximations to detect predictive gene-gene interaction. Entropy 2017, 19, 23. [Google Scholar] [CrossRef]
- Chen, L.; Yu, G.; Langefeld, C.D.; Miller, D.J.; Guy, R.T.; Raghuram, J.; Yuan, X.; Herrington, D.M.; Wang, Y. Comparative analysis of methods for detecting interacting loci. BMC Genom. 2011, 12, 344. [Google Scholar] [CrossRef]
- Chen, G.; Yuan, A.; Cai, T.; Li, C.M.; Bentley, A.R.; Zhou, J.; N. Shriner, D.; A. Adeyemo, A.; N. Rotimi, C. Measuring gene–gene interaction using Kullback–Leibler divergence. Ann. Hum. Genet. 2019, 83, 405–417. [Google Scholar] [CrossRef]
- Chanda, P.; Sucheston, L.; Zhang, A.; Brazeau, D.; Freudenheim, J.L.; Ambrosone, C.; Ramanathan, M. AMBIENCE: A novel approach and efficient algorithm for identifying informative genetic and environmental associations with complex phenotypes. Genetics 2008, 180, 1191–1210. [Google Scholar] [CrossRef] [PubMed]
- Chanda, P.; Sucheston, L.; Zhang, A.; Ramanathan, M. The interaction index, a novel information-theoretic metric for prioritizing interacting genetic variations and environmental factors. Eur. J. Hum. Genet. 2009, 17, 1274–1286. [Google Scholar] [CrossRef]
- Chanda, P.; Sucheston, L.; Liu, S.; Zhang, A.; Ramanathan, M. Information-theoretic gene-gene and gene-environment interaction analysis of quantitative traits. BMC Genom. 2009, 10, 509. [Google Scholar] [CrossRef] [PubMed]
- Knights, J.; Yang, J.; Chanda, P.; Zhang, A.; Ramanathan, M. SYMPHONY, an information-theoretic method for gene–gene and gene–environment interaction analysis of disease syndromes. Heredity 2013, 110, 548–559. [Google Scholar] [CrossRef] [PubMed]
- Chanda, P.; Zhang, A.; Ramanathan, M. Modeling of environmental and genetic interactions with AMBROSIA, an information-theoretic model synthesis method. Heredity 2011, 107, 320–327. [Google Scholar] [CrossRef]
- Knights, J.; Ramanathan, M. An information theory analysis of gene-environmental interactions in count/rate data. Hum. Hered. 2012, 73, 123–138. [Google Scholar] [CrossRef]
- Tritchler, D.L.; Sucheston, L.; Chanda, P.; Ramanathan, M. Information metrics in genetic epidemiology. Stat. Appl. Genet. Mol. Biol. 2011, 10. [Google Scholar] [CrossRef][Green Version]
- Sucheston, L.; Chanda, P.; Zhang, A.; Tritchler, D.; Ramanathan, M. Comparison of information-theoretic to statistical methods for gene-gene interactions in the presence of genetic heterogeneity. BMC Genom. 2010, 11, 487. [Google Scholar] [CrossRef]
- Ritchie, M.D.; Hahn, L.W.; Roodi, N.; Bailey, L.R.; Dupont, W.D.; Parl, F.F.; Moore, J.H. Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am. J. Hum. Genet. 2001, 69, 138–147. [Google Scholar] [CrossRef]
- Culverhouse, R. The use of the restricted partition method with case-control data. Hum. Hered. 2007, 63, 93–100. [Google Scholar] [CrossRef]
- Moore, J.H.; Hu, T. Epistasis analysis using information theory. In Epistasis; Springer: Berlin, Germany, 2015; pp. 257–268. [Google Scholar]
- Barabási, A.L.; Bonabeau, E. Scale-free networks. Sci. Am. 2003, 288, 60–69. [Google Scholar] [CrossRef] [PubMed]
- Piegorsch, W.W.; Weinberg, C.R.; Taylor, J.A. Non-hierarchical logistic models and case-only designs for assessing susceptibility in population-based case-control studies. Stat. Med. 1994, 13, 153–162. [Google Scholar] [CrossRef] [PubMed]
- Kang, G.; Yue, W.; Zhang, J.; Cui, Y.; Zuo, Y.; Zhang, D. An entropy-based approach for testing genetic epistasis underlying complex diseases. J. Theor. Biol. 2008, 250, 362–374. [Google Scholar] [CrossRef] [PubMed]
- De Andrade, M.; Wang, X. Entropy based genetic association tests and gene-gene interaction tests. Stat. Appl. Genet. Mol. Biol. 2011, 10. [Google Scholar] [CrossRef]
- Spielman, R.S.; McGinnis, R.E.; Ewens, W.J. Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM). Am. J. Hum. Genet. 1993, 52, 506. [Google Scholar]
- Zhao, J.; Boerwinkle, E.; Xiong, M. An entropy-based genome-wide transmission/disequilibrium test. Hum. Genet. 2007, 121, 357–367. [Google Scholar] [CrossRef]
- Yee, J.; Kwon, M.S.; Jin, S.; Park, T.; Park, M. Detecting Genetic Interactions for Quantitative Traits Using-Spacing Entropy Measure. BioMed. Res. Int. 2015, 2015, 523641. [Google Scholar] [CrossRef]
- Galas, D.J.; Kunert-Graf, J.M.; Uechi, L.; Sakhanenko, N.A. Towards an information theory of quantitative genetics. bioRxiv 2019, 811950. [Google Scholar] [CrossRef]
- Tahmasebi, B.; Maddah-Ali, M.A.; Motahari, A.S. Genome-wide association studies: Information theoretic limits of reliable learning. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 2231–2235. [Google Scholar]
- Tahmasebi, B.; Maddah-Ali, M.A.; Motahari, S.A. Information Theory of Mixed Population Genome-Wide Association Studies. In Proceedings of the 2018 IEEE Information Theory Workshop (ITW), Guangzhou, China, 25–29 November 2018; pp. 1–5. [Google Scholar]
- Jiang, D.; Wang, M. Recent developments in statistical methods for GWAS and high-throughput sequencing association studies of complex traits. Biostat. Epidemiol. 2018, 2, 132–159. [Google Scholar] [CrossRef]
- Hayes, B. Overview of statistical methods for genome-wide association studies (GWAS). In Genome-Wide Association Studies and Genomic Prediction; Springer: Berlin, Germany, 2013; pp. 149–169. [Google Scholar]
- Kubkowski, M.; Mielniczuk, J. Asymptotic distributions of empirical Interaction Information. Methodol. Comput. Appl. Probab. 2020, 1–25. [Google Scholar] [CrossRef]
- Goeman, J.J.; Solari, A. Multiple hypothesis testing in genomics. Stat. Med. 2014, 33, 1946–1978. [Google Scholar] [CrossRef] [PubMed]
- Chanda, P.; Zhang, A.; Ramanathan, M. Algorithms for Efficient Mining of Statistically Significant Attribute Association Information. arXiv 2012, arXiv:1208.3812. [Google Scholar]
- Wang, Y.; Liu, G.; Feng, M.; Wong, L. An empirical comparison of several recent epistatic interaction detection methods. Bioinformatics 2011, 27, 2936–2943. [Google Scholar] [CrossRef]
- Sevimoglu, T.; Arga, K.Y. The role of protein interaction networks in systems biomedicine. Comput. Struct. Biotechnol. J. 2014, 11, 22–27. [Google Scholar] [CrossRef]
- De Las Rivas, J.; Fontanillo, C. Protein–protein interactions essentials: key concepts to building and analyzing interactome networks. PLoS Comput. Biol. 2010, 6, 523641. [Google Scholar] [CrossRef]
- Braun, P.; Gingras, A.C. History of protein–protein interactions: From egg-white to complex networks. Proteomics 2012, 12, 1478–1498. [Google Scholar] [CrossRef] [PubMed]
- Droit, A.; Poirier, G.G.; Hunter, J.M. Experimental and bioinformatic approaches for interrogating protein–protein interactions to determine protein function. J. Mol. Endocrinol. 2005, 34, 263–280. [Google Scholar] [CrossRef] [PubMed]
- Shoemaker, B.A.; Panchenko, A.R. Deciphering protein–protein interactions. Part I. Experimental techniques and databases. PLoS Comput. Biol. 2007, 3, e42. [Google Scholar] [CrossRef] [PubMed]
- Xing, S.; Wallmeroth, N.; Berendzen, K.W.; Grefen, C. Techniques for the analysis of protein-protein interactions in vivo. Plant Phys. 2016, 171, 727–758. [Google Scholar] [CrossRef]
- Jansen, R.; Yu, H.; Greenbaum, D.; Kluger, Y.; Krogan, N.J.; Chung, S.; Emili, A.; Snyder, M.; Greenblatt, J.F.; Gerstein, M. A Bayesian Networks Approach for Predicting Protein-Protein Interactions from Genomic Data. Science 2003, 302, 449–453. [Google Scholar] [CrossRef]
- Pržulj, N. Protein-protein interactions: Making sense of networks via graph-theoretic modeling. BioEssays 2010, 33, 115–123. [Google Scholar] [CrossRef] [PubMed]
- Fryxell, K.J. The coevolution of gene family trees. Trends Genet. 1996, 12, 364–369. [Google Scholar] [CrossRef]
- Pazos, F.; Valencia, A. Similarity of phylogenetic trees as indicator of protein–protein interaction. Protein Eng. Des. Sel. 2001, 14, 609–614. [Google Scholar] [CrossRef] [PubMed]
- Pazos, F.; Ranea, J.A.; Juan, D.; Sternberg, M.J. Assessing Protein Co-evolution in the Context of the Tree of Life Assists in the Prediction of the Interactome. J. Mol. Biol. 2005, 352, 1002–1015. [Google Scholar] [CrossRef]
- Fraser, H.B.; Hirsh, A.E.; Wall, D.P.; Eisen, M.B. Coevolution of gene expression among interacting proteins. Proc. Natl. Acad. Sci. USA 2004, 101, 9033–9038. [Google Scholar] [CrossRef]
- Giraud, B.G.; Lapedes, A.; Liu, L.C. Analysis of correlations between sites in models of protein sequences. Phys. Rev. E 1998, 58, 6312–6322. [Google Scholar] [CrossRef]
- Wollenberg, K.R.; Atchley, W.R. Separation of phylogenetic and functional associations in biological sequences by using the parametric bootstrap. Proc. Natl. Acad. Sci. USA 2000, 97, 3288–3291. [Google Scholar] [CrossRef]
- Tillier, E.R.; Lui, T.W. Using multiple interdependency to separate functional from phylogenetic correlations in protein alignments. Bioinformatics 2003, 19, 750–755. [Google Scholar] [CrossRef]
- Dunn, S.; Wahl, L.; Gloor, G. Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics 2007, 24, 333–340. [Google Scholar] [CrossRef]
- Szurmant, H.; Weigt, M. Inter-residue, inter-protein and inter-family coevolution: bridging the scales. Curr. Opin. Struct. Biol. 2018, 50, 26–32. [Google Scholar] [CrossRef]
- Morcos, F.; Pagnani, A.; Lunt, B.; Bertolino, A.; Marks, D.S.; Sander, C.; Zecchina, R.; Onuchic, J.N.; Hwa, T.; Weigt, M.; et al. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. USA 2011, 108. [Google Scholar] [CrossRef] [PubMed]
- Kamisetty, H.; Ovchinnikov, S.; Baker, D. Assessing the utility of coevolution-based residue-residue contact predictions in a sequence- and structure-rich era. Proc. Natl. Acad. Sci. USA 2013, 110, 15674–15679. [Google Scholar] [CrossRef] [PubMed]
- Cong, Q.; Anishchenko, I.; Ovchinnikov, S.; Baker, D. Protein interaction networks revealed by proteome coevolution. Science 2019, 365, 185–189. [Google Scholar] [CrossRef] [PubMed]
- Rosato, A.; Tenori, L.; Cascante, M.; De Atauri Carulla, P.R.; Martins dos Santos, V.A.P.; Saccenti, E. From correlation to causation: analysis of metabolomics data using systems biology approaches. Metabolomics 2018, 14, 37. [Google Scholar] [CrossRef] [PubMed]
- Cakır, T.; Hendriks, M.M.; Westerhuis, J.A.; Smilde, A.K. Metabolic network discovery through reverse engineering of metabolome data. Metabolomics 2009, 5, 318–329. [Google Scholar] [CrossRef] [PubMed]
- Saccenti, E.; Menichetti, G.; Ghini, V.; Remondini, D.; Tenori, L.; Luchinat, C. Entropy-based network representation of the individual metabolic phenotype. J. Proteome Res. 2016, 15, 3298–3307. [Google Scholar] [CrossRef] [PubMed]
- Saccenti, E.; Suarez-Diez, M.; Luchinat, C.; Santucci, C.; Tenori, L. Probabilistic networks of blood metabolites in healthy subjects as indicators of latent cardiovascular risk. J. Proteome Res. 2015, 14, 1101–1111. [Google Scholar] [CrossRef]
- Everett, J.R.; Holmes, E.; Veselkov, K.A.; Lindon, J.C.; Nicholson, J.K. A unified conceptual framework for metabolic phenotyping in diagnosis and prognosis. Trends Pharmacol. Sci. 2019, 40, 763–773. [Google Scholar] [CrossRef]
- Marr, C.; Hütt, M.T. Topology regulates pattern formation capacity of binary cellular automata on graphs. Phys. A Stat. Mech. Appl. 2005, 354, 641–662. [Google Scholar] [CrossRef]
- Marr, C.; Müller-Linow, M.; Hütt, M.T. Regularizing capacity of metabolic networks. Phys. Rev. E 2007, 75, 041917. [Google Scholar] [CrossRef]
- Nykter, M.; Price, N.D.; Larjo, A.; Aho, T.; Kauffman, S.A.; Yli-Harja, O.; Shmulevich, I. Critical networks exhibit maximal information diversity in structure-dynamics relationships. Phys. Rev. Lett. 2008, 100, 058702. [Google Scholar] [CrossRef] [PubMed]
- Grimbs, S.; Selbig, J.; Bulik, S.; Holzhütter, H.G.; Steuer, R. The stability and robustness of metabolic states: identifying stabilizing sites in metabolic networks. Mol. Syst. Biol. 2007, 3, 146. [Google Scholar] [CrossRef] [PubMed]
- De Martino, D.; Mc Andersson, A.; Bergmiller, T.; Guet, C.C.; Tkačik, G. Statistical mechanics for metabolic networks during steady state growth. Nat. Commun. 2018, 9, 2988. [Google Scholar] [CrossRef] [PubMed]
- Shore, J.; Johnson, R. Axiomatic derivation of the principle of maximum entropy and the principle of minimum cross-entropy. IEEE Trans. Inf. Theory 1980, 26, 26–37. [Google Scholar] [CrossRef]
- Wagner, A. From bit to it: How a complex metabolic network transforms information into living matter. BMC Syst. Biol. 2007, 1, 33. [Google Scholar] [CrossRef]
- Heirendt, L.; Arreckx, S.; Pfau, T.; Mendoza, S.N.; Richelle, A.; Heinken, A.; Haraldsdóttir, H.S.; Wachowiak, J.; Keating, S.M.; Vlasov, V.; et al. Creation and analysis of biochemical constraint-based models using the COBRA Toolbox v.3.0. Nat. Protoc. 2019, 14, 639–702. [Google Scholar] [CrossRef]
- Covert, M.W.; Schilling, C.H.; Famili, I.; Edwards, J.S.; Goryanin, I.I.; Selkov, E.; Palsson, B.O. Metabolic modeling of microbial strains in silico. Trends Biochem. Sci. 2001, 26, 179–186. [Google Scholar] [CrossRef]
- Hammer, G.; Cooper, M.; Tardieu, F.; Welch, S.; Walsh, B.; van Eeuwijk, F.; Chapman, S.; Podlich, D. Models for navigating biological complexity in breeding improved crop plants. Trends Plant Sci. 2006, 11, 587–593. [Google Scholar] [CrossRef]
- Gomes de Oliveira Dal’Molin, C.; Quek, L.E.; Saa, P.A.; Nielsen, L.K. A multi-tissue genome-scale metabolic modeling framework for the analysis of whole plant systems. Front. Plant Sci. 2015, 6, 1–12. [Google Scholar] [CrossRef]
- Sen, P.; Orešič, M. Metabolic modeling of human gut microbiota on a genome scale: An overview. Metabolites 2019, 9, 22. [Google Scholar] [CrossRef]
- Chen, Y.; Li, G.; Nielsen, J. Genome-Scale Metabolic Modeling from Yeast to Human Cell Models of Complex Diseases: Latest Advances and Challenges. In Methods in Molecular Biology; Humana Press Inc.: Totowa, NJ, USA, 2019; Volume 2049, pp. 329–345. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum entropy production and plant optimization theories. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 1429–1435. [Google Scholar] [CrossRef] [PubMed]
- Cannon, W.; Zucker, J.; Baxter, D.; Kumar, N.; Baker, S.; Hurley, J.; Dunlap, J. Prediction of Metabolite Concentrations, Rate Constants and Post-Translational Regulation Using Maximum Entropy-Based Simulations with Application to Central Metabolism of Neurospora crassa. Processes 2018, 6, 63. [Google Scholar] [CrossRef]
- Martyushev, L.M. The maximum entropy production principle: Two basic questions. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 1333–1334. [Google Scholar] [CrossRef] [PubMed]
- Vallino, J.J. Ecosystem biogeochemistry considered as a distributed metabolic network ordered by maximum entropy production. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 1417–1427. [Google Scholar] [CrossRef]
- Himmelblau, D.M.; Jones, C.R.; Bischoff, K.B. Determination of rate constants for complex kinetics models. Ind. Eng. Chem. Fundam. 1967, 6, 539–543. [Google Scholar] [CrossRef]
- Sorzano, C.O.S.; Vargas, J.; Montano, A.P. A Survey of Dimensionality Reduction Techniques. arXiv 2014, arXiv:1403.2877. [Google Scholar]
- Pearson, K. Principal components analysis. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 6, 559. [Google Scholar] [CrossRef]
- Comon, P. Independent component analysis, A new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Andrews, J.G.; Dimakis, A.; Dolecek, L.; Effros, M.; Medard, M.; Milenkovic, O.; Montanari, A.; Vishwanath, S.; Yeh, E.; Berry, R.; et al. A perspective on future research directions in information theory. arXiv 2015, arXiv:1507.05941. [Google Scholar]
- Holzinger, A.; Hörtenhuber, M.; Mayer, C.; Bachler, M.; Wassertheurer, S.; Pinho, A.J.; Koslicki, D. On entropy-based data mining. In Interactive Knowledge Discovery and Data Mining in Biomedical Informatics; Springer: Berlin, Germany, 2014; pp. 209–226. [Google Scholar]
- Uda, S. Application of information theory in systems biology. Biophys. Rev. 2020, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Gohari, A.; Mirmohseni, M.; Nasiri-Kenari, M. Information theory of molecular communication: Directions and challenges. IEEE Trans. Mol. Biol. Multi-Scale Commun. 2016, 2, 120–142. [Google Scholar] [CrossRef]
- Navarro, F.C.; Mohsen, H.; Yan, C.; Li, S.; Gu, M.; Meyerson, W.; Gerstein, M. Genomics and data science: An application within an umbrella. Genome Biol. 2019, 20, 109. [Google Scholar] [CrossRef] [PubMed]
- Demchenko, Y.; De Laat, C.; Membrey, P. Defining architecture components of the Big Data Ecosystem. In Proceedings of the 2014 International Conference on Collaboration Technologies and Systems (CTS), Minneapolis, MN, USA, 19–23 May 2014; pp. 104–112. [Google Scholar]
- Greene, C.S.; Tan, J.; Ung, M.; Moore, J.H.; Cheng, C. Big data bioinformatics. J. Cell. Physiol. 2014, 229, 1896–1900. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, M.; Pratas, D.; Pinho, A.J. A survey on data compression methods for biological sequences. Information 2016, 7, 56. [Google Scholar] [CrossRef]
- Daily, K.; Rigor, P.; Christley, S.; Xie, X.; Baldi, P. Data structures and compression algorithms for high-throughput sequencing technologies. BMC Bioinform. 2010, 11, 514. [Google Scholar] [CrossRef]
- Xie, X.; Zhou, S.; Guan, J. CoGI: Towards compressing genomes as an image. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 12, 1275–1285. [Google Scholar] [CrossRef]
- Ochoa, I.; Hernaez, M.; Weissman, T. iDoComp: a compression scheme for assembled genomes. Bioinformatics 2015, 31, 626–633. [Google Scholar] [CrossRef]
- Mohamed, S.A.; Fahmy, M.M. Binary image compression using efficient partitioning into rectangular regions. IEEE Trans. Commun. 1995, 43, 1888–1893. [Google Scholar] [CrossRef]
- Yu, Y.W.; Daniels, N.M.; Danko, D.C.; Berger, B. Entropy-scaling search of massive biological data. Cell Syst. 2015, 1, 130–140. [Google Scholar] [CrossRef]
- Ishaq, N.; Student, G.; Daniels, N.M. Clustered Hierarchical Entropy-Scaling Search of Astronomical and Biological Data. arXiv 2019, arXiv:1908.08551. [Google Scholar]
- Cannon, W.R. Simulating metabolism with statistical thermodynamics. PLoS ONE 2014, 9, e103582. [Google Scholar] [CrossRef] [PubMed]
- Cannon, W.R.; Baker, S.E. Non-steady state mass action dynamics without rate constants: Dynamics of coupled reactions using chemical potentials. Phys. Biol. 2017, 14, 55003. [Google Scholar] [CrossRef] [PubMed]
- Thomas, D.G.; Jaramillo-Riveri, S.; Baxter, D.J.; Cannon, W.R. Comparison of optimal thermodynamic models of the tricarboxylic acid cycle from heterotrophs, cyanobacteria, and green sulfur bacteria. J. Phys. Chem. B 2014, 118, 14745–14760. [Google Scholar] [CrossRef]
- Webb, S. Deep learning for biology. Nature 2018, 554, 7693. [Google Scholar] [CrossRef]
- Angermueller, C.; Pärnamaa, T.; Parts, L.; Stegle, O. Deep learning for computational biology. Mol. Syst. Biol. 2016, 12, 878. [Google Scholar] [CrossRef]
- Wang, Y.; Ribeiro, J.M.L.; Tiwary, P. Past–future information bottleneck for sampling molecular reaction coordinate simultaneously with thermodynamics and kinetics. Nat. Commun. 2019, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Djordjevic, I.B. Quantum Information Theory and Quantum Mechanics-Based Biological Modeling and Biological Channel Capacity Calculation. In Quantum Biological Information Theory; Springer: Berlin, Germany, 2016; pp. 143–195. [Google Scholar]
- Djordjevic, I.B. Quantum-Mechanical Modeling of Mutations, Aging, Evolution, Tumor, and Cancer Development. In Quantum Biological Information Theory; Springer: Berlin, Germany, 2016; pp. 197–236. [Google Scholar]
- Djordjevic, I.B. Classical and quantum error-correction coding in genetics. In Quantum Biological Information Theory; Springer: Berlin, Germany, 2016; pp. 237–269. [Google Scholar]
| Area | Information Theoretic Methods | How Information Theory Is Used |
|---|---|---|
| Reconstructing Gene Regulatory Networks | Relevance Networks [34] | Used MI larger than a given threshold to construct GRNs |
| CLR [36] | Used MI to construct GRN, filters spurious edges by estimating its background distribution | |
| ARACNE and its extensions [37,38,39,40] | Used MI to construct GRN, filters edges using null distribution and DPI, higher order DPI to improve inference performance, adaptive binning strategy to estimate MI efficiently | |
| PIDC [27] | GRN constructed using PID to explore dependencies between triplets of genes in single-cell gene expression datasets | |
| Alignment-free phylogeny | FFP [54] | Calculated JSD as pairwise distances between two genomes using normalized k-mer frequencies |
| kWIP [55] | Constructed a sketch data structure using all k-mers from a genomic sequence, computed inner product between the two sketches weighted by their Shannon’s entropy across the given dataset | |
| Sequencing and Error Correction | Motahari et al. [66] | Used Renyi entropy of order 2 to find the minimum fragment length and coverage depth needed for the assembling reads to reconstruct the original DNA sequence with a given reliability |
| Chen et al. [65] | Analyzed the information redundancy in dual-base degenerate sequencing by comparing entropy information content of multiple DPL (degenerate polymer length) arrays | |
| Anavy et al. [77] | Proposed encoding and decoding for composite DNA based storage and error correction through developing composite DNA alphabets and using KLD to select the best alphabet model | |
| Choi et al. [77] | Used eleven degenerate bases as encoding characters in addition to ACGT to increase information capacity limit and reduce the cost of DNA per unit data | |
| Genome-wide disease-gene association mapping | Fan et al. [97], Yee et al. [98], Dong et al. [99] | Proposed test statistics based on MI and conditional entropy involving two SNPs and the disease phenotype from case-control studies |
| Varadan et al. [103], Anastassiou [104], Curk at al. [105], Hu et al. [106,108] | Used synergy to analyze GXG statistical interactions | |
| Chanda et al. [24,114,115,118], Tritchler et al. [120] | Used multivariate information theoretic metrics and higher order models (e.g., KWII) to analyze statistical GXG and GxE interactions | |
| Moore et al. [124] | Used KWII to represent edges in epistasis networks | |
| Tahmasebi et al. [133] | Used entropy to formulate the capacity of recovering the causal subsequence | |
| Chanda et al. [116], Knights et al. [117], Yee et al. [131], Galas et al. [132] | Discussion and analysis of Information theoretic methods dealing with quantitative phenotypes and environmental variables | |
| Andrade et al. [128], Kang et al. [127] | Developed information theoretic test statistics for single-group or case-only studies. | |
| Tzeng et al. [92], Zhao et al. [93,94] | Developed entropy-based tests using haplotypes | |
| Cui et al. [95] | Developed entropy-based association test for gene-centric analysis considering variants within one gene as testing units | |
| Zhao et al. [130], Brunel et al. [102], Wu et al. [88] | Designed and discussed entropy based disease association test metrics for family-based studies |
| Area | Information Theoretic Methods | How Information Theory Is Used |
|---|---|---|
| Reconstruction and analysis of Metabolic Networks | CLR [36], ARACNE [37], PCLRC [164] | Uses MI to construct metabolic networks from metabolite concentration data, filters spurious edges by estimating its background distribution [36,164] or DPI [37] |
| Marr. et al. [166,167] | Network analysis of metabolic networks using Shannon and word entropy to reveal regularization dynamics encoded in network topology | |
| Nykter et al. [168] | Studied network structure-dynamics relationships, using Kolmogorov complexity as a measure of distance between pairs of network structures and between their associated dynamic state trajectories | |
| Grimbs et al. [169] | Stoichiometric analysis to parameterize the metabolic states, assessed the effect of enzyme-kinetic parameters on the stability properties of a metabolic state using MI and Kolmogorov–Smirnov test | |
| Fuente et al. [11]. | Studied properties of dissipative metabolic structures at different organizational levels using entropy | |
| De Martino et al. [170] | Introduced a generalization of FBA to single-cell level based on maximum entropy principle | |
| Saccenti et al. [163] | Investigated the associations and the interconnections among different metabolites by means of network modeling using maximum entropy ensemble null model | |
| Wagner et al. [172] | Proposed an information theoretic way to relate the nutrient information to the error in a cell’s measurement of nutrient concentration in its environment | |
| Protein interaction analysis | Wollenberg et al. [154], Tillier et al. [155], Dunn et al. [156], Kamisetty et al. [159], Morcos et al. [158] | Mutual Information combined with evolutionary information and refined with structural information to identify protein interactions |
| Optimization, Dimensionality Reduction | Cannon et al. [202,203], Thomas et al. [204] | Used MEP to simulate central metabolism in the fungus Neurospora crassa [180], tricarboxylic acid cycle model optimization in microbes [204]. |
| Hyvarinen et al. [187], Comon et al. [186] | Used negentropy and minimization of MI to obtain the components in ICA |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chanda, P.; Costa, E.; Hu, J.; Sukumar, S.; Van Hemert, J.; Walia, R. Information Theory in Computational Biology: Where We Stand Today. Entropy 2020, 22, 627. https://doi.org/10.3390/e22060627
Chanda P, Costa E, Hu J, Sukumar S, Van Hemert J, Walia R. Information Theory in Computational Biology: Where We Stand Today. Entropy. 2020; 22(6):627. https://doi.org/10.3390/e22060627
Chicago/Turabian StyleChanda, Pritam, Eduardo Costa, Jie Hu, Shravan Sukumar, John Van Hemert, and Rasna Walia. 2020. "Information Theory in Computational Biology: Where We Stand Today" Entropy 22, no. 6: 627. https://doi.org/10.3390/e22060627
APA StyleChanda, P., Costa, E., Hu, J., Sukumar, S., Van Hemert, J., & Walia, R. (2020). Information Theory in Computational Biology: Where We Stand Today. Entropy, 22(6), 627. https://doi.org/10.3390/e22060627





